西安电子科技大学电磁场与电磁波实验报告与数据
- 格式:docx
- 大小:89.68 KB
- 文档页数:2

电磁场与电磁波实验报告电磁场与电磁波实验报告引言:电磁场和电磁波是物理学中非常重要的概念。
电磁场是由电荷产生的一种物理场,它的存在和变化会影响周围空间中的其他电荷。
而电磁波则是电磁场的一种传播形式,它以电磁场的振荡和传播为基础,具有波动性质。
本次实验旨在通过实际操作和测量,深入了解电磁场和电磁波的特性。
实验一:测量电磁场强度在实验一中,我们使用了一个电磁场强度计来测量不同位置的电磁场强度。
首先,我们将电磁场强度计放置在一个固定的位置,记录下此时的电磁场强度。
然后,我们将电磁场强度计移动到其他位置,重复测量过程。
通过这些数据,我们可以得出不同位置的电磁场强度的分布情况。
实验结果显示,电磁场强度随着距离的增加而逐渐减弱。
这符合电磁场的特性,即电荷产生的电磁场在空间中以一定的规律传播,而传播的强度会随着距离的增加而减弱。
这一实验结果验证了电磁场的存在和变化对周围环境的影响。
实验二:测量电磁波频率和波长在实验二中,我们使用了一个频率计和一个波长计来测量电磁波的频率和波长。
首先,我们将频率计和波长计设置好,并将它们与电磁波源连接。
然后,我们观察频率计和波长计的测量结果,并记录下来。
通过这些数据,我们可以得出电磁波的频率和波长的数值。
实验结果显示,不同频率的电磁波具有不同的波长。
频率越高的电磁波,波长越短;频率越低的电磁波,波长越长。
这符合电磁波的特性,即电磁波的振荡频率和波长之间存在一定的关系。
这一实验结果验证了电磁波的波动性质,以及频率和波长之间的关系。
实验三:观察电磁波的干涉和衍射现象在实验三中,我们使用了一块光栅和一个狭缝装置来观察电磁波的干涉和衍射现象。
首先,我们将光栅放置在光源前方,并调整光源的位置和光栅的角度。
然后,我们观察到在光栅后方的屏幕上出现了一系列明暗相间的条纹。
这些条纹是由电磁波的干涉和衍射效应引起的。
实验结果显示,当电磁波通过光栅时,会发生干涉和衍射现象。
干涉现象表现为明暗相间的条纹,而衍射现象表现为条纹的扩散和交替。

重庆大学电磁场与电磁波课程实践报告题目:点电荷电场模拟实验日期:2013 年12 月7 日N=28《电磁场与电磁波》课程实践点电荷电场模拟实验1.实验背景电磁场与电磁波课程内容理论性强,概念抽象,较难理解。
在电磁场教学中,各种点电荷的电场线成平面分布,等势面通常用等势线来表示。
MATLAB 是一种广泛应用于工程、科研等计算和数值分析领域的高级计算机语言,以矩阵作为数据操作的基本单位,提供十分丰富的数值计算函数、符号计算功能和强大的绘图能力。
为了更好地理解电场强度的概念,更直观更形象地理解电力线和等势线的物理意义,本实验将应用MATLAB 对点电荷的电场线和等势线进行模拟实验。
2.实验目的应用MATLAB 模拟点电荷的电场线和等势线3.实验原理根据电磁场理论,若电荷在空间激发的电势分布为V ,则电场强度等于电势梯度的负值,即:E V =-∇r真空中若以无穷远为电势零点,则在两个点电荷的电场中,空间的电势分布为: 1212010244q q V V V R R πεπε=+=+本实验中,为便于数值计算,电势可取为1212q q V R R =+4.实验内容应用MATLAB 计算并绘出以下电场线和等势线,其中q 1位于(-1,0,0),q 2位于(1,0,0),n 为个人在班级里的序号:(1) 电偶极子的电场线和等势线(等量异号点电荷对q 2:q 1 = 1,q 2为负电荷);(2) 两个不等量异号电荷的电场线和等势线(q 2:q 1 = 1 + n /2,q 2为负电荷);(3) 两个等量同号电荷的电场线和等势线;(4) 两个不等量同号电荷的电场线和等势线(q 2:q 1 = 1 + n /2);(5) 三个电荷,q 1、q 2为(1)中的电偶极子,q 3为位于(0,0,0)的单位正电荷。
、n=28(1)电偶极子的电场线和等势线(等量异号点电荷对q2:q1 = 1,q2为负电荷);程序1:clear allq=1;xm=;ym=2;x=linspace(-xm,xm);y=linspace(-ym,ym);[X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2);R2=sqrt((X-1).^2+Y.^2);U=1./R1-q./R2;u=-4::4;figurecontour(X,Y,U,u,'--');hold onplot(-1,0,'o','MarkerSize',12);plot(1,0,'o','MarkerSize',12);[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1));dth1=11;th1=(dth1:dth1:360-dth1)*pi/180;r0=;x1=r0*cos(th1)-1;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);dth2=11;th2=(dth2:dth2:360-dth2)*pi/180;x2=r0*cos(th2)+1;y2=r0*sin(th2);streamline(X,Y,-Ex,-Ey,x2,y2);axis equal tighttitle('μ×óμμ3oíμèê','fontsize',12)(2)两个不等量异号电荷的电场线和等势线(q2:q1 = 1 + n/2,q2为负电荷);程序2:clear allq=15;xm=;ym=2;x=linspace(-xm,xm);y=linspace(-ym,ym);[X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2);R2=sqrt((X-1).^2+Y.^2);U=1./R1-q./R2;u=-4::4;figurecontour(X,Y,U,u,'--');hold onplot(-1,0,'o','MarkerSize',12);plot(1,0,'o','MarkerSize',12);[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1));dth1=11;th1=(dth1:dth1:360-dth1)*pi/180;r0=;x1=r0*cos(th1)-1;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);dth2=11;th2=(dth2:dth2:360-dth2)*pi/180;x2=r0*cos(th2)+1;y2=r0*sin(th2);streamline(X,Y,-Ex,-Ey,x2,y2);axis equal tighttitle('μ×óμμ3oíμèê','fontsize',12)(3)两个等量同号电荷的电场线和等势线;程序3:clear allq=-1;xm=;ym=2;x=linspace(-xm,xm);y=linspace(-ym,ym);[X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2);R2=sqrt((X-1).^2+Y.^2);U=1./R1-q./R2;u=-4::4;figurecontour(X,Y,U,u,'--');hold onplot(-1,0,'o','MarkerSize',12);plot(1,0,'o','MarkerSize',12);[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1));dth1=11;th1=(dth1:dth1:360-dth1)*pi/180;r0=;x1=r0*cos(th1)-1;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);dth2=11;th2=(dth2:dth2:360-dth2)*pi/180;x2=r0*cos(th2)+1;y2=r0*sin(th2);streamline(X,Y,Ex,Ey,x2,y2);axis equal tighttitle('μ×óμμ3oíμèê','fontsize',12)(4)两个不等量同号电荷的电场线和等势线(q2:q1 = 1 + n/2);程序4:clear allq=-15;xm=;ym=2;x=linspace(-xm,xm);y=linspace(-ym,ym);[X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2);R2=sqrt((X-1).^2+Y.^2);U=1./R1-q./R2;u=-4::4;figurecontour(X,Y,U,u,'--');hold onplot(-1,0,'o','MarkerSize',12);plot(1,0,'o','MarkerSize',12);[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1)); dth1=11;th1=(dth1:dth1:360-dth1)*pi/180;r0=;x1=r0*cos(th1)-1;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);dth2=11;th2=(dth2:dth2:360-dth2)*pi/180;x2=r0*cos(th2)+1;y2=r0*sin(th2);streamline(X,Y,Ex,Ey,x2,y2);axis equal tighttitle('μ×óμμ3oíμèê','fontsize',12)(5)三个电荷,q1、q2为(1)中的电偶极子,q3为位于(0,0,0)的单位正电荷程序5:clear allq=1;q3=-1;xm=;ym=2;x=linspace(-xm,xm);y=linspace(-ym,ym);[X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2);R2=sqrt((X-1).^2+Y.^2);R3=sqrt(X.^2+Y.^2);U=1./R1-q./R2-q3./R3;u=-4::4;figurecontour(X,Y,U,u,'--');hold onplot(-1,0,'o','MarkerSize',12);plot(1,0,'o','MarkerSize',12);[Ex,Ey]=gradient(-U,x(2)-x(1),y(2)-y(1));dth1=11;th1=(dth1:dth1:360-dth1)*pi/180;r0=;x1=r0*cos(th1)-1;y1=r0*sin(th1);streamline(X,Y,Ex,Ey,x1,y1);dth2=11;th2=(dth2:dth2:360-dth2)*pi/180;x2=r0*cos(th2)+1;y2=r0*sin(th2);streamline(X,Y,-Ex,-Ey,x2,y2);dth3=11;th3=(dth3:dth3:360-dth3)*pi/180;x3=r0*cos(th3);y3=r0*sin(th3);streamline(X,Y,Ex,Ey,x3,y3);axis equal tighttitle('μ×óμμ3oíμèê','fontsize',12)从实验过程中学习到的东西:1.灵活学习,大胆求证,当不清楚E1,E2,前面符号的正负时,随便假设一个,再根据电荷的正负关系,看得到的图形是否正确,若不正确则再修改符号2.注意q的正负与两电荷是否异号有关,异号与同号q的正负不同3.学习初步使用matlab软件,为以后的学习打好基础4.更加深入地了解电荷的电场线与等势线。

实验一 静电场仿真1.实验目的建立静电场中电场及电位空间分布的直观概念。
2.实验仪器计算机一台3.基本原理当电荷的电荷量及其位置均不随时间变化时,电场也就不随时间变化,这种电场称为静电场。
点电荷q 在无限大真空中产生的电场强度E 的数学表达式为(1-1)真空中点电荷产生的电位为(1-2)其中,电场强度是矢量,电位是标量,所以,无数点电荷产生的电场强度和电位是不一样的,电场强度为4= (1-3) 电位为4= (1-4) 本章模拟的就是基本的电位图形。
4.实验内容及步骤(1)点电荷静电场仿真题目:真空中有一个点电荷-q,求其电场分布图。
程序1:负点电荷电场示意图clear[x,y]=meshgrid(-10:1.2:10);E0=8.85e-12;q=1.6*10^(-19);r=[];r=sqrt(x.^2+y.^2+1.0*10^(-10))m=4*pi*E0*r;m1=4*pi*E0*r.^2;E=(-q./m1).*r;surfc(x,y,E);负点电荷电势示意图clear[x,y]=meshgrid(-10:1.2:10); E0=8.85e-12;q=1.6*10^(-19);r=[];r=sqrt(x.^2+y.^2+1.0*10^(-10))m=4*pi*E0*r;m1=4*pi*E0*r.^2;z=-q./m1surfc(x,y,z);xlabel('x','fontsize',16)ylabel('y','fontsize',16)title('负点电荷电势示意图','fontsize',10)程序2clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.16:4;y=x; [X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2+1.0*10^(-10)); R2=sqrt((X-1).^2+Y.^2+1.0*10^(-10));Z=q*k*(1./R2-1./R1);[ex,ey]=gradient(-Z);ae=sqrt(ex.^2+ey.^2);ex=ex./ae;ey=ey./ae; cv=linspace(min(min(Z)),max(max(Z)),40); contour(X,Y,Z,cv,'k-');hold onquiver(X,Y,ex,ey,0.7);clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.15:4;y=x; [X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2+1.0*10^(-10));R2=sqrt((X-1).^2+Y.^2+1.0*10^(-10));U=q*k*(1./R2-1./R1);[ex,ey]=gradient(-U);ae=sqrt(ex.^2+ey.^2);ex=ex./ae;ey=ey./ae; cv=linspace(min(min(U)),max(max(U)),40); surfc(x,y,U);实验二恒定电场的仿真1.实验目的建立恒定电场中电场及电位空间分布的直观概念。

北京邮电大学电磁场与微波测量学院:电子工程学院班级:2013211212姓名:学号:实验四迈克尔逊干涉实验一、实验目的1、通过实验观察迈克尔逊干涉现象。
2、掌握利用迈克尔逊干涉测量平面波长的方法。
二、实验设备DH926B型微波分光仪、三厘米固态振荡器、喇叭天线、可变衰减器、晶体检波器、反射板、半透射玻璃板三、实验原理如图5.1所示,在平面电磁波前进的方向放置一块与传播方向成450夹角的半透射板(实验中用玻璃板),由于该板的作用,将入射的电磁波分成为两束,一束穿透玻璃板继续前进,向反射板B方向传播,另外一束被玻璃板反射后,向反射板A方可移动反射板B的波,被反射板B反射后,又到达玻璃板,其中一部分被玻璃板反射后到达接收喇叭;而到达反射板A的波,被反射板A反射后,又到达玻璃板,其中一部分穿过玻璃板也到达接收喇叭,因此接收喇叭接收到的是这两束电磁波的和,当两束电磁波的传播路程相同,或相差波长的整数倍时,接收喇叭接收的信号最强,当他们传播的路程相差为半个波长的奇数倍时,接收喇叭接收到的信号最弱。
通过移动反射板B,可以改变这两束电磁波的传播路程,使得接收喇叭接收到的信号由弱变强,或由强变弱,测得两个相邻最强或最弱时反射板所移动的距离L,就可以得到电磁波的波长,即=2L。
实验中直接观察电压表的读数,为当表头指的距离,由此距示从一次极小变到又一次极小时,则B处的反射板就移动了2离就可求得平面波的波长。
四、实验内容及步骤1、如图5.2,连接仪器。
2、使两喇叭口面互成900。
3、半透射板与两喇叭轴线互成450。
4、将读数机构通过它本身上带有的两个螺钉旋入底座上,使其固定在底座上,再插上反射扳,使固定反射板的法线与接受喇叭的轴线一致,可移反射板的法钱与发射喇叭轴线一致。
5、按信号源操作规程接通电源,调节衰减器使信号电平读数指示合适值。
图5.2 迈克尔逊干涉实验系统6、将可移反射板移到读数机构的一端,在此附近测出一个极小的位置,然后旋转读数机构上的手柄使反射板移动,从表头上测出(n +1)个极小值,并同时从读数机构上得到相应的位移读数,从而求得可移反射板的移动距离L ,则波长nL2=λ。

电磁场与电磁波实验报告(一)引言概述:电磁场与电磁波是近代物理学中的重要概念,对于理解电磁现象和应用电磁技术具有重要意义。
本实验报告旨在通过实验来探究电磁场和电磁波的基本特性,并深入了解其在不同情境下的行为和应用。
一、电磁场的产生与性质1. 静电场与磁场的产生机制2. 静电场与磁场的区别与联系3. 电磁场的力线分布与场强的概念4. 高斯定律与安培定律的应用5. 电磁场的矢量表示及其运算规则二、电磁辐射和电磁波的特性1. 辐射的概念与特点2. 电磁波的定义和分类3. 电磁波的传播速度和能量传播方式4. 电磁波的频率和波长关系5. 电磁波与物质的作用及与光的关系三、电磁波的实验测量1. 等幅比波法测量电磁波的速度2. 利用扩散法测量电磁波的波长3. 利用光栅光谱仪测量电磁波的频率和波长4. 利用双缝干涉测量电磁波的波长5. 利用驻波法测量电磁波的频率四、电磁波在通信中的应用1. 电磁波在无线通信中的传输原理2. 电磁波的调制与解调技术3. 电磁波的天线和传输介质选择4. 电磁波在卫星通信中的应用5. 电磁波在无线电和电视广播中的应用五、电磁波对人体健康的影响1. 电磁波对人体的生物效应与健康风险2. 电磁辐射的安全标准与防护措施3. 电磁波辐射源的评估与监测4. 电磁波辐射对儿童和孕妇的影响5. 电磁波辐射与癌症的关系研究总结:通过本实验的开展,我们深入了解了电磁场和电磁波的产生机制和特性,探讨了其在实验测量、通信技术和健康影响等方面的应用。
电磁场与电磁波作为现代科技中的基础理论和技术手段,对于推动科学技术发展和提高人们的生活水平具有重要意义。
在未来的研究中,我们将继续深入探索电磁场和电磁波的更多应用和相关问题,为推动科学进步和提高人类福祉做出贡献。

电磁场与微波测量实验报告学院:班级:组员:撰写人:学号:序号:实验一电磁波反射和折射实验一、实验目的1、熟悉S426型分光仪的使用方法2、掌握分光仪验证电磁波反射定律的方法3、掌握分光仪验证电磁波折射定律的方法二、实验设备与仪器S426型分光仪三、实验原理电磁波在传播过程中如遇到障碍物,必定要发生反射,本处以一块大的金属板作为障碍物来研究当电磁波以某一入射角投射到此金属板上所遵循的反射定律,即反射线在入射线和通过入射点的法线所决定的平面上,反射线和入射线分居在法线两侧,反射角等于入射角。
四、实验内容与步骤1、熟悉分光仪的结构和调整方法。
2、连接仪器,调整系统。
仪器连接时,两喇叭口面应相互正对,它们各自的轴线应在一条直线上,指示两喇叭的位置的指针分别指于工作平台的90刻度处,将支座放在工作平台上,并利用平台上的定位销和刻线对正支座,拉起平台上的四个压紧螺钉旋转一个角度后放下,即可压紧支座。
3、测量入射角和反射角反射金属板放到支座上时,应使金属板平面与支座下面的小圆盘上的某一对刻线一致。
而把带支座的金属反射板放到小平台上时,应使圆盘上的这对与金属板平面一致的刻线与小平台上相应90度的一对刻线一致。
这是小平台上的0刻度就与金属板的法线方向一致。
转动小平台,使固定臂指针指在某一角度处,这角度读书就是入射角,五、实验结果及分析记录实验测得数据,验证电磁波的反射定律表格分析:(1)、从总体上看,入射角与反射角相差较小,可以近似认为相等,验证了电磁波的反射定律。
(2)、由于仪器产生的系统误差无法避免,并且在测量的时候产生的随机误差,所以入射角不会完全等于反射角,由差值一栏可以看出在55度左右的误差最小。
越向两边误差越大,说明测量仪器在55度的入射角能产生最好的特性。
2、观察介质板(玻璃板)上的反射和折射实验将金属换做玻璃板,观察、测试电磁波在该介质板上的反射和折射现象,自行设计实验步骤和表格,计算反射系数和透射系数,验证透射系数和反射系数相加是否等于1 。

最新电磁场与电磁波实验报告
在本次实验中,我们深入研究了电磁场与电磁波的基本特性,并进行了一系列的实验来验证理论和观测实际现象。
以下是实验的主要部分和观察结果的概述。
实验一:静电场的建立与测量
我们首先建立了一个简单的静电场,通过使用高压电源对两个相对的金属板进行充电。
通过改变电源的电压,我们观察到金属板上的电荷积累情况,并使用电位差计测量了电场强度。
实验数据显示,电场强度与电压成正比,这与库仑定律的预测一致。
实验二:电磁波的产生与传播
接下来,我们通过振荡电路产生了电磁波。
在一个封闭的微波腔中,我们使用电磁波发生器产生不同频率的电磁波,并通过特殊的探测器来测量波的传播特性。
实验结果表明,电磁波的传播速度在不同的介质中有所变化,这与介质的电磁特性有关。
实验三:电磁波的极化与干涉
在这部分实验中,我们研究了电磁波的极化现象。
通过使用不同极化的波前,我们观察到了波的干涉效应。
特别是在双缝干涉实验中,我们观察到了明显的干涉条纹,这证明了电磁波的波动性质。
实验四:电磁波的吸收与反射
最后,我们探讨了电磁波与物质相互作用的过程。
通过将电磁波照射在不同材料的样品上,我们测量了波的吸收和反射率。
实验发现,吸收和反射率与材料的电磁性质密切相关,并且可以通过改变波的频率来调整这些性质。
通过这些实验,我们不仅验证了电磁场与电磁波的基本理论,而且加深了对这些现象在实际应用中的理解。
这些实验结果对于无线通信、雷达技术以及其他相关领域的研究和开发具有重要的指导意义。

电磁场与电磁波实验报告题目:校园无线信号场强特性的研究班级:学号:班内序号:姓名:目录【实验目的】 (1)【实验原理】 (1)【实验内容】 (6)【实验步骤】 (6)1.实验对象的选择 (6)2.数据采集 (6)3. 数据处理 (7)【实验结果分析】 (7)【实验心得】 (16)【附录】 (16)一、实验目的1.掌握在移动环境下阴影衰落的概念以及正确的测试方法;2.研究校园内各种不同环境下阴影衰落的分布规律;3.掌握在室内环境下场强的正确测量方法,理解建筑物穿透损耗的概念;4.通过实地测量,分析建筑物穿透损耗随频率的变化关系;5.研究建筑物穿透损耗与建筑材料的关系。
二、实验原理1.电磁波的传播方式无线通信系统是由发射机、发射天线、无线信道、接收机、接收天线所组成。
对于接受者,只有处在发射信号的覆盖区内,才能保证接收机正常接受信号,此时,电波场强大于等于接收机的灵敏度。
因此基站的覆盖区的大小,是无线工程师所关心的。
决定覆盖区的大小的主要因素有:发射功率,馈线及接头损耗,天线增益,天线架设高度,路径损耗,衰落,接收机高度,人体效应,接收机灵敏度,建筑物的穿透损耗,同播,同频干扰等。
电磁场在空间中的传输方式主要有反射﹑绕射﹑散射三种模式。
当电磁波传播遇到比波长大很多的物体时,发生反射。
当接收机和发射机之间无线路径被尖锐物体阻挡时发生绕射。
当电波传播空间中存在物理尺寸小于电波波长的物体﹑且这些物体的分布较密集时,产生散射。
散射波产生于粗糙表面,如小物体或其它不规则物体﹑树叶﹑街道﹑标志﹑灯柱。
2.尺度路径损耗在移动通信系统中,路径损耗是影响通信质量的一个重要因素。
大尺度平均路径损耗:用于测量发射机与接收机之间信号的平均衰落,即定义为有效发射功率和平均接受功率之间的(dB)差值,根据理论和测试的传播模型,无论室内或室外信道,平均接受信号功率随距离对数衰减,这种模型已被广泛的使用。
对任意的传播距离,大尺度平均路径损耗表示为:()[]()()=+010log/0PL d dB PL d n d d即平均接收功率为:()[][]()()()[]() =--=-d dBm Pt dBm PL d n d d d dBm n d dPr010log/0Pr010log/0其中,定义n为路径损耗指数,表明路径损耗随距离增长的速度,d0为近地参考距离,d为发射机与接收机之间的距离。

电磁场与电磁波实验报告09024126 张亦驰一.实验目的使用简单迭代法与超松弛迭代法求解电磁场金属槽边值问题二.实验步骤1.简单迭代法:源程序:#include<xxgc.h>main(){int i;double a[50][3][3];a[0][0][0]=a[0][1][0]=a[0][2][0]=25;a[0][0][1]=a[0][1][1]=a[0][2][1]=50;a[0][0][2]=a[0][1][2]=a[0][2][2]=75;for(i=0;i<50;i++){printf("a[%d][0][0]=%.3f,a[%d][1][0]=%.3f,a[%d][2][0]=%.3f\n",i,a[i][0][0],i,a[i][1][0],i,a[i ][2][0]);printf("a[%d][0][1]=%.3f,a[%d][1][1]=%.3f,a[%d][2][1]=%.3f\n",i,a[i][0][1],i,a[i][1][1],i,a[i ][2][1]);printf("a[%d][0][2]=%.3f,a[%d][1][2]=%.3f,a[%d][2][2]=%.3f\n\n",i,a[i][0][2],i,a[i][1][2],i,a[i][2][2]);getch();a[i+1][0][0]=0.25*(0+0+a[i][1][0]+a[i][0][1]);a[i+1][0][1]=0.25*(0+a[i][0][0]+a[i][1][1]+a[i][0][2]);a[i+1][0][2]=0.25*(0+a[i][0][1]+a[i][1][2]+100);a[i+1][1][0]=0.25*(a[i][0][0]+0+a[i][2][0]+a[i][1][1]);a[i+1][1][1]=0.25*(a[i][0][1]+a[i][1][0]+a[i][2][1]+a[i][1][2]);a[i+1][1][2]=0.25*(a[i][0][2]+a[i][1][1]+a[i][2][2]+100);a[i+1][2][0]=0.25*(a[i][1][0]+0+0+a[i][2][1]);a[i+1][2][1]=0.25*(a[i][1][1]+a[i][2][0]+0+a[i][2][2]);a[i+1][2][2]=0.25*(a[i][1][2]+a[i][2][1]+0+100);}getch();}实验结果如图2.超松弛迭代法源程序:#include<stdio.h>#include<math.h> #include<iostream> using namespace std;#define pi 3.1415926void Boundary_conditions_initialize(float Boundary_areas[5][5]) {for(int j=0;j<5;j++){ Boundary_areas[0][j]=0;Boundary_areas[4][j]=100; }for(int i=0;i<5;i++){Boundary_areas[i][0]=0;Boundary_areas[i][4]=0;j =100 Vj =0j =0}}void nodes_Field_region_Initialization(float Field_region[5][5]) {for(int i=1;i<4;i++){ for(int j=1;j<4;j++){Field_region[i][j]=0; }}}void Output_nodes_value (float all_nodes[5][5],int count){if(count==0){cout<<"场内各点的初始值为:"<<'\n' ;}else{cout<<"迭代次数N="<< count<<'\n'<<"迭代最终结果为:" <<'\n'; }for(int i=4;i>=0;i--){ for(int j=0;j<5;j++){cout<<all_nodes[i][j]<<'\t'<<'\t';}cout<<'\n';}}void main(void){int a=4 ;int h=a/4;float areas[5][5] ;int N=0 ;const float e=0.00001;float Maxerror ;float a0=2/(1+sin(pi/4));Boundary_conditions_initialize(areas);nodes_Field_region_Initialization(areas);Output_nodes_value (areas,N) ;cout<<"加速因子a="<<a0<<'\n';do{ N=N+1 ;for(int i=1;i<4;i++){ for(int j=1;j<4;j++){ float areasK=areas[i][j];areas[i][j]=areas[i][j]+(a0/4)*(areas[i-1][j]+areas[i][j-1]+areas[i+1 ][j]+areas[i][j+1]-4*areas[i][j]);float error=fabs(areas[i][j]-areasK);if(i==1&&j==1){Maxerror=error; }else{if (Maxerror<error) Maxerror=error ;}}}} while(Maxerror>e) ;Output_nodes_value(areas,N);}。

电磁场与电磁波实验报告实验题目:电磁场与电磁波实验实验目的:1.了解电磁场的产生原理和特性。
2.理解电磁波的概念和基本特性。
3.掌握测量和分析不同电磁波的实验方法。
实验器材:1.U形磁铁2.电磁铁3.直流电源4.交流电源5.电磁感应器6.示波器7.微波源8.微波接收器9.光栅片10.各种电磁波滤波器实验原理:1.电磁场的产生:电流通过电线时,会在周围产生磁场。
在一对平行导线中,当电流方向相同时,导线之间的磁场是叠加的;当电流方向相反时,导线之间的磁场互相抵消。
2.电磁场的特性:电磁场具有两种性质,即不能长距离传播和具有作用力。
通过电磁感应现象,可以观察到电磁场的作用力。
3.电磁波的产生与传播:当电场和磁场变化时,会激发并产生电磁波。
电磁波可根据频率不同被分为不同波段,如:无线电波、微波、红外线、可见光、紫外线、X射线和γ射线。
实验步骤:实验1:观察电磁场的产生和作用1.将磁铁插入U形磁铁中,并将直流电源连接到U形磁铁的两端;2.在U形磁铁下方放置一根金属杆,并用电磁感应器在金属杆上方测量磁感应强度;3.开启直流电源,记录不同电流强度下的磁感应强度,并绘制电流与磁感应强度的图线;4.在磁铁两端放置一磁性物体,观察其受力情况。
实验2:测量电磁波的特性1.将微波源和微波接收器分别连接至交流电源和示波器;2.将微波源调至一定频率,并记录该频率;3.调整示波器至合适的量程和垂直偏置,观察示波器上的微波信号;4.更换不同频率和波长的电磁波,重复步骤3;5.将光栅片放置在微波源与接收器之间,观察光栅片的衍射效应。
实验结果与分析:实验1:观察电磁场的产生和作用根据实验数据,绘制出电流与磁感应强度的图线,可以观察到磁感应强度与电流之间呈现线性关系,并且磁性物体受到磁力的作用。
实验2:测量电磁波的特性根据实验数据,可以观察到不同频率和波长的电磁波在示波器上表现出不同的振动形态,频率越高,波长越短。
通过光栅片的衍射效应,可以观察到电磁波的波长。
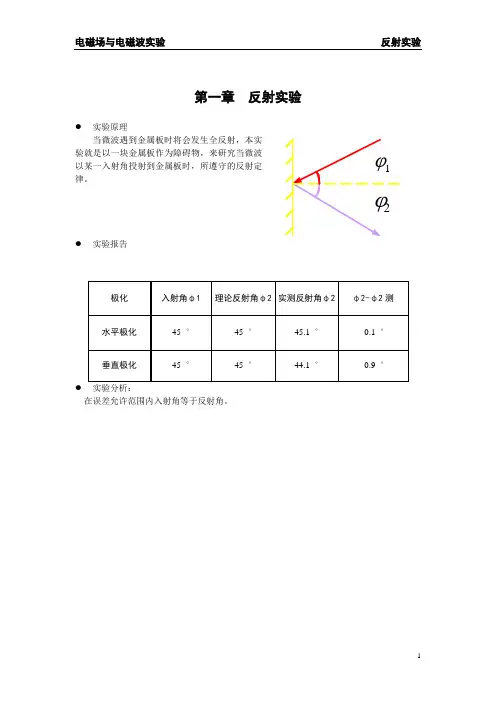
第一章反射实验●实验原理当微波遇到金属板时将会发生全反射,本实Array验就是以一块金属板作为障碍物,来研究当微波以某一入射角投射到金属板时,所遵守的反射定律。
●实验报告●在误差允许范围内入射角等于反射角。
第二章 衍射实验●实验原理:如图所示,当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象。
在缝后面出现的衍射波强度并不是均匀的,中央最强,同时也最宽。
在中央的两侧衍射波强度迅速减小,直至出现衍射波强度的最小值,即一级极小,此时衍射角为ϕ=sin-1(λ/a),其中λ是波长,a 是狭缝宽度。
两者取同一长度单位。
然后,随着衍射角增大,衍射波强度又逐渐增大,直至出现一级极大值,角度为:ϕ=sin-1(3λ/2a)。
Ф—I 曲线图(标注极大值点)-20204060801001202468101214161820222426283032343638404244464850● 实验分析随着角度的增加,电流强度出现两个峰值,证明这是两个加强点。
第三章 干涉实验●实验原理如图所示,当一平面波垂直入射到一金属板的两条狭缝上,则每一条狭缝就是次级波波源。
由两缝发出的次级波是相干波,因此在金属板的背面空间中,将产生干涉现象。
当然,通过每个缝也有衍射现象。
因此实验将是衍射和干涉两者结合的结果。
为了只观察双缝的两束中央衍射波相互干涉的现象,令双缝的缝宽a 接近λ,λ=32mm ,a=40mm 。
这时单缝的一级极小接近53︒。
因此取较大的b ,则干涉强度受狭缝衍射的影响小,当b 较小时,干涉强度受狭缝衍射影响大。
干涉加强的角度为:ϕ=sin -1(K ⋅λ/(a+b)),式中K=1、2、…。
干涉减弱的角度为:ϕ=sin -1((2K+1)⋅λ/2(a+b)),式中K=1、2、…。
实验报告 ()Ф—I 曲线图(标注极大值点)-2020406080100012345678910111213141516171819202122232425● 实验分析由于光的干涉,随着角度的增加,出现了光的加强的区和减弱区。
电磁场与电磁波实验报告实验一实验题目:阻抗匹配实验 成绩:学生姓名:李荣金 指导教师:黎波 学院名称:信息学院 专业:通信工程 年级:2010级实验时间:2011年10月29日10时30分 实验地址:信息学院楼2303一、实验目的了解掌握阻抗匹配的含义、原理、调整方法。
二、实验内容1、了解阻抗测量原理2、调整微波测量系统3、了解基本的阻抗匹配理论及阻抗变换器的设计方法4、利用实验模组实际测量以了解匹配电路的特性 三、实验仪器及器材(一) 基本阻抗匹配理论: 输入信号经过传输以后,其输出功率与输入功率之间存在以下关系,信号的当R L =R S 时可获得最大输出功率,此时为阻抗匹配状态。
推而广之,当输入阻抗Z S 与负载阻抗Z L 间成为Z S =Z L *的关系时,满足广义阻抗匹配的条件。
所以,阻抗匹配电路也可以称为阻抗变换器。
(二) 阻抗交换器的设计原理:阻抗交换器的设计方法,根据使用元件及工作频率高低,大致可分为无源元件型(Lumped Device Type )和传输线型(Transmission Line Type )两种。
无源元件型此种电路是利用电感及电容来设计。
根据工作频宽的大小,基本上可分为L形(L-Network)、T形(T-Network)及П(П-Network)等三种(A)T型匹配电路(T-type Matching Network)(以RS < RL为例)步骤一:决定工作频率fc、负载Q值、输入阻抗RS 及输出阻抗RL。
并求出Rsmall = MIN( RS,RL).步骤二:依图2-3(a)中所示及下列公式计算出XS1、XP1、XP2及XS2。
(B)、和匹配电路(П-type Matching Network)(以RS <RL为例)步骤一:决定工作频率fc、负载Q值、输入阻抗RS 及输出阻抗RL。
并求出RH = MAX ( RS, RL).步骤二:根据图2-4(a)中所示及下列公式计算出XP2、XS2、XP1及 XS1:五、实验步骤及实验内容记录1、测量MOD-2A: Π型阻抗转换器的S11及S21测量以了解Π型阻抗匹配电路的特性;测量MOD-2B: T型阻抗转换器的S11及S21测量以了解T型阻抗匹配电路的特性。
电磁场与电磁波实验报告实验一 电磁场参量的测量一、 实验目的1、 在学习均匀平面电磁波特性的基础上,观察电磁波传播特性互相垂直。
2、 熟悉并利用相干波原理,测定自由空间电磁波波长λ,并确定电磁波的相位常数β和波速υ。
二、 实验原理两束等幅、同频率的均匀平面电磁波,在自由空间从一样(或相反)方向传播时,由于初始相位不同发生干涉现象,在传播路径上可形成驻波场分布。
本实验正是利用相干波原理,通过测定驻波场节点的分布,求得自由空间电磁波波长λ的值,再由 λπβ2=,βωλν==f得到电磁波的主要参量:β和ν等。
本实验采取了如下的实验装置设入射波为φj i i e E E -=0,当入射波以入射角1θ向介质板斜投射时,则在分界面上产生反射波r E 和折射波t E 。
设介质板的反射系数为R ,由空气进入介质板的折射系数为0T ,由介质板进入空气的折射系数为c T ,另外,可动板2r P 和固定板1r P 都是金属板,其电场反射系数都为-1。
在一次近似的条件下,接收喇叭处的相干波分别为1001Φ--=j i c r e E T RT E ,2002Φ--=j i c r e E T RT E这里 ()13112r r r L L L ββφ=+=;()()231322222L L L L L L r r r r βββφ=+∆+=+=;其中12L L L -=∆。
又因为1L 为定值,2L 则随可动板位移而变化。
当2r P 移动L ∆值,使3r P 有零指示输出时,必有1r E 与2r E 反相。
故可采用改变2r P 的位置,使3r P 输出最大或零指示重复出现。
从而测出电磁波的波长λ和相位常数β。
下面用数学式来表达测定波长的关系式。
在3r P 处的相干波合成为()210021φφj j i c r r r e e E T RT E E E --+-=+=或写成 ()⎪⎭⎫⎝⎛+-∆Φ-=200212cos 2φφj i c r e E T RT E (1-2)式中L ∆=-=∆Φβφφ221为了测量准确,一般采用3r P 零指示法,即02cos =∆φ或 π)12(+=∆Φn ,n=0,1,2......这里n 表示相干波合成驻波场的波节点(0=r E )数。
电磁场与电磁波(天线部分实验报告班级:姓名:学号:实验一网络分析仪测量振子天线输入阻抗实验目的1.掌握网络分析仪校正方法;2.学习网络分析仪测量振子天线输入阻抗的方法;3.研究振子天线输入阻抗随振子电径变化的情况。
实验原理当双振子天线的一端变为一个无穷大导电平面后,就形成了单振子天线。
实际上当导电平面的径向距离大到0.2~0.3λ,就可以近似认为是无穷大导电平面。
这时可以采用镜像法来分析。
天线臂与其镜像构成一对称振子,则它在上半平面辐射场与自由空间对称振子的辐射场射相同。
由于使用坡印亭矢量法积分求其辐射功率只需对球面上半部分积分,故其辐射功率为等臂长等电流分布的对称振子的一半,其辐射电阻也为对称振子的一半。
当h<<λ时,可认为R≈40。
由于天线到地面的单位长度电容比到对称振子另一个臂的单位长度电容大一倍,则天线的平均特征阻抗也为等臂长对称振子天线的一半,为=60[ln(2h/a-1]。
实验步骤1.设置仪表为频域模式的回损连接模式后,校正网络分析仪;2.设置参数(BF=600,∆F=25,EF=2600,n=81并加载被测天线,开始测量输入阻抗;3.调整测试频率寻找天线的两个谐振点并记录相应阻抗数据;4.更换不同电径(φ1,φ 3,φ9)的天线,分析两个谐振点的阻抗变化情况。
实验数据当被测天线的电径为1mm时,可在Smith原图上得到如下阻抗点分布:当被测天线的电径为3mm时,可在Smith原图上得到如下阻抗点分布:当被测天线的电径为9mm时,可在Smith原图上得到如下阻抗点分布:实验结果分析由图可知,相同材质、不同电径的天线对应不同的输入阻抗,电径越大,谐振点输入阻抗越小,网络反射系数越小,回波损耗越小。
1被测天线的电径对天线的阻抗是基本不产生影响的,上述三图中阻抗有差别主要是因为三根阵子粗细不同因而对空间电磁场产生了一些影响导致了天线阻抗的变化,本质上是不影响的。
2天线的电阻随着频率的变化是不断变化的,频率变化范围为600KHz到2600KHz,变化的趋势为——在前20个点基本不变,后面的点基本随着频率的增加电阻增加。
电磁场与波实验报告电磁场与波实验报告引言:电磁场与波是物理学中重要的研究对象,对于我们理解光、电、磁等现象具有重要意义。
为了更好地探究电磁场与波的性质,我们进行了一系列实验,下面将对实验过程和结果进行详细报告。
实验一:电磁感应现象实验目的:通过实验观察电磁感应现象,验证法拉第电磁感应定律。
实验装置:实验装置由一根导线、一个磁铁和一个电流表组成。
实验步骤:1. 将导线绕在一个纸芯上,形成一个线圈。
2. 将磁铁靠近线圈,观察电流表的指示情况。
实验结果:当磁铁靠近线圈时,电流表指针发生偏转,表明在导线中产生了电流。
当磁铁远离线圈时,电流方向相反。
这一现象验证了法拉第电磁感应定律,即磁场的变化会引起导线中的电流。
实验二:电磁波的传播实验目的:通过实验观察电磁波的传播特性,验证电磁波的存在。
实验装置:实验装置由一个发射器和一个接收器组成。
实验步骤:1. 将发射器放置在一定距离内,接通电源。
2. 在接收器处设置一个示波器,调节示波器的参数。
3. 观察示波器上的波形变化。
实验结果:当发射器工作时,示波器上出现了一定频率的波形。
通过调节示波器参数,我们可以观察到电磁波的传播特性,包括波长、频率等。
这一实验结果验证了电磁波的存在,并且进一步揭示了电磁波的传播特性。
实验三:电磁波的干涉实验目的:通过实验观察电磁波的干涉现象,验证电磁波的波动性质。
实验装置:实验装置由一个光源、一个狭缝、一个屏幕和一个检测器组成。
实验步骤:1. 将光源置于一定位置,使其照射到狭缝上。
2. 在屏幕上观察到干涉条纹的出现。
3. 使用检测器测量干涉条纹的强度。
实验结果:在屏幕上观察到了明暗相间的干涉条纹,这表明电磁波具有波动性质。
通过检测器的测量,我们可以进一步研究干涉条纹的强度分布规律。
这一实验结果验证了电磁波的波动性质,并且揭示了电磁波的干涉现象。
结论:通过以上实验,我们验证了电磁感应定律、电磁波的存在以及电磁波的波动性质。
电磁场与波是物理学中重要的研究对象,对于我们理解光、电、磁等现象具有重要意义。
电磁场与电磁波实验报告实验项目: ________________________班级 _______, 实验日期 _______, 实验成绩 _______,姓名 _______, 学号_______, 同组成员姓名 _______, 学号 _______指导教师:卢露一、实验目的要求1.理解物理模拟法的实验原理和应用条件。
2.学习用物理模拟法研究静电场。
3.加深对静电场场强和电位的理解。
二、实验内容1.了解装置电路及实验原理。
2.描绘矩形水槽薄水层中两个点电极产生的二维静电场。
三、实验仪器与软件矩形水槽、坐标纸两张、稳压电源和电压表,模拟电极、导线、固定支架。
四、实验原理理论上讲,如果知道了电荷的分布,就可以确定静电场的分布。
电场既可以用电场强度E 0(电力线)来描述,又可以用电势U(等势面、线)来描述。
由于标量的测量和计算比矢量简便,因此,人们更愿意用电势来描述电场。
在给定条件下,确定系统静电场分布的方法,一般有解析法﹑数值模拟法和物理模拟法。
解析法只能求解一些简单的问题;数值模拟法,也就是数值计算方法,它能解决一些复杂的问题,虽计算量很大,但在计算机的帮助下,目前已经得到长足的发展,应用很广,数值模拟也有不足之处,对于一些形状比较复杂的带电体或电极周围静电场的分布,求解也非常困难。
模拟法作为一种重要的实验研究方法,它本质上是用一种易于实现﹑便于测量的物理状态或过程来模拟另一种不易实现﹑不便测量的物理状态或过程。
其条件是两种状态或过程有两组一一对应的物理量,并且满足相同形式的数学规律。
由于静电场中不存在电流,一般磁电式仪表,在有电流时才会有反应,因此难以确定静电场的等势线。
由于在一定条件下电介质中的稳恒电流场与静电场服从相同的数学规律,可以用恒定电流的电场模拟静电场。
如接到直流电源两端的小圆柱形电极之间形成的恒定电场,可以用来模拟等量异种电荷之间的静电场。
静电场与稳恒电流场的对应关系为静电场稳恒电流场导体上的电荷± Q极间电流± I 电场强度E电场强度 E 介电常数电导率电位移 D =E电流密度 J=E无电荷区E dS 0无源区E dS 0电位满足20电位满足20 U U根据上表中的对应关系可知,要想在实验上用稳恒电流场来模拟静电场,需要满足下面三个条件:⑴电极系统与导体几何形状相同或相似;⑵导电质与电介质分布规律相同或相似;⑶电极的电导率远大于导电质的电导率,以保证电极表面为等势面。
电磁场与电磁波实验报告班级:学号:姓名:实验一:验证电磁波的反射和折射定律1学时1、实验目的验证电磁波在媒质中传播遵循反射定理及折射定律;1研究电磁波在良好导体表面上的全反射;2研究电磁波在良好介质表面上的反射和折射;3研究电磁波全反射和全折射的条件;2、实验原理电磁波在传播过程中如遇到障碍物,必定要发生反射,本处以一块大的金属板作为障碍物来研究当电磁波以某一入射角投射到此金属板上所遵循的反射定律,即反射线在入射线和通过入射点的法线所决定的平面上,反射线和入射线分居在法线两侧,反射角等于入射角;3、实验结果:图1.1 电磁波在介质板上的折射图1.2 电磁波在良导体板上的反射实验二:电磁波的单缝衍射实验、双缝干涉实验;1、实验目的1研究当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象;在缝后面出现的衍射波强度不是均匀的,中央最强;2研究当一平面波垂直入射到一金属板的两条狭线上,则每一条狭缝就是次级波波源;由两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象;2、实验原理单缝衍射实验原理见下图 5:当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象;在缝后面将出现的衍射波强度不是均匀的,中央最强,同时也最宽,在中央的两侧衍射波强度迅速减小,直至出现衍射波强度的最小值,即一级极小,此时衍射角为,其中λ是波长,λ是狭缝宽度;两者取同一长度单位,然后,随着衍射角增大,衍射波强度又逐渐增大,直至一级极大值,角度为:图 5 单缝衍射实验原理图如图 8:当一平面波垂直入射到一金属板的两条狭缝上时,则每一条狭缝就是次级波波源,由于两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象;当然电磁波通过每个缝也有狭缝现象;因此实验将是衍射和干涉两者结合的结果;为了只研究主要是由于来自双缝的两束中央衍射波相互干涉的结果,令双缝的缝宽α接近入,例如:,这时单缝的一级极小接近53°;因此取较大的b,则干涉强受单缝衍射影响大;干涉加强的角度为:干涉减弱的角度为:3、实验结果图2.1 单缝衍射的I-α曲线图2.2双缝干涉的I-α曲线实验三:布朗格衍射的实验1、实验目的本实验是仿造X射线入射真实晶体发生衍射的基本原理,人为的制作了一个方形点阵的模拟晶体,以微波代替X射线,使微波向模拟晶体入射,观察从不同晶面上点阵的反射波产生干涉应符合的条件;这个条件就是布拉格方程;1掌握100面,110面点阵的反射波产生干涉的条件,得出布拉格方程;2了解直线极化和圆极化波特性参数的测试方法;2、实验原理任何的真实晶体,都具有自然外形和各向异性的性质,这和晶体的离子、原子或分子在空间按一定的几何规律排列密切相关;晶体内的离子、原子或分子占据着点阵的结构, 两相邻结点的距离叫晶体的晶格常数;真实晶体的晶格常数约在10−8厘米的数量级,X 射线的波长与晶体的常数属于同一数量级,实际上晶体是起着衍射光栅的作用,因此可以利用 X 射线在晶体点阵上的衍射现象来研究晶体点阵的间距和相互位置的排列,以达到对晶体结构得了解;本实验是仿造 X 射线入射真实晶体发生衍射的基本原理,人为的制作了一个方形点阵的模拟晶体,以微波代替 X 射线,使微波向模拟晶体入射,观察从不同晶面上点阵的反射波产生干涉应符合的条件,这个条件就是布拉格方程;它是这样说的,当波长为入的平面波射到间距为α的晶面上,入射角为Θ°,当满足条件时n为整数发生衍射;衍射线在所考虑的晶面反射线方向;在布拉格衍射实验中采用入射线与晶面的夹角即通称的入射角,是为了在实验时方便,因为当被研究晶面的法线与分光仪上度盘的 0 度刻度一致时,入射线与反射线的方向在度盘上有相同的示数,不容易搞错,操作方便;3、实验结果图3.1 布拉格衍射I-θ关系曲线由实验数据可得,两侧发生衍射的角度大约在34°和65°附近;根据布拉格方程nλ=2aCOSθ,将λ=32mm,a=40mm代入得:当n=1时,θ=66.42°;当n=2时,θ=36.87°.实验测得数据与理论计算值比较接近,可验证布拉格方程;69°附近产生的峰值可能是由其他实验组影响造成的,不计入考虑;实验四:均匀无损耗媒质参量的测量2学时1、实验目的了解电磁波在真空中传播特性和相干原理;1在学习均匀平面电磁波的基础上,观察电磁波传播特性,E、H、S互相垂直;2推导相干波理论数学模型,自行调节测量仪器,测量基本参量;3测定自由空间内电磁波波长λ、频率f,并确定电磁波的相位常数β和波速υη的测量;4了解电磁波的其他参量,如波阻抗5利用相干波接点位移法推导测量均匀无损耗媒质参量的ε和μ的数学模型6了解均匀无损耗媒质参量λ、β、的差别7熟悉均匀无损耗媒质分界面对电磁波的反射和折射的特性;2、实验原理迈克尔逊干涉试验的基本原理见下图 13 所示:在平面波前进的方向上放置一个成45°的半透射板,由于该板的作用,将入射波分成两束波:一束由于反射向 A 方向传播;另一束透过半透射板向B 方向传播;由于A﹑B 处全反射板的作用,两列波就再次回到半透射板并到达接收喇叭处,于是接收喇叭收到两束同频率且振动方向一致的两个波;如果这两个波的位相差为2π的整数倍,则干涉加强;当相位差为π的奇数倍则干涉减弱;因此在 A 处放一固定板,让 B 处的反射板移动,当表头指示从一次极小变到又一次极小时,则 B 处的反射板就移动λ⁄2的距离,因此有这个距离就可求得平面波的波长;3、实验结果()()mm 32.341-443.5-91.5621n 0L -3L 2=⨯=-⨯=λ实验五:利用微波衰减测量湿度、厚度2学时1、实验目的学习介质特性参量:相移常数和衰减常数的测量方法,自行推导出介质厚度和湿度的数学模型,设计实验方法;1了解被测量的物质所用波为TEM 波,TEM 波产生的条件; 2相移常数和衰减常数测量方法; 3湿度、厚度测量方法 4信号处理方法 2、实验原理同迈克尔干涉实验原理 3、实验结果491.5602.5592.4067.4172.2357.2643.532.13-+-+-+-=91.2=n33221100L L L L L L L L L -'+-'+-'+-'=∆()()mm80.271-432.13-2.05521n 0-32ˊ=⨯=-''⨯'L L λ()d L /1/∆+= λλ()d /91.21/32.3480.27+=mmd 6.12≈。