北京市昌平区2013届高三上学期期末考试理科数学试题
- 格式:doc
- 大小:652.00 KB
- 文档页数:12

北京市昌平区2012-2013学年第一学期高三年级期末考试数 学 试 卷(理科)(满分150分,考试时间 120分钟)2013.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A 等于 A .{|2}x x > B .{}20<<x xC .{}21<<x xD .{|01}x x <<(2)“2a =”是“直线214a y ax y x =-+=-与垂直”的A. 充分不必要条件 B 必要不充分条件C. 充要条件D.既不充分也不必要条件 (3)已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是A.(0,1)B. (1,2)C. (2,3)D. (3,4)(4)设不等式组22,42x y x y -+≥≥-⎧⎪⎨⎪⎩0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线+2=0y 的距离大于2的概率是A.413B.513C.825D.925(5)设n S 是公差不为0的等差数列{}n a 的前n 项和,且124,,S S S 成等比数列,则21a a 等于A.1B. 2C. 3D. 4(6)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为A. 24B. 36C. 48D.60(7)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为A. 10+B.10+C. 14+D.14++(8)已知函数:①2()2f x x x =-+,②()cos()22x f x ππ=-,③12()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是命题:p ()f x 是奇函数; 命题:q (1)f x +在(0),1上是增函数; 命题:r 11()22f >; 命题:s ()f x 的图像关于直线1x =对称A .命题p q 、B .命题q s 、C .命题r s 、D .命题p r 、第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. (9)若221ai i i=-+-,其中i是虚数单位,则实数a 的值是____________.(10)以双曲线221916xy-=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.(11)在A B C △中,若b =1c =,tan B =,则a = . (12)已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .(13)在R t A B C ∆中,90C ︒∠=,4,2AC BC ==,D 是B C 的中点,那么()AB AC AD -∙=uu u r uuu r uuu r____________;若E 是A B 的中点,P 是ABC ∆(包括边界)内任一点.则AD EP ⋅uuu r uur的取值范围是___________.(14)在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则① 到坐标原点O 的“折线距离”不超过2的点的集合所构成的平面图形面积是_________;② 坐标原点O 与直线20x y --=上任意一点的“折线距离”的最小值是_____________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知函数1sin cos )2sin sin32()(2+⋅-=xx x x x f .(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42ππ上的最值.OFEDCBA(16) (本小题满分14分)在四棱锥E A B C D -中,底面A B C D 是正方形,,AC BD O 与交于点EC ABCD F 底面,^为B E 的中点.(Ⅰ)求证:D E ∥平面A C F ; (Ⅱ)求证:BD AE ^; (Ⅲ)若,A B E =在线段E O 上是否存在点G ,使CG BDE 平面^?若存在,求出E G E O的值,若不存在,请说明理由.(17)(本小题满分13分)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: 甲厂乙厂93 9 6 5 8 18 4 5 6 9 0 31 5 0 32 1 0 3规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品. (Ⅰ)试用上述样本数据估计甲、乙两厂生产的优等品率;(Ⅱ)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数ξ的分布列及其数学期望()E ξ;(Ⅲ)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率.(18)(本小题满分13分)已知函数32()4f x x ax =-+-(a ∈R ).(19)(本小题满分13分)已知椭圆M 的对称轴为坐标轴, 离心率为2且抛物线2y =的焦点是椭圆M 的一个焦点. (Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中点P 在椭圆M 上,O 为坐标原点. 求点O 到直线l 的距离的最小值.(20)(本小题满分14分)已知每项均是正整数的数列123100,,,,a a a a ,其中等于i 的项有i k 个(1,2,3)i = ,设j j k k k b +++= 21(1,2,3j = ,12()100m g m b b b m =+++- (1,2,3).m =(Ⅰ)设数列1240,30,k k ==34510020,10,...0k k k k =====,求(1),(2),(3),(4)g g g g ; (Ⅱ)若123100,,,,a a a a 中最大的项为50, 比较(),(1)g m g m +的大小; (Ⅲ)若12100200a a a +++= ,求函数)(m g 的最小值.G ABCDEFO昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试卷 参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的二、填空题(本大题共6小题,每小题5分,共30分.) (9)4(10)22(5)16x y -+=(11) 3(12)4 (13) 2;[-9,9] (14) 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)(15)(本小题满分13分)解:(Ⅰ)由sin 0x ≠得πx k ≠(k ∈Z ),故()f x 的定义域为{x ∈R |π,x k ≠k ∈Z }.…………………2分 因为1sin cos )2sin sin32()(2+⋅-=xx x x x f2cos )cos 1x x x =-⋅+ 2cos 2x x=-π2sin(2)6x =-,………………………………6分所以()f x 的最小正周期2ππ2T ==.…………………7分(II )由 5[,],2[,],2[,],422636x x x πππππππ挝- …………..9分 当52,,()1662x x f x πππ-==即时取得最小值,…………….11分当2,,()2623x x f x πππ-==即时取得最大值.……………….13分(16)(本小题满分14分) 解:(I )连接O F .由A B C D 是正方形可知,点O 为BD 中点. 又F 为B E 的中点,所以O F ∥D E ………………….2分 又,,OF ACF DEACF 平面平面趟yx所以D E ∥平面A C F ………….4分(II) 证明:由EC ABCD BD ABCD 底面,底面,^ 所以,EC BD ^由A B C D 是正方形可知, ,AC BD ^又=,,AC EC C AC ECACE 平面,翘 所以,BD ACE 平面^………………………………..8分又AE ACE 平面,Ì所以BD AE ^…………………………………………..9分(III)解法一:在线段E O 上存在点G ,使CG BDE 平面^. 理由如下: 如图,取E O 中点G ,连接C G . 在四棱锥E A B C D -中,,2AB E C O AB C E ===,所以C G E O ^.…………………………………………………………………..11分 由(II )可知,,BD ACE 平面^而,BD BDE 平面Ì 所以,,ACE BDE ACE BDE EO 平面平面且平面平面,^? 因为,CG EO CG ACE 平面,^所以CG BDE 平面^…………………………………………………………. 13分 故在线段E O 上存在点G ,使CG BDE 平面^.由G 为E O 中点,得1.2E G E O=…………………………………………… 14分解法二:由EC ABCD 底面,^且底面A B C D 建立空间直角坐标系,C DBE -由已知,AB E =设(0)CE a a =>,则(0,0,0),,0,0),,0),(0,0,),C D B E a,,0),,,0),(0,,),,,).2222O a a BD BE a EO a a uuu ruuruuu r =-=-=-设G 为线段E O 上一点,且(01)EGEO λλ=<<,则,,),22EG EO a a a λλλλuuu r uuu r ==-,,(1)),22CG CE EO a a a λλλuuu r uur uuu r =+=-…………………………..12分由题意,若线段E O 上存在点G ,使CG BDE 平面^,则C G BD^uuu r uuu r,C G BE ^uuu r uur .所以,221(1)0,0,12a a λλλ解得,()-+-==, 故在线段E O 上存在点G ,使CG BDE 平面^,且1.2E G E O=…………………… 14分(17)(本小题满分13分)解:(I )甲厂抽取的样本中优等品有6件,优等品率为63.105=乙厂抽取的样本中优等品有5件,优等品率为51.102=………………..2分(II )ξ的取值为0,1,2,3.312555533101015(0),(1),1212C C C C P P C C ξξ⋅⋅======21355533101051(2),(3)1212C C C P P C C ξξ⋅======所以ξ的分布列为故155130123.121212122E ξξ=⨯+⨯+⨯+⨯=的数学期望为()……………………9分(III) 抽取的优等品数甲厂恰比乙厂多2件包括2个事件,即A=“抽取的优等品数甲厂2件,乙厂0件”,B=“抽取的优等品数甲厂3件,乙厂1件”2200333321127()()()()()5522500P A C C =⨯=331123331181()()()()5221000P B C C =⨯=抽取的优等品数甲厂恰比乙厂多2件的概率为278127()().5001000200P A P B +=+=…13分(18)(本小题满分13分)解:(I ).23)(2ax x x f +-=' …………………………. ……………1分根据题意,(1)tan1,321, 2.4f a a π'==∴-+==即 …………………3分此时,32()24f x x x =-+-,则2()34f x x x '=-+. 令124'()00,.f x x x ===,得∴当[]1,1x ∈-时,()f x 最小值为()04f =-. ………………………7分 (II )).32(3)(a x x x f --='①若0,0,()0,()(0,)a x f x f x '><∴+∞≤当时在上单调递减. 又(0)4,0,() 4.f x f x =-><-则当时000,0,()0.a x f x ∴>>当≤时不存在使…………………………………………..10分②若220,0,()0;,()0.33a a a x f x x f x ''><<>><则当时当时从而)(x f 在(0,23a )上单调递增,在(23a ,+)∞上单调递减..4274494278)32()(,),0(333max -=-+-==+∞∈∴a a aa f x f x 时当 根据题意,33440,27. 3.27aa a ->>∴>即 …………….............................. 13分综上,a 的取值范围是(3,)+∞. (19)(本小题满分13分)解:(I )由已知抛物线的焦点为0),故设椭圆方程为22221(0)x y a b ab+=>>, 则22, 2.2c e a b ====由得所以椭圆M的方程为22 1.42xy+=……5分(II )当直线l 斜率存在时,设直线方程为y kx m =+,则由22,1.42y kx m x y=+⎧⎪⎨+=⎪⎩消去y 得,222(12)4240k x km x m +++-=, …………………6分222222164(12)(24)8(24)0k m k m k m ∆=-+-=+->, ①…………7分设A B P 、、点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则:012012122242,()21212km m x x x y y y k x x m kk =+=-=+=++=++,…………8分由于点P 在椭圆M 上,所以2200142x y +=. ……… 9分从而2222222421(12)(12)k mmk k +=++,化简得22212m k =+,经检验满足①式.………10分 又点O 到直线l 的距离为:2d ====………11分当且仅当0k =时等号成立 ………12分当直线l 无斜率时,由对称性知,点P 一定在x 轴上,从而点P 的坐标为(2,0)(2,0)-或,直线l 的方程为1x =±,所以点O 到直线l 的距离为1 .所以点O 到直线l的距离最小值为2. ………13分(20)(本小题满分14分)解: (I) 因为数列1240,30,k k ==320,k =410k =, 所以123440,70,90,100b b b b ====,所以(1)60,(2)90,(3)100,(4)100g g g g =-=-=-=- …………………4分 (II) 一方面,1(1)()100m g m g m b ++-=-,根据j b 的含义知1100m b +≤,故0)()1(≤-+m g m g ,即 )1()(+≥m g m g ,①当且仅当1100m b +=时取等号.因为123100,,,,a a a a 中最大的项为50,所以当50m ≥时必有100m b =, 所以(1)(2)(49)(50)(51)g g g g g >>>===即当149m ≤<时,有()(1)g m g m >+; 当49m ≥时,有()(1)g m g m =+ …9分 (III )设M 为{}12100,,,a a a 中的最大值. 由(II )可以知道,()g m 的最小值为()g M . 根据题意,123100,M M b k k k k =++++=L123123123....M k k k M ka a a a ++++=++++L 下面计算()g M 的值.123()100M g M b b b b M =++++-1231(100)(100)(100)(100)M b b b b -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++- 23[2(1)]M k k M k =-+++-12312(23)()M M k k k M k k k k =-++++++++123100()M a a a a b =-+++++ 123100()100a a a a =-+++++ ,∵123100200a a a a ++++= , ∴()100g M =-,∴()g m 最小值为100-. ………………………………………….14分。

北京市2013届高三上学期期末数学试题分类汇编算法初步1.【北京市昌平区2013届高三上学期期末理】已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .【答案】42.【北京市朝阳区2013届高三上学期期末理】执行如图所示的程序框图.若输入3x =,则输出k 的值是A . 3B .4C . 5D . 6 【答案】C【解析】第一次循环358,1x k =+==;第二次循环8513,2x k =+==;第三次循环13518,3x k =+==;第四次循环18523,4x k =+==;第五次循环23528,5x k =+==,此时满足条件输出5k =,选C.3.【北京市东城区2013届高三上学期期末理】执行如图所示的程序框图,输出的k 的值为(A )4 (B )5 (C )6 (D )7 【答案】A【解析】第一次循环得0021,1S k =+==;第二次循环得1123,2S k =+==;第三次循环得33211,3S k =+==,第四次循环得111122059,4S k =+==,但此时100S <,不满足条件,输出4k =,所以选A.4.【北京市房山区2013届高三上学期期末理】运行相应的程序,则输出n 的值为【答案】95.【北京市丰台区2013届高三上学期期末理】执行如图所示的程序框图,则输出的S 值为([]x 表示不超过x 的最大整数)(A) 4 (B) 5(C) 7(D) 9【答案】C【解析】第一次循环,0S =,不满足条件,1n =;第二次循环,[1]1S ==,不满足条件,2n =;第三次循环,12,S =+=,不满足条件,3n =;第四次循环,23,S =+=,不满足条件,4n =;第五次循环,3[4]5S =+=,此时不满足条件,5n =。
第六次循环,5[5]7S =+=,此时满足条件,输出 7S =,选C.6.【北京市海淀区2013届高三上学期期末理】某程序的框图如图所示, 执行该程序,若输入的p 为24,则输出的,n S 的值分别为A.4,30n S ==B.5,30n S ==C.4,45n S ==D.5,45n S == 【答案】B【解析】第一次循环,24,3,2S S n <==;第二次循环,24,3329,3S S n <=+⨯==;第三次循环,24,93318,4S S n <=+⨯==;第四次循环,24,183430,5S S n <=+⨯==;第五次循环,3024,S =<不满足条件,输出30,5S n ==,选B.7.【北京市石景山区2013届高三上学期期末理】执行右面的框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4 【答案】C【解析】本程序为分段函数2212log 2x x y x x ⎧-≤=⎨>⎩,,,当2x ≤时,由213x -=得,24x =,所以2x =±。

北京市2013届高三上学期期末数学试题分类汇编 数列 一、填空、选择题 1.【北京市昌平区2013届高三上学期期末理】设是公差不为0的等差数列的前项和,且成等比数列,则等于A.1B. 2C. 3D. 4 【解析】因为成等比数列,即,即,所以,选C. 2.【北京市朝阳区2013届高三上学期期末理】已知数列等差数列,是等比数列,则的值为 . 【解析】因为是等差数列。
是等比数列,因为,所以,所以。
3.【北京市东城区2013届高三上学期期末理】已知为等差数列,其前项和为,若,,则公差等于 (A) (B) (C) (D) 【答案】C 【解析】因为,,所以,解得,所使用,解得,选C. 4.【北京市丰台区2013届高三上学期期末理】右表给出一个“三角形数阵”.已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第行第列的数为(),则等于 ,. 【答案】 (第一个空2分,第二个空3分) 满足且对任意的,都有,则的前项和_____. 【答案】 【解析】由可得,所以。
所以。
由得,令,得,即数列是公比为2的等比数列,所以。
6.【北京市海淀区2013届高三上学期期末理】数列满足(且),则“”是“数列成等差数列”的A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件 【答案】A 【解析】若,则,即,所以数列成等差数列。
若数列成等差数列,设公差为,则,即,若,则,若,则 ,即,此时。
所以是数列成等差数列的充分不必要条件,选A. 7.【北京市石景山区2013届高三上学期期末理】在等比数列中,,则公比 【答案】 【解析】在等比数列中,所以,即。
所以,所以,即数列是一个公比为2的等比 数列,所以。
8..【北京市西城区2013届高三上学期期末理】设等比数列的各项均为正数,其前项和为.若,,,则______. 【答案】6 【解析】设公比为,因为,所以,则,所以,又,即,所以。

x y O π2π1-1北京市东城区普通校2013届高三第二学期3月联考 数学(理科)命题校:北京27中学 2013年3月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分,考试时间120 分钟。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利! 第Ⅰ卷(选择题,共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的. 1.已知平面向量(1,2)=a , (2,)m =-b , 且a ∥b , 则m 的值为( ) (A )1- (B ) (C )4- (D )4 2.极坐标方程4cos ρθ=化为直角坐标方程是( )(A )22(2)4x y -+= (B )224x y += (C )22(2)4x y +-= (D )22(1)(1)4x y -+-= 3.平面α∥平面β的一个充分条件是( ) (A )存在一条直线a a ααβ,∥,∥(B )存在一条直线a a a αβ⊂,,∥(C )存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥ (D )存在两条异面直线a b a b a b αββα⊂⊂,,,,∥,∥ 4. 执行如图所示的程序,输出的结果为20, 则判断框中应填入的条件为( ) (A )2a ≥ (B )3a ≥ (C )4a ≥(D )5a ≥第4题图5. 如图,已知AB 是⊙O 的一条弦,点P 为AB 上一点, PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =,则PC 的长是( )(A )3 (B) (C )2 (D第5题图 6.已知函数sin()y A x ωϕ=+的图象如图所示,则该函数的解析式可能是( ) 第6题图ABCOP40 50 60 70 80 90 分数(分)频率(A)41sin(255y x =+ (B) 31sin(225y x =+ (C)441sin()555y x =- (D) 441sin()555y x =+ 7. 设0,0.a b >>1133a b a b +与的等比中项,则的最小值为( ) (A) 8 (B) 4 (C) 1 (D) 148.对实数a 与b ,定义新运算“⊗”:,1,, 1.a a b a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =-⊗-∈若函数()y f x c =-的零点恰有两个,则实数c 的取值范围是( )(A) (]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ (B)(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭ (C) 11,,44⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭ (D)第Ⅱ卷(非选择题,共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 在6)11(x+的展开式中,含1x 项的系数是________.(用数字作答)10.由1、2、3、4、5组成的无重复数字的五位数中奇数有 个. 11.从某校高三学生中随机抽取100名同学,将他们的考试成绩(单位:分)绘制成频率分布直方图(如图).则图中a= ,由图中数据可知此次成绩平均分为 . 第11题图12.已知区域1,{(,)0,}1,y x x y y x ≤+⎧⎪Ω=≥⎨⎪≤⎩,1,{(,)}0,y x M x y y ⎧≤-+⎪=⎨≥⎪⎩,向区域Ω内随机投一点P ,点P 落在区域M 内的概率为 .13.如图,1F 和2F 分别是双曲线22221(00)x y a b a b -=>>,311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭的两个焦点,A 和B 是以O 为圆心,以1OF 为半径的圆与该双曲线左支的两个交点,且2F AB △是等边三角形,则双曲线的离心率为 . 第13题图 14.设S 为复数集C 的非空子集.若对任意x,y S ∈,都有x y,x y,xy S +-∈, 则称S 为封闭集。

昌平区2012-2013学年第一学期高三年级期末质量抽测数学试卷(理科)(满分150分,考试时间 120分钟)2013.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A 等于 A .{|2}x x > B .{}20<<x xC .{}21<<x xD .{|01}x x <<(2)“2a =”是“直线214ay ax y x =-+=-与垂直”的 A. 充分不必要条件 B 必要不充分条件C. 充要条件D.既不充分也不必要条件 (3)已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是A.(0,1)B. (1,2)C. (2,3)D. (3,4) (4)设不等式组22,42x y x y -+≥≥-⎧⎪⎨⎪⎩0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线+2=0y 的距离大于2的概率是A.413B.513C.825D.925(5)设n S 是公差不为0的等差数列{}n a 的前n 项和,且124,,S S S 成等比数列,则21a a 等于 A.1 B. 2 C. 3 D. 4(6)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为A. 24B. 36C. 48D.60(7)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为A. 10+B .10+C. 14+D. 14+(8)已知函数:①2()2f x x x =-+,②()cos()22xf x ππ=-,③12()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是命题:p ()f x 是奇函数; 命题:q (1)f x +在(0),1上是增函数;命题:r 11()22f >; 命题:s ()f x 的图像关于直线1x =对称A .命题p q 、B .命题q s 、C .命题r s 、D .命题p r 、第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.(9)若221aii i=-+-,其中i 是虚数单位,则实数a 的值是____________.(10)以双曲线221916x y -=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.(11)在ABC △中,若b =1c =,tan B =,则a = . (12)已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .(13)在Rt ABC ∆中,90C ︒∠=,4,2AC BC ==,D 是BC的中点,那么()AB AC AD -∙=uu u r uu u r uuu r____________;若E 是AB 的中点,P 是ABC ∆(包括边界)内任一点.则AD EP ⋅uuu r uu r的取值范围是___________.(14)在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则① 到坐标原点O 的“折线距离”不超过2的点的集合所构成的平面图形面积是_________;OFEDCBA② 坐标原点O与直线20x y --=上任意一点的“折线距离”的最小值是_____________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知函数1sin cos )2sin sin 32()(2+⋅-=xxx x x f .(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42ππ上的最值.(16) (本小题满分14分)在四棱锥E ABCD -中,底面ABCD 是正方形,,AC BD O 与交于点EC ABCD F 底面,^为BE 的中点. (Ⅰ)求证:DE ∥平面ACF ; (Ⅱ)求证:BD AE ^;(Ⅲ)若,AB =在线段EO 上是否存在点G ,使CG BDE 平面^?若存在,求出EGEO的值,若不存在,请说明理由.(17)(本小题满分13分)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: 甲厂乙厂93 9 6 5 8 18 4 5 6 9 0 31 5 0 3 21 0 3规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品. (Ⅰ)试用上述样本数据估计甲、乙两厂生产的优等品率;(Ⅱ)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数ξ的分布列及其数学期望()E ξ;(Ⅲ)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率.(18)(本小题满分13分)已知函数32()4f x x ax =-+-(a ∈R ).(19)(本小题满分13分)已知椭圆M 的对称轴为坐标轴, 且抛物线2y =的焦点是椭圆M 的一个焦点.(Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中点P 在椭圆M 上,O 为坐标原点. 求点O 到直线l 的距离的最小值.(20)(本小题满分14分) 已知每项均是正整数的数列123100,,,,a a a a ,其中等于i 的项有i k 个(1,2,3)i =,设j j k k k b +++= 21(1,2,3)j =,12()100m g m b b b m =+++-(1,2,3).m =(Ⅰ)设数列1240,30,k k ==34510020,10,...0k k k k =====,求(1),(2),(3),(4)gg g g;(Ⅱ)若123100,,,,a a a a 中最大的项为50, 比较(),(1)g m g m +的大小; (Ⅲ)若12100200a a a +++=,求函数)(m g 的最小值.G BCEF昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试卷 参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符二、填空题(本大题共6小题,每小题5分,共30分.) (9)4 (10)22(5)16x y -+=(11) 3(12)4 (13)2; [-9,9] (14) 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)(15)(本小题满分13分)解:(Ⅰ)由sin 0x ≠得πx k ≠(k ∈Z ),故()f x 的定义域为{x ∈R |π,x k ≠k ∈Z }.…………………2分因为1sin cos )2sin sin 32()(2+⋅-=xxx x x f 2cos )cos 1x x x =-⋅+ 2cos 2x x -π2sin(2)6x =-,………………………………6分所以()f x 的最小正周期2ππ2T ==.…………………7分 (II )由 5[,],2[,],2[,],422636x x x πππππππ挝-?…………..9分 当52,,()1662x x f x πππ-==即时取得最小值,…………….11分 当2,,()2623x x f x πππ-==即时取得最大值.……………….13分 (16)(本小题满分14分) 解:(I )连接OF .由ABCD 是正方形可知,点O 为BD 中点. 又F 为BE 的中点,所以OF ∥DE ………………….2分 又,,OF ACF DEACF 平面平面趟所以DE ∥平面ACF ………….4分(II) 证明:由EC ABCD BD ABCD 底面,底面,^? 所以,EC BD ^由ABCD 是正方形可知, ,AC BD ^又=,,AC EC C AC EC ACE 平面,翘所以,BD ACE 平面^………………………………..8分又AE ACE 平面,Ì所以BD AE ^…………………………………………..9分(III)解法一:在线段EO 上存在点G ,使CG BDE 平面^. 理由如下: 如图,取EO 中点G ,连接CG .在四棱锥E ABCD -中,,2AB CO AB CE ===, 所以CG EO ^.…………………………………………………………………..11分 由(II )可知,,BD ACE 平面^而,BD BDE 平面Ì 所以,,ACE BDE ACE BDE EO 平面平面且平面平面,^?因为,CG EO CG ACE 平面,^?所以CG BDE 平面^…………………………………………………………. 13分 故在线段EO 上存在点G ,使CG BDE 平面^.由G 为EO 中点,得1.2EG EO =…………………………………………… 14分 解法二:y由EC ABCD 底面,^且底面ABCD 建立空间直角坐标系,C DBE -由已知,AB =设(0)CE a a =>,则(0,0,0),,0,0),,0),(0,0,),C D B E a(,,0),,,0),(0,,),,,).2222O a a BD BE a EO a a uu u r uuruu u r =-=-=-设G 为线段EO 上一点,且(01)EGEOλλ=<<,则,),22EG EO a a a λλλλuuu r uu u r ==-,,(1)),22CG CE EO a a a λλλλuuu r uur uu u r =+=-…………………………..12分由题意,若线段EO 上存在点G ,使CG BDE 平面^,则CG BD ^uuu r uu u r ,CG BE ^uu u r uur.所以,221(1)0,0,12a a λλλ解得,()-+-==?, 故在线段EO 上存在点G ,使CG BDE 平面^,且1.2EG EO =…………………… 14分 (17)(本小题满分13分)解:(I )甲厂抽取的样本中优等品有6件,优等品率为63.105= 乙厂抽取的样本中优等品有5件,优等品率为51.102=………………..2分 (II )ξ的取值为0,1,2,3.0312555533101015(0),(1),1212C C C C P P C C ξξ⋅⋅======21355533101051(2),(3)1212C C C P P C C ξξ⋅====== 所以ξ的分布列为故155130123.121212122E ξξ=⨯+⨯+⨯+⨯=的数学期望为()……………………9分(III) 抽取的优等品数甲厂恰比乙厂多2件包括2个事件,即A=“抽取的优等品数甲厂2件,乙厂0件”,B=“抽取的优等品数甲厂3件,乙厂1件”2200333321127()()()()()5522500P A C C =⨯=331123331181()()()()5221000P B C C =⨯=抽取的优等品数甲厂恰比乙厂多2件的概率为278127()().5001000200P A P B +=+=…13分 (18)(本小题满分13分)解:(I ).23)(2ax x x f +-=' …………………………. ……………1分根据题意,(1)tan1,321, 2.4f a a π'==∴-+==即 …………………3分 此时,32()24f x x x =-+-,则2()34f x x x '=-+. 令124'()00,.f x x x ===,得 …………………………………………………………………………………………. 6分∴当[]1,1x ∈-时,()f x 最小值为()04f =-. ………………………7分 (II )).32(3)(a x x x f --='①若0,0,()0,()(0,)a x f x f x '><∴+∞≤当时在上单调递减. 又(0)4,0,() 4.f x f x =-><-则当时000,0,()0.a x f x ∴>>当≤时不存在使…………………………………………..10分②若220,0,()0;,()0.33a aa x f x x f x ''><<>><则当时当时从而)(x f 在(0,23a )上单调递增,在(23a,+)∞上单调递减..4274494278)32()(,),0(333max-=-+-==+∞∈∴a a a a f x f x 时当根据题意,33440,27. 3.27a a a ->>∴>即 …………….............................. 13分 综上,a 的取值范围是(3,)+∞. (19)(本小题满分13分)解:(I )由已知抛物线的焦点为,故设椭圆方程为22221(0)x y a b a b +=>>,则22, 2.2c e a b ====由得所以椭圆M 的方程为22 1.42x y +=……5分 (II )当直线l 斜率存在时,设直线方程为y kx m =+,则由22,1.42y kx m x y=+⎧⎪⎨+=⎪⎩ 消去y 得,222(12)4240k x kmx m +++-=, …………………6分222222164(12)(24)8(24)0k m k m k m ∆=-+-=+->, ①…………7分设AB P 、、点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则: 012012122242,()21212km mx x x y y y k x x m k k =+=-=+=++=++,…………8分由于点P在椭圆M上,所以2200142x y+=. ……… 9分从而2222222421(12)(12)k m mk k+=++,化简得22212m k=+,经检验满足①式.………10分又点O到直线l的距离为:2d===≥=………11分当且仅当0k=时等号成立………12分当直线l无斜率时,由对称性知,点P一定在x轴上,从而点P的坐标为(2,0)(2,0)-或,直线l的方程为1x=±,所以点O到直线l的距离为1 . 所以点O到直线l的距离最小值为2. ………13分(20)(本小题满分14分)解: (I) 因为数列1240,30,k k==320,k=410k=,所以123440,70,90,100b b b b====,所以(1)60,(2)90,(3)100,(4)100g g g g=-=-=-=-…………………4分(II) 一方面,1(1)()100mg m g m b++-=-,根据j b的含义知1100mb+≤,故0)()1(≤-+mgmg,即)1()(+≥mgmg,①当且仅当1100mb+=时取等号.因为123100,,,,a a a a中最大的项为50,所以当50m≥时必有100mb=,所以(1)(2)(49)(50)(51)g g g g g>>>===即当149m≤<时,有()(1)g m g m>+;当49m≥时,有()(1)g m g m=+…9分(III )设M 为{}12100,,,a a a 中的最大值.由(II )可以知道,()g m 的最小值为()g M . 根据题意,123100,M M b k k k k =++++=L123123123....M k k k M k a a a a ++++=++++L 下面计算()g M 的值.123()100M g M b b b b M =++++-1231(100)(100)(100)(100)M b b b b -=-+-+-++- 233445()()()()M M M M k k k k k k k k k k =----+----+----++-23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++123100()M a a a a b =-+++++123100()100a a a a =-+++++,∵123100200a a a a ++++= , ∴()100g M =-,∴()g m 最小值为100-. ………………………………………….14分昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试 卷(理科)(满分150分,考试时间 120分钟)2013.1考生须知: 1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
北京市2013届高三上学期期末数学试卷分类汇编三角函数一、选择、填空题1.【北京市昌平区2013届高三上学期期末理】在ABC △中,若b =,1c =,tan B =,则a =.【答案】3【解读】由tan 0B =>,知02B π<<,得sin B =,1cos 3B =,由余弦定理可得2221cos 23a c b B ac +-==,即218123a a +-=,整理得232210a a --=,解得3a =或73a =-(舍去)。
2.【北京市东城区2013届高三上学期期末理】若3sin 5α=-,且tan 0α>,则cos α=.【答案】45-【解读】因为3sin 05α=-<,tan 0α>所以α为第三象限,所以cos 0α<,即4cos 5α==-。
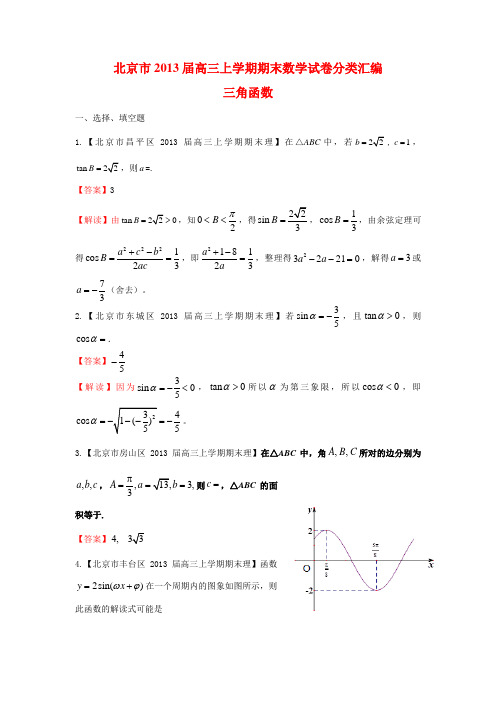
3.【北京市房山区2013届高三上学期期末理】在△ABC 中,角C B A ,,所对的边分别为c b a ,,,,3,3A a b π===则=c ,△ABC 的面积等于.【答案】4,4.【北京市丰台区2013届高三上学期期末理】函数2sin()y x ωϕ=+在一个周期内的图象如图所示,则此函数的解读式可能是(A) 2sin(2)4y x π=-(B) 2sin(2)4y x π=+ (C) 32sin()8y x π=+ (D) 72sin()216x y π=+【答案】B【解读】由图象可知52882T πππ=-=,所以函数的周期T π=,又2T ππω==,所以2ω=。
所以2sin(2)y x ϕ=+,又()2sin(2)288y f ππϕ==⨯+=,所以sin()14πϕ+=,即2,42k k Z ππϕπ+=+∈,所以24k πϕπ=+,所以2sin(2)4y x π=+,选B.5.【北京市石景山区2013届高三上学期期末理】在ABC ∆中,若2,60,a B b =∠=︒=,则BC 边上的高等于.【解读】由余弦定理得2222cos 60b a c ac =+-,即2174222c c =+-⨯⨯整理得2230c c --=,解得3c =。
昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试 卷(理科) (满分150分,考试时间 120分钟)2013.1考生须知: 1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
2. 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。
3. 答题卡上第I 卷(选择题)必须用2B 铅笔作答,第II 卷(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
请按照题号顺序在各题目的答题区内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
4. 修改时,选择题部分用塑料橡皮擦涂干净,不得使用涂改液。
保持答题卡整洁,不要折叠、折皱、破损。
不得在答题卡上做任何标记。
5. 考试结束后,考生务必将答题卡交监考老师收回,试卷自己妥善保存。
第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A 等于 A .{|2}x x > B .{}20<<x xC .{}21<<x xD .{|01}x x <<(2)“2a =”是“直线214ay ax y x =-+=-与垂直”的 A. 充分不必要条件 B 必要不充分条件C. 充要条件D.既不充分也不必要条件 (3)已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是A.(0,1)B. (1,2)C. (2,3)D. (3,4) (4)设不等式组22,42x y x y -+≥≥-⎧⎪⎨⎪⎩0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线+2=0y 的距离大于2的概率是A. 413B.513C.825D.925(5)设n S 是公差不为0的等差数列{}n a 的前n 项和,且124,,S S S 成等比数列,则21a a 等于 A.1 B. 2 C. 3D. 4(6)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为A. 24B. 36C. 48D.60(7)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为A. 10+ B.10+C. 14+D.14+(8)已知函数:①2()2f x x x =-+,②()cos()22xf x ππ=-,③12()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是命题:p ()f x 是奇函数; 命题:q (1)f x +在(0),1上是增函数;命题:r 11()22f >; 命题:s ()f x 的图像关于直线1x =对称A .命题p q 、B .命题q s 、C .命题r s 、D .命题p r 、第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.(9)若221aii i =-+-,其中i 是虚数单位,则实数a 的值是____________.(10)以双曲线221916x y -=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.(11)在ABC △中,若b =1c =,tan B =a = . (12)已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .(13)在Rt ABC ∆中,90C ︒∠=,4,2AC BC ==,D 是BC 的中点,那么()AB AC AD -∙=uu u r uuu r uuu r____________;若E 是AB 的中点,P 是ABC ∆(包括边界)内任一点.则AD EP ⋅uuu r uu r的取值范围是___________.(14)在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则① 到坐标原点O 的“折线距离”不超过2的点的集合所构成的平面图形面积是_________;② 坐标原点O 与直线20x y --=上任意一点的“折线距离”的最小值是_____________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知函数1sin cos )2sin sin 32()(2+⋅-=xxx x x f .(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42ππ上的最值.OFEDCBA(16) (本小题满分14分)在四棱锥E ABCD -中,底面ABCD 是正方形,,AC BD O 与交于点EC ABCD F 底面,^为BE 的中点. (Ⅰ)求证:DE ∥平面ACF ;(Ⅱ)求证:BD AE ^;(Ⅲ)若,AB =在线段EO 上是否存在点G ,使CG BDE 平面^?若存在,求出EGEO的值,若不存在,请说明理由.(17)(本小题满分13分)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: 甲厂乙厂93 9 6 5 8 18 4 5 6 9 0 31 5 0 3 21 0 3规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品. (Ⅰ)试用上述样本数据估计甲、乙两厂生产的优等品率;(Ⅱ)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数ξ的分布列及其数学期望()E ξ;(Ⅲ)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率.(18)(本小题满分13分)已知函数32()4f x x ax =-+-(a ∈R ).(19)(本小题满分13分)已知椭圆M 的对称轴为坐标轴, 离心率为2且抛物线2y =的焦点是椭圆M 的一个焦点.(Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中点P 在椭圆M 上,O 为坐标原点. 求点O 到直线l 的距离的最小值.(20)(本小题满分14分)已知每项均是正整数的数列123100,,,,a a a a ,其中等于i 的项有i k 个(1,2,3)i = ,设j j k k k b +++= 21(1,2,3)j = ,12()100m g m b b b m =+++- (1,2,3).m = (Ⅰ)设数列1240,30,k k ==34510020,10,...0k k k k =====,求(1),(2),(3),(4)g g g g;(Ⅱ)若123100,,,,a a a a 中最大的项为50, 比较(),(1)g m g m +的大小; (Ⅲ)若12100200a a a +++= ,求函数)(m g 的最小值.昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试卷 参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符二、填空题(本大题共6小题,每小题5分,共30分.) (9)4 (10)22(5)16x y -+=(11) 3 (12)4(13) 2; [-9,9] (14) 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)(15)(本小题满分13分)解:(Ⅰ)由sin 0x ≠得πx k ≠(k ∈Z ),故()f x 的定义域为{x ∈R |π,x k ≠k ∈Z }.…………………2分因为1sin cos )2sin sin 32()(2+⋅-=xxx x x f2cos )cos 1x x x =-⋅+2cos 2x x -π2sin(2)6x =-,………………………………6分所以()f x 的最小正周期2ππ2T ==.…………………7分 (II )由 5[,],2[,],2[,],422636x x x πππππππ挝- …………..9分 当52,,()1662x x f x πππ-==即时取得最小值,…………….11分 当2,,()2623x x f x πππ-==即时取得最大值.……………….13分G ABC DEFO(16)(本小题满分14分) 解:(I )连接OF .由ABCD 是正方形可知,点O 为BD 中点. 又F 为BE 的中点,所以OF ∥DE ………………….2分 又,,OF ACF DEACF 平面平面趟所以DE ∥平面ACF ………….4分(II) 证明:由EC ABCD BD ABCD 底面,底面,^ 所以,EC BD ^由ABCD 是正方形可知, ,AC BD ^又=,,AC EC C AC ECACE 平面,翘 所以,BD ACE 平面^………………………………..8分又AE ACE 平面,Ì所以BD AE ^…………………………………………..9分(III)解法一:在线段EO 上存在点G ,使CG BDE 平面^. 理由如下: 如图,取EO 中点G ,连接CG . 在四棱锥E ABCD -中,,AB CO AB CE ===, 所以CG EO ^.…………………………………………………………………..11分 由(II )可知,,BD ACE 平面^而,BD BDE 平面Ì 所以,,ACE BDE ACE BDE EO 平面平面且平面平面,^? 因为,CG EO CG ACE 平面,^所以CG BDE 平面^…………………………………………………………. 13分 故在线段EO 上存在点G ,使CG BDE 平面^.由G 为EO 中点,得1.2EG EO =…………………………………………… 14分 解法二:y由EC ABCD 底面,^且底面ABCD 建立空间直角坐标系,C DBE -由已知,AB =设(0)CE a a =>,则(0,0,0),,0,0),,0),(0,0,),C D B E a(,,0),,,0),(0,,),(,,).2222O a a BD BE a EO a a uu u r uuruu u r =-=-=-设G 为线段EO 上一点,且(01)EGEOλλ=<<,则,),EG EO a a a λλuu u r uu u r ==-(,,(1)),22CG CE EO a a a λλλλuu u r uur uu u r =+=-…………………………..12分由题意,若线段EO 上存在点G ,使CG BDE 平面^,则CG BD ^uu u r uu u r ,CG BE ^uu u r uur.所以,221(1)0,0,12a a λλλ解得,()-+-==, 故在线段EO 上存在点G ,使CG BDE 平面^,且1.2EG EO =…………………… 14分 (17)(本小题满分13分)解:(I )甲厂抽取的样本中优等品有6件,优等品率为63.105= 乙厂抽取的样本中优等品有5件,优等品率为51.102=………………..2分(II )ξ的取值为0,1,2,3.0312555533101015(0),(1),1212C C C C P P C C ξξ⋅⋅======21355533101051(2),(3)1212C C C P P C C ξξ⋅====== 所以ξ的分布列为故155130123.121212122E ξξ=⨯+⨯+⨯+⨯=的数学期望为()……………………9分(III) 抽取的优等品数甲厂恰比乙厂多2件包括2个事件,即A=“抽取的优等品数甲厂2件,乙厂0件”,B=“抽取的优等品数甲厂3件,乙厂1件”2200333321127()()()()()5522500P A C C =⨯=331123331181()()()()5221000P B C C =⨯=抽取的优等品数甲厂恰比乙厂多2件的概率为278127()().5001000200P A P B +=+=…13分 (18)(本小题满分13分)解:(I ).23)(2ax x x f +-=' …………………………. ……………1分根据题意,(1)tan1,321, 2.4f a a π'==∴-+==即 …………………3分 此时,32()24f x x x =-+-,则2()34f x x x '=-+. 令124'()00,.f x x x ===,得 …………………………………………………………………………………………. 6分∴当[]1,1x ∈-时,()f x 最小值为()04f =-. ………………………7分 (II )).32(3)(a x x x f --='①若0,0,()0,()(0,)a x f x f x '><∴+∞≤当时在上单调递减. 又(0)4,0,() 4.f x f x =-><-则当时000,0,()0.a x f x ∴>>当≤时不存在使…………………………………………..10分②若220,0,()0;,()0.33a aa x f x x f x ''><<>><则当时当时从而)(x f 在(0,23a )上单调递增,在(23a,+)∞上单调递减..4274494278)32()(,),0(333m ax-=-+-==+∞∈∴a a a a f x f x 时当根据题意,33440,27. 3.27a a a ->>∴>即 …………….............................. 13分 综上,a 的取值范围是(3,)+∞. (19)(本小题满分13分)解:(I )由已知抛物线的焦点为,故设椭圆方程为22221(0)x y a b a b+=>>,则22, 2.c e a b ====由得所以椭圆M 的方程为22 1.42x y +=……5分 (II )当直线l 斜率存在时,设直线方程为y kx m =+,则由22,1.42y kx m x y=+⎧⎪⎨+=⎪⎩ 消去y 得,222(12)4240k x kmx m +++-=, …………………6分222222164(12)(24)8(24)0k m k m k m ∆=-+-=+->, ①…………7分 设A B P 、、点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则: 012012122242,()21212km mx x x y y y k x x m k k =+=-=+=++=++,…………8分由于点P在椭圆M上,所以2200142x y+=. ……… 9分从而2222222421(12)(12)k m mk k+=++,化简得22212m k=+,经检验满足①式.………10分又点O到直线l的距离为:d====………11分当且仅当0k=时等号成立………12分当直线l无斜率时,由对称性知,点P一定在x轴上,从而点P的坐标为(2,0)(2,0)-或,直线l的方程为1x=±,所以点O到直线l的距离为1 . 所以点O到直线l的距离最小值为2. ………13分(20)(本小题满分14分)解: (I) 因为数列1240,30,k k==320,k=410k=,所以123440,70,90,100b b b b====,所以(1)60,(2)90,(3)100,(4)100g g g g=-=-=-=-…………………4分(II) 一方面,1(1)()100mg m g m b++-=-,根据j b的含义知1100mb+≤,故0)()1(≤-+mgmg,即)1()(+≥mgmg,①当且仅当1100mb+=时取等号.因为123100,,,,a a a a中最大的项为50,所以当50m≥时必有100mb=,所以(1)(2)(49)(50)(51)g g g g g>>>===即当149m≤<时,有()(1)g m g m>+;当49m≥时,有()(1)g m g m=+…9分(III )设M 为{}12100,,,a a a 中的最大值. 由(II )可以知道,()g m 的最小值为()g M . 根据题意,123100,M M b k k k k =++++=L123123123....M k k k M k a a a a ++++=++++L 下面计算()g M 的值.123()100M g M b b b b M =++++-1231(100)(100)(100)(100)M b b b b -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++- 23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++123100()M a a a a b =-+++++ 123100()100a a a a =-+++++ ,∵123100200a a a a ++++= , ∴()100g M =-, ∴()g m 最小值为100-. ………………………………………….14分。
数 学 试 卷(理科)(满分150分,考试时间 120分钟)2013.1考生须知: 1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
2. 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。
3. 答题卡上第I 卷(选择题)必须用2B 铅笔作答,第II 卷(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
请按照题号顺序在各题目的答题区内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
4. 修改时,选择题部分用塑料橡皮擦涂干净,不得使用涂改液。
保持答题卡整洁,不要折叠、折皱、破损。
不得在答题卡上做任何标记。
5. 考试结束后,考生务必将答题卡交监考老师收回,试卷自己妥善保存。
第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A 等于 A .{|2}x x > B .{}20<<x xC .{}21<<x xD .{|01}x x <<(2)“2a =”是“直线214ay ax y x =-+=-与垂直”的 A. 充分不必要条件 B 必要不充分条件C. 充要条件D.既不充分也不必要条件 (3)已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是A.(0,1)B. (1,2)C. (2,3)D. (3,4) (4)设不等式组22,42x y x y -+≥≥-⎧⎪⎨⎪⎩0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线+2=0y 的距离大于2的概率是A.413B.513C.825D.925(5)设n S 是公差不为0的等差数列{}n a 的前n 项和,且124,,S S S 成等比数列,则21a a 等于A.1B. 2C. 3D. 4(6)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为A. 24B. 36C. 48D.60(7)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为A. 1032+ B .102342+ C. 142342+ D. 144342+(8)已知函数:①2()2f x x x =-+,②()cos()22xf x ππ=-,③12()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是命题:p ()f x 是奇函数; 命题:q (1)f x +在(0),1上是增函数;命题:r 11()22f >; 命题:s ()f x 的图像关于直线1x =对称A .命题p q 、B .命题q s 、C .命题r s 、D .命题p r 、第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.(9)若221aii i=-+-,其中i 是虚数单位,则实数a 的值是____________.(10)以双曲线221916x y -=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.(11)在ABC △中,若22b =1c =,tan 22B =,则a = . (12)已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .(13)在Rt ABC ∆中,90C ︒∠=,4,2AC BC ==,D 是BC 的中点,那么()AB AC AD -•= ____________;若E 是AB 的OFEDCBA中点,P 是ABC ∆(包括边界)内任一点.则AD EP ⋅的取值范围是___________. (14)在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则① 到坐标原点O 的“折线距离”不超过2的点的集合所构成的平面图形面积是_________;② 坐标原点O与直线20x y --=上任意一点的“折线距离”的最小值是_____________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知函数1sin cos )2sin sin 32()(2+⋅-=xxx x x f .(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42ππ上的最值.(16) (本小题满分14分)在四棱锥E ABCD 中,底面ABCD 是正方形,,AC BD O 与交于点EC ABCD F 底面,为BE 的中点. (Ⅰ)求证:DE ∥平面ACF ; (Ⅱ)求证:BD AE ;(Ⅲ)若2,ABCE 在线段EO 上是否存在点G ,使CG BDE 平面?若存在,求出EGEO的值,若不存在,请说明理由.(17)(本小题满分13分)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: 甲厂乙厂9 03 9 6 5 8 1 8456 9 0 3 1 5 0 3 2 1 0 3规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品. (Ⅰ)试用上述样本数据估计甲、乙两厂生产的优等品率;(Ⅱ)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数ξ的分布列及其数学期望()E ξ;(Ⅲ)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率.(18)(本小题满分13分)已知函数32()4f x x ax =-+-(a ∈R ).(19)(本小题满分13分)已知椭圆M 的对称轴为坐标轴, 离心率为2且抛物线2y =的焦点是椭圆M 的一个焦点.(Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中点P 在椭圆M 上,O 为坐标原点. 求点O 到直线l 的距离的最小值.(20)(本小题满分14分) 已知每项均是正整数的数列123100,,,,a a a a ,其中等于i 的项有i k 个(1,2,3)i =,设j j k k k b +++= 21(1,2,3)j =,12()100m g m b b b m =+++-(1,2,3).m =(Ⅰ)设数列1240,30,k k ==34510020,10,...0k k k k =====,求(1),(2),(3),(4)g g g g ;(Ⅱ)若123100,,,,a a a a 中最大的项为50, 比较(),(1)g m g m +的大小; (Ⅲ)若12100200a a a +++=,求函数)(m g 的最小值.昌平区2012-2013学年第一学期高三年级期末质量抽测数 学 试卷 参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符二、填空题(本大题共6小题,每小题5分,共30分.) (9)4 (10)22(5)16x y -+=(11) 3 (12)4(13) 2; [-9,9] (14) 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.) (15)(本小题满分13分)解:(Ⅰ)由sin 0x ≠得πx k ≠(k ∈Z ),故()f x 的定义域为{x ∈R |π,x k ≠k ∈Z }.…………………2分因为1sin cos )2sin sin 32()(2+⋅-=xxx x x f2cos )cos 1x x x =-⋅+2cos 2x x -π2sin(2)6x =-,………………………………6分所以()f x 的最小正周期2ππ2T ==.…………………7分G ABC DEFO(II )由 5[,],2[,],2[,],422636x x x πππππππ…………..9分 当52,,()1662x x f x πππ-==即时取得最小值,…………….11分 当2,,()2623x x f x πππ-==即时取得最大值.……………….13分 (16)(本小题满分14分)解:(I )连接OF .由ABCD 是正方形可知,点O 为BD 中点. 又F 为BE 的中点,所以OF ∥DE ………………….2分 又,,OFACF DE ACF 平面平面所以DE ∥平面ACF ………….4分 (II) 证明:由EC ABCD BD ABCD 底面,底面,所以,ECBD由ABCD 是正方形可知, ,ACBD又=,,ACEC C AC EC ACE 平面,所以,BD ACE 平面………………………………..8分又AEACE 平面,所以BDAE …………………………………………..9分(III)解法一:在线段EO 上存在点G ,使CGBDE 平面. 理由如下:如图,取EO 中点G ,连接CG . 在四棱锥E ABCD 中,22,AB CE COAB CE ,所以CGEO .…………………………………………………………………..11分由(II )可知,,BD ACE 平面而,BDBDE 平面所以,,ACE BDE ACE BDE EO 平面平面且平面平面,因为,CG EO CGACE 平面,所以CGBDE 平面…………………………………………………………. 13分y故在线段EO 上存在点G ,使CGBDE 平面.由G 为EO 中点,得1.2EG EO …………………………………………… 14分 解法二: 由ECABCD 底面,且底面ABCD 建立空间直角坐标系,CDBE由已知2,ABCE 设(0)CEa a,则(0,0,0),,0,0),,0),(0,0,),C D B E a22(,,0),(2,2,0),(0,2,),(,,).2222O a a BD a a BE a a EO a a a 设G 为线段EO 上一点,且(01)EGEOλλ,则22(,,),2EG EO a a a λλλλ 22(,,(1)),22CG CE EO a a a λλλλ…………………………..12分 由题意,若线段EO 上存在点G ,使CG BDE 平面,则CGBD ,CGBE .所以,221(1)0,0,12aa λλλ解得,(), 故在线段EO 上存在点G ,使CG BDE 平面,且1.2EGEO…………………… 14分 (17)(本小题满分13分)解:(I )甲厂抽取的样本中优等品有6件,优等品率为63.105= 乙厂抽取的样本中优等品有5件,优等品率为51.102=………………..2分(II )ξ的取值为0,1,2,3.0312555533101015(0),(1),1212C C C C P P C C ξξ⋅⋅======21355533101051(2),(3)1212C C C P P C C ξξ⋅====== 所以ξ的分布列为故155130123.121212122E ξξ=⨯+⨯+⨯+⨯=的数学期望为()……………………9分(III) 抽取的优等品数甲厂恰比乙厂多2件包括2个事件,即A=“抽取的优等品数甲厂2件,乙厂0件”,B=“抽取的优等品数甲厂3件,乙厂1件”2200333321127()()()()()5522500P A C C =⨯=331123331181()()()()5221000P B C C =⨯=抽取的优等品数甲厂恰比乙厂多2件的概率为278127()().5001000200P A P B +=+=…13分 (18)(本小题满分13分)解:(I ).23)(2ax x x f +-=' …………………………. ……………1分根据题意,(1)tan1,321, 2.4f a a π'==∴-+==即 …………………3分 此时,32()24f x x x =-+-,则2()34f x x x '=-+. 令124'()00,.f x x x ===,得…………………………………………………………………………………………. 6分∴当[]1,1x ∈-时,()f x 最小值为()04f =-. ………………………7分 (II )).32(3)(a x x x f --=' ①若0,0,()0,()(0,)a x f x f x '><∴+∞≤当时在上单调递减. 又(0)4,0,() 4.f x f x =-><-则当时000,0,()0.a x f x ∴>>当≤时不存在使…………………………………………..10分②若220,0,()0;,()0.33a aa x f x x f x ''><<>><则当时当时从而)(x f 在(0,23a )上单调递增,在(23a,+)∞上单调递减. .4274494278)32()(,),0(333max-=-+-==+∞∈∴a a a a f xf x 时当根据题意,33440,27. 3.27a a a ->>∴>即 …………….............................. 13分综上,a 的取值范围是(3,)+∞. (19)(本小题满分13分)解:(I )由已知抛物线的焦点为,故设椭圆方程为22221(0)x y a b a b +=>>, 则22, 2.2c e a b ====由得所以椭圆M 的方程为22 1.42x y +=……5分(II )当直线l 斜率存在时,设直线方程为y kx m =+,则由22,1.42y kx m x y =+⎧⎪⎨+=⎪⎩消去y 得,222(12)4240k x kmx m +++-=, …………………6分222222164(12)(24)8(24)0k m k m k m ∆=-+-=+->, ①…………7分设AB P 、、点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则: 012012122242,()21212km mx x x y y y k x x m k k =+=-=+=++=++,…………8分 由于点P 在椭圆M 上,所以2200142x y +=. ……… 9分 从而2222222421(12)(12)k m m k k +=++,化简得22212m k =+,经检验满足①式. ………10分 又点O 到直线l 的距离为:2d ===≥= ………11分 当且仅当0k =时等号成立 ………12分当直线l 无斜率时,由对称性知,点P 一定在x 轴上,从而点P 的坐标为(2,0)(2,0)-或,直线l 的方程为1x =±,所以点O 到直线l 的距离为1 . 所以点O 到直线l的距离最小值为2. ………13分 (20)(本小题满分14分)解: (I) 因为数列1240,30,k k ==320,k =410k =, 所以123440,70,90,100b b b b ====,所以(1)60,(2)90,(3)100,(4)100g g g g =-=-=-=- …………………4分 (II) 一方面,1(1)()100m g m g m b ++-=-,根据j b 的含义知1100m b +≤,故0)()1(≤-+m g m g ,即 )1()(+≥m g m g , ①11 当且仅当1100m b +=时取等号.因为123100,,,,a a a a 中最大的项为50,所以当50m ≥时必有100m b =, 所以(1)(2)(49)(50)(51)g g g g g >>>===即当149m ≤<时,有()(1)g m g m >+; 当49m ≥时,有()(1)g m g m =+ …9分 (III )设M 为{}12100,,,a a a 中的最大值.由(II )可以知道,()g m 的最小值为()g M .根据题意,123100,M M b k k k k =++++= 12312310023....M k k k Mk a a a a ++++=++++下面计算()g M 的值.123()100M g M b b b b M =++++-1231(100)(100)(100)(100)M b b b b -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++-23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++123100()M a a a a b =-+++++123100()100a a a a =-+++++, ∵123100200a a a a ++++= , ∴()100g M =-,∴()g m 最小值为100-. ………………………………………….14分。
(满分150分,考试时间 120分钟)2013.1
考生须知: 1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
2. 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。
3. 答题卡上第I 卷(选择题)必须用2B 铅笔作答,第II 卷(非选择题)必须用黑色字迹的签字笔作
答,作图时可以使用2B 铅笔。
请按照题号顺序在各题目的答题区内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
4. 修改时,选择题部分用塑料橡皮擦涂干净,不得使用涂改液。
保持答题卡整洁,不要折叠、
折皱、破损。
不得在答题卡上做任何标记。
5. 考试结束后,考生务必将答题卡交监考老师收回,试卷自己妥善保存。
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
(1)设集合{}
{}>1,|(2)0A x x B x x x ==-<,则B A 等于 A .{|2}x x > B .{}
20<<x x
C .{}21<<x x
D .{|01}x x <<
(2)“2a =”是“直线214
a
y ax y x =-+=
-与垂直”的 A. 充分不必要条件 B 必要不充分条件
C. 充要条件
D.既不充分也不必要条件 (3)已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是
A.(0,1)
B. (1,2)
C. (2,3)
D. (3,4)
(4)设不等式组22,42x y x y -+≥≥-⎧⎪
⎨⎪⎩
0≤, 表示的平面区域为D .在区域D 内随机取一个点,则此点到直线
+2=0y 的距离大于2的概率是
A.
413
B.
513
C.
825
D.
925
(5)设n S 是公差不为0的等差数列{}n a 的前n 项和,且124,,S S S 成等比数列,则
2
1
a a 等于 A.1 B. 2 C. 3
D. 4
(6)在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为
A. 24
B. 36
C. 48
D.60 (7)已知一个空间几何体的三视图如图所示,根据图中标出的尺
寸,可得这个几何体的全面积为
A. 10+B
.10+
C. 14+
D.
14+(8)已知函数:①2
()2f x x x =-+,②()cos()22
x
f x π
π=-,③1
2()|1|f x x =-.则以下四个命题对已知的三个函数都能成立的是
命题:p ()f x 是奇函数; 命题:q (1)f x +在(0),1上是增函数;
命题:r 11
()22
f >; 命题:s ()f x 的图像关于直线1x =对称
A .命题p q 、
B .命题q s 、
C .命题r s
、
D .命题p r 、
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分. (9)若221ai
i i =-+-,其中i 是虚数单位,则实数
a 的值是
____________.
(10)以双曲线
22
1916
x y -=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.
(11)在ABC △
中,若b =1c =
,tan B =a = .
O
F
E
D
C
B
A
(12)已知某算法的流程图如图所示,则程序运行结束时输出的结果为 .
(13)在Rt ABC ∆中,90C ︒
∠=,4,2AC BC ==,D 是BC 的中点,那么()AB AC AD -∙=u u u r u u u r u u u r
____________;若E 是AB 的中点,P 是ABC ∆(包括边界)内任一点.则AD EP ⋅uuu r uu r
的取值范围是
___________.
(14)在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则
① 到坐标原点O 的“折线距离”不超过2的点的集合所构成的平面图形面积是_________; ② 坐标原点O
与直线20x y --=上任意一点的“折线距离”的最小值是_____________. 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知函数
1sin cos )2sin sin 32()(2+⋅-=x
x
x x x f .
(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42
ππ上的最值.
(16) (本小题满分14分)在四棱锥E ABCD -中,底面ABCD 是正方形,
,AC BD O 与交于点EC ABCD F 底面,^为BE 的中点. (Ⅰ)求证:
DE ∥平面ACF ;
(Ⅱ)求证:BD AE ^; (Ⅲ)
若,AB =
在线段EO 上是否存在点G ,
使C G B D E 平面^?若存在,求出
EG
EO
的值,若不存在,请说明理由.
(17)(本小题满分13分)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: 甲厂
乙厂
9
3 9 6 5 8 1 8
4
5
6 9 0 3 1 5 0 3 2 1 0 3
规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品. (Ⅰ)试用上述样本数据估计甲、乙两厂生产的优等品率;
(Ⅱ)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数ξ的分布列及其数学期望()E ξ;
(Ⅲ)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率.
(18)(本小题满分13分)已知函数32()4f x x ax =-+-(a ∈R ).
(19)(本小题满分13分)已知椭圆M 的对称轴为坐标轴, 离心率为
2
且抛物线
2y =的焦点是椭圆M 的一个焦点.
(Ⅰ)求椭圆M 的方程;
(Ⅱ)设直线l 与椭圆M 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中点P 在椭圆M 上,O 为坐标原点. 求点O 到直线l 的距离的最小值.
(20)(本小题满分14分)
已知每项均是正整数的数列123100,,,,a a a a ,其中等于i 的项有i k 个(1,2,3)i = ,设j j k k k b +++= 21(1,2,3)j =
,12()100m g m b b b m =+++- (1,2,3).m = (Ⅰ)设数列1240,30,k k ==34510020,10,...0k k k k =====,求(1),(2),(3),(4)g g g g ; (Ⅱ)若123100,,,,a a a a 中最大的项为50, 比较(),(1)g m g m +的大小;
(Ⅲ)若
12100200
a a a
+++=
,求函数)
(m
g的最小值.
所以()
f x的最小正周期
2π
π
2
T==.…………………7分
y
x
(III)解法一:
在线段EO 上存在点G ,使CG BDE 平面^. 理由如下: 如图,取EO 中点G ,连接CG . 在四棱锥E ABCD -
中,,2
AB CO AB === 所以
CG EO ^.…………………………………………………………………..11分
由(II )可知,,BD ACE 平面^而,BD BDE 平面Ì 所以,,ACE BDE ACE BDE EO 平面平面且平面平面,^?
因为,CG EO CG ACE 平面,^
所以CG BDE 平面^…………………………………………………………. 13分 故在线段EO 上存在点G ,使CG BDE 平面^.
由G 为EO 中点,得
1
.2
EG EO =…………………………………………… 14分
213
55533
101051
(2),(3)1212
C C C P P C C ξξ⋅====== 所以ξ的分布列为
故15513
0123.121212122E ξξ=⨯+⨯+⨯+⨯=的数学期望为(
)……………………9分
(II )).3
2(3)(a x x x f -
-=' ① 若0,0,()0,()(0,)a x f x f x '><∴+∞≤当时在上单调递减.
又(0)4,0,() 4.f x f x =-><-则当时
由于点P在椭圆M上,所以
22
001
42
x y
+=. ……… 9分
所以点O 到直线l 的距离最小值为2
. ………13分
(III )设M 为{}12100,,,a a a 中的最大值.
由(II )可以知道,()g m 的最小值为()g M .。