全国通用2017年高考数学大二轮专题复习第二编专题整合突破专题五立体几何第三讲空间向量与立体几何课件理
- 格式:ppt
- 大小:5.37 MB
- 文档页数:95
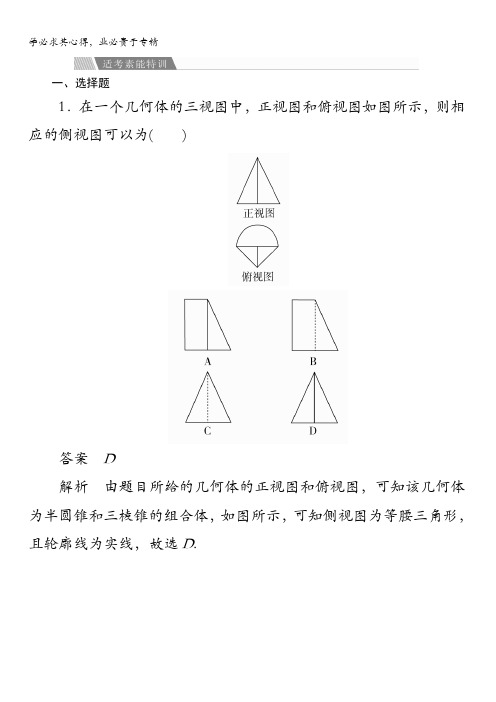
一、选择题1.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )答案D解析由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知侧视图为等腰三角形,且轮廓线为实线,故选D.2.[2016·重庆测试]某几何体的三视图如图所示,则该几何体的体积为( )A.错误!B。
错误!C.错误!D.错误!答案B解析依题意,题中的几何体是由一个直三棱柱与一个三棱锥所组成的,其中该直三棱柱的底面是一个直角三角形(腰长分别为1、2)、高为1;该三棱锥的底面是一个直角三角形(腰长分别为1、2)、高为1,因此该几何体的体积为错误!×2×1×1+错误!×错误!×2×1×1=错误!,选B 。
3.[2016·唐山统考]三棱锥P -ABC 中,PA⊥平面ABC 且PA =2,△ABC 是边长为错误!的等边三角形,则该三棱锥外接球的表面积为( ) A .4π3 B .4πC .8πD .20π 答案 C解析 由题意得,此三棱锥外接球即为以△ABC 为底面、以PA 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r =错误!×错误!×错误!=1,外接球球心到△ABC 的外接圆圆心的距离d =1,所以外接球的半径R =错误!=错误!,所以三棱锥外接球的表面积S =4πR 2=8π,故选C 。
4.[2016·武昌调研]某几何体的三视图如图所示,则该几何体的表面积为( )A.18+2πB.20+πC.20+π2D.16+π答案B解析由三视图可知,这个几何体是一个边长为2的正方体割去了相对边对应的两个半径为1、高为1的错误!圆柱体,其表面积相当于正方体五个面的面积与两个错误!圆柱的侧面积的和,即该几何体的表面积S=4×5+2×2π×1×1×错误!=20+π,故选B。

2017 年高考试题分类汇编之立体几何一、选择题(在每题给出的四个选项中,只有一项为哪一项切合题目要求的)1.( 2017 课标 I 理)某多面体的三视图如下图,此中正视图和左视图都由正方形和等腰直角三角形构成,正方形的边长为2 ,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形, 这些梯形的面积之和为() A.10B.12C.12D.16(第 1题)(第 2题)(第 3题)2.( 2017 课标 II1理)如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为()A.90B.63C.42D.363. ( 2017 北京理) 某四棱锥的三视图如下图,则该四棱锥的最长棱的长度为()A.3 2B.2 3C.2 2D.24.( 2017 课标 II 理)已知直三棱柱ABCA 1B 1C 1中, ABC 1200 , AB 2, BCCC 1 1,则异面直线AB 1 与 BC 1 所成角的余弦值为(3 15 C . 10 3) A. B.5D .2535. ( 2017 课标 III 理) 已知圆柱的高为 1,它的两个底面的圆周在直径为2 的同一个球的球面上,则该圆柱的体积为()A.B.3C.D .4246.( 2017 浙江)某几何体的三视图如下图(单位: cm ),则该几何体的体积 (单位: cm 3)是()A.2 1 B.3 C .31D.332227.( 2017 浙江)如图, 已知正四周体 D ABC (全部棱长均相等的三棱锥), P,Q, R 分别为 AB, BC, CA上的点, AP PB,BQCR 2 ,分别记二面角 D PR Q, DPQ R,D QRP 的平面角为 , ,QCRA则() A. B. C. D.O2OO1(第 6题)(第 7题)(第 8题)二、填空题(将正确的答案填在题中横线上)8.( 2017江苏)如图 ,在圆柱 O1 ,O2内有一个球 O ,该球与圆柱的上、下边及母线均相切.记圆柱 O1 , O2的体积为 V1,球 O 的体积为 V2 ,则V1的值是. V29. ( 2017 天津理)已知一个正方体的全部极点在一个球面上,若这个正方体的表面积为18 ,则这个球的积为.10. ( 2017 山东理)由一个长方体和两个1 圆柱体构成的几何体的三视图如右图,则该几何体的体积4为.(第10 题)(第11 题)11.( 2017课标I 理)如图,圆形纸片的圆心为O ,半径为5cm,该纸片上的等边三角形ABC 的中心为O.D,E,F为圆剪开后,分别以O 上的点,BC ,CA, ABDBC , ECA, FAB 分别是以 BC ,CA, AB 为底边的等腰三角形.沿虚线为折痕折起DBC , ECA , FAB ,使得 D , E, F 重合,获得三棱锥.当ABC 的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______.12. ( 2017课标III理)a,b 为空间中两条相互垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与 a, b都垂直,斜边AB 以直线AC 为旋转轴旋转,有以下结论:①当直线AB 与a 成 600角时,AB 与b 成300角;②当直线AB 与a成600角时,AB 与b 成600角;③直线AB 与a所成角的最小值为450;④直线AB与 a 所成角的最小值为600.________.(填写全部正确结论的编号)此中正确的选项是三、解答题(应写出必需的文字说明、证明过程或演算步骤)13.( 2017 课标I 理)如图,在四棱锥P ABCD 中,AB // CD,且BAP CDP90o.( 1)证明:平面PAB平面PAD ;( 2)若PA PD AB DC ,APD90 0,求二面角A PB C 的余弦值.14.( 2017 课标II 理)如图,四棱锥P ABCD 中,侧面PAD 为等比三角形且垂直于底面ABCD ,AB BC 1AD ,BAD ABC90o , E 是PD 的中点。
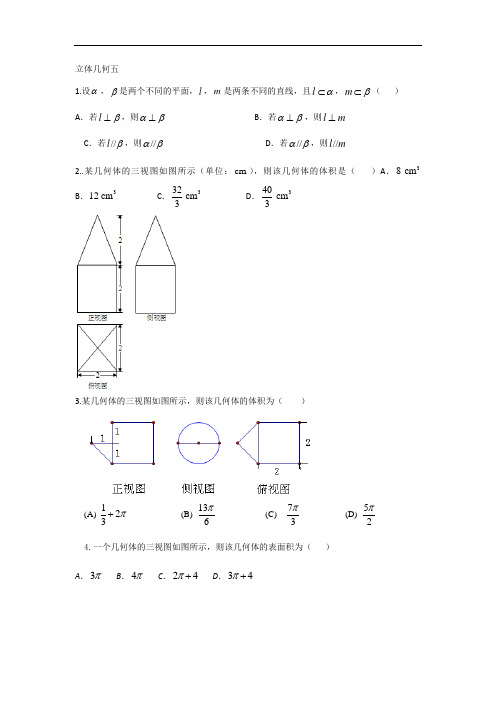
立体几何五1.设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m2..某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cm B .123cm C .3233cm D .4033cm3.某几何体的三视图如图所示,则该几何体的体积为( )(A)123π+ (B) 136π (C) 73π (D) 52π4.一个几何体的三视图如图所示,则该几何体的表面积为( ) A .3π B .4π C .24π+ D .34π+5.若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内, l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交 6.12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( ) A .p 是q 的充分条件,但不是q 的必要条件 B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件7.如图,三棱锥P -ABC 中,PA ⊥平面ABC ,1,1,2,60PA AB AC BAC ===∠=o.(Ⅰ)求三棱锥P -ABC 的体积;(Ⅱ)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PMMC的值.8.(本小题满分14分)如图,在三棱锥V C -AB 中,平面V AB ⊥平面C AB ,V ∆AB 为等边三角形,C C A ⊥B 且C C A =B =O ,M 分别为AB ,V A 的中点.(I )求证:V //B 平面C MO ; (II )求证:平面C MO ⊥平面V AB ; (III )求三棱锥V C -AB 的体积.1.A2. C3.B4.D5.A6.A 7(Ⅰ)6(Ⅱ)13PM MC = (Ⅰ)解:由题设AB =1,,2=AC60=∠BAC可得ABC S ∆︒⋅⋅⋅=60sin 21AC AB 23=.由⊥PA 面ABC 可知PA 是三棱锥ABC P -的高,又1=PA 所以三棱锥ABC P -的体积6331=⋅⋅∆PA S V ABC = (Ⅱ)证:在平面ABC 内,过点B 作AC BN ⊥,垂足为N ,过N 作PA MN //交PC 于M ,连接BM .由⊥PA 面ABC 知AC PA ⊥,所以AC MN ⊥.由于N MN BN =⋂,故⊥AC 面MBN ,又⊂BM 面MBN ,所以BM AC ⊥. 在直角BAN ∆中,21cos =∠⋅=BAC AB AN ,从而23=-=AN AC NC .由PA MN //,得31=NC AN MC PM =.8.【答案】((III .(Ⅱ)因为AC BC =,O 为AB 的中点, 所以OC AB ⊥.又因为平面V AB ⊥平面C AB ,且OC ⊂平面C AB , 所以OC ⊥平面V AB . 所以平面C MO ⊥平面V AB .(Ⅲ)在等腰直角三角形ACB 中,AC BC ==所以2,1AB OC ==.所以等边三角形V AB 的面积VAB S ∆=又因为OC ⊥平面V AB ,所以三棱锥C V -AB 的体积等于13VAB OC S ∆⨯⨯=. 又因为三棱锥V C -AB 的体积与三棱锥C V -AB 的体积相等,所以三棱锥V C -AB。

2017—2018年高考数学试题立体几何汇编及答案解析类型一 空间几何体的结构特征与三视图1.【2017浙江,3】某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .12+πB .32+πC .123+πD .323+π【答案】A 【解析】2π1211π3(21)1322V ⨯=⨯⨯+⨯⨯=+,选A. 2.【2017北京,理7】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A ) (B )(C ) (D )2 【答案】B 【解析】几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l == B.3.【2017山东,理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为 .【答案】22π+【解析】该几何体的体积为21112211242V π=π⨯⨯⨯+⨯⨯=+. 4.(2018年高考北京卷理科)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC=,CD=,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.5.(2018年高考数学全国卷1理科)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.故选:B.6.(2018年高考数学全国卷3理科)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B . C . D .【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A .故选:A .7.(2018年高考浙江卷)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( ) A .2B .4C .6D .8【解答】解:根据三视图:该几何体为底面为直角梯形的四棱柱.如图所示:故该几何体的体积为:V=.故选:C .8.某多面体的三视图如图所示,则该几何体的体积与其 外接球的体积之比为( )A .π186B .π96 C .π36 D .π26选A类型二 空间几何体与空间旋转体的面积、体积问题1、如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.解:如图,2、设球的一条半径与圆柱相应的母线的夹角为α,圆柱侧面积S =2π×4sin α×2×4cos α=32πsin2α,当α=π4时,S 取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.3、(2018年高考数学天津卷理科)已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M ﹣EFGH 的体积为 .【解答】解:正方体的棱长为1,M ﹣EFGH 的底面是正方形的边长为:,四棱锥是正四棱锥,棱锥的高为, 四棱锥M ﹣EFGH 的体积:=.故答案为:.4、(2014·课标Ⅱ)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解:原来毛坯体积为:π·32·6=54π(cm 3),由三视图知该零件由左侧底面半径为2cm ,高为4cm 的圆柱和右侧底面半径为3cm ,高为2cm 的圆柱构成,故该零件的体积为:π·22·4+π·32·2=34π(cm 3),切削掉部分的体积为54π-34π=20π(cm 3),故切削掉部分的体积与原来毛坯体积的比值为20π54π=1027 .故选C.6.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π4【答案】B【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径r =则圆柱体体积23ππ4V r h ==,故选B.7.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 【答案】92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=. 8.【2017江苏,6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 ▲ .【答案】32 【解析】设球半径为r ,则2132π2342π3V r r V r ⨯==.故答案为32. 9、(2018年高考数学全国卷3理科)10.(5分)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且面积为9,则三棱锥D ﹣ABC 体积的最大值为( ) A .12B .18C .24D .54【解答】解:△ABC 为等边三角形且面积为9,可得,解得AB=6,球心为O ,三角形ABC 的外心为O′,显然D 在O′O 的延长线与球的交点如图:O′C==,OO′==2,则三棱锥D ﹣ABC 高的最大值为:6, 则三棱锥D ﹣ABC 体积的最大值为:=18.故选:B .10、(2018年高考数学全国卷2理科)16.(5分)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,SA 与圆锥底面所成角为45°,若△SAB 的面积为5,则该圆锥的侧面积为40π .【解答】解:圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,可得sin ∠AMB==.△SAB 的面积为5,可得sin ∠AMB=5,即×=5,即SA=4.SA 与圆锥底面所成角为45°,可得圆锥的底面半径为:=2.则该圆锥的侧面积:π=40π.故答案为:40π.11、(2018年高考数学全国卷1理科)12.(5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .B .C .D .【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长明明就的最大值为:6×=.故选:A.12、(2018年江苏省高考数学试卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.类型三点共线、线共点问题1、如图,E,F,G,H分别是空间四边形内AB,BC,CD,DA上的点,且EH与FG交于点O.求证:B,D,O三点共线.证明:∵点E∈平面ABD,点H∈平面ABD,∴EH⊂平面AB D.∵EH∩FG=O,∴点O∈平面AB D.同理可证点O∈平面BC D.∴点O∈平面ABD∩平面BCD=B D.即B,D,O三点共线.类型四共面问题1、下列如图所示的正方体和正四面体,P、Q、R、S分别是所在棱的中点,则四个点共面的图形是____________.(填所有满足条件图形的序号)解:易知①③中PS ∥Q R ,∴四点共面.在②中构造如图所示的含点P ,S ,R ,Q 的正六边形,易知四点共面.在④中,由点P ,R ,Q 确定平面α,由图象观察知点S 在平面α外,因此四点不共面.综上知,故填①②③.类型五 异面直线问题1.【2017课标II ,理10】已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A ..5 C .5D 【答案】C【解析】如图所示,补成四棱柱1111ABCD A B C D - ,则所求角为1111,BC D BC BD C D AB ∠=====因此1cos 5BC D ∠== ,故选C 。


第1讲 空间几何体1.(2016·山东)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )A.13+23π B.13+23π C.13+26π D .1+26π 答案 C解析 由三视图知,半球的半径R =22,四棱锥是底面边长为1,高为1的正四棱锥,∴V =13×1×1×1+12×43π×⎝ ⎛⎭⎪⎫223=13+26π,故选C. 2.(2016·课标全国丙)在封闭的直三棱柱ABC —A 1B 1C 1内有一个体积为V 的球,若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4π B.9π2 C .6π D.32π3答案 B解析 由题意知,底面三角形的内切圆直径为4.三棱柱的高为3,所以球的最大直径为3,V 的最大值为9π2.3.(2015·山东)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3 B.4π3 C.5π3D .2π答案 C解析 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V 圆柱-V圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C.4.(2016·浙江)如图,已知平面四边形ABCD ,AB =BC =3,CD =1,AD =5,∠ADC =90°,沿直线AC 将△ACD 翻折成△ACD ′,直线AC 与BD ′所成角的余弦的最大值是________.答案66解析 设直线AC 与BD ′所成角为θ,平面ACD 翻折的角度为α,设点O 是AC 的中点,由已知得AC =6,如图,以OB 为x 轴,OA 为y 轴,过点O 与平面ABC 垂直的直线为z 轴,建立空间直角坐标系, 由A ⎝ ⎛⎭⎪⎫0,62,0,B ⎝ ⎛⎭⎪⎫302,0,0,C ⎝ ⎛⎭⎪⎫0,-62,0,作DH ⊥AC 于点H ,翻折过程中,D ′H 始终与AC 垂直,CH =CD 2CA =16=66,则OH =63,DH =1×56=306,因此可设D ′⎝ ⎛⎭⎪⎫-306cos α,-63,306sin α, 则BD ′——→=⎝ ⎛⎭⎪⎫-306cos α-302,-63,306sin α,与CA →平行的单位向量为n =(0,1,0),所以cos θ=|cos 〈BD ′——→,n 〉|=⎪⎪⎪⎪⎪⎪⎪⎪BD ′——→·n |BD ′——→|·|n |=639+5cos α, 所以cos α=-1时,cos θ取最大值66.1.以三视图为载体,考查空间几何体面积、体积的计算.2.考查空间几何体的侧面展开图及简单的组合体问题.热点一 三视图与直观图 1.一个物体的三视图的排列规则俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.2.由三视图还原几何体的步骤一般先从俯视图确定底面再利用正视图与侧视图确定几何体.例1 (1)(2016·课标全国甲)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π(2)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )答案 (1)C (2)D解析 (1)由三视图可知,组合体的底面圆的面积和周长均为4π,圆锥的母线长l =32+22=4,所以圆锥的侧面积为S 锥侧=12×4π×4=8π,圆柱的侧面积S 柱侧=4π×4=16π,所以组合体的表面积S =8π+16π+4π=28π,故选C.(2)所得几何体的轮廓线中,除长方体原有的棱外,有两条是原长方体的面对角线,它们在侧视图中落在矩形的两条边上,另一条是原长方体的体对角线,在侧视图中体现为矩形的自左下至右上的一条对角线,因不可见,故用虚线表示,由以上分析可知,应选D.思维升华 空间几何体的三视图是从空间几何体的正面、左面、上面用平行投影的方法得到的三个平面投影图,因此在分析空间几何体的三视图问题时,先根据俯视图确定几何体的底面,然后根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置,再确定几何体的形状,即可得到结果.跟踪演练1 (1)一个几何体的三视图如图所示,则该几何体的直观图可以是( )(2)一几何体的直观图如图,下列给出的四个俯视图中正确的是( )答案 (1)D (2)B解析 (1)由俯视图,易知答案为D.(2)由直观图可知,该几何体由一个长方体和一个截角三棱柱组合.从上往下看,外层轮廓线是一个矩形,矩形内部有一条线段连接的两个三角形.热点二 几何体的表面积与体积空间几何体的表面积和体积计算是高考中常见的一个考点,解决这类问题,首先要熟练掌握各类空间几何体的表面积和体积计算公式,其次要掌握一定的技巧,如把不规则几何体分割成几个规则几何体的技巧,把一个空间几何体纳入一个更大的几何体中的补形技巧. 例2 (1)(2016·北京)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16B.13C.12D .1 (2)如图,在棱长为6的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别在C 1D 1与C 1B 1上,且C 1E =4,C 1F =3,连接EF ,FB ,DE ,BD ,则几何体EFC 1-DBC 的体积为( )A .66B .68C .70D .72答案 (1)A (2)A解析 (1)由三视图知,三棱锥如图所示:由侧视图得高h =1, 又底面积S =12×1×1=12.所以体积V =13Sh =16.(2)如图,连接DF ,DC 1,那么几何体EFC 1-DBC 被分割成三棱锥D -EFC 1及四棱锥D -CBFC 1,那么几何体EFC 1-DBC 的体积为V =13×12×3×4×6+13×12×(3+6)×6×6=12+54=66.故所求几何体EFC 1-DBC 的体积为66.思维升华 (1)求多面体的表面积的基本方法就是逐个计算各个面的面积,然后求和.(2)求体积时可以把空间几何体进行分解,把复杂的空间几何体的体积分解为一些简单几何体体积的和或差.求解时注意不要多算也不要少算.跟踪演练2 某几何体的三视图如图所示,则这个几何体的体积为________.答案452解析 由三视图可知,该几何体为如图所示的多面体ABCDEF (置于长方体ABCD —MNFG 中去观察),且点E 为DG 的中点,可得AB =BC =GE =DE =3,连接AG ,所以多面体ABCDEF 的体积为V 多面体ABCDEF =V 三棱柱ADG —BCF -V 三棱锥A —GEF =12×(3+3)×3×3-13×(12×3×3)×3=452.热点三 多面体与球与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径.球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心(或“切点”“接点”)作出截面图. 例3 (1)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SA ⊥平面ABC ,SA =23,AB =1,AC =2,∠BAC =60°,则球O 的表面积为( ) A .4π B .12π C .16πD .64π(2)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.500π3cm 3B.866π3cm 3C.1 372π3cm 3D.2 048π3cm 3答案 (1)C (2)A 解析 (1)在△ABC 中,BC 2=AB 2+AC 2-2AB ·AC cos 60°=3,∴AC 2=AB 2+BC 2, 即AB ⊥BC , 又SA ⊥平面ABC ,∴三棱锥S -ABC 可补成分别以AB =1,BC =3,SA =23为长、宽、高的长方体, ∴球O 的直径=12+32+32=4,故球O 的表面积为4π×22=16π. (2)过球心与正方体中点的截面如图,设球心为点O ,球半径为R cm ,正方体上底面中心为点A ,上底面一边的中点为点B , 在Rt△OAB 中,OA =(R -2)cm ,AB =4 cm , OB =R cm ,由R 2=(R -2)2+42,得R =5, ∴V 球=43πR 3=5003π(cm 3).故选A.思维升华 三棱锥P -ABC 可通过补形为长方体求解外接球问题的两种情形: (1)点P 可作为长方体上底面的一个顶点,点A 、B 、C 可作为下底面的三个顶点; (2)P -ABC 为正四面体,则正四面体的棱都可作为一个正方体的面对角线.跟踪演练3 在三棱锥A -BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ABD 的面积分别为22,32,62,则三棱锥A -BCD 的外接球体积为________. 答案6π解析 如图,以AB ,AC ,AD 为棱把该三棱锥扩充成长方体,则该长方体的外接球恰为三棱锥的外接球,∴三棱锥的外接球的直径是长方体的体对角线长.据题意⎩⎨⎧AB ·AC =2,AC ·AD =3,AB ·AD =6,解得⎩⎨⎧AB =2,AC =1,AD =3,∴长方体的体对角线长为AB 2+AC 2+AD 2=6, ∴三棱锥外接球的半径为62. ∴三棱锥外接球的体积为V =43π·(62)3=6π.1.一个几何体的三视图及其尺寸如图所示,则该几何体的表面积为( )A .16B .82+8C .22+26+8D .42+46+8押题依据 求空间几何体的表面积或体积是立体几何的重要内容之一,也是高考命题的热点.此类题常以三视图为载体,给出几何体的特征,求几何体的表面积或体积. 答案 D解析 由三视图知,该几何体是底面边长为22+22=22的正方形,高PD =2的四棱锥P -ABCD ,因为PD ⊥平面ABCD ,且四边形ABCD 是正方形,易得BC ⊥PC ,BA ⊥PA , 又PC =PD 2+CD 2=22+22=23,所以S △PCD =S △PAD =12×2×22=22,S △PAB =S △PBC =12×22×23=2 6.所以几何体的表面积为46+42+8.2.在正三棱锥S -ABC 中,点M 是SC 的中点,且AM ⊥SB ,底面边长AB =22,则正三棱锥S -ABC 的外接球的表面积为( )A .6πB .12πC .32πD .36π押题依据 多面体的外接球一般借助补形为长方体的外接球解决,解法灵活,是高考的热点. 答案 B解析 因为三棱锥S -ABC 为正三棱锥,所以SB ⊥AC ,又AM ⊥SB ,AC ∩AM =A ,所以SB ⊥平面SAC ,所以SB ⊥SA ,SB ⊥SC ,同理,SA ⊥SC ,即SA ,SB ,SC 三线两两垂直,且AB =22,所以SA =SB =SC =2,所以(2R )2=3×22=12,所以球的表面积S =4πR 2=12π,故选B.3.已知半径为1的球O 中内接一个圆柱,当圆柱的侧面积最大时,球的体积与圆柱的体积的比值为________.押题依据 求空间几何体的体积是立体几何的重要内容之一,也是高考的热点问题之一,主要是求柱体、锥体、球体或简单组合体的体积.本题通过球的内接圆柱,来考查球与圆柱的体积计算,设问角度新颖,值得关注. 答案423解析 如图所示,设圆柱的底面半径为r ,则圆柱的侧面积为S =2πr ×21-r 2=4πr1-r2≤4π×r 2+-r22=2π(当且仅当r 2=1-r 2,即r =22时取等号). 所以当r =22时, V 球V 圆柱=4π3×13π222×2=423.A 组 专题通关1.如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )答案 B解析由所截几何体可知,FC 1被平面AD 1E 遮挡,可得B 图.2.下图是棱长为2的正方体的表面展开图,则多面体ABCDE 的体积为( )A .2 B.23 C.43 D.83答案 D解析 多面体ABCDE 为四棱锥(如图),利用割补法可得其体积V =4-43=83,选D.3.某几何体的三视图如图所示,该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4答案 B解析 由三视图可知,该几何体是由一个棱长为2的正方体切去两个四分之一圆柱而成,所以该几何体的体积为V =(22-2×14×π×12)×2=8-π.4.(2015·课标全国Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r 等于( )A .1B .2C .4D .8 答案 B 解析 如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r ,圆柱的底面半径为r ,高为2r ,则表面积S =12×4πr 2+πr 2+4r 2+πr ·2r =(5π+4)r 2.又S =16+20π,∴(5π+4)r 2=16+20π,∴r 2=4,r =2,故选B.5.如图所示,平面四边形ABCD 中,AB =AD =CD =1,BD =2,BD ⊥CD ,将其沿对角线BD 折成四面体A ′BCD ,使平面A ′BD ⊥平面BCD ,若四面体A ′BCD 的顶点在同一个球面上,则该球的体积为( )A.32π B .3π C.23π D .2π答案 A解析 如图所示,取BD 的中点E ,BC 的中点O ,连接A ′E ,EO ,A ′O ,OD .因为平面A ′BD ⊥平面BCD ,A ′E ⊥BD , 平面A ′BD ∩平面BCD =BD ,A ′E ⊂平面A ′BD ,所以A ′E ⊥平面BCD .因为A ′B =A ′D =CD =1,BD =2, 所以A ′E =22,EO =12,所以OA ′=32. 在Rt△BCD 中,OB =OC =OD =12BC =32,所以四面体A ′BCD 的外接球的球心为O ,球的半径为32,所以V 球=43π(32)3=32π.故选A.6.有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC =45°,AB =AD =1,DC ⊥BC ,则这块菜地的面积为________.答案 2+22解析 如图,在直观图中,过点A 作AE ⊥BC ,垂足为点E ,则在Rt△ABE 中,AB =1,∠ABE =45°,∴BE =22. 而四边形AECD 为矩形,AD =1, ∴EC =AD =1,∴BC =BE +EC =22+1. 由此可还原原图形如图.在原图形中,A ′D ′=1,A ′B ′=2,B ′C ′=22+1, 且A ′D ′∥B ′C ′,A ′B ′⊥B ′C ′, ∴这块菜地的面积为S =12(A ′D ′+B ′C ′)·A ′B ′=12×(1+1+22)×2=2+22. 7.(2016·浙江)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm 2,体积是________cm 3.答案 72 32解析 由三视图可知,该几何体为两个相同长方体的组合,长方体的长、宽、高分别为4 cm 、2 cm 、2 cm ,其直观图如下:其体积V =2×2×2×4=32(cm 3),由于两个长方体重叠部分为一个边长为2的正方形,所以表面积为S =2(2×2×2+2×4×4)-2×2×2=2×(8+32)-8=72(cm 2).8.如图所示,从棱长为6 cm 的正方体铁皮箱ABCD —A 1B 1C 1D 1中分离出来由三个正方形面板组成的几何图形.如果用图示中这样一个装置来盛水,那么最多能盛的水的体积为________ cm 3.答案 36解析 最多能盛多少水,实际上是求三棱锥C 1—CD 1B 1的体积. 又111111——C CD B C B C D V V 三棱锥三棱锥==13×(12×6×6)×6=36(cm 3), 所以用图示中这样一个装置来盛水,最多能盛36 cm 3体积的水.9.一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于____________.答案 2解析 由三视图可知该几何体是一个直三棱柱,如图所示.由题意知,当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆相同时,该球的半径最大,故其半径r =12×(6+8-10)=2.10.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ; (2)求该几何体的侧面积S .解 由已知可得,该几何体是一个底面为矩形,高为4,顶点在底面的投影是矩形中心的四棱锥E -ABCD .(1)V =13×(8×6)×4=64.(2)四棱锥E -ABCD 的两个侧面EAD ,EBC 是全等的等腰三角形,且BC 边上的高h 1=42+822=42;另两个侧面EAB ,ECD 也是全等的等腰三角形,AB 边上的高h 2= 42+622=5.因此S =2×(12×6×42+12×8×5)=40+24 2.B 组 能力提高11.(2015·湖南)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A.89πB.169πC.2-3πD.2-3π答案 A解析 设三视图对应的几何体为底面半径为1,高为2的圆锥.如图,设长方体的长、宽、高分别为a 、b 、c ,上、下底面中心分别为O 1,O 2,上方截得的小圆锥的高为h ,底面半径为r ,则a 2+b 2=4r 2.由三角形相似,得SO 1SO 2=O 1A O 2B, 即h 2=r 1,则h =2r .长方体的体积为V =abc =ab (2-2r )≤a 2+b 22×(2-2r )=2r 2(2-2r )=4r2-4r 3(当且仅当a =b 时取等号,且0<r <1).设y =4r 2-4r 3(0<r <1),则y ′=8r -12r 2.由y ′=0,得r =0或r =23.由y ′>0,得0<r <23;由y ′<0,得23<r <1.故当r =23时,y max =4×⎝ ⎛⎭⎪⎫232-4×⎝ ⎛⎭⎪⎫233=1627,即V max =1627.∴原工件材料的利用率为162713π×12×2=89π,故选A.12.已知在三棱锥P —ABC 中,PA ⊥平面ABC ,AB =AC =PA =2,且在△ABC 中,∠BAC =120°,则三棱锥P —ABC 的外接球的体积为________. 答案205π3解析 由余弦定理得:BC 2=AB 2+AC 2-2AB ·AC ·cos∠BAC , ∴BC 2=22+22-2×2×2×(-12)=12,∴BC =2 3.设平面ABC 截球所得截面圆半径为r ,则2r =23sin 120°=4,所以r =2.由PA=2且PA ⊥平面ABC 知球心到平面ABC 的距离为1,所以球的半径为R =12+22=5,所以V 球=43πR 3=205π3. 13.如图,侧棱长为23的正三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =40°,过点A 作截面△AEF ,则截面△AEF 的周长的最小值为____________.答案 6解析沿着侧棱VA 把正三棱锥V -ABC 展开在一个平面内,如图,则AA ′即为截面△AEF 周长的最小值,且∠AVA ′=3×40°=120°. 在△VAA ′中,由余弦定理可得AA ′=6,故答案为6.14.如图,在Rt△ABC 中,AB =BC =4,点E 在线段AB 上.过点E 作EF ∥BC 交AC 于点F ,将△AEF 沿EF 折起到△PEF 的位置(点A 与点P 重合),使得∠PEB =30°.(1)求证:EF ⊥PB ;(2)试问:当点E 在何处时,四棱锥P —EFCB 的侧面PEB 的面积最大?并求此时四棱锥P —EFCB 的体积.(1)证明 ∵EF ∥BC 且BC ⊥AB , ∴EF ⊥AB ,即EF ⊥BE ,EF ⊥PE . 又BE ∩PE =E ,∴EF ⊥平面PBE , 又PB ⊂平面PBE ,∴EF ⊥PB .(2)解 设BE =x ,PE =y ,则x +y =4. ∴S △PEB =12BE ·PE ·sin∠PEB=14xy ≤14⎝ ⎛⎭⎪⎫x +y 22=1. 当且仅当x =y =2时,S △PEB 的面积最大. 此时,BE =PE =2.由(1)知EF ⊥平面PBE ,∴平面PBE ⊥平面EFCB , 在平面PBE 中,作PO ⊥BE 于点O , 又平面PBE ∩平面EFCB =BE , ∴PO ⊥平面EFCB .即PO 为四棱锥P —EFCB 的高. 又PO =PE ·sin 30°=2×12=1,S EFCB =12×(2+4)×2=6,∴V P —BCFE =13×6×1=2.。
一、选择题1.[2016·银川一中一模]已知直线m、n和平面α,则m∥n的必要非充分条件是()A.m、n与α成等角B.m⊥α且n⊥αC.m∥α且n⊂α D.m∥α且n∥α答案A解析m∥n⇒m、n与α成等角,若m、n与α成等角,m、n 不一定平行,故选A.2.[2016·“江南十校”高三联考]下列结论正确的是()A.若直线l∥平面α,直线l∥平面β,则α∥βB.若直线l⊥平面α,直线l⊥平面β,则α∥βC.若两直线l1、l2与平面α所成的角相等,则l1∥l2D.若直线l上两个不同的点A、B到平面α的距离相等,则l∥α答案B解析A选项,α与β可能相交;C选项,l1,l2可能相交或异面;D选项,l可能与α相交,A、B在平面α两侧;B正确,故选B.3.[2015·广东高考]若空间中n个不同的点两两距离都相等,则正整数n的取值()A.至多等于3 B.至多等于4C.等于5 D.大于5答案B解析首先我们知道正三角形的三个顶点满足两两距离相等,于是可以排除C、D.又注意到正四面体的四个顶点也满足两两距离相等,于是排除A,故选B.4.如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是()A.MN与CC1垂直B.MN与AC垂直C.MN与BD平行D.MN与A1B1平行答案D解析如图,连接C1D,BD,AC,在△C1DB中,易知MN∥BD,故C正确;∵CC1⊥平面ABCD,∴CC1⊥BD,∴MN与CC1垂直,故A正确;∵AC⊥BD,MN∥BD,∴MN与AC垂直,故B正确;∵A1B1与BD异面,MN∥BD,∴MN与A1B1不可能平行,故D错误,选D.5.如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1.点E,F分别为棱B1C1,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,HP2的最小值是()A .7- 2B .27-6 2C .51-14 2D .14-2 2答案 B 解析 如图所示,以EF 为直径,在平面BCC 1B 1内作圆,易知点P 在该圆上,该圆的半径为12EF =2,再过点H 引BB 1的垂线,垂足为G ,连接GP ,∴HP 2=HG 2+GP 2,其中HG 为4,因此当GP 最小时,HP 取得最小值,此时GP =3-2,∴HP 2=(3-2)2+42=9-62+2+16=27-62,∴HP 2的最小值为27-6 2.故选B .6.如图,在Rt △AOB 中,∠OAB =π6,斜边AB =4.Rt △AOC 可以通过Rt △AOB 以直线AO 为轴旋转得到,且二面角B -AO -C 是π3.点D 为斜边AB 的中点,则异面直线AO 与CD 所成角的大小为( )A .π2B .π4C .π3D .π6答案 B解析 如图,∵AO ⊥OB ,AO ⊥OC ,∴∠BOC =π3,∵AB =4,∠OAB =π6,∴OB =OC =2,过点D 作DE ⊥OB ,垂足为E ,连接CE ,则DE ∥AO ,∴∠CDE 为异面直线AO 与CD 所成的角,∵OE=1,OC =2,∠BOC =π3,∴CE =3,∵点D 为AB 的中点,∴DE =3,∴Rt △DEC 是等腰直角三角形,∴∠CDE =π4,即异面直线AO 与CD 所成角的大小为π4.二、填空题7.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是________.(写出所有真命题的序号)答案 ②④解析 对于①,若一个平面内的两条直线与另一个平面都平行,那么这两个平面平行或相交,所以①不正确.对于②,若一个平面经过另一个平面的垂线,那么这两个平面相互垂直,这是判定定理,②正确.对于③,垂直于同一直线的两条直线可能相互平行,也可能是异面直线,③不正确.对于④,若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直,④正确.8.[2016·江南十校联考]已知△ABC 的三边长分别为AB =5,BC =4,AC =3,M 是AB 边上的点,P 是平面ABC 外一点.给出下列四个命题:①若PA ⊥平面ABC ,则三棱锥P -ABC 的四个面都是直角三角形;②若PM ⊥平面ABC ,且M 是AB 边的中点,则有PA =PB =PC ;③若PC =5,PC ⊥平面ABC ,则△PCM 面积的最小值为152;④若PC =5,P 在平面ABC 上的射影是△ABC 内切圆的圆心,则点P 到平面ABC 的距离为23.其中正确命题的序号是________.(把你认为正确命题的序号都填上)答案 ①②④解析 由题意知AC ⊥BC ,对于①,若PA ⊥平面ABC ,则PA ⊥BC ,又PA ∩AC =A ,∴BC ⊥平面PAC ,∴BC ⊥PC ,因此该三棱锥P -ABC 的四个面均为直角三角形,①正确;对于②,由已知得M 为△ABC 的外心,所以MA =MB =MC.∵PM ⊥平面ABC ,则PM ⊥MA ,PM ⊥MB ,PM ⊥MC ,由三角形全等可知PA =PB =PC ,故②正确;对于③,要使△PCM 的面积最小,只需CM 最短,在Rt △ABC 中,(CM)min =125,∴(S △PCM )min =12×125×5=6,故③错误;对于④,设P 点在平面ABC 内的射影为O ,且O 为△ABC 的内心,由平面几何知识得△ABC 的内切圆半径r =1,且OC =2,在Rt △POC 中,PO =PC 2-OC 2=23,∴点P 到平面ABC 的距离为23,故④正确.9. [2015·大连高三双基测试]如图,∠ACB =90°,DA ⊥平面ABC ,AE ⊥DB 交DB 于E ,AF ⊥DC 交DC 于F ,且AD =AB =2,则三棱锥D -AEF 体积的最大值为________.答案 26解析 因为DA ⊥平面ABC ,所以DA ⊥BC ,又BC ⊥AC ,所以BC ⊥平面ADC ,BC ⊥AF ,又AF ⊥CD ,所以AF ⊥平面DCB ,AF ⊥DB ,又DB ⊥AE ,所以DB ⊥平面AEF ,所以DE 为三棱锥D -AEF 的高,且AF ⊥EF.AE 为等腰三角形ABD 斜边上的高,所以AE =2,设AF =a ,FE =b ,则底面△AEF 的面积S =12ab ≤12·a 2+b 22=12×22=12,所以三棱锥D -AEF 的体积V ≤13×12×2=26(当且仅当a =b =1时等号成立).三、解答题10.[2016·湖南六校联考]如图,在直角梯形ABCD 中,AB ∥CD ,AB ⊥AD ,且AB =AD =12CD =1.现以AD 为一边向梯形外作矩形ADEF ,然后沿边AD 将矩形ADEF 翻折,使平面ADEF 与平面ABCD 垂直.(1)求证:BC ⊥平面BDE ;(2)若点D 到平面BEC 的距离为63,求三棱锥F -BDE 的体积.解 (1)证明:在矩形ADEF 中,ED ⊥AD ,因为平面ADEF ⊥平面ABCD ,所以ED ⊥平面ABCD ,所以ED ⊥BC.又在直角梯形ABCD 中,AB =AD =1,CD =2,∠BDC =45°,所以BC =2,在△BCD 中,BD =BC =2,CD =2,所以BD 2+BC 2=CD 2, 所以BC ⊥BD ,所以BC ⊥平面BDE.(2)由(1)得,平面DBE ⊥平面BCE ,作DH ⊥BE 于点H ,则DH ⊥平面BCE ,所以DH =63.在△BDE 中,BD·DE =BE·DH ,即2·DE =63(DE 2+2),解得DE =1.所以V F -BDE =V B -EFD =13×12×1×1×1=16.11.[2016·广州五校联考]如图,四棱锥P -ABCD 中,底面ABCD 是菱形,PA =PD ,∠BAD =60°,E 是AD 的中点,点Q 在侧棱PC 上.(1)求证:AD ⊥平面PBE ;(2)若Q 是PC 的中点,求证:PA ∥平面BDQ ;(3)若V P -BCDE =2V Q -ABCD ,试求CP CQ 的值.解 (1)证明:由E 是AD 的中点,PA =PD 可得AD ⊥PE.又底面ABCD 是菱形,∠BAD =60°,所以AB =BD ,又因为E 是AD 的中点,所以AD ⊥BE ,又PE ∩BE =E ,所以AD ⊥平面PBE.(2)证明:连接AC ,交BD 于点O ,连接OQ.因为O 是AC 的中点,Q 是PC 的中点,所以OQ ∥PA ,又PA ⊄平面BDQ ,OQ ⊂平面BDQ ,所以PA ∥平面BDQ.(3)设四棱锥P -BCDE ,Q -ABCD 的高分别为h 1,h 2.所以V P -BCDE =13S 四边形BCDE h 1,V Q -ABCD =13S 四边形ABCD h 2.又因为V P -BCDE =2V Q -ABCD ,且S 四边形BCDE =34S 四边形ABCD ,所以CP CQ =h 1h 2=83. 12.[2016·郑州质检]如图,已知三棱柱ABC -A ′B ′C ′的侧棱垂直于底面,AB =AC ,∠BAC =90°,点M ,N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面AA ′C ′C ;(2)设AB =λAA ′,当λ为何值时,CN ⊥平面A ′MN ,试证明你的结论.解 (1)证明:取A ′B ′的中点E ,连接ME ,NE.因为M ,N 分别为A ′B 和B ′C ′的中点,所以NE ∥A ′C ′,ME ∥AA ′.又因为A ′C ′⊂平面AA ′C ′C ,A ′A ⊂平面AA ′C ′C ,NE ⊄平面AA ′C ′C ,ME ⊄平面AA ′C ′C ,所以ME ∥平面AA ′C ′C ,NE ∥平面AA ′C ′C ,所以平面MNE ∥平面AA ′C ′C ,因为MN ⊂平面MNE ,所以MN ∥平面AA ′C ′C.(2)连接BN ,设AA ′=a ,则AB =λAA ′=λa ,由题意知BC =2λa ,NC =BN =a 2+12λ2a 2,因为三棱柱ABC -A ′B ′C ′的侧棱垂直于底面,所以平面A ′B ′C ′⊥平面BB ′C ′C ,因为AB =AC ,点N 是B ′C ′的中点,所以A ′N ⊥平面BB ′C ′C ,所以CN ⊥A ′N ,要使CN ⊥平面A ′MN ,只需CN ⊥BN 即可,所以CN 2+BN 2=BC 2,即2⎝ ⎛⎭⎪⎫a 2+12λ2a 2=2λ2a 2, 解得λ=2,故当λ=2时,CN ⊥平面A ′MN.。
五年高考真题分类汇编:立体几何一、选择题1.(2015安徽高考,理5)已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )(A )若α,β垂直于同一平面,则α与β平行 (B )若m ,n 平行于同一平面,则m 与n 平行(C )若α,β不平行,则在α内不存在与β平行的直线 (D )若m ,n 不平行,则m 与n 不可能垂直于同一平面【解析】选D. 由A ,若α,β垂直于同一平面,则α,β可以相交、平行,故A 不正确;由B ,若m ,n 平行于同一平面,则m ,n 可以平行、重合、相交、异面,故B 不正确;由C ,若α,β不平行,但α平面内会存在平行于β的直线,如α平面中平行于α,β交线的直线;由D 项,其逆否命题为“若m 与n 垂直于同一平面,则m ,n 平行”是真命题,故D 项正确.所以选D.2.(2015北京高考,理4)设α,β是两个不同的平面,m 是直线且m α⊂.“m β∥”是“αβ∥”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】选B. 因为α,β是两个不同的平面,m 是直线且m α⊂.若“m β∥”,则平面、αβ可能相交也可能平行,不能推出//αβ,反过来若//αβ,m α⊂,则有m β∥,则“m β∥”是“αβ∥”的必要而不充分条件.3.(2015新课标全国卷I ,理6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )(A)14斛 (B)22斛 (C)36斛 (D)66斛 【答案】B4.(2015陕西高考,理5)一个几何体的三视图如图所示,则该几何体的表面积为( ) A .3π B .4π C .24π+ D .34π+【解析】选D.由三视图知:该几何体是半个圆柱,其中底面圆的半径为1,母线长为2,所以该几何体的表面积是()1211222342ππ⨯⨯⨯++⨯=+,故选D . 5.(2015新课标全国卷I ,理11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r =( )(A )1 (B )2 (C )4 (D )8【解析】选B.由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r =2,故选B.6.(2015重庆高考,理5)某几何体的三视图如图所示,则该几何体的体积为A 、13π+ B 、23π+ C 、 123π+ D 、223π+【解析】选A.这是一个三棱锥与半个圆柱的组合体,2111112(12)12323V ππ=⨯⨯+⨯⨯⨯⨯⨯=+,选A .7.(2015北京高考,理5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )正(主)视图11俯视图侧(左)视图21A .25+B .45+C .225+D .5 【答案】C52=,三棱锥表面积表252S =+.8.(2015安徽高考,理7)一个四面体的三视图如图所示,则该四面体的表面积是( )(A )13+ (B )23+ (C )122+ (D )22【解析】选B.由题意,该四面体的直观图如下,,ABD BCD ∆∆是等腰直角三角形,,ABC ACD ∆∆是等边三角形,则113221,22sin 60222BCD ABD ABC ACD S S S S ∆∆∆∆==⨯⨯===⨯⨯=,所以四面体的表面积3212232BCD ABD ABC ACD S S S S S ∆∆∆∆=+++=⨯+⨯=+,故选B. 9.(2015新课标全国卷II ,理9)已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( ) A .36π B.64π C.144π D.256π 【答案】CBOAC10.(2015山东高考,理7)在梯形ABCD 中,2ABC π∠=,//,222AD BC BC AD AB === .将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )(A )23π (B )43π (C )53π (D )2π 【解析】选C. 直角梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为1,母线长为2的圆柱挖去一个底面半径同样是1、高为1的圆锥后得到的组合体,所以该组合体的体积为:2215121133V V V πππ=-=⨯⨯-⨯⨯⨯=圆柱圆锥,故选C. 11.(2015浙江高考,理8)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆折成A CD '∆,所成二面角A CD B '--的平面角为α,则( )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≤D. A CB α'∠≤【解析】B.试题分析:设ADC θ∠=,设2AB =,则由题意1AD BD ==,在空间图形中,设A B t '=,在A CB '∆中,2222222112cos 22112A D DB AB t t A DB A D DB '+-+--'∠==='⨯⨯⨯,在空间图形中,过A '作AN DC ⊥,过B 作BM DC ⊥,垂足分别为N ,M , 过N 作//NP MB ,连结A P ',∴NP DC ⊥,则A NP '∠就是二面角A CD B '--的平面角,∴A NP α'∠=,在Rt A ND '∆中,cos cos DN A D A DC θ''=∠=,sin sin A N A D A DC θ'''=∠=,同理,sin BM PN θ==,cos DM θ=,故2cos BP MN θ==, 显然BP ⊥面A NP ',故BP A P '⊥,在Rt A BP '∆中,2222222(2cos )4cos A P A B BP t t θθ''=-=-=-,在A NP '∆中,222cos cos 2A N NP A P A NP A N NP α''+-'=∠='⨯2222sin sin (4cos )2sin sin t θθθθθ+--=⨯12.(2015湖南高考,理10)某工件的三视图如图3所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A.89πB.169πC.34(21)π-D.312(21)π-【解析】选A.分析题意可知,问题等价于圆锥的内接长方体的体积的最大值,设长方体体的长,宽,高分别为x ,y ,h ,长方体上底面截圆锥的截面半径为a ,则22224)2(a a y x ==+,如下图所示,圆锥的轴截面如图所示,则可知a h ha 22221-=⇒-=,而长方体的体积)22(2222222a a h a h y x xyh V -==+≤= 322162()327a a a ++-≤⨯=,当且仅当y x =,3222=⇒-=a a a 时,等号成立,此时利用率为ππ98213127162=⨯⨯,故选A.13.(2015浙江高考,理2)某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A.38cm B. 312cm C.3323cm D. 3403cm【答案】C.14.(2015福建高考,理7)若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“//l α 的 ( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】选B. 若l m ⊥,因为m 垂直于平面α,则//l α或l α⊂;若//l α,又m 垂直于平面α,则l m ⊥,所以“l m ⊥ ”是“//l α 的必要不充分条件,故选B .学优高考网15.(2015新课标全国卷II ,理6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( ) A .81 B .71 C .61 D .51【解析】选 D. 由三视图得,在正方体1111ABCD A B C D -中,截去四面体111A A B D -,如图所示,,设正方体棱长为a ,则11133111326A A B D V a a -=⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51,故选D . CBADD 1C 1B 1A 116.(2015浙江高考,文4)设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m 【解析】选A. 采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.17.(2015新课标全国卷I ,文6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛 【解析】选 B. 设圆锥底面半径为r ,则12384r ⨯⨯=,所以163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B. 18.(2015浙江高考,文2)某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A .83cm B .123cm C .3233cm D .4033cm【解析】选C. 由三视图可知,该几何体是一个棱长为2的正方体与一个底面边长为2,高为2的正四棱锥的组合体,故其体积为32313222233V cm =+⨯⨯=.故选C. 19.(2015重庆高考,文5)某几何体的三视图如图所示,则该几何体的体积为( )(A) 123π+ (B)136π (C) 73π (D) 52π【解析】选B. 由三视图可知该几何体是由一个底面半径为1,高为2的圆柱,再加上一个半圆锥:其底面半径为1,高也为1,构成的一个组合体,故其体积为61311612122πππ=⨯⨯⨯+⨯⨯,故选B. 20.(2015陕西高考,文5)一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .24π+D .34π+【解析】选D . 由几何体的三视图可知该几何体为圆柱的截去一半,所以该几何体的表面积为21121222342πππ⨯⨯+⨯⨯⨯+⨯=+,故答案选D21.(2015广东高考,文6)若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交【解析】选A. 若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则l 至少与1l ,2l 中的一条相交,故选A .22.(2015浙江高考,文7)如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支【解析】选C. 由题可知,当P 点运动时,在空间中,满足条件的AP 绕AB 旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C.23.(2015湖北高考,文5)12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( ) A .p 是q 的充分条件,但不是q 的必要条件 B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件【解析】选A . 若p :12,l l 是异面直线,由异面直线的定义知,12,l l 不相交,所以命题q :12,l l 不相交成立,即p 是q 的充分条件;反过来,若q :12,l l 不相交,则12,l l 可能平行,也可能异面,所以不能推出12,l l 是异面直线,即p 不是q 的必要条件,故应选A .24.(2015新课标全国卷I ,文11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( )(A )1 (B )2 (C )4 (D )8【解析】选B. 由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B.25.(2015福建高考,文9)某几何体的三视图如图所示,则该几何体的表面积等于( )A .822+B .1122+C .1422+D .15 【解析】选B. 由三视图还原几何体,该几何体是底面为直角梯形,高为2的直四棱柱,且底面直角梯形的两底分别为12,,直角腰长为1, 1112斜腰为2.底面积为12332⨯⨯=,侧面积为2+2+4+22=8+22, 所以该几何体的表面积为1122+,故选B .26.(2015山东高考,文9)已知等腰直角三角形的直角边的长为,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) (A )223π(B )423π()22π()42π【解析】选B . 由题意知,该等腰直角三角形的斜边长为22,斜边上的高为2,所得旋转体为同底等高的全等圆锥,所以,其体积为2142(2)22,33ππ⨯⨯=,故选B . 27.(2015湖南高考,文10)某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)( )A 、89πB 、827πC 、224(21)π-D 、28(21)π-【答案】A28.(2015北京高考,文7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B.2 C.3 D.2【解析】选C.四棱锥的直观图如图所示:AB,S A是四棱锥最长的棱,由三视图可知,SC⊥平面CD222223=+=++=,故选C.SA SC AC SC AB BC29(2015安徽高考,文9)一个四面体的三视图如图所示,则该四面体的表面积是()(A )13+ (B )122+ (C )23+ (D )22 【解析】选C. 由该几何体的三视图可知,该几何体的直观图,如下图所示:其中侧面PAC ⊥底面ABC ,且PAC ∆≌ABC ∆,由三视图中所给数据可知:2====BC AB PC PA ,取AC 中点,O 连接BO PO ,,则POB Rt ∆中,1==BO PO ⇒2=PB ∴3222212432+=⋅⋅+⋅⋅=S ,故选C . 30.(2014·湖北高考文科·T7)在如图所示的空间直角坐标系O-xyz 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为 ( )A.①和②B.③和①C.④和③D.④和②【解题提示】由已知条件,在空间坐标系中作出几何体的大致形状,进一步得到正视图与俯视图. 【解析】选D.在坐标系中标出已知的四个点,根据三视图的画图规则判断三棱锥的正视图为④,俯视图为②,故选D.31. (2014·湖北高考文科·T10)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h,计算其体积V 的近似公式2136V L h ≈.它实际上是将圆锥体积公式中的圆周率π近似取为 3.那么,近似公式2275V L h ≈相当于将圆锥体积公式中的π近似取为 ( ) A.227 B.258 C. 15750 D.355113【解题提示】考查圆锥的体积公式以及学生的阅读理解能力.根据近似公式V ≈275L 2h,建立方程,即可求得结论.【解析】选 B.设圆锥底面圆的半径为r,高为h,依题意,L=(2πr)2,V=13Sh=13πr 2h=112π(2πr)2h ≈275L 2h, 所以112π≈275,即π的近似值为258.32.(2014·湖北高考理科·T5).在如图所示的空间直角坐标系xyz O -中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为A.①和②B.③和①C. ④和③D.④和②【解题提示】 考查由已知条件,在空间坐标系中作出几何体的大致形状,进一步得到正视图与俯视图 【解析】选D. 在坐标系中标出已知的四个点,根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②,故选D .33.(2014·湖北高考理科·T8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,另相乘也。