下载文档原格式
习题五5-1 求下列齐次差分方程的解。
（1）()3(1)0,(0)1y k y k y +-== （2）()2(1)0,(0)3y k y k y --== 5-2 求下列齐次差分方程的解。
（1）()3(1)2(2)0,(1)2,(2)1y k y k y k y y +-+-=-=-= （2）()2(1)(2)0,(1)1,(2)3y k y k y k y y +-+-=-=-=- 5-3 求下列差分方程的零输入响应。
（1）()2(1)(2)()2(2),(0)(1)1y k y k y k f k f k y y +-+-=+-=-= （2）15()3(1)2(2)(),(1),(2)24y k y k y k f k y y +-+-=-=--= 5-4 用经典法求下列差分方程所描述因果离散系统的全响应。
（1）()3(1)2(2)6()y k y k y k f k +-+-=,()(),(1)1,(2)0f k k y y ε=-=-= （2）()4(1)4(2)()y k y k y k f k +-+-=,()2(),(0)0,(1)1k f k k y y ε===- 5-5 求下列差分方程所描述的LTI 离散系统的零输入响应、零状态响应和全响应。
(1) ()4(1)4(2)()(1)y k y k y k f k f k +-+-=+-()(),(0)1,(1)2f k k y y ε=== （2）()3(1)2(2)(),y k y k y k f k +-+-=()(),(1)1,(2)0f k k y y ε=-=--=（3）()2(1)(2)(),y k y k y k f k +-+-=1()3(),(1)3,(2)52kf k k y y ε⎛⎫=-=-=- ⎪⎝⎭5-6 下列差分方程所描述的系统，若激励()2cos 3k f k π⎛⎫= ⎪⎝⎭,k ≥。
求各系统的稳态响应。
信号系统(第3版)习题解答《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。
1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。
[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。
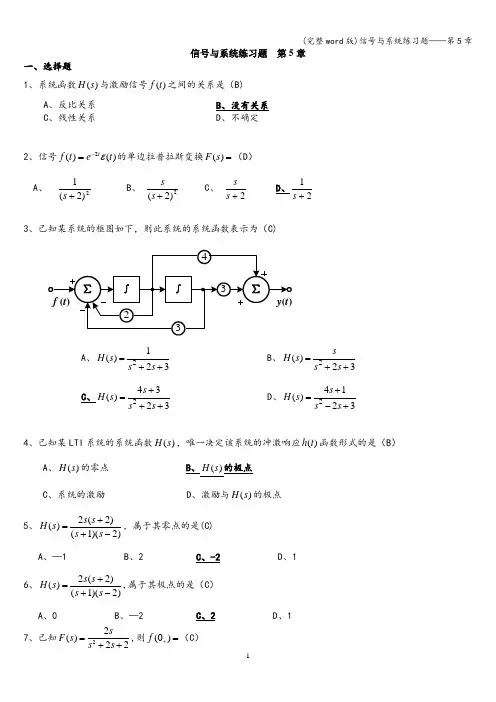
信号与系统练习题 第5章一、选择题1、系统函数()H s 与激励信号()f t 之间的关系是（B)A 、反比关系B 、没有关系C 、线性关系D 、不确定2、信号)()(2t e t f t ε-=的单边拉普拉斯变换=)(s F （D ） A 、2)2(1+s B 、 2)2(+s sC 、 2+s sD 、21+s3、已知某系统的框图如下，则此系统的系统函数表示为（C)A 、21()23H s s s =++ B 、2()23s H s s s =++C 、243()23s H s s s +=++ D 、241()23s H s s s +=-+4、已知某LTI 系统的系统函数()H s ，唯一决定该系统的冲激响应()h t 函数形式的是（B ）A 、()H s 的零点B 、()H s 的极点C 、系统的激励D 、激励与()H s 的极点 5、2(2)()(1)(2)s s H s s s +=+-，属于其零点的是(C)A 、—1B 、2C 、-2D 、1 6、2(2)()(1)(2)s s H s s s +=+-,属于其极点的是（C ）A 、0B 、—2C 、2D 、1 7、已知22()22sF s s s =++,则(0)f +=（C ）8、已知2()22F s s s =++，则()f ∞=（A) A 、0 B 、—2 C 、2 D 、不确定 9、信号2(1)()()t f t e t ε--=的单边拉普拉斯变换=)(s F （A ）A 、2()2e F s s =+B 、2()2s F s s =+ C 、1()2F s s =+ D 、()2s F s s =+10、信号2(1)()(1)t f t e t ε--=-的单边拉普拉斯变换=)(s F (A ）A 、()2s e F s s -=+B 、2()2e F s s =+ C 、1()2F s s =+ D 、()2s F s s =+11、已知信号()cos(2)f t t =的单边拉普拉斯变换2()4s F s s =+，则()[cos(2)]dy t t dt=的单边拉普拉斯变换()Y s =(B ）A 、2se s -+ B 、244s -+ C 、224s s + D 、24s s +12、已知信号()cos(2)f t t =的单边拉普拉斯变换2()4s F s s =+,则()[cos(2)()]dy t t t dtε=的单边拉普拉斯变换()Y s =（C ）A 、2se s -+ B 、244s -+ C 、224s s + D 、24s s +13、已知信号()f t 的单边拉普拉斯变换为()F s ，则()[()]dy t f t dt=的单边拉普拉斯变换()Y s =（A ） A 、()(0)sF s f -- B 、()(0)sF s f -+ C 、()sF s D 、()F s s14、已知信号()f t 的单边拉普拉斯变换为()F s ，则()[()()]dy t f t t dtε=的单边拉普拉斯变换()Y s =（C ）A 、()(0)sF s f --B 、()(0)sF s f -+C 、()sF sD 、()F s s15、已知223()21s F s s s +=++，则(0)f +=(C ）A 、0B 、-2C 、2D 、不确定 16、已知223()21s F s s s +=++，则()f ∞=（A ）A 、0B 、—2C 、2D 、不确定 17、已知1()1F s s =+，则(0)f +=(C ）18、已知()1F s s =+，则()f ∞=（A ） A 、0 B 、—1 C 、3 D 、不确定 19、信号5(1)()t f t e --=的单边拉普拉斯变换=)(s F (A)A 、5()5e F s s =+B 、5()5s F s s =+ C 、1()5F s s =+ D 、()5s F s s =+二、填空题1、某LTI 连续系统的系统函数为235)(2+++=s s s s H ，描述该系统的微分方程为)(5)()(2)(3)(''''t f t f t y t y t y +=++。
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
第5章 连续时间信号的抽样与量化5.1 试证明时域抽样定理。
证明： 设抽样脉冲序列是一个周期性冲激序列，它可以表示为∑∞-∞=-=n sT nT t t )()(δδ由频域卷积定理得到抽样信号的频谱为：[])()(21)(ωδωπωT s F F *=()[]∑∞-∞=-=n ssn F T ωω1式中)(ωF 为原信号)(t f 的频谱，)(ωδT 为单位冲激序列)(t T δ的频谱。
可知抽样后信号的频谱)(ωs F 由)(ωF 以 s ω为周期进行周期延拓后再与s T 1相乘而得到，这意味着如果m s ωω2≥，抽样后的信号)(t f s 就包含了信号)(t f 的全部信息。
如果m s ωω2<，即抽样间隔ms f T 21>，则抽样后信号的频谱在相邻的周期内发生混叠，此时不可能无失真地重建原信号。
因此必须要求满足ms f T 21≤，)(t f 才能由)(t f s 完全恢复，这就证明了抽样定理。
5.2 确定下列信号的最低抽样频率和奈奎斯特间隔： （1）)50(t Sa（2）)100(2t Sa（3） )100()50(t Sa t Sa +（4）)60()100(2t Sa t Sa +解：抽样的最大间隔m s f T 21=称为奈奎斯特间隔，最低抽样速率m s f f 2=称为奈奎斯特速率，最低采样频率m s ωω2=称为奈奎斯特频率。
（1）)]50()50([50)50(--+↔ωωπu u t Sa ，由此知s rad m /50=ω，则π25=m f ，由抽样定理得：最低抽样频率π502==m s f f ，奈奎斯特间隔501π==s s f T 。
（2）)2001(100)100(2ωπ-↔t Sa脉宽为400，由此可得s rad m /200=ω，则π100=m f ，由抽样定理得最低抽样频率π2002==m s f f ，奈奎斯特间隔2001π==s s f T 。
（3）)]50()50([50)50(--+↔ωωπu u t Sa ，该信号频谱的s rad m /50=ω)]100()100([100)100(--+↔ωωπu u t Sa ,该信号频谱的s rad m /100=ω)100()50(t Sa t Sa +信号频谱的s rad m /100=ω,则π50=m f ，由抽样定理得最低抽样频率π1002==m s f f ，奈奎斯特间隔1001π==s s f T 。
（4）)]100()100([100)100(--+↔ωωπu u t Sa ,该信号频谱的100=m ω)1201(60)60(2ωπ-↔t Sa ，该信号频谱的s rad m /120=ω所以)60()100(2t Sa t Sa +频谱的s rad m /120=ω, 则π60=m f ，由抽样定理得最低抽样频率π1202==m s f f ，奈奎斯特间隔1201π==s s f T 。
5.3 系统如题图 5.3所示，)1000()(1t Sa t f π=，)2000()(2t Sa t f π=，∑∞-∞=-=n nT t t p )()(δ，)()()(21t ft f t f =，)()()(t p t f t f s =。
（1）为从)(t f s 中无失真地恢复)(t f ，求最大采样间隔m ax T 。
（2）当max T T =时，画出)(t f s 的幅度谱)(ωs F 。
题图 5.3解：（1）先求)(t f 的频谱)(ωj F 。
)]1000()1000([10001)()1000()(11πωπωωπ--+=⇒=u u j F t Sa t f)]2000()2000([20001)()2000()(22πωπωωπ--+=⇒=u u j F t Sa t f )]}3000()1000()[3000()]1000()1000([2000)]1000()3000()[3000{(1041)]2000()2000((20001))1000()1000((10001[21)()(21)(621πωπωπωπωπωππωπωπωππωπωπωπωπωωπω---+-+--+++-++⨯⨯=--+*--+=*=-u u u u u u u u u u j F j F j F 由此知)(ωj F 的频谱宽度为π6000，且s rad m /3000πω=，则Hz f m 1500=，抽样的最大允许间隔s f T m 3000121max ==（2）∑∞-∞=-=n nT t t p )()(δ，所以为用冲激序列对连续时间信号为)(t f 进行采样，设原输入信号)(t f 的频谱密度为)(ωF ，而单位冲激序列的频谱密度为：∑∞-∞=-=n sn Tp )(2)(ωωδπω 其中Ts πω2=则根据频域卷积定理得抽样信号)(t f s 的频谱为：∑∞-∞=-==n s s n F T p F F )(1)](*)([21)(ωωωωπω而max T T =，则s rad T s /6000230002maxπππω=⨯==，幅度谱如下图所表示。
5.4 对信号)()(t u e t f t-=进行抽样，为什么一定会产生频率混叠效应？画出其抽样信号的频谱。
解： 由第三章知识知，该单边指数信号的频谱为：ωωj j F +=11)(其幅度频谱和相位频谱分别为211)(ωω+=j Fωωϕarctan )(-=单边非因果指数函数的波形)(t f 、 幅度谱)(ωj F 、相位谱)(ωϕ如下图所示，其中1=a 。
单边指数信号的波形和频谱显然该信号的频谱范围为整个频域，故无论如何抽样一定会产生频率混叠效应。
抽样后的频谱是将原信号频谱以抽样频率s ω为周期进行周期延拓，幅度变为原来的sT 1而得到。
图略。
5.5 题图5.5所示的三角形脉冲，若以20Hz 频率间隔对其频率抽样，则抽样后频率对应的时域波形如何？以图解法说明。
题图 5.5解：三角形脉冲的频谱可根据傅里叶变换的时域微分特性得到，具体求解可参考课本第三章。
由此可知，脉宽为τ幅度为E 的三角形脉冲其频谱为2)4(2ωττSa E。
其波形如图所示。
三角函数的频谱在)(t x 中，s ms 1.0100==τ易求得)(t x 的频谱为：2E τ()X j ω4πτ8πτ4πτ-8πτ-ω()ϕω0 50 -50 t /msx (t )2)025.0(05.0)(ωωESa j X =在)(404为整数k k k πτπω⋅==处，)(ωj X 为零，图略。
由频域卷积定理，抽样信号的频谱为：()[]∑∞-∞=-=n sss n j X T j X ωωω1)(其中s Hzf T s s 05.02011===，s rad f s s /402ππω==。
抽样后的频谱是将三角形频谱以s ω为周期做了周期延拓，幅度则变为原来的sT 1，可见发生了频谱混叠现象。
5.6 若连续信号)(t f 的频谱)(ωF 是带状的)(21ωω～，利用卷积定理说明当122ωω=时，最低抽样频率只要等于2ω就可以使抽样信号不产生频谱混叠。
证明：由频域卷积定理的抽样信号的频谱为[])()(21)(ωδωπωT s F F *=()[]∑∑∞-∞=∞-∞=-=-=n ssn ss n F T n w T F ωωωδπωπ1])(2*)([21抽样后的频谱是以抽样频率s ω为周期做了周期延拓，幅度则变为原来的sT 1。
由于频谱)(ωF 是带状的且122ωω=，所以当2ωω=s 时频谱不会混叠。
5.7 如题图5.7所示的系统。
求：（1）求冲激响应函数)(t h 与系统函数)(s H ；（2）求系统频率响应函数)(ωH ，幅频特性)(ωH 和相频特性)(ωϕ，并画出幅频和相频特性曲线；（3）激励[])()()(T t u t u t f --=，求零状态响应)(t y ，画出其波形； （4）激励∑+∞=-=)()()(n s nT t nT f t f δ，其中T 为奈奎斯特抽样间隔，)(nT f 为点上)(t f 的值，求响应)(t y 。
解：（1）由图可知()()()[]()t u T t f t f t y *--=两边求拉氏变换可得()()()se s F s Y Ts--=1所以()()se s H Ts--=1（2）图略（3）)(t f 的拉氏变换为()se s F Ts--=1零状态响应得拉氏变换为()()()()221s e s F s H s Y Ts --==求拉氏反变换可得()()()()()()T t u T t T t u T t ut t y 222-++---=（4）由()()se s H Ts--=1可得()()T t u t u t h --=)(而()()()()()()()[]T t u t u nT t nT f t h t f t y sn ss ---==∑+∞=**0δ()()()[]T nTt u nT t u nT f ssn s----=∑+∞=0)t。
