等腰三角形和等边三角形的综合题

等腰三角形和等边三角形的综合题哎呀，说到等腰三角形和等边三角形的综合题，那可真是让不少同学头疼，但别怕，咱们一起来好好琢磨琢磨。

我记得有一次，在课堂上我给同学们出了一道关于等腰三角形和等边三角形的综合题。

题目是这样的：一个等腰三角形，其中一个角是60 度，让大家求其他角的度数。

我就看着同学们有的抓耳挠腮，有的眉头紧皱，还有的在草稿纸上不停地写写画画。

咱们先来说说等腰三角形，它可是有两条边长度相等的哟。

如果已知顶角，那底角的度数就可以通过用（180 顶角）÷ 2 来算。

要是已知一个底角，那顶角就是 180 底角× 2 啦。

再看看等边三角形，这可就更有趣了，它的三条边都相等，三个角也都相等，每个角都是 60 度。

比如说有这样一道题：一个等腰三角形的周长是 20 厘米，其中一条腰长 8 厘米，求底边的长度。

这时候咱们就得先知道等腰三角形两腰相等，所以另一条腰也是 8 厘米，那底边就是 20 8× 2 ＝ 4 厘米。

还有这样的题：一个等边三角形的边长是 10 厘米，它的周长是多少？这就太简单啦，因为等边三角形三边相等，所以周长就是 10× 3 ＝30 厘米。

我再给大家出一道有点难度的综合题：已知一个三角形是等腰三角形，其中一个角是 50 度，求其他两个角的度数。

这时候就得分情况讨论啦，如果这个 50 度的角是顶角，那底角就是（180 50）÷ 2 ＝ 65 度；要是 50 度的角是底角，那另一个底角也是 50 度，顶角就是 180 50× 2 ＝ 80 度。

在做这些综合题的时候，大家一定要认真分析题目给出的条件，千万不能马虎。

就像上次，有个同学做题的时候，明明题目说的是等腰三角形，他愣是给当成等边三角形来做，结果答案全错啦，那叫一个可惜哟！所以呀，同学们，对于等腰三角形和等边三角形的综合题，只要咱们掌握了它们的特点和性质，多做几道练习题，就一定能轻松应对。

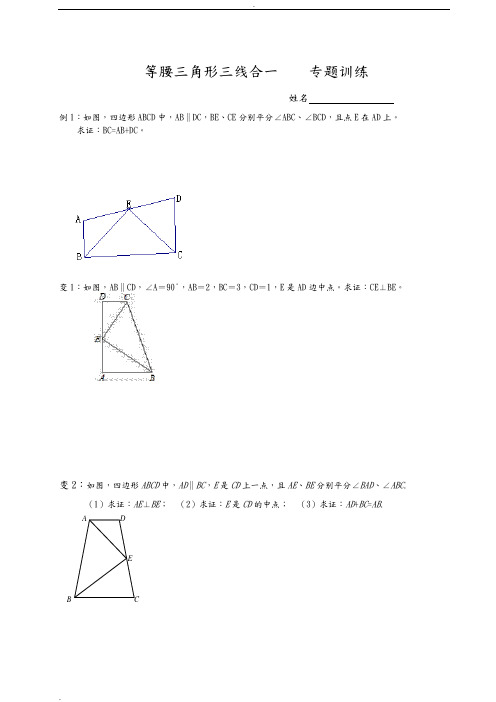
等腰三角形三线合一专题训练姓名例1：如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

求证：BC=AB+DC。

变1：如图，AB∥CD，∠A＝90°，AB＝2，BC＝3，CD＝1，E是AD边中点。

求证：CE⊥BE。

变2：如图，四边形ABCD中，AD∥BC，E是CD上一点，且AE、BE分别平分∠BAD、∠ABC.（1）求证：AE⊥BE；（2）求证：E是CD的中点；（3）求证：AD+BC=AB.变3：△ABC 是等腰直角三角形 ，∠BAC=90°,AB=AC.⑴若D 为BC 的中点，过D 作DM ⊥DN 分别交AB 、AC 于M 、N ，求证：（1）DM ＝DN 。

⑵若DM ⊥DN 分别和BA 、AC 延长线交于M 、N 。

问DM 和DN 有何数量关系。

(1) 已知：如图，AB=AC ，E 为AB 上一点，F 是AC 延长线上一点，且BE=CF ，EF 交BC 于点D ． 求证：DE=DF ．M N D C BAM ND CB ADBCF AE(2)已知：如图，AB=AC ，E 为AB 上一点，F 是AC 延长线上一点，且，EF 交BC 于点D ，且D 为EF 的中点． 求证：BE=CF ．DBCF AE利用面积法证明线段之间的和差关系1、如图，在△ABC 中，AB=AC ，P 为底边BC 上的一点，PD ⊥AB 于D ，PE ⊥AC 于E ，•CF ⊥AB 于F ，那么PD+PE 与CF 相等吗？变1：若P点在直线BC上运动，其他条件不变，则PD 、PE与CF的关系又怎样，请你作图，证明。

ＦＦ1、已知等腰三角形的两边长分别为4、9，则它的周长为（ ）A 17B 22C 17或22D 13根据等腰三角形的性质寻求规律 例1．在△ABC 中，AB=AC ，∠1=12∠ABC ，∠2=12∠ACB ，BD 与CE 相交于点O ，如图，∠BOC 的大小与∠A 的大小有什么关系？ 若∠1=13∠ABC ，∠2=13∠ACB ，则∠BOC 与∠A 大小关系如何？ 若∠1=1n ∠ABC ，∠2=1n∠ACB ，则∠BOC 与∠A 大小关系如何？会用等腰三角形的判定和性质计算与证明例2．如图，等腰三角形ABC 中，AB=AC ，一腰上的中线BD•将这个等腰三角形周长分成15和6两部分，求这个三角形的腰长及底边长．利用等腰三角形的性质证线段相等例3．如图，P 是等边三角形ABC 内的一点，连结PA 、PB 、PC ，•以BP 为边作∠PBQ=60°，且BQ=BP ，连结CQ ．（1）观察并猜想AP 与CQ 之间的大小关系，并证明你的结论．（2）若PA ：PB ：PC=3：4：5，连结PQ ，试判断△PQC 的形状，并说明理由．例1、等腰三角形底边长为5cm ，腰上的中线把三角形周长分为差是3cm 的两部分，则腰长为（ ） A 、2cm B 、8cm C 、2cm 或8cm D 、不能确定例2、已知AD 为△ABC 的高，AB=AC ，△ABC 周长为20cm ，△ADC 的周长为14cm ，求AD 的长。

等腰三角形与等边三角形的综合练习题在几何学中，等腰三角形和等边三角形是两个基本的三角形类型。

虽然它们具有一些共同点，但也有一些不同之处。

本文将为您提供一些相关的综合练习题，以帮助您更好地理解和应用这两种三角形。

练习题1：等边三角形的性质和相关计算题目：已知一个等边三角形ABC，边长为a。

请计算以下内容：1. 三角形ABC的内角和是多少？2. 计算三角形ABC的高和面积。

3. 求三角形ABC的外接圆半径。

4. 若等边三角形ABC的周长为15cm，求边长a的值。

解答：1. 由于等边三角形的三个内角相等，所以三角形ABC的内角和为180°。

2. 等边三角形ABC的高等于边长，因此三角形ABC的高为a。

根据三角形面积公式，三角形ABC的面积S = 1/2 * a * a * sin60°= a² * √3 / 4。

3. 由于等边三角形的外接圆半径等于边长的一半，所以三角形ABC 的外接圆半径为a / 2。

4. 根据等边三角形的性质，边长a乘以3即为等边三角形的周长。

所以3a = 15，解得a = 5。

练习题2：等腰三角形的性质和相关计算题目：已知一个等腰三角形DEF，底边DE = 8cm，等腰边DF = EF = 6cm。

请计算以下内容：1. 三角形DEF的内角和是多少？2. 求三角形DEF的高和面积。

3. 已知等腰三角形DEF的底边DE = 8cm，求EF的值，使得三角形DEF的面积为12平方厘米。

解答：1. 由于等腰三角形的两个底角相等，所以三角形DEF的内角和为180°。

2. 等腰三角形DEF的高可以通过勾股定理计算，即高h = √(DF² - (DE/2)²) = √(6² - (8/2)²) = √16 = 4。

根据三角形面积公式，三角形DEF的面积S = 1/2 * DE * h = 1/2 * 8 * 4 = 16 平方厘米。

精心整理等腰三角形与等边三角形 学习目标 掌握等腰三角形、等边三角形的性质和判定本课重点 1．理解等腰三角形的性质和判定．2．理解等边三角形的性质和判定．3．灵活运用性质和判定定理解决实际问题本课难点 综合应用等腰三角形的性质和判定解决实际问题，理解性质和判定的区别．1．已知等腰三角形一腰上的高与另一腰的夹角为45°，这个等腰三角形顶角的度数为．2．已知等腰三角形的两边长分别为5和6，则这个等腰三角形的周长为（ ）A ．11B ．16C ．17D ．16或173．下列说法，正确的个数是（）①等腰三角形的底角一定是锐角；②等腰三角形的角平分线、中线、高线是同一条线段；③等腰三角形两腰上的高一定相等；④等腰三角形两腰上的中线一定相等A ．0B ．1C ．2D ．34．如图，∠B =∠C =36°，∠ADE =∠AED =72°，则图中的等腰三角形的个数为（ ）A ．3个B ．4个C ．5个D ．6个知识点一、等腰三角形三线合一 【例1】如图，在△ABC 中AB =AC ，点F 在AC 上，在BA 延长线上截取AE =AF 求证：EF ⊥BC名校精析名校导读名校互动【变式1】求证：一边上的中线与这边所对的角的角平分线互相重合的三角形是等腰三角形．知识点二、等腰三角形边关系【例2】已知：如图，点D 是∠ABC 的角平分线与∠ACB 的外角平分线的交点，DE ∥BC ，DE 交AB 于点E ，交AC 于点F ．求证：EF ＝BE －CF ．【变式2】等腰三角形ABC 中，AB AC =，90A ∠=，BD 平分ABC ∠，DE BC ⊥，且10BC =，求DCE ∆的周长．知识点三、等腰三角形角的关系【例3【变式3】在Rt ABC ∆中，90ACB ∠=，AD AC =，BE BC =，求DCE ∠的度数．知识点四、等边三角形与直角三角形含30°角的性质【例4】将ABC ∆绕顶点A 顺时针旋转60，得到AB C ''∆，且C '为BC 的中点．则求:C D '：DB '的值．【变式4】如图所示，在△ABC 中，∠A =30°，∠ACB =90°，M 是AB 上一点，CM =21AB ，D 是BM 的中点，求证：CD ⊥AB ．【例5】，作∠求证：【变式5】已知ABC ∆为等边三角形，D 是BC 上一点，再延长BA 到E ，使AE BD =．求证：CE DE =知识点六、等腰直角三角形【例6】如图，在Rt △ABC 中，AB =AC ，∠BAC =90°，点O 是BC 的中点，连结OA ，（1）OA =OB =OC 成立吗？请说明理由．（2）若点M ，N 分别在线段AB ，AC 上移动，在移动中始终保持AN =BM ，请判断△OMN 的形状，并说明理由．（3）若点O 分别在线段BA 、AC 的延长线上移动，在移动中始终保持AN =BM ，请判断△OMN 的形状，并说明理由．【变式6PF 分别交AB ，=AP ⑤S 四边形AEPF 证明．A 夯实基础1．若等腰三角形有一个角的度数是70°，则这个三角形的顶角是___________．2．等腰三角形的底边长为3，周长为15，则一腰长为．3．如图，已知△ABC 是等边三角形，点B ，C ，D ，E 在同一直线上，且CG=CD ，DF =DE ，则∠E = ．4．已知：如图，B 、D 分别在AC 、CE 上，AD 是∠CAE 的平分线，BD ∥AE ，AB ＝BC ．求证：AC ＝AE ．5．长方形球桌ABCD 上，一球从AB 边上某处P 点击出，分别撞击球桌的边BC 、CD 、DA 各一次后，又回到出发点P 处，每次球撞击桌边时，撞击前后的路线与桌边所成德角相等（如图中αβ∠=∠）．已知3AB =，4BC =，求此球所走路线的长度．名校拓展B能力提高6．如图，已知，在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．7．△ABC为等边三角形，点M是BC上任意一点，点N是CA上任意一点，且BM=CN，BN与AM相交于Q点，则∠AQN等于多少度？C综合创新，连接DE．则BD与DE有什么关系？8．在等边三角形ABC中，BD⊥AC，延长BC到E，使CE CD名校小结。

1、一个等腰三角形的两边长分别为2和5，则它的周长为_____________。

2、已知等腰三角形的两边长分别为8cm 和10cm ，求周长。

3、已知等腰三角形的一个角是另一个角的4倍，求各个内角的度数。

4、已知等腰三角形的一个外角等于150°，求它的各个内角。

5、已知等腰三角形一腰上的高与另一边的夹角是25°，求各个内角的度数。

6、在三角形ABC 中，AB=AC ，AB 边上的垂直平分线与AC 边所在的直线想交所得的锐角是40°，求底角B 的度数。

7、等腰三角形的底边长为5cm ，一腰上的中线把它的周长分为两部分的差为3cm ，求它的腰长。

8、等腰三角形一腰上的高与另一腰的夹角为70°，其底角为________．9、在△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为________．10、已知点A 的坐标为（1，1），点B 是x 轴上一点，且△OAB 为等腰三角形，求点B 的坐标11、坐标平面内一点A （2，﹣1），O 为原点，P 是x 轴上的一个动点，如果以点P 、O 、A 为顶点的三角形是等腰三角形，那么符合条件的动点P 的个数为（ ）A ． 2 B ．3 C ．4 D ．512、在平面直角坐标系xOy 中，已知A(2，－2)，在y 轴确定点P ，使△AOP 为等腰三角形，则符合条件的点有 ( )A ．2个 D ．3个 C ．4个 D ．5个13、△ABC 中，AB=AC ，AB 边的中垂线与直线AC 所成的角为50°，则∠B 等于（ ）A ．70°B ．20°或70°C ．40°或70°D ．40°或20°14、如图,把一张对边平行的纸条如图折叠，重合部分是( )A. 等边三角形 B ．等腰三角形 C. 直角三角形 D ．无法确定ED CA B HF G15、如图，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB=BC=CD=DE=EF ，若∠A=18°，则∠GEF 的度数是（ ） A ．80° B ．90° C ．100° D ．108°16、在等腰△ABC 中，AB=AC ，中线BD 将这个三角形的周长分为15和12两个部分，则这个等腰三角形的腰长是( ) A. 11 B. 4或5 C. 7或11 D. 8或1017、如图，在△ACB 的边BC 所在直线上找一点P ，使得△ACP 为等腰三角形，则满足条件的点P 共有( )A. 2个B. 3个C. 4个D. 5个18、等腰三角形一腰上的高与一边的夹角为50°，则该等腰三角形的底角度数（ ）A. 50°B. 40°或20°或70°C. 70°或20°D. 40°或70°19、已知△ABC 的三条边长分别为3，4，6，在△ABC 所在平面内画一条直线，将△ABC 分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）A ．6条B ．7条C ．8条D ．9条20、已知：如图，下列三角形中，AB=AC ，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（ ） A ． ①③④ B ． ①②③④ C ． ①②④ D ． ①③1．已知，如图，△ABC 中，AB=AC ，DE 是AB 的中垂线，点D 在AB 上，点E 在AC 上，若△ABC 的周长为25cm ，△EBC 的周长为16cm ，则AC 的长度为（ ）A ． 16cmB ． 9cmC ． 8cmD ． 7cm（1图） （2图） （3图）2．如图，在△ABC 中，∠B=∠C ，点F 为AC 上一点，FD ⊥BC 于D ，过D 点作DE ⊥AB 于E ．若∠AFD=158°，则∠EDF 的度数为（ ）A ． 90°B ． 80°C ． 68°D ．60° 3．如图所示，在△ABC 中，点D 是BC 上一点，∠BAD=80°，AB=AD=DC ，则∠C 的大小为（ ） A ． 50° B ． 40° C ． 20° D ．25°4．下列说法正确的是（ ）A .等腰三角形的两条高相等B ．等腰三角形一定是锐角三角形C ．有一个角是60°的锐角三角形是等边三角形D ．三角形三条角平分线的交点到三边的距离相等 5．已知等腰三角形ABC ，∠A 是顶角，且∠A 等于∠C 的一半，BD 是△ABC 的角平分线，则该图中共有等腰三角形的个数是（ ）A ． 4个B ． 3个C ． 2个D ．1个6．边长为2的等边三角形的面积是（ ）A ．B ．C ． 3D ． 6 7．如图，在等边△ABC 中，∠BAD=20°，AE=AD ，则∠CDE 的度数是（ ）（7图） （8图） （9图）A ． 10°B ． 12.5°C ． 15°D ．20°8．如图，在△ABC 中，∠C=90°，∠ABC=15°，点D 、E 分别在BC 、AB 上，且DE 垂直平分AB ，BD=3，则DC 等于（ ）A ．B ．C ． 3D ． 9．如图，等边△ABC 的边长为4，AD 是BC 边上的中线，F 是AD 边上的动点，E 是AC 边上一点，若AE=2，当EF+CF 取得最小值时，则∠ECF 的度数为（ ）A 15°B 22.5°C 30°D 45°． ． ． ．10．如图，钢架中∠A=16°，焊上等长的钢条P 1P 2，P 2P 3，P 3P 4…来加固钢架，若AP 1=P 1P 2，则这样的钢条至多需要（ ）根．（10图） （11图） （13图） A ． 4 B ． 5 C ． 6 D ． 711．如图，已知等边△ABC 的周长为6，BD 是AC 边的中线，E 为BC 延长线上一点，CD=CE ，那么△BDE 的周长是（ ）A ． 5+2B ． 5+C ． 3+2D ．3+12．以下关于等边三角形的判定：①三条边相等的三角形是等边三角形；②有一个角是60°的等腰三角形是等边三角形；③有两个角为60°的三角形是等边三角形④三个角相等的三角形是等边三角形 其中正确的是（ ）A ． 只有①②③B ． 只有①②④C ． 只有①③④D ．①②③④13．如图，△ABC 为边长是5的等边三角形，点E 在AC 边上，点F 在AB 边上，ED ⊥BC ，且ED=AE ，DF=AF ，则CE 的长是（ ）A ．B ．C ． 20+10D ．20﹣10 14．已知△ABC 是等腰三角形，BC 边上的高恰好等于BC 的一半，则∠BAC 的度数是（ ）A ． 75°B ． 90°或75°或25°C ． 75°或15°D ． 90°或75°或15°15．如图，已知∠AOB=40°，点P 关于OA 、OB 的对称点分别为C 、D ，CD 交OA 、OB 于M 、N 两点，则∠MPN 的度数是（ ）（15图） （17图） （19图）A ． 70°B ． 80°C ． 90°D ．100° 16．在△ABC 中，∠A 和∠B 的度数如下，能判定△ABC 是等腰三角形的是（ ）A ． ∠A=50°，∠B=70°B ． ∠A=70°，∠B=40°C ． ∠A=30°，∠B=90°D ． ∠A=80°，∠B=60°17．如图∠AOP=∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=10，则PD 等于（ ）A ． 10B ．C ． 5D ． 2.5 18．等腰三角形的一边长为4，另一边长为9，则它的周长为（ ）19．如图所示，共有等腰三角形（ ）A ． 4个B ． 5个C ． 3个D ．2个20．如图，AD ⊥BC ，D 为BC 的中点，以下结论正确的有几个？（ ）①△ABD ≌△ACD ；②AB=AC ；③∠B=∠C ；④AD 是△ABC 的角平分线．A ． 1B ． 2C ． 3D ． 421．如图，已知△ABC 是等边三角形，点O 是BC 上任意一点，OE ，OF 分别于两边垂直，等边三角形的高为2，则OE+OF 的值为（ ）（21图） （22图） （23图）A ． 1B ． 3C ． 2D ． 422．如图，在Rt △ABC 中，已知，∠ACB=90°，∠B=15°，AB 边的垂直平分线交AB 于E ，交BC 于D ，且BD=13cm ，则AC 的长是（ ）A ． 13cmB ． 6.5cmC ． 30cmD ．6cm23．如图所示，AB=AD ，∠ABC=∠ADC=90°，则①AC 平分∠BAD ；②CA 平分∠BCD ；③AC 垂直平分BD ；④BD 平分∠ABC ，其中正确的结论有（ ）A ． ①②B ． ①②③C ． ①②③④D ．②③ 24．已知a ，b ，c 是△ABC 的三边，且a 2+b 2+c 2=ab+ac+bc ，则△ABC 是（ ）A ． 等腰三角形B ． 直角三角形C ． 等边三角形D ． 等腰直角三形25．如图，△ABC 中，AB=BC=AD ，D 在BC 的延长线上，则角α和β的关系是（ ）（25图） （26图） （28图）A ． α+β=180°B ． 3α+2β=180°C ． 3α+β=180°D ．2β=α26．如图，等边三角形ABC 内有一点P ，过点P 向三边作垂线，垂足分别为S 、Q 、R ，且PQ=6，PR=8，PS=10，则△ABC 的面积等于（ ）27．在边长为1的等边三角形内任意放一些点，要使得至少存在2个点之间的距离不超过，那么至少应该放几个点（）A ．n2+1 B．2n+1 C．2n D．n+128．如图所示，△ABC为正三角形，P是BC上的一点，PM⊥AB，PN⊥AC，设四边形AMPN，△ABC的周长分别为m、n，则有（）A ．B．C．D．29．如图，D，E，F为等边三角形ABC三边中点，AE、BF、CD交于O，DE，EF，FD为三条中位线，则图中能数出不同的直角三角形的个数是（）A ．36 B．32 C．30 D．2830．等腰△ABC中，∠B=50°，那么另外两个角的度数分别是_________．31．如图，已知：AB=AC=AD，∠BAC=50°，∠DAC=30°，则∠BDC=_________．32．如图，在△ABC中，∠BAC=135°，AD⊥BC于D，且AB+BD=DC，那么∠C=_________°．33．如图，Rt△ABC中，∠C=90°，BD=2CD，AD是∠BAC的角平分线，则∠B=_________度．34．若一腰上的中线把一个等腰三角形的周长分为12cm和21cm两部分，则其底边长为_________cm．36．如果一个三角形三边长为a、b、c，且满足（a+b+c）（a﹣c）=0，则该三角形的形状是_________．37．边长为a的等边三角形的面积为_________．38．如图，△ABC中，AB=AC，点P、Q分别在AC、AB上，且AP=PQ=QC=BC，则∠A的大小是_________．39．如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于E，交BC于D，BD=8，则AC=_________．41．如图，在△ABC中，∠ACD=90°，CA=CB，AD是△ABC的角平分线，点E在AB上，如果DE=2CD，那么∠ADE=_________度．42．等腰三角形的周长为24，腰长为x，则x的取值范围是_________．43．如图，点C、E和点B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=12°，则∠GEF=_________度．44．如图，AB=AC，∠BAC=120°，点D在BC上，DB=DA=4，那么BC=_________．45．如图，D是等边△ABC的AC边上的中点，点E在BC的延长线上，DE=DB，△ABC的周长是9，则∠E=_________°，CE=_________．46．如图，在△ABC中，AB=AC=5，BC=6，AD=4，点E、F是中线AD上的两点，则图中阴影部分的面积是_________．47．如果一个三角形一边上的中线和这边上的高重合，那么这个三角形是_________三角形．48．△ABC是等腰三角形，AB=AC，分别以两腰为边向外作等边△ADB和等边△ACE，若∠DAE=∠DBC，则∠BAC 的度数为_________．49．如图，等边△RST的顶点R、S、T分别在等腰△ABC的边AB、BC、CA上，设∠ART=x度，∠RSB=y度，∠STC=z度，用含y、z的代数式表示x是：_________．50．等腰三角形一腰上的高与另一腰的夹角为30°，腰长为2，则其底边的高为_________．51．如图所示，△ABC是等边三角形，点是AC的中点，过D点作DM⊥BE，垂足是MD；延长BC到E，使CE=CD，求证：BM=EM．52．如图，△ABC中，AB=AC，DE是AB的垂直平分线，D为垂足，交AC于E．若AD=5cm，△ABC的周长为27cm，求△BCE的周长．53．小明在找等边三角形ABC一边的三等分点时，他是这样做的，先做∠ABC、∠ACB的角平分线并且相交于点O，然后做线段BO、CO的垂直平分线，分别交BC于E、F，他说：“E、F就是BC边的三等分点．”你同意他的说法吗？请说明你的理由．54．如图，已知：等边三角形ABC，点D是AB的中点，过点D作DF⊥AC，垂足为F，过点F作FE⊥BC，垂足为E，若三角形ABC的边长为4．求：（1）线段AF的长度；（2）线段BE的长度．55．如图AF是△ABC的角平分线，BD⊥AF，交AF的延长线于D，DE∥AC交AB于E，求证：AE=BE．56．已知如图，△ABC中，AB=AC，D是AB的中点，DE⊥AB交AC于E，（1）若BE平分∠ABC，求∠A的度数．（2）若△ABC的周长为10，△BCE的周长为6，求BC的长度．57．如图，在△ABC中，∠B=45°，AD是∠BAC的角平分线，EF垂直平分AD，交BC的延长线于点F．求∠FAC 的大小．58．如图，在△ABC中，AB=AC，CD平分∠ACB交加于D点，AE∥DC交BC的延长线于点E，已知∠E=36°，求∠B的度数．59．已知：如图，∠ACB=90°，D、E是AB上的两点，且AE=AC，BD=BC，EF⊥CD于F，求证：CF=EF．60．已知：如图，Rt△ABC中，∠ACB=90°，边AC的垂直平分线DE交AB于点D，交AC于E，连接DC．求证：DA=DC=DB．61．如图，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数．62．等腰三角形中，一边与另一边之比为3：2，该三角形周长为56，求腰长是多少？63．如图：△ABC中，∠B=2∠C，AD是BC边上的高．求证：AB+BD=DC．64．如图，在△ABC中，AB=BC=AC，BD是中线，延长BC到E，使CE=CD．（1）已知CD=3，求BE的长；（2）求证：BD=ED；（3）若点F是BE边的中点，试判断DF与BE的位置关系并简要说明理由．65．如图所示，在△ABC中，∠C=90°，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，过点D 作DF⊥AB于点F，说明：BC=DE+EF成立的理由．66．如图，△ABC为等边三角形，D为BC上一点，∠ADE=60°，DE交∠ACB外角平分线于E．（1）AB与CE平行吗？请说明理由．（2）请说明∠BAD=∠EDC的理由．67．如图，在等腰△ABC中，∠A=80°，∠B和∠C的平分线相交于点O（1）连接OA，求∠OAC的度数；（2）求：∠BOC．68．如图，AD是△ABC的角平分线，过点D作直线DF∥BA，交△ABC的外角平分线AF于点F，DF与AC交于点E．求证：DE=EF．69．如图，在△ABC中，AB=AC=10，点D为BC上一点，过点D分别作DE∥AB交AC于点E，DE∥AC交AB 于点F．求四边形AFDE的周长．70．如图，AD是△ABC的角平分线，且∠B=∠ADB，过点C作AD的延长线的垂线，垂足为M．（1）若∠DCM=α，试用α表示∠BAD；（2）求证：AB+AC=2AM．72．已知：如图，在△ABC中，∠B=∠C，点D、E、F分别是边BC、AB、AC上的点，BE=CD，连接DE、DF，有∠EDF=∠C，那么DE和DF相等吗？试说明理由．73．如图，在等腰△ABC中，AB=AC，点D在BC上，且AD=AE．（1）若∠BAC=90°，∠BAD=30°，求∠EDC的度数？（2）若∠BAC=a（a＞30°），∠BAD=30°，求∠EDC的度数？（3）猜想∠EDC与∠BAD的数量关系？（不必证明）74．已知一个等腰三角形的周长为18cm．（1）如果腰长是底边的2倍，那么各边的长是多少？（2）如果一腰上的中线将该等腰三角形的周长分为1：2两部分，那么各边的长为多少？75．△ABC中，∠B=40°，过点A的直线将这个三角形分成2个等腰三角形，试确定∠C的度数．76．已知一个等腰三角形的两个内角分别为（2x﹣2）°和（3x﹣5）°，求这个等腰三角形各内角的度数．77．如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．（1）求∠ECD的度数；（2）若CE=5，求BC长．78．如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°，∠DAB=45°．（1）求∠DAC的度数；（2）求证：DC=AB．79．如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．（1）DE，DF，CG的长之间存在着怎样的等量关系？并加以证明；（2）若D在底边的延长线上，（1）中的结论还成立吗？若不成立，又存在怎样的关系？请说明理由．80．如图，已知在△ABC中，AB=AC，D是AB上一点，DE⊥BC，E是垂足，ED的延长线交CA的延长线于点F，求证：AD=AF．参考答案：1．∵DE是AB的垂直平分线，∴AE=BE，∵△ABC的周长为25cm，△EBC的周长为16cm，AC=AB，∴2AC+BC=25cm，BE+CE+BC=AE+EC+BC=AC+BC=16cm，即，解得：AC=9cm，故选B．2．∵AB=AC∴∠B=∠C∵FD⊥BC于D，DE⊥AB于E∴∠BED=∠FDC=90°∵∠AFD=158°∴∠EDB=∠CFD=180°﹣158°=22°∴∠EDF=90°﹣∠EDB=90°﹣22°=68°．故选C3．∵AB=AD，∴∠B=∠ADB，由∠BAD=80°得∠B==50°=∠ADB，∵AD=DC，∴∠C=∠ACD，∴∠C=∠ADB=25°故选D．4．A、等腰三角形两腰上的高相等，故错误；B、等腰三角形不一定是锐角三角形，故错误；C、有一个角是60°的等腰三角形是等边三角形，故错误；D、三角形三条角平分线的交点到三边的距离相等，故正确，故选D5．∵AB=AC，∴△ABC是等腰三角形，∵∠A是顶角，且∠A等于∠C的一半，∴∠A+∠C+∠ABC=∠A+2∠A+2∠A=180°，∴∠A=36°，∠C=∠ABC=72°，BD平分∠ABC交AC于D，∴∠ABD=∠DBC=36°，∵∠A=∠ABD=36°，∴△ABD是等腰三角形．∠BDC=∠A+∠ABD=36°+36°=72°=∠C，∴△BDC是等腰三角形．∴共有3个等腰三角形．故选B．6．AB=2，∵等边三角形高线即中点，∴BD=CD=1，在Rt△ABD中，AB=2，BD=1，∴AD==，∴等边△ABC 的面积为BC•AD=×2×=，故选：B．7．∵△ABC是等边三角形，∴∠B=∠BAC=60°，∵∠BAD=20°，∴∠DAE=∠BAC﹣∠BAD=40°，∵AD=AE，∴∠ADE=∠AED，∵∠ADE+∠AED+∠DAE=180°，∴∠ADE=∠AED=×（180°﹣40°）=70°，∵∠ADC=∠B+∠BAD=60°+20°=80°，∴∠CDE=∠CDA﹣∠ADE=80°﹣70°=10°．故选A8．连接AD．∵DE垂直平分AB，BD=3，∴BD=AD=3；∴∠B=∠BAD（等边对等角）；又∵∠ABC=15°，∴∠BAC=15°；∴∠ADC=2∠BAC=30°（外角定理），∴=cos∠ADC，∴DC=AD•cos30°=．故选A．9．过E作EM∥BC，交AD于N，∵AC=4，AE=2，∴EC=2=AE，∴AM=BM=2，∴AM=AE，∵AD是BC边上的中线，△ABC是等边三角形，∴AD⊥BC，∵EM∥BC，∴AD⊥EM，∵AM=AE，∴E和M关于AD对称，连接CM交AD于F，连接EF，则此时EF+CF的值最小，∵△ABC是等边三角形，∴∠ACB=60°，AC=BC，∵AM=BM，∴∠ECF=∠ACB=30°，故选C．10．∵∠A=∠P1P2A=16°∴∠P2P1P3=32°，∠P1P3P2=32°∴∠P1P2P3=116°∴∠P3P2P4=48°∴∠P3P2P4=48°∴∠P2P3P4=96°∴∠P4P3P5=52°∴∠P3P5P4=52°∴∠P3P4P5=52°∴∠P5P4P6=76°∴∠P4P6P5=76°∴∠P4P5P6=28°∴∠P6P5P7=86°，此时就不能在往上焊接了，综上所述总共可焊上5条．故选B．11．△ABC的周长为6，∴AB=BC=AC=2，DC=CE=1，又∵∠ACB=∠CDE+∠CED∴∠CED=30°，△BDE为等腰三角形，DE=BD=∴BD+DE+BE=2+2+1=3+2．故选C12．①三条边相等的三角形是等边三角形符合等边三角形的定义，故正确；②有一个角是60°的等腰三角形是等边三角形，正确；③有两个角为60°的三角形是等边三角形，正确；④三个角相等的三角形是等边三角形，正确．故选D13．∵ED⊥BC，∠C=60°，∴∠CED=30°，设DE=x，则AE=x，且CE=x，又∵AE+CE=5，∴x+x=5，解得x=10﹣15，∴CE=5﹣（10﹣15）=20﹣10．故选D14．①BC边为底边时，AD=BC=BD=CD，所以△ABD和△ADC为等腰直角三角形，∠BAC=∠BAD+∠CAD=90°．②BC 边为腰时可分为和两种情况，垂足在三角形内部时，AD==AC，所以∠C=30°，又因为AC=BC，所以∠BAC=∠ABC=（180°﹣∠C）=75°．垂足落在三角形外时，由图知AD=AB，所以∠ABD=30°，所以∠BAC=∠C=∠ABD=15°．故答案为D15．∵P关于OA、OB的对称∴OA垂直平分PC，OB垂直平分PD∴CM=PM，PN=DN∴∠PMN=2∠C，∠PNM=2∠D，∵∠PRM=∠PTN=90°，∴在四边形OTPR中，∴∠CPD+∠O=180°，∴∠CPD=180°﹣40°=140°∴∠C+∠D=40°∴∠MPN=180°﹣40°×2=100°故选D16．当顶角为∠A=50°时，∠B=65°，当顶角为∠B=70°时，∠A=55°所以A选项错误．当顶角为∠B=40°时，∠A=70°，所以B选项正确．当顶角为∠A=30°时，∠B=75°，当顶角为∠B=90°时，∠A=45°所以C选项错误．当顶角为∠A=80°时，∠B=50°，当顶角为∠B=60°时，∠A=60°所以D选项错误．故选B17．∵PC∥OA，∴∠CPO=∠POA，∵∠AOP=∠BOP=15°，∴∠AOP=∠BOP=∠CPO=15°，过点P作∠OPE=∠CPO交于AO于点E，则△OCP≌△OEP，∴PE=PC=10，∵∠PEA=∠OPE+∠POE=30°，∴PD=10×=5．故选C．18．4是腰长时，三角形的三边分别为4、4、9，∵4+4=8＜9，∴不能组成三角形，4是底边时，三角形的三边分别为4、9、9，能组成三角形，周长=4+9+9=22，综上所述，该等腰三角形的周长为22．故选D 19．根据三角形的内角和定理，得：∠ABO=∠DCO=36°，根据三角形的外角的性质，得∠AOB=∠COD=72°．再根据等角对等边，得等腰三角形有△AOB，△COD，△ABC，△CBD和△BOC．故选B20．∵AD⊥BC，D为BC的中点，∴∠ADB=∠ADC=90°，BD=BC，AD为公共边，∴△ABD≌△ACD，∴AB=AC，∠B=∠C，∠BAD=∠CAD，即AD是△ABC的角平分线．故选D21．∵△ABC是等边三角形，∴AB=BC=AC，∠A=∠B=∠C=60°又∵OE⊥AB，OF⊥AC，∠B=∠C=60°，∴OE=OB•sin60°=OB，同理OF=OC．∴OE+OF=（OB+OC）=BC．在等边△ABC中，高h=AB=BC．∴OE+OF=h．又∵等边三角形的高为2，∴OE+OF=2，故选C22．∵AB边的垂直平分线交AB于E，交BC于D（已知）∴AD=BD（线段垂直平分线的性质）∴∠DAE=∠B=15°且AD=BD=13cm（等腰三角形的性质）∴∠ADC=30°（外角性质）∴AC=AD=6.5cm．故选B23．在Rt△ABC和Rt△ADC中，AB=AD，AC=AC，所以Rt△ABC≌Rt△ADC（HL）．所以∠ACB=∠ACD，∠BAC=∠DAC，即AC平分∠BAD，CA平分∠BCD．故①②正确；在△ABD中，AB=AD，∠BAO=∠DAO，所以BO=DO，AO⊥BD，即AC垂直平分BD．故③正确；不能推出∠ABO=∠CBO，故④不正确．故选B24．原式可化为2a2+2b2+2c2=2ab+2ac+2bc，即a2+b2+c2+a2+b2+c2﹣2ab﹣2ac﹣2bc=0；根据完全平方公式，得：（a﹣b）2+（c﹣a）2+（b﹣c）2=0；由非负数的性质，可知：a﹣b=0，c﹣a=0，b﹣c=0；即：a=b=c．所以△ABC是等边三角形．故选C．25．∵AB=AD，∴∠B=∠D=α，∵AB=BC∴∠BAC=∠BCA，∵∠ACB=α+β∴在等腰三角形ABC中，2（α+β）+α=180°∴3α+2β=180°，故选B26．连接AP、BP、CP，过点A作AD⊥BC于D，等边三角形面积S=BC•（PQ+PR+PS）=BC•AD故PQ+PR+PS=AD，∴AD=6+8+10=24，∵∠ABC=60°∴AB=24×=16，∴△ABC的面积S=BC•AD=×24×16=192，故选B．27．把三角形每条边分成n份，相应点之间连线，可以把三角形分成n2个边长为的小三角形，至少n2+1个点可以保证至少有两个点落在同一个小三角形内，所以那两个点的距离是不超过的．故选A28．设BM=x，CN=y则BP=2x，PC=2y，PM=x，PN=yAM+AN=2BC﹣（BM+CN）=3（x+y），故==≈0.7887．故选D．29．①∵DE，EF，FD为等边△ABC三条中位线，∴AB=AC=BC，∴EF AB，ED AC，∴四边形CEDF是菱形，∴EF⊥CD，∴在菱形CEDF中有6个不同的直角三角形：Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG；同理，在菱形ADEF、菱形BEFD中各有6个不同的直角三角形；②∵D为等边三角形ABC三边中点，∴CD⊥AB，∴△ADC、△BDC、AOD、△BOD是直角三角形；同理，以BF、AE为直角边的三角形各有4个；综上所述，图中能数出的直角三角形由6×3+4×3=30（个）；故选C30. 当∠B=50°为顶角时，此时∠A=∠C==65°；当∠B=50°为底角时，此时另一底角为50°，顶角为80°，故答案为：50°，80°或65°，65°31．根据题意，可以以点A为圆心，以AB为半径作圆，即可得出点B、C、D均在圆周上，故有∠BAC=2∠BDC=50°，即∠BDC=25°．故答案为：25°32．在DC上截取DE=BD，连接AE，∵AD⊥BC，∴∠ADB=∠ADE=90°，∵AD=AD，∴△ADB≌△ADE，∴∠B=∠AED，AE=AB，∵AB+BD=DC，DE+EC=DC，∴AE=AB=EC，∴∠AEB=2∠EAC=2∠C，∴∠B=2∠C，∵∠BAC=135°，∠B+∠C+∠BAC=180°，∴3∠C=45°，∴∠C=15°．故答案为：1533．过D作DE⊥AB于E，∵AD是∠BAC的角平分线，∠C=90°，DE⊥AB，∴CD=DE，∵BD=2CD，∴BD=2DE，∵∠BED=90°，∴∠B=30°．故答案为：3034．设等腰三角形的腰长是xcm，底边是ycm．根据题意，得：或，解得或．再根据三角形的三边关系，知：8，8，17不能组成三角形，应舍去．所以它的底边是5cm．故答案为：535．如图：△ABC中，AB=AC，BD是边AC上的高．∵∠A=80°，且AB=AC，∴∠ABC=∠C=（180°﹣80°）÷2=50°；在Rt△BDC中，∠BDC=90°，∠C=50°；∴∠DBC=90°﹣50°=40°．故答案为：40°36．∵（a+b+c）（a﹣c）=0，∴a+b+c=0或a﹣c=0，∵a、b、c，为三角形三边，∴a+b+c=0（舍去），∴a=c∴该三角形为等腰三角形，故答案为：等腰三角形37．如图作AD⊥BC于点D．∵△ABC为等边三角形，∴∠B=60°，∴AD=AB×sin∠B=a，∴边长为a 的等边三角形的面积为×a ×a=a2，故答案为：a238．∵AB=AC，AP=PQ，QP=QC，QC=BC，∴∠ABC=∠ACB，∠A=∠AQP，∠QPC=∠QCP，∠BQC=∠B（等边对等角），设∠A=x°，则∠AQP=x°，∵在△AQP中，∠QPB是外角，∴∠QPC=∠A+∠AQP=2x°（三角形的一个外角等于和它不相邻的两个内角的和），∵在△BCQ中，∠BQC是外角，∴∠BQC=∠ACQ+∠A（三角形的一个外角等于和它不相邻的两个内角的和），∴∠BQC=3x°，∴∠B=3x°，∴∠ABC=3x°，∵在△ABC中，∠A+∠ACB+∠B=180°，∴x°+3x°+3x°=180°（三角形三个内角的和等于180°），解得x=（）°，∴∠A=（）°．39．∵△ABC中，∠C=90°，∠B=15°，∴∠BAC=180°﹣∠C﹣∠B=180°﹣90°﹣15°=75°．连接AD．∵ED是AB的垂直平分线，∴AD=BD=8，∠B=∠1=15°，∴∠2=∠BAC﹣∠1=75°﹣15°=60°．在Rt△ACD中，∠2=60°，∠C=90°，∴∠3=180°﹣∠C﹣∠2=180°﹣90°﹣60°=30°．∴AC=AD=BD=×8=4．40．∵OC为等边三角形的高，且等边三角形的边长为1，∴NC=，∵△OCD为等边三角形，∴∠OCD=60°，∴OE⊥CD，∴OE==（）2，以此类推，当ON与OA重合时，一共旋转了10次，∴ON 的长为（）10，故答案为（）1041．作DF⊥AB于点F∵△ABC中，∠ACD=90°，CA=CB，∴∠CAB=∠B=45°，∵AD是△ABC的角平分线，∴DF=DC，∠DAB=22.5°，∵DE=2CD，∴DE=2DF，∴∠DEB=30°，∴∠ADE=∠DEB=﹣∠DAB=30°﹣22.5°=7.5°，故答案为7.5°．42．底边是24﹣2x，根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边．得：0＜24﹣2x＜2x．解得6＜x＜12．故填6＜x＜1243．∵∠A=12°，AB=BC，∴∠A=∠ACB=12°，∠CBD=∠A+∠ACB=12°+12°=24°；∵BC=CD，∴∠CBD=∠CDB=24°，∴∠ECD=∠A+∠CDA=36°（外角定理）；∵CD=DE，∴∠DCE=∠DEC=36°，∴∠EDF=∠A+∠AED=48°；又∵DE=EF，∴∠EDF=∠EFD=48°，∴∠GEF=∠A+∠EFD=12°+48°=60°．故答案是：6044．∵AB=AC，∠BAC=120°，∴∠B═∠C=（180°﹣∠A）=30°，∵DB=DA=4，∴∠B=∠BAD=30°，∴∠ADC=∠B+∠BAD=60°，∴∠DAC=180°﹣∠C﹣∠ADC=90°，∵∠C=30°，∴DC=2AD=2×4=8，∴BC=BD+DC=4+8=12，故答案为：1245．∵△ABC为等边三角形，D为AC边上的中点，∴BD为∠ABC的平分线，且∠ABC=60°，即∠DBE=30°，又DE=DB，∴∠E=∠DBE=30°，∵等边△ABC的周长为9，∴AC=3，且∠ACB=60°，∴∠CDE=∠ACB﹣∠E=30°，即∠CDE=∠E，∴CD=CE=AC=．故答案为：30；46．∵AB=AC，BC=6，AD是△ABC的中线，∴BD=DC=BC=3，AD⊥BC，∴△ABC关于直线AD对称，∴B、C关于直线AD对称，∴△CEF和△BEF关于直线AD对称，∴S△BEF=S△CEF，∵△ABC 的面积是：×BC×AD=×6×4=12，∴图中阴影部分的面积是S△ABC=6．故答案为：647．∵BD=CD，AD⊥BC，∴AB=AC，即三角形是等腰三角形．故填等腰．48．∵AB=AC，∴∠ABC=∠ACB，故2∠ABC+∠BAC=180°，∵等边三角形各内角为60°，∠DAE=∠DBC，∴120°+∠BAC=60°+∠ABC，又∵2∠ABC+∠BAC=180°，∴∠BAC=20°．故答案为：20°49．∵∠BRS+y=∠TSC+z，∴∠BRS﹣∠TSC=z﹣y，又∠BRS+x=y+∠TSC=120°，∴∠BRS﹣∠TSC=y﹣x，∴z﹣y=y﹣x，∴x=2y﹣z．故答案为：x=2y﹣z．50．①如图1，已知AB=AC=2，BD为腰AC上的高，可知∠ABD=30°，可得∠A=60°，即证△ABC为正三角形，即可得出底边AC 上的高等于腰上的高等于．②如图2，AB=AC=2，CD⊥BA交BA是延长线于点D，且∠CAD=30°，可得AD=1，CD=，可得BC=2，即BE=，在Rt△ABE中，AB=2，BE=，即AE=1．故答案为：1或．51．∵△ABC是等边三角形，D是AC的中点，∴BD平分∠ABC（三线合一），∴∠ABC=2∠DBE；∵CE=CD，∴∠CED=∠CDE．又∵∠ACB=∠CED+∠CDE，∴∠ACB=2∠E；又∵∠ABC=∠ACB，∴2∠DBC=2∠E，∴∠DBC=∠E，∴BD=DE．又∵DM⊥BE，∴BM=EM．52．∵DE是AB的垂直平分线．∴AB=2AD，EA=EB．∵AD=5cm，∴AB=10cm．∵△ABC的周长为27cm，∴AC+BC+AB=2cm7，AC+BC=17cm即AE+EC+BC=17cm．∴EB+EC+BC=17．即△BCE的周长为17cm53．E，F是BC的三等分点．理由：连接OE，OF，∵DE垂直平分OB∴BE=OE（线段垂直平分线上的点到线段两端点距离相等），同理OF=CF，∴∠EBO=∠BOE，∠FCO=∠FOC，∵等边三角形ABC中，∴∠ABC=∠ACB=60°（等边三角形各角相等且为60°）∵BO平分∠ABC，CO平分∠ACB∴∠EBO=∠ABC=30°，∠FCO=∠ACB=30°∴∠BOE=∠EBO=30°，∠FOC=∠FCO=30°∴∠OEF=∠BOE+∠EBO=60°，∠OFE=∠FOC+∠FCO=60°，∴△OEF是等边三角形（有两个内角60°的三角形是等边三角形）∴OE=OF=EF（等边三角形各边相等）∴BE=EF=FC，即E，F是BC的三等分点54．（1）∵D是AB的中点，∴AD==2，∵等边三角形ABC中∠A=∠C=60°，且DF⊥AC，∴∠ADF=180°﹣90°﹣60°=30°，在Rt△ADF中，AF==1；（2）FC=AC﹣AF=4﹣1=3，同理，在Rt△FEC中，EC==1.5，∴BE=BC﹣EC=4﹣1.5=2.5．故答案为：AF=1，BE=2.555．∵AF平分∠BAC，∴∠BAD=∠CAD，∵DE∥AC，∴∠EDA=∠CAD=∠BAD，∴AE=ED，∵∠EDB+∠ADE=90°，∴∠BDE+∠BAD=90°，∵∠EBD+∠BAD=90°，∴∠BDE=∠EBD，∴BE=ED，∴AE=BE．56．（1）∵D是AB的中点，DE⊥AB交AC于E，∴EB=EA，∴∠A=∠ABE，∵BE平分∠ABC，∴∠ABE=∠CBE，∵AB=AC，∴∠C=∠ABC=2∠ABE=2∠A，∵∠A+∠ABC+∠C=180°，即：5∠A=180°∴∠A=36°；（2）∵△ABC的周长为10，∴AB+AC+BC=10，∵△BCE的周长为6，∴BE+EC+BC=AE+EC+BC=AC+BC=6，∴AB=AC=4．∴BC=257．∵EF垂直平分AD，∴FA=FD，∴∠ADF=∠DAF，又∵∠ADF=∠B+∠BAD，∠DAF=∠FAC+∠DAC，∵∠BAD=∠DAC，∴∠FAC=∠B=45°．58．∵AE∥DC，∴∠BCD=∠E=36°，又∵CD平分∠ACB，∴∠ACB=2∠BCD=72°，∵AB=AC，∴∠B=∠ACD=72°．答：∠B的度数为72°．59．连接CE．∵AE=AC，∴∠1+∠2=∠AEC=∠3+∠B．①同理，∠2+∠3=∠1+∠A．②①+②得2∠2=∠A+∠B．∵∠ACB=90°，∴∠A+∠B=90°．∴∠2=45°．∵EF⊥CD，∴∠CFE=90°．∴∠CEF=45°=∠2，∴EF=CF．60．∵AC的垂直平分线DE，∴AD=DC，∴∠A=∠ACD，∵∠ACB=90°，∴∠A+∠B=90°，∠ACD+∠BCD=90°，∴∠B=∠BCD，∴DC=BD，∴DA=DC=DB61．∵AB=BC=CD=DE，∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，根据三角形的外角性质，∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，又∵∠EDM=84°，∴∠A+3∠A=84°，解得：∠A=21°62．∵等腰三角形中，一边与另一边之比为3：2，∴设两边分别为3x，2x，根据题意得：3x+3x+2x=56或3x+2x+2x=56解得：x=7，此时腰长3x=21，或x=8，此时腰长2x=16，所以腰长为21或1663．在线段DC上取一点E，使DE=DB，连接AE，∵AD⊥BC，∴AD垂直平分BE，∴AB=AE，∴∠AEB=∠B，∵∠B=2∠C，∴∠AEB=2∠C，∴∠EAC=∠AEB﹣∠C=2∠C﹣∠C=∠C，∴AE=CE，∴CE=AE=AB，∴DC=DE+CE=AB+BD，∴AB+BD=DC．64．（1）∵AB=BC=AC，BD是中线，∴BC=AC=2CD∵CD=3，∴BC=2CD=6，CE=CD=3∴BE=BC+CE=6+3=9（2）∵△ABC是等边三角形，BD是中线，∴∠ABC=∠ACB=60°．∠DBC=30°（等腰三角形三线合一）．又∵CE=CD，∴∠CDE=∠CED．又∵∠BCD=∠CDE+∠CED，∴∠CDE=∠CED=∠BCD=30°．∴∠DBC=∠DEC．∴DB=DE（等角对等边）．（3）∵点F是BE边的中点，∴DF是BE边的中线，∵BD=ED∴DF⊥BE65．∵BD平分∠ABC，DF⊥AB，∠C是直角，∴CD=DF，∠DBC=∠DBE，∠DFB=∠C，∴△BCD≌△BFD，∴BC=BF，∵DE∥BC，∴∠DBC=∠EDB，即∠DBC=∠DBE，∴△BDE是等腰三角形，∴BE=DE，∴BF=BC=DE+EF66．（1）∵等边三角形各内角为60°∴∠ACF=180°﹣60°=120°，CE为∠ACF的角平分线，∴∠ECF=60°，∵∠ABC=60°∴EC∥AB．（2）∵∠EDC+∠ADE+∠ADB=180°，∴∠EDC+∠ADB=120°，∵∠ABD+∠BAD+∠ADB=180°，∴∠BAD+∠ADB=120°，∴∠BAD=∠EDC．67．（1）连接AO，∵在等腰△ABC中，∠B和∠C的平分线相交于点O，∴等腰△ABC关于线段AO所在的直线对称，∵∠A=80°，∴∠OAC=40°（2）∵BO、CO分别平分∠ABC和∠ACB，∴∠OBC=∠ABC，∠OCB=∠ACB，∴∠BOC=180°﹣（∠OBC+∠OCB）=180°﹣（∠ABC+∠ACB）=180°﹣（∠ABC+∠ACB）=180°﹣（180°﹣∠A）=90°+∠A．∴当∠A=80°时，=130°．68．证明：∵AD是△ABC的角平分线，AF平分△ABC 的外角，∴∠1=∠2，∠3=∠4，∵DF∥BA，∴∠4=∠ADE，∠1=∠F∴∠3=∠ADE，∠2=∠F∴DE=EA EF=EA∴DE=EF69．∵AB=AC=10，∴∠B=∠C，由DF∥AC，得∠FDB=∠C=∠B，∴FD=FB，同理，得DE=EC．∴四边形AFDE的周长=AF+AE+FD+DE=AF+FB+AE+EC=AB+AC=10+10=20．∴四边形AFDE的周长为2070．（1）∵CM⊥AM，∠DCM=α，∴∠CDM=∠ADB=∠B=90°﹣α，∴∠BAD=180°﹣2∠ABD=180°﹣2（90°﹣α）=2α；（2）延长AM到F使MF=AM，则有AC=CF∵AD平分∠CAB∴∠CAF=∠BAF=∠F∴CF∥AB∴∠FCD=∠ABD=∠ADB=∠CDF∴CF=DF∵AD+DF=2MA∴AB+AC=2MA71．∵王宏和张新他们两家和学校正好构成一个等腰三角形，而且王宏家距学校2千米，张新家距学校4千米，∴此等腰三角形的底边长为2，两腰均为4，∴王宏与张新两家的距离是4千米；当王宏家与学校相距2千米，而张新家与学校相距3千米时，王宏与张新两家相距可能是2千米也可能是3千米72．DE=DF．证明：∵∠CDF+∠EDF+∠BDE=180°，∠CDF+∠C+∠CFD=180°∴∠BDE=∠CFD在△EBD和△DCF中∠BDE=∠CFDBE=CD∠B=∠C∴△EBD≌△DCF∴DE=DF73．（1）解：∵∠BAC=90°，AB=AC，∴∠B=∠C=（180°﹣∠BAC）=45°，∴∠ADC=∠B+∠BAD=45°+30°=75°，∵∠DAC=∠BAC﹣∠BAD=90°﹣30°=60°，∵AD=AE，∴∠ADE=∠AED=（180°﹣∠DAC）=60°，∴∠EDC=∠ADC﹣∠ADE=75°﹣60°=15°，答：∠EDC的度数是15°．（2）解：与（1）类似：∠B=∠C=（180°﹣∠BAC）=90°﹣α，∴∠ADC=∠B+∠BAD=90°﹣α+30°=120°﹣α，∵∠DAC=∠BAC﹣∠BAD=α﹣30°，∴∠ADE=∠AED=（180°﹣∠DAC）=105°﹣α，∴∠EDC=∠ADC﹣∠ADE=（120°﹣α）﹣（105°﹣α）=15°，答：∠EDC的度数是15°．（3）∠EDC与∠BAD的数量关系是∠EDC=∠BAD．74.（1）解：设底边BC=acm，则AC=AB=2acm，∵三角形的周长是18cm，∴2a+2a+a=18，∴a=，2a=，答：等腰三角形的三边长是cm ，cm ，cm．（2）解：设BC=acm，AB=AC=2bcm，∵中线BD将△ABC的周长分为1：2两部分，18×=12，18×=6，∴2b+b=6，b+a=12或2b+b=12，b+a=6，解得：a=10，b=2或b=4，a=2，∴①三角形三边长是10cm，4cm，4cm，因为4+4＜10，不符合三角形三边关系定理，∴此种情况舍去，②三角形的三边长是2cm，8cm，8cm，符合三角形的三边关系定理，综合上述：符合条件的三角形三边长是8cm，8cm，2cm，答：等腰三角形的边长是8cm，8cm，2cm．75．分成两类进行研究：（1）∠B为△ABD的底角，如果∠BAD=40°，那么∠ADC=80°；如果∠ADC为△ACD的底角，那么∠C=80°或20°；如果∠ADC为△ACD的顶角，那么∠C=50°；如果∠ADB=70°，那么∠ADC=140°，所以∠C=20°（2）∠B为△ABD的顶角，这时∠ADB=70°，∠ADC=110°，所以∠C=35°；综上所述，∠C的值为20°或35°或50°或80°76．①当（2x﹣2）°和（3x﹣5）°是两个底角时，2x﹣2=3x﹣5，x=3°，∴三个内角分别是4°，4°，172°；②当2x﹣2是顶角时，2x﹣2+2（3x﹣5）=180°，解得x=24°，∴三个内角分别是46°，67°，67°；③当3x﹣5是顶角时，3x﹣5+2（2x﹣2）=180°，解得x=27°，∴三个内角分别是76°52°，52°77．（1）∵DE垂直平分AC，∴CE=AE，∴∠ECD=∠A=36°；（2）∵AB=AC，∠A=36°，∴∠B=∠ACB=72°，∴∠BEC=∠A+∠ECD=72°，∴∠BEC=∠B，∴BC=EC=5．答：（1）∠ECD的度数是36°；（2）BC长是578．1）解：∵AB=AC，∴∠B=∠C=30°，∵∠C+∠BAC+∠B=180°，∴∠BAC=180°﹣30°﹣30°=120°，∵∠DAB=45°，∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°；（2）证明：∵∠DAB=45°，∴∠ADC=∠B+∠DAB=75°，∴∠DAC=∠ADC，∴DC=AC，∴DC=AB79．（1）DE+DF=CG．证明：连接AD，则S△ABC=S△ABD+S△ACD ，即AB•CG=AB•DE+AC•DF，∵AB=AC，∴CG=DE+DF．（2）当点D在BC延长线上时，（1）中的结论不成立，但有DE﹣DF=CG．理由：连接AD，则S△ABD=S△ABC+S△ACD，即AB•DE=AB•CG+AC•DF∵AB=AC，∴DE=CG+DF，即DE﹣DF=CG．同理当D点在CB的延长线上时，则有DE﹣DF=CG，说明方法同上．80．证明：∵AB=AC，∴∠B=∠C，∵DE⊥BC，∴∠C+∠F=90°，∠B+∠BDE=90°，∵∠ADF=∠BDE，∴∠F=∠ADF，∴AD=AF。

备考2023年中考数学一轮复习-图形的性质_三角形_等腰三角形的性质-综合题专训及答案等腰三角形的性质综合题专训1、(2016北京.中考真卷) 在等边△ABC中，（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．①依题意将图2补全；②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：要证明PA=PM，只需证△APM是等边三角形；想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．2、(2015葫芦岛.中考真卷) 在△ABC中，AB=AC，点F是BC延长线上一点，以CF 为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．3、(2017杭州.中考模拟) 如图1，O为线段AB上一点，AB=6，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．（1）若AO=4，=；①当t=1秒时，OP=，S△ABP②当△ABP是直角三角形时，求t的值；（2）如图2，若点O为AB中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQ•BP的值．4、(2016巢湖.中考模拟) 如图，有一块分别均匀的等腰三角形蛋糕（AB=AC且AB≠BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．这条分割直线既平分了三角形的面积，又平分了三角形的周长，我们称这条直线为三角形的“等分积周线”．（1）小明很快就想到了一条经过点A分割直线，请你用尺规作图在图1中画出这条“等分积周线（不写画法）．（2）小华觉得小明的方法很好，所以自己模仿着在图2中过点C画了一条直线CD交AB于点D．你觉得小华会成功吗？请说明理由．（3）若AB=BC=5，BC=6，请你通过计算，在图3中找出△ABC不经过顶点的一条“等分积周线”．5、(2018南宁.中考模拟) 如图，矩形ABCD中，AB=4，BC=6，E是BC边的中点，点P在线段AD上，过P作PF⊥AE于F，设PA=x．（1）求证：△PFA∽△ABE；（2）当点P在线段AD上运动时，设PA=x，是否存在实数x，使得以点P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，请说明理由；（3）探究：当以D为圆心，DP为半径的⊙D与线段AE只有一个公共点时，请直接写出x满足的条件：．6、(2017洛阳.中考模拟) 如图，在△ABD中，AB=AD，以AB为直径的⊙F交BD于点C，交AD于点E，CG⊥AD于点G，连接FE，FC．（1）求证：GC是⊙F的切线；（2）填空：①若∠BAD=45°，AB=2 ，则△CDG的面积为．②当∠GCD的度数为时，四边形EFCD是菱形．7、(2017衡阳.中考模拟) 如图△ABC中，AB=AC=10厘米，BC=12厘米，D是BC的中点，点P从B出发，以a厘米/秒（a＞0）的速度沿BA匀速向点A运动，点Q 同时以1厘米/秒的速度从D出发，沿DB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为t秒．（1）若a=2，△BPQ∽△BDA，求t的值；（2）设点M在AC上，四边形PQCM为平行四边形．①若a= ，求PQ的长；②是否存在实数a，使得点P在∠ACB的平分线上？若存在，请求出a的值；若不存在，请说明理由．8、(2018永州.中考真卷) 如图1．在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB上的高，CD交GH于点I．若CI＝4，HI＝3，AD ．矩形DFGI恰好为正方形．（1）求正方形DFGI的边长；（2）如图2，延长AB至P．使得AC＝CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M、N，求△MNG′的周长．9、(2019广东.中考模拟) 如图M2-11，Rt△ABC中，∠C=90°，BD为△ABC的角平分线，以AD为直径的⊙O交AB于点E，BD的延长线交⊙O于点F，连接AF，EF，ED．（1）求证：∠BDC=∠BDE；（2）求证：FA=FE；（3）若BC=4，CD=3，求AF的长．10、(2019柳州.中考模拟) 如图，已知直线与双曲线交于A，B两点点A在点B的上方.（1）求点A与点B的坐标；（2）点C在x轴上，若AC是等腰的腰，求符合条件的所有点C坐标.11、(2017遵义.中考真卷) 边长为2 的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．（1）连接CQ，证明：CQ=AP；（2）设AP=x，CE=y，试写出y关于x的函数关系式，并求当x为何值时，CE= BC；（3）猜想PF与EQ的数量关系，并证明你的结论．12、(2017云南.中考真卷) 如图，△ABC是以BC为底的等腰三角形，AD是边BC上的高，点E，F分别是AB，AC的中点．（1）求证：四边形AEDF是菱形；（2）如果四边形AEDF的周长为12，两条对角线的和等于7，求四边形AEDF的面积S．13、(2020衡阳.中考真卷) 如图1，平面直角坐标系中，等腰的底边在x轴上，，顶点A在y的正半轴上，，一动点从出发，以每秒1个单位的速度沿向左运动，到达的中点停止．另一动点F从点C出发，以相同的速度沿向左运动，到达点O停止．已知点E、F同时出发，以为边作正方形，使正方形和在的同侧．设运动的时间为秒（）．（1）当点H落在边上时，求t的值；（2）设正方形与重叠面积为S，请问是存在t值，使得？若存在，求出t值；若不存在，请说明理由；（3）如图2，取的中点D，连结，当点E、F开始运动时，点N从点O出发，以每秒个单位的速度沿运动，到达点O停止运动．请问在点E的整个运动过程中，点M可能在正方形内（含边界）吗？如果可能，求出点M在正方形内（含边界）的时长；若不可能，请说明理由．14、(2020温州.中考模拟) 如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，AB、BC的长分别是一元二次方程x2﹣7x+12＝0的两个根（BC＞AB），OA＝2OB，边CD交y轴于点E，动点P以每秒1个单位长度的速度，从点E出发沿折线段ED﹣DA向点A运动，运动的时间为t（0≤t＜6）秒，设△BOP与矩形AOED 重叠部分的面积为S.（1）求点D的坐标；（2）求S关于t的函数关系式，并写出自变量的取值范围；（3）在点P的运动过程中，是否存在点P，使△BEP为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由.15、(2020路北.中考模拟) 如图，在中，，点从点出发沿向点运动，点从点出发沿向点运动，点和点同时出发，速度相同，到达点或点后运动停止．（1）求证：；（2）若，求的度数；（3）若的外心在其内部时，直接写出的取值范围．等腰三角形的性质综合题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：11.答案：12.答案：13.答案：14.答案：15.答案：。

初中数学综合复习等腰三角形（含等边三角形）部分4一、选择题1. 如图，梯形ABCD中，AD∥BC，DE∥AB，DE=DC，∠C=80°．则∠A等于（）A．80°B．90°C．100°D．110°【答案】C2.如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是A、85°B、80°C、75°D、70°【答案】A3.如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第n个三角形中以A n为顶点的内角度数是( )A．(12)n·75°B．(12)n－1·65°C．(12)n－1·75°D．(12)n·85°【答案】C4.如图，坐标平面上，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB＝BC＝5．若A点的坐标为(﹣3，1)，B、C两点在方程式y＝﹣3的图形上，D、E两点在y轴上，则F点到y轴的距离为何？()A1A2A3A4CBDEF…第11题图第10题图AB CDEA ．2B ．3C ．4D ．5分析：如图，作AH 、CK 、FP 分别垂直BC 、AB 、DE 于H 、K 、P ．由AB ＝BC ，△ABC ≌△DEF ，就可以得出△AKC ≌△CHA ≌△DPF ，就可以得出结论．解：如图，作AH 、CK 、FP 分别垂直BC 、AB 、DE 于H 、K 、P ． ∴∠DPF ＝∠AKC ＝∠CHA ＝90°． ∵AB ＝BC ， ∴∠BAC ＝∠BCA ． 在△AKC 和△CHA 中。

专题05 高分必刷题-等腰三角形、等边三角形压轴题真题（原卷版）题型一：等腰三角形、等边三角形中的动点问题1．（湘一芙蓉）如图，已知△ABC中，AB＝AC＝12cm，BC＝10cm，点D为AB的中点．如果点P在线段BC上以2cm/s的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s的速度运动．（1）若点P、Q两点分别从B、A两点同时出发，经过2秒后，△BPD与△CQP是否全等？请说明理由；（2）若点P、Q两点分别从B、A两点同时出发，△CPQ的周长为16cm，设运动时间为t，问：是否存在某一时刻t，使得△CPQ是等腰三角形？如存在，请求出t的值，若不存在，请说明理由．2．（中雅）如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P 从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；（2）何时△PBQ是直角三角形？（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．3．（青竹湖）已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．（1）如图1，设点P的运动时间为t（s），那么t为何值时，△PBC是直角三角形；（2）若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P、Q都以1cm/s 的速度同时出发．①如图2，设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？②如图3，连接PC，请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．4．（广益）如图1，在平面直角坐标系中，直线AB分别交x轴、y轴于A（a，0）、B（0，b）两点，且a，b满足（a﹣b）2+|a﹣4t|＝0，且t＞0，t是常数．直线BD平分∠OBA，交x轴于D点．（1）若AB的中点为M，连接OM交BD于N，求证：ON＝OD；（2）如图2，过点A作AE⊥BD，垂足为E，猜想AE与BD间的数量关系，并证明你的猜想；（3）如图3，在x轴上有一个动点P（在A点的右侧），连接PB，并作等腰Rt△BPF，其中∠BPF＝90°，连接F A并延长交y轴于G点，当P点在运动时，OG的长是否发生改变？若改变，请求出它的变化范围；若不变，求出它的长度．5．（长郡、雅礼）如图，在平面直角坐标系中，点O为原点，△OAB为等边三角形，P、Q分别为AO、AB边上的动点，点P、点Q同时从点A 出发，且当其中一点停止运动时，另一点也立即停止运动；若P以2个单位长度每秒的速度从点A向终点O运动，点Q以3个单位长度每秒的速度从点A向终点B运动，设运动时间为t，已知点A坐标为（a，b），且满足（a﹣6）2+|a﹣b|＝0．（1）求A点坐标；（2）如图1，连接BP、OQ交于点C，请问当t为何值时，∠OCP＝60°；（3）如图2，D为OB边上的中点，P，Q在运动过程中，D，P，Q三点是否能构成使∠PDQ＝120°的等腰三角形，若能，求运动时间t并直接写出四边形APDQ的面积：若不能，请说明理由．6．（师梅）如图，在平面直角坐标系中，A（﹣3，0），点B是y轴正半轴上一动点，点C、D在x正半轴上．（1）如图，若∠BAO＝60°，∠BCO＝40°，BD、CE是△ABC的两条角平分线，且BD、CE交于点F，直接写出CF的长．（2）如图，△ABD是等边三角形，以线段BC为边在第一象限内作等边△BCQ，连接QD并延长，交y轴于点P，当点C运动到什么位置时，满足PD＝DC？请求出点C的坐标；（3）如图，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．7．（郡维）等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A、点B分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC 交y轴于点E．（1）如图（1），已知C点的横坐标为﹣1，直接写出点A的坐标；（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；（3）如图（3），若点A在x轴上，且A（﹣4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连接CD交y轴于点P，问当点B在y 轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度．8．（长郡）如图，在△ABC中．AB ＝AC，点E在线段BC上，连接AE并延长到G，使得EG＝AE，过点G作GD∥BA分别交BC，AC 于点F，D．（1）求证：△ABE≌△GFE；（2）若GD＝3，CD＝1，求AB的长度；（3）过点D作DH⊥BC于H，P是直线DH上的一个动点，连接AF，AP，FP，若∠C＝45°，在（2）的条件下，求△AFP周长的最小值．9．（广益）如图，在平面直角坐标系中，点O为坐标原点，点A（0，3）与点B关于x轴对称，点C（n，0）为x轴的正半轴上一动点．以AC为边作等腰直角三角形ACD，∠ACD＝90°，点D在第一象限内．连接BD，交x轴于点F．（1）如果∠OAC＝38°，求∠DCF的度数；（2）用含n的式子表示点D的坐标；（3）在点C运动的过程中，判断OF的长是否发生变化？若不变求出其值，若变化请说明理由．题型二：等腰三角形、等边三角形综合类压轴题10．（雅境）（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．①∠AEB的度数为②猜想线段AD，BE之间的数量关系为：，并证明你的猜想．（2）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E 在同一直线上，CM为△DCE中DE边上的高，连接BE，请求出∠AEB的度数及线段CM，AE，BE之间的数量关系．11．（郡维）如图1，已知△ABC和△EFC都是等边三角形，且点E在线段AB上．（1）求证：BF∥AC；（2）过点E作EG∥BC交AC于点G，试判断△AEG的形状并说明理由；（3）如图2，若点D在射线CA上，且ED＝EC，求证：AB＝AD+BF．12．（北雅）已知：△ABC为等边三角形，点E为射线AC 上一点，点D为射线CB上一点，AD＝DE．（1）如图1，当E在AC 的延长线上且CE＝CD时，求证：BD＝CD；（2）如图2，当E在AC的延长线上时，AB+BD等于AE吗？请说明理由；（3）如图3，当D在线段CB的延长线上，E在线段AC上时，请直接写出AB、BD、AE的数量关系，并证明．13．（中雅）已知△ABC为等边三角形，取△ABC的边AB，BC中点D，E，连接DE，如图1，易证△DBE 为等边三角形，将△DBE绕点B顺时针旋转，设旋转的角度∠ABD＝α，其中0＜α＜180°．（1）如图2，当α＝30°，连接AD，CE，求证：AD＝CE；（2）在△DBE旋转过程中，当α超过一定角度时，如图3，连接AD，CE会交于一点，记交点为点F，AD交BC于点P，CE交BD于点Q，连接BF，请问BF是否会平分∠CBD？如果是，求出α，如果不是，请说明理由；（3）在第（2）问的条件下，试猜想线段AF，BF和CF之间的数量关系，并说明理由．14．（雅实）如图1，△ABC 为等腰三角形，∠ABC＝90°，点P在线段BC上（不与B、C重合），以点A为直角顶点作等腰直角△P AQ，且点Q在AP的左下方，过点Q作QE⊥AB于点E．（1）求证：△P AB≌△AQE；（2）连接CQ交AB于M，若PC＝2PB，求的值．（3）如图2，过点Q作QF⊥AQ于AB的延长线于点F，过P点作DP⊥AP交AC于点D，连接DF，当点P在线段BC上运动时（不与B，C重合），式子的值会变化吗？若不变，求出该值；若变化，请说明理由．15．（师梅）如图1，在平面直角坐标系中，点A在y轴上，点B在x轴上，AB＝AC，∠BAC＝90°，CM⊥y轴，交y轴于点M．（1）求证∠ABO＝∠CAM；（2）如图2，D，E为y轴上的两个点，BD＝BE，BD⊥BE，求∠CEM的度数；（3）如图3，△P AQ是等腰直角三角形，∠P AQ为顶角，点Q在x轴负半轴上，连接CB，交y轴于点H，AC与x轴交于点G，连接PC，交AQ于点K，交x轴于点N，若CN＝CM，NG＝3，HM＝2，求GH．16．（博才）如图1，OA＝2，OB＝4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC，（1）求C点的坐标；（2）如图2，P为y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，以P为顶点，P A为腰作等腰Rt△APD，过D作DE⊥x轴于E点，求OP﹣DE的值；（3）如图3，已知点F坐标为（﹣2，﹣2），当G在y轴的负半轴上沿负方向运动时，作Rt△FGH，始终保持∠GFH＝90°，FG与y轴负半轴交于点G（0，m），FH与x轴正半轴交于点H（n，0），当G点在y 轴的负半轴上沿负方向运动时，以下两个结论：①m﹣n为定值；②m+n为定值，其中只有一个结论是正确的，请找出正确的结论，并求出其值．17．（青竹湖）如图，四边形OABC 的位置在平面直角坐标系中如图所示，且A（0，a），B（b，a），C（b，0），又a，b满足﹣+b2+4b+8＝0，点P在x轴上且横坐标大于b，射线OD是第一象限的一条射线，点Q在射线OD上，BP＝PQ．并连接BQ交y轴于点M．（1）求点A，B，C的坐标为A、B、C．（2）当BP⊥PQ时，求∠AOQ的度数．（3）在（2）的条件下，若点P在x轴的正半轴上，且OP＝3AM，试求点M的坐标．专题05 高分必刷题-等腰三角形、等边三角形压轴题真题（解析版）题型一：等腰三角形、等边三角形中的动点问题1.如图，已知△ABC中，AB＝AC＝12cm，BC＝10cm，点D为AB的中点．如果点P在线段BC上以2cm/s 的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s的速度运动．（1）若点P、Q两点分别从B、A两点同时出发，经过2秒后，△BPD与△CQP是否全等？请说明理由；（2）若点P、Q两点分别从B、A两点同时出发，△CPQ的周长为16cm，设运动时间为t，问：是否存在某一时刻t，使得△CPQ是等腰三角形？如存在，请求出t的值，若不存在，请说明理由．【解答】解：（1）∠CMQ＝60°不变．∵等边三角形中，AB＝AC，∠B＝∠CAP ＝60°，又由条件得AP＝BQ，∴△ABQ≌△CAP（SAS），∴∠BAQ＝∠ACP，∴∠CMQ＝∠ACP+∠CAM ＝∠BAQ+∠CAM＝∠BAC＝60°．（2）设时间为t，则AP＝BQ＝t，PB＝4﹣t①当∠PQB＝90°时，∵∠B＝60°，∴PB＝2BQ，得4﹣t＝2t，t＝；②当∠BPQ＝90°时，∵∠B＝60°，∴BQ＝2BP，得t＝2（4﹣t），t＝；∴当第秒或第秒时，△PBQ为直角三角形．（3）∠CMQ＝120°不变．∵在等边三角形中，BC＝AC，∠B＝∠CAP＝60°∴∠PBC＝∠ACQ＝120°，又由条件得BP＝CQ，∴△PBC≌△QCA（SAS）∴∠BPC＝∠MQC又∵∠PCB＝∠MCQ，∴∠CMQ＝∠PBC＝180°﹣60°＝120°2．如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B 同时出发，且它们的速度都为1cm/s，（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；（2）何时△PBQ是直角三角形？（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ 变化吗？若变化，则说明理由，若不变，则求出它的度数．【解答】解：（1）∠CMQ＝60°不变．∵等边三角形中，AB＝AC，∠B＝∠CAP＝60°，又由条件得AP＝BQ，∴△ABQ≌△CAP（SAS），∴∠BAQ＝∠ACP，∴∠CMQ＝∠ACP+∠CAM＝∠BAQ+∠CAM＝∠BAC＝60°．（2）设时间为t，则AP＝BQ＝t，PB＝4﹣t，①当∠PQB＝90°时，∵∠B＝60°，∴PB＝2BQ，得4﹣t＝2t，t＝；②当∠BPQ＝90°时，∵∠B＝60°，∴BQ＝2BP，得t＝2（4﹣t），t＝；∴当第秒或第秒时，△PBQ为直角三角形．（3）∠CMQ＝120°不变．∵在等边三角形中，BC＝AC，∠B＝∠CAP＝60°∴∠PBC＝∠ACQ＝120°，又由条件得BP＝CQ，∴△PBC≌△QCA（SAS）∴∠BPC＝∠MQC又∵∠PCB＝∠MCQ，∴∠CMQ＝∠PBC＝180°﹣60°＝120°3.已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．（1）如图1，设点P的运动时间为t（s），那么t为何值时，△PBC是直角三角形；（2）若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．①如图2，设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？②如图3，连接PC，请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．【解答】解：（1）当△PBC是直角三角形时，∠B＝60°，∠BPC＝90°，所以BP＝1.5cm，所以t＝，（2）①∵∠DCQ＝120°，当△DCQ是等腰三角形时，CD＝CQ，∴∠PDA＝∠CDQ＝∠CQD＝30°，∵∠A＝60°，∴AD＝2AP，∴2t+t＝3，解得t＝1（s）；②相等，如图所示：作PE垂直AD，QG垂直AD延长线，则PE∥QG，∴∠G＝∠AEP，在△EAP 和△GCQ，，∴△EAP≌△GCQ（AAS），∴PE＝QG，∴△PCD和△QCD同底等高，所以面积相等．4.如图1，在平面直角坐标系中，直线AB分别交x轴、y轴于A（a，0）、B（0，b）两点，且a，b满足（a ﹣b）2+|a﹣4t|＝0，且t＞0，t是常数．直线BD平分∠OBA，交x轴于D点．（1）若AB的中点为M，连接OM交BD于N，求证：ON＝OD；（2）如图2，过点A作AE⊥BD，垂足为E，猜想AE与BD间的数量关系，并证明你的猜想；（3）如图3，在x轴上有一个动点P（在A点的右侧），连接PB，并作等腰Rt△BPF，其中∠BPF＝90°，连接F A并延长交y轴于G点，当P点在运动时，OG的长是否发生改变？若改变，请求出它的变化范围；若不变，求出它的长度．【解答】（1）证明：∵直线AB分别交x 轴、y轴于A（a，0）、B（0，b）两点，且a，b满足（a﹣b）2+|a﹣4t|＝0，且t＞0，∴a＝b＝4t，当x＝0时，y＝4t，当y＝0时，﹣x+4t＝0，解得x＝4t，∴点A、B的坐标是A（4t，0），B（0，4t），∴△AOB是等腰直角三角形，∵点M是AB的中点，∴OM⊥AB，∴∠MOA＝45°，∵直线BD平分∠OBA，∴∠ABD＝∠ABO＝22.5°，∴∠OND＝∠BNM＝90°﹣∠ABD＝90°﹣22.5°＝67.5°，∠ODB＝∠ABD+∠BAD＝22.5°+45°＝67.5°，∴∠OND＝∠ODB，∴ON ＝OD（等角对等边）；（2）答：BD＝2AE．理由如下：延长AE交BO于C，∵BD平分∠OBA，∴∠ABD＝∠CBD，∵AE⊥BD 于点E，∴∠AEB＝∠CEB＝90°，在△ABE≌△CBE中，，∴△ABE≌△CBE（ASA），∴AE＝CE，∴AC＝2AE，∵AE⊥BD，∴∠OAC+∠ADE＝90°，又∠OBD+∠BDO＝90°，∠ADE＝∠BDO （对顶角相等），∴∠OAC＝∠OBD，在△OAC与△OBD中，，∴△OAC≌△OBD（ASA），∴BD＝AC，∴BD＝2AE；（3）OG的长不变，且OG＝4t．过F作FH⊥OP，垂足为H，∴∠FPH+∠PFH＝90°，∵∠BPF＝90°，∴∠BPO+∠FPH＝90°，∴∠FPH＝∠BPO，∵△BPF是等腰直角三角形，∴BP＝FP，在△OBP与△HPF 中，，∴△OBP≌△HPF（AAS），∴FH＝OP，PH＝OB＝4t，∵AH＝PH+AP＝OB+AP，OA＝OB，∴AH＝OA+AP＝OP，∴FH＝AH，∴∠GAO＝∠F AH＝45°，∴△AOG是等腰直角三角形，∴OG＝OA＝4t．5.如图，在平面直角坐标系中，点O为原点，△OAB为等边三角形，P、Q分别为AO、AB边上的动点，点P、点Q同时从点A出发，且当其中一点停止运动时，另一点也立即停止运动；若P以2个单位长度每秒的速度从点A向终点O运动，点Q以3个单位长度每秒的速度从点A向终点B运动，设运动时间为t，已知点A坐标为（a，b），且满足（a﹣6）2+|a﹣b|＝0．（1）求A点坐标；（2）如图1，连接BP、OQ交于点C，请问当t为何值时，∠OCP＝60°；（3）如图2，D为OB边上的中点，P，Q在运动过程中，D，P，Q三点是否能构成使∠PDQ＝120°的等腰三角形，若能，求运动时间t并直接写出四边形APDQ的面积：若不能，请说明理由．【解答】解：（1）∵（a﹣6）2+|a ﹣b|＝0，又∵（a﹣6）2，≥0，|a﹣b|≥0，∴a＝6，b＝6∴点A（6，6）．（2）如图1中，∵△AOB是等边三角形，点A（6，6），∴AO＝BO＝AB＝12，∠AOB＝∠ABO ＝60°＝∠A，∵∠OCP＝60°＝∠AOB，∴∠AOB＝∠QOB+∠AOQ＝∠QOB+∠PBO＝∠PCO，∴∠AOQ ＝∠PBO，且AO＝BO，∠A＝∠AOB，∴△AOQ≌△OBP（ASA），∴OP＝AQ，∴12﹣2t＝3t∴t＝2.4∴当t＝2.4时，∠OCP＝60°．（3）如图2中，过点D作DF⊥AO，DE⊥AB，连接AD，∵△ABO是等边三角形，D是OB中点，点A（6，6），∴OD＝BD＝6，∠AOB ＝∠ABO＝60°，AD＝6，又∵∠DFO＝∠DEB＝90°，∴△ODF≌△BDE（AAS），∴OF＝BE，DF＝DE，∵AO＝AB，∴AO﹣OF＝AB﹣BE，∴AF＝AE，∵DF＝DE，PD＝DQ，∴Rt△DFP≌Rt△DEQ（HL），∴PF＝EQ，∵OD＝6，∠AOD＝60°，∠DFO＝90°，∴∠ODF＝30°∴OF＝3，DF＝OF＝3，∴AF＝AO﹣OF＝9＝AE，BE＝OF＝3，∵AP+AQ＝AP+AE+EQ＝AP+PF+AE＝AF+AE＝2AF，∴2t+3t＝18∴t＝3.6，∴当t＝，3.6时，D，P，Q三点是能构成使∠PDQ＝120°的等腰三角形，∵Rt△DFP≌Rt△DEQ，∴S△DFP＝S△DEQ，∴S四边形APDQ＝S四边形AFDQ＝S△AOB﹣2S△OFD＝×12×6﹣2××3×3＝27．6．如图，在平面直角坐标系中，A（﹣3，0），点B是y轴正半轴上一动点，点C、D在x正半轴上．（1）如图，若∠BAO＝60°，∠BCO＝40°，BD、CE是△ABC的两条角平分线，且BD、CE交于点F，直接写出CF的长6．（2）如图，△ABD是等边三角形，以线段BC为边在第一象限内作等边△BCQ，连接QD并延长，交y轴于点P，当点C运动到什么位置时，满足PD＝DC？请求出点C的坐标；（3）如图，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．【解答】解：（1）作∠DCH＝10°，CH交BD的延长线于H，∵∠BAO＝60°，∴∠ABO＝30°，∴AB＝2OA＝6，∵∠BAO＝60°，∠BCO＝40°，∴∠ABC＝180°﹣60°﹣40°＝80°，∵BD是△ABC的角平分线，∴∠ABD＝∠CBD＝40°，∴∠CBD＝∠DCB，∠OBD＝40°﹣30°＝10°，∴DB＝DC，在△OBD和△HCD中，，∴△OBD≌△HCD（ASA），∴OB＝HC，在△AOB和△FHC中，，∴△AOB≌△FHC（ASA），∴CF＝AB＝6，故答案为：6；（2）∵△ABD和△BCQ是等边三角形，∴∠ABD＝∠CBQ＝60°，∴∠ABC＝∠DBQ，在△CBA和△QBD中，，∴△CBA≌△QBD（SAS），∴∠BDQ＝∠BAC＝60°，∴∠PDO ＝60°，∴PD＝2DO＝6，∵PD＝DC，∴DC＝9，即OC＝OD+CD＝12，∴点C的坐标为（12，0）；（3）如图3，以OA为对称轴作等边△ADE，连接EP，并延长EP交x轴于点F．由（2）得，△AEP≌△ADB，∴∠AEP＝∠ADB＝120°，∴∠OEF＝60°，∴OF＝OA＝3，∴点P在直线EF上运动，当OP⊥EF时，OP则OP的最小值为．最小，∴OP＝OF＝，7.等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A、点B 分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E．（1）如图（1），已知C点的横坐标为﹣1，直接写出点A的坐标；（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；（3）如图（3），若点A在x轴上，且A（﹣4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连接CD交y轴于点P，问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度．【解答】解：（1）如图（1），过点C作CF⊥y轴于点F，∵CF⊥y轴于点F，∴∠CF A＝90°，∠ACF+∠CAF＝90°，∵∠CAB＝90°，∴∠CAF+∠BAO＝90°，∴∠ACF＝∠BAO，在△ACF和△ABO中，，∴△ACF≌△ABO（AAS），∴CF＝OA＝1，∴A（0，1）；（2）如图2，过点C作CG⊥AC交y轴于点G，∵CG⊥AC，∴∠ACG＝90°，∠CAG+∠AGC＝90°，∵∠AOD＝90°，∴∠ADO+∠DAO＝90°，∴∠AGC＝∠ADO，在△ACG和△ABD中，，∴△ACG≌△ABD（AAS），∴CG＝AD＝CD，∠ADB＝∠G，∵∠ACB＝45°，∠ACG＝90°，∴∠DCE＝∠GCE＝45°，在△DCE和△GCE中，，∴△DCE≌△GCE（SAS），∴∠CDE＝∠G，∴∠ADB＝∠CDE；（3）BP的长度不变，理由如下：如图（3），过点C作CE⊥y轴于点E．∵∠ABC＝90°，∴∠CBE+∠ABO ＝90°．∵∠BAO+∠ABO＝90°，∴∠CBE＝∠BAO．∵∠CEB＝∠AOB＝90°，AB＝AC，∴△CBE≌△BAO （AAS），∴CE＝BO，BE＝AO＝4．∵BD＝BO，∴CE＝BD．∵∠CEP＝∠DBP＝90°，∠CPE＝∠DPB，∴△CPE≌△DPB（AAS），∴BP＝EP＝2．8．如图，在△ABC中．AB＝AC，点E在线段BC上，连接AE并延长到G，使得EG＝AE，过点G作GD∥BA分别交BC，AC于点F，D．（1）求证：△ABE≌△GFE；（2）若GD＝3，CD＝1，求AB的长度；（3）过点D作DH⊥BC于H，P是直线DH上的一个动点，连接AF，AP，FP，若∠C＝45°，在（2）的条件下，求△AFP周长的最小值．【解答】（1）证明：如图1中，∵GD∥AB，∴∠B＝∠EFG，在△ABE和△GFE中，，∴△ABE≌△GFE（AAS）．（2）解：如图1中，∵AB＝AC，∴∠B＝∠ACB，∵DF∥AB，∴∠DFC＝∠B，∴∠DFC＝∠DCF，∴DC＝DF＝1，∵DG＝3，∴FG＝DG﹣DF＝2，∵△ABE≌△GFE，∴AB＝GF＝2．（3）解：如图2中，∵AB＝AC＝2，∴∠B＝∠C＝45°，∴∠BAC＝90°，∵AB∥FD，∴∠FDC＝∠BAC ＝90°，即FD⊥AC∵AC＝AB＝2，CD＝1，∴DA＝DC，∴F A＝FC，∴∠C＝∠F AC＝45°，∴∠AFC＝90°，∴DF＝DA＝DC＝1，∴AF＝，∵DH⊥CF，∴FH＝CH，∴点F与点C关于直线PD对称，∴当点P与D重合时，△P AF的周长最小，最小值＝△ADF的周长＝2+．9.如图，在平面直角坐标系中，点O为坐标原点，点A（0，3）与点B关于x轴对称，点C（n，0）为x轴的正半轴上一动点．以AC为边作等腰直角三角形ACD，∠ACD＝90°，点D在第一象限内．连接BD，交x轴于点F．（1）如果∠OAC＝38°，求∠DCF的度数；（2）用含n的式子表示点D的坐标；（3）在点C运动的过程中，判断OF的长是否发生变化？若不变求出其值，若变化请说明理由．【解答】解：（1）∵∠AOC＝90°，∴∠OAC+∠ACO＝90°，∵∠ACD＝90°，∴∠DCF+∠ACO＝90°，∴∠DCF＝∠OAC，∵∠OAC＝38°，∴∠DCF＝38°；（2）如图，过点D作DH⊥x轴于H，∴∠CHD＝90°∴∠AOC＝∠CHD＝90°，∵等腰直角三角形ACD，∠ACD＝90°∴AC＝CD，由（1）知，∠DCF＝∠OAC，∴△AOC≌△CHD（AAS），∴OC＝DH＝n，AO ＝CH＝3，∴点D的坐标（n+3，n）；（3）不会变化，理由：∵点A（0，3）与点B关于x轴对称，∴AO＝BO，又∵OC⊥AB，∴x轴是AB垂直平分线，∴AC＝BC，∴∠BAC＝∠ABC，又∵AC＝CD，∴BC＝CD，∴∠CBD＝∠CDB，∵∠ACD＝90°，∴∠ACB+∠DCB＝270°，∴∠BAC+∠ABC+∠CBD+∠CDB＝90°，∴∠ABC+∠CBD＝45°，∵∠BOF＝90°，∴∠OFB＝45°，∴∠OBF＝∠OFB＝45°，∴OB＝OF＝3，∴OF的长不会变化．题型二：等腰三角形、等边三角形综合类压轴题10．（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．①∠AEB的度数为②猜想线段AD，BE之间的数量关系为：，并证明你的猜想．（2）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请求出∠AEB的度数及线段CM，AE，BE之间的数量关系．【解答】解：（1）①∵△ACB和△DCE均为等边三角形，∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝60°，∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，即∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE，∴∠CEB＝∠CDA＝120°，∴∠AEB＝60°，故答案为：60°；②AD＝BE，证明：∵△ACD≌△BCE，∴AD＝BE，故答案为：AD＝BE；（2）∠AEB＝90°，AE﹣BE＝2CM，证明：∵△DCE是等腰直角三角形，CM是中线，∴CM＝DM＝EM＝DE，在△ACD和△BCE中，，∴△ACD≌△BCE，∴∠CDA＝∠CEB，∵∠CDA＝135°，∴∠AEB＝135°﹣45°＝90°，∴BE＝AD，∴AE﹣AD＝DE＝2CM，∴AE﹣BE＝2CM．11.如图1，已知△ABC和△EFC都是等边三角形，且点E在线段AB上．（1）求证：BF∥AC；（2）过点E作EG∥BC交AC于点G，试判断△AEG的形状并说明理由；（3）如图2，若点D在射线CA上，且ED＝EC，求证：AB＝AD+BF．【解答】（1）证明：∵△ABC和△EFC都是等边三角形，∴∠A＝∠ABC＝∠ACB＝∠ECF＝60°，AC＝BC，CE＝FC，∴∠ACE＝∠BCF，在△ACE与△FCB中，，∴△ACE≌△FCB（SAS），∴∠A＝∠CBF＝60°，∵∠ABC＝60°，∴∠A+∠ABC+∠CBF＝180°，∴∠A+∠ABF＝180°，∴AC∥BF；（2）解：△AEG是等边三角形，理由如下：如图1所示：∵△ABC是等边三角形，∴∠A＝∠ABC＝∠ACB ＝60°，∵EG∥BC，∴∠AEG＝∠ABC＝60°，∠AGE＝∠ACB＝60°，∴∠A＝∠AEG＝∠AGE＝60°，∴△AEG是等边三角形；（3）证明：如图2，过E作EM∥BC交AC于M，则∠AEM＝∠ABC＝60°，∠AME＝∠ACB＝60°，∵∠A＝∠ABC＝∠ACB＝60°，∴∠A＝∠AEM＝∠AME＝60°，∴△AEM是等边三角形，∴AE＝EM＝AM，∴∠DAE＝∠EMC＝120°，∵DE＝CE，∴∠D＝∠MCE，在△ADE和△MCE中，，∴△ADE≌△MCE（AAS），∴AD＝CM，∴AC＝AM+CM，由（1）得△ACE≌△FCB，∴BF＝AE，∴BF＝AM，∴AC＝BF+AD，∴AB＝AD+BF．12．已知：△ABC为等边三角形，点E为射线AC上一点，点D为射线CB上一点，AD＝DE．（1）如图1，当E在AC的延长线上且CE＝CD时，求证：BD＝CD；（2）如图2，当E在AC的延长线上时，AB+BD等于AE吗？请说明理由；（3）如图3，当D在线段CB的延长线上，E在线段AC上时，请直接写出AB、BD、AE的数量关系，并证明．【解答】（1）证明：∵△ABC是等边三角形，∴AB＝AC，∠BAC＝∠B＝∠ACB＝60°，∵CD＝CE，∴∠CDE＝∠E，∵∠ACD＝∠CDE+∠E＝60°，∴∠E＝30°，∵DA＝DE，∴∠DAC＝∠E＝30°，∵∠BAC＝60°，∴∠DAB＝∠CAD，∵AB＝AC，∴BD＝DC；（2）结论：AB+BD＝AE，理由如下：如图2，在AB上取BH＝BD，连接DH，∵BH＝BD，∠B＝60°，∴△BDH为等边三角形，AB﹣BH＝BC﹣BD，即AH＝DC，∴∠BHD＝60°，BD＝DH，∵AD＝DE，∴∠E＝∠CAD，∴∠BAC﹣∠CAD＝∠ACB﹣∠E，即∠BAD＝∠CDE，∵∠BHD＝60°，∠ACB＝60°，∴180°﹣∠BHD＝180°﹣∠ACB，即∠AHD＝∠DCE，在△AHD和△DCE，，∴△AHD≌△DCE（AAS），∴DH＝CE，∴BD＝CE，∴AE＝AC+CE＝AB+BD；（3）AB＝BD+AE；如图3，在AB上取AF＝AE，连接DF，∵△ABC为等边三角形，∴∠BAC＝∠ABC＝60°，∴△AFE是等边三角形，∴∠F AE＝∠FEA＝∠AFE＝60°，∴EF∥BC，∴∠EDB＝∠DEF，∵AD＝DE，∴∠DEA＝∠DAE，∴∠DEF ＝∠DAF，在△AFD和△EFD中，，∴△AFD≌△EFD（SSS），∴∠ADF＝∠EDF，∠DAF＝∠DEF，∴∠FDB＝∠EDF+∠EDB，∠DFB＝∠DAF+∠ADF，∵∠EDB＝∠DEF，∴∠FDB＝∠DFB，∴DB＝BF，∵AB＝AF+FB，∴AB＝BD+AE．13．已知△ABC为等边三角形，取△ABC的边AB，BC中点D，E，连接DE，如图1，易证△DBE为等边三角形，将△DBE绕点B顺时针旋转，设旋转的角度∠ABD＝α，其中0＜α＜180°．（1）如图2，当α＝30°，连接AD，CE，求证：AD＝CE；（2）在△DBE旋转过程中，当α超过一定角度时，如图3，连接AD，CE会交于一点，记交点为点F，AD 交BC于点P，CE交BD于点Q，连接BF，请问BF是否会平分∠CBD？如果是，求出α，如果不是，请说明理由；（3）在第（2）问的条件下，试猜想线段AF，BF和CF之间的数量关系，并说明理由．【解答】证明：（1）∵△ABC，△DBE都是等边三角形，∴AB＝BC，BD＝BE，∠ABC＝∠DBE＝60°，∴∠ABD＝∠CBE，在△ABD和△CBE中，，∴△ABD≌△CBE（SAS），∴AD＝CE；（2）不存在，理由如下：如图3，过点B作BN⊥AD于N，过点B作BH⊥CE于H，∵△ABC，△DBE都是等边三角形，∴AB＝BC，BD＝BE，∠ABC＝∠DBE ＝60°，∴∠ABD＝∠CBE，在△ABD和△CBE中，，∴△ABD≌△CBE（SAS），∴AD＝CE，S△ABD＝S△CBE，∠BAD ＝∠BCE，∴×AD×BN＝×CE×BH，∴BN＝BH，又∵BF＝BF，∴Rt△BFN≌Rt△BFH（HL），∴∠AFB＝∠EFB，∵∠BAD＝∠BCE，∠CPF＝∠APB，∴∠AFC＝∠ABC＝60°，∴∠AFB＝∠EFB＝60°，∴∠CFB＝∠DFB＝120°，当BF平分∠CBD时，则∠CBF＝∠DBF，∴∠BCF＝180°﹣∠CBF﹣∠CFB＝180°﹣∠DBF﹣∠DFB＝∠ADB，∴∠DAB＝∠ADB，∴AB＝DB，与题干DB＝BC＝AB相矛盾，∴BF不会平分∠CBD；（3）AF＝CF+BF，理由如下：如图4，在AF上截取MF＝BF，连接BM，∵∠AFB＝60°，MF＝FB，∴△MFB是等边三角形，∴MB＝BF，∠MBF ＝∠ABC＝60°，∴∠ABM＝∠CBF，在△ABM和△CBF中，，∴△ABM≌△CBF（SAS），∴AM＝CF，∵AF＝AM+MF，∴AF＝CF+BF．14．如图1，△ABC为等腰三角形，∠ABC＝90°，点P在线段BC上（不与B、C重合），以点A为直角顶点作等腰直角△P AQ，且点Q在AP的左下方，过点Q作QE⊥AB于点E．（1）求证：△P AB≌△AQE；（2）连接CQ交AB于M，若PC＝2PB，求的值．（3）如图2，过点Q作QF⊥AQ于AB的延长线于点F，过P点作DP⊥AP交AC于点D，连接DF，当点P在线段BC上运动时（不与B，C重合），式子的值会变化吗？若不变，求出该值；若变化，请说明理由．【解答】（1）证明：∵△ACB 为等腰三角形，∠ABC＝90°，△P AQ是等腰直角三角形，QE⊥AB于E．∴AP＝AQ，∠ABP＝∠QEA＝90°，∠QAE+∠BAP＝∠BAP+∠APB＝90°，∴∠QAE＝∠APB，在△P AB和△AQE中，，∴△P AB≌△AQE（AAS）；（2）解：∵△P AB≌△AQE，∴AE＝PB，∵AB＝CB，∴QE＝CB．在△QEM和△CBM中，，∴△QEM≌△CBM（AAS），∴ME＝MB，∵AB＝CB，AE＝PB，PC＝2PB，∴BE＝PC，∵PC＝2PB，∴PC＝2MB，∴＝2；（3）解：式子的值不会变化，理由如下：过A作HA⊥AC交QF于点H，如图2所示：∵QA⊥AP，HA⊥AC，AP⊥PD，∴∠QAH+∠HAP＝∠HAP+∠P AD＝90°，∠AQH＝∠APD＝90°，∴∠QAH＝∠P AD，∵△P AQ为等腰直角三角形，∴AQ＝AP，在△AQH和△APD中，，∴△AQH≌△APD（ASA），∴AH＝AD，QH＝PD，∵HA⊥AC，∠BAC＝45°，∴∠HAF＝∠DAF，在△AHF和△ADF中，，∴△AHF≌△ADF（SAS），∴HF＝DF，∴＝＝＝1．15．如图1，在平面直角坐标系中，点A在y轴上，点B在x轴上，AB＝AC，∠BAC＝90°，CM⊥y轴，交y轴于点M．（1）求证∠ABO＝∠CAM；（2）如图2，D，E为y轴上的两个点，BD＝BE，BD⊥BE，求∠CEM的度数；（3）如图3，△P AQ是等腰直角三角形，∠P AQ为顶角，点Q在x轴负半轴上，连接CB，交y轴于点H，AC与x轴交于点G，连接PC，交AQ于点K，交x轴于点N，若CN＝CM，NG＝3，HM＝2，求GH．【解答】（1）证明：∵∠BOA＝90°，∴∠BAO+∠ABO＝90°，又∵∠BAC＝∠BAO+∠CAM＝90°，∴∠ABO＝∠CAM；（2）解：∵CM⊥y轴，∴∠AMC＝∠BOA＝90°，∵AB＝AC，∠ABO＝∠CAM，∴△AMC≌△BOA（AAS），∴CM＝AO，AM＝BO，∵BD＝BE，BD⊥BE，∴△BDE是等腰直角三角形，∴∠BDE＝∠BED＝45°，∠EBO ＝∠DBE＝45°，∴∠EBO＝∠BEO，∴BO＝EO＝AM，∴EO﹣OM＝AM﹣OM，∴EM＝AO＝CM，∴△CME是等腰直角三角形，∴∠CEM＝45°；（3）解：∵AB＝AC，∠BAC＝90°，∴∠ACB＝45°，∵△P AQ是等腰直角三角形，∴P A＝QA，∠P AQ＝∠CAB＝90°，∴∠P AQ+∠QAC＝∠CAB+∠QAC，即∠P AC＝∠QAB，∵AC＝AB，∴△P AC≌△QAB（SAS），∴∠APC＝∠AQB，∵∠AKP＝∠QKN，∴∠QNK＝∠P AK＝90°，∵CM⊥y轴，∴CM∥NO，∴∠NCM＝∠KNO＝90°，在ON的延长线上截取NI＝MH，连接CI，如图3所示：∵CN＝CM，∠CNI＝∠CMH＝90°，∴△CNI≌△CMH（SAS），∴∠NCI＝∠MCH，CI＝CH，∴∠NCG+∠NCI ＝∠NCG+∠MCH＝∠NCM﹣∠GCH＝90°﹣45°＝45°＝∠GCH＝∠GCI，∴△GCI≌△GCH（SAS），∴GI ＝GH，∵GI＝IN+NG＝HM+NG＝2+3＝5，∴GH＝5．16．如图1，OA＝2，OB＝4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC，（1）求C点的坐标；（2）如图2，P为y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，以P为顶点，P A为腰作等腰Rt△APD，过D作DE⊥x轴于E点，求OP﹣DE的值；（3）如图3，已知点F坐标为（﹣2，﹣2），当G在y轴的负半轴上沿负方向运动时，作Rt△FGH，始终保持∠GFH＝90°，FG与y轴负半轴交于点G（0，m），FH与x轴正半轴交于点H（n，0），当G点在y 轴的负半轴上沿负方向运动时，以下两个结论：①m﹣n为定值；②m+n为定值，其中只有一个结论是正确的，请找出正确的结论，并求出其值．【解答】解：（1）过C 作CM⊥x轴于M点，如图1，∵CM⊥OA，AC⊥AB，∴∠MAC+∠OAB＝90°，∠OAB+∠OBA＝90°则∠MAC＝∠OBA在△MAC和△OBA中，则△MAC≌△OBA（AAS），则CM＝OA＝2，MA＝OB ＝4，则点C的坐标为（﹣6，﹣2）；（2）过D作DQ⊥OP于Q点，如图2，则OP﹣DE＝PQ，∠APO+∠QPD＝90°∠APO+∠OAP＝90°，则∠QPD＝∠OAP，在△AOP和△PDQ中，则△AOP≌△PDQ（AAS），∴OP﹣DE＝PQ＝OA＝2；（3）结论②是正确的，m+n＝﹣4，如图3，过点F分别作FS⊥x轴于S点，FT⊥y轴于T点，则FS＝FT＝2，∠FHS＝∠HFT＝∠FGT，在△FSH和△FTG中，则△FSH≌△FTG（AAS），则GT＝HS，又∵G（0，m），H（n，0），点F坐标为（﹣2，﹣2），∴OT═OS＝2，OG＝|m|＝﹣m，OH＝n，∴GT＝OG﹣OT＝﹣m﹣2，HS＝OH+OS＝n+2，则﹣2﹣m＝n+2，则m+n＝﹣4．17．如图，四边形OABC的位置在平面直角坐标系中如图所示，且A（0，a），B（b，a），C（b，0），又a，b满足﹣+b2+4b+8＝0，点P在x轴上且横坐标大于b，射线OD是第一象限的一条射线，点Q在射线OD上，BP＝PQ．并连接BQ交y轴于点M．（1）求点A，B，C的坐标为A、B、C．（2）当BP⊥PQ时，求∠AOQ的度数．（3）在（2）的条件下，若点P在x轴的正半轴上，且OP＝3AM，试求点M的坐标．【解答】解：（1）∵﹣+b2+4b+8＝0，∴﹣+（b﹣4）2＝0，∴a＝4，b＝4，∴A（0，4），B（﹣4，4），C（﹣4，0），故答案为（0，4），（﹣4，4），（﹣4，0）；（2）由（1）知，A（0，4），B（﹣4，4），C（﹣4，0），∴AB ＝BC＝OC＝OA＝4，∴四边形OABC是菱形，∵∠AOC＝90°，∴菱形OABC是正方形，过点Q作QN⊥x轴于N，∴∠PNQ＝90°，∴∠QPN+∠PQN＝90°，∵BP⊥BQ，∴∠BPQ＝90°，∴∠BPC+∠QPN＝90°，∴∠PQN＝∠BPC，由（1）知，B（﹣4，4），C（﹣4，0），∴BC＝4，BC⊥x，∴∠BCP＝∠PNQ＝90°，在△BCP和△PNQ中，，∴△BCP≌△PNQ（AAS），∴CP＝QN，BC＝PN，∴OC＝PN＝4，①当点P在x轴负半轴时，如图1、OC＝CP+OP，PN＝OP+ON，∴CP＝ON，∵CP＝QN，∴ON＝QN，∵∠PNQ＝90°，∴∠QON＝45°，∴∠AOQ＝45°，②当点P在x轴正半轴时，如图2、OC＝CP﹣OP，PN＝ON﹣OP，∴CP＝ON，∵CP＝QN，∴ON＝QN，∵∠PNQ＝90°，∴∠QON＝45°，∴∠AOQ＝45°，即：∠AOQ＝45°；（3）如图2，过点Q作QN⊥x轴于N，设P（m，0）（m＞0），∵OP＝3AM，∴AM＝OP＝m，∴M（0，m+4），∵点B（﹣4，4），∴直线BM的解析式为y＝mx+m+4，由（2）知，PN＝OC＝4，∴N（m+4，0），∴Q（m+4，m+4），∵点Q在直线BM上，∴m（m+4）+m+4＝m+4，∴m＝0（舍）或m＝4，∴M（0，）．。

一、选择题 9．（2020·绍兴）如图，等腰直角三角形ABC 中，∠ABC ＝90°，BA ＝BC ，将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，连结CP ，过点A 作AH ⊥CP 交CP 的延长线于点H ，连结AP ，则∠P AH 的度数（ ）A ．随着θ的增大而增大B ．随着θ的增大而减小C ．不变D ．随着θ的增大，先增大后减小 {答案}C{解析}本题考查了等腰三角形的性质，三角形的内角和，旋转的性质．由旋转得BC=BP=BA ，∴△BCP 和△ABP 均是等腰三角形.在△BCP 中，∠CBP=θ，BC=BP ，∴∠BPC=90°-12θ.在△ABP 中，∠ABP=90°-θ，同理得∠APB=45°+12θ，∴∠APC=∠BPC +∠APB =135°，又∵∠AHC=90°，∴∠PAH=45°，即其度数是个定值，不变．因此本题选C ．7．（2020·铜仁）已知等边三角形一边上的高为2，则它的边长为（ ） A ．2 B ．3 C ．4 D ．4{答案}C {解析}设等边三角形的边长为2x ，过等边三角形的一个顶点作对边的高，由等边三角形“三线合一”的性质得直角三角形的一条直角边为x ，由勾股定理得x2＋（2）2=（2x ）2，解得x=4，因此本题选C ．3．（2020·聊城）如图，在△ABC 中，AB ＝AC ，∠C ＝65°，点D 是BC 边上任意一点，过点D 作DF ∥AB 交AC 于点E ，则∠FEC 的度数是（ ）A ．120°B ．130°C ．145°D ．150°{答案}B{解析}可利用三角形的外角性质求∠ FEC 的度数，结合等腰三角形与平行线的性质，可得∠ EDC 、∠B 均与∠C 相等．即：∵AB ＝AC ，∴∠B ＝∠C ＝65°．∵DF ∥AB ，∴∠ EDC ＝∠B ＝65°．∴∠FEC ＝∠EDC ＋∠C ＝65°＋65°＝130°．10．（2020·河南）如图，在△ABC 中，AB =BC =3，∠BAC =30°，分别以点A ，C 为圆心，AC 的长为半径作弧，两弧交于点D ，连接DA ，DC ，则四边形ABCD 的面积为( ) A.63 B.9 C.6 D. 33{答案}D{解析}∵分别以点A 、C 为圆心，AC 的长为半径作弧，两弧交于点D ， ∴AD=AC=CD ，∴△ACD 是等边三角形，∴∠DAC=60°.∵AB=BC ，AD=CD ，连接BD 交AC 于点E ，∴BD 垂直平分AC ，∴∠AEB=90°.ABCD E F在Rt △ADE 中，∵∠DAC=60°，∠AED=90°，AE=32，∴323∴四边形ABCD 的面积为：3333221=⨯⨯．9．(2020自贡)如图，在Rt△ABC 中，△ACB ＝90°，△A ＝50°，以点B 为圆心，BC 长为半径画弧，交AB 于点D ，连接CD ，则△ACD 的度数是（ ）A ．50°B ．40°C ．30°D ．20°{答案} D ．{解析}本题考查了直角三角形，圆，等腰三角形等知识，∵在Rt △ABC 中，∠ACB ＝90°，∠A ＝50°，∴∠B ＝40°，∵BC ＝BD ，∴∠BCD ＝∠BDC =12（180°﹣40°）＝70°，∴∠ACD ＝90°﹣70°＝20°，因此本题选D ．5．（2020·福建）如图，AD 是等腰三角形ABC 的顶角平分线，5=BD ，则CD 等于（ ）A.10B.5C.4D.3{答案}B{解析}本题考查了等腰三角形三线合一的性质，∵AD 是等腰三角形ABC 的顶角平分线，5=BD，∴CD=BD=5，因此本题选B ．(2020·南充） 6.如图，在等腰三角形ABC 中，BD 为∠ABC 的平分线，∠A=36°，AB=AC=a ，BC=b ，则CD=（ ）（第6题） A.2b a + B.2ba - C.a-b D.b-a {答案}C{解析}∵AB=AC ，∠A=36°，∴∠ABC=∠ACB=72°，∵BD 平分∠ABC ，∴∠ABD=12∠ABC=12×72°=36°，∴∠BDC=∠A+∠ABD=36°+36°=72°，∴∠C=∠BDC=36°，∴BD=BC=b ，同理：AD=BD=b ，∴CD=AC-AD=a-b ，故选C ．（2020·济宁）5.一条船从海岛A 出发，以15海里/时的速度向正北航行，2小时后到达海岛B 处.灯塔C 在海岛在海岛A 的北偏西42°方向上，在海岛B 的北偏西84°方向上.则海岛B 到灯塔C 的距离是（）A.15海里B.20海里C. 30海里D.60海里 {答案}C{解析}根据题意画图，如图，∠A=42°，∠DBC=84°，AB=15×2=30(海里), ∴∠C=∠DBC-∠A=42°,∴BC=BA=30(海里).10．（2020·无锡）如图，等边△ABC 的边长为3，点D 在边AC 上，AD ＝12，线段PQ 在边BA 上运动，PQ＝12，有下列结论：NMHG AB CD EFC B FE ABC P QDD Q C B(P)AE①CP 与QD 可能相等； ②△AQD 与△BCP 可能相似； ③四边形PCDQ 面积的最大值为31316； ④四边形PCDQ 周长的最小值为3＋372.其中，正确结论的序号为（ ）A ．①④B ．②④C ．①③D ．②③{答案} D{解析}设AQ ＝x ，则BP ＝52—x①如图1，当点P 与B 重合时，此时QD 为最大，过点Q 作QE ⊥AC ，∵AQ ＝52，∴AE ＝54，QE ＝534，∴DE ＝34，∴此时QD ＝212，即0≤QD ≤212；而332≤CP ≤3，两个范围没有交集，即不可能相等；①错误②若△AQD ∽△BCP ，则AD BP ＝AQ BC ，代入得2x 2—5x +3＝0，解得x 1＝1，x 2＝32，∴都存在，∴②正确；③如图2，过点D 作DE ⊥AB ，过点P 作PF ⊥BC ，S 四边形PCDQ =S △ABC —S △AQD —S △BPC ＝34×32－12⋅x ⋅34－12×3×34（52－x ）＝34 x ＋21316，∵52—x ≥0，即x ≤52，∴当x =52时面积最大为31316；③正确； ④如图，将D 沿AB 方向平移12个单位得到E ，连接PE ，即四边形PQDE 为平行四边形，∴QD =PE ，四边形周长为PQ +QD +CD +CP =3+PE +PC ，即求PE +PC 的最小值，作点E 关于AB 的对称点F ，连接CF ，线段CF 的长即为PE +PC 的最小值；过点D 作DG ⊥AB ，∴AG ＝14，EN =FN =HM =34，∴CH ＝332＋34＝734，FH ＝MN ＝32－14－12＝34，∴FC ＝392，∴四边形PCDQ 周长的最小值为3＋392，④错误.DQ PCB A13.（2020·湖北孝感）某型号飞机的机翼形状如图所示，根据图中数据计算AB的长为________米．（结果保留根号）（第13题）{答案}（533-1.6）．{解析}如图，过点A作AM⊥CM于M，则CM=5m，在Rt△BCM中，∠BCM＝30°,所以BM=CM∙tan30°=53.由题意可知△DCN是等腰直角三角形，所以CN=CD=3.4m,所以MN=5-3.4=1.6(m),因为△AMN是等腰直角三角形，所以MN=AM=1.6m，所以AB=BM-AM=（533-1.6）m.故答案为（533-1.6）．第13题答图6．(2020·荆门)如图3，△ABC中，AB＝AC，∠BAC＝120°，BC＝23，D为BC的中点，AE＝14AB，则△EBD的面积为( )A．334B．338C．34D．38{答案}BDECAB图3{解析}连结AD ．∠B ＝∠C ＝12×(180°－∠A )＝30°．由等腰三角形的“三线合一”可知AD ⊥BC ．∴AD＝BD ·tan B ＝1．∴S △ABC ＝12BC ·AD ＝12××1AE ＝14AB ，∴S △EBD ＝34S △ABD＝38S △ABC ．故选B ．7. （2020·张家界）已知等腰三角形的两边长分别是一元二次方程2680x x -+=的两根，则该等腰三角形的底边长为（ ） A. 2 B. 4C. 8D. 2或4{答案}A{解析}本题考查了等腰三角形的性质，三角形的三边关系，解一元二次方程，能求出方程的解并能够判断三角形三边存在的条件是解此题的关键．解一元二次方程求出方程的解，得出三角形的边长，用三角形存在的条件分类讨论边长，即可得出答案． 解：x 2－6x+8=0 （x －4）（x －2）=0 解得：x=4或x=2，当等腰三角形的三边为2，2，4时，不符合三角形三边关系定理，此时不能组成三角形； 当等腰三角形的三边为2，4，4时，符合三角形三边关系定理，此时能组成三角形， 所以三角形的底边长为2， 故选：A ．14．(2020·青海)等腰三角形的一个内角为70°，则另外两个内角的度数分别是( ) A ．55°，55° B ．70°，40°或70°，55° C ．70°，40° D ．55°，55°或70°，40° {答案}D{解析}(1)当70°是顶角时，另两个角相等，都等于12×(180°－70°)＝55°；(2)当70°是底角时，另一个底角也是70°，顶角＝180°－70°×2＝40°．因此另外两个内角的底数分别是55°，55°或70°，40°．故选D ． 5．（2020·临沂）如图，在ABC ∆中，AB AC =，40A ∠=︒，//CD AB ，则BCD ∠=（ ）A.40°B.50°C.60°.D.70°{答案}D{解析} 根据三角形内角和定理和等腰三角形的等边对等角且AB AC =，40A ∠=，可得：70ABC ACB ∠=∠=；然后根据两直线平行内错角相等且//CD AB 可得：70BCD ABC ∠=∠=，所以选D ． 11．（2020·宜宾）如图，△ABC 和△ECD 都是等边三角形，且点B 、C 、D 在一条直线上，连结BE 、AD ，点M 、N 分别是线段BE 、AD 上的两点，且BM ＝13BE ，AN ＝13AD ，则△CMN 的形状是（ ）A ．等腰三角形B ．直角三角形C ．等边三角形D ．不等边三角形{答案} C{解析} 由△ABC 和△ECD 都是等边三角形，可得△BCE ≌△ACD （SAS ），∴∠MBC ＝∠NAC ，BE ＝AD ，∵BM ＝13BE ，AN ＝13AD ，∴BM ＝AN ，∴△MBC ≌△NAC （SAS ），∴MC ＝NC ，∠BCM ＝∠ACN ，∵∠BCM+∠MCA ＝60°，∴∠NCA+∠MCA ＝60°，∴∠MCN ＝60°，∴△MCN 是等边三角形．9．（2020·玉林）如图，A ，B ，C 三岛的平面图，C 岛在A 岛的北偏东35°方向，B 岛在A 岛的北偏东80°方向，C 岛在B 岛的北偏西55°方向，则A ，B ，C 三岛组成一个（ ）A ．等腰直角三角形B ．等腰三角形C ．直角三角形D ．等边三角形 {答案}A{解析}如图所示： ∵C 岛在A 岛的北偏东35°方向，∴∠CAD ＝35°，∵B 岛在A 岛的北偏东80°方向，∴∠BAD ＝80°，∴∠CAB ＝∠BAD －∠CAD ＝45°， ∵C 岛在B 岛北偏西55°方向，∴∠CBE ＝55°， 又∵DA ∥EB ，∴∠ABE＋∠BAD＝180°，∴∠ABE＝100°，∵∠CBE＝55°，∴∠CBA＝100°－55°＝45°，∴∠CBA＝∠CAB，∴CA＝CB，在△ABC中，∴∠C＝180°－∠ABC－∠CAB＝180°－45°－45°＝90°，∴△ABC为等腰直角三角形，故选：C．9．（2020·毕节）已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（）A．13 B．17 C．13或17 D．13或10{答案}B，{解析}本题考查等腰三角形的三边关系．解：分两种情况讨论：若3为底边，腰长为7，则此等腰三角形的周长为3＋7＋7=17；若7为底边，腰长为3，则此等腰三角形不存在，因为3＋3＜7，不符合三角形的三边关系，故选B.9．（2020·烟台）七巧板是我们祖先的一项创造，被誉为“东方魔板”．在一次数学活动课上，小明用边长为4cm的正方形纸片制作了如图所示的七巧板，并设计了下列四幅作品﹣﹣“奔跑者”，其中阴影部分的面积为5cm2的是（）A．B．C．D．【解析】最小的等腰直角三角形的面积=18×12×42＝1（cm2），平行四边形面积为2cm2，中等的等腰直角三角形的面积为2cm2，最大的等腰直角三角形的面积为4cm2，则A、阴影部分的面积为2+2＝4（cm2），不符合题意；B、阴影部分的面积为1+2＝3（cm2），不符合题意；C、阴影部分的面积为4+2＝6（cm2），不符合题意；D、阴影部分的面积为4+1＝5（cm2），符合题意．故选：D．10．（2020·天门仙桃潜江）如图，已知△ABC和△ADE都是等腰三角形，△BAC=△DAE=90°，BD，CE 交于点F，连接AF．下列结论：△BD=CE；△BF△CF；△AF平分△CAD；△△AFE=45°．其中正确结论的个数有A．1 B．2个C．3个D．4个{答案}C{解析}∵△ABC 和△ADE 都是等腰直角三角形， ∴AB=AC ，AD=AE ， ∵∠BAD=90°+∠CAD ， ∠CAE=90°+∠CAD ， ∴∠BAD=∠CAE ， 在△AEC 与△ADB 中，AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩， ∴△AEC ≌△ADB(SAS)， ∴BD=CE ，故①正确； ∴∠ADB=∠AEC ，∵∠DEF+∠AEC+∠EDA=90°， ∴∠DEF+∠ADB+∠EDA=90° ∴∠DEF+∠EDF=90∘， ∴BD ⊥CE ，故②正确； ∵作AN ⊥CE ，AM ⊥BD ∵△AEC ≌△ADB(SAS)， ∴AM=AN ，∵AF 是∠BFE 的角平分线， ∠BFE=90°，∴∠AFE=45°，故④正确 ，故③正确；因为QF ≠PF ，故③错误。