DSP-第二章维纳滤波器
- 格式：pdf
- 大小：1.64 MB
- 文档页数：20
下载文档原格式
合集下载
维纳滤波器
w
* 1
m in
w
* 0
w
0
w
1
记 为 w w , w w
* T N 1
( w ) 若 使最 ( w )小 ， 须 0 w 即
( w ) ( w ) ( w ) ( w ) ， ,, 2 R w 2 p 0 w w w w 0 1 N 1
E dn () 2 w () n E d () n xn () N
2
T
期 望 响 应 的 平 均 功 率
2 d
( n ) 是 w 的 函 数 , 即 ( n ) ( w )
T w () n E xn () xn () w () n N N T
——维纳-霍甫夫(Wiener-Hopf)方程
它反映了相关函数与最佳单位脉冲响应之间的关系。
Wiener-Hopf方程的矩阵形式
R hR s x x x
自相关矩阵 故最佳单位脉冲响应 其中
s () n 与的 x () n互 相 关
h RR s x o p t
R 0, N1 R 1, N1 RN1,N1
xn 观察/测量数据
s n 真实信号
vn 加性噪声/干扰
ˆ s n x n h n h i x n i 线性估计问题 i
ˆ e n s n s n
2
估计误差
n E en m i n h n 最小均方误差(MMSE)估计
得到：
E [] e x 0 i 0 , 1 ,, N 1 i
或
N 1 E h x sx 0 i j j j 0
第2章 维纳滤波讲解
横向滤波器的二次误差性能曲面和等高 线
15
第2章 维纳滤波
相关矩阵R的特征分解与化为标准形
det[R I] 0
0 , 1 ,, M 1
0 0 Λ 0 0
Q q 0
q1 q M 1 R来自 QΛQT1 0
0 0 M 1
3
第2章 维纳滤波
得到维纳滤波器的另一个充要条件，即著名的维纳-霍夫（Wiener-Hopf）方程为
w
i 0
oi
r (i k ) p(k ) k 0,1,2,
2.3 离散形式维纳滤波器的性质 2.3.1 正交原理的几何解释
d (1 )
eo (1)
u (1 )
yo
u (0 )
p E[u(n)d (n)] [ p(0), p(1),, p(1 M )]T
则横向滤波器的维纳-霍夫方程式的矩阵表示形式为 Rwo p ，即维纳解为 w o R 1p 式中： w o [wo,0 , wo,1 ,, wo,M 1 ]T 是横向滤波器最优抽头权向量。
8
第2章 维纳滤波
2.4.2 横向滤波器的误差性能 一、误差性能曲面 M 1 输出： y(n) w u(n k ) u T (n)w(n) w T (n)u(n)
k 0
k
估计误差： 均方误差：
e(n) d (n) y(n) d (n) wT (n)u(n)
J E[e 2 (n)] E{[d (n) y (n)]2 } E{[d (n) wT (n)u(n)]2 } E[d 2 (n)] wT (n) E[u(n)uT (n)]w (n) 2wT (n) E[d (n)u(n)]
维纳滤波
m 0 N 1
e 2 (n) [ s(n) X (n) H ][ s(n) H T X (n)] s 2 ( n) 2 s ( n) X ( n) H H X (n) X (n)]H
E[e 2 n ] E[ s 2 n ] 2 E[ sn X T n ]H H T E[ X n X T n ]H
x(
我们已知
X ( z ) B( z )W ( z )
则信号功率谱为
2 Pxx ( z) B( z) B( z 1 )
如果已知信号的Pxx(z)，即可求得B(z) 。
非因果IIR维纳滤波器的求解
计算Hopt (z)：
1 B( z )
x( n )
w(n)
G(z)
ˆ( n ) y ( n) s
正交性原理：最优估计 误差正交于任一个进入 估计的输入信号或信号 空间。
由正交方程可得：
E[enxn m] E[{sn hmxn m}xn m]
E[snxn m] E[xn mxn p ]h p 0
m
m 0
k ≥ 0的约束使得上式不能直接转到Z域求解。如
能将其转化为非因果问题，则求解会大大简化。
如果滤波器的输入x(n)是方差为 w 的白噪声w(n)
2
因果维纳滤波器的维纳－霍夫方程变为：
2 2 xs m ws m h p w m p w hm m 0
代入可得： (h) s2 2P H H RH (二次型问题）
其解为：HOP R1P， 且
2 T H H 即 op s op P
结论：在所有N阶FIR滤波器中，最优滤波器的均 方误差值是最小的。其阶数越高，采用的已知信 息越多，最小均方误差越小，计算量也越大。
e 2 (n) [ s(n) X (n) H ][ s(n) H T X (n)] s 2 ( n) 2 s ( n) X ( n) H H X (n) X (n)]H
E[e 2 n ] E[ s 2 n ] 2 E[ sn X T n ]H H T E[ X n X T n ]H
x(
我们已知
X ( z ) B( z )W ( z )
则信号功率谱为
2 Pxx ( z) B( z) B( z 1 )
如果已知信号的Pxx(z)，即可求得B(z) 。
非因果IIR维纳滤波器的求解
计算Hopt (z)：
1 B( z )
x( n )
w(n)
G(z)
ˆ( n ) y ( n) s
正交性原理：最优估计 误差正交于任一个进入 估计的输入信号或信号 空间。
由正交方程可得：
E[enxn m] E[{sn hmxn m}xn m]
E[snxn m] E[xn mxn p ]h p 0
m
m 0
k ≥ 0的约束使得上式不能直接转到Z域求解。如
能将其转化为非因果问题，则求解会大大简化。
如果滤波器的输入x(n)是方差为 w 的白噪声w(n)
2
因果维纳滤波器的维纳－霍夫方程变为：
2 2 xs m ws m h p w m p w hm m 0
代入可得： (h) s2 2P H H RH (二次型问题）
其解为：HOP R1P， 且
2 T H H 即 op s op P
结论：在所有N阶FIR滤波器中，最优滤波器的均 方误差值是最小的。其阶数越高，采用的已知信 息越多，最小均方误差越小，计算量也越大。
维纳滤波器
z(n) Hw(z)
w(n) H2(z)
ˆ s ( n)
1 Hw(z) = + Gz (z)
维纳滤波器
+ H2 (z) = Gsw(z) =[Hw(z−1)Gsz (z)]+
1 Gsz (z) H(z) = + + −1 Gz (z) Gz (z )
+
维纳滤波器
Rsw (n1 , n2 ) = E {s (n1 ) w(n2 )} = E s (n1 )∑ z (n2 − k )hw (k ) k =0 = ∑ Rsz (n1 , n2 − k )hw (k )
维纳滤波器
维纳滤波器
波形估计 维纳滤波器频域解 维纳滤波器时域解
维纳滤波器
一、波形估计一般概念
z(n) = s(n) + v(n)
波形估计有三种类型 ：
n = n0, n0 +1 nf ,...,
(1)滤波： 根据当前和过去的观测值 滤波： 滤波 {z(k),k= n0, n0+1,...,n}对信号 对信号s(n)进行估计 对信号 进行估计 (2)预测 根据当前和过去的观测值 预测: 根据当前和过去的观测值{z(k),k= n0, n0+1,...,nf} 预测 对未来时刻n(n>nf)的信号 的信号s(n)进行估计，预测也称为外 进行估计， 对未来时刻 的信号 进行估计 推。
维纳滤波器 (3)内插 根据某一区间的观测数据 内插: 根据某一区间的观测数据{z(k),k= 内插 n0,n0+1,...,nf}对区间内的某一个时刻 0<n<nf)的信 对区间内的某一个时刻n(n 对区间内的某一个时刻 的信 号进行估计，内插也称为平滑。 号进行估计，内插也称为平滑。 波形估计的目的： 波形估计的目的： 选取线性滤波器的冲激响应函数或传输函数， 选取线性滤波器的冲激响应函数或传输函数， 使估计的均方误差达到最小。 使估计的均方误差达到最小。
维纳滤波概述
2 2
E[ x(t ) h(t ) y (t )d ]2
0
E[ x(t )]2 2 h( )( E[ y (t ) y ( )]d
0
h( )d h( ) E[ y (t ) y (t )]d
0 0
Rxx (0) 2 h( ) Ryx ( )d
E[e 2 (n)] lim
(2-25)
1 T 2T
T
T
(n) s (n)]2 dn [s
滤波器在n时刻复现信号s(n)显然是滤波问题。这是一种简单的过滤，滤除 噪声v(n)是唯一的目的。 但输出在时间上的简单的超前或者滞后，都不失为线性
(n a) ，这显然是一种超前的情况，输 滤波问题。在n时刻，滤波器输出如果为 s (n a) 是 s(n a) 的估计值，它比x(n)超前了 时间。这个时候滤波器所完成 出s
2 J1 2 J 2 0( 3 )
(2-15) 则将导致
J[ h h( t )] J [ o p t( t ) oh p t (t ) ]
(2-16) 这明显与最佳冲击响应将使均方误差最小的假设相矛盾。所以，我们只能取
J1 =0，即满足式(2-11)。由式(2-13)知，若使 J1 =0成立，则必须使式(2-13)中的方
第 2 章 维纳滤波理论
2.1 维纳滤波的概述
维纳 （Wiener） 滤波是用来解决从噪声中提取信号问题的一种过滤 （或滤波） 的方法。 实际上这种线性的滤波问题，可以看成是一种估计问题或是一种线性估 计问题。 维纳滤波器是一种基于最小均方误差准则下的估计滤波器。 滤波器的输入包 括有真实信号值x(t)和干扰噪声w(t)，信号值与噪声是统计独立的，则两者的合 成输入信号是
E[ x(t ) h(t ) y (t )d ]2
0
E[ x(t )]2 2 h( )( E[ y (t ) y ( )]d
0
h( )d h( ) E[ y (t ) y (t )]d
0 0
Rxx (0) 2 h( ) Ryx ( )d
E[e 2 (n)] lim
(2-25)
1 T 2T
T
T
(n) s (n)]2 dn [s
滤波器在n时刻复现信号s(n)显然是滤波问题。这是一种简单的过滤，滤除 噪声v(n)是唯一的目的。 但输出在时间上的简单的超前或者滞后，都不失为线性
(n a) ，这显然是一种超前的情况，输 滤波问题。在n时刻，滤波器输出如果为 s (n a) 是 s(n a) 的估计值，它比x(n)超前了 时间。这个时候滤波器所完成 出s
2 J1 2 J 2 0( 3 )
(2-15) 则将导致
J[ h h( t )] J [ o p t( t ) oh p t (t ) ]
(2-16) 这明显与最佳冲击响应将使均方误差最小的假设相矛盾。所以，我们只能取
J1 =0，即满足式(2-11)。由式(2-13)知，若使 J1 =0成立，则必须使式(2-13)中的方
第 2 章 维纳滤波理论
2.1 维纳滤波的概述
维纳 （Wiener） 滤波是用来解决从噪声中提取信号问题的一种过滤 （或滤波） 的方法。 实际上这种线性的滤波问题，可以看成是一种估计问题或是一种线性估 计问题。 维纳滤波器是一种基于最小均方误差准则下的估计滤波器。 滤波器的输入包 括有真实信号值x(t)和干扰噪声w(t)，信号值与噪声是统计独立的，则两者的合 成输入信号是
第二章维纳滤波2-3
2 -1
解 得 B ( z )。 因 B ( z ) 是 xx ( z ) 单 位 园 内 的 零 、 极 点 组 成 ， 所 以 B ( z )和 1 B(z) 都是物理可实现的因果系统。
G ( z )也 可 分 为 因 果 性 与 非 因 果 性 的 情 况 ， 但它是将激励信号白化后所得的白噪声， 使 求 解 G ( z )比 直 接 求 解 H
2 -1
又 因 为 x ( n ) s ( n ) ( n ), x ( n )的 信 号 模 型 为 ：
v(n)
w (n) A( z)
s(n)
x(n)
当 x ( n )的 功 率 谱 密 度 也 是 z的 有 理 式 时 ， 显 然 可 将 x (n )表 示 如 下 信 号 模 型 ：
2
1
2
ws (k )
2
ws ( z )=
xs
(z)
1
w k -
B(z
)
E e (n) m in =
2 -1 1 1 xs ( z ) xs ( z ) -1 c ss ( z ) - 2 B ( z -1 ) B ( z ) z d z 2 j w
x s (- m ) b ( m ) w s (- m )
x s ( m ) b (- m ) w s ( m )
(z) B(z xs
ws 1
)
1
ws
(z)
( z )=
xs
(z) )
B(z
H
opt
(z)
G (z) B(z)
xs 1
ˆ s ( n )的 均 方 误 差 ：
解 得 B ( z )。 因 B ( z ) 是 xx ( z ) 单 位 园 内 的 零 、 极 点 组 成 ， 所 以 B ( z )和 1 B(z) 都是物理可实现的因果系统。
G ( z )也 可 分 为 因 果 性 与 非 因 果 性 的 情 况 ， 但它是将激励信号白化后所得的白噪声， 使 求 解 G ( z )比 直 接 求 解 H
2 -1
又 因 为 x ( n ) s ( n ) ( n ), x ( n )的 信 号 模 型 为 ：
v(n)
w (n) A( z)
s(n)
x(n)
当 x ( n )的 功 率 谱 密 度 也 是 z的 有 理 式 时 ， 显 然 可 将 x (n )表 示 如 下 信 号 模 型 ：
2
1
2
ws (k )
2
ws ( z )=
xs
(z)
1
w k -
B(z
)
E e (n) m in =
2 -1 1 1 xs ( z ) xs ( z ) -1 c ss ( z ) - 2 B ( z -1 ) B ( z ) z d z 2 j w
x s (- m ) b ( m ) w s (- m )
x s ( m ) b (- m ) w s ( m )
(z) B(z xs
ws 1
)
1
ws
(z)
( z )=
xs
(z) )
B(z
H
opt
(z)
G (z) B(z)
xs 1
ˆ s ( n )的 均 方 误 差 ：
第二章维纳滤波2-4
{
}
{
}
（1）因果系统
取反变换：用b(n)表示B ( z )的逆变换。
E e2 (n + N )
∞ n=-∞
{
}
min ∞
2 2 = σ w ∑ b2 (n) - σ w ∑ b(n + N ) [b(n + N )u(n)] n=-∞
e2 (n + N ) 说明N 增大将导致E
N
Φ xyd ( z )
及 = 1
ˆ E [ s (n + N )-s (n + N ) ]
ss
{
c
2
}
min -1 -1
∫ Φ 2π j
( z ) - H opt ( z ) z Φ xs ( z ) z dz
-N
(2)物理可实现约束的(因果)维纳预测器
1 Φ xyd ( z ) H opt ( z ) = 2 -1 σ w B( z ) B( z ) + 1 Z Φ xs ( z ) = 2 -1 σ w B( z ) B( z ) +
因而，具有
2 Φ xx ( z) = Φss ( z) = Φ xs ( z) = σ w B( z) B( z -1 )
x(n) = s(n)
H ( z)
纯预测器
ˆ y (n) = s(n + N )
纯预测在工程上的意义： 当噪声小到一定程度以后可将该噪声忽略 或不再作更多考虑。 为此，可先用维纳滤波器等将噪声抑制到一定水准 之后再以纯预测方法作相应的预测处理。
φx y =∑hiφx x
j d
∞
i =1
j i
第二章—维纳滤波和卡尔曼滤波
H
c
(z)
2
1 B(
z)
[
Ssx (z) B(z 1 )
]
• 计算步骤如下：
•
(1)对
S xx
(z)
进行谱分解（因式分解）
S
x
x
(
z)
2
B(
z)
B(
z
1
)
• (2)对 Ssx (z)
进行因果和逆因果分解
B(z 1 )
Ssx (z) B(z 1 )
[
Ssx (z B(z 1
) )
]
[
Ssx (z B(z 1
N
• 称y(n) 是 sˆ(n)的估计值。 h(n) 为估计器。这种滤波器
称为最佳滤波器。
• 如果：s(n) 和 v(n) 的谱在频域上是分离的，容易设计一个
线性滤波器抑制噪声并提取信号。这是本科中经典数字信号 处理理论中详细讨论过的数字滤波器的设计问题。但是
• s(n) 和 v(n) 的谱有一部分相互重叠，则问题就要复杂的
E[e(n) x(n j)] 0
• 上式称为正交方程。（这是讲当用两个矢量正交时它们的 点乘等于零的关系，正交性原理可借用几何图形表示）
• 可见，满足正交性原理与满足最小均方误差的条件是等价
的。由图知，sˆ(n) 最满足最小均方误差的估计值。
• 正交方程表明，任何时刻的估计误差与用于估计的所有数 据（即滤波器的输入）正交。
• （2）
Ssx (z) B( z 1 )
[
Ssx (z B( z 1
) )
]
[
Ssx (z B( z 1
) )
]
0.36
(1 0.8z 1 )(1 0.8z)
维纳滤波器
维纳滤波器(第二讲)维纳去卷积•一般的去卷积并不考虑噪声，因此，当有噪声时，去卷积传递函数（在高频时它的幅度值常常很大）是不实用的。
图11.17表示在去卷积之后紧跟着维纳滤波器。
期望的信号s(t)首先被一个冲激响应为f(t)的线性系统所退化，其输出又被附加的噪声源n(t)所污染形成了观察到的信号x(t).维纳滤波在图象上的应用匹配检测器举例•第一种情况：假定噪声的频谱是白的；即因为式（99）中的C 是任意的常数，因此我们可以令，在这种情况下，匹配检测器变为：K 0(s) = M*(s)2)(N s P n =20N C =)()()}({)(2*1t m ds e s M t K t k st j o o −==ℑ=∫∞∞−−π•对于白噪声情况，冲激响应就是信号本身的反转。
输出端的信号分量为:而噪声分量为:因为式（107）中K 0(t)正好是我们企图信号的反转，所以匹配滤波器K 0(t)只是一个互相关算子，它把进来的信号加噪声与已知形式的期望信号做相关运算，所得输出为)()()()(*)()(t R d t m m t k t m t u m o −=+−==∫∞∞−τττ)()()()(*)()(t R d t m n t k t n t v mn o −=+−==∫∞∞−τττ)()()()()(t R t R t v t u t y mn m −+−=+=•矩形脉冲检测器假定，即设计用来检测淹没在白的矩形脉冲的匹配检测器。
还假定输入是x(t) = s(t)+ n(t)，这里，n(t)是白噪声。
我们知道矩形脉冲的自相关函数由下式给出：滤波器的输出就是:)()(t t m C =)()(T t t s −=C )()(*)()(ττΛ=∏∏=t t R x )()()(t R T t t y mn +−Λ=•从图11.23可以看出匹配检测器是如何抑制噪声而对信号做出响应。
输出有一峰值出现在信号的t=T时刻，但在其他的地方，幅度值相当小。
维纳滤波器的原理和应用
维纳滤波器的原理和应用维纳滤波器简介维纳滤波器是一种经典的信号处理滤波器，它基于维纳滤波理论，通过对信号进行统计分析和模型建立，实现信号的优化处理。
维纳滤波器能够降低信号中的噪声成分，提高信号的质量和可靠性，在许多领域中得到广泛的应用。
维纳滤波器原理维纳滤波器的原理是基于最小均方误差的思想，通过最小化信号与噪声之间的均方误差，实现对信号的最优估计。
其数学模型可以表示为：维纳滤波器原理公式维纳滤波器原理公式其中，x(n)是输入信号，h(n)是滤波器的冲激响应，y(n)是滤波器的输出信号，w(n)是噪声信号，E[w(n)w(m)]是噪声信号的自相关函数，Rxx(k)是输入信号的自相关函数，Rxy(k)是输入信号和噪声之间的互相关函数。
维纳滤波器根据输入信号、噪声信号和系统参数的统计特性，通过最小化均方误差优化系统参数，使得滤波器能够有效地抑制噪声成分，提取出原始信号。
维纳滤波器的设计需要基于输入信号和噪声的统计特性的准确估计，以及对滤波器参数的优化求解。
维纳滤波器应用维纳滤波器在实际应用中具有广泛的用途，以下列举了几个常见的应用领域：1.图像去噪：维纳滤波器可以应用于数字图像处理中的去噪问题，通过最小化图像中的噪声与图像信号的误差，实现对图像噪声的抑制，提高图像的质量和清晰度。
2.语音增强：在语音信号处理中，维纳滤波器可以应用于语音增强问题，通过对语音信号进行建模和分析，实现对噪声的抑制，提高语音信号的清晰度和可听性。
3.视频恢复：在视频信号处理中，维纳滤波器可以应用于视频恢复问题，通过对视频帧进行建模和分析，实现对噪声和失真的抑制，提高视频的质量和稳定性。
4.无线通信：在无线通信系统中，维纳滤波器可以应用于信号解调和接收问题，通过对接收信号进行建模和分析，实现对噪声和干扰的抑制，提高信号的可靠性和传输速率。
5.生物信号处理：在生物医学信号处理中，维纳滤波器可以应用于生物信号的去噪和增强问题，通过对生物信号进行建模和分析，实现对噪声和干扰的抑制，提高生物信号的可读性和分析能力。
数字信号处理第2章(3、4)
-∞＜k＜∞ (2.3.10)
gopt ( k ) =
对上式两边同时做Z变换，得到
rωs (k ) (k
σω
2
-∞＜k＜∞ (2.3.11)
Gopt ( z ) =
Sωs ( z )
2 σω
(2.3.12)
第二章 维纳滤波和卡尔曼滤波 这样，非因果维纳滤波器的最佳解为 Gopt ( z ) 1 Sωs ( z ) H opt ( z ) = = 2 B( z ) σ ω B( z ) (1.4.15)式, 得到
G( z) H ( z) = B( z )
(2.3.7)
因此，维纳滤波器的传输函数H(z)的求解转化为G(z)的求解。
x(n)
1 B( z )
ω(n)
G(z)
^ y(n)＝ s(n)
图 2.3.3 维纳滤波解题思路
第二章 维纳滤波和卡尔曼滤波 2.3.1 非因果维纳滤波器的求解 假设待求维纳滤波器的单位脉冲响应为ω(n)，期望信号 d(n)=s(n)，系统的输出信号
ω(n)
B(z)
x(n)
x(n)
B －1(z)
ω(n)
图 2.3.2 x(n)的时间序列信号模型及其白化滤波器
第二章 维纳滤波和卡尔曼滤波 具体思路如图2.3.3所示。用白噪声作为待求的维纳滤波器 的输入，设定1/B(z)为信号x(n)的白化滤波器的传输函数，那么 维纳滤波器的传输函数G(z)的关系为
第二章 维纳滤波和卡尔曼滤波 下面我们推出该滤波器的最小均方误差E［|e(n)|2］ min 的计 算, 重新写出(2.3.9)式的最佳解
E[| e(n) | ]min = rss (0) −
2
k = −∞
DSP_维纳滤波器的计算机实现
实验一维纳滤波器的计算机实现一实验目的1.利用计算机编程实现加性噪声信号的维纳滤波。
2.将计算机模拟实验结果与理论分析结果相比较，分析影响维纳滤波效果的各种因素，从而加深对维纳滤波的理解。
3.利用维纳滤波一步纯预测方法实现对信号生成模型的参数估计。
二实验原理1.维纳滤波器是一种从噪声中提取信号的最佳线性估计方法，假定一个随机信号形式为：x(n)=s(n)+v(n),其中s(n)为有用信号，v(n)为噪声信号。
而维纳滤波的作用就是让x(n)通过一个系统h(n)尽可能滤掉噪声，提取近似s(n),h(n)的选择以最小均方误差为准则。
由维纳-霍夫方程知，只要求出φxx 及φxs就可求出h（h=φ-1xxφxs）。
但要求h(n)满足因果性要求，维纳-霍夫方程便是一个难题，这里利用最佳FIR 维纳滤波方法求解h(n)的近似，这也便于在计算机上实现，公式为：h =R-1xx rxs。
实验中s(n)由信号生成模型：s(n)=as(n-1)+w(n)确定，其中a=0.95,w(n)是均值为0，方差为бw2=1的高斯白噪声，v(n)为均值为0，方差为1的高斯白噪声，且s(n)与v(n)不相关。
实验中s(n)是已知的，但实际中如果s(n)已知，维纳滤波也就失去意义了，因此实验纯粹是为了理解维纳滤波原理而设计。
2.维纳一步纯预测问题S(n)的生成模型：s(n)+a1(n-1)+…+a p s(n-p)=w(n),已知φxx（n）,利用Yule-walker方程即可得到信号生成模型参数a i(i=1,2…p)和б2w 。
三实验步骤及结果分析1.仔细阅读维纳滤波原理，根据图 1.1 给出的框图编制维纳滤波程序。
(程序见附录)2.运行维纳滤波程序，选择L=5000,N=10，观察并记录实验结果，分析比较下列三个问题：①与s(n)比较，信号x(n)在维纳滤波前后有何差别？滤波效果如何？（注意：比较噪声方差时应取多次实现的平均值,在本实验中我们统一取100 次实现的平均）可知滤波前后x(n)围绕s(n)的波动比较大，这种变化是由滤波前有很大噪声造成的。
第二章 维纳滤波与卡尔曼滤波
k0
xs (k ) h0 pt * xx (k )
又称互相关定理
共128页 12
解Wiener-Hopf 方程 存在的问题及解决的思路
存在的问题： 1。假设设计的是因果系统，由于存在 k>0的约 束条件，卷积定理（双边Z变换）不能用。 2。实际物理系统为因果系统。 解决思路： 1。设计一个非因果性系统（滤波器）。 2。用有限长的因果序列h(n)来逼近hopt(n).实 质为设计FIR型滤波器。
s (k ) g opt (k ) 0
共128页
k
31
s (k ) g opt (k ) 2
k
Gopt ( z )
1
2
s ( z )
s ( z ) B( z )
32
G( z ) 1 H opt ( z ) 2 B( z )
共128页 5
2.2 维纳滤波器的离散形式(I) —— 时域解
ˆ(n) h(m) x(n m) y(n) s
m
h(n)=0
当n<0， 因果系统
ˆ(n) h(m) x(n m) y ( n) s
m 0
ˆ(n) hi xi 为表示简单，记：s
共128页
i 1
Es(n) (n m) 0
xs (m) Ex(n)s(n m) Es(n) (n) s(n m) Es(n)s(n m) ss (m) xx ( z ) ss ( z ) ( z )
X ( z ) B( z )W ( z )
1 W ( z) X ( z) B( z ) 则维纳滤波器的设计变为：
第二章1 维纳滤波
16
S(n)
x(n)
例2.1
解：由题知信号的自相关与噪声的自相关为:
ss ( m ) 0.6
m
, ww ( m ) 1( m )
[fxs ] [fxx ][hopt ] fxs fss fxx fss fvv
代入维纳－霍夫方程得: k0 1 2h(0) 0.6h(1) k 1 0.6 0.6h(0) 2h(1) 求出: h(0)=0.451，h(1)=0.165 最小均方误差为：
10
2.2.2 有限脉冲响应法求解维纳－霍夫方程
xs ( k ) = å hopt ( m ) xx ( k - m )
m =0 ¥
k = 0,1, 2...
从维纳－霍夫方程中求出h，就是最小均方误差下的最优 hopt。设h(n)是一个因果序列可以且用有限长度为N的 （h(n)是一个长度为N的FIR滤波器）序列逼近它。
xi x j E [ x i x j ] sx j E[ sx j ]
¥ ì ü i = m + 1 或 m = i 1 ï ï j ³ 1 2 E [( s h x ) x ] = 0 ï ï å i i j ï ï ï hi = h( i - 1) = h( m ) i =1 ý ï í ¥ ï ï x = x ( n i + 1) = x ( n m ) ï ï i ï þ = h j ³ 1 å ï xj s i x j xi ï i =1 ï î 正交性原理的另一表达式
i =1
均方误差最小原则
要求使均方差最小的h(n)，将上式对hj求偏导，并令其 为零：
2 E[( s - å hi xi ) x j ] = 0
i =1
S(n)
x(n)
例2.1
解：由题知信号的自相关与噪声的自相关为:
ss ( m ) 0.6
m
, ww ( m ) 1( m )
[fxs ] [fxx ][hopt ] fxs fss fxx fss fvv
代入维纳－霍夫方程得: k0 1 2h(0) 0.6h(1) k 1 0.6 0.6h(0) 2h(1) 求出: h(0)=0.451，h(1)=0.165 最小均方误差为：
10
2.2.2 有限脉冲响应法求解维纳－霍夫方程
xs ( k ) = å hopt ( m ) xx ( k - m )
m =0 ¥
k = 0,1, 2...
从维纳－霍夫方程中求出h，就是最小均方误差下的最优 hopt。设h(n)是一个因果序列可以且用有限长度为N的 （h(n)是一个长度为N的FIR滤波器）序列逼近它。
xi x j E [ x i x j ] sx j E[ sx j ]
¥ ì ü i = m + 1 或 m = i 1 ï ï j ³ 1 2 E [( s h x ) x ] = 0 ï ï å i i j ï ï ï hi = h( i - 1) = h( m ) i =1 ý ï í ¥ ï ï x = x ( n i + 1) = x ( n m ) ï ï i ï þ = h j ³ 1 å ï xj s i x j xi ï i =1 ï î 正交性原理的另一表达式
i =1
均方误差最小原则
要求使均方差最小的h(n)，将上式对hj求偏导，并令其 为零：
2 E[( s - å hi xi ) x j ] = 0
i =1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
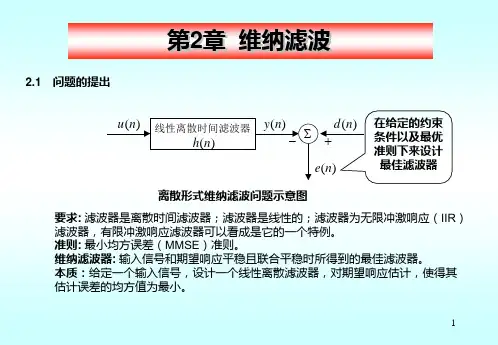
第二章维纳滤波
其中：x(n)=s(n)+v(n)s(n)为真实有用信号v(n)为加性噪声
滤波的目的：在接收端得到s(n)的值，最好把v(n)全部给滤除掉
实际情况：不可能把噪声v(n)全部滤掉，只能让接收端接收的信号尽可能接近s(n),性能最好的这种线性滤波器就叫做维纳滤波器。
性能指标：最小均方误差MMSE（minimum mean square error）
滤波的目的：不断逼近S(n)
滤波的分类：
性能指标：最小均方误差MMSE（minimum mean square error）
◆维纳滤波器的设计（求解），实际上是找出一个滤波器，当输入x(n)=s(n)+v(n)时，滤
波器的输出最接近
s(n)。
◆确定一个滤波器：得到滤波器的单位冲击响应
h(n)
或者系统函数H(w)◆对于非因果的滤波器（Z域求解简单）：维纳滤波器时域求解
对于因果的滤波器：
维纳滤波器的Z域解（改进后的模型）
◆信号分解（通过白噪声获得色噪声）：
互逆操作◆白化滤波器（由色噪声得到白噪声）：
引入白化滤波器后的维纳滤波器滤波器的结构：
改进后的滤波器：
非因果维纳滤波器Z域求解（应用改进模型）
ΦXX z=σω2·B z·B(z−1)
最小均方误差：
因果维纳滤波器Z域求解（应用改进模型）
最小均方误差：
维纳预测器
◆维纳滤波器：
◆维纳预测器：
◆分类：
◆纯预测：x(n)中没有噪声，纯粹已知S(n),S(n-1)···对S(n + N)进行预测◆一般预测：带有噪声，已知x(n),x(n-1)···对S(n + N)进行预测
期望输出：y d(n)=S(n + N)
实际输出：y(n)=S(n+N)
◆非因果维纳预测器：
◆因果维纳预测器：
N步纯预测
一步纯线性预测时域求算
Yule-Walker方程：
自相关矩阵的的性质：
◆1.当x(n)为实数，自相关矩阵为对称阵Φxx=Φxx T
◆当x(n)为复数，自相关矩阵为厄米特阵Φxx=Φxx H
◆2.自相关矩阵为托普列兹阵，对角线上的元素相同。
◆3.自相关矩阵为正定阵。
习题。