最简单的单片机PID控制算法程序
- 格式:pdf
- 大小:132.81 KB
- 文档页数:4

PID算法的单片机实现PID控制算法是目前应用较为广泛的一种控制算法,PID控制具有参数可调、应用范围广、控制精度高等优点。
在实际工程中,PID算法可以应用于机电控制、工业自动化、机器人控制、微处理器控制等多个领域。
以单片机实现PID算法为例,以下是一个简要的介绍。
1. 调节PID算法的三个参数:比例常数Kp,积分时间常数Ti,微分时间常数Td。
不同系统需要设置不同的PID参数,一般需要经过实验和调试来获取最优参数。
比例常数Kp调节比例,调节控制系统运行中的输出与反馈误差的比例;积分时间常数Ti调节积分,调节控制系统运行中误差的积累情况;微分时间常数Td调节微分,调节控制系统中误差的变化率。
2. 精度调节。
精度调节是指根据控制系统应用的需要,调节系统的精度。
对于不同领域的应用,需要根据具体的应用而精心调节PID算法的参数。
例如,对于机器人控制领域,精度通常要求高于工业控制领域。
3. 微处理器程序实现。
(1)获取输入信号,包括控制问题、机器状态等。
常见的输入信号包括温度、保护、安全等信号。
本例中,我们可以设置单片机的ADC(模拟数字转换器)以获取输入信号。
(2)实现PID算法。
PID算法的实现涉及到计算最终输出量以驱动控制。
此过程通常涉及采样和累积误差等方面。
具体实现中,对单片机某一设备的比特定位进行控制以输入输出。
例如,控制计数器在定期间隔内进行错误信息统计。
(3)输出信号。
输出信号指控制器输出的电路,通过该电路实现机械运动的控制。
例如,通过调节电机的转速或转矩,控制锅炉的温度或控制航空发动机的转速。
综上所述,PID算法是一种常用的控制算法,在单片机实现中需要先确定PID算法的参数,根据实际应用需要进行精度调节,并针对实际应用场景编写微处理器程序。
PID算法在机电控制、工业自动化、机器人控制、微处理器控制等多个领域的应用都有广泛的运用。

单片机中的PID公式
在自动化控制领域,PID(比例-积分-微分)控制器是一种广泛使用的控制算法。
单片机,作为一种集成度高、功能丰富的微控制器,在很多自动化设备中发挥着核心控制作用。
将PID算法应用到单片机中,可以实现精确、快速的控制,提高设备的性能和稳定性。
PID控制器的核心公式如下:
误差= 设定值- 实际值
比例项= Kp * 误差
积分项= Ki * 误差的积分
微分项= Kd * 误差的微分
输出= 比例项+ 积分项+ 微分项
其中,Kp、Ki和Kd是比例、积分和微分系数,需要根据具体的控制系统进行调整,以获得最佳的控制效果。
在单片机中实现PID算法,需要编写相应的程序。
一般来说,程序会包括以下几个部分:
1.初始化部分:设置PID控制器的参数,如设定值、比例系数、积分系数和
微分系数。
2.输入部分:读取实际值,与设定值进行比较,计算误差。
3.计算部分:根据误差计算比例项、积分项和微分项,得出输出值。
4.输出部分:将输出值转换为控制信号,控制执行机构。
在实际应用中,单片机中的PID算法还需要考虑一些其他因素,如抗干扰能力、系统稳定性等。
此外,为了方便调整和控制,许多单片机还提供了PID库函数或相关模块,可以直接调用。
总之,将PID算法应用到单片机中,可以实现精确、快速的控制,提高设备的性能和稳定性。
通过合理设置参数和优化程序,可以充分发挥单片机和PID算法的优势,推动自动化设备的发展和应用。

51单片机pid算法程序51单片机是一种广泛应用于嵌入式系统开发的微控制器。
PID算法是一种常用的控制算法,用于实现系统的闭环控制。
本文将介绍如何在51单片机上实现PID算法。
PID算法是一种经典的控制算法,它能够根据系统的反馈信息,自动调整控制量,使系统的输出接近期望值。
PID算法由比例项(P 项)、积分项(I项)和微分项(D项)组成。
比例项用来根据当前误差大小调整控制量,积分项用来根据过去误差的累积值调整控制量,微分项用来根据误差的变化速度调整控制量。
在51单片机上实现PID算法,首先需要编写程序来读取系统的反馈信息和期望值。
例如,可以通过ADC模块读取传感器的信号,然后通过计算得到当前误差。
接下来,根据比例项、积分项和微分项的系数,计算PID控制量。
最后,将PID控制量输出到执行机构,例如电机或舵机,来控制系统的输出。
在编写PID算法程序时,需要注意一些细节。
首先,要根据实际系统的特点和要求来选择合适的PID参数。
比例项的系数决定了控制量对误差的敏感程度,积分项的系数决定了控制量对误差累积值的敏感程度,微分项的系数决定了控制量对误差变化速度的敏感程度。
其次,要注意处理PID算法中的积分项和微分项的累积误差。
积分项的累积误差可能会导致系统出现超调或震荡,需要适当地进行限制或清零。
微分项的累积误差可能会导致系统出现噪声放大或不稳定,需要进行滤波或限制。
最后,要注意程序的效率和实时性。
PID算法通常需要以一定的频率进行计算和更新,要保证程序能够及时响应系统的变化。
除了基本的PID算法,还可以根据具体的应用需求进行算法的优化和改进。
例如,可以引入自适应调整PID参数的方法,使系统能够根据实时的工作条件自动调整PID参数。
还可以引入前馈控制或模糊控制等方法,进一步提高系统的控制性能和鲁棒性。
51单片机是一种常用的嵌入式系统开发平台,可以很方便地实现PID算法。
通过合理选择PID参数和优化算法,可以实现对系统的精确控制。

51单片机PID算法程序增量式PID控制算法增量式PID控制算法是一种常用的控制算法,可以应用于各种控制系统中。
该算法的原理是通过计算目标值与实际值之间的差异,来调整控制系统的输出,使其逐渐接近目标值。
增量式PID控制算法的核心思想是通过对目标值与实际值之间的差异进行积分和微分计算,来调整控制系统的输出。
这样可以使得控制系统对误差的响应更加敏感,从而实现更精确的控制效果。
在51单片机中实现增量式PID控制算法,可以按照以下步骤进行:1.参数设置:首先需要设置PID控制算法的参数,包括比例系数Kp、积分系数Ki和微分系数Kd。
这些参数可以根据实际控制系统的需求进行调整。
2.变量定义:定义控制系统所需的变量,包括目标值、实际值、误差值、上一次的误差值、累积误差值等。
3.计算误差:将目标值与实际值之间的差异作为误差值进行计算。
4.计算增量输出:根据误差值以及上一次的误差值和累积误差值,计算控制系统的增量输出。
增量输出的计算公式为:增量输出=Kp*(当前误差-上一次误差)+Ki*当前误差+Kd*(当前误差-上一次误差)5.更新变量:更新控制系统所需的变量,包括上一次的误差值和累积误差值。
6.输出信号:将增量输出作为控制系统的输出信号,并进行相应的处理。
通过上述步骤,就可以实现51单片机的增量式PID控制算法。
在实际应用中,可以根据具体情况对算法进行优化和改进,以满足实际控制的需求。
总结起来,增量式PID控制算法是一种常用的控制算法,可以通过计算目标值与实际值之间的差异,调整控制系统的输出,从而实现精确的控制效果。
在51单片机中实现增量式PID控制算法,可以按照参数设置、变量定义、计算误差、计算增量输出、更新变量和输出信号等步骤进行。
根据具体情况可以对算法进行优化和改进,以满足实际控制的需求。

单片机PID算法实现在网络上收集了一个PID控制程序,看到很多研友的毕业设计可能涉及到PID控制,这是一个PID的程序,希望能做到抛砖引玉,仅供大家参考。
/*/////////////////////////////////////////////////////////////*//* initial interrupter *//*/////////////////////////////////////////////////////////////*/void init_interrupter(void) /**/{TMOD=0x21; /* 设置计时器0工作于模式1,设置计时器1工作于模式2*/TL0=0x00; /* T0=0000定时时间为71.1ms;71.1ms*15=1.066s*/TH0=0xdc; /*T0=DC00定时时间为10ms;10ms*100=1s*/ /*T0=FC66定时时间为1m s;10ms*1000=1s*/TL1=0xfd; /* 设置串口通信速率9600bps*/TH1=0xfd;PCON=0x00; /* SMOD=0, 速率不倍增*/SCON=0x50; /* 8位数据通信,串行通信方式1,允许单片机接收数据*/IP=0x10; /*serial com is preferential*/IE=0x92; /* 定时器0, 串口中断允许;定时器1中断禁止*/rs485_receive=0;rs485_transmitte=0;TR0=1; /* 启动定时器0*/TR1=1; /* 启动定时器1*/}void tim er0_server(void) interrupt 1 using 1 /**/{TL0=0x00; TH0=0xdc;/*T0=DC00 timing interval is 10ms;10ms*100=1s*//*T0=FC66 timing interval is 1ms;10ms*1000=1s*/if (flag_serial==1){tim er0_counter_3++;if (tim er0_counter_3>11){tim er0_counter_3=0;flag_serial=0;pointer_serial_com_data=serial_com_data;counter_serial_com_data=0;}}dog=!dog;/*Tim er0 is full(10ms), feed dog*/if (timing_interval==0) {timing_interval=1;} /*tim ing_interval is lost then set it to 1 second*/tim er0_counter_1++;/*tim er0_counter_1 is software tim er. when timer0 interrupt is full, it increase autom atically*/if ((unsigned char) (tim er0_counter_1/100)==timing_interval) /*tim ing_interval arrives*/{out_flag=1;/*indexing 占空比high level begin*//*-scan 0809 to get current equipment's tem perature-*/scan_current_Tem perature();origina_address=0x82;display1_Temperature(current_Tem perature,origina_address);/*-calculate out_value-*/PID_algorithm_function(PID_mode,PP,II,DD,BB,current_Tem perature,seted_t em perature);//out_value=0.5;if (out_value>0.0) /*out_value=0.0, then 占空比is zero*/{control_0=1;ledctrl_address=0x8c;leddata_address=0xff;}//reset tim er0_counter_1 and timer0_counter_2,tim er0_counter_1=0; //indexing timing_interval's timingtim er0_counter_2=0; //indexing 占空比's timing}if(out_flag==1){tim er0_counter_2++;if (out_value<1.0){if( (unsigned char) (timer0_counter_2/out_value/100) >= timing_interval){tim er0_counter_2=0;control_0=0;ledctrl_address=0x8c;leddata_address=0x00;out_flag=0;}}}}float PID_algorithm_function(uchar PID_mode_2,floatP_2,I_2,D_2,B_2,current_Temperature_2,seted_tem perature_2){float idata delta;switch (PID_mode_2){case 1: break;/*PID mode*/case 2: D_2=0; break;/*PI m ode*/case 3: I_2=0; break;/*PD m ode*/case 4: I_2=0; D_2=0; break;/*P m ode*/}if (PID_mode_2<5)/*PID algorithm*/ek=(seted_tem perature_2-current_Tem perature_2)/99.9;delta=P_2*(ek-ek1)+I_2*ek+D_2*(ek-2.0*ek1+ek2);out_value=out_value+de lta;ek2=ek1;ek1=ek;if (out_value>1.0){out_value=1;}else if (out_value<=0){out_value=0.0;}if (PID_mode_2==5) /*BB algorithm*/{if (current_Tem perature_2-seted_temperature_2>=B_2) {out_value=0.0;} if (seted_tem perature_2-current_Temperature_2>=B_2) {out_value=1.0;} }return (out_value);}软件练习十二:将十六进制数据转换成十进制数据熟悉51 单片机指令系统,掌握程序设计方法。

单片机P I D算法程序公司内部编号:(GOOD-TMMT-MMUT-UUPTY-UUYY-DTTI-51单片机P I D算法程序(二)位置式P I D控制算法由51单片机组成的数字控制系统控制中,PID控制器是通过PID控制算法实现的。
51单片机通过AD对信号进行采集,变成数字信号,再在单片机中通过算法实现PID运算,再通过DA把控制量反馈回控制源。
从而实现对系统的伺服控制。
位置式PID控制算法位置式PID控制算法的简化示意图上图的传递函数为:(2-1)在时域的传递函数表达式(2-2)对上式中的微分和积分进行近似(2-3)式中n是离散点的个数。
于是传递函数可以简化为:(2-4)其中u(n)——第k个采样时刻的控制;KP——比例放大系数;Ki——积分放大系数;Kd——微分放大系数;T ——采样周期。
如果采样周期足够小,则(2-4)的近似计算可以获得足够精确的结果,离散控制过程与连续过程十分接近。
(2-4)表示的控制算法直接按(2-1)所给出的PID控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式PID控制算法。
缺点:1)由于全量输出,所以每次输出均与过去状态有关,计算时要对e(k)(k=0,1,…n)进行累加,工作量大。
2)因为计算机输出的u(n)对应的是执行机构的实际位置,如果计算机出现故障,输出u(n)将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实际生产中是不允许的。
位置式PID控制算法C51程序具体的PID参数必须由具体对象通过实验确定。
由于单片机的处理速度和ram资源的限制,一般不采用浮点数运算,而将所有参数全部用整数,运算到最后再除以一个2的N次方数据(相当于移位),作类似定点数运算,可大大提高运算速度,根据控制精度的不同要求,当精度要求很高时,注意保留移位引起的“余数”,做好余数补偿。
这个程序只是一般常用pid算法的基本架构,没有包含输入输出处理部分。

基于单片机pid算法的直流电机速度控制方法基于单片机PID算法的直流电机速度控制方法是一种常用的技术,其基本原理是通过调节PWM(脉宽调制)信号的占空比来控制电机的输入电压,从而实现电机的速度控制。
以下是基于单片机PID算法的直流电机速度控制方法的基本步骤:1.设定目标速度:首先,需要设定电机的目标速度。
这可以通过按键或其他输入设备来实现。
2.采集实际速度:为了实现精确的控制,需要实时获取电机的实际速度。
这可以通过在电机转轴上安装光电编码器或霍尔传感器来实现,这些传感器可以实时检测电机的转速并将其转换为电信号。
3.计算偏差:单片机通过比较目标速度和实际速度,计算出速度偏差。
如果实际速度小于目标速度,偏差为负;反之,偏差为正。
4.应用PID算法:单片机使用PID算法来处理速度偏差。
PID控制器通过比例、积分和微分三个环节来计算控制量,以尽可能消除偏差。
具体的PID参数(如Kp、Ki、Kd)可以根据实际情况进行调整,以获得最佳的控制效果。
5.生成PWM信号:基于PID控制器的输出,单片机生成PWM信号来调节电机的输入电压。
占空比决定了电机输入电压的大小,进而影响电机的转速。
6.实时调整:在整个控制过程中,单片机不断采集电机的实际速度,计算偏差,并调整PWM信号的占空比,以使电机尽可能接近目标速度。
7.显示和保存数据:为了方便调试和观察,可以通过单片机的显示屏实时显示电机的实际速度和偏差。
此外,也可以将重要的数据保存在单片机的内部或外部存储器中。
8.安全保护:为了防止电机过载或意外事故,单片机应具备安全保护功能。
例如,当电机实际速度超过设定速度一定时间时,单片机应自动切断电源或发出报警信号。
基于单片机PID算法的直流电机速度控制方法具有精度高、稳定性好、适应性强等优点,广泛应用于各种需要精确控制电机速度的场合。

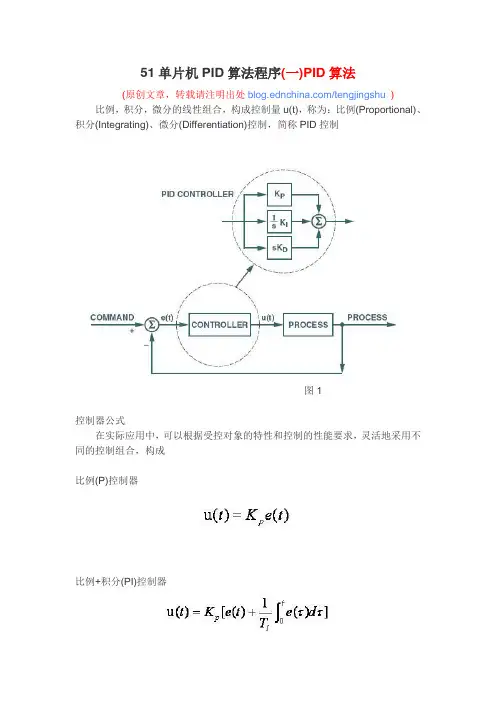
51单片机PID算法程序(一)PID算法(原创文章,转载请注明出处/tengjingshu) 比例,积分,微分的线性组合,构成控制量u(t),称为:比例(Proportional)、积分(Integrating)、微分(Differentiation)控制,简称PID控制图1控制器公式在实际应用中,可以根据受控对象的特性和控制的性能要求,灵活地采用不同的控制组合,构成比例(P)控制器比例+积分(PI)控制器比例+积分+微分(PID)控制器式中或式中控制系统中的应用在单回路控制系统中,由于扰动作用使被控参数偏离给定值,从而产生偏差。
自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算,并输出统一标准信号,去控制执行机构的动作,以实现对温度、压力、流量、也为及其他工艺参数的自动控制。
比例作用P只与偏差成正比;积分作用I是偏差对时间的积累;微分作用D 是偏差的变化率;比例(P)控制比例控制能迅速反应误差,从而减少稳态误差。
除了系统控制输入为0和系统过程值等于期望值这两种情况,比例控制都能给出稳态误差。
当期望值有一个变化时,系统过程值将产生一个稳态误差。
但是,比例控制不能消除稳态误差。
比例放大系数的加大,会引起系统的不稳定。
图2比例(P)控制阶跃响应积分(I)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
为了减小稳态误差,在控制器中加入积分项,积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即使误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减少,直到等于零。
积分(I)和比例(P)通常一起使用,称为比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
如果单独用积分(I)的话,由于积分输出随时间积累而逐渐增大,故调节动作缓慢,这样会造成调节不及时,使系统稳定裕度下降。
图3积分(I)控制和比例积分(PI)控制阶跃相应微分(D)控制在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。

51单片机PID算法程序(三)增量式PID控制算法前言在之前的两篇文章中,我们分别介绍了基础PID算法和位置式PID控制算法。
在本文中,我们将介绍另一种常见的PID算法——增量式PID控制算法,以及如何在51单片机上实现增量式PID控制算法。
增量式PID控制算法简介增量式PID控制算法与位置式PID控制算法最大的区别在于输出控制量的计算方式不同。
位置式PID算法的输出控制量是与目标值的误差和历史误差之和的积分和误差的比例和微分,而增量式PID算法的输出控制量只与误差和历史误差的差值有关。
在增量式PID控制算法中,输出控制量的计算方式如下:$$ OutPut=K_p \\cdot Err+K_i \\cdot \\Delta Err+K_d \\cdot \\Delta^2 Err $$ 其中,K p、K i和K d分别是比例、积分和微分系数。
增量式PID控制算法的优点在于可以避免积分饱和、能够快速响应控制量变化,因此在某些要求高响应速度的应用中,常选择使用增量式PID控制算法。
51单片机上的增量式PID控制算法相比较于位置式PID控制算法,增量式PID控制算法的实现更加复杂,需要考虑历史误差的存储、误差的差值计算等问题。
因此,在51单片机上实现增量式PID控制算法需要一些特殊的处理方式。
我们可以通过以下三个步骤来实现增量式PID控制算法:步骤一:初始化变量在增量式PID控制算法中,需要定义一些变量,如上一次的误差值和输出控制量等。
因此,在使用增量式PID控制算法之前,需要先初始化这些变量。
//定义变量double set_point=0; //目标值double process_pv=0; //实际值double Kp=1,Ki=1,Kd=1; //PID参数double last_error=0,prev_error=0; //历史误差double output=0, dInput=0; //输出控制量和误差的差值double output_max=100.0,output_min=-100.0; //控制量范围//初始化变量void PID_Init(){last_error = 0;prev_error = 0;dInput = 0;output = 0;}步骤二:控制量计算根据增量式PID控制算法的公式,我们可以计算控制量的值。

51单片机PID算法程序51单片机(也称为STC单片机)是一种常见的单片机型号,它可以使用PID(Proportional-Integral-Derivative,比例-积分-微分)算法来实现控制系统。
PID算法可以根据系统当前的误差、误差的积分以及误差的变化率来动态调整系统的输出,使得系统达到期望的目标。
下面是一个使用51单片机实现PID算法的程序示例:```c#include <reg52.h>#include <intrins.h>//定义PID参数#define Kp 1 // 比例系数#define Ki 0.1 // 积分系数#define Kd 0.01 // 微分系数//定义控制输出范围#define OutputMax 100#define OutputMin 0//定义系统参数#define SetPoint 100 // 设定值#define SampleTime 100 // 采样时间(单位:ms)//全局变量unsigned int SetPointValue;unsigned int ProcessValue;signed int PIDOutput;unsigned int LastProcessValue;signed long Integral;signed int Error;signed int LastError;//初始化函数void InitSetPointValue = SetPoint;ProcessValue = 0;PIDOutput = 0;LastProcessValue = 0;Integral = 0;Error = 0;LastError = 0;//PID计算函数signed int PIDCalculation(signed int input)Error = SetPointValue - input; // 当前误差Integral += Error * SampleTime; // 积分项signed int dError = Error - LastError; // 当前误差的变化率PIDOutput = Kp * Error + Ki * Integral + Kd * dError; // PID 输出//限制输出在控制范围内if (PIDOutput > OutputMax)PIDOutput = OutputMax;}else if (PIDOutput < OutputMin)PIDOutput = OutputMin;}LastError = Error;return PIDOutput;//主函数void mainInit(;while (1)//获取传感器测量值ProcessValue = GetProcessValue(; // 自定义函数,获取传感器测量值//PID控制signed int controlValue = PIDCalculation(ProcessValue);//输出控制信号SetControlOutput(controlValue); // 自定义函数,设置输出控制信号//延时采样时间Delay(SampleTime); // 自定义函数,延时指定的时间}```上述示例程序在使用51单片机编写PID算法时,首先定义了PID参数(比例系数Kp、积分系数Ki和微分系数Kd)、控制输出范围(OutputMax和OutputMin)以及系统参数(设定值SetPoint和采样时间SampleTime)。
pid控制算法系列(2)pid控制算法1.PID控制算法的基本思想PID算法是一种具有预见性的控制算法,其核心思想是:1>. PID算法不但考虑控制对象的当前状态值(现在状态),而且还考虑控制对象过去一段时间的状态值(历史状态)和最近一段时间的状态值变化(预期),由这3方面共同决定当前的输出控制信号;2>.PID控制算法的运算结果是一个数,利用这个数来控制被控对象在多种工作状态(比如加热器的多种功率,阀门的多种开度等)工作,一般输出形式为PWM,基本上满足了按需输出控制信号,根据情况随时改变输出的目的。
2.PID算法分析:设某控制系统:用户设定值为SV(也就是希望通过PID控制算法使被控制对象的状态值保持在SV的附近)。
1>从系统投入运行开始,控制算法每隔一段时间对被控制对象的状态值进行采样。
由此,可得到开机以来由各个采样时间点被控制对象的状态值所形成的数据序列:X1,X2, X3, X4, .... Xk-2,Xk-1,Xk说明:X1:开机以来的第一次采样值Xk: 目前的采样值(最近一次的采样值)2> 从这个采样值序列中提取出三方面信息:①当前采样值Xk与用户设定值SV之间的差值:EkEk =Sv - Xk分析Ek:Ek >0:说明当前状态值未达标Ek=0:说明当前控制状态值正好满足要求Ek<0:说明当前状态值已经超标结论:Ek反应了控制对象当前值与设定值的偏差程度,可以根据Ek的大小对输出信号OUT进行调整:偏差程度大OUT增大,偏差程度小OUT减小。
即输出信号的强弱与当前偏差程度的大小成比例,所以根据Ek的大小来给出控制信号OUT的当前值的算法称为比例控制(Proportion)。
用数学模型可以表示为:POUT=(Kp*Ek)+ Out0Kp:一般称之为比例系数,可以理解为硬件上的放大器(或衰减器),适当选取Kp将当前误差值Ek按一定的增益放大或缩小,以提高控制算法的相应速度。
式中或式中控制系统中的应用在单回路控制系统中,由于扰动作用使被控参数偏离给定值,从而产生偏差。
自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算,并输出统一标准信号,去控制执行机构的动作,以实现对温度、压力、流量、也为及其他工艺参数的自动控制。
比例作用P只与偏差成正比;积分作用I是偏差对时间的积累;微分作用D是偏差的变化率;比例(P)控制比例控制能迅速反应误差,从而减少稳态误差。
除了系统控制输入为0和系统过程值等于期望值这两种情况,比例控制都能给出稳态误差。
当期望值有一个变化时,系统过程值将产生一个稳态误差。
但是,比例控制不能消除稳态误差。
比例放大系数的加大,会引起系统的不稳定。
图2比例(P)控制阶跃响应积分(I)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
为了减小稳态误差,在控制器中加入积分项,积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即使误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减少,直到等于零。
积分(I)和比例(P)通常一起使用,称为比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
如果单独用积分(I)的话,由于积分输出随时间积累而逐渐增大,故调节动作缓慢,这样会造成调节不及时,使系统稳定裕度下降。
图3积分(I)控制和比例积分(PI)控制阶跃相应微分(D)控制在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
由于自动控制系统有较大的惯性组件(环节)或有滞后(delay)组件,在调节过程中可能出现过冲甚至振荡。
解决办法是引入微分(D)控制,即在误差很大的时候,抑制误差的作用也很大;在误差接近零时,抑制误差的作用也应该是零。
图4微分(D)控制和比例微分(PD)控制阶跃相应总结:PI比P少了稳态误差,PID比PI反应速度更快并且没有了过冲。
单片机pid算法程序
PID控制算法是一种常用的控制算法,适用于各种控制系统的设
计中。
下面是基于单片机的PID算法程序:
1. 初始化参数
在程序开始时,需要先对PID控制算法的三个参数——比例、积
分和微分系数进行初始化,一般设置为:Kp=1.2、Ki=1.0、Kd=0.001,然后将误差值、上次误差值和累积误差值都设置为0。
2. 计算PID输出值
在每个控制周期内,先读取被控制的变量的实际值和期望值,计
算出两者之间的误差值err。
然后按照PID控制算法公式,分别计算出比例、积分和微分三个修正量的值,最后将它们相加,得到PID输出值。
3. 更新参数
PID控制算法是一种自适应算法,需要不断地根据实际情况来更
新算法参数。
如果当前的误差值较大,说明控制效果不佳,应当增加
比例系数Kp和微分系数Kd,以提高控制效果。
否则,应当增加积分系数Ki,以提高稳定性。
4. 输出控制信号
最后,将PID输出值转换成相应的控制信号,输出给执行机构,
实现对被控制系统的控制。
以上就是单片机PID算法程序的基本步骤,可以根据实际需求进
行适当的优化和改进。
pid控制原理及编程方法PID控制是一种常用的控制算法,可以根据给定的目标值和实际值,通过不断调整输出值,使得实际值尽可能接近目标值。
PID控制的原理可以通过以下几个步骤来理解和实现。
1. 比例控制(P控制):根据目标值和实际值的偏差,乘以一个比例增益系数Kp得到控制量的变化量,作为输出。
控制量的变化量 = Kp * (目标值 - 实际值)2. 积分控制(I控制):将偏差的累积值乘以一个积分增益系数Ki得到控制量的变化量,作为输出。
这个步骤主要是为了解决系统存在的偏差问题。
控制量的变化量 += Ki * (目标值 - 实际值)* Δt3. 微分控制(D控制):根据偏差的变化率乘以一个微分增益系数Kd得到控制量的变化量,作为输出。
这个步骤主要是为了解决系统存在的过渡问题。
控制量的变化量 += Kd * (目标值变化率 - 实际值变化率) / Δt以上三个步骤得到的控制量的变化量之和即为最终的输出。
在编程实现PID控制时,可以按照以下步骤进行:1. 定义并初始化相关变量,包括比例增益系数Kp、积分增益系数Ki、微分增益系数Kd、目标值、实际值、偏差、偏差的累积值、上次偏差等。
2. 循环执行以下操作:a. 更新实际值。
b. 计算偏差(目标值 - 实际值)。
c. 计算控制量的变化量,包括比例控制量、积分控制量和微分控制量。
d. 更新偏差的累积值。
e. 计算最终输出值。
f. 控制执行相应操作(根据最终输出值控制系统)。
g. 等待一定时间间隔。
3. 重复步骤2直至达到控制目标。
需要注意的是,PID控制算法需要根据具体的应用场景,仔细选择合适的增益系数,以达到良好的控制效果。
51单片机PID算法程序PID控制(比例-积分-微分)是一种经典的控制算法,常用于单片机控制系统中。
PID控制算法结合了比例、积分和微分三个控制项,可以有效地调节系统的输出,使系统快速稳定地达到设定值。
PID控制算法的基本原理是通过比例、积分和微分三个部分来调节系统输出。
比例部分根据系统当前误差的大小来调节输出,积分部分根据系统过去误差的积累来调节输出,微分部分根据系统误差的变化率来调节输出。
通过合理地调节这三个部分的比例系数,可以使系统快速稳定地达到设定值,并且具有较好的鲁棒性。
下面给出一个单片机上实现PID控制算法的示例程序。
该程序使用C 语言编写,可以在常见的单片机开发环境中运行。
```c#include<reg52.h>sbit PWM=P1^0;sbit DIR=P1^1;sbit EN=P1^2;sbit Kp=0x30;sbit Ki=0x31;sbit Kd=0x32;int SetPoint = 100; //设定值int Kp = 1; //比例系数int Ki = 0.1; //积分系数int Kd = 0.2; //微分系数int GetFeedback//获取反馈值的函数,这里使用ADC等方式获取反馈值return feedback;void SetPWM(int pwm_value)//设置PWM输出的函数PWM = pwm_value;void PIDControlint Feedback = GetFeedback(;int Error = SetPoint - Feedback;static int LastError = Error;static int Integral = 0;int Derivative = Error - LastError;Integral += Error;int Output = Kp * Error + Ki * Integral + Kd * Derivative; SetPWM(Output);LastError = Error;void mainwhile(1)PIDControl(;}```在这个示例程序中,我们定义了一个PID控制函数PIDControl,用于控制系统的输出。
PID闭环控制算法原理与程序设计摘要:本文主要介绍了基于STC15 单片机作为控制器,运用PID闭环控制算法的原理,设计自动调节稳定无人机飞行高度的控制程序,采用基于单片机c语言的编程方法来实现;关键词:PID算法原理; STC15单片机;高度控制; PID算法闭环反馈式设计方法;一.PID连续系统离散化及表达形式PID控制其实是对偏差量的自动调节的控制过程;如果偏差为0,则比例环节不起作用,只有存在偏差时,比例环节才起作用;积分环节主要是用来消除静态误差,所谓静态误差,就是系统稳定后输出值和期望值做差的值,积分环节实际上就是对偏差量累计的过程,把累计的偏差量加到原有系统上以抵消系统造成的静态误差;而微分信号则是对偏差量的变化规律进行提前预见,或者说是变化趋势,根据偏差量的变化趋势来进行提前干预,从而增加了系统的高效性和快速性。
二.各参数作用及各环节形象解读P环节(比例部分--现在状态)作用:比例部分的作用就是加快系统的反应速率,精简系统的调节精度,反作用是会导致系统调节超调。
形象描述:假设要让无人机保持飞行在200米的高度,如果现在无人机飞行在180米的高度,超声波测距模块会读出相应的距离反馈给CPU,CPU进行比较得到实际值比期望值小,则会发出指令增加无刷电机的占空比,驱动无刷电机转速加快使无人机往期望值靠近。
但是这种调节只有两种状态:第一就是100%占空比、第二就是0%占空比,就是只会加速和不加速。
就比如正处于190米处时,无刷电机以100%占空比一下使无人机飞到了210米,而飞到210米处时,无刷电机以0%的占空比一下子使无人机掉到190米处,从而来回运动,所以会存在稳态误差,而且这样来回摆动,上下波动过大,稳定性比较差,也会一定的损坏无人机的器件。
相关参数:Kp(比例参数)。
比例参数越大,系统的响应灵敏度越高、调节精度越精准,但是容易产生调节超调,甚至会使系统稳定性降低,比例参数越小,则反正。