双曲线抛物线知识点总结

圆椭圆双曲线抛物线知识点汇总一、圆椭圆双曲线抛物线的定义1. 圆：圆是平面上到定点距离相等的所有点的集合。

圆由圆心和半径唯一确定。

2. 椭圆：椭圆是平面上到两个定点的距离之和为常数的所有点的集合。

椭圆由两个焦点和两个半轴唯一确定。

3. 双曲线：双曲线是平面上到两个定点的距离之差为常数的所有点的集合。

双曲线由两个焦点和两个实轴唯一确定。

4. 抛物线：抛物线是平面上到定点距离等于到定直线的距离的所有点的集合。

抛物线由焦点和直线唯一确定。

二、圆椭圆双曲线抛物线的方程1. 圆：圆的标准方程为(x-a)² + (y-b)² = r²，其中圆心为(a, b)，半径为r。

2. 椭圆：椭圆的标准方程为x²/a² + y²/b² = 1，其中a和b分别为x轴和y轴上的半轴长。

3. 双曲线：双曲线的标准方程为x²/a² - y²/b² = 1或者y²/a² - x²/b² = 1，取决于焦点的位置。

4. 抛物线：抛物线的标准方程为y² = 4ax或者x² = 4ay，取决于抛物线开口的方向。

三、圆椭圆双曲线抛物线的性质1. 圆：圆的直径是圆上任意两点之间的最大距离，且所有直径相等。

2. 椭圆：椭圆的离心率介于0和1之间，离心率越接近0，椭圆越接近于圆。

3. 双曲线：双曲线分为两支，每一支的焦点到定点的距离之差相等。

4. 抛物线：抛物线的焦点在抛物线上方，开口方向取决于系数a的正负号。

四、圆椭圆双曲线抛物线的应用1. 圆：在几何中常常与角度和三角函数结合，用于描述正弦和余弦函数的周期性。

2. 椭圆：在天体力学中用于描述行星轨道的形状，以及通信中的极化椭圆。

3. 双曲线：在光学和电磁学中用于描述折射和反射现象。

4. 抛物线：在物理学中用于描述自由落体运动和抛物线运动。

双曲线抛物线知识点⼤总结绝对好和全第⼆章 2.3 双曲线双曲线标准⽅程（焦点在x 轴）)0,0(12222>>=-b a by a x 标准⽅程（焦点在y 轴）)0,0(12222>>=-b a bx a y 定义第⼀定义：平⾯内与两个定点1F ，2F 的距离的差的绝对值是常数（⼩于12F F ）的点的轨迹叫双曲线。

这两个定点叫做双曲线的焦点，两焦点的距离叫焦距。

{}a MFMF M 221=-()212F F a <第⼆定义：平⾯内与⼀个定点F 和⼀条定直线l 的距离的⽐是常数e ，当1e >时，动点的轨迹是双曲线。

定点F 叫做双曲线的焦点，定直线叫做双曲线的准线，常数e （1e >）叫做双曲线的离⼼率。

范围 x a ≥，y R ∈ y a ≥，x R ∈对称轴x 轴，y 轴；实轴长为2a ,虚轴长为2b对称中⼼原点(0,0)O焦点坐标1(,0)F c - 2(,0)F c1(0,)F c - 2(0,)F c焦点在实轴上，22c a b =+；焦距：122F F c =顶点坐标（a -,0） (a ,0) (0, a -,) (0，a )xy P1F 2F xy P xyP1F2FxyxyP1F 2F xyxyP1F 2F xy P离⼼率 e ace (=>1)= 准线⽅程 ca x 2±=ca y 2±=准线垂直于实轴且在两顶点的内侧；两准线间的距离：c a 22顶点到准线的距离顶点1A （2A ）到准线1l （2l ）的距离为ca a 2-顶点1A （2A ）到准线2l （1l ）的距离为a ca +2焦点到准线的距离焦点1F （2F ）到准线1l （2l ）的距离为cac 2-焦点1F （2F ）到准线2l （1l ）的距离为c ca +2渐近线⽅程x a b y ±= x b a y ±=共渐近线的双曲线系⽅程k b y a x =-2222（0k ≠） k b x a y =-2222（0k ≠）1. 双曲线的定义①当|MF 1|－|MF 2|=2a 时，则表⽰点M 在双曲线右⽀上；当a MF MF 212=-时，则表⽰点M 在双曲线左⽀上；②注意定义中的“（⼩于12F F ）”这⼀限制条件，其根据是“三⾓形两边之和之差⼩于第三边”。

椭圆双曲线抛物线知识点汇总一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数（大于|F1F2|）的动点 P 的轨迹，F1、F2 称为椭圆的焦点，两焦点的距离|F1F2|称为椭圆的焦距。

1、椭圆的标准方程焦点在 x 轴上：＼（＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\）），其中\（a\）为长半轴长，＼（b\）为短半轴长，＼（c\）为半焦距，满足\（c^2 ＝ a^2 b^2\）。

焦点在 y 轴上：＼（＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\））。

2、椭圆的性质范围：对于焦点在 x 轴上的椭圆，＼（a ＼leq x ＼leq a\），＼（b＼leq y ＼leq b\）；对于焦点在 y 轴上的椭圆，＼（b ＼leq x ＼leq b\），＼（a ＼leq y ＼leq a\）。

对称性：椭圆关于 x 轴、y 轴和原点对称。

顶点：焦点在 x 轴上时，顶点坐标为\（（＼pm a, 0)＼），＼（（0, ＼pm b)＼）；焦点在 y 轴上时，顶点坐标为\（（0, ＼pm a)＼），＼（（＼pm b, 0)＼）。

离心率：椭圆的离心率\（e ＝＼frac{c}｛a}＼）（＼（0 ＜ e ＜1\）），它反映了椭圆的扁平程度，＼（e\）越接近0，椭圆越接近圆；＼（e\）越接近 1，椭圆越扁。

3、椭圆的参数方程焦点在 x 轴上：＼（＼begin{cases}x ＝ a\cos\theta ＼＼ y ＝b\sin\theta\end{cases}＼）（＼（＼theta\）为参数）焦点在 y 轴上：＼（＼begin{cases}x ＝ b\cos\theta ＼＼ y ＝a\sin\theta\end{cases}＼）（＼（＼theta\）为参数）4、椭圆中的焦点三角形设 P 为椭圆上一点，F1、F2 为焦点，＼（＼angle F1PF2 ＝＼theta\），则三角形 PF1F2 的面积为\（S ＝ b^2\tan\frac{＼theta}｛2}＼）。

抛物线双曲线椭圆知识点抛物线、双曲线、椭圆，这三个名词似乎很陌生的样子，但它们实际上是我们经常在生活中接触到的数学概念。

高中数学中，关于这三个曲线的内容是必修的。

虽然它们各有不同的性质，但它们都有一个共同的特征，那就是它们是二次函数图像。

本文将详细介绍抛物线、双曲线与椭圆的知识点，并探讨它们的性质和应用。

1. 抛物线抛物线是平面内的一条曲线，其形状类似于一个开口朝下或开口朝上的 U 形。

在数学中，抛物线是由一条直线（半轴）和一个固定点（焦点）构成的图形。

在图像上，焦点位于抛物线的顶点处，而半轴则与抛物线相切。

根据它的方程式，我们可以将抛物线分为两种类型：开口朝上的抛物线和开口朝下的抛物线。

开口朝上的抛物线方程式为：y = ax² + bx + c，其中a > 0 。

开口朝下的抛物线方程式为：y = ax² + bx + c，其中a < 0 。

在现实生活中，抛物线通常用来描述物体的运动轨迹。

例如，抛体在空气中的运动轨迹就是一个抛物线。

此外，抛物线也广泛用于建筑设计、工程、电信和电子等领域。

2. 双曲线双曲线是平面内一种曲线，以其非对称的形状而著称。

它看上去像两个并排的抛物线，我们也可以将两条抛物线相减得到双曲线的方程。

不同于抛物线的开口朝上或开口朝下的 U 形，双曲线的形状可以在横轴和纵轴两个方向都无限延伸。

双曲线方程式为：y²/a² − x²/b² = 1，其中a和b是该双曲线长度的参数。

当 a 和 b 相等，即a = b时，双曲线便可以转化为下面要介绍的椭圆。

双曲线在现代科学中有着广泛的应用，例如，它们可以被用于描述电磁波传播的方式、质能传播、黑洞引力等一系列现象。

此外，双曲线也被广泛应用到天文学、航空航天、电磁学和通讯领域等。

3. 椭圆椭圆是平面内一种闭合曲线，以其对称的 U 形或胎心形状而著称。

它看上去像两个抛物线，其一侧延伸，形成一个“尖角”，而另一侧则弯曲的更严密、圆润。

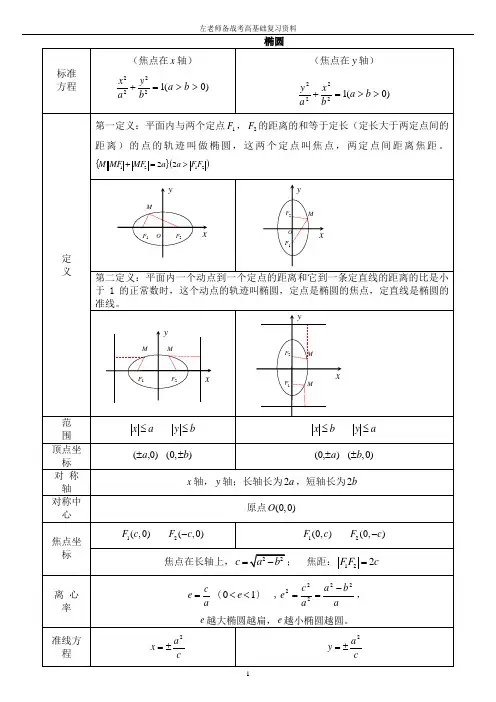
椭圆、双曲线、抛物线相关知识点总结一、椭圆的标准方程及其几何性质椭圆的定义：我们把平面内与两个定点F, F2的距离的和等于常数大于F1F21的点的轨迹叫做椭圆。

符号语言：|MF,| |MF2| 2a 2a 2c将定义中的常数记为2a,贝①.当2a卩人时，点的轨迹是椭圆_____________双曲线的标准方程及其几何性质双曲线的定义：我们把平面内与两个定点F, F2的距离的差的绝对值等于常数小于F”的点的轨迹叫做双曲线。

符号语言：MF t - MF22a 2a 2c将定义中的常数记为2a，贝①.当2a FE时，点的轨迹是双曲线_____________________ ②•当2a |吋2时，点的轨迹是两条射线③.当2a卩占时，点的轨迹不存在焦点位置不确定的双曲线方程可设为：mn 02 2与双曲线仔笃1共焦点的双曲线系方程可设为:a b2y1 ba kb kx22 2 2 2与双曲线笃 耸1共渐近线的双曲线系方程可设为： $ 爲a ba b三、抛物线的标准方程及其几何性质抛物线的定义：我们把平面内与一个定点 F 和一条定直线I （I 不经过点F ）距离相等 的点的轨迹叫做AB x , x 2 p -2^（为弦AB 的倾斜角）sin直线与椭圆（或与双曲线、抛物线）相交于 A （x i ,y i ）,B x 2,y 2，则椭圆（或双曲线、抛 物线）的弦长公式：AB x , x 2| —k 2J x , x 2 2 4%卷—k22 2 2 2与椭圆負b 2 1共焦点的椭圆系方程可设为：和冷1 k b 2标准方程2y 2px (p o )图形焦点坐标(p ,0) 2 (匕0) 2 （0月2(0,上) 2准线方程x& 2x E 2 y 舟 yi范围x 0, y R x 0, y Ry 0,x Ry 0,x R对称性 关于x 轴关于y 轴顶点坐标 (0,0)焦半径M X o ,y o|MF | X 。

双曲线和抛物线双曲线和抛物线⼀、知识梳理1. 双曲线的定义（1）定义：平⾯内与两个定点F 1、F 2的距离之差的绝对值为常数2a (122a F F <)的动点P 的轨迹叫双曲线，其中两个定点F 1、F 2叫双曲线的焦点.当12122PF PF a F F -=<时， P 的轨迹为双曲线; 当12122PF PF a F F -=>时， P 的轨迹不存在;当12122PF PF a F F -==时， P 的轨迹为以F 1、F 2为端点的两条射线. 2. 双曲线的标准⽅程和⼏何性质a b a b3.抛物线的定义平⾯内与⼀个定点F 和⼀条定直线l （l 不经过点F ）距离相等的点的轨迹叫做抛物线，点F 叫做抛物线的焦点，直线l 叫做抛物线的准线.注：当定点F 在定直线l 时，动点的轨迹是过点F 与直线l 垂直的直线. 4.抛物线的标准⽅程和⼏何性质⼆、⽅法归纳1.(1)求双曲线离⼼率必须分两种情况，共渐近线的双曲线⽅程为：λ=-2222by a x )0(≠λ的形式，它们的渐近线为x aby ±=. (2)关于双曲线的渐近线，可做如下⼩结：若已知双曲线⽅程为12222=-b y a x 或12222=-bx a y ，则它们的渐近线⽅程只需将常数“1”换成“0”，再写成直线⽅程的形式即可；若已知双曲线的两渐近线，先写成⼀个⽅程即02222=-b y a x 的形式，再设出双曲线⽅程λ=-2222b y a x )0(≠λ.2.抛物线题型：利⽤定义，实现抛物线上的点到焦点的距离与到准线的距离之间的转换题型⼀：双曲线的定义及标准⽅程【例1】双曲线⽅程为，则它的右焦点坐标为【例2】已知双曲线C 与双曲线221164x y -=有公共焦点，且过点（2）.求双曲线C的⽅程.【适时导练】1.根据下列条件，求双曲线的标准⽅程.（1）过点??? ??4153，P ，??-5316，Q . （2）6=c ，经过点（－5，2），焦点在x 轴上.2.求中⼼在原点，对称轴为坐标轴，经过点()31-，P ，且离⼼率为2的双曲线⽅程.题型⼆：与渐近线有关的问题【例1】已知双曲线的渐近线⽅程是12y x =±，焦点在坐标轴上且焦距是10，则此双曲线的⽅程为 .【例2】若双曲线()222210,0x y a b a b -=>>的焦点到渐近线的距离等于实轴长，则双曲线的离⼼率为2221x y -=【例3】设双曲线12222=-by a x （a>0,b>0）中，离⼼率e ∈[2,2],则两条渐近线夹⾓（锐⾓或直⾓）θ的取值范围是________；【适时导练】1. 焦点为（0，6），且与双曲线2212x y -=有相同的渐近线的双曲线⽅程是2. 经过点（3，2），且与双曲线2212x y -=有相同的渐近线的双曲线⽅程是3.(2014·苏州⼀调)与双曲线x 29－y216＝1有公共渐近线且经过点A (－3,23)的双曲线的⽅程是________．题型三：求离⼼率或离⼼率的范围【例1】已知点12,F F 分别是双曲线)0,0(12222>>=-b a by a x 的左、右焦点，过1F 且垂直于x 轴的直线与双曲线交于A ，B 两点，若2ABF ?是锐⾓三⾓形，则该双曲线离⼼率的取值范围是变式1．(2013·南京、盐城三模)在平⾯直⾓坐标系xOy 中，点F 是双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点，过点F 作双曲线C 的⼀条渐近线的垂线，垂⾜为A ，延长F A 与另⼀条渐近线交于点B .若FB ＝2FA ，则双曲线的离⼼率为________．变式2. 如图所⽰，F1，F 2是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的两个焦点，以坐标原点O 为圆⼼，|OF 1|为半径的圆与该双曲线左⽀的两个交点分别为A ，B ，且△F 2AB 是等边三⾓形，则双曲线的离⼼率为________．变式3．(2014·苏州调研)在平⾯直⾓坐标系xOy 中，双曲线E ：x 2a 2－y 2b2＝1(a >0，b >0)的左顶点为A ，过双曲线E 的右焦点F 作与实轴垂直的直线交双曲线E 于B ，C 两点，若△ABC 为直⾓三⾓形，则双曲线E 的离⼼率为________．变式4．(2014·苏州摸底)过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦点垂直于x 轴的弦长为a 2，则双曲线x 2a 2－y 2b 2＝1的离⼼率为________．变式5．(2014·南通模拟)设F 是双曲线x 2a 2－y 2b2＝1的右焦点，双曲线两条渐近线分别为l 1，l 2，过点F 作直线l 1的垂线，分别交l 1，l 2于A ，B 两点．若OA ，AB ，OB 成等差数列，且向量BF 与FA 同向，则双曲线的离⼼率e ＝________.变式6．已知F 1，F 2分别是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，过F 1的直线l 与双曲线的左、右两⽀分别交于A ，B 两点．若△ABF 2是等边三⾓形，则该双曲线的离⼼率为________．变式7．(2013·镇江质检)设双曲线x 2a 2－y 2b 2＝1的左、右焦点分别为F 1，F 2，点P 在双曲线的右⽀上，且PF 1＝4PF 2，则此双曲线离⼼率的最⼤值为________．变式8. 已知F 1，F 2是双曲线的两个焦点，以线段F 1F 2为边作正三⾓形MF 1F 2，若边MF 2的中点在此双曲线上，则此双曲线的离⼼率为________．题型四：抛物线的定义和⽅程【例1】动点到点的距离与它到直线的距离相等，则的轨迹⽅程为 .【例2】设斜率为2的直线过抛物线的焦点F ，且和轴交于点A ，若△OAF (O 为坐标原点)的⾯积为4，则抛物线的⽅程为【例3】．(2013·扬州期末)若抛物线y 2＝2px (p >0)的焦点也是双曲线x 2－y 2＝8的⼀个焦点，则p ＝________.【例4】．(2014·苏州模拟)顶点在原点且以双曲线x 23－y 2＝1的右准线为准线的抛物线⽅程是________．【例5】．已知抛物线y 2＝2px (p ＞0)，过其焦点且斜率为1的直线交抛物线于A ，B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线⽅程为________．【适时导练】1.抛物线的焦点坐标是 .2.若抛物线22y px =的焦点与双曲线2213x y -=的右焦点重合，则P 的值 .3.抛物线x 2＝2py (p >0)的焦点为F ，其准线与双曲线x 23－y 23＝1相交于A ，B 两点，若△ABF为等边三⾓形，则p ＝________.P (2,0)F 20x +=P l 2(0)y ax a =≠y 28y x =题型五：抛物线的⼏何性质【例1】已知点P在抛物线y2= 4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和的最⼩值为.变式：已知抛物线C的顶点在坐标原点，焦点为F(1,0)，直线l与抛物线C相交于A，B两点．若AB的中点的坐标为(2,2)，则直线l的⽅程为________．【适时导练】1.已知直线l1：4x－3y＋6＝0和直线l2：x＝－1，抛物线y2＝4x上⼀动点P到直线l1和直线l2的距离之和的最⼩值是2.若抛物线y2＝2x上的⼀点M到坐标原点O的距离为3，则M到该抛物线焦点的距离为________．3.已知抛物线y2＝2px(p>0)上⼀点M(1，m)(m>0)到其焦点F的距离为5，该抛物线的顶点在直线MF上的射影为点P，则点P的坐标为________．题型六：双曲线、抛物线的综合2b）是正三⾓形的三个顶点，（1）求：双曲线的离⼼率；（2）若双曲线经过点Q（4，6），求双曲线的⽅程。

高考双曲线抛物线知识点高考数学考试中，高中数学知识占据了很大的比重，其中双曲线和抛物线是高考必考的重要知识点。

本文将对双曲线和抛物线的相关概念、特点以及应用进行介绍，帮助考生全面理解和掌握这两个知识点。

1. 双曲线的概念和特点双曲线是由二次方程的图像所得，常见的双曲线方程有两种形式：$x^2/a^2 - y^2/b^2 = 1$ 和 $y^2/a^2 - x^2/b^2 = 1$，其中 a 和b 是正实数。

双曲线的形状特点是两支分离，且与坐标轴无交点。

双曲线的中心在坐标原点 O(0,0) 处。

在坐标平面上，双曲线的两个分支分别向 x 轴和 y 轴无限延伸。

2. 双曲线的应用双曲线在现实生活中有许多应用。

例如，光的折射是双曲线的一个重要应用。

当一束光从一个介质折射到另一个介质中时，光的传播路径将形成一个双曲线。

这个现象在眼镜、显微镜、望远镜等光学仪器中都有应用。

此外，双曲线还广泛应用于电磁场、无线通信和经济学等领域。

在电磁场中，电荷的分布和电场力线之间的关系可以由双曲线来描述。

在无线通信中，天线辐射和接收的信号模式也可以用双曲线表示。

在经济学中，供求关系也可以通过双曲线来进行分析和预测。

3. 抛物线的概念和特点抛物线是由二次方程的图像所得，常见的抛物线方程是 $y = ax^2 + bx + c$，其中 a、b 和 c 是实数且a ≠ 0。

抛物线的形状特点是开口方向，即上开或下开，取决于抛物线方程中 a 的正负。

抛物线的对称轴是与 y 轴平行的直线，其方程为 x = h，其中 h 是实数。

抛物线的顶点是位于对称轴上的点，其坐标为 (h, k)，其中 k 是实数。

4. 抛物线的应用抛物线在现实生活中也有许多实际应用。

例如，抛物线的形状是喷泉水柱的弹射轨迹，喷泉中的水从喷嘴射出后形成一个抛物线形状的水柱。

这种形状使得喷泉的水能够均匀地覆盖大面积区域，增加景观效果。

此外，抛物线还广泛应用于桥梁设计、体育运动和火箭发射等领域。

双曲线和抛物线的知识点双曲线和抛物线是高中数学中常见的两种曲线，它们有着丰富的几何和物理意义，被广泛应用在各个学科中。

本文将从基本概念、公式和性质，以及应用角度出发，全面探讨这两种曲线的知识点。

一、基本概念1. 双曲线双曲线是由平面上离心率大于1的两个点F1和F2，到该平面上任意一点P的距离之差等于常数2a（a>0）所确定的点集。

通常我们用双曲线的标准方程来表示，即：x^2/a^2-y^2/b^2=1 或 y^2/b^2-x^2/a^2=1其中，a表示离心率，b表示双曲线的半轴长。

2. 抛物线抛物线是由平面上一个定点F（称为焦点）和到该点的距离等于其到某一条定直线L（称为准线或对称轴）的距离d所确定的点集。

通常我们用抛物线的标准方程来表示，即：y=ax^2+bx+c其中，a、b、c分别表示抛物线的系数。

二、公式和性质1. 双曲线双曲线的标准方程可以化为下面的形式：y=b/a*sqrt(x^2-a^2) 或 y=b/a*sqrt(a^2-x^2)由此可以得到双曲线的几何性质：（1）双曲线的渐近线方程为y=±b/a*x，它们分别与x轴成正负45度的角。

（2）双曲线有两个分支，两个分支关于y轴对称。

（3）双曲线关于它的两个渐近线对称，任意一点到其中一条渐近线的距离与到另一条渐近线的距离之差等于常数2a（a>0）。

2. 抛物线抛物线的顶点坐标为（-b/2a，c-b^2/4a），正负号取决于a的符号。

抛物线的渐近线是y=±∞（当a=0时）或y=ax+b（当a≠0时），从而可以得到抛物线的几何性质：（1）抛物线关于它的准线对称。

（2）焦距等于抛物线的半轴长。

（3）抛物线的平面曲率半径在顶点处为无穷大，其他点处为y 轴的绝对值与一阶导数的比值。

（4）当抛物线的焦点在x轴上时，它是一个完美的反射面，任何入射到抛物线上的线段都会被反射到焦点（这就是开普勒使用抛物面反射望远镜原理的基础）。

注：（1）双曲线中的焦点三角问题椭圆上的点00(,)P x y 与两焦点构成的12PF F ∆称作焦点三角形，12F PF θ∠=，110220,r PF a ex r PF a ex ==+==-，1222121201sin sin cot 21cos 2PF F S PF PF F PF b b c y θθθ∆=⋅⋅∠===- （2）两种特殊的双曲线①等轴双曲线：22(0)()x y a b λλ-=≠=，渐近线方程：y x =±，两条渐近线夹角2π，e =②共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.具有共同渐近线，相等的焦距.离心率倒数的平方和为1，222222221,1x y x y a b b a-=-=(,0)a b >为共轭双曲线 7、双曲线的参数方程sec tan x a y b θθ=⎧⎨=⎩1、抛物线的定义及标准方程（1）定义：平面内与一个定点F （焦点）和一条定直线l （准线）的距离相等的点的轨迹叫做抛物线.（2）标准方程：22222,2,2,2(0)y px y px x py x py p ==-==-> 2、焦半径公式及焦点弦问题（标准方程22(0)y px p =>）（1）焦半径：00(,)P x y 是抛物线上一点，F 是焦点，则PF 为焦半径，长为02p x +（2）焦点弦：过焦点F 的直线l 与抛物线相交于1122(,),(,)A x y B x y 两点，AB 即为抛物线22(0)y px p =>的焦点弦，则有：2124p x x =；212y y p =-；12AB x x p =++，12x x p +≥=，当12x x =时，焦点弦最短，是通径，长为2p ；3、抛物线的简单性质：标准方程22(0)y px p =>（1）范围：0x ≥ （2）对称性：关于x 轴对称，对称轴为x 轴 （3）顶点：原点(0,0) （4）离心率：1e =。