原子物理——量子力学初步

量子力学的基本原理及其在原子物理学中的应用量子力学是一门研究微观世界的物理学分支，它描述了微观粒子的行为和性质。

量子力学的基本原理包括波粒二象性、不确定性原理和量子叠加原理等。

这些原理不仅令人惊叹，而且在原子物理学中有着广泛的应用。

首先，波粒二象性是量子力学的核心概念之一。

根据波粒二象性，微观粒子既可以表现出粒子的特性，如位置和质量，又可以表现出波的特性，如干涉和衍射。

这一概念最早由德布罗意提出，他认为粒子的动量与波长之间存在着关系。

这一理论在实验中得到了验证，如电子衍射实验和双缝干涉实验。

波粒二象性的发现彻底改变了人们对微观世界的认识，揭示了微观粒子的奇妙行为。

其次，不确定性原理是量子力学的另一个重要原理。

由于测量的干扰，我们无法准确地同时确定微观粒子的位置和动量。

不确定性原理指出，位置和动量的精确测量是不可能的，我们只能通过概率的方式来描述微观粒子的状态。

这一原理的提出颠覆了经典物理学中对于可测量量的确定性认识，引发了人们对于自然界本质的思考。

最后，量子叠加原理是量子力学中的又一重要原理。

根据量子叠加原理，微观粒子可以处于多个状态的叠加态中，直到被测量时才会坍缩到一个确定的状态。

这一原理在原子物理学中有着广泛的应用。

例如，在核磁共振中，原子核可以处于自旋向上和自旋向下的叠加态，通过外界的磁场作用，可以使原子核坍缩到一个确定的自旋状态，从而实现核磁共振的测量。

除了以上基本原理，量子力学还有许多应用在原子物理学中。

例如，量子力学成功解释了原子光谱的现象。

根据玻尔的量子化条件，电子在原子中只能存在于特定的能级上，并且能级之间的跃迁会产生特定波长的光谱线。

这一理论为原子光谱的解释提供了重要的依据。

此外，量子力学还应用于原子核物理学中的核衰变过程的描述。

根据量子力学，核衰变是由微观粒子的随机性决定的，无法准确预测某个核子何时会发生衰变。

通过量子力学的描述，我们可以用概率的方式来描述核衰变的发生概率，并且可以计算衰变的半衰期等相关参数。

物理学中的量子力学是什么量子力学是描述微观世界的一种理论框架，它是物理学中最重要的理论之一。

它的发展对我们理解原子、分子、固体、核子和基本粒子等微观世界现象具有重要的意义。

本文将介绍量子力学的基本原理、其在物理学研究中的作用，以及一些与量子力学相关的重要概念。

一、量子力学的基本原理在量子力学中，粒子的状态被描述为波函数，波函数可以用来确定粒子的位置、动量、能量等物理量。

根据薛定谔方程，波函数的演化可以用来预测粒子在时间上的变化。

而波函数的模方则给出了粒子出现在不同位置的概率分布。

这种概率性描述与经典物理的确定性描述截然不同，是量子力学的一个核心特征。

二、量子力学的重要概念1. 超位置原理：根据超位置原理，粒子可以处于多个位置的叠加态。

这导致了著名的薛定谔猫思想实验，其中猫可以同时处于死亡和存活的状态。

2. 不确定性原理：根据不确定性原理，无法同时准确测量粒子的位置和动量。

即我们无法同时知道粒子的精确位置和动量，只能给出它们的不确定性范围。

3. 量子纠缠：两个或多个粒子在某些情况下可以相互纠缠在一起，纠缠状态的改变会立即影响到其他纠缠粒子的状态，即使它们之间的距离非常远。

三、量子力学在物理学研究中的作用1. 原子物理学：量子力学的发展使我们能够准确描述电子在原子轨道中的行为，解释了原子中电子能级的结构和电子交互引力。

2. 分子物理学：通过量子力学的理论，我们可以解释分子中化学键的形成和分子的光谱特性。

3. 固体物理学：量子力学描述了固体中的电子行为，帮助我们理解导电性、磁性和绝缘特性等。

4. 粒子物理学：量子力学为粒子物理学提供了重要的工具，帮助我们研究基本粒子的行为和相互作用。

总结：量子力学是物理学中非常重要的一个理论框架，它描述了微观世界中粒子的行为。

通过量子力学的研究，我们能够深入了解原子、分子、固体和基本粒子等微观世界的特性。

量子力学的发展促进了现代科学技术的进步，为我们提供了更深入的理解和探索微观世界的能力。

原子物理与量子力学习题参考答案目录原子物理学（褚圣麟编） (1)第一章原子的基本状况 (1)7．α粒子散射问题（P21） (1)第二章原子的能级和辐射 (1)5．能量比较（P76） (1)7．电子偶素（P76） (1)8．对应原理（P77） (1)9．类氢体系能级公式应用（P77） (1)11．Stern-Gerlach实验（P77） (2)第三章量子力学初步 (2)3．de Broglie公式（P113） (2)第四章碱金属原子 (2)2．Na原子光谱公式（P143） (2)4．Li原子的能级跃迁（P143） (2)7．Na原子的精细结构（P144） (2)8．精细结构应用（P144） (3)第五章多电子原子 (3)2．角动量合成法则（P168） (3)3．LS耦合（P168） (3)7．Landé间隔定则（P169） (4)第六章磁场中的原子 (4)2．磁场中的跃迁（P197） (4)3．Zeeman效应（P197） (4)7．磁场中的原子能级（P197） (5)8．Stern-Gerlach实验与原子状态（P197） (5)10．顺磁共振（P198） (5)第七章原子的壳层结构 (6)3．原子结构（P218） (6)第八章X射线 (6)2．反射式光栅衍射（P249） (6)3．光栅衍射（P249） (6)量子力学教程（周世勋编） (7)第一章绪论 (7)1.1 黑体辐射（P15） (7)1.4 量子化通则（P16） (7)第二章波函数和Schrödinger方程 (8)2.3 一维无限深势阱（P52） (8)2.6 对称性（P52） (8)2.7 有限深势阱（P52） (9)第三章力学量 (10)3.5 转子的运动（P101） (10)3.7 一维粒子动量的取值分布（P101） (10)3.8 无限深势阱中粒子能量的取值分布（P101） (11)3.12 测不准关系（P102） (11)第四章态和力学量的表象 (12)4.2 力学量的矩阵表示（P130） (12)4.5 久期方程与本征值方程的应用（P130） (13)第五章微扰理论 (16)5.3 非简并定态微扰公式的运用（P172） (16)5.5 含时微扰理论的应用（P173） (16)第七章自旋与全同粒子 (17)7.1 Pauli算符的对易关系（P241） (17)7.2 自旋算符的性质（P241） (17)7.3 自旋算符x、y分量的本征态（P241） (17)7.4 任意方向自旋算符的特点（P241） (17)7.5 任意态中轨道角动量和自旋角动量的取值（P241） (18)7.6 Bose子系的态函数（P241） (19)原子物理与量子力学习题 (20)一、波函数几率解释的应用 (20)二、态叠加原理的应用 (20)三、态叠加原理与力学量的取值 (20)四、对易关系 (21)五、角动量特性 (22)1原子物理学（褚圣麟编）第一章 原子的基本状况7．α粒子散射问题（P21）J 106.1105.3221962-⨯⨯⨯⨯==E M υ232323030m )2/3(109.1071002.61060sin 1060sin 10----⊥-⨯⨯⨯⨯=⨯⨯=⋅⨯=A N t A N Nt s ρρ C 1060.119-⨯=e ，11120m AsV 1085.8---⨯=ε，61029-⨯=n dn32521017.412.0100.6--⨯=⨯==ΩL dS d ， 20=θ 2.48)4(sin 202422=⋅Ω⋅⋅=Nt d n dn eM Z πευθ第二章 原子的能级和辐射5．能量比较（P76）Li Li Li Li v hcR hcR E E hv E )427()211(32212=-⋅=-==H e H e H e H e hcR hcR E E 4)1/2(0221=⋅=-=++∞ +∞>H e v E E ，可以使He +的电子电离。

原子物理与量子力学唐敬友笔记《深入理解原子物理与量子力学：唐敬友笔记》序言1. 引言在现代物理学领域中，原子物理与量子力学一直是极具挑战性和深远影响的研究方向之一。

唐敬友教授的相关著作让我们对这一领域有了更深入的了解和认识。

在本文中，我将对原子物理与量子力学的相关概念进行深入剖析，并共享我个人对这些主题的观点和理解。

2. 原子物理的基础概念我们需要了解原子物理的基础概念。

原子是构成一切物质的基本单位，其结构和性质对物质的行为有着重要影响。

在唐敬友笔记中，对于原子的组成、结构及其内部粒子的运动规律有着详细的描述和解释。

原子物理的基础概念是我们深入理解量子力学的基础。

3. 量子力学的发展历程量子力学作为描述微观世界的理论，对于人类对于世界本质的认识产生了深远的影响。

在《唐敬友笔记》中，对于量子力学概念的演变和发展历程进行了全面的阐述。

从早期的波动方程到薛定谔方程的提出，再到后来的波粒二象性理论，唐敬友教授对于量子力学的发展历程进行了系统性的总结和探讨。

4. 量子力学的主要原理量子力学的主要原理是深入理解这一理论的关键。

唐敬友教授在笔记中对于不确定性原理、波函数及其统计解释等重要概念进行了详尽的分析，帮助人们更好地理解这些复杂而又深刻的原理。

量子力学的主要原理是我们理解量子世界的基石，也是探索微观世界的关键。

5. 应用与展望在我想对于原子物理与量子力学的应用与展望进行一些讨论。

这些理论不仅深刻影响着我们对于物质世界的认识，也在信息技术、材料科学等领域中有着重要的应用。

随着科学技术的不断进步，原子物理与量子力学的应用前景也会变得更加广阔和重要。

结论通过对《唐敬友笔记》中的原子物理与量子力学相关内容进行深入的剖析与探讨，我对于这些理论有了更为深刻和全面的理解。

我也认识到这些理论对于现代科学和技术的重要性，以及对人类对于世界本质的认识所产生的深远影响。

希望我对这一主题的探讨能够给您带来一些启发和思考。

在撰写本文的过程中，我深感唐敬友教授对于原子物理与量子力学的深厚造诣和卓越成就。

量子力学概述量子力学是一门研究微观粒子的物理学科，它的发展始于20世纪早期。

量子力学揭示了微观粒子行为的本质，改变了我们对于宇宙的认知。

本文将概述量子力学的基本概念和原理，并探讨其在科学研究和技术应用中的重要性。

1. 波粒二象性量子力学的核心概念之一是波粒二象性。

实验观察表明，微观粒子既具有粒子特性，又具有波动特性。

例如，光既可以被看作是粒子（光子）也可以被看作是一种电磁波。

这一观点由德布罗意提出，并由实验验证，成为了量子力学的基础。

2. 波函数和叠加原理波函数是量子力学描述微观粒子行为的数学工具。

它能够用来计算和预测微观粒子的性质和行为。

根据叠加原理，微观粒子的波函数可以同时处于多个可能的状态，并在观测之前不确定其具体状态。

观测时，波函数会崩塌为其中一个确定的状态。

3. 测量和不确定性原理量子力学中的测量与经典物理不同。

在经典物理中，测量一个物理量并不会对其他物理量造成干扰。

然而，在量子力学中，测量一个物理量会对其他物理量的测量结果产生影响。

这是由于测量过程本身引入了不确定性。

不确定性原理表明了人们无法同时准确测量微观粒子的位置和动量（或其他共轭变量），这对我们了解微观世界的基本粒子行为有着重要影响。

4. 薛定谔方程和定态薛定谔方程是量子力学中描述系统演化的基本方程。

通过求解薛定谔方程，可以得到系统的定态和能量谱。

定态是指系统处于一种稳定的状态，且不随时间演化。

一个定态可以由一个或多个量子数来描述，每个量子数对应于系统的一个可观测的物理量。

5. 相对论和量子力学的结合相对论和量子力学是现代物理学的两大支柱。

相对论揭示了宏观物体和高速粒子行为的规律，而量子力学揭示了微观粒子行为的规律。

尽管两者各自都能很好地解释和预测实验结果，但在高能物理和宇宙学等领域中，需要将相对论和量子力学结合起来，即量子场论。

量子场论的发展使得我们能够研究更高能量和更小尺度的粒子行为。

6. 应用和前景量子力学是许多科学和技术领域的基石。

1.1解：根据卢瑟福散射公式:可能达到的最粒子间的势能时，两粒子间的作用距离最小。

根据上面的分析可得:79 (1.60 10 19 )213 6诂 1.14 10 一1310 6 1.60 10 _19由上式看出：r min 与入射粒子的质量无关，所以当用相同能量质量和相同电量得到核 代替质子时，其与靶核的作用的最小距离仍为1.14 10“米。

1 .原子的基本状况ctg0—b = 4- 2 Ze 2「b Ze 2得到:e24二；°K79 (1.60 1019)2ctg 曹6…,小二915 r(4 二 8.85 10-12) (7.68 106 10J9^ 3.97 10 米 式中K 一. =2 Mv 2是〉粒子的功能。

1.2已知散射角为二的:•粒子与散射核的最短距离为212 Z e 2 1r m =()77^(1-)，4 二； 试问上题：•粒子与散射的金原子核之间的最短距离r m 多大?212 Ze 21解：将1.1题中各量代入r m 的表达式，得：r min = ()^(1)192=9 109 I ：。

俨寫10)。

靑心02 10_14 米1.3若用动能为1兆电子伏特的质子射向金箔。

问质子与金箔。

问质子与金箔原子核解：当入射粒子与靶核对心碰撞时，散射角为180：。

当入射粒子的动能全部转化为两1 Mv 2Ze 24 二；0 r min，故有：r minZe 2oK p1・7能量为3.5兆电子伏特的细「粒子束射到单位面积上质量为1.05 10-公斤/米2的银 箔上，：•粒解：设靶厚度为t '。

非垂直入射时引起：粒子在靶物质中通过的距离不再是靶物质的 厚度t '，而是t=t '/si n60，，如图1-1所示。

因为散射到与之间茁立体角内的粒子数dn 与总入射粒子数n 的比为：式中立体角元 d ； -ds/L 2,t =t '/sin60° =2t '/-3门-20°N 为原子密度。

原子物理与量子力学Atomic Physics and Quantum Mechanics哈尔滨理工大学应用科学学院应用物理系相关说明一、课程名称原子物理与量子力学二、计划学时108（每周3次6学时）三、课程性质技术基础课四、适用专业应用物理学、材料物理学、光信息科学与技术、电子科学与技术五、主要内容本课程内容主要可分为两大部分：1、原子物理学；2、量子力学。

原子物理学主要介绍原子物理学的发展。

从光谱学、X射线等方面的实验事实总结出能级规律，进一步分析原子结构的特点。

量子力学是二十世纪初建立起来的一门崭新的学科。

通过五个基本原理的引入，逐步构筑了量子力学的理论框架。

教学过程中，尽可能将两部分的相关内容结合讲授，利于学生理解和吸收。

原子物理学与量子力学是物理类学生的理论基础。

通过该课程的学习，学生应掌握有关原子等微观粒子的基本物理概念及反映其物理性质的基本规律，使学生了解和掌握现代一些重要的物理观念，并为应用技术准备理论基础。

六、教材与参考书《原子物理学》，褚圣麟，高教出版社《量子力学教程》，周世勋，高教出版社七、备注本课程采用多媒体教学，重点难点等采用特定的文字表现方式或动画声音等形式体现，可在“《原子物理与量子力学》课件”的相关章节观察效果。

目录绪论 (1)本章小结 (1)第一章原子的基本状况 (2)§1.1 原子的质量和大小 (2)§1.2 原子的核式结构 (2)本章小结 (3)第二章原子的能级和辐射 (4)§2.1 原子光谱的一般情况与氢原子光谱 (4)§2.2 经典理论的困难和光的波粒二象性 (4)§2.3 玻尔氢原子理论 (5)§2.4 类氢体系光谱 (5)§2.5 夫兰克-赫兹实验 (5)§2.6 量子化通则 (6)§2.7 电子的椭圆轨道 (6)§2.8 史特恩-盖拉赫实验与原子空间取向的量子化 (7)§2.9 量子理论与经典理论的对应关系对应原理 (7)本章小结 (7)第三章量子力学的运动方程—Schrödinger方程 (8)§3.1 物质的波粒二象性 (8)§3.2 波函数的统计解释 (8)§3.3 态叠加原理 (9)§3.4 薛定谔方程 (9)§3.5 几率守恒定律与定态薛定谔方程 (9)§3.6 一维无限深势阱 (10)§3.7 势垒贯穿 (10)§3.8 线性谐振子 (10)§3.9 电子在库仑场中的运动 (11)§3.10 氢原子 (11)本章小结 (12)第四章量子力学中的力学量 (13)§4.1 力学量算符 (13)§4.2 动量算符与角动量算符 (13)§4.3 厄密算符的本征函数 (14)§4.4 力学量的取值分布 (14)§4.5 算符的对易关系 (14)§4.6 测不准关系 (15)§4.7 守恒定律 (15)本章小结 (16)第五章碱金属原子的光谱和能级 (17)§5.1 碱金属原子的光谱和结构特点 (17)§5.2 碱金属原子光谱的精细结构 (17)§5.3 电子自旋与轨道运动的相互作用 (18)§5.4 单电子跃迁的选择定则 (18)*§5.5 氢原子光谱的精细结构与蓝姆移动 (18)本章小结 (19)第六章多电子原子 (20)§6.1 氦与第二族元素的光谱和能级 (20)§6.2 具有两个价电子的原子态 (20)§6.3 泡利原理与同科电子 (21)§6.4 复杂原子光谱的一般规律 (21)§6.5 辐射跃迁的普适选择定则 (21)§6.6 He-Ne激光器 (22)本章小结 (22)第七章磁场中的原子 (23)§7.1 原子的磁矩 (23)§7.2 外磁场对原子的作用 (23)§7.3 史特恩-盖拉赫实验的结果 (23)§7.4 顺磁共振 (24)*§7.5 物质的磁性 (24)§7.6 塞曼效应 (25)本章小结 (25)第八章原子的壳层结构 (26)§8.1 元素性质的周期性 (26)§8.2 原子的电子壳层结构 (26)§8.3 原子基态的电子组态 (26)本章小结 (27)第九章X射线 (28)§9.1 X射线的产生及测量 (28)§9.2 X射线的发射谱及相关能级 (28)*§9.3 X射线的吸收和散射 (28)*§9.4 X射线在晶体中的衍射 (29)本章小结 (29)第十章态和力学量的表象 (30)§10.1 态的表象 (30)§10.2 算符的矩阵表示 (30)§10.3 量子力学公式的矩阵表述 (31)§10.4 幺正变换 (31)§10.5 狄拉克符号 (31)§10.6 占有数表象 (32)本章小结 (32)第十一章微扰理论 (33)§11.1 非简并定态微扰理论及其应用 (33)§11.2 简并情况下的微扰理论及其应用 (33)§11.3 变分法与氦原子基态 (34)§11.4 与时间有关的微扰理论 (34)§11.5 跃迁几率 (34)§11.6 光的发射与吸收 (35)*§11.7 选择定则 (35)本章小结 (36)第十二章散射 (37)§12.1 碰撞过程与散射截面 (37)§12.2 中心力场中的弹性散射（分波法） (37)本章小结 (37)第十三章自旋与全同粒子 (39)§13.1 电子的自旋 (39)§13.2 电子自旋的描述 (39)§13.3 简单塞曼效应 (40)§13.4 角动量的耦合及应用 (40)§13.5 光谱的精细结构 (41)§13.6 全同粒子体系 (41)§13.7 全同粒子体系的波函数 (41)§13.8 两个电子的自旋函数 (42)本章小结 (42)绪论绪论本章主要介绍原子物理与量子力学的发展过程，并指出学习新理论应注意的问题。

第二章 量子力学初步为什么要学？量子力学已经从理论物理的一个分支学科，发展成为技术专家手中的一门有力的工具：纳米（10－9M ）科学与技术, STM 和AFM ，…对物理专业的学生，导论和准备；对应用物理专业的学生，掌握量子力学的基本知识。

为什么在这时候学？在波尔与索末菲的旧量子理论中：问题1：L （轨道角动量数值）＝n ϕℏ，L z （轨道角动量的方向）= m ℏ；即：定态条件，作为“规定”的量子化条件引入。

这种强制性“规定”不符合数学逻辑。

问题2：氢原子基态的电子空间分布： 波尔理论：n =1的“轨道”，r n ＝n 2a 1＝a 1＝0.53A ； 中学物理中的“电子云”。

孰是孰非？“电子云”概念是正确的，“轨道”概念是错误的。

正确的原子概念的建立，必须学习量子力学。

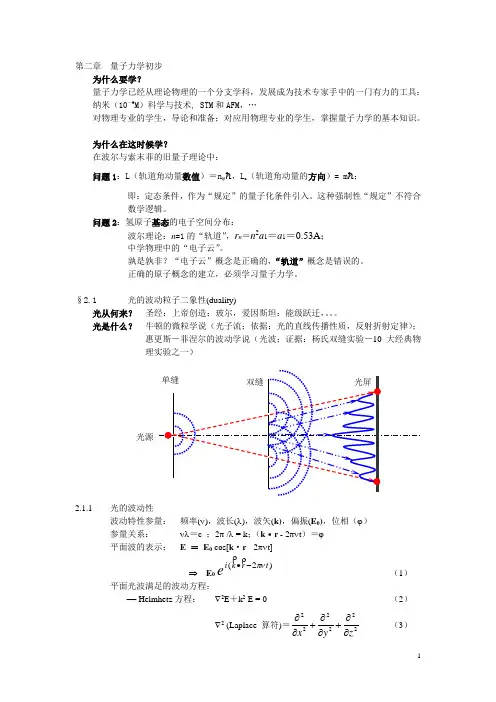
§2.1 光的波动粒子二象性(duality)光从何来？ 圣经：上帝创造；玻尔，爱因斯坦：能级跃迁，。

光是什么？ 牛顿的微粒学说（光子流；依据：光的直线传播性质，反射折射定律）；惠更斯－菲涅尔的波动学说（光波；证据：杨氏双缝实验－10大经典物理实验之一）2.1.1 光的波动性波动特性参量： 频率(ν)，波长(λ)，波矢(k)，偏振(E 0)，位相（ϕ） 参量关系： νλ＝c ；2π /λ = k ；（k ·r - 2πνt ）＝ϕ 平面波的表示： E ＝ E 0 cos[k ·r - 2πνt]⇒ E 0)2(t r k i eπν-∙（1）平面光波满足的波动方程：− Helmhetz 方程： ∇2E ＋k 2 E = 0 （2）∇2(Laplace 算符)＝222222zy x ∂∂+∂∂+∂∂（3）光源2.1.2光的粒子性粒子特性参量：能量E ，动量p 。

粒子特性参量（E ，p ）和波动特性参量（ν，λ)由Einstein 关系联系起来： E ＝ h ν ＝hc / λ （4）p ＝ h / λ ＝ h ν / c ＝ ℏk（5） p ＝ℏk ＝ (h / λ) k 0 (k 0 ：光传播的方向)（5'）光子能量（4）式的实验证实：光电效应实验装置：结果：仅当入射光的频率 ν > νmin ，才有光电流（光电子）。

物理学量子力学与原子物理学物理学量子力学是研究微观世界中的物质和能量交互作用的理论。

它涉及到原子、分子和基本粒子的行为，被认为是20世纪最伟大的科学理论之一。

原子物理学是量子力学的一个分支，专注于研究原子、原子核和原子中的电子运动。

1. 量子力学的发展历程量子力学的发展可以追溯到20世纪初。

1900年，普朗克提出了量子假设，认为能量是离散的，存在于不同的固定数值上，称为量子。

随后，爱因斯坦、玻尔等科学家为量子力学的发展做出了重要贡献。

1925年，薛定谔提出了薛定谔方程，奠定了现代量子力学的基础。

2. 量子力学的基本原理量子力学的基本原理包括波粒二象性、不确定性原理和量子叠加原理。

波粒二象性表明微观粒子既可以表现出波动性质，又可以表现出粒子性质。

不确定性原理指出，无法同时准确测量粒子的位置和动量，测量结果存在一定的不确定性。

量子叠加原理描述了微观粒子可能存在的多个状态，直到被观测时才会确定一个具体状态。

3. 原子物理学的研究内容原子物理学主要研究原子的结构和性质。

尤其是电子在原子中的能级结构和电子云分布。

根据波尔模型，原子的电子存在于不同的轨道上，每个轨道对应一个特定的能级。

这些能级可以通过吸收或发射光子的方式实现跃迁。

原子物理学的研究还包括原子光谱、原子碰撞和原子核结构等内容。

4. 量子力学在原子物理学中的应用量子力学为解释原子物理现象提供了有效的理论框架，并且在实际应用上也有广泛的应用。

通过量子力学的计算和模拟，我们可以了解原子的能级结构、原子光谱的特性。

量子力学还为原子物理学中的激光、原子钟、量子计算等领域的研究提供了理论基础。

5. 量子力学的发展挑战与展望尽管量子力学在物理学和应用领域取得了巨大成功，但仍然存在一些未解决的问题和挑战。

例如，量子力学与相对论的统一、量子纠缠、量子计算的可实现性等。

随着科学技术的发展，我们有望揭示更多的量子力学奥秘，并将其应用于更广泛的领域。

总结：物理学量子力学与原子物理学为我们理解微观世界提供了重要的理论基础。

量子力学知识的总结归纳量子力学是20世纪初由诺贝尔物理学家波尔、玻恩、海森堡等人发展起来的一门基础物理学理论。

它描述了微观世界中的粒子行为，涉及到微观粒子的波粒二象性、不确定性原理以及量子态叠加等概念。

本文将对量子力学的重要知识进行总结归纳，帮助读者更好地理解量子力学的基本原理。

一、波粒二象性在经典物理学中，我们将物质看作是粒子，具有确定的位置和动量。

然而，通过许多实验观察发现，微观粒子如电子、光子等却同时表现出粒子和波的性质。

这就是波粒二象性的基本概念。

根据德布罗意的物质波假设，每个物质粒子都与波动现象相对应。

粒子的波长和动量之间存在关系，称为德布罗意关系：λ = h / p其中，λ表示波长，h表示普朗克常数，p表示动量。

二、量子力学的基本原理1.波函数和薛定谔方程在量子力学中，用波函数（Ψ）来描述粒子的状态。

波函数的平方（|Ψ|^2）给出了在空间中找到粒子的概率。

薛定谔方程是描述波函数随时间演化的方程。

它是一个偏微分方程，其解决了波函数随时间的变化，从而可以预测粒子的行为。

2.不确定性原理由海森堡提出的不确定性原理是量子力学的重要概念之一。

它表明，无法同时准确地确定粒子的位置和动量。

不确定性原理可以用数学形式表示为：Δx * Δp >= h / 2π其中，Δx表示位置的不确定度，Δp表示动量的不确定度，h为普朗克常数。

3.量子态叠加和测量在量子力学中，粒子的状态可以叠加为多个态的线性组合。

这种叠加被称为叠加原理。

当我们对粒子进行观测时，测量结果只能是某个确定态，而不是叠加态。

测量之后，粒子的波函数将塌缩到某个确定态，概率由波函数的平方给出。

三、量子力学的应用量子力学不仅仅是一门理论学科，它也有着广泛的应用。

以下是量子力学的一些重要应用领域。

1.原子物理学量子力学解释了原子结构、电子轨道和元素周期表等现象。

它的应用使我们能够理解和探索原子和分子之间的相互作用，进而推动材料科学和化学的发展。

第二章 量子力学初步光的波动粒子二象性(duality) 光的波动性波动特性参量： 频率(ν)，波长(λ)，波矢(k)，偏振(E 0)，位相（ϕ） 参量关系：νλ＝c ；2π /λ = k ；（k ·r - 2πνt ）＝ϕ平面波的表示： E ＝ E 0 cos[k ·r - 2πνt]＝ E 0)2(t r k i eπν-∙光的粒子性粒子特性参量：能量E ，动量p 。

粒子特性参量（E ，p ）和波动特性参量（ν，λ)由Einstein 关系联系起来：E ＝ h ν ＝hc / λ ，p ＝ h / λ ＝ h ν / c ＝ ℏkp ＝ℏk ＝ (h / λ) k 0 (k 0 ：光传播的方向)光子能量的实验证实：光电效应实验光子动量的实验证实：康普顿－吴有训散射实验物质的波粒二象性德布罗意（法国人，1924，巴黎大学文理学院本科生）的类比假设；物质波的物理诠释：物质波是一种慨率波。

如果用波函数ψ ( r , t)表示物质波，∣ψ ( r , t)∣2d τ (d τ：体积元)表示粒子在t 时刻，在d τ中出现的慨率。

− 量子力学基本原理之一。

不确定关系（测不准关系 − 量子力学基本原理之二） 坐标和动量的不确定性：∆q ∆p ≥ ℏ/2；能量和动时间的不确定性：∆E ∆t ＝∆p ∆q ≥ ℏ/2 波函数和量子态1， 波函数的规一化2, 波函数的完备性 3, 量子态的表象4，本征态，本征函数，本征值 态叠加原理（量子力学基本原理之三）薛定谔方程1, 含时薛定谔方程（量子力学基本原理之四：量子力学中的牛顿定律）i ℏt∂∂ψ ( r , t) = [m222∇-+V(r , t)] ψ ( r , t)2， 定态薛定谔方程[m222∇-+V(r )] ψ (r )＝E ψ (r )1D 无限深势阱中的粒子：E =mk 222 ＝22222mLn π ＝E nψ (x)＝A sin(Ln πx) = ψ n (x) ＝21)2(Lsin (Ln πx)量子力学中的一些理论和方法1，平均值和算符的引入2，力学量用算符表示（在位置表象中）3，力学量Q 的平均值：<Q （p, r ）> ＝τψψd r r i Q r )(),()(*∇-⎰∞∞-本征函数，本征值，本征值方程的定义和性质轨道角动量1， L在直角坐标系中的算符表示 2， L在球坐标系中的表示3， z l ˆ和2ˆl 的本征函数和本征值2ˆl Y l, m （θ, ϕ）＝l (l +1) ℏ2Y l, m （θ, ϕ）；z l ˆ Y l, m （θ, ϕ）＝z l ˆΦm （ϕ）Θl, m （θ）= m ℏ Y l, m （θ, ϕ）。

原子物理第三章习题答案第三章量子力学初步3.1 波长为οA 1的X 光光子的动量和能量各为多少？解：根据德布罗意关系式，得：动量为：12410341063.6101063.6----=?==秒米千克λhp 能量为：λ/hc hv E==焦耳151083410986.110/1031063.6---?==。

3.2 经过10000伏特电势差加速的电子束的德布罗意波长?=λ 用上述电压加速的质子束的德布罗意波长是多少？解：德布罗意波长与加速电压之间有如下关系：meV h 2/=λ 对于电子：库仑公斤，19311060.11011.9--?=?=e m把上述二量及h 的值代入波长的表示式，可得：οοολA A A V 1225.01000025.1225.12===对于质子，库仑公斤，19271060.11067.1--?=?=e m ，代入波长的表示式，得：ολA 319273410862.2100001060.11067.1210626.6----?==3.3 电子被加速后的速度很大，必须考虑相对论修正。

因而原来ολA V25.12=的电子德布罗意波长与加速电压的关系式应改为：ολA V V)10489.01(25.126-?-=其中V 是以伏特为单位的电子加速电压。

试证明之。

证明：德布罗意波长：p h /=λ对高速粒子在考虑相对论效应时，其动能K 与其动量p 之间有如下关系：222022c p c Km K =+而被电压V 加速的电子的动能为：eV K =2200222/)(22)(c eV eV m p eV m ceV p +=+=∴因此有：2002112/c m eV eVm h p h +==λ一般情况下，等式右边根式中202/c m eV 一项的值都是很小的。

所以，可以将上式的根式作泰勒展开。

只取前两项，得：)10489.01(2)41(260200V eVm h c m eV eVm h -?-=-=λ 由于上式中οA VeV m h 25.122/0≈，其中V 以伏特为单位，代回原式得：ολA V V)10489.01(25.126-?-=由此可见，随着加速电压逐渐升高，电子的速度增大，由于相对论效应引起的德布罗意波长变短。

第一章．原子的基本状况1. 若卢瑟福散射用的α粒子是放射性物质镭C'放射的，其动能为7.68×106电子伏特.散射物质是原子序数Z=79的金箔.试问散射角θ=1500所对应的瞄准距离b 多大？解：根据卢瑟福散射公式：222cot42Mv b Zeθπε= 而动能212k E mv =则20222cot442k E Mv b b Ze Zeθπεπε== 由此，瞄准距离为20cot 24kZe b E θπε=其中：79Z =12-1-108.854210A s V m ε-=⨯⋅⋅⋅191.6021910e C -=⨯0150θ=, 0cotcot 750.26802θ==3.14159π=6197.687.6810 1.6021910k E MeV J -==⨯⨯⨯得到：219215022126190cot 79(1.6021910)cot 4(4 3.141598.854210)(7.6810 1.6021910)k Ze b m E οθπε---⨯⨯==⨯⨯⨯⨯⨯⨯⨯153.969710m -=⨯2.已知散射角为θ的α粒子与散射核的最短距离为2202121()(1)4sin mZe r Mv θπε=+,试问上题α粒子与散射的金原子核之间的最短距离m r 多大？解：2min202121()(1)4sin Ze r Mv θπε=+ 2min0211()(1)4sin k Ze r E θπε=+ 其中，0150θ=, 0sinsin 750.965932θ==把上题各参数代入，得到192min12619179(1.6021910)1(1)4 3.141598.8542107.6810 1.60219100.96593r m ---⨯⨯=⨯⨯+⨯⨯⨯⨯⨯⨯143.014710m -=⨯4. 钋放射的一种α粒子的速度为71.59710⨯米/秒，正面垂直入射于厚度为710-米、密度为41.93210⨯3/公斤米的金箔。