八年级数学正方形判定

正方形定义：有一个角是直角且一组邻边相等的平行四边形叫正方形。

正方形性质：1、正方形四个角都是直角； 2、正方形四条边都相等；3、正方形对角线垂直相等，每一条对角线平分一组对边。

正方形判定：1、有一个角是直角的菱形是正方形； 2、有－组邻边相等的矩形是正方形； 3、既是矩形又是菱形的四边形是正方形。

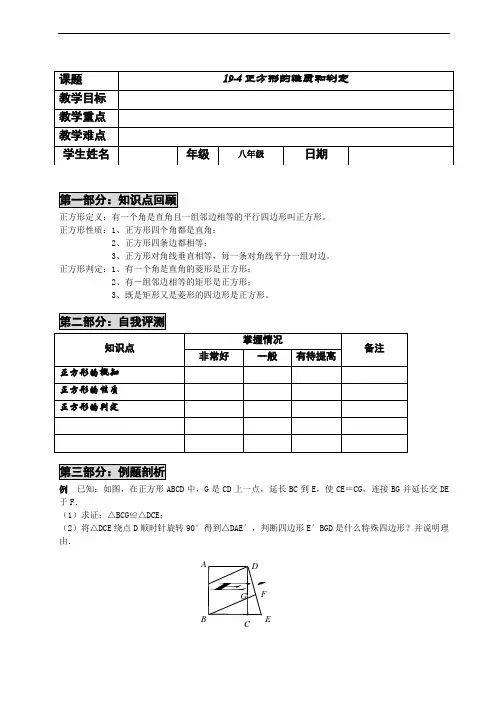
例 已知：如图，在正方形ABCD 中，G 是CD 上一点，延长BC 到E ，使CE ＝CG ，连接BG 并延长交DE 于F ．（1）求证：△BCG ≌△DCE ；（2）将△DCE 绕点D 顺时针旋转90°得到△DAE ′，判断四边形E ′BGD 是什么特殊四边形？并说明理由．ABCDEF EG分析：（1）由正方形ABCD 知，DC=BC ，∠DCB=90°，又由∠DCB=90°得∠DCE=90°，所以，根据SAS 得到△BCG ≌△DCE ；（2）四边形E ′BGD 是平行四边形。

理由： ∵ 四边形ABCD 是正方形∴ AB//CD,AB=CD ∵ CG=CE=A E ′ ∴ BE//DG,BE=DG∴ 四边形 E ′BGD 是平行四边形第四部分：典型例题例1、有一块面积为1的正方形ABCD ，M 、N 分别为AD 、BC 边上的中点，将C 点折至MN 上，落在P 点位置，折痕为BQ ，连结PQ. 求MP 的长.【变式练习】1. 四边形ABCD 中，AC 、BD 相交于点O ，能判别这个四边形是正方形的条件是（ ） A.OA =OB =OC =OD ，AC ⊥BD B.AB ∥CD ，AC =BDC.AD ∥BC ，∠A =∠CD.OA =OC ，OB =OD ，AB =BC2. 在正方形ABCD 中，AB =12 cm ，对角线AC 、BD 相交于O ，则△ABO 的周长是（ ） A.12+122B.12+62C.12+2D.24+623. 已知四边形ABCD 是菱形，当满足条件_________时，它成为正方形(填上你认为正确的一个条件即可).4. 下列命题中的假命题是( )．A ．一组邻边相等的平行四边形是菱形B ．一组邻边相等的矩形是正方形c 一组对边平行且相等的四边形是平行四边形D ．一组对边相等且有一个角是直角的四边形是矩形 5. 正方形的一条边长是3，那么它的对角线长是_______.例2、如图1，在正方形ABCD 中，点E 、F 分别是BC 、CD 的中点，AF 、DE 相交于点G ，则可得得结论：①DE AF =；②DE AF ⊥。

判定正方形的方法
一、基于几何性质的判定方法：
正方形是一种特殊的四边形，具有以下几何性质：
1.四边相等：正方形的四条边长度完全相等，可以通过测量四边的长度来判断。

2.四角相等：正方形的四个角度完全相等，每个角度为90度。

3.对角线相等：正方形的两条对角线完全相等，在已知四边长的情况下，可以通过勾股定理判断对角线是否相等。

综上所述，如果满足以上几何性质，就可以判定为正方形。

二、基于数学公式的判定方法：
正方形是一种特殊的矩形，具有以下数学公式：
1.周长：正方形的周长公式为4a，其中a为边长。

2.面积：正方形的面积公式为a²，其中a为边长。

在已知周长或面积的情况下，可以通过计算公式得到边长，并判断四边是否相等来判断是否为正方形。

三、基于编程算法的判定方法：
除了几何性质和数学公式的判定方法外，还可以通过编程算法来判定正方形。

1.输入四个点的坐标：首先，需要输入四个点的坐标，分别表示正方形的四个顶点。

2.计算边长：利用欧几里得距离公式计算四条边的长度，然后判断四边是否相等。

3.计算角度：利用向量的概念计算相邻两条边的夹角，然后判断四个角度是否相等且为90度。

4.判断对角线长度：利用勾股定理，计算对角线的长度，然后判断是否相等。

通过上述算法，可以判断输入的四个点是否构成正方形。

综上所述，判断正方形的方法可以从几何性质、数学公式和编程算法等方面进行判定。

根据不同需求和条件，选择适合的方法进行判断。

八年级数学下册《正方形的判定》教学反思1、八年级数学下册《正方形的判定》教学反思正方形的判定是八年级数学下册18章的内容，前边已经学习了平行四边形、矩形、菱形的判定方法，正方形的判定是平行四边形、矩形、菱形的判定的综合。

可以通过本节的学习总结、归纳前面所学内容，澄清学习中存在的一些模糊概念。

正方形的有关知识在日常生活中的应用也非常广泛，是近年中考命题的热点之一。

利用正方形的性质和判定进行解题，有助于我们发展演绎推理能力，培养证明过程的严谨性，发展学生初步的综合推理能力。

今天上正方形这节课整体比较满意，主要体现在以下几方面：第一、利用图形进行比较教学，学生比较容易理解，同时很清楚各种图形之间的关系。

结合矩形和菱形的条件得到正方形的定义，有一个角是直角，有一组邻边相等的平行四边形是正方形。

在分析定义时，强调了正方形定义和前面两类特殊平行四边形的异同。

突出要得到正方形的三个条件，1、一个角是直角；2、有一组邻边相等；3、是平行四边形。

并指出每一个条件它的作用。

第二、通过归纳矩形和菱形的性质得到正方形的性质，有前面学习的基础，学生掌握的比较轻松。

第三、正方形的判定，教材的处理没有用专门的判定，对于正方形的证明主要是通过定义，但是在证明的过程中又进行相应的结合，并不是纯粹的证明出三个条件。

首先根据定义，由平行四边形直接得到。

然后由矩形增加条件得到，还有菱形增加一个条件得到。

虽然没有专门用黑体字表示，但是实际上证明都可以用，总的其实就是用到了定义进行证明。

正方形的判定方法：(1)有一组邻边相等并且有一个角是直角的平行四边形是正方形；(2)有一个角是直角的菱形是正方形；(3)有一组邻边相等的矩形是正方形；(4)对角线相等的菱形是正方形；(5)对角线互相垂直的矩形是正方形。

第四、详细讲解范例，主要是引导学生，对于正方形的'证明的思路以及书写的格式。

在复习提问时，思路条理，能够清晰的和学生一起理顺知识点间的联系和区别，为后边学习正方形的判定打下良好的基础。

第2课时正方形的判定1．掌握正方形的判定条件；(重点)2．能熟练运用正方形的性质和判定进行有关的证明和计算．(难点)一、情境导入老师给学生一个任务：从一张彩色纸中剪出一个正方形．小明剪完后，这样检验它：比较了边的长度，发现4条边是相等的，小明就判定他完成了这个任务．这种检验可信吗？小兵用另一种方法检验：量对角线，发现对角线是相等的，小兵就认为他正确地剪出了正方形．这种检验对吗？小英剪完后，比较了由对角线相互分成的4条线段，发现它们是相等的．按照小英的意见，这说明剪出的四边形是正方形．你的意见怎样？你认为应该如何检验，才能又快又准确呢？二、合作探究探究点一：正方形的判定【类型一】利用“一组邻边相等的矩形是正方形”证明四边形是正方形如图，在Rt△ABC中，∠ACB＝90°，CD为∠ACB的平分线，DE⊥BC于点E，DF⊥AC于点F.求证：四边形CEDF是正方形．解析：要证四边形CEDF是正方形，则要先证明四边形CEDF是矩形，再证明一组邻边相等即可．证明：∵CD平分∠ACB，DE⊥BC，DF⊥AC，∴DE＝DF，∠DFC＝90°，∠DEC ＝90°.又∵∠ACB＝90°，∴四边形CEDF是矩形．∵DE＝DF，∴矩形CEDF是正方形．方法总结：要注意判定一个四边形是正方形，必须先证明这个四边形为矩形或菱形．【类型二】利用“有一个角是直角的菱形是正方形”证明四边形是正方形如图，在四边形ABFC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF＝AE.(1)试判断四边形BECF是什么四边形？并说明理由；(2)当∠A的大小满足什么条件时，四边形BECF是正方形？请回答并证明你的结论．解析：(1)根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，有BE＝EC，BF＝FC.又∵CF＝AE，∴可证BE＝EC＝BF＝FC.根据“四边相等的四边形是菱形”，∴四边形BF是菱形；(2)菱形对角线平分一组对角，即当∠ABC＝45°时，∠EBF＝90°，有菱形为正方形．根据“直角三角形中两个角锐角互余”得∠A＝45°.解：(1)四边形BECF是菱形．理由如下：∵EF垂直平分BC，∴BF＝FC，BE ＝EC，∴∠3＝∠1.∵∠ACB＝90°，∴∠3＋∠4＝90°，∠1＋∠2＝90°，∴∠2＝∠4，∴EC＝AE，∴BE＝AE.∵CF＝AE，∴BE＝EC＝CF＝BF，∴四边形BECF是菱形；(2)当∠A＝45°时，菱形BECF是正方形．证明如下：∵∠A＝45°，AB＝90°，∴∠3＝45°，∴∠EBF＝2∠3＝90°，∴菱形BECF是正方形．方法总结：正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；②先判定四边形是菱形，再判定这个菱形有一个角为直角；③还可以先判定四边形是平行四边形，再用判定定理1或判定定理2进行判定．探究点二：正方形的判定的应用【类型一】正方形的性质和判定的综合应用错误!未找到引用源。

八年级数学—正方形的性质和应用正方形的性质：正方形同时具备平行四边形，矩形，菱形的所有性质。

①正方形四个角都是直角②四条边都相等③对角线互相垂直平分④每一条对角线平分一组对角⑤正方形是轴对称图形，有四条对称轴。

正方形的判定：同时满足菱形和矩形的判定即可。

常用判定有：①先证菱形后证一个角是直角②先证矩形后证一组邻边相等基础篇：例一、已知四边形ABCD是平行四边形，再从①AB=BC②∠ABC=90°③AC=BD④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，下列选法错误的是（）A、①②B、②③C、①③D、②④例二、如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形。

（1）求证：四边形ABCD是菱形；（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形。

例三、如图，在正方形ABCD中，点P，Q是CD边上的两点，且DP=CQ，过D作DG⊥AP于H，分别交AC、BC于E、G，AP，EQ的延长线相交于R。

（1）求证：DP=CG；（2）判断△PQR的形状，并说明理由例四、如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。

（1）求证：CE=CF；（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？提高篇：例五、如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB、EA，延长BE交边AD于点F。

（1）求证：△ADE≌△BCE；（2）求∠AFB的度数。

变式练习1：如图，在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED 。

（1）求证：△BEC ≌△DEC（2）延长BE 交AD 于F ，当∠BED=120°时，求∠EFD 的度数。

例六、如图，正方形ABCD 中，点E 、F 分别在边BC 、CD 上，且AE=EF=FA 。