20181120鲁教版初中数学九年级下册《5.4 圆周角和圆心角的关系(3)》课件
- 格式:ppt
- 大小:1.43 MB
- 文档页数:12


《圆周角和圆心角的关系》教案教学目标知识技能:掌握圆周角的概念,理解掌握圆周角定理的证明并会进行简单的计算和证明.过程与方法:经历圆周角定理证明过程,体会“特殊到一般”和“分类讨论”的数学思想方法.情感与态度:通过观察、猜想、验证推理,培养学生探索数学问题的能力和方法.教学重点圆周角概念及圆周角定理.教学难点认识圆周角定理需分三种情况证明的必要性.教学方法指导探索法、讲授法.教学过程一、复习回顾,引入新课1.圆心角:顶点在圆心的角叫圆心角.2.圆心角的度数和它所对的弧的度数的大小关系是:相等.当角的顶点在圆心时,就是圆心角.这时角与圆两种不同的图形产生了联系,在圆中还有比较特殊的点吗?如果有,把这样的点作为角的顶点,会是怎样的图形?二、探索新知:圆周角的概念(观察圆心角的顶点的变化,导出圆周角的概念)(1)(2)(3)图(3)中的∠BAC,顶点在什么位置?角的两边有什么特点?圆周角的定义:顶点在圆上,并且两边分别与圆还有另一个交点的角叫圆周角.1.强调两个要点:(1)角的顶点在圆上;(2)角的两边都与圆相交2.跟踪训练:判断下列图示中,各图形中的角是不是圆周角,并说明理由.研究圆周角和圆心角的关系.证一证1.当圆心O 在圆周角∠ABC 的一边BC 上时,圆周角∠ABC 与圆心角∠AOC 的大小关系. 解:∠ABC =12∠AOC .理由是: ∵ ∠AOC 是△ABO 的外角,∴∠AOC =∠ABO +∠BAO .∵OA =OB ,∴∠ABO =∠BAO .∴∠AOC =2∠ABO .即∠ABC =12∠AOC . 2.如果∠ABC 的两边都不经过圆心(如下图),结果会怎样?特殊情况会给我们什么启发吗?能否将下 图中的两种情况分别转化成上图中的情况去解决吗?(学生互相交流、讨论)如图(1),点O 在∠ABC 内部时,只要作出直径BD ,将这个角转化为上述情况的两个角的和即可证出.(体现“分”的数学思想)由1的结论可知:∠ABD =12∠AOD ,∠CBD =12∠COD ,∴∠ABD +∠CBD =12 (∠AOD +∠COD ),即∠ABC =12∠AOC . 在图(2)中,当点O 在∠ABC 外部时,仍然是作出直径BD ,将这个角转化成上述情形的两个角的差即可证出.(体现“补”的数学思想)由1的结论可知:∠ABD =12∠AOD ,∠CBD =12∠COD . ∴∠ABD -∠CBD =12 (∠AOD -∠COD ),即∠ABC =12∠AOC . 综上所述,我们可以得到:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.(提问:条件是什么?结论是什么?)圆周角的度数等于它所对的弧的度数的一半.老师提示:圆周角定理是承上启下的知识点,要予以重视.如图1,圆中一段»AC 对着许多个圆周角,这些个角的大小有什么关系?为什么? 如图2,圆中»AB =»EF ,那么∠C 和∠G 的大小有什么关系?为什么? 如图2,圆中∠C =∠G , 那么»AB 与»EF 的大小有什么关系?为什么?C AE C图1 图2圆周角定理的推论同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.实际应用:当球员在B ,D ,E 处射门时,他所处的位置对球门AC 分别形成三个张角∠ABC , ∠ADC ,∠AEC .这三个角的大小有什么关系?3.圆周角与直径的关系1.如图(1),BC 是⊙O 的直径,A 是⊙O 上任一点,你能确定∠BAC 的度数吗?2.如图(2),圆周角∠BAC =90º,弦BC 经过圆心O 吗?为什么?图1BC图2BC圆周角定理的推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.定理的应用例题分析:如图,在△ABC 中AB=AC ,以AB 为直径的⊙O 交BC 于D ,BD 与CD 的大小有什么关系?为什么? 解析:BD=CD如图连接AD .∵AB 是⊙O 的直径,∴∠ADB =90°∵AC=AB ,∴BD=CD .C练一练:1.如图,在⊙O 上中, ∠BOC = 50°求∠BAC 的大小.2.如图,哪个角与∠BAC 相等?你还能找到哪些相等的角? 3.指出图中的圆周角.第1题图 第2题图 第3题图三、课堂小结(一)这节课主要学习了四个知识点:1.圆周角:顶点在圆上,并且两边分别与圆还有另一个交点的角叫圆周角.2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.3.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:(1)构造直径上的圆周角.(2)构造同弧所对的圆周角.4.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.四、拓展延伸圆外角:顶点在圆外,并且两边都和圆相交的角.如下图中,∠DPB 是圆外角,那么∠DPB 的度数与它所夹的两段弧»BD和»AC 的度数有什么关系? 1.你的结论: ________;2.证明你的结论.1.圆外角等于它所夹弧的度数差的一半.2.证明:边结BC .P DB五、布置作业.。







周次: 学科: 数学 主备人: 审核人: 备课日期: 授课日期: 授课人: 课题 5.4圆周角和圆心角的关系(第2课时) 课型新授课时: 1教学目标知识目标:掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径的性质,并能运用此性质解决问题能力目标:灵活运用性质,掌握做辅助线的方法。
情感态度与价值观:激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活.重点掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径的性质,并能运用此性质解决问题.难点 灵活运用性质,掌握做辅助线的方法。
学习过程二次备课预习案【课前预习】学习任务一:阅读教材第21—23页内容,思考并总结本节课学习的主要内容,写在下面的横线上:1.如图,在⊙O 中,△ABC 是等边三角形,AD 是直径,则∠ADB=______________,∠DAB=___________。
2.如图,AB 是⊙O 的直径,若AB=AC ,求证:BD=CD 。
探究案例 如图5-27(1),在△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于点D 。
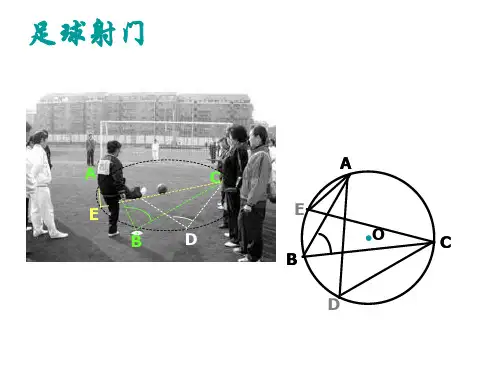
BD 与CD 的大小有什么关系?为什么?做一做轮船在航行过程中,船长常常通过测定角度来确定轮船是否会遇到暗礁,如图,A,B 表示灯塔,暗礁分布在经过A,B 两点的一个圆形区域内,C 表示一个危险临界点,∠ACB 就是“危险角”,当轮船与两个灯塔的夹角大于危险角时,就有可能触礁。
(1)当轮船与两个灯塔的夹角∠α大于危险角时,轮船位于哪个区域?为什么?(2)当轮船与两个灯塔的夹角∠α小于危险角时,轮船位于哪个区域?为什么?ODCBA第1题ODCBA第2题训练案1、如图,⊙O的直径AB=10cm,C为⊙O上的一点,∠ABC=30°,求AC的长。
2、如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2,以AB为直径的圆与BC相交于点D,求AD和CD的长。
初三下学期数学圆周角和圆心角的关系知识点精讲知识点总结圆心角与圆周角:圆心角是指顶点在圆心的角,而圆周角则指顶点在圆上的角,二者注意区分。
重要结论:①同弧(同弦)所对的圆周角是圆心角的一半(即½)②直径所对的圆周角是直角,即90º解题思路:结合垂径定理、圆心角和圆周角的转化关系,加上以前学过的直角三角形性质、三角形的外角性质和角平分线的性质,去解决具体题目,注意分析过程中灵活运用相关知识点。
要点1:圆周角1.圆周角定义:像图中∠AEB、∠ADB、∠ACB这样的角,它们的顶点在圆上,并且两边都与圆相交的角叫做圆周角.2圆周角定理:一条弧所对的圆周角等于它所对圆心角度数的一半。
3.圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;推论2:直径所对的圆周角是直角,90°的圆周角所对的弦是直径。
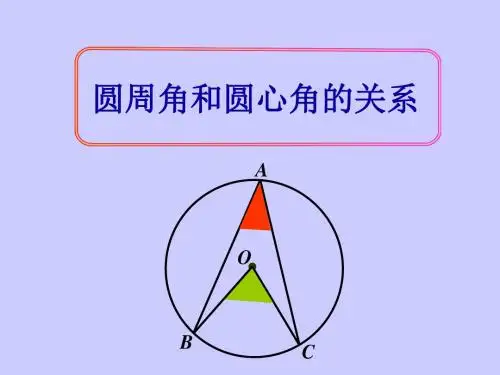
要点诠释:(1)圆周角必须满足两个条件:①顶点在圆上:②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.(3)圆心与圆周角存在三种位置关系:圆心在圆周角的一边上:圆心在圆周角的内部:圆心在圆周角的外部,(如下图)要点2:圆内接四边形1.圆内接四边形定义:四边形的四个顶点都在同一个圆上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.2.圆内接四边形性质:圆内接四边形的对角互补.如图,四边形ABCD是00的内接四边形,则∠A+∠C=180°,∠B+∠D=180°.要点诠释:当四边形的四个顶点不同时在一个圆上时,四边形的对角是不互补.习题讲析练习题:图文导学教学设计圆周角和圆心角的关系一、教材分析1、教材的地位和作用本课是在学习了圆心角后进而要学习的圆的又一个重要的性质,它在推理、论证和计算中应用比较广泛,是圆这章的重点内容之一。
2、依学情定目标我们面对的是已具备一定知识储备和一定认知能力的个性鲜明的学生,他们有较强的自我发展意识,根据新课程标准的学段目标要求,结合学生实际情况制订以下三个方面的教学目标:1)知识目标:了解圆周角和圆心角的关系,有机渗透由特殊到一般思想、分类思想、化归思想。