测量集成霍尔传感器的灵敏度

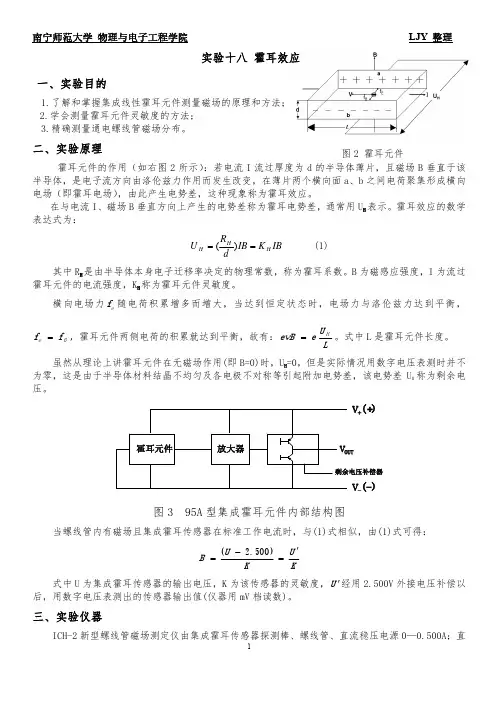
图2 霍耳元件南宁师范大学 物理与电子工程学院 LJY 整理实验十八 霍耳效应一、实验目的1.了解和掌握集成线性霍耳元件测量磁场的原理和方法；2.学会测量霍耳元件灵敏度的方法；3.精确测量通电螺线管磁场分布。

二、实验原理霍耳元件的作用（如右图2所示）：若电流I 流过厚度为d 的半导体薄片，且磁场B 垂直于该半导体，是电子流方向由洛伦兹力作用而发生改变，在薄片两个横向面a、b 之间电荷聚集形成横向电场（即霍耳电场），由此产生电势差，这种现象称为霍耳效应。

在与电流I、磁场B 垂直方向上产生的电势差称为霍耳电势差，通常用U H 表示。

霍耳效应的数学表达式为：IB K IB dR U H HH ==((1) 其中R H 是由半导体本身电子迁移率决定的物理常数，称为霍耳系数。

B 为磁感应强度，I 为流过霍耳元件的电流强度，K H 称为霍耳元件灵敏度。

横向电场力e f 随电荷积累增多而增大，当达到恒定状态时，电场力与洛伦兹力达到平衡，B e f f =，霍耳元件两侧电荷的积累就达到平衡，故有：LU eevB H=。

式中L 是霍耳元件长度。

虽然从理论上讲霍耳元件在无磁场作用(即B=0)时，U H =0，但是实际情况用数字电压表测时并不为零，这是由于半导体材料结晶不均匀及各电极不对称等引起附加电势差，该电势差U 0称为剩余电压。

图3 95A 型集成霍耳元件内部结构图当螺线管内有磁场且集成霍耳传感器在标准工作电流时，与(1)式相似，由(1)式可得：KU KU B '=-=)500.2( 式中U 为集成霍耳传感器的输出电压，K 为该传感器的灵敏度，U '经用2.500V 外接电压补偿以后，用数字电压表测出的传感器输出值(仪器用mV 档读数)。

三、实验仪器ICH-2新型螺线管磁场测定仪由集成霍耳传感器探测棒、螺线管、直流稳压电源0—0.500A；直流稳压电源输出二档(2.4V—2.6V 和4.8V—5.2V)；四位半数字电压表(19.999V 和1999.9mV 二档)；导线若干组成。

华南农业大学实验报告组别201130010110题目集成霍尔传感器测量圆线圈和亥姆霍线兹圈的磁场姓名梁志雄日期实验目的学会用霍尔传感器测量圆线圈和亥姆霍兹线圈的磁场实验器材亥姆霍兹磁场测定仪、高灵敏度毫特计和数字式直流稳压电源实验原理亥姆霍兹线圈磁场实验仪采用恒流源，产生恒定的磁场，用集成霍尔传感器测量载流圈线圈和亥姆霍兹线圈线上各点的磁感应强度，研究亥姆霍兹线圈的磁场分布。

若在一条直线上两个完全相同共轴密绕的圆形线圈，两线圈半径都则在两线圈轴线附都是R，匝数都是N，且两线圈间距也是R，通入大小和方向都相同的电流，则在两线圈间轴线附近，磁场叠加结果保持基本均匀，产生均匀磁场区。

实验步骤1、接好仪器，测量电流I=100mA时单线圈a轴上各点的磁感应强度Ba，每隔1cm测量一次；2、计算线圈中的轴线上各点的磁感应强度；3、在轴线上某点转动探头观察该点磁感应强度变化规律；4、调节ab之间的距离d=10cm，组成一个亥姆霍兹线圈，取I=10mA，分别测量两线圈单独通电时各点磁感应强度Ba+Bb。

记录数据的表格位置/cm-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 测量值-0.134 -0.152 -0.176 -0.205 -0.23 -0.266 -0.291 -0.315 -0.328 -0.337 -0.332 -0.325 -0.301 -0.274 -0.243 -0.213 -0.185 -0.156 -0.14 理论值-0.129 -0.150 -0.173 -0.198 -0.225 -0.251 -0.276 -0.296 -0.309 -0.314 -0.309 -0.296 -0.279 -0.251 -0.225 -0.198 -0.173 -0.150 -0.129 百分误差% 3.88 1.33 1.73 3.54 2.22 5.98 5.43 6.42 6.15 7.32 7.44 9.80 7.89 9.16 8.00 7.58 6.94 4.00 8.53 单线圈轴线上的磁感应强度亥姆霍兹线圈轴线上磁感应强度位置/cm -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 单线圈磁场Ba -0.257 -0.282 -0.311 -0.316 -0.332 -0.330 -0.316 -0.297 -0.272 -0.241 -0.214 -0.186 -0.161 -0.139 -0.120 -0.103 -0.089 -0.078 -0.068 单线圈磁场B b-0.063 -0.071 -0.083 -0.097 -0.110 -0.128 -0.148 -0.170 -0.196 -0.230 -0.258 -0.288 -0.308 -0.328 -0.353 -0.337 -0.317 -0.296 -0.273 Ba+Bb -0.32 -0.35 -0.39 -0.41 -0.44 -0.46 -0.46 -0.47 -0.47 -0.47 -0.47 -0.47 -0.47 -0.47 -0.47 -0.44 -0.41 -0.37 -0.34 亥姆霍兹线圈的磁场B -0.318 -0.353 -0.398 -0.426 -0.450 -0.467 -0.475 -0.466 -0.470 -0.481 -0.460 -0.473 -0.475 -0.470 -0.457 -0.440 -0.413 -0.383 -0.342数据处理（见附表）思考题1、为什么在实验中每测一点的磁感应强度之前都必须调零？在实验中，测量坐标板上的每一点，由于所处的环境不同，所受到周围环境的电磁波大小就有一个差异，因为我们在实验中主要是研究在该点由这个线圈所激发的磁场的磁感应强度是多少，所以绝对有这个必要在测量每一点之前调零来排除周围环境的电磁波的影响。

霍尔元件灵敏度参数单位霍尔元件是一种用来测量磁场的传感器元件。

它的灵敏度是指在给定的电场条件下，每个磁场单位变化对该元件输出电压的影响程度。

霍尔元件的灵敏度通常以电压/V（V/T）表示，其中V/T是对磁场单位的度量。

本文将详细介绍霍尔元件的灵敏度参数单位，并对其进行全面的分析。

一、霍尔元件的工作原理霍尔元件是由一块晶体片制成的，它包含有金属触点和感应结构。

当感应结构过电流时，它会在两个触点之间产生横向电场（霍尔电场），这个电场会受到磁场的影响，从而引起触点之间的电势差产生变化。

这种电势差的变化可以通过读取该元件的输出电压来衡量。

霍尔元件的灵敏度参数单位通常有两种：一种是电压/V（V/T），另一种是电流/A（V/A T）。

其中电压/V（V/T）是对于每个磁场单位的电势差变化量的度量，而电流/A（V/A T）是入射磁场下输出电流与磁力度之间的比例。

S = ΔV/ΔB其中S表示霍尔元件的灵敏度，ΔV表示输入磁场单位下的输出电势差变化量，ΔB表示磁场单位的变化量。

该公式可以用来计算霍尔元件在不同磁场条件下的灵敏度，从而确定将使用什么样的元件来实现所需的测量精度。

霍尔元件的灵敏度参数受多种因素影响，其中包括：1. 硅片的薄膜质量：硅片的薄膜质量会影响霍尔晶体的导电性、生长质量和磁场响应。

2. 温度：温度是影响霍尔元件灵敏度的一个重要因素。

在不同的温度下，霍尔元件的灵敏度会发生变化。

3. 磁场的方向和大小：不同方向和大小的磁场对霍尔元件的灵敏度有影响。

对于特定方向和大小的磁场，霍尔元件会表现出不同的灵敏度值。

4. 霍尔元件的尺寸和形状：霍尔元件的尺寸和形状也会对其灵敏度产生影响。

对于不同的尺寸和形状的霍尔元件，其灵敏度也不同。

霍尔元件的灵敏度参数单位是电压/V（V/T）和电流/A（V/A T）。

灵敏度受多种因素影响，包括硅片的薄膜质量、温度、磁场的方向和大小以及霍尔元件的尺寸和形状。

了解这些因素对霍尔元件灵敏度的影响可以帮助我们选择合适的元件来实现所需的测量精度。

【实验步骤】(一)清点主要仪器（二）测量1.调节仪器①将仪器按照如图4所示安装：将弹簧固定在焦利秤上部的横梁上，在一个刻有水平线的小平面镜杆下端挂上砝码盘，小平面镜杆穿过固定在立柱上的玻璃管，其上端与弹簧的下端相连，②调节焦利秤的底脚螺旋，使焦利秤立柱竖直；调节螺旋E使小平面镜上水平线与玻璃管壁上的水平线重合作为平衡位置，并调节支架让小镜面及其它参于振动的物体竖直。

2.测量弹簧的倔强系数K2.1利用新型焦利秤（静态法）测定弹簧倔强系数K①调节实验装置底脚螺丝，使焦利秤立柱垂直（目测）；②将弹簧固定在焦利秤上部悬臂上，旋转悬臂，使挂于弹簧下放的砝码盘的尖针（1）靠拢游标尺上的小镜；（2）在砝码盘放入10个1g的砝码，然后依次取出。

在三线重合（小钩中的平面镜中有一水平刻线G，玻璃管上有一水平刻线D，D在平面镜中有一像D’，通过转动标尺调节旋钮可将弹簧上下移动，则平面镜同时上下移动。

当G、D、D’三者重合时称“三线重合”。

）时，记录各次标尺读数y1,y2, (10)K g （3）作Mi～Yi图，验证Mi～Yi满足线性关系，并求出斜率'K，'/即为弹簧的倔强系数K。

2.2测量弹簧振子振动周期求弹簧倔强系数K（动态法）（1）用电子秒表测弹簧振子振动50次的时间，然后求得弹簧振子的周期T。

（2）用集成开关型霍尔传感器测量弹簧振动周期，求弹簧倔强系数。

（3）将集成霍尔开关的三个引脚分别与电源和周期测试仪相接。

OUT 接周期测试仪正级，V-接电源负极，并和周期测试仪负级连接，V+接电源正级，见图3；（4） 将钕铁硼磁钢粘于20g 砝码下端，使S 极面向下。

把集成霍尔开关感应面对准S 极，其与磁钢间距在10cm ～20cm 之间。

轻轻拉动弹簧使其上下振动，记录振动50次的时间，求出弹簧振子周期。

进行4次测量。

3.测量集成开关霍尔传感器的参数。

（1） 如图5将95A 型集成线性霍尔传感器接线，把小磁钢放在远处，接通电源，调节电压使电压表示数为2.500V ；（2） 将95A 型集成线性霍尔传感器换成集成开关型霍尔传感器（简称集成霍尔开关）接线不变，把小块钕铁硼磁钢粘在固定支架上，使小磁钢的S 极与集成霍尔开关的感应面(有文字面)紧密相对（接触）；（3） 记录集成霍尔和小磁钢接触时，电路板在固定支架上的位置x0,将集成霍尔开关拉出然后又向内线移动。

实验名称：用霍尔传感器测定螺线管磁场姓 名学 号 班 级桌 号 教 室 基础教学楼1108 实验日期 20 年月 日 时段同组同学 指导教师一、实验目的（请先参阅实验教材上《磁场测量》的内容，然后充分阅读实验报告！） 1、验证霍尔传感器输出电势差与螺线管内磁感应强度成正比。

2、测量集成线性霍尔传感器的灵敏度。

3、测量螺线管内磁感应强度与位置之间的关系，求得螺线管均匀磁场范围及边缘的磁感应强度。

4、学习补偿原理在磁场测量中的应用。

二、实验仪器FD-ICH-II 新型螺线管磁场测定仪，包括：实验主机、螺线管、集成霍尔传感器探测棒、单刀双掷开关、双刀双掷换向开关、、连接导线（4红，4黑）若干组成。

其仪器装置如图1所示。

图1 新型螺线管磁场测定仪仪器装置三、实验原理把一块半导体薄片（锗片或硅片）放在垂直于它的磁场B 中，如图2所示，当沿AA ′方向（Y 轴方向）通过电流I 时，薄片内定向移动的载流子受到洛伦兹力f B 的作用而发生偏转。

从而在DD ′间产生电位差U H ，这一现象称为 。

这个电位差称为 。

由电磁理论可得：U H ＝ （1）式中，K H ＝ned1称为霍尔元件的灵敏度，n 为载流子浓度，e 为载流子电荷电量。

d 为半导体薄片厚度虽然从理论上讲霍尔元件在无磁场作用(即B=0)时，U H =0，但实际中，在产生霍尔效应的同时，还伴随着几个副效应，它们分别是； ； ； 。

所以用数字电压表测时U H 并不为零，这是由于半导体材料结晶不均匀及各电极不对称等引起附加电势差，该电势差U 0称为剩余电压。

随着科技的发展，新的集成化(IC)元件不断被研制成功。

本实验采用SS95A 型集成霍尔传感器(结构示意图如图3所示)是一种高灵敏度集成霍尔传感器，它由霍尔元件、放大器和薄膜电阻剩余电压补偿组成。

测量时输出信号大，并且剩余电压的影响已被消除。

对SS95A 型集成霍尔传感器，它由三根引线，分别是:“V +”、“V -”、“V out ”。

实验报告班级： 姓名： 学号：一、实验名称集成霍尔传感器测量圆形线圈和亥姆霍兹线圈的磁场二、实验目的1、掌握霍尔效应原理测量磁场；2、测量单匝载流原线圈和亥姆霍兹线圈轴线上的磁场分布。

三、实验仪器亥姆霍兹线圈磁场测定仪、包括圆线圈和亥姆霍兹线圈平台（包括两个圆线圈、固定夹、不锈钢直尺等）、高灵敏度毫特计和数字式直流稳压电源。

四、实验原理1、圆线圈的磁场根据毕奥—萨伐尔定律，载流线圈在轴线上某点的磁感应强度为：NI x R RB 232220)(2+=μ式中I 为通过线圈的电流强度，R 为线圈平均半径，x 为圆心到该点的距离，N 为线圈的匝数，A m T /10470⋅⨯=-πμ，为真空磁导率。

因此，圆心处的磁感应强度为NIRB 20μ=2、亥姆霍兹线圈的磁场亥姆霍兹线圈：两个半径和匝数完全相同的线圈，其轴向距离等于线圈的半径。

这种线圈的特点是当线圈串联连接并通以稳定的直流电后，就可在线圈中心区域内产生较为均匀性较好的磁场，因而成为磁测量等物理实验的重要组成部件，与永久磁铁相比，亥姆霍兹线圈所产生的磁场在一定范围内具有一定的均匀性，且产生的磁场具有一定的可调性，可以产生极微弱的磁场直至数百高斯的磁场，同时在不通电的情况下不会产生环境磁场。

亥姆霍兹线圈如图所示，是一对彼此平行且连通的共轴圆形线圈，两线圈内电流方向一致，大小相同，线圈之间距离d 正好等于圆形线圈的半径R 。

设z 为亥姆霍兹线圈中轴线上某点离中心点O处的距离，根据毕奥—萨伐尔定律及磁场叠加原理可以从理论上计算出亥姆霍兹线圈轴上任意一点的磁感应强度为⎭⎬⎫⎩⎨⎧-++++⋅⋅⋅='--2322232220]z 2([]z 2([21））R R R R R I N B μ而在亥姆霍兹线圈上中心O 处的磁感应强度'B 为R IN B ⋅⋅=023'058μ 当线圈通有某一电流时，两线圈磁场合成如图可看出，两线圈之间轴线上磁感应强度在相当大的范围内是均匀的。

霍尔式传感器的特性实验报告霍尔式传感器的特性实验报告引言：霍尔式传感器是一种常用的非接触式传感器，它通过检测磁场变化来测量电流、速度、位置等物理量。

本实验旨在研究和分析霍尔式传感器的特性，并通过实验数据验证其性能和准确度。

实验一：霍尔传感器的灵敏度在这个实验中，我们使用了一台霍尔传感器测量不同电流下的输出电压，并记录了相应的数据。

通过分析实验数据，我们可以计算出霍尔传感器的灵敏度。

实验结果显示，当电流增加时，霍尔传感器的输出电压也随之增加。

通过绘制电流与输出电压之间的关系曲线，我们可以观察到一个线性关系。

通过对实验数据进行线性回归分析，我们可以得到霍尔传感器的灵敏度。

实验二：霍尔传感器的响应时间在这个实验中，我们使用了一个霍尔传感器来测量一个旋转的磁场源的位置。

我们记录了霍尔传感器的输出电压随时间的变化，并通过分析实验数据来计算霍尔传感器的响应时间。

实验结果显示，当旋转磁场源时，霍尔传感器的输出电压随之变化。

通过绘制时间与输出电压之间的关系曲线，我们可以观察到一个明显的响应时间。

通过对实验数据进行分析，我们可以计算出霍尔传感器的响应时间。

实验三：霍尔传感器的线性度在这个实验中，我们使用了一个霍尔传感器来测量一个恒定电流下的位置变化。

我们记录了霍尔传感器的输出电压随位置的变化，并通过分析实验数据来计算霍尔传感器的线性度。

实验结果显示，当位置变化时，霍尔传感器的输出电压也随之变化。

通过绘制位置与输出电压之间的关系曲线，我们可以观察到一个线性关系。

通过对实验数据进行线性回归分析，我们可以得到霍尔传感器的线性度。

讨论：通过以上实验，我们可以得出以下结论：1. 霍尔传感器的灵敏度是通过实验数据计算得出的，它反映了传感器对电流变化的敏感程度。

灵敏度越高，传感器的测量精度越高。

2. 霍尔传感器的响应时间是通过实验数据计算得出的，它反映了传感器对磁场变化的响应速度。

响应时间越短，传感器的实时性越好。

3. 霍尔传感器的线性度是通过实验数据计算得出的，它反映了传感器输出电压与被测物理量之间的线性关系。

霍尔元件的灵敏度测量原理霍尔元件是一种基于霍尔效应的传感器，用于测量磁场的强度和方向。

它的灵敏度是指对于磁场的变化，传感器输出信号的变化程度。

本文将详细介绍霍尔元件的灵敏度测量原理。

首先，我们需要了解一下霍尔效应。

霍尔效应是指当电流通过导体时，如果该导体处于磁场中，会在导体的两侧产生电势差，这个现象就被称为霍尔效应。

霍尔元件中常用的是纵向霍尔效应，即磁场方向与电流方向垂直。

在霍尔元件中，通常有三个引脚，分别是电源引脚（Vcc）、接地引脚（GND）和输出引脚（OUT）。

电源引脚连接正电源，接地引脚连接地线，输出引脚连接电路的输入端。

在测量霍尔元件的灵敏度时，我们需要将霍尔元件放置在已知磁场中，并通过测量输出信号的变化来确定其灵敏度。

具体步骤如下：1. 构建实验电路。

首先，将霍尔元件与其他电路连接起来，例如，将电源引脚连接正电源，接地引脚连接地线，输出引脚连接电路的输入端。

2. 定义基准信号。

在没有外部磁场作用时，测量霍尔元件输出的基准信号，将其作为后续测量的基准值。

3. 放置霍尔元件。

将霍尔元件放置在已知磁场中，并保持稳定。

可以使用磁铁或电磁铁产生磁场，确保磁场强度可控且恒定。

4. 测量输出信号。

通过连接的电路，测量霍尔元件输出的信号大小和方向。

可以使用示波器或模拟信号处理器来获取输出信号。

5. 计算灵敏度。

通过比较基准信号和测量信号的差异，计算出霍尔元件的灵敏度。

通常，灵敏度被定义为单位磁场变化引起的电压变化。

需要注意的是，为了获得准确的灵敏度测量结果，我们应该尽量避免外界因素对测量的干扰。

例如，应保持磁场稳定且恒定，避免其它磁场源的影响；还要注意电源稳定和抗干扰电路的设计，以减小测量误差。

此外，为了获得更准确的灵敏度测量结果，可以进行多次测量并取平均值。

同时，还可以通过改变磁场的强度来测量不同磁场下的输出信号，以确定灵敏度的变化规律。

总之，霍尔元件的灵敏度测量原理是通过将霍尔元件放置在已知磁场中，测量输出信号的变化来确定其灵敏度。

霍尔传感器参数霍尔传感器是一种常用的传感器，常用于测量磁场强度和进行位置检测。

它由霍尔元件和信号处理电路组成，通过检测磁场的变化来实现相应的测量和控制功能。

在实际应用中，霍尔传感器的参数对于其性能和精度起着至关重要的作用。

本文将针对霍尔传感器的参数进行详细的介绍和解析，以便读者能够更好地理解和应用这一传感器。

我们来介绍一下霍尔传感器的主要参数：1. 灵敏度：霍尔传感器的灵敏度是指在单位磁场变化下输出电压的变化量。

通常以mV/mT（毫伏/毫特斯拉）或V/T（伏特/特斯拉）为单位。

灵敏度越高，说明传感器对磁场变化的响应越快，能够更准确地进行测量和控制。

2. 饱和磁场：霍尔传感器在磁场作用下，当输出信号达到一个特定的数值后，信号将不再随磁场的增加而线性增加，而是趋于饱和。

饱和磁场是传感器能够测量的最大磁场强度。

3. 工作电压：霍尔传感器的工作电压范围，通常以V（伏特）为单位。

超出该范围，传感器可能无法正常工作或者寿命将受到影响。

4. 工作温度范围：霍尔传感器能够正常工作的温度范围，通常以摄氏度（℃）为单位。

超出该范围，传感器的性能可能会下降。

5. 输出类型：霍尔传感器的输出类型有两种，一种是模拟输出，以电压或电流的形式输出测量值；另一种是数字输出，以数字信号的形式输出测量值。

6. 尺寸和安装方式：霍尔传感器的尺寸和安装方式对于实际应用有着重要的影响，包括外形尺寸、安装孔径、连接方式等。

除了上述参数外，霍尔传感器的响应时间、线性度、稳定性、精度等参数也是衡量其性能的重要指标。

在选择和应用霍尔传感器时，需要根据具体的应用场景和要求来综合考虑这些参数，并进行适当的选择和设计。

在实际应用中，不同类型的霍尔传感器有着不同的参数要求。

用于测量磁场强度的霍尔传感器需要具有较高的灵敏度和较大的饱和磁场，而用于位置检测的霍尔传感器则需要具有较好的线性度和稳定性。

在选择霍尔传感器时，需要充分了解其参数要求，并根据具体需求来进行选择。

Vol.18No.4Dec .2019第18卷第4期2019年12月浙江工商职业技术学院学报Journal o f Zhejiang Business Technology InstituteLabCorder 是一款数据采集仪,在工作中与电脑组成测量采集系统。

它的工作特性是测量二个物理量的函数关系,在控制元件操作窗口显示其特征曲线关系。

所测数据是以采集形式获得,采样频率可以人为调节,最大采样频率是每秒40次。

其特点是只能采集电压而不能采集电流,采集范围是-5-+5V ,超出此范围的物理量都视作是极限值。

采集到的数据以Excel 格式保存,其保存数据有三列,第一列是采集时间,第二列是CH 1通道采集数据,第三列是CH 2通道采集的数据,采集的电压单位为伏(V )。

1霍耳效应与灵敏度将一导电体(金属或半导体)薄片放在磁场中,并使薄片平面垂直于磁场方向,如图1。

当薄片纵向端面有电流I 流过时,在与电流I 和磁场B 垂直的薄片横向端面a 、b 间就会产生一电势差,这种现象称为霍耳效应(Hall effect ),所产Experimental Design of Susceptivity Mensuration of Hall Sensor Basedon the LabCorderZHANG Guo-rong(Ningbo University of Technology ,Ningbo 315016,China )Abstract :LabCorder is a kind of the data acquisition instrument ,which combines with a computer to form a measurement acquisition system.It is mainly used for measuring the relationship between two physical quantities ,visually displaying in the form of images ,and saving the measurement data in Excel format.The sensitivity mea ⁃surement experiment of the integrated Hall sensor mainly achieves the measurement purpose by the relationshipbetween the Hall voltage and the magnetic induction intensity in the Hall effect phenomenon ,thus applying Lab ⁃Corder to build design experiments.Key words :LabCorder ;Hall effect ;exciting current ;magnetic flux density ;susceptivtiy基于LabCorder 对霍尔传感器灵敏度测量实验的设计章国荣(宁波工程学院,浙江宁波315016)摘要：LabCorder 是一款数据采集仪,与电脑组成测量采集系统。

探测识别技术设计0811020207 徐超本系统模拟声磁探测系统。

SS95A型集成霍尔传感器测磁场（线性测量范围为-67mT~67mT,灵敏度31.3±1.3V/T）。

工作电压为5V，他的输出电压与磁感应强度成线性关系：B=KU模拟传感器的电压输出变化，测出附近的磁场强度。

当声音传来时，声音传感器由高电平变成低电平，可由一个开关代替控制，当声音靠近时，则报警灯闪烁，发出报警声。

原理图：C语言程序：#include<reg52.h>#define uchar unsigned char #define uint unsigned int sbit p20=P2^0;sbit p21=P2^1;sbit p22=P2^2;sbit p23=P2^3;sbit oe=P1^0;sbit eoc=P1^1;sbit st=P1^2;sbit clk=P1^3;sbit s1=P2^7;sbit r1=P2^4;uchar code tab1[]={0x3F,0x06,0x5B,0x4F,0x66,0x6D,0x7D,0x07,0x7F,0x6F}; uchar code tab2[]={0xbf,0x86,0xdb,0xcf,0xe6,0xed,0xfd,0x87,0xff,0xef}; void delay(uint z){uint x,y;for(x=z;x>0;x--)for(y=110;y>0;y--);}void display(uchar date){uchar qian,bai,shi,ge;uint zhi;float a=0.26275;zhi=a*date*100/1;qian=zhi/1000;bai=zhi%1000/100;shi=zhi%1000%100/10;ge=zhi%10;p20=0;P0=tab1[qian];delay(1);p20=1;p21=0;P0=tab2[bai];delay(1);p21=1;p22=0;P0=tab1[shi];delay(1);p22=1;p23=0;P0=tab1[ge];delay(1);p23=1;}void main(){TMOD=0x02;TH0=245;TL0=0;IE=0x82;TR0=1;P1=0x0f;while(1){st=0;st=1;st=0;while(eoc==0);oe=1;display(P3);oe=0;if(s1==0){r1=~r1;delay(5);}}}void timer0() interrupt 1 {clk=~clk;}。