傅里叶变换和小波变换简介-课件

格式：ppt
大小：633.00 KB
文档页数：19

下载文档原格式

一看就懂的小波变换ppt

8
8
[32.5,0, 0.5,0.5,31,-29,27,-25]
Haar小波反变换：
1 1 1 0 1 0 0 0 32.5 64
1
1
1
0 -1
0
0
0
0
2
1 1 -1 0 0 1 0 0 0.5 3
1 1 -1 1 -1 0
0 1
0 -1 00
0 1
0 0
0.5
31
61 60
傅立叶变换： Of M log2 M
小波变换：
Ow M
设有信号f(t):
其傅里叶变
换为F(jΩ):
即：
f (t) 1 F ( j)e jtd
2
பைடு நூலகம் =
1
0. 8
0. 6
0. 4
0. 2
0 -0. 2 -0. 4 -0. 6
Ψ（t）
-0. 8
-1 0
2
4
6
8
10
12
14
16
18
+
1
0. 8
0. 6
二维金字塔分解算法
令I(x,y)表达大小为M N旳原始图像，l(i)表达相对于分析
小波旳低通滤波器系数，i=0,1,2,…,Nl-1， Nl表达滤波器L旳支撑长度； h(i)表达相对于分析小波旳高通滤波器系数，
i=0,1,2,…,Nh-1， Nh表达滤波器H旳支撑长度，则
IL x,
y
1 Nl
1.2 二维小波变换（二维多尺度分析）
二维小波变换是由一维小波变换扩展而来旳，二维尺度函数和二维小波函数可由一维尺度函数和小波函数张量积得到，即：

小波变换入门.ppt

f f
(2 j , x, (2 j , x,
y)
y)
2
j
x
y
f f
(x, (x,
y) y)
a a
(x, (x,
y)
y)
2
j
grad
f
(x,
y)
a
(x,
y)
37/103
整个图像的二进小波变换即矢量：
W (1) f (2 j , x, y)
T
W
(
T
2)
f
(2
j,
x,
y)
WT
f
(2
j,
x,
尺度空间的递归嵌套关系： 0 V1 V0 V1 L2 R
小波空间 W是j 和V j 之V间j1 的差，即时丢V 失j 的信息V j。1 推出：
V0 W0 W1 Wj V j1
V0
Vj，它Wj 捕 V捉j1 由逼近
V j1
L2 R
V j1
Vj
多分辨率的空间关系图
19/103
两尺度方程
1 ( x, y)
(x) (y)
2 ( x, y)
(x)(y)
3 ( x, y)
(x) (y)
与 (x, y)一起就建立了二维小波变换的基础。
26/103
图像的小波变换实现
1. 正变换图像小波分解的正变换可以依据二维小波变换按如下方式扩展，在变换的每一层次，图像都被分解为4个四分之一大小的图像。
线性
设： xt g t ht
WTx a,b WTg a,b WTh a,b 平移不变性
若 xt WTx a,b，则 xt WTx a,b
伸缩共变性

小波变换理论与方法ppt课件

R
其中 g,t (t) g(t )eit g(t )eit ，窗口函数g(t)起着时
限作用，eit 起着频限作用。该变化具有不变化宽度（由时间宽度决定）和不变的窗口面积4g∆g∆
10
短时傅里叶变换示意图
11
cos(440 t) x(t) cos(660 t)
傅里叶变换傅里叶变换小波变换小波变换小波变换的一些应用小波变换的一些应用1822年法国数学家傅里叶jfourier发表的研究热传导理论的热的力学分析提出每一个周期函数都可以表示成三角函数之和奠定了傅里叶级数的理论基础
1
主要内容
1. 傅里叶变换 2. 小波变换 3. 小波变换的一些应用
2
一傅里叶变换
E(|Wn(j,t)|2)=0
D(|Wn(j,t)|2)= Ψ t 2
j
26
3.1.1小波包去噪步骤
① 选择小波基并确定最佳分解的层次,对信号进行小波包分解; ② 对步骤(1)获得的小波包树,选择一定的嫡标准,计算最优树; ③ 估计阈值,并应用该阈值对最优树的小波包系数进行阈值量化; ④ 将经量化处理的小波包系数,重构回原始信号。
Gabor变换的基本思想为：取时间函数 g(t) 1/ e4 t2/2 作为窗口函数，然后用 g(t ) 通待分析函数相乘，τ是时间延迟，是窗函数 g(t)的中心，窗函数根据τ进行时移，然后再进行傅里叶变换：
Gf (, ) f (t)g(t )eitdt f (t), g,t (t)
小波包阈值消噪有两个关键点：1、如何估计阈值；2 如何利用阈值量化小波包系数。
27
熵的确定
熵：用来确定最优树的标准，熵值越小，对应的小波包基越好。
1）香农熵：约定0log(0)=0，则香农熵定义为： Es si2 logsi2

小波变换简介PPT课件

[H,V,D] = detcoef2 ('all',C,S,N) returns the horizontal H, vertical V, and diagonal D detail coefficients at level N.
47
X = waverec2(C,S,'wname')
reconstructs the matrix X based on the multi-level wavelet decomposition structure [C,S]
从小波和正弦波的形状可以看出，变化剧烈的信号，用不规则的小波进行分析比用平滑的正弦波更好，即用小波更能描述信号的局部特征。
18
连续小波基函数
将小波母函数进行伸缩和平移后得到函数
a,b(t)a1 2(t ab),a0,bR
称该函数为依赖于参数a,τ的小波基函数。a 为尺度因子，b为位移因子。
39
小波重构
重构概念
把分解的系数还原成原始信号的过程叫做小波重构 (wavelet reconstruction)或合成(synthesis)，数学上叫做逆离散小波变换(inverse discrete wavelet transform， IDWT)
两个过程
在使用滤波器做小波变换时包含滤波和降采样 (downsampling)两个过程，在小波重构时也包含升采样(upsampling)和滤波两个过程。
Wavevlet “dB1”二级分解
水平细节分量cH
近似分量cA 垂直细节分量cV 对角细节分量cD
[C,S] = wavedec2(X,N,'wname')
returns the wavelet decomposition of the matrix X at level N, using the wavelet named in string 'wname‘. Outputs are the decomposition vector C and the corresponding bookkeeping matrix S.

001第1讲小波分析与傅里叶变换201104

dt
从频率至时间（逆变换）

it F ( ) e d

短时傅立叶变换实现信号局部分析
WFT ( , )

f (t ) g * (t )e i 2t dt
小波分析的基本理论短时傅里叶变换(STFT )
1 傅里叶变换到小波分析
S ( , ) f (t ) g (t )e
令 Wb, t eit wt b，则短时FT为
Parseval 恒等式
1 ˆ ˆ ~ (Gb f ) f t Wb, t dt f ,Wb, f ,Wb, 2

ˆ 都是窗函数，其确定可以证明 Wb, 和 W b , 的矩形窗口为
窗函数的举例
Gaussian 函数
1
短时Fourier变换
ˆ 都是窗函数，若wt , w 则短时Fourier变换定义为
~ (Gb f )

f t eit wt bdt
短时Fourier变换也叫窗口Fourier变换短时FT是说明时频局部化分析思想的很好例子
实际中信号分析的要求：

信号高频部分对应时域中的快变成分，如陡峭的前沿、后沿、尖脉冲等，分析时对时域分辨率要求高，对频域分辨率要求低。信号低频成分对应时域中的慢变成分，分析对时域分辨率要求低，对频域分辨率要求高。
因此，短时Fourier变换不能敏感地反映信号的突变，不能很好地刻画信息。
信号时频分析的重要性：
时间和频率是描述信号的两个最重要的物理量。信号的时域和频域之间具有紧密的联系。

Fourier变换（FT）:

小波变换原理与应用ppt课件

3.小波变换的基本原理与性质
信号的时域表示和频域表示只适用于平稳信号，对于
非平稳信号而言，在时间域各种时间统计量会随着时间的变化而变化，失去统计意义；而在频率域，由于非平稳信号频谱结构随时间的变化而变化导致谱值失去意义
幅度 A |Y(f)|
信号 x(t)的时域波形 1
0.5
0
-0.5
2
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
1.小波的发展历史——工程到数学
小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的，通过物理的直观和信号处理的实际需要经验的建立了反演公式，当时未能得到数学家的认可。幸运的是，1986年著名数学家 Y.Meyer偶然构造出一个真正的小波基，并与S.Mallat 合作建立了构造小波基的同一方法枣多尺度分析之后，小波分析才开始蓬勃发展起来。
1.小波的发展历史——工程到数学
1909: Alfred Haar——发现了Haar小波 1980：Morlet——Morlet小波，并分别与20世纪70年代提
出了小波变换的概念，20世纪80年代开发出了连续小波变换CWT（ continuous wavelet transform ） 1986：Y.Meyer——提出了第一个正交小波Meyer小波 1988： Stephane Mallat——Mallat快速算法（塔式分解和重构算法）
Rx(t1,t2)ExE(t)x(t1)x ( tx2)f(x)dRxx()m,x t2 t1
Ex2(t)
非平稳信号不满足平稳性条件至少是宽平稳条件的信号

小波分析理论ppt课件

S(w,t ) f (t)g*(w t ) eiwt d t R
(1.12)
25
其中，“*”表示复共轭；g(t)为有紧支集的函数；f(t)为被分析的信号。在这个变换中，ejwt起着频限的作用，g(t)起着时限的作用。随着时间t的变化，g(t)所确定的“时间窗” 在t轴上移动，使f(t)“逐渐”进行分析。因此g(t)往往被称为
(1.4)
为序列{X(k)}的离散傅里叶逆变换(IDFT)。在式(1.4)中，n相当于对时间域的离散化，k相当于频
率域的离散化，且它们都是以N点为周期的。离散傅里叶变换序列{X(k)}是以2p为周期的，且具有共轭对称性。
9
若f(t)是实轴上以2p为周期的函数，即f(t)∈L2(0，2p) ，则f(t)可以表示成傅里叶级数的形式，即
(1.1)
F(w)的傅里叶逆变换定义为
f (t) 1 eiwt F (w)dw 2 π -
(1.2)
6
为了计算傅里叶变换，需要用数值积分，即取f(t)在R 上的离散点上的值来计算这个积分。在实际应用中，我们希望在计算机上实现信号的频谱分析及其他方面的处理工作，对信号的要求是：在时域和频域应是离散的，且都应是有限长的。下面给出离散傅里叶变换(Discrete Fourier Transform，DFT)的定义。
。将母函数y(t)经伸缩和平移后，就可以得到一个小波序
列。
对于连续的情况，小波序列为
y a,b (t)
2
其中，短时傅里叶变换和小波变换也是因传统的傅里叶变换不能够满足信号处理的要求而产生的。短时傅里叶变换分析的基本思想是：假定非平稳信号在分析窗函数g(t)的一个短时间间隔内是平稳(伪平稳)的，并移动分析窗函数，

详细版小波变换原理与应用复习课件.ppt

精选
如果我们有一个无限长的窗口，然后做傅里叶变换，会得到完美的频率分辨率，但是结果中不包含时间信息。更进一步为了获得信号的平稳性，我们需要一个宽度足够短的窗函数，窗口越短，时间分辨率越高，信号的稳定性越高，但是频率分辨率却越来越低。
窄窗=高时间分辨率，低频率分辨率宽窗=高频率分辨率，低时间分辨率
精选
2.4 塔式算法
(1) 信号在小波空间的展开为：
f t
fWj
f t, j,k t j,k t
jZ ,kZ
精选
2.2.1 连续小波变换
如果函数 x满足以下容许性条件：
2
C d
则称 x为一容许性小波，并定义如下的积分变
换：
W
f
a,b
a
1 2
f
x
x
b a
dx,
f
x
L2 R
以上积分变换为 f x以 x为母小波的积分连
续小波变换，a为尺度因子，表示与频率相关的伸缩，
b为时间平移因子。
精选
2.2.2离散小波变换
33
其中，va为构造函数Meyer的辅助函数，且有：
2 -1/2
2
1/
2
c
os
2
v
3 2
1
0
精选
2 3
2 4
3
3
4 3
（3）其他常用小波
① Daubechies(dbN)小波系 ② Biorthogonal(biorNr.Nd)小波系 ③ Symlets(symN)小波系 ④ Morlet(morl)小波 ⑤ Coiflet(CoifN)小波系
cos(2ft) j sin(2ft)
即信号是由一些不同频率的正弦项叠加起来的，如果信号中频率为f的分量幅度较大，那么这个分量就和正弦项重叠，他们的即就比较大，这表明信号有一个频率为f的主要分量。精选

傅里叶小波变换

小波变换的应用
信号处理
小波变换广泛应用于信号处理领域，如语音、图像、雷达、地震等信号的分析和处理。
故障诊断
在机械、电力、航空航天等领域，小波变换被用于监测设备的运行状态，通过分析设备的振动、声音等信号，实现故障的早期发现和诊断。
图像压缩
小波变换可以用于图像压缩，通过对图像进行多尺度分解，提取关键信息并进行压缩，从而实现高效的图像存储和传输。
傅里叶小波变换具有良好的局部化特性，能够更好地捕捉信号的突变和奇异性。
傅里叶小波变换的应用
傅里叶小波变换在信号处理、图像处理、语音识别等领域有着广泛的应用。
在图像处理中，傅里叶小波变换可以用于图像的压缩、去噪、增强和特征提取等任务。
ABCD
在信号处理中，傅里叶小波变换可以用于信号的滤波、去噪、压缩和特征提取等任务。
金融分析
在金融领域，小波变换被用于分析股票、期货等金融市场的数据，提取市场趋势和波动特征，为投资者提供决策支持。
03
傅里叶小波变换
傅里叶小波变换的定义
傅里叶小波变换是一种信号处理方法，通过将信号分解成不同频率和时间的小波分量，以便更好地分析信号的时频特性。
小波变换的基本思想是将信号分解成一系列的小波函数，这些小波函数具有不同的尺度（或频率）和位移（或时间），以便更好地适应信号的时频特性。
编码效率
傅里叶小波变换在压缩编码过程中能够保留信号的重要特征，同时实现较高的压缩比和较小的失真，具有较高的编码效率和较好的重建效果。
05
傅里叶小波变换与图像处理
图像的分解与重构
图像的分解
傅里叶小波变换可以将图像分解成不同频率和方向的小波分量，从而提取出图像在不同频率和方向上的特征。

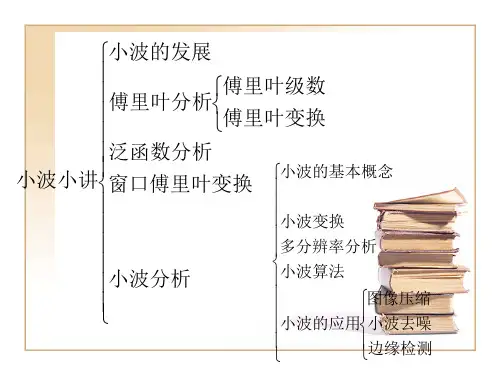
小波分析全节讲解精品PPT课件

x x, en en n 1
并且有Parseval等式，即
x 2
x, en 2
n 1
（5）双正交基
对于不满足规范正交条件的基底 {ek } 来说，如果存在另一组对偶基底{en} 使得
en , em
(m n)
0, m n 1, m n
对应的傅里叶展开式为
f f , en en n 1
X ()
x[n] e jn
n
x[n] 1 X ()e jnd
2
2.DFT
X[k]
N 1
j 2 nk
x[n]e N
N 1
x[n]WNnk , k
0,1,..., N
1
n0
n0
x[n]
1 N
N 1
j 2 nk
X [k]e N
n0
1 N
N 1
X [k]WNnk , n
F (t) F 2 f ()
2.位移时域位移将导致信号频谱增加一个附加相位，但是幅频特性不变，即
f (t a) F F ()e ja
3.卷积
卷积特性分为时域卷积和频域卷积，即
f1(t) * f2 (t) F F1()F2
1
2
F1() F2 ()
4.Parseval定理（内积定理）
2.基底及展开
（1）由函数序列张成的空间
设 {ek (t)}为函数序列，令集合 X 为
X
ak
ek
(t),
t,
ak
R,
k
Z
k
即 X 为函数序列{ek (t)} 的所有可能的
线性组合构成的集合，则称 X 为
序列 {ek (t)}张成的线性空间，简记为

《傅里叶变换》课件

特点
小波变换具有多尺度分析的特点，能够同时获得信号在时间和频率域的信息，并且在时频域具有很好的局部化能力。
应用
在信号处理、图像处理、语音识别等领域广泛应用。
周期性和共轭对称性
总结词
周期性和共轭对称性是傅里叶变换的重要性质。
详细描述
由于傅里叶变换将时间域的函数映射到频率域，因此频谱具有周期性，即F(ω) = F(ω+2πn)，其中n为整数。此外，频谱还具有共轭对称性，即F*(ω) = F(-ω)，这意味着频谱在频率轴上关于原点对称。这些性质在信号处理、图像处理等领域有着广泛的应用。
线性性质
如果a和b是常数，f(t)和g(t)是可傅里叶变换的函数，那么 a*f(t)+b*g(t)也是可傅里叶变换的，并且其频域表示为 a*F(ω)+b*G(ω)。
时移性质
如果f(t)是可傅里叶变换的，那么f(t+a)也是可傅里叶变换的，并且其频域表示为F(ω)e^(iωa)。
频移性质
如果f(t)是可傅里叶变换的，那么f(t)e^(iω0t)也是可傅里叶变换的，并且其频域表示为F(ω-ω0)。
04
傅里叶逆变换
傅里叶逆变换的定义
01
傅里叶逆变换是将频域函数转换为时域函数的过程。
02
它与傅里叶变换是可逆的，即给定一个频域函数，通过傅里叶逆变换可以恢复原始的时域函数。
03
傅里叶逆变换的公式为：f(t) = ∫F(ω)e^(iωt)dω，其中f(t)是时域函数，F(ω)是频域函数。
傅里叶逆变换的性质
在图像处理中的应用
图像频域滤波
通过傅里叶变换将图像从空间域转换到频域，可以在频域中对图像进行滤波处理，如去除噪声、

傅里叶变换跟小波变换

傅里叶变换跟小波变换一、傅里叶变换和小波变换傅里叶变换和小波变换是常见的数学工具，用于分析数据的频率分布的特征。

它们是经典的数学工具，可以用来处理信号和图像处理，以及其他复杂的技术和科学问题。

1. 傅里叶变换傅里叶变换是一种把连续的时域信号变换为频率域信号的数学工具，用于分析信号的复杂性和节律。

它的基本思想是，信号可以分解为若干完全正交的正弦波，每一个正弦波代表一个不同的频率，然后进行叠加。

傅里叶变换的优点：(1) 分析复杂信号。

傅里叶变换可以用来对较复杂的信号进行分析，从而找出它们中包含的基本信号成分，进而提取出与其有关联的特征。

(2) 分析信号的频率分布。

傅里叶变换可以用来分析信号的频率分布，从而找出其中的不同频率信号，进而分析不同频率信号对人类感知的影响。

然而，傅里叶变换也有一些缺点：(1) 计算复杂。

傅里叶变换的计算较为复杂，需要计算多个正弦波的叠加，这需要大量的计算资源。

(2) 无法处理极快的信号变化。

由于傅里叶变换是基于完全正交的正弦波估计的，因此对于极快的信号变化，无法很好地模拟，甚至可能导致频率和时域分析的偏差。

2.小波变换小波变换是一种把连续的时域信号变换为频率域信号的数学工具，与傅里叶变换不同，它使用小波函数作为基本函数，在处理极快的信号变化时，具有更强的稳定性和准确性。

小波变换的优点：(1) 模拟极快的信号变化。

由于小波变换的基本函数是小波函数，在处理极快的信号变化时，具有更强的稳定性和准确性。

(2) 实时处理非常复杂的信号。

小波变换可以对非常复杂的信号进行实时处理，而不需要太多的计算资源，因此可以有效地提高处理效率。

然而，小波变换也有一些缺点：(1) 计算量大。

小波变换的精确度比傅里叶变换高，但是它的计算量也比傅里叶变换大得多，比较耗费计算资源。

(2) 无法处理非常复杂的信号。

尽管小波变换具有很强的稳定性，但是对于非常复杂的信号，它仍然无法很好地处理，因此，在处理复杂信号时，仍然需要考虑其他技术的应用。

《傅里叶变换详解》课件

单击添加标题
原理：利用信号的稀疏性，通过测量矩阵将高维信号投影到低维空间，再利用优化算法重构出原始信号。
单击添加标题
应用：在图像处理、通信、雷达、医学成像等领域有广泛应用，能够实现高分辨率和高帧率成像，降低数据采集成本和存储空间。
单击添加标题
展望：随着压缩感知技术的不断发展，未来有望在人工智能、物联网、无人驾驶等领域发挥重要作用，为信号处理领域带来更多创新和突破。
应用：傅里叶逆变换在信号处理、图像处理等领域有着广泛的应用
逆变换的应用场景
信号处理：用于信号的滤波、去噪、压缩等图像处理：用于图像的增强、去噪、边缘检测等音频处理：用于音频的滤波、去噪、压缩等通信系统：用于信号的调制、解调、编码、解码等
06
傅里叶变换的计算机实现
离散傅里叶变换（DFT）
傅里叶变换的分类
连续傅里叶变换：适用于连续信号，将信号分解为不同频率的正弦波
离散傅里叶变换：适用于离散信号，将信号分解为不同频率的正弦波
快速傅里叶变换：适用于快速计算傅里叶变换，通过FFT算法实现短时傅里叶变换：适用于分析非平稳信号，将信号分解为不同频率的正弦波，同时考虑时间因素
03
傅里叶变换的性质
04
傅里叶变换的应用
在信号处理中的应用
滤波器设计：设计滤波器以消除或增强特定频率的信号
信号分解：将信号分解为不同频率的谐波
信号压缩：通过傅里叶变换进行信号压缩，减少数据量
信号分析：分析信号的频率成分，了解信号的特性和变
化规律
在图像处理中的应用
傅里叶变换可以用于图像的平滑处理，去除噪声傅里叶变换可以用于图像的锐化处理，增强图像的细节傅里叶变换可以用于图像的频域滤波，去除图像中的特定频率成分傅里叶变换可以用于图像的压缩和编码，减少图像的数据量

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

精品jing
傅里叶变换和小波变换简介
傅里叶变换
• 1807年傅立叶提出“ 任何周期信号都可用正弦函数级数表示”
• 1829年狄里赫利第一个给出收敛条件
• 拉格朗日反对发表
• 1822年傅立叶首次发表在“热的分析理论”
• 一书中
傅立叶，1768年生于法国
2
傅氏变换简介
傅立叶变换历史： 1822年，法国数学家傅里叶(J.Fourier,1768-1830)
4
《热的分析理论》
书中处理了各种边界条件下的热传导问题，以系统地运用三角级数和三角积分而著称，他的学生以后把它们称为傅里叶级数和傅里叶积分，这个名称一直沿用至今。傅里叶在书中断言：“任意”函数（实际上要满足一定的条件,例如分段单调）都可以展开成三角级数,他列举大量函数并运用图形来说明函数的这种级数表示的普遍性，但是没有给出明确的条件和完整的证明。
在研究热传导理论时发表了“热的分析理论”，提出并证明了将周期函数展开为正弦级数的原理，奠定了傅里叶级数的理论基础。泊松(Poisson)、高斯(Guass)等人把这一成果应用到电学中去，得到广泛应用。 19世纪末，人们制造出用于工程实际的电容器。进入20世纪以后，谐振电路、滤波器、正弦振荡器等一系列具体问题的解决为正弦函数与傅里叶分析的进一步应用开辟了广阔的前景。在通信与控制系统的理论研究和工程实际应用中，傅里叶变换法具有很多的优点。 “FFT”快速傅里叶变换为傅里叶分析法赋予了新的生命力。
幸运的是，早在七十年代，A.Calderon表示定理的发现、Hardy空间的原子分解和无条件基的深入研究为小波变换的诞生做了理论上的准备，而且J.O.Stromberg还构造了历史上非常类似于现在的小波基；1986年著名数学家Y.Meyer偶然构造出一个真正的小波基，并与S.Mallat合作建立了构造小波基的同意方法枣多尺度分析之后，小波分析才开始蓬勃发展起来，其中比利时女数学家 I.Daubechies撰写的《小波十讲（Ten Lectures on Wavelets）》对小波的普及起了重要的推动作用。
傅里叶的创造性工作为偏微分方程的边值问题提供了基本的求解方法-傅里叶级数法,从而极大地推动了微分方程理论的发展，特别是数学物理等应用数学的发展；其次，傅里叶级数拓广了函数概念，从而极大地推动了函数论的研究，其影响还扩及纯粹数学的其他领域。
傅里叶深信数学是解决实际问题的最卓越的工具，并且认为“对自然界的深刻研究是数学最富饶的源泉。” 这一见解已成为数学史上强调通过实际应用发展数学的
为了使他的研究成果能让法兰西研究院接受并发表,在经过了几次其他的尝试以后,傅里
叶才把他的成果以另一种方式出现在"热的分析理论"这本书中。这本书出版于1822
年,也即比他首次在法兰西研究院宣读他的研究成果时晚十五年。这本书已成为数学史上一部经典性的文献，其中基本上包括了他的数学思想和数学成就。
作为一名出色的数学家，傅立叶更清楚两点之间线段最短，但特殊情况下，也许曲线更有生命力，他的曲线不仅解决了个人问题更是解决了数学应用上的大问题。
但是在实际应用中的绝大多数信号是非稳定的，而特别适用于非稳定信号的工具就是小波分析。
小波(Wavelet)这一术语，顾名思义，“小波”就是小区域、长度有限、均值为0的波形。所谓“小”是指它具有衰减性；而称之为“波” 则是指它的波动性，其振幅正负相间的震荡形式。与Fourier变换相比，小波变换是时间(空间)频率的局部化分析，它通过伸缩平移运算对信号(函数) 逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。
一种代表性的观点。
5
一、三角函数的傅里叶级数:
f1(t)a0 (anco n1 stbnsin n1t) n 1
直流
基波分量
谐波分量
分量
n =1
n>1
ቤተ መጻሕፍቲ ባይዱ
1
2 T1
n1
6
求上式中的系数
∫ 直流分量
a0=
1 T1
t0 T1 f t .dt
t0
余弦分量
系数
anT21
t0T1 t0
f(t)c. ons1t.dt
在1759年拉格朗日(grange)表示：
不可能用三角级数来表示一个具有间断点的函数,因此三角级数的应用非常有限。
傅里叶很早就开始并一生坚持不渝地从事热学研究，1807年他在向法国科学院呈交一篇关于热传导问题的论文中宣布了任一函数都能够展成三角函数的无穷级数。
这篇论文经 J.-L.拉格朗日, P.-S.拉普拉斯, A.-M.勒让德等著名数学家审查，由于文中初始温度展开为三角级数的提法与拉格朗日关于三角级数的观点相矛盾，而遭拒绝。由于拉格朗日的强烈反对,傅里叶的论文从未公开露面过。
9
小波分析 (Wavelet)
小波变换历史：小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的，通过物理
的直观和信号处理的实际需要经验的建立了反演公式，当时未能得到数学家的认可。正如
1807年法国的热学工程师J.B.J.Fourier提出任一函数都能展开成三角函数的无穷级数的创新概念未能得到著名数学家 grange，place以及A.M.Legendre的认可一样。
傅立叶变换在物理的数据处理中占据着举足轻重的地位，在后面将展示我们物理学院与之相关的实验。
8
小波分析与傅立叶变换
从数学地角度来看，信号与图象处理可以统一看作是信号处理(图象可以看作是二维信号)，在小波分析地许多分析的许多应用中，都可以归结为信号处理问题。现在，对于其性质随时间是稳定不变的信号，处理的理想工具仍然是傅立叶分析。
正弦分量
系数
bn
2 T1
t0T1 t0
f(t)s. inn1t.dt
7
傅立叶变换应用
傅里叶变换应用：傅里叶变换在物理学、声学、光学、结构动力学；数论、组
合数学、概率论、统计学、信号处理、密码学、通讯、海洋学等领域都有着广泛的应用。例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值分量和频率分量。