C语言输入两个正整数m和n求其最大公约数和最小公倍数

输入两个正整数m和n,求其最大公约数和最小公倍
数
求m和n的最大公约数和最小公倍数：最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

求两个正整数m和n的最大公约数可用欧几里德算法（辗转相除法）。

求两个正整数m和n的最小公倍数=两个数的乘积÷两个数的最大公约数。

用欧几里德算法（辗转相除法）求两个数的最大公约数的步骤如下：
先用小的一个数除大的一个数，得第一个余数；
再用第一个余数除小的一个数，得第二个余数；
又用第二个余数除第一个余数，得第三个余数；
这样逐次用后一个数去除前一个余数，直到余数是0为止。

那么，最后一个除数就是所求的最大公约数（如果最后的除数是1，那么原来的两个数是互质数）。

两个正整数的最小公倍数=两个数的乘积÷两个数的最大公约数。

由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。

这就是说，求两个数的最小公倍数，可以先求出两个数的最大公约数，再用这两个数的最大公约数去除这两个数的积，所得的商就是两个数的最小公倍数。

输入两个正整数,m和n,求其最大公约数和最小公倍数。

1. 输入两个正整数，m和n，求其最大公约数和最小公倍数。

2. 输入一行字符，分别统计出其中字母、空格、数字和其他字符的个数。

3. 输入一个正整数求出它是几位数;输出原数和位数。

4. 输入一个正整数，输出原数并逆序打印出各位数字。

5. 从键盘上输入若干学生的一门课成绩，统计并输出最高成绩和最低成绩及相应的序号，当输入负数时结束输入。

6. 从键盘上输入若干学生的一门课成绩，计算出平均分，当输入负数时结束输入。

将结果输出。

7. 求1!+2!+3!+……+20!，将结果输出。

8. 打印以下图案: ****************9. 打印以下图案:**********10. 求下列试子的值:1-1/2+1/3-1/4+……+1/99-1/100，将结果输出。

11. 打印出100,999之间的所有水仙花数。

12. 求S(Sn)=a+aa+aaa+…+aa…a之值，n,a由键盘输入。

n13. 打印以下图案:****************************14.打印以下图案:112112321123432115. 打印以下图案:123432112321121116.编写一个统计学生成绩程序，完成以下功能:输入4个学生的2门课成绩;求出全班的总平均分，将结果输出。

17. 打印以下图案:*************************18.给出年、月、日，计算该日是该年的第几天。

19.求一个3*3的整型矩阵对角线元素之和。

将原矩阵和求出的和输出。

20.求一个4*3的矩阵各行元素的平均值;将原矩阵和求出的平均值全部输出。

21.求一个3*4的矩阵各列元素的平均值;将原矩阵和求出的平均值全部输出。

22.求一个3*5的矩阵各列元素的最大值，将原矩阵和求出的最大值全部输出。

23.求一个4*3的矩阵各行元素的最大值，将原矩阵和求出的最大值全部输出。

24.求一个M*N的矩阵中元素的最大值，将原矩阵和求出的最大值全部输出。

1、用下面的scanf函数输入数据，使a=10, b=20, c1='A', c2='a', x=1.5, y=-3.75, z=67.8，请问在键盘上如何输入数据？scanf("%5d%5d%c%c%f%f%*f,%f", &a,&b,&c1,&c2,&x,&y,&z);2、设圆半径r=1.5，圆柱高h=3，求圆周长、圆面积、圆球表面积、圆球体积、圆柱体积。

用scanf函数输入数据，输出计算结果，输出时要求有文字说明，取小数点后2位数字第三次作业1、有3个整数a,b,c，由键盘输入，输出其中最大的数。

2、有一个函数：x x<1y= 2x-1 1<=x<103x-11 x>=10写一段程序，输入x，输出y的值。

3、给出一百分制成绩，要求输出成绩等级A、B、C、D、E。

90分以上为A，80－89分为B，70－79为C，60－69为D，60分以下为E。

4、给一个不多于5位的正整数，输出这个数是几位数。

第四次作业1、给一个不多于5位的正整数，要求：a.求出它是几位数；+b.分别输出每一位数字；c.按逆序输出各位数字，例如：原数为321，应输出123。

2、教材P112页第5.8题（if语句解法创建一个独立文件，switch语句解法创建一个独立文件第五次作业1、输入两个正整数m和n，求其最大公约数和最小公倍数。

（经典题）2、输入一行字符，分别统计出其中英文字母、空格、数字和其他字符的个数，并输出。

3、求s=a+aa+aaa+aaaa+....+(a...a)之值，其中a是一个数字，n表示a的位数。

1、输入两个字符串，使用指针p将两个字符串按次序复制到数组c中。

例：输入“zhe"和"jiang"，将"zhejiang"保存在数组c中。

c语言求最大公约数和最小公倍数函数调用
以下是一个简单的 C 语言程序，使用函数调用求两个数的最大公约数和最小公倍数：
```c
include <>
// 定义求最大公约数的函数
int gcd(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
// 定义求最小公倍数的函数
int lcm(int a, int b) {
return a b / gcd(a, b);
}
int main() {
int a, b;
printf("请输入两个整数：");
scanf("%d %d", &a, &b);
printf("最大公约数为：%d\n", gcd(a, b));
printf("最小公倍数为：%d\n", lcm(a, b));
return 0;
}
```
在这个程序中，我们首先定义了两个函数 `gcd` 和 `lcm`，分别用于求两个数的最大公约数和最小公倍数。

在 `gcd` 函数中，我们使用递归的方式实现了欧几里得算法，而在 `lcm` 函数中，我们使用了公式 `a b / gcd(a, b)` 来计算最小公倍数。

在 `main` 函数中，我们通过调用这两个函数来计算并输出最大公约数和最小公倍数。

输入两个正整数m和n,求其最大公约数和最小公倍数最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

求两个正整数m和n的最大公约数可用欧几里德算法（辗转相除法）。

求两个正整数m和n的最小公倍数=两个数的乘积÷两个数的最大公约数。

用欧几里德算法（辗转相除法）求两个数的最大公约数的步骤如下：先用小的一个数除大的一个数，得第一个余数；再用第一个余数除小的一个数，得第二个余数；又用第二个余数除第一个余数，得第三个余数；这样逐次用后一个数去除前一个余数，直到余数是0为止。

那么，最后一个除数就是所求的最大公约数（如果最后的除数是1，那么原来的两个数是互质数）。

两个正整数的最小公倍数=两个数的乘积÷两个数的最大公约数。

由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。

这就是说，求两个数的最小公倍数，可以先求出两个数的最大公约数，再用这两个数的最大公约数去除这两个数的积，所得的商就是两个数的最小公倍数。

main(){int p,r,n,m,temp;printf("Please enter 2 numbers n,m:");scanf("%d,%d",&n,&m);//输入两个正整数.if(n\u003cm)//把大数放在n中,把小数放在m中. {temp=n;n=m;m=temp;}p=n*m;//P是原来两个数n,m的乘积.while(m!=0)//求两个数n,m的最大公约数.{r=n%m;n=m;m=r;}printf("Its MAXGongYueShu:%d\\n",n);//打印最大公约数. printf("Its MINGongBeiShu:%d\\n",p/n);打印最小公倍数.。

输入两个正整数m和n,求其最大公约数和最小公倍数+欧几里得算法
欧几里得算法，又称辗转相除法，是求最大公约数的一种常用算法。

假设有两个正整数m和n，且m>n，不断用n去除m，直到余数为0，此时n的值即为m和n的最大公约数。

最小公倍数是指在自然数中，同时整除两个数的最小正整数，可以通过最大公约数求得：
两个数的最小公倍数 = 两数积÷ 最大公约数。

下面是Python代码实现：
```
m = int(input("请输入第一个正整数m："))
n = int(input("请输入第二个正整数n："))
# 求最大公约数
while (n != 0):
r = m % n
m = n
n = r
gcd = m
# 求最小公倍数
lcm = int((m * n) / gcd)
print("最大公约数是：", gcd)
print("最小公倍数是：", lcm)
```
输入：
```
请输入第一个正整数m：12
请输入第二个正整数n：18 ```
输出：
```
最大公约数是： 6
最小公倍数是： 36
```。

习题2参考答案一、基础题1．若二维数组a有m列，则在a[i][j]前的元素个数为：A）j*m+i B）i*m+jC）i*m+j-1 D）i*m+j+1B2．在C语言中（以16位PC机为例），五种基本数据类型存储空间长度的排列顺序是：A) char<int<long int<=float<doubleB) char=int<long int<=float<doubleC) char<int<long int=float=doubleD) char=int=long int<=float<doubleA3．在C语言的变量类型说明中，int，char，float等类型的长度是：A) 固定的B) 由用户自己定义的C) 任意的D) 与机器字长有关的D4. 设变量a是整型，f是实型，i是双精度型，则表达式10+'a'+i*f的数据类型是：A) int型B)float型C) double型D)不确定C5．C语言中的变量名只能由字母，数字和下划线三种字符组成，且第一个字符：A) 必须为字母B) 必须为下划线C) 必须为字母或下划线D) 可以是字母,数字或下划线中的任意一种C6．设a=1，b=2，c=3，d=4，则表达式a<b?a：c<d?a：d的值是：A) 4 B) 3 C) 2 D) 1D7．以下程序的输出结果是：main(){ int a=12, b=12;printf("%d,%d\n",--a,++b);}A) 10,10 B) 12,12 C) 11,10 D) 11,13D8．若有代数式(3ae)/(bc)，则下面不正确的C语言表达式是：A) a/b/c*e*3 B) 3*a*e/b/c C) 3*a*e/b*c D) a*e/c/b*3C9．已知x=43，ch='A'，y=0，则表达式(x>=y&&ch<'B'&&!y)的值是：A) 0 B) 语法错C) 1 D) "假"C10．下面程序的输出结果是：main(){ int a=-1, b=4, k;k=(a++<=0)&&(!(b--<=0));printf("%d,%d,%d\n",k,a,b);}A) 1,1,2 B) 1,0,3 C) 0,1,2 D) 0,0,3B11．已知字母A的ASCII码为十进制的65，下面程序的输出是：main(){ char ch1,ch2;ch1='A'+'5'-'3';ch2='A'+'6'-'3';printf("%d,%c\n",ch1,ch2);}A) 67,D B) B,C C) C,D D) 不确定的值A12．下面程序的输出的是main(){ int x=10,y=3;printf("%d\n",y=x/y);}A) 0 B) 1 C) 3 D) 不确定的值C二、程序设计题1．从键盘上输入一个小写字母，编程输出其对应的大写字母以及它们的十进制ASCII码。

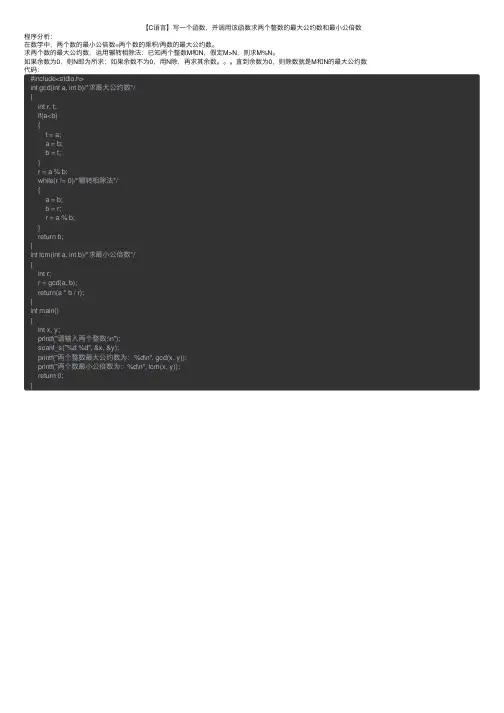
【C语⾔】写⼀个函数，并调⽤该函数求两个整数的最⼤公约数和最⼩公倍数程序分析：
在数学中，两个数的最⼩公倍数=两个数的乘积/两数的最⼤公约数。

求两个数的最⼤公约数，运⽤辗转相除法：已知两个整数M和N，假定M>N，则求M%N。

如果余数为0，则N即为所求；如果余数不为0，⽤N除，再求其余数。

直到余数为0，则除数就是M和N的最⼤公约数代码：
#include<stdio.h>
int gcd(int a, int b)/*求最⼤公约数*/
{
int r, t;
if(a<b)
{
t = a;
a = b;
b = t;
}
r = a % b;
while(r != 0)/*辗转相除法*/
{
a = b;
b = r;
r = a % b;
}
return b;
}
int lcm(int a, int b)/*求最⼩公倍数*/
{
int r;
r = gcd(a, b);
return(a * b / r);
}
int main()
{
int x, y;
printf("请输⼊两个整数:\n");
scanf_s("%d %d", &x, &y);
printf("两个整数最⼤公约数为：%d\n", gcd(x, y));
printf("两个数最⼩公倍数为：%d\n", lcm(x, y));
return 0;
}。