电路分析中互易双口和互易定理

单片机原理互易定理
单片机原理中的互易定理是指在电路中，两个端口之间的电压和电流可以互相替换，即电压可以视作电流，电流也可以视作电压。

这个定理在单片机设计中起着非常重要的作用，可以帮助工程师更好地理解和分析电路。

在单片机设计中，我们经常需要对电路进行建模和分析，以确保电路能够正常工作。

而互易定理提供了一个简单而有效的方法来简化电路的分析过程。

通过将电压源替换为电流源，或者将电流源替换为电压源，我们可以更容易地对电路进行分析和计算。

以电压源和电流源的互相替换为例，当我们需要计算电路中的电流时，可以将电压源替换为等效的电流源，然后根据电流源的特性来计算电路中的电流。

同样地，当我们需要计算电路中的电压时，可以将电流源替换为等效的电压源，然后根据电压源的特性来计算电路中的电压。

通过互易定理，我们可以更灵活地应用不同的电路分析方法，从而更好地理解和优化单片机电路的设计。

在实际的单片机设计中，工程师经常会根据具体的需求和情况选择合适的电压源或电流源来进行分析，以确保电路能够正常工作并满足设计要求。

除了在电路分析中的应用，互易定理还可以帮助工程师更好地理解电路中的能量转换和传递过程。

通过将电压和电流互相替换，我们
可以更清晰地看到电路中能量的流动路径，从而更好地优化电路设计，提高电路的效率和性能。

总的来说，单片机原理中的互易定理是一个非常重要且实用的概念，可以帮助工程师更好地理解和分析电路，在单片机设计中发挥重要作用。

通过灵活运用互易定理，工程师可以更好地优化电路设计，提高电路的性能和可靠性，从而实现更好的单片机应用。

实验九双口网络参数的测定一、实验目的1. 加深理解双口网络的基本理论。

2. 掌握直流双口网络传输参数和混合参数的测量方法。

3. 验证互易双口的互易条件和对称互易双口的对称条件。

二、原理说明1. 双口网络的基本理论根据需要将其拆分为两个单口网络和一个双口网络。

对双口网络来说它的每一个口端都只有一个电流变量和一个电压变量。

在电路参数未知的情况下，我们可以通过实验测定方法，求取一个极其简单的等值双口电路来替代原双口网络，此即“墨盒理论”的基本内容。

2.双口网络参数方程9-1所示的无源双口网络，四个电压电流变量之间的关系，可以用多种形式的参数方程来表示。

本实验只研究传输参数方程和混合参数方程。

①传输(T)参数方程以输出口变量U2、I2为自变量，输入口变量U1、I1为应变量，采用关联参考方向，可以列出传输型参数方程：U1＝AU2-BI2I1＝CU2-DI2式中A、B、C、D为双口网络的T参数。

②混合(H)参数方程以入口电流I1和出口电压U2为自变量，入口电压U1和出口电流I2为应变量的混合型参数方程为：U1=H11I1+H12U2I2=H21I1+H22U2式中H11、H12、H21和H22为双口网络的H参数。

3.双口网络参数的测试(1)同时测量法传输方程中四个T 参数0I 221==U U A 0 U I 221==U B 0I I 221==U C 0 U I I 221==D 故可在输出端(I 2=0)或短路(U 2=0)的情况下，在输入口加上电压，在两个端口同时测量其电压、电流值，即可求出四个T 参数，这种方法称之为同时测量法。

(2)混合测量法混合型参数方程中的四个H 参数0 U I U H 21111==0I U U H 12112== 0 U I I H 21221==I U I H 12222==因此四个H 参数可以先在输入口加上电压，将输出端短路(U 2=0)，测出U 1、I 1和I 2；再在输出口加电压，将输入端开路(I 1=0)，测出U 2、I 2和U 1，再计算得出，这种方法称之为混合测量法。

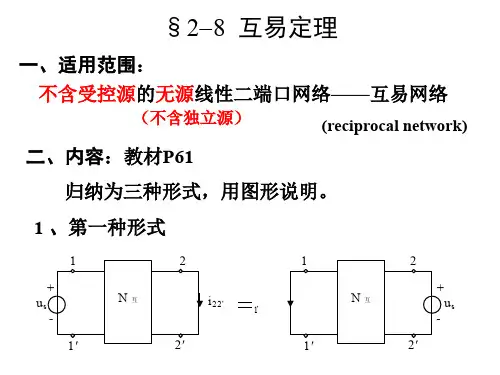
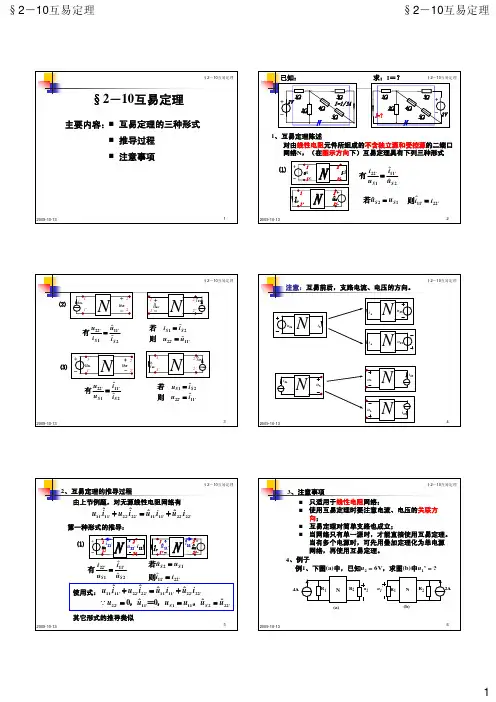
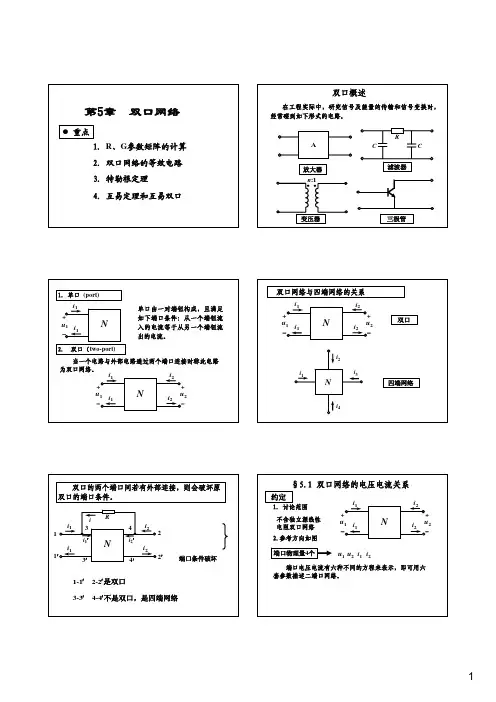
3.4 互易定理1. 互易定理的内容互易定理：对于一个线性电阻网络而言，如果只有一个激励和一个响应，那么当激励与响应互换位置后，激励与响应的比值保持不变。

这里的激励指电压源或电流源，响应指电压或电流。

互易定理的示意图如图1所示。

u 1i 2u 2i 1212u u i i =图1 互易定理示意图根据互易定理和图1，1212(u u i i =激励）（互换位置后的激励）（响应）（互换位置后的响应） （1）由式（1）可以看出，如果激励（电压源电压）相同，则互换位置后的响应（电流）也相同。

这是互易定理的一种特殊情况。

由互易定理的内容可以看出，互易定理是很难自己想象出来的。

由于互易定理很难想象，要证明互易定理自然也是一件非常困难的事情。

不过，为了令人信服，下面我们来证明一下互易定理。

2. 互易定理的证明在证明互易定理之前，需要先证明两个定理和一个定理推论，即特勒根定理1、特勒根定理2和特勒根定理2推论。

特勒根定理1的内容是，任意一个电路，如果每一条支路的电流参考方向都是从电压参考方向的正极流入，则所有支路的电压电流乘积加起来一定等于零。

电压电流乘积就是功率，可见特勒根定理1的物理含义就是任何一个电路总的功率为零，也就是发出功率等于吸收功率，即功率守恒。

下面我们来证明特勒根定理1。

假设任意一个电路总计有b 条支路，n 个结点，第p 、q 个结点之间的电压记为pq u ，电流记为pq i ，则1111111111111()02222bn n n n n n nnk kpq pq p q pq p pq q pq k p q p q p q q p u i u i u u i u i u i ===========−=−=∑∑∑∑∑∑∑∑∑ （2）由式（2）即证明了特勒根定理1。

式（2）乍一看很难理解，下面对其中的细节进行解释。

式（2）中第一个等号是将支路电压电流乘积之和转化为结点与结点之间电压与电流乘积之和。

电路的互易定理
什幺是互易定理
在只含一个电压源（或电流源），不含受控源的线性电阻电路中，电压源（或电流源）与电流表（电压表）互换位置，电流表（电压表）读数不变。

这种性质称为互易定理。

在电磁学上，互易定理为洛仑兹互易定理（Lorentz Reciprocity Theorem），由卡森（J.R. Carson）导出而被称为卡森形式的互易定理。

互易定理即论述某些网络具有的互易性质的定理。

互易性质表现为：将网络的输入和特定输出互换位置后，输出不因这种换位而有所改变。

具有互易性质的网络称为互易网络。

互易性不仅一些电网络有，某些声学系统、力学系统等也有。

互易定理是一个较有普遍意义的定理。

互易定理的性质
从图中可以得出结论，图（a）的电压u2=R21/S与图（b）的电压
u1=R12/S相同。

也就是说，在互易网络中电流源与电压表互换位置，电压表读数不变。