固体物理习题答案PPT课件
- 格式：ppt
- 大小：585.00 KB
- 文档页数：43
下载文档原格式
合集下载
固体物理习题解答 ppt课件
设n为一个晶胞中的刚性原子球数，r表示刚性原子球半径， V表示晶胞体积，则致密度为
n 4r3
x 3 V
(1) 简单立方
a 任意一个原子球有6个最近邻，若原子 以刚性球堆积，则有 a 2r,V a3
晶胞内包含一个原子，所以有： (2) 体心立方
x
4 (a)3
32
a3
6
任意一个原子球有8个最近邻，若原子
Vc
ac 3 2
单位体积内原子数（即密度）为
1 Vc
六角密堆积每个晶胞包含6个原子，一个原子所占的体积为
Vs a
3 2
a
3
c
/
6
3 a2c 4
1
3
a2 8
2
a
4 3
2 a3 2
因为密度不变，所以
1 Vc
1 Vs
即：
ac3 / 2
2 a3 2
1
a ac / 2 6 0.377nm
r h3b3
)
(
r a1 h1
r a3 h3
)
r h1b1
r ga1 h1
h3
r b3
r ga3 h3
0
同理可证
v uuur Kh1h2h3 CB 0
v 所以晶面族（h1h2h3）与和倒格矢 Kh1h2h3 正交
v K h1h2 h3
2.6 试导出倒格矢的长度与晶面族面间距间的关系 2.8 试画出周期为的一维布喇菲格子的第一和第 二布里渊区。
第一章 习题
1.1 何谓布喇菲格子？试画出NaCl晶体的结点所构成的布喇 菲格子。
答：所谓布喇菲格子是指晶体由完全相同的原子组成， 原子与晶格的格点相重合，而且每个格点周围的情况都 一样。（Bravais格子） 氯化钠结构：面心立方Na+布氏格子和面心立方Cl-的 布氏格子套构而成的复式格子。
n 4r3
x 3 V
(1) 简单立方
a 任意一个原子球有6个最近邻，若原子 以刚性球堆积，则有 a 2r,V a3
晶胞内包含一个原子，所以有： (2) 体心立方
x
4 (a)3
32
a3
6
任意一个原子球有8个最近邻，若原子
Vc
ac 3 2
单位体积内原子数（即密度）为
1 Vc
六角密堆积每个晶胞包含6个原子，一个原子所占的体积为
Vs a
3 2
a
3
c
/
6
3 a2c 4
1
3
a2 8
2
a
4 3
2 a3 2
因为密度不变，所以
1 Vc
1 Vs
即：
ac3 / 2
2 a3 2
1
a ac / 2 6 0.377nm
r h3b3
)
(
r a1 h1
r a3 h3
)
r h1b1
r ga1 h1
h3
r b3
r ga3 h3
0
同理可证
v uuur Kh1h2h3 CB 0
v 所以晶面族（h1h2h3）与和倒格矢 Kh1h2h3 正交
v K h1h2 h3
2.6 试导出倒格矢的长度与晶面族面间距间的关系 2.8 试画出周期为的一维布喇菲格子的第一和第 二布里渊区。
第一章 习题
1.1 何谓布喇菲格子？试画出NaCl晶体的结点所构成的布喇 菲格子。
答：所谓布喇菲格子是指晶体由完全相同的原子组成， 原子与晶格的格点相重合，而且每个格点周围的情况都 一样。（Bravais格子） 氯化钠结构：面心立方Na+布氏格子和面心立方Cl-的 布氏格子套构而成的复式格子。
固体物理+胡安版+部分习题答案ppt课件
1.1 a
1
解：是由红色代表的碳原子构成的二维菱形格子与黑色代 表的碳原子构成的二维菱形格子沿正六边形边长方向相互移 动一个边长长度 a 套购而成的复式格子。
其二维点阵和其元胞基矢如图所示：
a2
a1
2
1.2
(a)
Rl l1i l2 j l3k (l1,l2 ,l3 0, 1, 2, 3,)
a1
2
ai
2
a2 aj
元胞体积
i jk
k
a1
a2
k
2 2
0
0 2 a2 2
0 a0
23
（110）面二维晶格倒格子基矢，
b1
b2
2 2
a2 k k a1
2 2
a2
aj k
cos a2 , a3
a2 a3 a2 a3
1 109027 3
cos a1, a3
a1 a3 a1 a3
1 109027
3
7
(b)
kj i
金刚石晶胞
1
3a (i j k ) 4
2
3a (i j k ) 4
1
i
h 2
3k 2
3l 2
i
3h 2
3k 2
l 2
i
3 2
h
k 2
3l 2
fj
1 ei (hk )
1
解：是由红色代表的碳原子构成的二维菱形格子与黑色代 表的碳原子构成的二维菱形格子沿正六边形边长方向相互移 动一个边长长度 a 套购而成的复式格子。
其二维点阵和其元胞基矢如图所示：
a2
a1
2
1.2
(a)
Rl l1i l2 j l3k (l1,l2 ,l3 0, 1, 2, 3,)
a1
2
ai
2
a2 aj
元胞体积
i jk
k
a1
a2
k
2 2
0
0 2 a2 2
0 a0
23
（110）面二维晶格倒格子基矢，
b1
b2
2 2
a2 k k a1
2 2
a2
aj k
cos a2 , a3
a2 a3 a2 a3
1 109027 3
cos a1, a3
a1 a3 a1 a3
1 109027
3
7
(b)
kj i
金刚石晶胞
1
3a (i j k ) 4
2
3a (i j k ) 4
1
i
h 2
3k 2
3l 2
i
3h 2
3k 2
l 2
i
3 2
h
k 2
3l 2
fj
1 ei (hk )
固体物理学习题解答(完整版)[1]
![固体物理学习题解答(完整版)[1]](https://img.taocdn.com/s1/m/b770b80b7cd184254b353568.png)
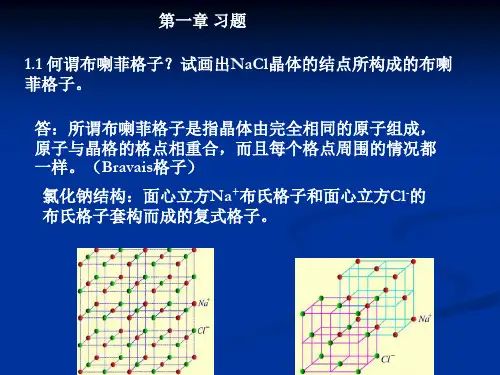
《固体物理学》部分习题参考解答第一章1.1 有许多金属即可形成体心立方结构，也可以形成面心立方结构。
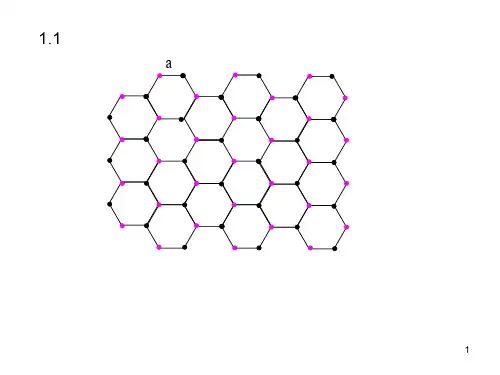
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略，并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离，试问R f /R b 等于多少？答：由题意已知，面心、体心立方结构同一棱边相邻原子的距离相等，都设为a ：对于面心立方，处于面心的原子与顶角原子的距离为：R f=2 a对于体心立方，处于体心的原子与顶角原子的距离为：R b=2a那么，R f R b31.2 晶面指数为（123）的晶面ABC 是离原点O 最近的晶面，OA 、OB 和OC 分别与基失a 1，a 2和a 3重合，除O 点外，OA ，OB 和OC 上是否有格点？若ABC 面的指数为（234），情况又如何？答：根据题意，由于OA 、OB 和OC 分别与基失a 1，a 2和a 3重合，那么 1.3 二维布拉维点阵只有5种，试列举并画图表示之。
答：二维布拉维点阵只有五种类型：正方、矩形、六角、有心矩形和斜方。
分别如图所示：1.4 在六方晶系中，晶面常用4个指数（hkil ）来表示，如图所示，前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1，a 2，a 3上的截距a 1/h ，a 2/k ，a 3/i ，第四个指数表示该晶面的六重轴c 上的截距c/l.证明：i=-（h+k ） 并将下列用（hkl ）表示的晶面改用（hkil ）表示：（001）(133)(110)(323)（100）（010）(213)答：证明设晶面族（hkil ）的晶面间距为d ，晶面法线方向的单位矢量为n °。
因为晶面族（hkil ）中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ，a 2/k ，a 3/i ，因此123oo o a n h da n kd a n id=== ……… (1) 正方 a=b a ^b=90° 六方 a=b a ^b=120° 矩形 a ≠b a ^b=90° 带心矩形 a=b a ^b=90° 平行四边形 a ≠b a ^b ≠90°由于a 3=–（a 1+ a 2）313()ooa n a a n =-+把（1）式的关系代入，即得()id hd kd =-+ ()i h k =-+根据上面的证明，可以转换晶面族为 （001）→（0001），(13)→(1323)，(110)→(1100)，(323)→(3213)，（100）→(1010)，（010）→(0110)，(213)→(2133)1.5 如将等体积的硬球堆成下列结构，求证球可能占据的最大面积与总体积之比为（1）简立方：6π（28（3）面心立方：6（4）六方密堆积：6（5）金刚石：16。
固体物理第一章习题
15
得到：
d 1 h 2 k l a 2 s h i n 2 2 b k 2 2 c 2 s l i n 2 2 a 2 c h s c i o n s 2 s i n 1 2 a h 2 2 c l 2 2 2 h l a c c o s b k 2 2
即：
1
1 h2 l2 2hlcos k22 dhkl sin2a2c2 ac b2
bc
•
ca
0
b*•c* 42 2
ca
•
ab
0
将以上诸式代入：
d 1 h 2 k l 4 1 2 h 2 a 2 k 2 b 2 l 2 c 2 2 h k a * • b * 2 k lb * • b * 2 h la * • c *
编辑版pppt
1
1
2p K h 1 h 2h 32p (h 1 b 1h 2 b 2h 3 b 3)
Kh1h2h3 与晶面族(h1h2h3)正交。
因此，若已知晶面族的密勒指数(hkl)，则原胞坐标 系中的面指数
(h1h2h3)1 p{(kl)(lh)(hk)} 其中p是(k+l)(l+h)(h+k)的公约数。
编辑版pppt
只有当 n(4 3h2 3kl)奇数时才出现衍射消光
编辑版pppt
23
（a）n为奇数时：若l是偶数，nl也是偶数 为保证n(4/3h+2/3k+l)=奇数成立， 须n(4/3h+2/3k)=奇数 由此，2n(2h+k)=3奇数=奇数。 由于h, k为整数，上式左端是偶数，右端为奇数，显
然不成立。
矛盾的产生是l为偶数的条件导致的，所以l不能为偶 数，只能为奇数。因而n(4/3h+2/3k)=偶数，即(2h+k)=3 整数/n=整数。
中科大固体物理课程作业答案说课.ppt
57
精心整理
58
精心整理
59
精心整理
60
精心整理
61
对非简并的半导体采用玻尔兹曼统计处理，在玻尔兹曼统计中E=3/2kBT
精心整理
62
晶格振动
精心整理
63
精心整理
64
精心整理
65
精心整理
66
精心整理
67
此题的计算说明了电子只有在极低温度下才会奉献晶格热容，在室温时电子对 热容的奉献可以忽略不计
精心整理
68
精心整理
69
精心整理
70
精心整理
71
精心整理
72
精心整理
73
精心整理
74
固体中的原子键合
精心整理
75
精心整理
76
精心整理
77
精心整理
78
精心整理
79
Madelung常数
精心整理
80
精心整理
81
精心整理
82
精心整理
83
精心整理
84
精心整理
85
精心整理
86
精心整理
42
= V 1 ( G c ) ( 1 + 1 + e x p ( - i2 ) + 3 e x p ( - i) )
精心整理
43
精心整理
44
精心整理
45
精心整理
46
精心整理
47
精心整理
48
精心整理
49
晶体中的电子运动
精心整理
50
对于能带宽度分别求出带顶和带底能量〔两种极值情况〕，即可获得能带的宽度 对于半经典模型，一维情况有：
固体物理习题4 ppt课件
的球壳内的状态数为 2V 4k 2dk ， 由此得到，费密球内
电子的总能量
E0
k kF
h2k 2 2m
2V
4k 2dk
式中 kF 是费密球半径。当V比较大时，波矢 k 在 k 空间的
分布非常密集，可以看作准连续，上式的求和可用积分代替，
于是
E0 2V
k12 m12
k22 m22
k32 m32
求能量E ~ E dE 之间的状态数。
解： 因为
E k
2 2
k12 m12
k
2 2
m22
k32 m32
能量为E的等能面的方程式可写为
k12
k
2 2
k32
1
2m1E 2m2 E 2m3 E
2
2
2
z
z
L
z
z
则从(3)(4)两式可得行波解
Ae i2 kx xky ykzz
波矢各分量分别为
kx
nx L
,ky
ny L
,kz
nz L
(7)
nx , n y , nz 取正负整数，电子的能量仍然表示为
E
h2k 2 2m
h2 2m
(k
2 x
k
2 y
(5)
(3).按照定义，电子的平均能量(T=0K)
1
E0 N
E
0 F
Ef
固体物理-第一章习题解答参考 ppt课件
绕对边中心的联线转180度，共3条；
绕对顶点联线转180度，共3条；
以上每个对称操作加上中心反演仍然为对称操作，共24个对称操作
ppt课件
4
1.2 面心立方晶格在晶胞基矢坐标系中，某一晶面族的密勒指为 (hkl)，求在
原胞基矢坐标系中，该晶面族的晶面指数。
晶胞基矢：a
ai ,
b
aj ,
c
ak
ab c
c
a1
a2
b
a3
a
与晶胞坐标系对应的倒格子基矢：
a
2
i ,b
2
j,
c
2
k
a
a
a
原胞基矢
a1
a 2
(
j
k)
a2
a 2
(i
k)
a1 a2 a3
a3
a 2
(i
熔点固定 --达到某温度时开始熔化，继续加热，在晶体没有完全熔化之前，温度不再
上升。
各向异性 -- 晶体的性质与方向有关 对称性 -- 晶体性质在某些特定方向上完全相同
非晶体 没有固定熔点、没有固定几何形状、各项同性、没有解理性
多晶体 各项同性、具有固定熔点、没有固定的几何形状、没有解理性
准晶体
ppt课件
准晶体 粒子有序排列介于晶体和非 晶体之间。但没有平移对称 性、只具有5重旋转对称性。
单晶体 粒子在整个固体中严格周期性排 列，具有严格的平移对称性、具 有8种基本点对称操作性。
多晶体 粒子在微米尺度内有序排 列形成晶粒，晶粒随机堆积
绕对顶点联线转180度，共3条；
以上每个对称操作加上中心反演仍然为对称操作，共24个对称操作
ppt课件
4
1.2 面心立方晶格在晶胞基矢坐标系中，某一晶面族的密勒指为 (hkl)，求在
原胞基矢坐标系中，该晶面族的晶面指数。
晶胞基矢：a
ai ,
b
aj ,
c
ak
ab c
c
a1
a2
b
a3
a
与晶胞坐标系对应的倒格子基矢：
a
2
i ,b
2
j,
c
2
k
a
a
a
原胞基矢
a1
a 2
(
j
k)
a2
a 2
(i
k)
a1 a2 a3
a3
a 2
(i
熔点固定 --达到某温度时开始熔化，继续加热，在晶体没有完全熔化之前，温度不再
上升。
各向异性 -- 晶体的性质与方向有关 对称性 -- 晶体性质在某些特定方向上完全相同
非晶体 没有固定熔点、没有固定几何形状、各项同性、没有解理性
多晶体 各项同性、具有固定熔点、没有固定的几何形状、没有解理性
准晶体
ppt课件
准晶体 粒子有序排列介于晶体和非 晶体之间。但没有平移对称 性、只具有5重旋转对称性。
单晶体 粒子在整个固体中严格周期性排 列，具有严格的平移对称性、具 有8种基本点对称操作性。
多晶体 粒子在微米尺度内有序排 列形成晶粒，晶粒随机堆积
固体物理习题解答-完整版
n
2.3
若一晶体的相互作用能可以表示为 u ( r ) = − 求 1 ）平衡间距 r 0
α
r
m
+
β
rn
3 ）体弹性模量 4 ）若取
2 ）结合能 W （单个原子的）
m = 2, n = 10, r0 = 0.3 nm, W = 4 eV ，计算 α , β 值。
解 1）晶体内能 U ( r ) =
N α β (− m + n ) 2 r r
⎛ ε 11 3ε 22 ⎜ + 4 4 0 ⎞ ⎜ ⎟ ⎜ 3ε 11 3ε 22 ε 23 ⎟ = ⎜ − + 4 4 ⎜ ε 33 ⎟ ⎠ ⎜ 3ε 23 − ⎜ 2 ⎝ − 3ε 11 3ε 22 + 4 4 3ε 11 ε 22 + 4 4 − − 3ε 23 ⎞ ⎟ 2 ⎟ ε ⎟ − 23 ⎟ 2 ⎟ ε 33 ⎟ ⎟ ⎠
h k l ( )2 + ( )2 + ( )2 a b c
说明面指数简单的晶面，其面密度较大，容易解理 证 简单正交系 a ⊥ b ⊥ c 倒格子基矢 b1 = 2π
a1 = ai , a2 = bj , a3 = ck b2 = 2π a3 × a1 a1 ⋅ a2 × a3 b3 = 2π a1 × a2 a1 ⋅ a2 × a3
⎛ ε 11 ε 12 ⎜ 假 设 六 角 晶 系 统 的 介 电 常 数 为 ε = ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
⎛ ε 11 ε 12 ⎜ ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
ε 13 ⎞ ⎟ ε 23 ⎟ 则 由 ε = AT ε Ax 得 ε 33 ⎟ ⎠
x
ε 13 ⎞ ⎛ ε 11 − ε 12 − ε 13 ⎞ 0 ⎞ ⎛ ε 11 0 ⎟ ⎟ ⎜ ⎟ ⎜ ε 23 ⎟ = ⎜ − ε 21 ε 22 ε 23 ⎟ 可见 ε = ⎜ 0 ε 22 ε 23 ⎟ 将上式代入 ε = AzT ε Az ⎜ ⎜0 ε ε 33 ⎟ ε 33 ⎟ ε 33 ⎟ 32 ⎠ ⎠ ⎝ ⎠ ⎝ − ε 31 ε 32
2.3
若一晶体的相互作用能可以表示为 u ( r ) = − 求 1 ）平衡间距 r 0
α
r
m
+
β
rn
3 ）体弹性模量 4 ）若取
2 ）结合能 W （单个原子的）
m = 2, n = 10, r0 = 0.3 nm, W = 4 eV ，计算 α , β 值。
解 1）晶体内能 U ( r ) =
N α β (− m + n ) 2 r r
⎛ ε 11 3ε 22 ⎜ + 4 4 0 ⎞ ⎜ ⎟ ⎜ 3ε 11 3ε 22 ε 23 ⎟ = ⎜ − + 4 4 ⎜ ε 33 ⎟ ⎠ ⎜ 3ε 23 − ⎜ 2 ⎝ − 3ε 11 3ε 22 + 4 4 3ε 11 ε 22 + 4 4 − − 3ε 23 ⎞ ⎟ 2 ⎟ ε ⎟ − 23 ⎟ 2 ⎟ ε 33 ⎟ ⎟ ⎠
h k l ( )2 + ( )2 + ( )2 a b c
说明面指数简单的晶面，其面密度较大，容易解理 证 简单正交系 a ⊥ b ⊥ c 倒格子基矢 b1 = 2π
a1 = ai , a2 = bj , a3 = ck b2 = 2π a3 × a1 a1 ⋅ a2 × a3 b3 = 2π a1 × a2 a1 ⋅ a2 × a3
⎛ ε 11 ε 12 ⎜ 假 设 六 角 晶 系 统 的 介 电 常 数 为 ε = ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
⎛ ε 11 ε 12 ⎜ ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
ε 13 ⎞ ⎟ ε 23 ⎟ 则 由 ε = AT ε Ax 得 ε 33 ⎟ ⎠
x
ε 13 ⎞ ⎛ ε 11 − ε 12 − ε 13 ⎞ 0 ⎞ ⎛ ε 11 0 ⎟ ⎟ ⎜ ⎟ ⎜ ε 23 ⎟ = ⎜ − ε 21 ε 22 ε 23 ⎟ 可见 ε = ⎜ 0 ε 22 ε 23 ⎟ 将上式代入 ε = AzT ε Az ⎜ ⎜0 ε ε 33 ⎟ ε 33 ⎟ ε 33 ⎟ 32 ⎠ ⎠ ⎝ ⎠ ⎝ − ε 31 ε 32
医科大学精品课件：固体物理作业及答案
久期方程变为
E eikb 0 eikb* E
E2 ( )E ( 2 ) 0
E ( )2 42
2
2
6.5 一维单原子链，原子间距a，总长度为L＝Na
1) 用紧束缚近似方法求出与原子s态能级相对应的能带函数
2) 求出其能态密度函数
的表达式
3) 如每个原子s态中只有一个电子，计算T=0K时的费密能级
6.4 由相同原子组成的一维原子链，每个原胞中有两个原子，
原胞长度为a，原胞内两个原子的相对距离为b ：
(1) 根据紧束缚近似，只计入近邻相互作用，写出原子 s态
相对应的晶体波函数的形式。
(2) 求出相应能带的 E (K) 函数。
黄昆书 4.6 题
解：这是相同原子组成的一维复式格子，设第一套原子格点位置为xn，则第二套原子 格点位置为xn+b
解：（1）
势能的平均值
势能的平均值
令
V a2 m2 b2 m 2
96
6
在近自由电子近似模型中，势能函数的第n个傅里叶系数
第一个带隙宽度
Eg1 2V1
8b2
3
m 2
a2
2 3
m 2
第二个带隙宽度
Eg2 2V2
b2
2
m 2
a2
16
2
m 2
6.3 设有二维正方晶格，晶体势场为
U (x, y)
—— s态原子能级相对应的能带函数
—— s原子态波函数具有球对称性
—— 任选取一个格点为原点 —— 最近邻格点有12个
O
12个最邻近格点的位置
O
—— 类似的表示共有12项 —— 归并化简后得到面心立方s态原子能级相对应的能带
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上述八个矢量的垂直平分面，形成了第一布里渊 区。
5 解： A2 b c,B 2 c a,C 2 a b
V c
V c
V c
V A (B C ) (2)3( b c )[ c ( a ) ( a b )] V c
A (B C )(A C )B (A B )C
6解：当 KCl 取 ZnS 结构时，晶体总相互作用
能为 utotN(zeRR q2)
已知：N=6.023*1023/mol, ρ=0.326埃，αZnS=1.6381,（见P103) 为NaCl结构时，Zλ=2.05*10-8erg, Z=6 当为ZnS 结构时，Z=4, Zλ=（4/6）*2.05*10-8erg
设ZnS 结构时，其晶格常数与NaCl结构相同， （为原子最近邻距离）
即 a=6.294埃（见P20，图20配位数为6，参见表10，表11， a=2*1.33+1.81=6.2埃），31/2a/4=2.72埃（为原子最近邻距
离）
u to 6 . 0 t 1 2 2 [ 3 0 6 4 2 2 . 0 1 5 8 e 0 0 2 . 3 . 7 2 2 1 . 6 6 2 . ( 3 7 4 . 8 1 8 2 1 8 0 1 0 e 1 5 0 0 ) 3 ] s 1 u . 8 K 5/ m 3 C
第二章 习题答案
3解:
（c)衍射先只出现在同时满足以下二个方程的方
向上：（1）acosθ1=nλ,(2) bcosθ2=mλ
(
a,b
为二个方向矢量）
所以在二个锥面的交线上出现衍射极大。当底板
//原子面时，衍射花样为二个锥面的交线与底板
的交点。
（d）反射式低能电子衍射(LEED)中，只有表面 层原子参与衍射，故为二维衍射，衍射点的周期 大小与晶体表面原子排列方向上周期大小成反比。
'pi j6,B
p ' 12 ij
对fcc结构:Afcc=14.45392, Bfcc=12.13188
对bcc结构：Abcc=12.2533, Bbcc=9.11418
而
utot12N4[A2 B]
(uuttoo)t)tbfccccA Abfcc2c2c
Bfcc1.04533 Bfcc
∴取fcc结构更稳定。
(b)设该方程有如下形式的解： ul,m=u0ei(lkxa+mkya-wt)式中：a=最近邻原子距离 代入运动方程有： w2M=-c(eikxa+e-ikxa+eikya+e-ikya-4)=2c(2-coskya)
（c） 由上式可知，kxa,kya 的单值范围为： kxa∈(-π,π], kya∈(-π,π] 亦即：-π/a<kx≤π/a , -π/a<ky≤π/a 全部独立解区域为第一布里渊区。
V c
3 a a V c c
(c) 倒易矢量：
G h A k B lC 2( h k ) x 2( h k ) y 2lz
3 a
a
c
离原点最近的八个倒易格点（hkl):
( 1 ,0 ,0 ) ( 0 , ,1 ,0 ) ( 0 ,0 ,, 1 ) ( 1 , 1 ,0 ) ( 1 , 1 ,0 )
(2,2,0) (3,1,1) (2,2,2) (4,0,0)……
第三章
习题答案
2 解：
1 u to t2N 4[j
'( )1 2 p iR j j
'( )6] p iR j
平衡时，dutot/dR|R=R0=0，得
[ R0 2
'
6 1
pij
6
] ' 12
pij
[ A]16 2B
此时设
A
图1
图2
4 解： (a) V c a ( b c ) (2 3 a x a 2 y )[ (2 3 a x a 2 y ) c z ]2 3 a 2 c
(b)
2 2 3a 2 A b c ( a x y ) cz (x 3y )
V c V c 2 2
3 a
B 2 c a 2x 2y ,C 2 a b 2z
而由表6知， KCl 取 NaCl结构时 ，
(uto)计 t 算 16.6K 1 C/m alol
∴取fcc结构更为稳定。
第四章 习题答案
1 解: (a)只考虑四个近邻时，其运动方程为：
Md2ul,m/dt2=c[ul+1,m+ul-1,m-2ul,m]+[ul,m+1+ul,m-1-2ul,m]
( c a ) ( a b ) [c (a )b ] a [c (a )a ] b V c a
V (2 V c)3( b c)V c a(2 V c)3V 3c(2 V c)3
8:解： （a）金刚石晶胞中的八个原子位置为：
( 0 , 0 , 0 ) ( 1 , , 1 , 0 ) ( 1 , , 0 , 1 ) ( 0 , , 1 , 1 ) ( 1 , , 1 , 1 ) ( 3 , , 3 , 1 ) ( 3 , , 1 , 3 ) ( 1 , , 3 , 3 ) 2 22 22 2 4 4 4 4 4 4 4 4 4 4 4 4
f{ 1 e 2 i(h k l)} { 1 e i(h k ) e i(k l) e i(k l)}
（1） 对于后一项来讲为FCC结构因子，不为零 的条件是为hkl全奇或全偶。
（2）对于第一项而言，是由于复式格子错 位（沿对角线）1/4距离而产生，不为零条 件要求：(h+k+l)/2=2n, 即(h+k+l)=4n 因此，得到 Fhkl2≠0的条件为： ⅰhkl 为全偶，且h+k+l=4n ⅱhkl为全奇, 即下述衍射线会出现:(1,1,1) (2,0,0)
F fe fe hkl
iriG i
2i(xih yik zih k ) e i( k l ) e i( k l ) e 2 i ( h k l ) e 2 i ( h 3 k 3 l ) e 2 i ( 3 h k 3 l ) e 2 i ( 3 h 3 k l ) }
5 解： A2 b c,B 2 c a,C 2 a b
V c
V c
V c
V A (B C ) (2)3( b c )[ c ( a ) ( a b )] V c
A (B C )(A C )B (A B )C
6解：当 KCl 取 ZnS 结构时，晶体总相互作用
能为 utotN(zeRR q2)
已知：N=6.023*1023/mol, ρ=0.326埃，αZnS=1.6381,（见P103) 为NaCl结构时，Zλ=2.05*10-8erg, Z=6 当为ZnS 结构时，Z=4, Zλ=（4/6）*2.05*10-8erg
设ZnS 结构时，其晶格常数与NaCl结构相同， （为原子最近邻距离）
即 a=6.294埃（见P20，图20配位数为6，参见表10，表11， a=2*1.33+1.81=6.2埃），31/2a/4=2.72埃（为原子最近邻距
离）
u to 6 . 0 t 1 2 2 [ 3 0 6 4 2 2 . 0 1 5 8 e 0 0 2 . 3 . 7 2 2 1 . 6 6 2 . ( 3 7 4 . 8 1 8 2 1 8 0 1 0 e 1 5 0 0 ) 3 ] s 1 u . 8 K 5/ m 3 C
第二章 习题答案
3解:
（c)衍射先只出现在同时满足以下二个方程的方
向上：（1）acosθ1=nλ,(2) bcosθ2=mλ
(
a,b
为二个方向矢量）
所以在二个锥面的交线上出现衍射极大。当底板
//原子面时，衍射花样为二个锥面的交线与底板
的交点。
（d）反射式低能电子衍射(LEED)中，只有表面 层原子参与衍射，故为二维衍射，衍射点的周期 大小与晶体表面原子排列方向上周期大小成反比。
'pi j6,B
p ' 12 ij
对fcc结构:Afcc=14.45392, Bfcc=12.13188
对bcc结构：Abcc=12.2533, Bbcc=9.11418
而
utot12N4[A2 B]
(uuttoo)t)tbfccccA Abfcc2c2c
Bfcc1.04533 Bfcc
∴取fcc结构更稳定。
(b)设该方程有如下形式的解： ul,m=u0ei(lkxa+mkya-wt)式中：a=最近邻原子距离 代入运动方程有： w2M=-c(eikxa+e-ikxa+eikya+e-ikya-4)=2c(2-coskya)
（c） 由上式可知，kxa,kya 的单值范围为： kxa∈(-π,π], kya∈(-π,π] 亦即：-π/a<kx≤π/a , -π/a<ky≤π/a 全部独立解区域为第一布里渊区。
V c
3 a a V c c
(c) 倒易矢量：
G h A k B lC 2( h k ) x 2( h k ) y 2lz
3 a
a
c
离原点最近的八个倒易格点（hkl):
( 1 ,0 ,0 ) ( 0 , ,1 ,0 ) ( 0 ,0 ,, 1 ) ( 1 , 1 ,0 ) ( 1 , 1 ,0 )
(2,2,0) (3,1,1) (2,2,2) (4,0,0)……
第三章
习题答案
2 解：
1 u to t2N 4[j
'( )1 2 p iR j j
'( )6] p iR j
平衡时，dutot/dR|R=R0=0，得
[ R0 2
'
6 1
pij
6
] ' 12
pij
[ A]16 2B
此时设
A
图1
图2
4 解： (a) V c a ( b c ) (2 3 a x a 2 y )[ (2 3 a x a 2 y ) c z ]2 3 a 2 c
(b)
2 2 3a 2 A b c ( a x y ) cz (x 3y )
V c V c 2 2
3 a
B 2 c a 2x 2y ,C 2 a b 2z
而由表6知， KCl 取 NaCl结构时 ，
(uto)计 t 算 16.6K 1 C/m alol
∴取fcc结构更为稳定。
第四章 习题答案
1 解: (a)只考虑四个近邻时，其运动方程为：
Md2ul,m/dt2=c[ul+1,m+ul-1,m-2ul,m]+[ul,m+1+ul,m-1-2ul,m]
( c a ) ( a b ) [c (a )b ] a [c (a )a ] b V c a
V (2 V c)3( b c)V c a(2 V c)3V 3c(2 V c)3
8:解： （a）金刚石晶胞中的八个原子位置为：
( 0 , 0 , 0 ) ( 1 , , 1 , 0 ) ( 1 , , 0 , 1 ) ( 0 , , 1 , 1 ) ( 1 , , 1 , 1 ) ( 3 , , 3 , 1 ) ( 3 , , 1 , 3 ) ( 1 , , 3 , 3 ) 2 22 22 2 4 4 4 4 4 4 4 4 4 4 4 4
f{ 1 e 2 i(h k l)} { 1 e i(h k ) e i(k l) e i(k l)}
（1） 对于后一项来讲为FCC结构因子，不为零 的条件是为hkl全奇或全偶。
（2）对于第一项而言，是由于复式格子错 位（沿对角线）1/4距离而产生，不为零条 件要求：(h+k+l)/2=2n, 即(h+k+l)=4n 因此，得到 Fhkl2≠0的条件为： ⅰhkl 为全偶，且h+k+l=4n ⅱhkl为全奇, 即下述衍射线会出现:(1,1,1) (2,0,0)
F fe fe hkl
iriG i
2i(xih yik zih k ) e i( k l ) e i( k l ) e 2 i ( h k l ) e 2 i ( h 3 k 3 l ) e 2 i ( 3 h k 3 l ) e 2 i ( 3 h 3 k l ) }