三角形的三线——导学案

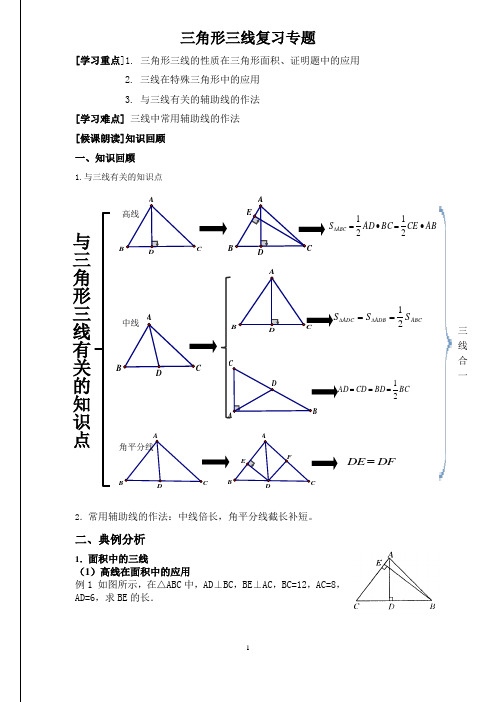
教学设计三角形的三线与三心导学案
一、教学内容：
三角形的三线与三心
二、教学目标
1.理解三角形的三线与三心的概念；
2.通过练习让学生熟练运用所学的三角形的三线与三心的概念进行求解；
3.通过学习，使学生能够根据所给条件判断三角形是否符合三角形的三线与三心的定义。

三、教学重点
理解三角形的三线与三心的概念；
四、教学难点
运用所学的三角形的三线与三心的概念进行求解
五、教学准备
准备相关的课件、例题和练习题
六、教学过程
（一）课前准备：
1.
先用ppt展示图形，让学生了解三角形的三条边及三个内角；
让学生分析图形，总结三角形的三线与三心的性质；
（二）正式教学：
1.
老师讲解三角形的三线与三心，引导学生学习如何求解三角形；
2.
老师可以分组活动，让学生总结三角形的三线与三心；
3.
多设计例题，让学生学会运用三角形的三线与三心的概念进行求解；
4.
教师给出练习题，让学生自主解答，老师帮助指导，检查学生的答案是否正确；
（三）课后作业：
1.
让学生完成上课未完成的练习题；
2.
让学生多练习，巩固学过的三角形的三线与三心的概念；
3.
让学生尝试从三条边或三个角度求解三角形；
布置适当的变形题，让学生体会新形的三角形。

11.1.2三角形的高、中线与角平分线主编：王强【预习归纳】1．三角形的三线（1）从三角形的一个顶点向它所对边的直线画___，顶点与______之间的________叫做做三角形的高。

（2）在三角形中，连接顶点和它所对的边的______所得的____ 叫做三角形的中线。

三角形三条中线的交点叫做三角形的_______（3）三角形的一个内角的角平分线与这个内角所对的边相交，这个内角的顶点与交点之间_____叫做_____________（4）一个三角形的高、中线、角平分线各有___条，且都是______，可以度量2.三角形具有______，而其他多边形不具________. 【典例精析】知识点一:三角形的三线例1：如图，在△ABC中.（1）画出AC边上的高，标出垂足D；（2）画出AB边上的中线CE，写出两条相等的线段，它们与边AB有什么关系？（3）画出∠BAC处的角平分线AF，写出两个相等的角，它们与∠BAC有什么关系？针对训练：1.如图，△ABC中，∠1=∠2，G为AD中点，延长BG 交AC于E，其满足BE⊥AC；F为AB上一点，且CF ⊥AD于H，下列判断：①线段AG是△ABE的角平分线；②BE是△ABD边AD上的中线；③线段AE是△ABG的边BG上的高；④∠1+∠FBC+∠FCB=90∘.其中正确的个数是( ) A. 1 B. 2 C. 3 D. 4知识点二：三角形的三线的运用例2：如图,在直角三角形ABC中,∠ACB=90∘，CD 是AB边上的高，AB=13cm，BC=12cm，AC=5cm.求：(1)△ABC的面积；(2)CD的长；(3)作出△ABC的边AC上的中线BE，并求出△ABE的面积；(4)作出△BCD的边BC边上的高DF，当BD=11cm时，试求出DF的长。

针对训练：2.如图，在△ABC中，BC=4cm，BC边上的高AD=4cm，AC=5cm.（1）试求△ABC的面积及AC边上的高BE的长；（2）试求AD:BE的值.知识点三：三角形的稳定性例3（1）下列图形中具有稳定性是_______；（只填图形序号）（2）对不具有稳定性的图形，请适当地添加线段，使之具有稳定性．针对训练：3如图,要使四边形木架(用四根木条钉成)不变形，至少要再钉上几根木条?五边形木架和六边形木架呢?请在下面画出草图。

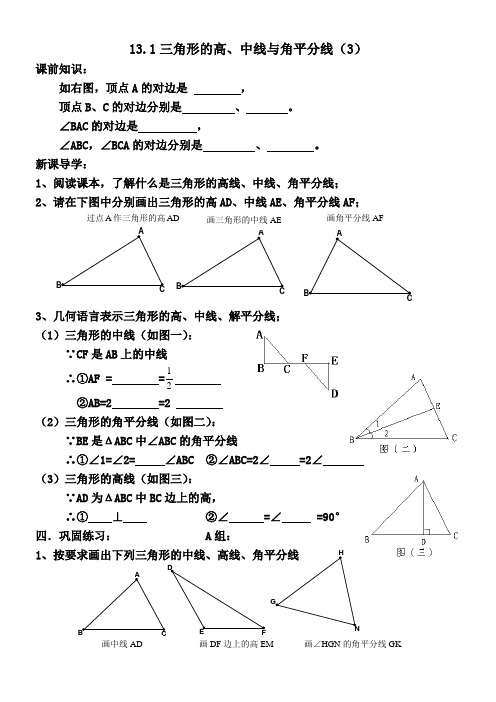
13.1三角形的高、中线与角平分线（3）课前知识：如右图，顶点A 的对边是 ，顶点B 、C 的对边分别是 、 。

∠BAC 的对边是 ，∠ABC ，∠BCA 的对边分别是 、 。

新课导学：1、阅读课本，了解什么是三角形的高线、中线、角平分线；2、请在下图中分别画出三角形的高AD 、中线AE 、角平分线AF ；3、几何语言表示三角形的高、中线、解平分线； （1）三角形的中线（如图一）：∵CF 是AB 上的中线∴①AF = =21②AB=2 =2 （2）三角形的角平分线（如图二）：∵BE 是ΔABC 中∠ABC 的角平分线∴①∠1=∠2= ∠ABC ②∠ABC=2∠ =2∠ （3）三角形的高线（如图三）：∵AD 为ΔABC 中BC 边上的高，∴① ⊥ ②∠ =∠ =90° 四．巩固练习： A 组：1A画三角形的中线AE过点A 作三角形的高ADA画角平分线AFCEF 画中线AD 画DF 边上的高EM 画∠HGN 的角平分线GK图2图12、如图1：∠BAC=60°，AD 是三角形ABC 的角平分线，则∠BAD= °，∠CAD= °3、如图2，AD 为ΔABC 中BC 边上的高，∠B=35°，∠C=45°，则∠BDA= °∠BAD= °，∠CAD= °。

4、如图3，ΔABC 的周长为20，AB=6，AC=8，AD 是BC 边上的中线，则BC= ，BD= ，CD= 。

5、下列三个图中三个∠B 有什么不同？过点A 作画出下列三角形的高，这三个三角形ABC 的边BC 上的高AD 在各自三角形的什么位置上？你能说出其中的规律？解：图一∠B 是 角，这个三角形ABC 的边BC 上的高AD 在图二∠B 是 角，这个三角形ABC 的边BC 上的高AD 在 图三∠B 是 角，这个三角形ABC 的边BC 上的高AD 在B 组：6、在△ABC 中，AD 是中线，AE 是角平分线、AF 是高，填空：（1）BD= =12；（2）12BAE ∠=⎽⎽⎽⎽⎽⎽=⎽⎽⎽⎽⎽⎽⎽⎽ （3）90BFA ∠=⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽=︒ （4）12ABCS =⎽⎽⎽⎽⨯⎽⎽⎽⎽⎽7、如图，在ΔABC 中，∠BAC=60°，∠B=45°， AD 是ΔABC 的一条角平分线，求∠ADB 的度数。

A D BC第三课时11.1.2 三角形的高、中线与角平分线【学习目标】1、认识与准确画出三角形的高、中线与角平分线；2、通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于点.【学习重点】了解三线的概念, 会准确画出三线.了解三线合一【学习难点】了解高的画法、位置、与垂线的区别一、学前准备1、三角形的定义是：2、三角形的三边有怎样的关系?二、探索思考1、 三角形的高、中线、角平分线的概念及表示探究一：(1)三角形的高与垂线有何区别和联系?(2)连结两点的线段与过两点的直线有何区别和联系? (3)三角形的角平分线与角平分线有何区别和联系?练习12、画一画：(1).画出下面三个三角形三条高.观察这三条高所在的直线的位置有何关系?(2)画三角形,并在这个三角形中画出它的三条中线.(锐角三角形,直角三角形和钝角三角形的中线在哪里)?观察这三条中线的位置有何关系? (3).画三角形,并在这三角形中画出它的三条角平分线,观察这三条角平分线的位置有何关系?三、当堂反馈1、下列各组图形中，哪一组图形中A D 是△A B C 的高( )2.如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ） 第4题图A.锐角三角形B.直角三角形C.钝角三角形D.锐角三角形3.三角形的三条高相交于一点，此一点定在（ ）A. 三角形的内部B.三角形的外部C.三角形的一条边上D. 不能确定 4.如图：在ΔABC 中,CD 是中线,已知BC-AC=5cm, ΔDBC 的周长为25cm,求ΔADC 的周长.四、学习反思B AB AB AA D CB A BC DA B C DAB C D (A ) (B ) (C ) (D )。

“三角形的高、中线、角平分线及三角形的稳定性”教学案例一、三维目标：1、了解三角形的角平分线、中线、高线的概念以及三角形的稳定性；2、经历探索与三角形有关的线段的过程，感受三角形稳定性的内涵：3、培养良好的几何推理意识和简单的分析思想，感受三角形“三线”的应用价值。

二、教学重点、难点及切入点：1、教学重点：理解三角形角平分线、高线、中线的概念，懂得画出三角形的“三线段”。

2、教学难点：会画出钝角三角形的高。

3、切入点：通过拆线画图等实践操作活动，让学生体验“三线段”并感受“三线”的异同。

三、教学过程：（一）创设情境，导入新课：操作：在一张薄纸上任意画出一个三角形，通过折纸的方法，你能设计画出一个三角形内角的角平分线吗？学生活动：在薄纸上画任意三角形，对折一个角，折痕就是所要作的内角平分线。

师：一个三角形角平分线有几条？这几条角平分线是否交于同一点？试试看！生：我对折一个角找到了它的角平分线，再对折另外两个角找到了它们的角平分线，所以一个三角形有三条角平分线，我还发现这三条角平分线交于同一点。

师生共识：在三角形中，一个内角平分线与它的对边相交，这个顶点与交战之间的线段叫做三角形的角平分线；一个三角形有三条角平分线，且交于一点。

如图：图1 AB C DFE O操作感知：锐角三角形、钝角三角形、直角三角形纸片各一个。

1、用拆线的办法，画出这三种三角形的内角平分线；2、在每一个三角形中，寻找三条角平分线交点与三角形的位置关系。

师：一个三角形的三条内角平分线交点在三角形的什么位置？生：交点在三角形的内部，不可能在在角形上，也不在三角形的外部。

二、知识牵移，构建理论引导学生动手操作：1、分别画一个锐角三角形、直角三角形和一个钝角三角形；2、取它们各边的中点；3、连接每一个顶点与对边的中点，观察这三条线段是否交在一点上。

师：在三角形中，连接一个顶点与它对边中点的线段，我们把叫作什么呢？生：中线。

师：画三角形的中线可以像角平分线那样用折叠的方法吗？试试看！生操作：把三角形一这对折，找到中点，再与对角的顶点连接就是中线。

AB C(1)AB C(2)AB C(3)课题：三角形的高、中线与角平分线【学】7022学习目标：1.经历折纸，画图等实践过程认识三角形的高、中线与角平分线.2.会用工具准确画出三角形的高、中线与角平分线，通过画图了解三角形的三条高(及所在直线)交于一点，三角形的三条中线、三条角平分线等都交于点.3.注意(1)三角形平分线与角平分线的区别，三角形的高与垂线的区别.(2)钝角三角形高的画法.(3)不同的三角形三条高的位置关系.【预习案】【探究案】例１如图，（1）（2）（3）中的三个∠B有什么不同？分别画出BC边的高。

这三个△ABC的边BC上的高AD在各自三角形的什么位置？你能说出来其中的规律吗？例2．填空：（1）如图（1），AD、BE、CF是△ABC的三条中线，则AB＝2 ，BD＝，AE＝1 2（2）如图（2）AD、BE、CF是△ABC的三条角平分线，则∠1＝，∠3＝12，AB D E CAC B FD H G E21ABCD∠ACB ＝2 .ABCB CAD E FDEF1234(1)(2)例3．如图，已知AD 、AE 分别是△ABC 的中线、高，且AB =5cm ，AC =3cm ，则△ABD 和△ACD的周长之差为 ，则△ABD 和△ACD 的面积关系为 .例4．如图，在△ABC 中，AB =AC ，AC 上的中线BD 把三角形的周长分为12cm 和15cm 两个部分，求三角形各边的长.【训练案】1．如图，在△ABC 中，∠1＝∠2，G 为AD 中点，延长BG 交AC 于E ， F 为AB 上一点，CF⊥AD 于H ，下面判断正确的有（ ）①AD 是△ABE 的角平分线；②BE 是△ABD 的边AD 上的中线； ③CH 是△ACD 的边AD 上的高；④AH 是△ACF 的角平分线和高线；A ．1个B ．2个C ．3个D ．4个 2．已知三角形的两条边长相等，周长是10，边长为整数，求这个三角形的三边长.A CB AC B ADC B A BD C A B C D课题：三角形的高、中线与角平分线班级 小组 姓名 得分1．在下列画图中，分别画出了△ABC 中BC 边上的高AD ，其中正确的是（ ）2．如图，AD ⊥BC 于D ，则以AD 为高的三角形有（ ） A ．3个B ．4个C ．5个D ．6个（2） （3）3．如图，图中共有三角形 （ ）A ．10个B ．11个C ．12个D ．13个 4．至少有两条高在三角形内部的三角形是（ ）A ． 锐角三角形B ．钝角三角形C ．直角三角形D ．以上都有可能 5．以下四个命题中正确的是 （ ）A ．三角形的角平分线是射线B ．过三角形一边中点的线段一定是三角形的中线C ．三条线段一定能组成一个三角形D ．三角形的中线是线段 6．下列命题：①首尾相连的三条线段组成的图形是三角形；②在三角形中，连接一个顶点和它对边中点的直线叫做三角形的中线； ③任何三角形都有三条中线、三条角平分线，并且都交于一点；④△ABC 中，如果射线AD 平分∠BAC ，那么AD 是△ABC 的角平分线， 其中正确的命题有（ ）A ．1个B ．2个C ．3个D ．4个 7．一个三角形的三条角平分线的交点在（ ）A ．三角形内B ．三角形外C ．可能三角形内，也可能三角形外D ．可能在三角形的一边上 8．若CD 是△ABC 的高，则∠CDA ＝∠ ＝ °9. 若CD 上△AB C 的角平分线，∠ACD ＝45°，∠DCB ＝ ，∠ACB ＝ 。