第三章_3 MG1型排队系统

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。

它是数学运筹学的分支学科。

也是研究服务系统中排队现象随机规律的学科。

广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。

排队论研究的内容有3个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。

其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。

一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中虚线所包括的部分。

排队系统又称服务系统。

服务系统由服务机构和服务对象（顾客）构成。

服务对象到来的时刻和对他服务的时间（即占用服务系统的时间）都是随机的。

描述一个排队系统一般需要分析其三个组成部分：输入过程、排队规则和服务机构。

输入过程输入过程考察的是顾客到达服务系统的规律。

它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述，一般分为确定型和随机型两种。

例如，在生产线上加工的零件按规定的间隔时间依次到达加工地点，定期运行的班车、班机等都属于确定型输入。

随机型的输入是指在时间t内顾客到达数n（t）服从一定的随机分布。

如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布，即式中λ为单位时间顾客期望到达数，称为平均到达率；1/λ为平均间隔时间。

在排队论中，讨论的输入过程主要是随机型的。

排队规则排队规则分为等待制、损失制和混合制三种。

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。

它是数学运筹学的分支学科。

也是研究服务系统中排队现象随机规律的学科。

广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。

排队论研究的内容有3个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。

其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。

一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中虚线所包括的部分。

排队系统又称服务系统。

服务系统由服务机构和服务对象（顾客）构成。

服务对象到来的时刻和对他服务的时间（即占用服务系统的时间）都是随机的。

描述一个排队系统一般需要分析其三个组成部分：输入过程、排队规则和服务机构。

输入过程输入过程考察的是顾客到达服务系统的规律。

它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述，一般分为确定型和随机型两种。

例如，在生产线上加工的零件按规定的间隔时间依次到达加工地点，定期运行的班车、班机等都属于确定型输入。

随机型的输入是指在时间t内顾客到达数n（t）服从一定的随机分布。

如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布，即式中λ为单位时间顾客期望到达数，称为平均到达率；1/λ为平均间隔时间。

在排队论中，讨论的输入过程主要是随机型的。

排队规则排队规则分为等待制、损失制和混合制三种。

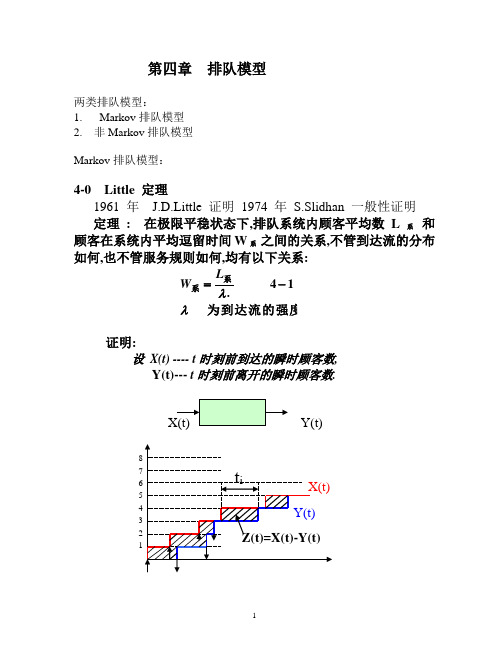
第四章 排队模型两类排队模型：1. Markov 排队模型2. 非Markov 排队模型Markov 排队模型：4-0 Little 定理1961 年 J.D.Little 证明 1974 年 S.Slidhan 一般性证明定理 : 在极限平稳状态下,排队系统内顾客平均数L 系 和 顾客在系统内平均逗留时间W 系 之间的关系,不管到达流的分布如何,也不管服务规则如何,均有以下关系:为到达流的强度系系λλ14.-=L W证明:设 X(t) ---- t 时刻前到达的瞬时顾客数, Y(t)--- t 时刻前离开的瞬时顾客数.Y(t)在稳定后,流入与流出的顾客数应相等, 则在t 时刻留在系统内的顾客数为:Z(t)=X(t)-Y(t)在足够长的时间T 来考虑有:队队系系系系同理可以证明所以有逗留时间系统内每个顾客的平均时间的总和所有顾客在系统内逗留时间个顾客在系统内的逗留第其中的小面积的总和高度为长度为阴影部分的面积W L W L W Tt t i t t Tt T t T T dtt Z T L iiii i iiii i T.:.:...,:.11]1*[1][1)(10λλλλλ==--=--=⨯====∑∑∑∑⎰4-1 M/M/1/0 (单通道损失制)服务员数：n=1 队长：m=0M -- 到达流为Poisson,流强λM -- 服务时间服从指数分布：)0()(>=⋅-t e t f t μμ 状态为系统内顾客数，I={0,1}"0"表示服务员闲，其概率为：P 0(t)；"1"表示服务员忙，其概率为：P 1(t)； 状态转换图：Fokker-Plank k 方程：可得:)0(1)0(:341)()(24)()()(14)()()(1010011100==-=+-+-=-+-=∙∙P P t P t P t P t P t P t P t P t P 初始条件λμμλ联立求解4-1与4-3得：λμλλμλμμλλμλλλμλλμμμμλμλμλμλ+=∞+=∞∞→==+-+=-=+++=-++-=-+-=+----+-∙∙)(,)()0(,1)0(0)(1)()(44)()()()(1[)()(1010)(01)(000000P P t P P t e t P t P e t P t P t P t P t P t P tt定义：系统负载能力：μλρ=指标：(1) ρμλμ+=+===110P Q 请求服务的顾客数被服务顾客数 (2) 绝对通过能力：ρλμλλμλ+=+===1Q A 数单位时间被服务的顾客(3) 损失概率(即顾客来时，系统服务员忙，顾客离去)ρρμλλμλμ+=+=+-=-==1111Q P P 损例一：一条电话线，呼叫率为：0.8次/分(λ=0.8)，每次平均通话时间为：τ=1.5分。

非强占有限优先权MG排队系统针对部分数据帧有完全优先权发送的计算机网络数据服务系统存在的网络拥塞风险问题，提出了一种非强占有限优先权M/G/1排队系统模型的方法。

该系统模型引入控制完全优先权的参数n，使得数据帧的完全优先权变成有限优先权，考虑了不同优先级队伍之间的公平性，降低了计算机网络数据服务系统拥塞的风险，使得网络系统在有限优先权下有较好的稳定性。

在模型研究中，运用全概率拆解方法获得各级队伍平均等待时间、平均逗留时间和平均队长的理论结果。

对模型采用Matlab 2010a软件实验仿真，实验得到的各级队伍平均等待时间和理论平均等待时间的平均绝对误差为0.951%。

实验中，有限优先权条件下各级顾客的平均等待时间比值显著小于完全优先权条件下各级顾客的平均等待时间比值。

实验结果表明对非强占有限优先权M/G/1排队系统模型研究的理论结果是正确的，该模型具有更稳定的系统特性。

0引言排队论是运筹学的分支，其理论得广泛应用于计算机网络数据发送服务[1]、通信系统[2]、道路交通[3]、银行[4]、地铁[5]、医院[6]等一些服务领域。

对不同领域的服务系统需要建立与之对应的排队系统模型进行研究。

当前已有很多文献对排队系统进行过深入研究。

文献[7]对强占及非强占优先权排队系统作了基础研究;文献[8]研究了非强占优先权的多服务器排队系统，将非强占优先权排队系统服务器扩充到多台经行研究;文献[9]引入绩效评价将排队系统应用在银行自动取款机(Automatic Teller Machine， ATM)系统，展示排队论在其他领域中有效的应用，此后排队论更是广泛应用于各种服务领域之中。

之后研究人员纷纷研究了多级适应性M/G/1可修排队系统[10]、M/G/1休假排队系统[11]、基于多重休假的min(N，V)策略M/G/1排队系统[12]等。

现在文献对休假排队系统和可修排队系统研究颇多，其排队系统在计算机网络[13]和通信领域[14]也有较好的应用，但对于计算机网络应用中待解决的优先权拥堵问题相关文献比较少[15]。

多级适应性休假的M/G/1型排队系统的稳态理论随着信息技术、计算机技术及管理系统等领域的迅猛发展，排队论已被广泛地应用到上述领域的性能分析上。

但是，由于空竭服务的M／G／1型排队系统理论往往不能满足对大量复杂问题建立数学模型的需要，越来越多的数学、计算机、管理等方面的学者不断地研究非空竭服务休假策略，建立了多种非空竭服务的M ／G／1型休假排队系统，丰富了非空竭服务休假的M／G／1型排队系统的理论，对大量系统的性能指标分析起到了非常重要的作用。

本文以前人所研究的M／G／1型排队理论为基础，研究了一类多级适应性休假的M／G／1型排队系统，给出了系统稳态指标的随机分解结果，通过数值例子描绘出了一些系统的稳态指标的变化趋势，比较了这些系统的稳态指标的差异，从而建立了多级适应性休假的M／G／1型排队系统的稳态理论。

首先，总结、归纳了多级适应性休假的M／G／1排队系统，空竭服务的M／G／1边界状态变体模型，多级适应性休假的Geom／G／1排队，阐述了稳态队长和等待时间的随机分解结果，分析了系统的忙期，导出了系统处于每种状态的概率，通过若干特例展示了稳态指标的随机分解结果的一般性。

在此基础上，本文提出了空竭服务的Geom／G／1边界状态变体模型，平行于连续时间M／G／1排队模型的解析结果，给出了离散时间的隐态队长与等待时间的随机分解结果，从而使这一类排队系统具有更加完善的理论框架，丰富了空竭服务的M／G／1型休假排队系统的理论。

其次，将闸门服务规则和多级适应性休假策略结合，建立了新的M／G／1型排队系统，利用再生循环法得到系统的稳态指标的随机分解结果，分析了平均服务周期等性能指标，通过数值例子，比较系统参数对系统性能指标的影响。

大量已经被研究过的闸门服务的M／G／1型休假排队系统都是该类模型的特例，如Takagi研究的闸门服务的多重休假和单重休假的M／G／1型排队系统，Leung、Alfa等研究的单服务台闸门服务的M／G／1型排队系统等。

《带负顾客的M-M-1休假排队系统驱动的流模型》篇一带负顾客的M-M-1休假排队系统驱动的流模型一、引言在现代服务行业中，排队系统是衡量服务效率和顾客满意度的关键因素之一。

特别是在高流量、高需求的场景中，如何有效地管理和优化排队系统显得尤为重要。

本文将探讨一个特殊的排队系统模型——带负顾客的M/M/1休假排队系统，并对其驱动的流模型进行深入分析。

二、M/M/1排队系统概述M/M/1排队系统是一种典型的随机服务系统，其中M代表指数分布，即顾客到达时间和服务时间的随机性。

在M/M/1系统中，只有一个服务台提供服务。

本文将关注这种排队系统在存在负顾客时的特性及其对服务流程的影响。

三、负顾客的概念及其影响负顾客是指在排队系统中，不仅存在等待接受服务的正常顾客，还存在一类特殊的顾客，他们到达系统后并不接受服务，反而带走正在服务的顾客或未接受服务的顾客（称为“取消”或“离开”的顾客）。

这种特殊现象在现实生活中并不罕见，如网络购物中的退单、餐厅中的取消预约等。

负顾客的存在对排队系统的运行效率和服务质量产生显著影响。

四、带负顾客的M/M/1休假排队系统模型本文将探讨带负顾客的M/M/1休假排队系统模型。

在这种模型中，服务台在空闲时会进入休假状态，以节省成本和提高效率。

当有顾客到达时，如果服务台处于休假状态，则顾客需等待服务台结束休假并开始服务；如果服务台正在服务其他顾客，则新到达的顾客需排队等待。

同时，负顾客的到达也会影响这一过程，他们可能会取消正在进行的服务或使正在等待的顾客离开。

五、流模型分析为了更好地理解带负顾客的M/M/1休假排队系统的运行机制，我们建立了一个流模型。

该模型主要关注以下几个方面：1. 顾客到达流：分析正常顾客和负顾客的到达规律，包括到达间隔时间的分布、到达率的计算等。

2. 服务流：研究服务台的服役过程，包括服务时间的分布、服务率的计算以及服务台在休假和服役状态之间的切换规律。

3. 负顾客影响流：探讨负顾客对正在服务的顾客和等待的顾客的影响，包括负顾客取消服务的概率、导致其他顾客离开的概率等。

MG1型非空竭服务休假排队系统的随机分解的开题报告一、研究目的和意义随机分解法是一种常用的优化算法，可以有效地解决多种实际问题。

非空竭排队系统是一种常见的服务系统，如银行、医院等场所，对其进行优化可以提高系统效率和顾客满意度。

本文旨在利用随机分解法对MG1型非空竭服务休假排队系统进行优化，提高系统的服务能力和效率，从而为实际应用提供可靠参考。

二、研究内容与思路1. 系统模型建立本文采用MG1型排队系统作为研究对象，建立相应的系统模型，并对系统中的各要素进行描述，如到达率、服务时间分布、休假时间、排队规则等。

2. 随机分解算法研究随机分解算法是一种常用的优化算法，包括两个部分：全局搜索和局部搜索。

在全局搜索阶段，通过对目标函数进行随机扰动，得到局部最优解；在局部搜索阶段，则对当前解进行局部优化，以得到更优解。

本文将对随机分解算法进行深入研究，并运用到MG1型非空竭服务休假排队系统优化中。

3. MG1型非空竭服务休假排队系统优化本文将通过随机分解算法对MG1型非空竭服务休假排队系统进行优化。

具体步骤为：首先建立系统模型，然后利用随机分解算法求解系统最优解，最后对优化结果进行验证和评价。

三、研究预期成果通过本文的研究，预期达到以下成果：1. 建立MG1型非空竭服务休假排队系统模型，对系统中的各要素进行描述。

2. 深入研究随机分解算法，包括全局搜索和局部搜索等关键步骤。

3. 运用随机分解算法对MG1型非空竭服务休假排队系统进行优化，提高系统的服务能力和效率。

4. 对优化结果进行验证和评价，为实际应用提供可靠参考。

综上所述，本文的研究具有一定的理论与实际意义，在服务系统优化领域具有一定的推广价值和应用前景。

M／Mr／1／N排队系统
何启明
【期刊名称】《应用概率统计》
【年(卷),期】1993(009)003
【摘要】本文讨论了等待空间有限的成批服务排队系统M/M^r/1/N,给出队长平稳分布的精确解.还得到了系统损失概率和平均输出间隔的精确值.
【总页数】5页(P266-270)
【作者】何启明
【作者单位】无
【正文语种】中文
【中图分类】O226
【相关文献】
1.一种新的排队系统在CDMA2000 1X数据业务吞吐量优化中的应用——
M/M/m变速率自适应优先服务排队系统 [J], 杨谦;赵东风
2.M／M／C／∞排队系统模型及其应用实例分析-以建行某储蓄所M／M／C／∞排队系统为例 [J], 黄志芳;肖英才
3.基于排队系统的队长管理分析 [J], 张笑雨;郭永江
4.基于GI/M/1型Markov过程的Geo/Geo/1多重工作休假排队系统分析 [J], 张宏波;彭培让
5.具有反馈和不耐烦顾客的可修 M/M/1排队系统 [J], 池夏夏;李冰冰
因版权原因，仅展示原文概要，查看原文内容请购买。