2018js高考

2018江西省高考信息技术真题试卷含答案（word版）信息技术基础（必修）第一部分信息技术（100分）第I卷必修模快(70分)一、选择题(本大题20小题毎小題2分.共40分。

毎小题给出的四个选项中,只有一项是符合题目要求的)1.省电教馆发布通知，“2018年中小学生电脑制作比赛”参赛作品必须在3月22日前上传到省基础教育资源公共服务平台。

小明3月23日才看到这则通知.结果无法上传作品,以致错过比赛。

这主要体现了信息的A.时效性B.依附性C.共享性D.普遍性2.下列智能手机操作中,属于人工智能技术应用范畴的是A.通过APP购买电影票B.使用翻译工具与外国人士交流C.查询本人高考成绩D.收发电子邮件3.2018年3月，国家互联网应急中心发现多个锁屏勒索类病毒变种。

该类病毒通过锁屏用户手机，勒索用户付费解锁,对手机安全和用户财产均造成严重威胁。

为了防止病毒侵害.下列行为合理的是①手机上安装杀毒软件并定期升级在条病毒②公共场所通过免费无线网络进行手机支付③将手机连接到公共电脑上作为U盘使用④通过手机厂商的应用商城下载APP软件A.①④B.①③C.②④D.②③4.“喂,张立宪吗?这里是社保中心医保核查部您上个月十七号,在华西医科大学附属医院开药740元,医保支付620元,医保监察系统发现,您的医保卡存在违规开药的现象，涉嫌骗保，请按照我说的进行以下操作……，这是某电影中的片段,受害人在5分钟内被骗走4万元人民币。

假如你接到陌生人电话,对方要求你汇款或对银行卡进行相关操作,下列做法最可靠的是A.接到电话后,立即按照对方的要求进行汇款B.根据对方自报的身份进行判断后决定是否汇款C.根据对方所说事件的真实性决定是否汇款D.接到此类电话,立即挂断不予理睬5.已知十六进制数(12B) :转换为十进制数的运算过程为:(12B)16 =1x16^2 +2x16^1 +11x16^0=299,则(6F)H转换为十进制数的结果为A.109B.110C.111D.1126.目前有些超市提供自助结算系统，对顾客所购商品进行结算,此类自助结算系统属于A.操作系统B.数据库应用系统C.数据库管理系统D.编译系统7.小明诵读明朝张居正的诗句“瘦筇又逐孤鸿远,浪迹还如落叶分”时，遇到生僻字“筇”,他用Word的“拼音指南”工具，获知“筇”的读音为"qióng"。

江苏省2018年高考：数学卷考试真题与答案解析一、填空题本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1．已知集合{0,1,2,8}A =，{1,1,6,8}B =-，那么A B =．2．若复数z 满足i 12i z ⋅=+，其中i 是虚数单位，则z 的实部为．3．已知5位裁判给某运动员打出的分数的茎叶图如图所示，那么这5位裁判打出的分数的平均数为．4．一个算法的伪代码如图所示，执行此算法，最后输出的S 的值为 ．5．函数()f x =的定义域为．6．某兴趣小组有2名男生和3名女生，现从中任选2名学生去参加活动，则恰好选中2名女生的概率为．7．已知函数sin(2)(22y x ϕϕππ=+-<<的图象关于直线3x π=对称，则ϕ的值是 ．8．在平面直角坐标系xOy 中，若双曲线22221(0,0)x y a b a b-=>>的右焦点(,0)F c 到一条渐近线的距，则其离心率的值是 ．9．函数()f x 满足(4)()()f x f x x +=∈R ，且在区间(2,2]-上，cos ,02,2()1||,20,2x x f x x x π⎧<≤⎪⎪=⎨⎪+<≤⎪⎩-则((15))f f 的值为 ．10．如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．11．若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点，则()f x 在[1,1]-上的最大值与最小值的和为．12．在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为．13．在ABC △中，角,,A B C 所对的边分别为,,a b c ，120ABC ∠=︒，ABC ∠的平分线交AC 于点D ，且1BD =，则4a c +的最小值为．14．已知集合*{|21,}A x x n n ==-∈N ，*{|2,}n B x x n ==∈N ．将A B 的所有元素从小到大依次排列构成一个数列{}n a ．记n S 为数列{}n a 的前n 项和，则使得112n n S a +>成立的n 的最小值为．二、解答题本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．在平行六面体1111ABCD A B C D -中，1111,AA AB AB B C =⊥．求证：（1）11AB A B C 平面∥；（2）111ABB A A BC ⊥平面平面．16．已知,αβ为锐角，4tan 3α=，cos()αβ+=（1）求cos 2α的值；（2）求tan()αβ-的值．17．某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD ，大棚Ⅱ内的地块形状为CDP △，要求,A B 均在线段MN 上，,C D 均在圆弧上．设OC 与MN 所成的角为θ．（1）用θ分别表示矩形ABCD 和CDP △的面积，并确定sin θ的取值范围；（2）若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．18．如图，在平面直角坐标系xOy 中，椭圆C 过点12，焦点12(F F ，圆O 的直径为12F F ．（1）求椭圆C 及圆O 的方程；（2）设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程．19．记(),()f x g x ''分别为函数(),()f x g x 的导函数．若存在0x ∈R ，满足00()()f x g x =且00()()f x g x ''=，则称0x 为函数()f x 与()g x 的一个“S 点”．（1）证明：函数()f x x =与2()22g x x x =+-不存在“S 点”；（2）若函数2()1f x ax =-与()ln g x x =存在“S 点”，求实数a 的值；（3）已知函数2()f x x a =-+，e ()xb g x x=．对任意0a >，判断是否存在0b >，使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”，并说明理由．20．设{}n a 是首项为1a ，公差为d 的等差数列，{}n b 是首项为1b ，公比为q 的等比数列．（1）设110,1,2a b q ===，若1||n n a b b -≤对1,2,3,4n =均成立，求d 的取值范围；（2）若*110,,a b m q =>∈∈N ，证明：存在d ∈R ，使得1||n n a b b -≤对2,3,,1n m =+ 均成立，并求d 的取值范围（用1,,b m q 表示）．答案解析一、填空题1、{1，8}2、23、904、85、[2，+∞）6、3107、π6-8、2910、4311、–312、3 13、914、27二、解答题15．证明：（1）在平行六面体ABCD -A 1B 1C 1D 1中，AB ∥A 1B 1．因为AB ⊄平面A 1B 1C ，A 1B 1⊂平面A 1B 1C ，所以AB ∥平面A 1B 1C ．（2）在平行六面体ABCD -A 1B 1C 1D 1中，四边形ABB 1A 1为平行四边形．又因为AA 1=AB ，所以四边形ABB 1A 1为菱形，因此AB 1⊥A 1B ．又因为AB 1⊥B 1C 1，BC ∥B 1C 1，所以AB 1⊥BC ．又因为A 1B ∩BC =B ，A 1B ⊂平面A 1BC ，BC ⊂平面A 1BC ，所以AB 1⊥平面A 1BC ．因为AB 1⊂平面ABB 1A 1，所以平面ABB 1A 1⊥平面A 1BC ．16．解：（1）因为4tan 3α=，sin tan cos ααα=，所以4sin cos 3αα=．因为22sin cos 1αα+=，所以29cos 25α=，因此，27cos 22cos 125αα=-=-．（2）因为,αβ为锐角，所以(0,π)αβ+∈．又因为cos()αβ+=sin()αβ+==，因此tan()2αβ+=-．因为4tan 3α=，所以22tan 24tan 21tan 7ααα==--，因此，tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+．17．解：（1）连结PO 并延长交MN 于H ，则PH ⊥MN ，所以OH =10．过O 作OE ⊥BC 于E ，则OE ∥MN ，所以∠COE =θ，故OE =40cos θ，EC =40sin θ，则矩形ABCD 的面积为2×40cos θ（40sin θ+10）=800（4sin θcos θ+cos θ），△CDP 的面积为12×2×40cos θ（40–40sin θ）=1600（cos θ–sin θcos θ）．过N 作GN ⊥MN ，分别交圆弧和OE 的延长线于G 和K ，则GK =KN =10．令∠GOK =θ0，则sin θ0=14，θ0∈（0，π6）．当θ∈[θ0，π2）时，才能作出满足条件的矩形ABCD ，所以sin θ的取值范围是[14，1）．答：矩形ABCD 的面积为800（4sin θcos θ+cos θ）平方米，△CDP 的面积为1600（cos θ–sin θcos θ），sin θ的取值范围是[14，1）．（2）因为甲、乙两种蔬菜的单位面积年产值之比为4∶3，设甲的单位面积的年产值为4k ，乙的单位面积的年产值为3k （k >0），则年总产值为4k ×800（4sin θcos θ+cos θ）+3k ×1600（cos θ–sin θcos θ）=8000k （sin θcos θ+cos θ），θ∈[θ0，π2）．设f （θ）= sin θcos θ+cos θ，θ∈[θ0，π2），则．令()=0f θ′，得θ=π6，当θ∈（θ0，π6）时，()>0f θ′，所以f （θ）为增函数；当θ∈（π6，π2）时，()<0f θ′，所以f （θ）为减函数，因此，当θ=π6时，f （θ）取到最大值．答：当θ=π6时，能使甲、乙两种蔬菜的年总产值最大．18．解：（1）因为椭圆C的焦点为12(),F F -，可设椭圆C 的方程为22221(0)x y a b a b +=>>．又点1)2在椭圆C 上，所以2222311,43,a b a b ⎧+=⎪⎨⎪-=⎩，解得224,1,a b ⎧=⎪⎨=⎪⎩因此，椭圆C 的方程为2214x y +=．因为圆O 的直径为12F F ，所以其方程为223x y +=．（2）①设直线l 与圆O 相切于0000(),,(00)P x y x y >>，则22003x y +=，所以直线l 的方程为0000()x y x x y y =--+，即0003x y x y y =-+．由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩，消去y ，得222200004243640()x y x x x y +-+-=．（*）因为直线l 与椭圆C 有且只有一个公共点，所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=．因为00,0x y >，所以001x y ==．因此，点P的坐标为．②因为三角形OAB，所以12AB OP ⋅=AB =．设1122,,()(),A x y B x y ，由（*）得1,2x =所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+．因为22003x y +=，所以22022016(2)32(1)49x AB x -==+，即42002451000x x -+=，解得22005(202x x ==舍去），则2012y =，因此P的坐标为．综上，直线l的方程为y =+．19．解：（1）函数f （x ）=x ，g （x ）=x 2+2x -2，则f ′（x ）=1，g ′（x ）=2x +2．由f （x ）=g （x ）且f ′（x ）= g ′（x ），得222122x x x x ⎧=+-⎨=+⎩，此方程组无解，因此，f （x ）与g （x ）不存在“S ”点．（2）函数21f x ax =-（），()ln g x x =，则12f x ax g x x'='=（），（）．设x 0为f （x ）与g （x ）的“S ”点，由f （x 0）=g （x 0）且f ′（x 0）=g ′（x 0），得200001ln 12ax x ax x ⎧-=⎪⎨=⎪⎩，即200201ln 21ax x ax ⎧-=⎪⎨=⎪⎩，（*）得01ln 2x =-，即120e x -=，则1221e 22(e )a -==．当e2a =时，120e x -=满足方程组（*），即0x 为f （x ）与g （x ）的“S ”点．因此，a 的值为e 2．（3）对任意a >0，设32()3h x x x ax a =--+．因为(0)0(1)1320h a h a a =>=--+=-<，，且h （x ）的图象是不间断的，所以存在0x ∈（0，1），使得0()0h x =，令03002e (1)x x b x =-，则b >0．函数2e ()()xb f x x a g x x=-+=，，则2e (1)()2()x b x f x x g x x -=-=′，′．由f （x ）=g （x ）且f ′（x ）=g ′（x ），得22e e (1)2xx b x a x b x x x ⎧-+=⎪⎪⎨-⎪-=⎪⎩，即00320030202e e (1)2e (1)2e (1)x x xx x x a x x x x x x x ⎧-+=⋅⎪-⎪⎨-⎪-=⋅⎪-⎩（**）此时，0x 满足方程组（**），即0x 是函数f （x ）与g （x ）在区间（0，1）内的一个“S 点”．因此，对任意a >0，存在b >0，使函数f （x ）与g （x ）在区间（0，+∞）内存在“S 点”．20．解：（1）由条件知：112(,)n nn a n d b -=-=．因为1||n n a b b -≤对n =1，2，3，4均成立，即1 12|()1|n n d---≤对n =1，2，3，4均成立，即1≤1，1≤d ≤3，3≤2d ≤5，7≤3d ≤9，得7532d ≤≤．因此，d 的取值范围为75[,32．（2）由条件知：111(1),n nn a b n d b b q -=+-=．若存在d ，使得1||n n a b b -≤（n =2，3，···，m +1）成立，即1111|1|2,3,,(1())n b n d b q b n m -+--≤=+ ，即当2,3,,1n m =+ 时，d 满足1111211n n q q b d b n n ---≤≤--．因为(q ∈，则112n m q q -<≤≤，从而11201n q b n --≤-，1101n q b n ->-，对2,3,,1n m =+ 均成立．因此，取d =0时，1||n n a b b -≤对2,3,,1n m =+ 均成立．下面讨论数列12{}1n q n ---的最大值和数列1{}1n q n --的最小值（2,3,,1n m =+ ）．①当2n m ≤≤时，1112222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---，当112mq <≤时，有2n m q q ≤≤，从而1() 20n n n n q q q ---+>．因此，当21n m ≤≤+时，数列12{}1n q n ---单调递增，故数列12{}1n q n ---的最大值为2m q m-．②设()()21x f x x =-，当x >0时，ln 21(0(n )l 22)xf x x '=--<，所以()f x 单调递减，从而()f x <f （0）=1．当2n m ≤≤时，111112111()()()nn n q q n n f q n n n n --=≤-=<-，因此，当21n m ≤≤+时，数列1{}1n q n --单调递减，故数列1{}1n q n --的最小值为m q m ．因此，d 的取值范围为11(2)[,]m mb q b q m m-．。

2018江西省高考信息技术真题试卷含答案（word版）信息技术基础（必修）含网络技术应用（选修I）+多媒体技术应用(选修II)第一部分信息技术（100分）第I卷必修模快(70分)一、选择题(本大题20小题毎小題2分.共40分。

毎小题给出的四个选项中,只有一项是符合题目要求的)1.省电教馆发布通知，“2018年中小学生电脑制作比赛”参赛作品必须在3月22日前上传到省基础教育资源公共服务平台。

小明3月23日才看到这则通知.结果无法上传作品,以致错过比赛。

这主要体现了信息的A.时效性B.依附性C.共享性D.普遍性2.下列智能手机操作中,属于人工智能技术应用范畴的是A.通过APP购买电影票B.使用翻译工具与外国人士交流C.查询本人高考成绩D.收发电子邮件3.2018年3月，国家互联网应急中心发现多个锁屏勒索类病毒变种。

该类病毒通过锁屏用户手机，勒索用户付费解锁,对手机安全和用户财产均造成严重威胁。

为了防止病毒侵害.下列行为合理的是①手机上安装杀毒软件并定期升级在条病毒②公共场所通过免费无线网络进行手机支付③将手机连接到公共电脑上作为U盘使用④通过手机厂商的应用商城下载APP软件A.①④B.①③C.②④D.②③4.“喂,张立宪吗?这里是社保中心医保核查部您上个月十七号,在华西医科大学附属医院开药740元,医保支付620元,医保监察系统发现,您的医保卡存在违规开药的现象，涉嫌骗保，请按照我说的进行以下操作……，这是某电影中的片段,受害人在5分钟内被骗走4万元人民币。

假如你接到陌生人电话,对方要求你汇款或对银行卡进行相关操作,下列做法最可靠的是A.接到电话后,立即按照对方的要求进行汇款B.根据对方自报的身份进行判断后决定是否汇款C.根据对方所说事件的真实性决定是否汇款D.接到此类电话,立即挂断不予理睬5.已知十六进制数(12B) :转换为十进制数的运算过程为:(12B)16 =1x16^2 +2x16^1 +11x16^0=299,则(6F)H转换为十进制数的结果为A.109B.110C.111D.1126.目前有些超市提供自助结算系统，对顾客所购商品进行结算,此类自助结算系统属于A.操作系统B.数据库应用系统C.数据库管理系统D.编译系统7.小明诵读明朝张居正的诗句“瘦筇又逐孤鸿远,浪迹还如落叶分”时，遇到生僻字“筇”,他用Word的“拼音指南”工具，获知“筇”的读音为"qióng"。

绝密★启用前2018年普通高等学校招生全国统一考试理科综合能力测试试题卷注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.作答时，务必将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3.考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 P 31 S 32 Fe 56一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

学@科网1.下列关丁人体中蛋白质功能的叙述，错误的是A.浆细胞产生的抗体可结合相应的病蠹抗原B.肌细胞中的某些蛋白质参与肌肉收缩的过程C蛋白质结合M#形成的血红蛋白参与Q运输D.细胞核中某些蛋白质是染色体的重要组成成分2.下列有关物质跨膜运输的叙述，正确的是A.巨噬细胞摄入病原体的过程届丁协助扩散B.固醇类激素进入靶细胞的过程届丁主动运输C神经细胞受到刺激时产生的Nc+内流届丁被动运输D.护肤品中的甘油进入皮肤细胞的过程届丁主动运输3.下列有关人体内激素的叙述，正确的是A.运动时，肾上腺素水平■升高，可使心率加快。

说明激素是高能化合物B.饥饿时，胰高血糖素水平升高，促进糖原分解，说明激素具有酶的催化活性C进食后，胰岛素水平升高，其既可加速糖原合成，也可作为细胞的结构组分D.宵春期，性激素水平■升高，随体液到达靶细胞，与受体结合可促进机体发育4.有些作物的种子入库前需要经过风干处理，与风干前相比，下列说法错误的是A.风干种子中有机物的消耗减慢B.风干种子上微生物不易生长繁殖C风干种子中细胞呼吸作用的强度高D.风干种子中结合水与自由水的比值大5.下列关丁病蠹的叙述，错误的是A.从烟草花叶病蠹中可以提取到RNAB.T2噬菌体可感染肺炎双球菌导致其裂解C HIV可引起人的获得性免疫缺陷综合征D.阻断病蠹的传播可降低其所致疾病的发病率6.在致癌因子的作用下，正常动物细胞可转变为癌细胞，有关癌细胞特点的叙述错误的是A.细胞中可能发生单一基因突变，细胞问黏着性增加B.细胞中可能发生多个基因突变，细胞的形态发生变化C细胞中的染色体可能受到损伤，细胞的增殖失去控制D.细胞中遗传物质可能受到损伤，细胞表面的糖蛋白减少7.化学与生活密切相关。

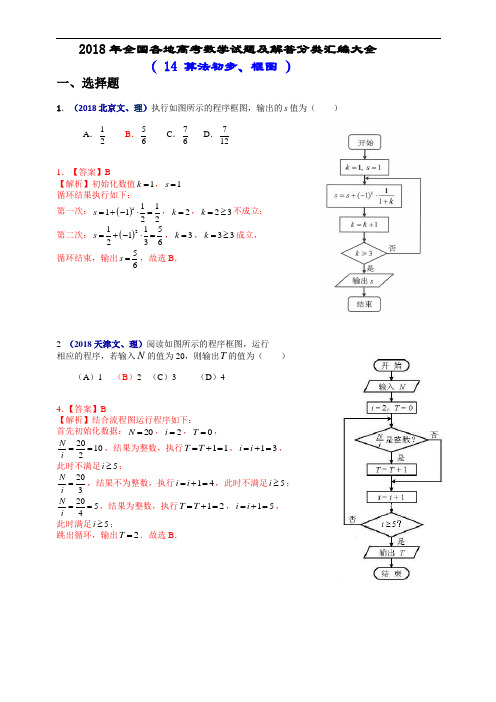
2018年全国各地高考数学试题及解答分类汇编大全（ 14 算法初步、框图 ）一、选择题1．（2018北京文、理）执行如图所示的程序框图，输出的s 值为（ ）A ．12B ．56C ．76D ．7121．【答案】B【解析】初始化数值1k =，1s = 循环结果执行如下：第一次：()1111122s =+-⋅=，2k =，23k =≥不成立；第二次：()21151236s =+-⋅=，3k =，33k =≥成立，循环结束，输出56s =，故选B ．2 （2018天津文、理）阅读如图所示的程序框图，运行相应的程序，若输入N 的值为20，则输出T 的值为（ ）（A ）1 （B ）2 （C ）3 （D ）4 4．【答案】B【解析】结合流程图运行程序如下：首先初始化数据：20N =，2i =，0T =， 20102N i ==，结果为整数，执行11T T =+=，13i i =+=， 此时不满足5i ≥； 203N i =，结果不为整数，执行14i i =+=，此时不满足5i ≥； 2054N i ==，结果为整数，执行12T T =+=，15i i =+=， 此时满足5i ≥；跳出循环，输出2T =．故选B ．3．（2018全国新课标Ⅱ文、理）为计算11111123499100S =-+-++-，设计了如图的程序框图， 则在空白框中应填入（ ）A ．1i i =+B ．2i i =+C ．3i i =+D ．4i i =+ 3．【答案】B【解析】由11111123499100S =-+-+⋯+-得程序框图先对奇数项累加，偶数项累加，最后再相减． 因此在空白框中应填入2i i =+，选B ．二、填空1．（2018江苏）一个算法的伪代码如图所示，执行此算法，最后输出的S 的值为 ▲ ．1．【答案】8【解析】由伪代码可得3I =，2S =；5I =，4S =；7I =，8S =；因为76>，所以结束循环，输出8S =．三、解答题。

绝密＊考试结束前2018年4月浙江省普通高校招生选拦考科目考试技术试题考生须知：姓名：准考证号：本试题卷分两部分，第一部分信息技术，第二部分通用技术。

全卷共16页，第一部分1至10页，第二部分11至16页。

满分100分，考试时间90分钟。

其中加试题部分为30分，用【加试题】标出。

1. 答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

2答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

3. 非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上相应区域内，作图时可先使用2B铅笔， 确定后须用黑色字迹的签字笔或钢笔描黑， 答案写在本试题卷上无效。

第一部分信息技术（共50分）一、选择题（本大题共12小题，每小题2分，共24分，每小题列出的四个备选项中只有一个是符合题目要求的，不选、错选、多选均不得分。

）1. 下列有关信息的说法，正确的是（）A. 信息在计算机内部采用二进制代码表示B. 只有最新的信息才具有价值C.只能借助计算机才能处理信息D. 信息不能脱离它所反应的事物被存储答案：A【解析】A.计算机处理信息，本质上是对二进制数进行计算处理，信息在计算机内部采用二进制代码表示，计算机才能处理。

B. 信息具有时效性，但是过期的信息也具有历史研究价值。

C.计算机只是处理信息的其中一种技术D .信息可以脱离它所反应的事物被存储，但不能脱离载体2. 超文本标记语言用于描述网页的内容，该语言的简称是（）A. WWWB. URLC. HTIPD.H TML 答案：D【解析】WWW:万维网，全称为"Wo r dWi d We b ")。

URL 统一资源地址（网址）。

HTTP :超文本传输协议（浏览器与服务器传输）。

HTML :超文本标记语言（用千描述网页）3使用某OCR软件进行字符识别，发现识别正确率较低，可能的原因有（）＠识别前没有进行倾斜校正＠识别前没有进行合理的区域划分＠识别前没有放大显示＠扫描原始文稿时设置的扫描分辨率较低A .CD@® B. CD@© C.CD®© D.@®©答案： B【解析】识别率和图像的切斜度、分辨率、区域类型划分等有关。

B.邮崗寄送申请材料山去接岀国逮交材料C. 103D. 1042018年江西省高考技术试题第一部分倍息技术加分） 第I 卷必修模块（70分）一、选择題（本大题20小题'毎小题2分，井枷分。

每小題给出的四个选项中•只有一顼是苻合超目要求的）1，知电教馆发布通知「20悟年中小罕牛.电棘制作比軽”參赛作晶必须在3月22 H 前匕传到省幕础教育资源 金共服务半台七小明3月23 H 才看到这则適却*结果尤法上传作品•以敷倍过比赛。

这主要洋取「信息的 乩时效性«. ssm&製孚性 （1曾涸性2•下列钢能手机操作中•属于入王押能技术应用范畴的眉 A,通过AI 屮购买电影粟 B 使用翻译工具与外国人士交流C 僅询本人高易成绩I ）收发电子邮件工那用年了 ”，啊烹互联倒应急中也发现*个锁屏勒索类病再变种「该类屈事通过锁屛用八于机•勒家囲门 村费解锁・对手机安全和用户財产均造成严用咸胁为r 防止情旅侵害.下列行为令理的是 ① 手机上安然杀誓软件井定期升级、査杀摘毒 ② 公共场所通过见费无线网塔进行手机支付I 融将手机连搖到公共电脑上作为u 盘使用④iS 过手机厂商的应用商城卜皱AFT 软件A.®@H ®@G ②©•D.②®4邛亂张立罐眄？这里壘社保中心戾煤枝査部”您上牛”1七号•在华西医科大学附网低院开药7北元.医保 支H 62Q 元•医保监察系统发现，您的展保卡存在违规开细的现象削嫌骗保册按將税说的进行戍卜操件 ……”.这是某电影屮的片段*受富人在5分仲内被骗走瑰万无人民「氐 假如称接到陌生人电话」寸方要求 你汇款或对丫艮行卡进行相黄撫作■下列做的是 乩楼到电话肓’丈即按照对方的要求进行?T.款 乩根据对方自报的身份逬行判断后决定是否汇款C 根据对方所说聊件的直实性涯宦层否汇款 D.接到此类电话•立即挂断不予理睬工已抑十六进制数（12B ）.转换为十进制数的运算过程为L （12B ）1^lxl61+2xl6^11Mi^99T M （6F ）l （W 换为十进制数的结果为A. 109B. HOC. HlD. 1126. 目前有些趙市提供n 朋給算系统，对顾客所购商甜进行給惊,此类白的结n 系统屈于 A 襟件杲统B.故邺库应用泵统C.数据库管俚乘统L.编译系竦7. 小期前读明朝张居正的诗旬懺飾又逐孤鸿远，独迹还如講叶分欄时.谓到牛僻字“幣，他用Word 的浄音指南"工民嵌知沖的好为虫瞬叭 小明萩取肚信息的来源是 九啦申媒介B.纸质媒介C 事物D •专业人士乩随看技术的进步*检索方式也发生『改变:在稟校开展的*传统中戡药知识进校园"活动中，同学们借助手 机拍照，使用照片搜索的方法辨识苔种中草药材.TMfitJ 的喀称3g 态和生长周期等特性口上述新型检索 方式賦于 儿目录检嬢B.关键说检離C •图粽楡盍D ，个牲flS 检寮9.某校运动会开將式的稈序为:升国旗、壽国歌,校领导讲话'运动员入场，裁舛员代表发言，运动员代表壇言。

2018年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ1． 已知集合{}8,2,1,0=A ，{}8,6,1,1-=B ，那么_____=B A I2． 若复数z 满足i z i 21+=⋅，其中i 是虚数单位，则z 的实部为_____ 3． 已知5位裁判给某运动员打出的分数的茎叶图如图所示，那么这5位 裁判打出的分数的平均数为_____4． 一个算式的伪代码如图所示，执行此算法，最后输出的S的值为______5． 函数1log )(2-=x x f 的定义域为______ 6． 某兴趣小组有2名男生和3名女生，现从中选2名学生去参加，则恰好有2名女生的概率为_______7． 已知函数)22)(2sin(πϕπϕ<<-+=x y 的图象关于直线3π=x 对称，则ϕ的值是______8． 在平面直角坐标系xOy 中．若双曲线0)b 0(12222>>=-，a by a x 的右焦点F(c ，0)到一条渐近线的距离为c 23，则其离心率的值是_____ 9． 函数f(x)满足f(x ＋4)＝f(x)(x ∈R)，且在区间]2,2(-上，⎪⎪⎩⎪⎪⎨⎧≤<-+≤<=,02,21,20,2cos )(x x x x x f π则))15((f f 的值为______10． 如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为_______11． 若函数)(12)(23R a ax x x f ∈+-=在),0(+∞内有且只有一个零点，则)(x f 在[－1，1]上的最大值与最小值的和为_______12． 在平面直角坐标系xOy 中，A 为直线l ：x y 2=上在第一象限内的点，B (5，0)，以 8 99 9 011(第3题)I ←1S ←1While I<6I ←I+2S ←2SEnd WhilePnint S (第4题)AB 为直径的圆C 与l 交于另一点D ，若0=⋅CD AB ，则点A 的横坐标为_______ 13． 在ABC ∆中角A ，B ，C 所对的边分别为a ，b ，c ，︒=∠120ABC ，ABC ∠的平分线交AC 与点D ，且BD ＝1，则4a ＋c 的最小值为_______ 14． 已知集合},12|{*N n n x x A ∈-==，},2|{*N n x x B n∈==， 将A Y B 的所有元素从小到大依次排列构成一个数列}{n a ．记n S 为数列}{n a 的前n 项的和，则使得1n 12+>n a S 成立的n 的最小值为______15． 在平行六面体ABCD —A 1B 1C 1D 1中，AA 1＝AB ，AB 1⊥B 1C 1．求证：(1)AB //平面A 1B 1C ；(2)平面ABB 1A 1⊥A 1BC ．16． 已知βα,为锐角，34tan =α，55)cos(-=+βα，(1)求α2cos 的值；(2)求)tan(βα-的值．17． 某农场有一块农田，如图所示，宽、它的边界由圆O 的一段弧MPN(P 为圆弧的中点)和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米，先规划在此 农田上修建两个温室大棚，大棚Ⅰ内的地形为矩形ABCD ，大棚Ⅱ内的地块形状为CDP ∆，要求A ，B 均在线段MN 上，C ，D 均在圆弧上．设OC 与MN 所成的角为θ．(1)用θ分别表示矩形ABCD 和CDP ∆的面积，并确定θsin 的取值范围；(2)若大棚Ⅰ内种值甲种蔬菜，大棚Ⅱ内种值乙种蔬菜，甲、乙两种蔬菜的单位两种 年产值之比为4：3．求当θ为何值时，能使甲、乙两种蔬菜折总产值最大．18． 如图，在平面直角坐标系xOy 中，椭圆C 过点)21,3(，焦点)0,3(),0,3(21F F -圆O 的直径为F 1F 2．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标； ②直线l 与椭圆C 交于A ，B 两点，若OAB ∆的面积为762，求直线l 的方程．19． 记)('),('x g x f 分别为函数)(),(x g x f 的导函数，若存在R x ∈0，满足)()(00x g x f =且)(')('00x g x f =，则称0x 为函数)(x f 与)(x g 的一个“S 点”． (1)证明：函数x x f =)(与22)(2-+=x x x g 不存在“S 点”； (2)若函数1)(2-=ax x f 与x x g ln )(=存在“S 点”，求实数a 的值；(3)已知函数a x x f +-=2)(，xbe x g x =)(，对任意0>a ，判断是否存在b>0，使函数)(x f 与)(x g 在区间),0(+∞内存在“S 点”，并说明理由．20． 设}{n a 是首项为1a ，公差为d 的等差数列， }{n b 是首项为1b ，公比为q 的等比数列．(1)设1a ＝0，1b ＝1，q ＝2，若1b b a n n ≤-对n ＝1，2，3，4均成立，求d 的取值范围； (2)若1a ＝1b >0，*N m ∈，]2,1(m q ∈，证明：存在R d ∈，使得1b b a n n ≤-对n ＝1，2，3，……m ＋1均成立，并求d 的取值范围(用1b ，m ，q 表示)．。