2014届数学试题选编29：算法初步(教师版) Word版含答案

算法初步【课前回顾】1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．(2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题．2．程序框图程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．3．三种基本逻辑结构及相应语句【课前快练】1．如图所示的程序框图的运行结果为________．解析：因为a ＝2，b ＝4，所以输出S ＝24＋42＝2.5.答案：2.52．执行如图所示的程序框图，如果输出的结果为0，那么输入的x 的值为________．解析：当x ≤0时，由－x 2＋1＝0，得x ＝－1；当x ＞0时，第一次对y 赋值为3x ＋2，第二次对y 又赋值为－x 2＋1，最后y ＝－x 2＋1，于是由－x 2＋1＝0，得x ＝1，综上知输入的x 的值为－1或1.答案：－1或13．执行如图所示的程序框图，则输出的结果为________．解析：进行第一次循环时，S ＝1005＝20，i ＝2，S ＝20>1；进行第二次循环时， S ＝205＝4，i ＝3，S ＝4>1；进行第三次循环时， S ＝45，i ＝4，S ＝45<1，此时结束循环，输出的i ＝4. 答案：44．执行如图所示的程序框图，则输出的结果为________．解析：第一次循环：S ＝12，n ＝4；第二次循环：n ＝4<8，S ＝12＋14，n ＝6；第三次循环：n ＝6<8，S ＝12＋14＋16，n ＝8；第四次循环：n ＝8<8不成立，输出S ＝12＋14＋16＝1112.答案：1112考点一 基本算法语句1．解决算法语句的3步骤(1)通读全部语句，把它翻译成数学问题； (2)领悟该语句的功能；(3)根据语句的功能运行程序，解决问题． 2．算法语句应用的4关注1．根据下列算法语句，当输入x 为60时，输出y 的值为( )A ．25B ．30C ．31D ．61解析：选C 该语句表示分段函数y ＝⎩⎪⎨⎪⎧0.5x ，x ≤50，25＋0.6×(x －50)，x >50， 当x ＝60时，y ＝25＋0.6×(60－50)＝31. 故输出y 的值为31.2．按照如图程序运行，则输出K 的值是________．解析：第一次循环，X ＝7，K ＝1； 第二次循环，X ＝15，K ＝2； 第三次循环，X ＝31，K ＝3，X >16， 终止循环，则输出K 的值是3. 答案：3考点二 顺序结构和条件结构顺序结构和条件结构的运算方法(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可．(2)条件结构中条件的判断关键是明确条件结构的功能，然后根据“是”的分支成立的条件进行判断．(3)对于条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．【典型例题】1．执行如图所示的程序框图．若输出y ＝－3，则输入角θ＝( )A.π6B ．－π6 C.π3 D ．－π3解析：选D 由输出y ＝－3<0，排除A 、C ，又当θ＝－π3时，输出y ＝－3，故选D.2．某程序框图如图所示，现输入如下四个函数，则可以输出的函数为( )A ．f (x )＝cos x x ⎝⎛⎭⎫－π2<x <π2，且x ≠0B．f(x)＝2x－1 2x＋1C．f(x)＝|x| xD．f(x)＝x2ln(x2＋1)解析：选B由程序框图知该程序输出的是存在零点的奇函数，选项A、C中的函数虽然是奇函数，但在给定区间上不存在零点，故排除A、C.选项D中的函数是偶函数，故排除D.选B.3．定义[x]为不超过x的最大整数，例如[1.3]＝1.执行如图所示的程序框图，当输入的x为4.7时，输出的y值为()A．7B．8.6C．10.2D．11.8解析：选C当输入的x为4.7时，执行程序框图可知，4.7>3，4.7－[4.7]＝0.7，即4.7－[4.7]不等于0，因而可得y＝7＋([4.7－3]＋1)×1.6＝10.2，即输出的y值为10.2.考点三循环结构角度(一)由程序框图求输出(输入)结果循环结构程序框图求输出结果的方法解决此类问题最常用的方法是列举法，即依次执行循环体中的每一步，直到循环终止，但在执行循环体的过程中：第一，要明确是当型循环结构还是直到型循环结构，根据各自特点执行循环体；第二，要明确框图中的累加变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；第三，要明确循环终止的条件是什么，什么时候要终止执行循环体．1．(2017·全国卷Ⅱ)执行如图所示的程序框图，如果输入的a＝－1，则输出的S＝()A．2B．3C．4 D．5解析：选B运行程序框图，a＝－1，S＝0，K＝1，K≤6成立；S＝0＋(－1)×1＝－1，a＝1，K＝2，K≤6成立；S＝－1＋1×2＝1，a＝－1，K＝3，K≤6成立；S＝1＋(－1)×3＝－2，a＝1，K＝4，K≤6成立；S＝－2＋1×4＝2，a＝－1，K＝5，K≤6成立；S＝2＋(－1)×5＝－3，a＝1，K＝6，K≤6成立；S＝－3＋1×6＝3，a＝－1，K＝7，K≤6不成立，输出S＝3.2．(2017·全国卷Ⅲ)执行如图所示的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为()A．5 B．4C．3 D．2解析：选D法一：执行程序框图，S＝0＋100＝100，M＝－10，t＝2；S＝100－10＝90，M＝1，t＝3，S<91，输出S，此时，t＝3不满足t≤N，所以输入的正整数N的最小值为2.法二：要求的是最小值，观察选项，发现选项中最小的为2，不妨将2代入检验．当输入的N为2时，第一次循环，S＝100，M＝－10，t＝2；第二次循环，S＝90，M＝1，t＝3，此时退出循环，输出S＝90，符合题意，故选D.3．(2017·山东高考)执行两次如图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为()A．0,0 B．1,1C．0,1 D．1,0解析：选D当输入x＝7时，b＝2，因为b2>x不成立且x不能被b整除，故b＝3，这时b2>x成立，故a＝1，输出a的值为1.当输入x＝9时，b＝2，因为b2>x不成立且x不能被b整除，故b＝3，这时b2>x不成立且x能被b整除，故a＝0，输出a的值为0.角度(二)完善程序框图程序框图补全问题的求解方法(1)先假设参数的判断条件满足或不满足；(2)运行循环结构，一直到运行结果与题目要求的输出结果相同为止；(3)根据此时各个变量的值，补全程序框图．4．(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n－2n>1 000的最小偶数n，那么在◇和▭两个空白框中，可以分别填入()A ．A >1 000和n ＝n ＋1B ．A >1 000和n ＝n ＋2C ．A ≤1 000和n ＝n ＋1D ．A ≤1 000和n ＝n ＋2解析：选D 程序框图中A ＝3n －2n ，且判断框内的条件不满足时输出n ，所以判断框中应填入A ≤1 000，由于初始值n ＝0，要求满足A ＝3n －2n >1 000的最小偶数，故执行框中应填入n ＝n ＋2.5．(2018·广东五校协作体诊断)已知函数f (x )＝ax 3＋12x 2在x ＝－1处取得极大值，记g (x )＝1f ′(x ).执行如图所示的程序框图，若输出的结果S >2 0172 018，则判断框中可以填入的关于n的判断条件是( )A ．n ≤2 017?B ．n ≤2 018?C ．n >2 017?D ．n >2 018?解析：选B f ′(x )＝3ax 2＋x ，则f ′(－1)＝3a －1＝0，解得a ＝13，g (x )＝1f ′(x )＝1x 2＋x ＝1x (x ＋1)＝1x －1x ＋1，则g (n )＝1n －1n ＋1，即S ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1，因为输出的结果S >2 0172 018，分析可知判断框中可以填入的判断条件是“n ≤2 018？”，选B.【针对训练】1．(2017·北京高考)执行如图所示的程序框图，输出的s 值为( )A ．2 B.32C.53D.85解析：选C 运行该程序，k ＝0，s ＝1，k <3； k ＝0＋1＝1，s ＝1＋11＝2，k <3；k ＝1＋1＝2，s ＝2＋12＝32，k <3；k ＝2＋1＝3，s ＝32＋132＝53，此时不满足循环条件，输出s ，故输出的s 值为53.2．(2017·天津高考)阅读如图所示的程序框图，运行相应的程序，若输入N 的值为24，则输出N 的值为( )A ．0B ．1C ．2D ．3解析：选C 第一次循环，24能被3整除，N ＝243＝8>3；第二次循环，8不能被3整除，N ＝8－1＝7>3； 第三次循环，7不能被3整除，N ＝7－1＝6>3； 第四次循环，6能被3整除，N ＝63＝2<3，结束循环，故输出N 的值为2.3．如图，给出的是计算12＋14＋…＋1100的值的一个程序框图，则图中判断框内(1)处和执行框内的(2)处应填的语句是( )A ．i >100，n ＝n ＋1B ．i >100，n ＝n ＋2C ．i >50，n ＝n ＋2D ．i ≤50，n ＝n ＋2解析：选C经第一次循环得到的结果是⎩⎪⎨⎪⎧S ＝12，n ＝4，i ＝2；经第二次循环得到的结果是⎩⎪⎨⎪⎧ S ＝12＋14，n ＝6，i ＝3；经第三次循环得到的结果是⎩⎪⎨⎪⎧S ＝12＋14＋16，n ＝8，i ＝4.据观察S 中最后一项的分母与i 的关系是分母＝2(i －1)， 令2(i －1)＝100，解得i ＝51，即需要i ＝51时输出S .故图中判断框内(1)处和执行框中的(2)处应填的语句分别是i >50，n ＝n ＋2.【课后演练】1．对任意非零实数a ，b ，若a ⊗b 的运算原理如图所示，则log 24⊗⎝⎛⎭⎫13－1的值为( )A.13 B ．1 C.43D ．2解析：选B log 24＝2<3＝⎝⎛⎭⎫13－1，由题意知所求值为3－12＝1.2.执行如图所示的程序框图，如果输入的t ∈[－1,3]，则输出的s ∈( )A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]解析：选A 当－1≤t ＜1时，s ＝3t ， 则s ∈[－3,3)．当1≤t ≤3时，s ＝4t －t 2.函数s ＝4t －t 2在[1,2]上单调递增，在[2,3]上单调递减． ∴s ∈[3,4]． 综上知s ∈[－3,4]．3．(2017·山东高考)执行如图所示的程序框图，当输入的x 的值为4时，输出的y 的值为2，则空白判断框中的条件可能为( )A．x＞3 B．x＞4C．x≤4 D．x≤5解析：选B当x＝4时，若执行“是”，则y＝4＋2＝6，与题意矛盾；若执行“否”，则y＝log24＝2，满足题意，故应执行“否”．故判断框中的条件可能为x＞4.4．(2018·合肥质检)执行如图所示的程序框图，如果输出的k的值为3，则输入的a的值可以是()A．20 B．21C．22 D．23解析：选A根据程序框图可知，若输出的k＝3，则此时程序框图中的循环结构执行了3次，执行第1次时，S＝2×0＋3＝3，执行第2次时，S＝2×3＋3＝9，执行第3次时，S＝2×9＋3＝21，因此符合题意的实数a的取值范围是9≤a<21，故选A.5．执行如图所示的程序框图，若输入的n＝4，则输出的s＝()A．10 B．16C．20 D．35解析：选C执行程序框图，第一次循环，得s＝4，i＝2；第二次循环，得s＝10，i＝3；第三次循环，得s＝16，i＝4；第四次循环，得s＝20，i＝5.不满足i≤n，退出循环，输出的s＝20.6．如图所示的程序框图的算法思想源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图(图中“m MOD n”表示m除以n的余数)，若输入的m，n分别为495,135，则输出的m＝()A．0 B．5C．45 D．90解析：选C该程序框图是求495与135的最大公约数，由495＝135×3＋90,135＝90×1＋45,90＝45×2，所以495与135的最大公约数是45，所以输出的m＝45，故选C.7．(2018·石家庄模拟)程序框图如图，若输入的S＝1，k＝1，则输出的S为________．解析：执行程序框图，第一次循环，k＝2，S＝4；第二次循环，k＝3，S＝11；第三次循环，k＝4，S＝26；第四次循环，k＝5，S＝57.此时，终止循环，输出的S＝57.答案：578．执行如图所示的程序框图，如果输入的a，b的值分别为56,140，则输出的a＝________.解析：执行程序框图，第一次循环：a＝56，b＝140－56＝84；第二次循环：a＝56，b＝84－56＝28；第三次循环：a＝56－28＝28，b＝28，退出循环，输出的a＝28.答案：289．执行如图所示的程序框图，若输入的N＝20，则输出的S＝________.解析：依题意，结合题中的程序框图知，当输入的N ＝20时，输出S 的值是数列{2k －1}的前19项和，即19(1＋37)2＝361.答案：36110．(2018·宝鸡质检)阅读如图所示的程序框图，运行相应的程序，若输入x 的值为1，则输出S 的值为________．解析：依题意，执行题中的程序框图，当输入x 的值为1时，进行第一次循环，S ＝1<50，x ＝2；进行第二次循环，S ＝1＋23＝9<50，x ＝4； 进行第三次循环，S ＝9＋43＝73>50， 此时结束循环，输出S 的值为73. 答案：7311．(2018·合肥质检)执行如图所示的程序框图，则输出n 的值为( )A ．9B ．11C ．13D ．15解析：选C 由程序框图可知，S 是对1n 进行累乘，直到S <12 018时停止运算，即当S ＝1×13×15×17×19×111<12 018时循环终止，此时输出的n ＝13.12.如图所示，程序框图的功能是( )A ．求⎩⎨⎧⎭⎬⎫1n 的前10项和B ．求⎩⎨⎧⎭⎬⎫12n 的前11项和C ．求⎩⎨⎧⎭⎬⎫1n 的前11项和D ．求⎩⎨⎧⎭⎬⎫12n 的前10项和解析：选D 依题意可得S ＝12＋14＋16＋…＋12n ，故程序框图的功能是求⎩⎨⎧⎭⎬⎫12n 的前10项和，选D.13.(2018·长春质检)运行如图所示的程序框图，则输出的结果为( ) A ．1 008 B ．1 009 C ．2 017 D ．2 018解析：选B 由程序框图知，此题是求当k 取1,2，…，2 018这些值时，(－1)k ·k 的和，所以输出的S ＝0－1＋2－3＋4－…＋2 016－2 017＋2 018＝0＋(－1＋2)＋(－3＋4)＋…＋(－2 017＋2 018)＝1 009.14．(2018·湘中名校联考)执行如图所示的程序框图，如果运行结果为5 040，那么判断框中应填入( )A ．k <6?B ．k <7?C ．k >6?D ．k >7?解析：选D 执行程序框图，第一次循环，得S ＝2，k ＝3； 第二次循环，得S ＝6，k ＝4； 第三次循环，得S ＝24，k ＝5； 第四次循环，得S ＝120，k ＝6； 第五次循环，得S ＝720，k ＝7； 第六次循环，得S ＝5 040，k ＝8，此时满足题意，退出循环，输出的S ＝5 040， 故判断框中应填入“k >7？”．15．(2018·惠州三调)执行如图所示的程序框图，则输出的结果为________．解析：法一：i ＝1，S ＝lg 13＝－lg 3>－1；i ＝3，S ＝lg 13＋lg 35＝lg 15＝－lg 5>－1；i ＝5，S ＝lg 15＋lg 57＝lg 17＝－lg 7>－1；i ＝7，S ＝lg 17＋lg 79＝lg 19＝－lg 9>－1；i ＝9，S ＝lg 19＋lg 911＝lg 111＝－lg 11<－1，故输出的i ＝9.法二：因为S ＝lg 13＋lg 35＋…＋lg i i ＋2＝lg 1－lg 3＋lg 3－lg 5＋…＋lg i －lg(i ＋2)＝－lg(i＋2)，当i ＝9时，S ＝－lg(9＋2)<－lg 10＝－1，所以输出的i ＝9.答案：916．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为________．解析：当条件x ≥0，y ≥0，x ＋y ≤1不成立时，输出S 的值为1，当条件x ≥0，y ≥0，x ＋y ≤1成立时，输出S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分所示，由图可知当直线S ＝2x ＋y 经过点M (1,0)时S 最大，其最大值为2×1＋0＝2，故输出S 的最大值为2.答案：2。

算法初步测试题及答案work Information Technology Company.2020YEAR2第一章 算法初步一、选择题1．看下面的四段话，其中是解决问题的算法的是( ).A ．把高一5班的同学分成两组，高个子参加篮球赛，矮个子参加拔河比赛B ．把高一5班的同学分成两组，身高达到170 cm 的参加篮球赛，不足170 cm 的参加拔河比赛C ．把a ，b 的值代入x ＝ab ，求方程ax ＝b 的解D ．从2开始写起，后一个数为前一个数与2的和，不断地写，写出所有偶数2．任何一个算法都必须有的基本结构是( ). A ．顺序结构 B ．条件结构 C ．循环结构D ．三个都有3．右边的程序框图(如图所示)，能判断任意输入的整数x 的奇偶性：其中判断框内的条件是( ).A ．m ＝0B ．x ＝0C ．x ＝1D ．m ＝14．给出以下一个算法的程序框图(如图所示)，该程序框图的功能是( ).A ．求输出a ，b ，c 三数的最大数B ．求输出a ，b ，c 三数的最小数C ．将a ，b ，c 按从小到大排列D ．将a ，b ，c 按从大到小排列5．右图给出的是计算21＋41＋61＋ … ＋201的值的 一个程序框图，其中判断框内应填入的条件是( ).A ．i ＞10B ．i ＜10C ．i ＞20D ．i ＜206．直到型循环结构为( ).ABC D7．下列给出的赋值语句中正确的是().A．4＝M B．M＝－MC．2B＝A－3 D．x＋y＝08．右边程序执行后输出的结果是().A．－1 B．0 C．1 D．29．我国古代数学发展曾经处于世界领先水平，特别是宋、元时期的“算法”，其中可以同欧几里德辗转相除法相媲美的是().A．割圆术B．更相减损术C．秦九韶算法D．孙子乘余定理10．下面是一个算法的程序．如果输入的x的值是20，则输出的y的值是().A．100 B．50 C．25 D．150二、填空题11．下列关于算法的说法正确的是. (填上正确的序号)①某算法可以无止境地运算下去②一个问题的算法步骤不能超过1万次③完成一件事情的算法有且只有一种④设计算法要本着简单方便可操作的原则12．下列算法的功能是.S1输入A，B；(A，B均为数据)S2A＝A＋B；S3B＝A－B；S4A＝A－B；S5输出A，B．13．如图，输出的结果是.14 如图，输出的结果是.15 已知函数y＝⎩⎨⎧-+，x，x232流程图表示的是给定x值，求其相应函数值的算法．请将该流程图补充完整．其中①处应填，②处应填．若输入x＝3，则输出结果为.x≤3316．如图，输出结果为.三、解答题17．某小区每月向居民收取卫生费，计费方法是：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费，并画出程序框图.18．编写程序，计算一个学生数学、语文、英语三门课的平均成绩.19．假定在银行中存款10 000元，按11.25％的利率，一年后连本带息将变为11 125元，若将此款继续存人银行，试问多长时间就会连本带利翻一番请用直到型和当型两种语句写出程序.20．用辗转相除法求91和49的最大公约数.第一章算法初步参考答案一、选择题1．解析：A．何为高个子，何为矮个子，标准不明确.C．当a＝0时公式是无效的.D．非有限步可以完成.只有B符合算法的三个要求，所以答案是B.解：选B.2．A 解析：顺序结构是最简单的结构，也是最基本的结构.3．A 解析：x除以2，如余数为0，则x为偶数；余数不为0，则x为奇数.4．B 解析：从程序框图可知：输出的是三个数中的最小值.5．A 解析：这是一个10项求和问题.6．B 解析：直到型循环在执行了一次循环体之后，对控制循环条件进行判断，当条件不满足时反复做，满足则停止.7．B 解析：依据赋值语句的概念，选B是正确的.8．B 解析：程序执行后输出的结果是0，故选B.9．B10．D 解析：∵20＞5，∴y＝20×7.5＝150，∴选 D.二、填空题11．答案：④.解析：由算法的特点所确定.12．答案：实现数据A，B的互换.解析：利用赋值语句的意义与题中算法的步骤进行分析.13．答案：12. 解析：m＝2，p＝7，m＝12.4x＝10 000r＝11.25／100y＝0WHILE x＜20 000 y＝y＋1 x＝10 000y＝0r＝11.25／100 Doy＝y＋114．答案：105. 解析：T＝1，I＝1，T＝1，I＝3，不满足条件；T＝3，I＝5，不满足条件；T＝15，I＝7，不满足条件；T＝105，I＝9，满足条件．输出T.15．答案：①x≤3；②y＝－3x2；5. 解析：根据给出函数的解析式分析可填出.16．答案：9．解析：逐个取值计算．三、解答题17．解析：根据题意，可考虑用条件结构来进行算法设计.解：算法步骤：第一步，输入人数x，设收取的卫生费为m(元)．第二步，判断x与3的大小．若x＞3，则费用为m＝5＋(x－3)×1.2；若x≤3，则费用为m＝5．第三步，输出m．18．分析：先写出算法，画出程序框图，再进行编程．程序框图：程序：19．解：用当型用直到型20．解析：由 91＝49×1＋42，得 42＝91－49×1．因为余数42≠0，所以由辗转相除法，得 49＝42×1＋7，即 7＝49－42×1； 42＝7×6，即 0＝42－7×6．所以，91和49的最大公约数等于7．5。

L 单元 算法初步与复数目录L 单元 算法初步与复数 ............................................................................................................... 1 L1 算法与程序框图 ...................................................................................................................... 1 L2 基本算法语句 .......................................................................................................................... 9 L3 算法案例 .................................................................................................................................. 9 L4 复数的基本概念与运算 .......................................................................................................... 9 L5 单元综合 . (13)L1 算法与程序框图【数学（理）卷·2015届浙江省重点中学协作体高考摸底测试（201408）】L112．如右图，如果执行右面的程序框图，输入正整数m n ,，满足m n ，那么输出的P 等于 。

【知识点】循环结构的程序框图；排列公式.【答案解析】mn A 解析 ：解：第一次循环：1,1,+1k p p n m ===-； 第二次循环：()()2,12k p n m n m ==-+-+； 第三次循环：()()()3,123k p n m n m n m ==-+-+-+; …第m 次循环：()()(),12...1k m p n m n m n n ==-+-+- 此时结束循环，输出()()()12...1m n p n m n m n n A =-+-+-=故答案为：mn A .【思路点拨】分析程序中各变量、各语句的作用，再根据流程图所示的顺序可知：该程序的作用是利用循环计算并输出变量P 的值，用表格对程序运行过程中各变量的值进行分析即可．【数学（文）卷·2015届湖北省部分重点中学高三上学期起点考试（201408）】L1D23．若开始某程序框图如图所示，则输出的n 的值是 ( )A. 3B. 4C. 5D. 6【知识点】程序框图，等差数列的前n 项和公式.【答案解析】C 解析 ：解：框图首先给循环变量n 赋值1，给累加变量p 赋值1， 执行n=1+1=2，p=1+（2×2-1）=1+3=4； 判断4＞20不成立，执行n=2+1=3，p=1+3+（2×3-1）=1+3+5=9； 判断9＞20不成立，执行n=3+1=4，p=1+3+5+（2×4-1）=1+3+5+7=16； …由上可知，程序运行的是求首项为1，公差为2的等差数列的前n 项和， 由()2121202n n p n+-==>，且n ∈N *，得n=5．故选C ．【思路点拨】框图首先给循环变量n 赋值1，给累加变量p 赋值1，然后执行运算n=n+1，p=p+2n-1，然后判断p ＞20是否成立，不成立循环执行n=n+1，p=p+2n-1，成立时算法结束，输出n 的值．且由框图可知，程序执行的是求等差数列的前n 项和问题．当前n 项和大于20时，输出n 的值．【数学（文）卷·2015届浙江省重点中学协作体高考摸底测试（201408）】L1 4．如图给出的是计算11124108+++的值的一个程序框图， 则图中判断框内（1）处和执行框中的（2）处应填的语句是 （ ）。

第十四章算法初步、推理与证明、复数第1讲算法的含义及流程图对应学生用书P201考点梳理1．算法与流程图(1)算法通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成．(2)设计算法要注意的问题①认真分析问题，找出解决此问题的一般方法．②借助有关的变量或参数对算法加以表述．③将解决问题的过程划分为若干步骤．④用简练的语言将各个步骤表示出来．(3)流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作的内容，流程线表示操作的先后次序.2.三种基本逻辑结构(1)顺序结构是由若干个依次执行的处理步骤组成的，这是任何一个算法都离不开的基本结构．其结构形式为(2)选择结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式，也称为分支结构．其结构形式为(3)循环结构是指在算法中，需要重复执行同一操作的结构．反复执行的处理步骤称为循环体．循环结构又分为当型和直到型．循环结构主要用在一些有规律的重复计算的算法中，如累加求和，累乘求积等问题常常需要用循环结构来设计算法．其结构形式为【助学·微博】一个复习指导算法初步是必考内容之一，试题难度不大，属基础题，以填空题形式出现，主要考查流程图知识，但往往与其他章节知识结合，常与数列等知识融合在一起．两种循环语句的区别在当型语句中，是当条件满足时执行循环体，而在直到型语句中是当条件不满足时执行循环体，二者是有区别的，在解决问题时用两种循环语句编写应注意条件的不同．考点自测1．阅读如图所示的流程图，若输入的x是2，则输出的值为________．解析∵2>0，故输出的值为1.答案 12．如图所示的是一个算法的流程图，已知a1＝3，输出的结果为7，则a2的值是________．解析已知图形是一个顺序结构的框图，表示的算法的功能是求两数a1、a2的算术平均数，已知a1＝3，输出结果为7，有a1＋a22＝7，解得a2＝11.答案113．(2012·泰州模拟)如图是一个算法的流程图，则输出a的值是________．解析a＝log2256＝log228＝8＞2；a＝log28＝3＞2；a＝log23＜2，所以输出a＝log23.答案log234．(2011·湖南卷)若执行如图所示的框图，输入x1＝1，x2＝2，x3＝4，x4＝8，则输出的数为________．解析解读框图可知，本题的实质是求4个数x1，x2，x3，x4的平均数，其平均数为1＋2＋4＋84＝154.答案15 45.(2011·课标全国卷改编)执行如图所示的流程图，如果输入的N是6，那么输出的p是________．解析当输入的N是6时，由于k＝1，p＝1，因此p＝p·k＝1.此时k＝1，满足k<6.故k＝k＋1＝2.当k＝2时，p＝1×2，此时满足k<6，故k＝k＋1＝3.当k＝3时，p＝1×2×3，此时满足k<6，故k＝k＋1＝4.当k＝4时，p＝1×2×3×4，此时满足k<6，故k＝k＋1＝5.当k＝5时，p＝1×2×3×4×5，此时满足k<6，故k＝k＋1＝6.当k＝6时，p＝1×2×3×4×5×6＝720，此时k<6不再成立，因此输出p＝720.答案720对应学生用书P202考向一算法的意义与设计及顺序结构的应用【例1】已知点P(x0，y0)和直线l：Ax＋By＋C＝0，求点P(x0，y0)到直线l的距离d，写出其算法并画出流程图．解算法如下：第一步，输入x0，y0及直线方程的系数A，B，C.第二步，计算Z1←Ax0＋By0＋C.第三步，计算Z2←A2＋B2.第四步，计算d←|Z1| Z2.第五步，输出d.该算法对应的流程图如图所示：[方法总结] 给出一个问题，设计算法应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)将解决问题的过程划分为若干个步骤；(4)用简练的语言将各个步骤表示出来．【训练1】已知f(x)＝x2－2x－3.求f(3)、f(－5)、f(5)，并计算f(3)＋f(－5)＋f(5)的值．设计出解决该问题的一个算法，并画出流程图．解算法如下：S1x←3.S2y1←x2－2x－3.S3x←－5.S4y2←x2－2x－3.S5 x ←5.S6 y 3←x 2－2x －3. S7 y ←y 1＋y 2＋y 3.S8 输出y 1，y 2，y 3，y 的值． 该算法对应的流程图如图所示：考向二 算法的选择结构【例2】 已知函数y ＝⎩⎨⎧－2x (x >0)，0 (x ＝0)，2x (x <0)，写出求该函数的函数值的算法及流程图．解 算法如下： S1 输入x ；S2 如果x >0，转S3，如果x ＝0，转S4，否则转S5； S3 y ←－2x ； S4 y ←0； S5 y ←2x ； S6 输出y .相应的流程图如图所示：[方法总结] 利用选择结构解决算法问题时，要引入判断框，要根据题目的要求引入一个或多个判断框．而判断框内的条件不同，对应的下一图框中的内容和操作也相应地进行变化，故应逐个分析判断框内的条件．【训练2】 (1)如图(1)是某个函数求值的流程图，则满足该程序的函数解析式为________．(2)(2010·山东卷)执行如图(2)所示的流程图，若输入x ＝4，则输出y 的值为________．解析 (1)依题意得当x <0时，f (x )＝2x －3； 当x ≥0时，f (x )＝5－4x .因此f (x )＝⎩⎨⎧2x －3，x <05－4x ，x ≥0.(2)当x ＝4时，y ＝1，不满足|y －x |<1， 因此由x ＝y 知x ＝1.当x ＝1时，y ＝－12，不满足|y －x |<1， 因此由x ＝y 知x ＝－12. 当x ＝－12时，y ＝－54， 此时，⎪⎪⎪⎪⎪⎪－54＋12<1成立．答案 (1)f (x )＝⎩⎨⎧2x －3，x <05－4x ，x ≥0(2)－54考向三 算法的循环结构【例3】 设计算法求11×2＋12×3＋13×4＋…＋12 011×2 012的值，并画出流程图．解 算法如下： S1 S ←0，i ←1；S2 如果i ≤2 011，则转S3，否则，转S5； S3 S ←S ＋1i (i ＋1)； S4 i ←i ＋1，转S 2； S5 输出S . 流程图：法一 当型循环流程图： 法二 直到型循环流程图：[方法总结] 利用循环结构表示算法，第一要确定是利用当型循环结构，还是直到型循环结构；第二要注意根据条件，设计合理的计数变量、累加变量等，特别要注意循环结构中条件的表述要恰当、精确，以免出现多一次循环或少一次循环的情况．【训练3】(1)(2012·江苏卷)如图(1)是一个算法流程图，则输出的k的值是________．(2)(2011·浙江卷)某流程图如图(2)所示，则该程序运行后输出的k的值是________．解析(1)∵条件语句为k2－5k＋4>0，即k<1或k>4.∴当k＝5时，满足此条件，此时输出5.(2)初始值：k＝2，执行“k＝k＋1”得k＝3，a＝43＝64，b＝34＝81，a>b不成立；k＝4，a＝44＝256，b＝44＝256，a>b不成立；k＝5，a＝45＝1 024，b＝54＝625，a>b成立，此时输出k＝5.答案(1)5(2)5对应学生用书P203规范解答24算法流程图的识别与读取2014年高考，算法初步为必考知识，估计试题难度为中、低档题，一般是以流程图为考查重点，考查对算法思想和流程图的应用．【示例】(2012·山东卷改编)执行右面的程序框图，如果输入a＝4，那么输出的n的值为________．[审题路线图] (1)这是一个累加求和的当型循环结构．(2)P、Q是累加变量，n是计数变量．[解答示范] n＝0，P＝0＋40＝1，Q＝2＋1＝3；n＝1，P＝1＋41＝5，Q＝6＋1＝7；n＝2，P＝5＋42＝21，Q＝14＋1＝15；n＝3，P>Q.故n值为3.(5分)[点评] (1)在解决循环结构问题时，一定要弄明白计数变量和累加变量是用什么字母表示的，再把这两个变量的变化规律弄明白，就能理解这个流程图的功能了，问题也就清楚了．(2)在解决带有循环结构的流程图问题时，循环结构的终止条件是至关重要的，这也是考生非常容易弄错的地方，考生一定要根据问题的情境弄清楚这点．高考经典题组训练1．(2012·福建卷)阅读如图所示的程序框图，运行相应的程序，输出的s值等于________．解析第1次s＝1，k＝1；第2次s＝1，k＝2，；第3次s＝0，k＝3；第4次s＝－3，k＝4.结束．答案－32．(2012·浙江卷)若某程序框图如图所示，则该程序运行后输出的值是________．解析第1次，T＝1，第2次，T＝12，第3次，T＝16，第4次，T＝124，第5次，T＝1120，i＝6结束．答案1 1203．(2012·安徽卷改编)如图所示，程序框图(算法流程图)的输出结果是________．解析答案 44．(2012·湖北卷)阅读如图所示的程序框图，运行相应的程序，输出的结果s ＝________.解析第1次，n＝1，s＝1，a＝3，第2次，n＝2，s＝4，a＝5，第3次，n＝3，s＝9，输出s＝9.答案95．(2010·江苏卷)如图是一个算法的流程图，则输出S的值是________．解析执行过程如下表：答案63对应学生用书P377分层训练A级基础达标演练(时间：30分钟满分：40分)1．关于流程图的图形符号的理解，正确的是________(填序号)．①任何一个流程图都必须有起止框；②输入框只能在开始框之后，输出框只能放在结束框之前；③判断框是唯一具有超过一个退出点的图形符号；④对于一个流程图来说，判断框内的条件是唯一的．解析任何一个程序都有开始和结束，因而必须有起止框；输入和输出可以放在算法中任何需要输入、输出的位置；判断框内的条件不是唯一的，如a>b，亦可写为a≤b.故只有①③对．答案①③2．(2011·天津卷改编)阅读如图所示流程图，运行相应的程序，若输入x的值为－4，则输出y的值为________．解析当x＝－4时，|x|＝4>3，x赋值为x＝|－4－3|＝7>3，∴x赋值为x＝|7－3|＝4>3，x再赋值为x＝|4－3|＝1<3，则y＝21＝2，输出2.答案 23．(2012·盐城市期末考试)执行如图所示的流程图，则输出的y的值是________．解析当x＝16时，经循环得x＝4，再循环得x＝2，此时不满足x>2，故y＝e2－2＝1.答案 14.执行如图所示流程图，得到的结果是________．解析由题意，得S＝12＋14＋18＝78.答案7 85．(2013·无锡调研)某算法的流程图如图所示，若输入a＝4，b＝2，c＝6，则输出的结果为________．(第4题图)解析 原执行程序是在输入的a ，b ，c 中，选出最大的数， ∴结果为6. 答案 66．(2012·南通调研一)如图是求函数值的算法流程图，当输入值为2时，则输出值为________．解析 本题的流程图其实是一个分段函数 y ＝⎩⎨⎧2x －3，x <0，5－4x ，x ≥0.当输入x ＝2时，y ＝5－4×2＝－3. 答案 －37．(2011·天津卷)阅读下面的程序框图，运行相应的程序，则输出i 的值为________． 解析 第一次运行结束：i ＝1，a ＝2； 第二次运行结束：i ＝2，a ＝5； 第三次运行结束：i ＝3，a ＝16；第四次运行结束：i ＝4，a ＝65，故输出i ＝4. 答案 48．(2012·天津卷改编)阅读如图算法流程图，运行相应的程序，当输入x 的值为－25时，输出x 的值为________．解析 当输入x ＝－25时，|－25|>1成立，因此x ＝|－25|－1＝4，x ＝4时，|4|>1成立，因此x ＝|4|－1＝1；x ＝1时，1>1不成立，因此x ＝2×1＋1＝3，输出x 为3. 答案 3分层训练B 级 创新能力提升1．(2011·江西卷)如图是某算法的流程图，则程序运行后输出的结果是________．解析 n ＝1，s ＝0＋(－1)1＋1＝0，n＝2时，s＝0＋(－1)2＋2＝3，n＝3时，s＝3＋(－1)3＋3＝5，n＝4时，s＝5＋(－1)4＋4＝10>9，故运行输出结果为10.答案102．(2011·陕西卷)如图中，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分，当x1＝6，x2＝9，p＝8.5时，x3等于________．解析由题意知x1＝6，x2＝9，此时|x1－x2|＝3>2，若|x3－6|<|x3－9|，则p＝6＋x3 2＝8.5，解得x3＝11，不满足|x3－6|<|x3－9|，舍去；若|x3－6|≥|x3－9|，则p＝x3＋9 2＝8.5，解得x3＝8，符合题意．答案83．(2011·辽宁卷改编)执行如图流程图，如果输入的n是4，则输出的p是________．解析由k＝1，n＝4，知1<4⇒p＝1＝0＋1⇒s＝1，t＝1⇒k＝2⇒2<4⇒p＝1＋1＝2⇒s＝1，t＝2⇒k＝3⇒3<4⇒p＝1＋2＝3⇒s＝2，t＝3⇒k＝4⇒4<4――→否输出p＝3.答案 34．(2010·广东卷)某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x1，…，x n(单位：吨)．根据如图所示的程序框图，若n＝2，且x1，x2分别为1,2，则输出的结果s为________．解析当i＝1时，s1＝1，s2＝1，s＝1×(1－1)＝0，当i＝2时，s1＝3，s2＝1＋4＝5，s＝12×⎝⎛⎭⎪⎫5－12×9＝14.答案1 45．(2012·苏州调研一)如图是一个算法的流程图，则最后输出W的值是________．解析由流程图，执行过程为：故输出答案146．(2012·泰州调研二)2010年上海世博会园区每天9：00开园，20：00停止入园．在如图所示的框图中，S表示上海世博会官方网站在每个整点报道的入园总人数，a表示整点报道前1个小时内入园人数，则空白的处理框内应填________．解析框图表示的是每天入园参观的人数统计，报道的入园总人数的时间为整点，但入园的时间有整点入园和非整点入园．举例说明如11点报道的入园人数为10点钟以后到11点整入园的人数与之前入园的人数之和．答案S←S＋a7．(2011·苏锡常镇调研)如图给出的是计算1＋13＋15＋…＋119的值的一个流程图，其中判断框内应填入的条件是________．解析按算法的运算本质，执行到n＝19时，结束输出．即：答案i>108.(2011·湖南卷)若执行如图所示的流程图，输入x1＝1，x2＝2，x3＝3，x＝2，则输出的数为________．解析通过流程图可以看出本题的实质是求数据x1，x2，x3的方差，根据方差公式，得S＝13[(1－2)2＋(2－2)2＋(3－2)2]＝23.答案2 3第2讲基本算法语句对应学生用书P204考点梳理1．基本算法语句五种基本算法语句分别是赋值语句、输入语句、输出语句、条件语句、循环语句．2．赋值语句、输入语句、输出语句赋值语句用符号“←”表示，其一般格式是变量←表达式(或变量)，其作用是对程序中的变量赋值；输入语句“Read a，b”表示输入的数据依次递给a，b，输出语句“Print x”表示输出运算结果x.3．算法的选择结构由条件语句来表达，条件语句有两种，一种是If－Then－Else另一种是If－Then语句，其格式是If A ThenBEnd If，对应的流程图为.4．算法中的循环结构，可以运用循环语句来实现．(1)当循环的次数已经确定，可用“For”语句表示“For”语句的一般形式为对应的流程图为说明：上面“For”和“End For”之间缩进的步骤称为循环体，如果省略“Step步长”，那么重复循环时，I每次增加1.(2)不论循环次数是否确定都可以用下面循环语句来实现循环结构当型和直到型两种语句结构．对应的流程图为对应的流程图为【助学·微博】关于赋值语句，有以下几点需要注意：(1)赋值号左边只能是变量名字，而不是表达式，例如3←m是错误的．(2)赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y←x，表示用x的值替代变量Y的原先的取值，不能改写为x←Y.因为后者表示用Y的值替代变量x的值．(3)在一个赋值语句中只能给一个变量赋值，不能出现多个“←”．考点自测1．(课本改编题)阅读右面伪代码，则输出的结果为________．解析a＝5，b＝3，c＝(a＋b)2＝4.答案 42．(2012·南通一模)计算机执行下面的伪代码后，输出的结果是________．解析a＝3＋1＝4，b＝4－3＝1.答案4,13．当a＝1，b＝3时，执行以下伪代码输出的结果为________．解析因为1<3满足a<b，所以x＝1＋3＝4.答案 44．要使下面的“For”循环语句循环执行15次，“初值”应为________．For I From“初值”To 5 Step－1解析由x－5＋1＝15，得x＝19.答案 195．(2012·南京模拟)当x ＝2时，下面的伪代码执行后的结果是________． 解析 当i ＝1时，s ＝0×2＋1＝1， 当i ＝2时，s ＝1×2＋1＝3， 当i ＝3时，s ＝3×2＋1＝7， 当i ＝4时，s ＝7×2＋1＝15. 答案 15i ←1s ←0While i ≤4s ←s ·x ＋1i ←i ＋1End While Print s对应学生用书P205考向一 输入、输出和赋值语句【例1】 要求输入两个正数a 和b 的值，输出a b 与b a 的值，画出流程图，写出伪代码．解 流程图： 伪代码如下： Read a ，b A ←a bB ←b aPrint A ，B[方法总结] 编写伪代码的关键在于搞清问题的算法，特别是算法结构，然后确定采取哪一种算法语句．【训练1】 编写伪代码，求用长度为l 的细铁丝分别围成一个正方形和一个圆时的面积．要求输入l 的值，输出正方形和圆的面积．(π取3.14) 解 伪代码如下：错误!【例2】 已知分段函数y ＝⎩⎨⎧－x ＋1，x ＜0，0，x ＝0，x ＋1，x ＞0.编写伪代码，输入自变量x 的值，输出其相应的函数值，并画出流程图． 解 伪代码如下： 流程图 Read xIf x ＜0 Then y ←－x ＋1ElseIf x ＝0 Theny ←0Else y ←x ＋1 End If End If Print y[方法总结] 这是一个分段函数问题，计算函数值必须先判断x 的范围，因而设计求函数值的算法必须用到选择结构，相应程序的书写应用条件语句来书写．【训练2】 已知函数f (x )＝⎩⎨⎧x 2－1(x ≥0)，2x 2－5(x <0)，设计一个算法并用伪代码实现每输入一个x 的值，都得到相应的函数值．解 用x ，y 分别表示自变量和函数值，则相应的算法如下： S1 输入x 的值；S2 判断x 的取值范围，如果x ≥0，则y ←x 2－1，求函数值，否则y ←2x 2－5； S3 输出函数值y . 伪代码如下： Read xIf x ≥0 Then y ←x 2－1Else y ←2×x 2－5End If Print y【例3】编写伪代码，求1＋12＋13＋…＋1n>1 000的最小自然数n的值．解本题不等号的左边1＋12＋13＋…＋1n是有规律的累加，故可引入和变量S，转化为求S>1 000的最小自然数n的值，故可以用“While S≤1 000”来控制循环．伪代码如下：错误![方法总结] 通过本题掌握While语句的特点，注意与For语句的区别．在设计算法时要注意循环体的构成，不能颠倒．【训练3】某算法的伪代码如下：错误!则输出的结果是________．解析伪代码所示的算法是一个求和运算．答案50 101对应学生用书P206规范解答25算法语句的识别与读取结合江苏高考以及实施新课标省份的高考试题来看，对算法的考查深度、难度并不大．考查基本上集中在两个方面：一是流程图表示的算法；二是伪代码表示的算法．【示例】(2011·江苏卷)根据如图所示的伪代码，当输入a，b分别为2,3时，最后输出的m的值是________．[审题路线图] (1)本题是一个含条件语句的伪代码．(2)利用流程图和伪代码的关系、算法语句的意义解题．[解答示范] 由题意知，m为a，b中的最大值，故最后输出的m值为3.Read a，bIf a>b Thenm←aElsem←bEnd IfPrint m(5分)[点评] 计算机在执行条件语句时，首先对If后的条件进行判断，如果条件符合，就执行Then后的语句1，若条件不符合，对于If—Then—Else语句就执行Else后的语句2，然后结束这一条件语句．对于If—Then语句，则直接结束该条件语句．高考经典题组训练1．下列伪代码的运行结果是________．a←3b←5Print a＋b答案82．(2012·无锡模拟)当x＝3时，下面算法输出结果是________．解析这是一个条件语句，x＝3满足x<10，所以y＝2x＝6.答案 63．下面伪代码运行后输出的结果为________．解析由于x＝5，所以条件不满足，程序执行Else语句后面的y＝y＋3，所以y＝－17，从而得x－y＝5－(－17)＝22；y－x＝－17－5＝－22.答案22，－224．为了在运行下面的伪代码后输出y＝16，应输入的整数x的值是________．解析当x<0时，由(x＋1)2＝16得x＝－5；当x≥0时，由1－x2＝16得x2＝－15，矛盾．答案－55．(2013·南京外国语学校调研)如图所示的伪代码的输出结果为________．解析S＝1＋1＋3＋5＋7＋9＝26.答案26对应学生用书P379分层训练A级基础达标演练(时间：30分钟满分：60分)一、填空题(每小题5分，共30分)1．按照下面的算法进行操作：S1x←2.35S2y←Int(x)S3Print y最后输出的结果是________．解析Int(x)表示不大于x的最大整数．答案 22．下面是一个算法的伪代码，如果输入的x的值是20，则输出的y的值是________．解析∵x＝20>5，∴执行赋值语句y＝7.5x＝7.5×20＝150.答案150Read xIf x≤5Then y←10xElsey←7.5xEnd IfPrint y Read xIf x<3Theny←2xElseIf x>3Theny←x2－1Elsey←2End IfEnd If3．以上给出的是用条件语句编写的一个伪代码，该伪代码的功能是________． 答案 求下列函数当自变量输入值为x 时的函数值f (x )，其中f (x )＝⎩⎨⎧2x ，x <32，x ＝3x 2－1，x >34．(2013·南通调研)根据如图的算法，输出的结果是________．S ←0For I From 1 to 10 S ←S ＋IEnd For Print S End解析 S ＝1＋2＋3＋…＋10＝10×112＝55.答案 555．(2012·苏州调研)根据如图所示的伪代码，最后输出的t ＝________. 解析 由题意，得t ＝1＋3＋5＋7＋9＝25. 答案 256．(2012·苏北四市质检(一))根据如图所示的伪代码，可知输出的S ＝________. 解析 i ＝1时第一次循环：i ＝3，S ＝9；第二次循环：i ＝5，S ＝13；第三次循环：i ＝7，S ＝17；第四次循环：i ＝9，S ＝21，此时不满足条件“i <8”，停止循环，输出S ＝21. 答案 21二、解答题(每小题15分，共30分)7．已知分段函数y ＝⎩⎨⎧x ＋3(x ＜0)，0(x ＝0)，x ＋8(x ＞0)，编写伪代码，输入自变量x 的值，输出其相应的y 值，并画出流程图．解 伪代码如下： 流程图如下： Read xIf x ＜0 Then y ←x ＋3ElseIf x ＝0 Theny ←0Else y ←x ＋8 End If End If Print y8．用伪代码写出求1＋3＋32＋33＋34的值的算法． 解S ←0For I From 0 to 4 Step 1 S ←S ＋3I End For Print S分层训练B 级 创新能力提升1．(2012·盐城调研)如图所示的伪代码运行的结果为________． 解析 a ＝1＋1＝2，b ＝2＋1＝3，c ＝2＋3＝5； a ＝2＋3＝5，b ＝5＋3＝8，c ＝5＋8＝13； a ＝5＋8＝13，b ＝13＋8＝21，c ＝13＋21＝34. 答案 34(第1题图) (第2题图)2．(2012·高邮模拟)根据如图所示伪代码，可知输出结果S＝________，I＝________.解析S＝2×7＋3＝17，I＝7＋2＝9.答案1793．(2012·泰州调研)如图，运行伪代码所示的程序，则输出的结果是________．a←1b←2I←2While I≤6a←a＋bb←a＋bI←I＋2End WhilePrint b解析流程图的执行如下：当I＝8时，答案344．(2012·南京调研)写出下列伪代码的运行结果．(1)图1的运行结果为________；(2)图2的运行结果为________．解析(1)图1的伪代码是先执行S←S＋i，后执行i←i＋1∴S＝0＋1＋2＋…＋(i－1)＝(i－1)i2>20，∴i的最小值为7.(2)图2的伪代码是先执行i←i＋1，后执行S←S＋i，∴S＝0＋1＋2＋…＋i＝i(i＋1)2>20.∴i的最小值为6.答案(1)7(2)65．(2012·常州调研)根据下列伪代码画出相应的流程图，并写出相应的算法．S←1n←1While S<1 000S←S×nn←n＋1End WhilePrint n解流程图如图：算法如下：S1S←1；S2n←1；S3如果S<1 000，那么S←S×n，n←n＋1，重复S3；S4输出n.6．(2012·苏北四市调研)设计算法，求1－3＋5－7＋…－99＋101的值，用伪代码表示．解用“For”语句表示，S ←1a ←1For I From 3 To 101 Step 2 a ←a ×(－1) S ←S ＋a ×I End For Print S用“While”语句表示， S ←1I ←3a ←1While I ≤101a ←a ×(－1) S ←S ＋a ×I I ←I ＋2End While Print S 第3讲 合情推理与演绎推理对应学生用书P207考点梳理1．归纳推理(1)定义：根据一类事物中部分事物具有某种属性，推断该类事物中每一个事物都有这种属性的推理．或者由个别事实概括出一般结论的推理，称为归纳推理(简称归纳)． (2)归纳推理的特点①归纳推理是由部分到整体，由个别到一般的推理； ②归纳推理的结论不一定为真；③归纳的个别情况越多，越具有代表性，推广的一般性命题就越可靠． 2．类比推理(1)定义：由于两类不同对象具有某些类似的特征，在此基础上，根据一类对象的其他特征，推断另一类对象也具有类似的其他特征的推理，称为类比推理．类比推理是两类事物特征之间的推理．(2)类比推理的特点①类比推理是由特殊到特殊的推理；②类比推理属于合情推理，其结论具有或然性，可能为真，也可能为假；③类比的相似性越多，相似的性质与推测的性质之间越相关，类比得出的命题就越可靠．3．演绎推理(1)定义：演绎推理是根据已知的事实和正确的结论，按照严格的逻辑法则得到新结论的推理过程．(2)演绎推理的特点①演绎推理是由一般到特殊的推理；②当前提为真时，结论必然为真．(3)演绎推理的主要形式是三段论，其一般模式为：①大前提——已知的一般原理；②小前提——所研究的特殊情况；③结论——根据一般原理，对特殊情况作出的判断．【助学·微博】一个命题解读本部分内容是新课标内容，高考考查的几率非常大．对归纳推理与类比推理仍会以填空形式考查，主要是由个别情况归纳出一般结论，或运用类比的形式给出某个问题的结论．而演绎推理以解答题出现的可能性较大，因此要求学生具备一定的逻辑推理能力．两个防范(1)合情推理是从已知的结论推测未知的结论，发现与猜想的结论都要经过进一步严格证明．(2)演绎推理是由一般到特殊的推理，它常用来证明和推理数学问题，注意推理过程的严密性，书写格式的规范性．考点自测1．(2012·盐城市第一学期摸底考试)在平面上，若两个正方形的边长的比为1∶2，则它们的面积比为1∶4；类似地，在空间内，若两个正方体的棱长的比为1∶2，则它们的体积比为________．解析 由正方体的体积之比等于棱长的立方之比可得． 答案 1∶82．给出下列三个类比结论．①(ab )n ＝a n b n 与(a ＋b )n 类比，则有(a ＋b )n ＝a n ＋b n ；②log a (xy )＝log a x ＋log a y 与sin(α＋β)类比，则有sin(α＋β)＝sin αsin β； ③(a ＋b )2＝a 2＋2ab ＋b 2与(a ＋b )2类比，则有(a ＋b )2＝a 2＋2a ·b ＋b 2. 其中结论正确的序号是________． 答案 ③3．“因为指数函数y ＝a x 是增函数(大前提)，而y ＝⎝ ⎛⎭⎪⎫13x 是指数函数(小前提)，所以函数y ＝⎝ ⎛⎭⎪⎫13x是增函数(结论)”，上面推理的错误在于________错误导致结论错．解析 “指数函数y ＝a x 是增函数”是本推理的大前提，它是错误的，因为实数a 的取值范围没有确定，所以导致结论是错误的． 答案 大前提错4．(2010·陕西卷)观察下列等式：13＋23＝32,13＋23＋33＝62,13＋23＋33＋43＝102，…，根据上述规律，第五个等式为________．解析 13＋23＝32＝(1＋2)2,13＋23＋33＝62＝(1＋2＋3)2,13＋23＋33＋43＝102＝(1＋2＋3＋4)2，则13＋23＋…＋n 3＝(1＋2＋…＋n )2＝⎣⎢⎡⎦⎥⎤n (n ＋1)22，故第五个等式即为当n ＝6时，13＋23＋33＋43＋53＋63＝⎝⎛⎭⎪⎫6×722＝212. 答案 13＋23＋33＋43＋53＋63＝2125．(2011·盐城调研)观察下列几个三角恒等式： ①tan 10°tan 20°＋tan 20°tan 60°＋tan 60°tan 10°＝1； ②tan 5°tan 100°＋tan 100°tan(－15°)＋tan(－15°)tan 5°＝1； ③tan 13°tan 35°＋tan 35°tan 42°＋tan 42°tan 13°＝1.一般地，若tan α，tan β，tan γ都有意义，你从这三个恒等式中猜想得到的一个结论为________．解析 由于三个等式中，角度之间满足10°＋20°＋60°＝90°，5°＋100°－15°＝90°，13°＋35°＋42°＝90°.于是通过类比可得．答案 当α＋β＋γ＝90°时，tan αtan β＋tan βtan γ＋tan γtan α＝1对应学生用书P207考向一 归纳推理【例1】 观察下列等式： 1＝1，1＋2＝3，1＋2＋3＝6，1＋2＋3＋4＝10，1＋2＋3＋4＋5＝15， 13＝1，13＋23＝9，13＋23＋33＝36，13＋23＋33＋43＝100，13＋23＋33＋43＋53＝225.可以推测：13＋23＋33＋…＋n 3＝________(n ∈N *，用含有n 的代数式表示)． 解析 第二列等式的右端分别是1×1,3×3,6×6,10×10,15×15，∵1,3,6,10,15，…第n 项a n ，与第n －1项a n －1(n ≥2)的差为：a n －a n －1＝n ，∴a 2－a 1＝2，a 3－a 2＝3，a 4－a 3＝4，…，a n －a n －1＝n ，各式相加得，a n ＝a 1＋2＋3＋…＋n ，其中a 1＝1，∴a n ＝1＋2＋3＋…＋n ，即a n ＝n (n ＋1)2，∴a 2n ＝14n 2(n ＋1)2.答案 14n 2(n ＋1)2[方法总结] 所谓归纳，就是由特殊到一般，因此在归纳时就要分析所给条件之间的变化规律，从而得到一般结论． 【训练1】 (2011·山东)设函数f (x )＝xx ＋2(x >0)，观察： f 1(x )＝f (x )＝xx ＋2，f 2(x )＝f (f 1(x ))＝x3x ＋4， f 3(x )＝f (f 2(x ))＝x7x ＋8， f 4(x )＝f (f 3(x ))＝x15x ＋16，……根据以上事实，由归纳推理可得：当n ∈N *且n ≥2时，f n (x )＝f (f n －1(x ))＝________. 解析 由f (x )＝x x ＋2(x >0)得，f 1(x )＝f (x )＝x x ＋2， f 2(x )＝f (f 1(x ))＝x 3x ＋4＝x(22－1)x ＋22， f 3(x )＝f (f 2(x ))＝x 7x ＋8＝x (23－1)x ＋23， f 4(x )＝f (f 3(x ))＝x 15x ＋16＝x(24－1)x ＋24，……∴当n ≥2且n ∈N *时，f n (x )＝f (f n －1(x ))＝x(2n－1)x ＋2n.答案x(2n －1)x ＋2n考向二 类比推理【例2】 在平面几何里，有“若△ABC 的三边长分别为a ，b ，c ，内切圆半径为r ，则三角形面积为S △ABC ＝12(a ＋b ＋c )r ”，拓展到空间，类比上述结论，“若四面体ABCD 的四个面的面积分别为S 1，S 2，S 3，S 4，内切球的半径为r ，则四面体的体积为________”．解析 三角形的面积类比为四面体的体积，三角形的边长类比为四面体四个面的面积，内切圆半径类比为内切球的半径．二维图形中12类比为三维图形中的13，得V 四面体ABCD ＝13(S 1＋S 2＋S 3＋S 4)r .答案 V 四面体ABCD ＝13(S 1＋S 2＋S 3＋S 4)r[方法总结] (1)类比是从已经掌握了的事物的属性，推测正在研究的事物的属性，是以旧有的认识为基础，类比出新的结果；(2)类比是从一种事物的特殊属性推测另一种事物的特殊属性；(3)类比的结果是猜测性的，不一定可靠，但它却有发现的功能．【训练2】 (2012·盐城模拟)记等差数列{a n }的前n 项和为S n ，利用倒序求和的方法，可将S n 表示成首项a 1、末项a n 与项数n 的一个关系式，即公式S n ＝n (a 1＋a n )2；类似地，记等比数列{b n }的前n 项积为T n ，且b n >0(n ∈N *)，试类比等差数列求和的方法，可将T n 表示成首项b 1、末项b n 与项数n 的一个关系式，即公式T n ＝________.解析 利用等比数列性质，即若m ＋n ＝p ＋q ，则b m ·b n ＝ b p ·b q ，得T 2n ＝(b 1b 2…b n )·(b n b n －1…b 2b 1)＝(b 1b n )n，即T n ＝(b 1b n )n 2. 答案 (b 1b n )n 2考向三 演绎推理【例3】 数列{a n }的前n 项和记为S n ，已知a 1＝1，a n ＋1＝n ＋2n S n (n ∈N ＋)，证明：(1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列；(2)S n ＋1＝4a n .证明 (1)∵a n ＋1＝S n ＋1－S n ，a n ＋1＝n ＋2n S n ， ∴(n ＋2)S n ＝n (S n ＋1－S n )，即nS n ＋1＝2(n ＋1)S n . ∴S n ＋1n ＋1＝2·S nn ，(小前提) 故⎩⎨⎧⎭⎬⎫S n n 是以2为公比的等比数列．(结论)(大前提是等比数列的定义，这里省略了)(2)由(1)可知S n＋1n＋1＝4·S n－1n－1(n≥2)，∴S n＋1＝4(n＋1)·S n－1n－1＝4·n－1＋2n－1·S n－1＝4a n(n≥2)(小前提)又a2＝3S1＝3，S2＝a1＋a2＝1＋3＝4＝4a1，(小前提)∴对于任意正整数n，都有S n＋1＝4a n(结论)(第(2)问的大前提是第(1)问的结论以及题中的已知条件)[方法总结] 演绎推理是从一般到特殊的推理；其一般形式是三段论，应用三段论解决问题时，应当首先明确什么是大前提和小前提，如果前提是显然的，则可以省略．【训练3】已知函数f(x)＝2x－12x＋1(x∈R)，(1)判定函数f(x)的奇偶性；(2)判定函数f(x)在R上的单调性，并证明．解(1)对∀x∈R有－x∈R，并且f(－x)＝2－x－12－x＋1＝1－2x1＋2x＝－2x－12x＋1＝－f(x)，所以f(x)是奇函数．(2)f(x)在R上单调递增，证明如下：任取x1，x2∈R，并且x1＞x2，f(x1)－f(x2)＝2x1－12x1＋1－2x2－12x2＋1＝(2x1－1)(2x2＋1)－(2x2－1)(2x1＋1)(2x1＋1)(2x2＋1)＝2(2x1－2x2) (2x1＋1)(2x2＋1).∵x1＞x2，∴2x1＞2x2＞0，即2x1－2x2＞0，又∵2x1＋1＞0,2x2＋1＞0.∴2(2x1－2x2)(2x1＋1)(2x2＋1)＞0.∴f(x1)＞f(x2)．∴f(x)在R上为单调递增函数．。

高一数学算法初步试题答案及解析1.我国《算经十书》之一《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二.问物几何？答曰：二十三.”你能用程序解决这个问题吗？【答案】见解析。

【解析】设物共m个，被3，5，7除所得的商分别为x、y、z，则这个问题相当于求不定方程的正整数解.m应同时满足下列三个条件：（1）m MOD 3=2；（2）m MOD 5=3；（3）m MOD 7=2.因此，可以让m从2开始检验，若3个条件中有任何一个不成立，则m递增1，一直到m同时满足三个条件为止.程序：m=2f=0WHILE f=0IF m MOD 3=2 AND m MOD 5=3AND m MOD 7=2 THENPRINT “物体的个数为：”；mf=1ELSEm=m+1END IFWENDEND【考点】本题主要考查算法的基本概念及算法的程序语言。

点评：经典题目。

在理解解方程组算理的基础上，首先用语言表示算法，再写出程序语言。

2.下面程序的运行结果不为4的【答案】C【解析】本题考查的是简单程序语言的运行。

A考查的是条件语句，由a←3，b←5得b＞a，应执行c←， Print c所以运行结果为4。

B考查的也是条件语句，由a←3，b←4得，应执行a←a+1，Print a所以运行结果为4。

C考查的是条件语句，由a←3，b←4得a≤b，应执行c←a+b，Print c运行结果为7。

故应选C。

【考点】程序中条件语句，赋值语句的运行。

点评：解决此类问题，先根据变量的初始值判断条件是否成立，然后再根据“是”和“否”分别执行的语句来计算运行结果。

3.设计一个解关于x的方程：ax+b=0的程序．图中给出了程序的一部分，请在横线上填上适当的语句，使程序完整．【答案】①：x= -；②：“方程无解”；③：“解为一切实数”【解析】根据题意要解关于x的方程应先判断a是否为0，如a≠0，则方程的根为所以①为；若，再判断把是否为0，若输b≠0，方程无解，②应为“方程无解”；若，则方程为，则“解为一切实数”。

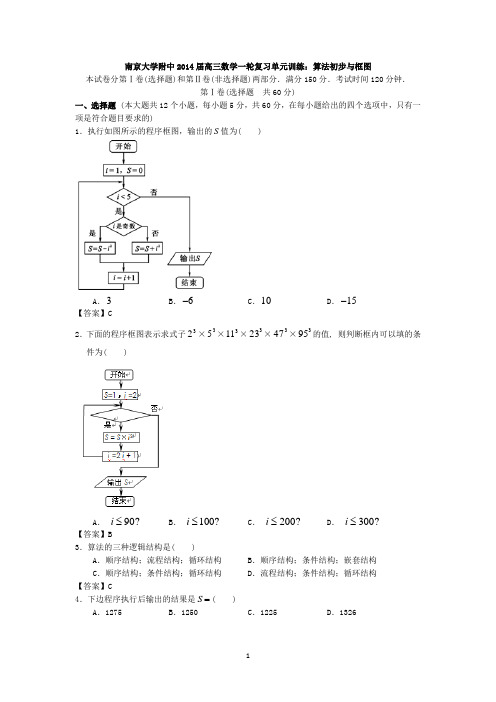
南京大学附中2014届高三数学一轮复习单元训练：算法初步与框图本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．执行如图所示的程序框图，输出的S 值为( )A ．3B ．6-C ．10D ．15-【答案】C2．下面的程序框图表示求式子32×35×311×323×347×395的值, 则判断框内可以填的条件为( )A ． ?90≤iB ． ?100≤iC ． ?200≤iD ． ?300≤i【答案】B3．算法的三种逻辑结构是( )A ．顺序结构；流程结构；循环结构B ．顺序结构；条件结构；嵌套结构C ．顺序结构；条件结构；循环结构D ．流程结构；条件结构；循环结构【答案】C4．下边程序执行后输出的结果是S =( )A ．1275B ．1250C ．1225D ．1326【答案】A5．把十进制数15化为二进制数为( )A． 1011 B．1001 (2）C． 1111（2）D．1111【答案】C6．下列说法正确的是( )A．算法就是某个问题的解题过程；B．算法执行后可以产生不同的结果；C．解决某一个具体问题算法不同结果不同；D．算法执行步骤的次数不可以为很大，否则无法实施。

【答案】B7．阅读如图所示的程序框图，运行相应的程序，输出的结果是( )A．3 B．11C．38 D．123【答案】B8．为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路，现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里）则能把电力输送到这四个村庄的输电线路的最短总长度应该是( )A．19．5 B．20．5 C．21．5 D．25．5【答案】B9．在下列各数中，最大的数是( )A ．)9(85B ．)6(210C ．C )4(1000D ．)2(11111【答案】B10．某程序的框图如图所示，则运行该程序后输出的B 的值是( )A ．63B ．31C ．15D ．7【答案】A11．执行如图所示的程序框图，若输入x=3，则输出y 的值为( )A ．5B ．9C ．17D ．33【答案】D12．执行下面的程序框图，如果输入的n 是4，则输出的p 是( )A ．8B ．5C ．3D ．2【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．已知某程序框图如图所示，则执行该程序后输出的结果为 .【答案】1214．若执行如图所示的框图，输入12341,2,4,8,x x x x ====则 输出的数等于 _ __．15【答案】415．阅读如图所示的流程图，运行相应的程序，输出的结果是____________．【答案】816．如图，是一程序框图，则输出结果为________．【答案】1011三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．写出用二分法求方程x3－x －1=0在区间［1，1.5］上的一个解的算法（误差不超过0.001），并画出相应的程序框图及程序. 【答案】用二分法求方程的近似值一般取区间［a ，b ］具有以下特征： f （a ）＜0，f （b ）＞0. 由于f （1）=13－1－1=－1＜0， f （1.5）=1.53－1.5－1=0.875＞0，所以取［1，1.5］中点25.11 =1.25研究，以下同求x2－2=0的根的方法.相应的程序框图是：开始a =1b =1.5c =0.001是是是否否否f a a a ()=--1f x x x ()=--1f x ()=0?f a f x ()()＜033x =a b +2a x=b x=a b -＜c?输出x程序：a=1 b=1.5 c=0.001DO x=（a+b ）2 f （a ）=a ∧3－a －1 f （x ）=x ∧3－x －1 IF f （x ）=0 THEN PRINT “x=”；x ELSEIF f （a ）*f （x ）＜0 THEN b=x ELSE a=xEND IFEND IFLOOP UNTIL ABS（a－b）＜=cPRINT “方程的一个近似解x=”；xEND18．修订后的《中华人民共和国个人所得税》法规定，公民全月工资、薪金所得税的起征点为1600元，即月收入不超过1600元，免于征税；超过1600元的按以下税率纳税；超过部分在500元以内（含500元）税率为5％，超过500元至2000元的部分（含2000元）税率为10％，超过2000元至5000元部分，税率为15％，已知某厂工人的月最高收入不高于5000元。

2014年高考数学试题汇编 算法初步一．选择题1. (2014北京)当7,3m n ==时，执行如图所示的程序框图，输出的S 值为（ ）.7A .42B .210C .840D2 (2014江西)阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为（ ）A.7B.9C.10D.11 【答案】B 【解析】1357910lg lg lg lg lg lg 135791111S =+++++=<-，9i ∴=，选B3 (2014新课标I).执行下图的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =A .203 B .165 C .72 D .158【答案】：D【解析】：输入1,2,3a b k ===；1n =时：1331,2,222M a b =+===； 2n =时：28382,,3323M a b =+===；3n =时：3315815,,28838M a b =+===；4n =时：输出158M = . 选D.4. (2014新课标II)执行右图程序框图，如果输入的x,t 均为2，则输出的S= （ ）A. 4B. 5C. 6D. 7 【答案】 D 【KS5U 解析】5 (2014天津)阅读右边的程序框图，运行相应的程序，输出的S 的值为（ ）（A ）15 （B ）105 （C ）245 （D ）945 【答案】B 【解析】法一..∴1057*5*3*1B S 选==法二：1i =时，3T =，3S =；2i =时，5T =，15S =；3i =时，7T =，105S =，4i =输出105S =.6(2014湖南)执行如图1所示的程序框图，如果输入的]2,2[-∈t ，则输出的S 属于（ ）A.]2,6[--B.]1,5[--C.]5,4[-D.]6,3[-7、(2014四川)执行如图的程序框图，如果输入的,x y R ，那么输出的S 的最大值为（ ） A 、0 B 、1 C 、2 D 、3 【答案】C【解析】..2)0,1(2.2,1,0,0.C y x S y x S y x y x 选处取最大值在点，目标函数画出可行区域为三角形的最大值求限制条件为相性规划问题+=+=≤+≥≥8. (2014陕西)根据右边框图，对大于2的整数N ，输出数列的通项公式是（ ）.2n Aa n = .2(1)n B a n =- .2n n C a = 1.2n n D a -=【答案】 C 【解析】C q a a a a a n 选的等比数列是.2,2∴,8,4,21321=====9(2014安徽)如图所示，程序框图（算法流程图）的输出结果是（A ）34 （B ）55 （C ）78 （D ）89 3 B10. （2014福建）阅读右图所示的程序框图，运行相应的程序，输出的S 得值等于（ ）.18A .20B .21C .40DB11. (2014重庆)执行如题（5）图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是。

数学L单元算法初步与复数L1 算法与程序框图3．L1如图1­1所示，程序框图(算法流程图)的输出结果是( )图1­1A．34 B．53 C．78 D．893．B 由程序框图可知，变量的取值情况如下：第一次循环，x＝1，y＝1，z＝2；第二次循环，x＝1，y＝2，z＝3；第三次循环，x＝2，y＝3，z＝5；第四次循环，x＝3，y＝5，z＝8；第五次循环，x＝5，y＝8，z＝13；第六次循环，x＝8，y＝13，z＝21；第七次循环，x＝13，y＝21，z＝34；第八次循环，x＝21，y＝34，z＝55，不满足条件，跳出循环．4．L1当m＝7，n＝3时，执行如图1­1所示的程序框图，输出的S值为( )图1­1A．7 B．42C．210 D．8404．C S＝1×7×6×5＝210.5．L1阅读如图1­3所示的程序框图，运行相应的程序，输出的S的值等于( )图1­3A．18B．20C．21D．405．B 输入S＝0，n＝1，第一次循环，S＝0＋2＋1＝3，n＝2；第二次循环，S＝3＋22＋2＝9，n＝3；第三次循环，S＝9＋23＋3＝20，n＝4，满足S≥15，结束循环，输出S＝20.13．L1设a是一个各位数字都不是0且没有重复数字的三位数．将组成a的3个数字按从小到大排成的三位数记为I(a)，按从大到小排成的三位数记为D(a)(例如a＝815，则I(a)＝158，D(a)＝851)．阅读如图1­2所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b＝________．图1­213．495 取a1＝815⇒b1＝851－158＝693≠815⇒a2＝693；由a2＝693⇒b2＝963－369＝594≠693⇒a3＝594；由a3＝594⇒b3＝954－459＝495≠594⇒a4＝495；由a4＝495⇒b4＝954－459＝495＝a4⇒b＝495.6．L1执行如图1­1所示的程序框图．如果输入的t∈，则输出的S属于( )A． B．C． D．图1­16．D (特值法)当t＝－2时，t＝2×(－2)2＋1＝9，S＝9－3＝6，所以D正确．7．L1阅读如图1­3所示的程序框图，运行相应的程序，则程序运行后输出的结果为( )图1­3A．7 B．9 C．10 D．117．B 由程序框图可知，运算过程如下表：图1­213.299 当x ＝9时，y ＝5，则|y －x |＝4；当x ＝5时，y ＝113，则|y －x |＝43；当x ＝113时，y ＝299，则|y －x |＝49<1.故输出y ＝299.7．L1 执行如图1­2所示的程序框图，若输入的a ，b ，k 分别为1，2，3，则输出的M ＝( )图1­2A.203 B.165 C.72 D.1587．D 逐次计算，依次可得：M ＝32，a ＝2，b ＝32，n ＝2；M ＝83，a ＝32，b ＝83，n ＝3；M＝158，a ＝83，b ＝158，n ＝4.此时输出M ，故输出的是158. 7．L1 执行如图1­2所示的程序框图，如果输入的x ，t 均为2，则输出的S ＝( )图1­2A ．4B ．5C ．6D ．77．D 逐次计算，可得M ＝2，S ＝5，k ＝2；M ＝2，S ＝7，k ＝3，此时输出S ＝7. 11．L1 执行如图1­2所示的程序框图，若输入的x 的值为1，则输出的n 的值为____．图1­211．3 x＝1满足不等式，执行循环后，x＝2，n＝1；x＝2满足不等式，执行循环后，x＝3，n＝2；x＝3满足不等式，执行循环后，x＝4，n＝3；x＝4不满足不等式，结束循环，输出的n的值为3.4．L1根据如图1­1所示的框图，对大于2的整数N，输出的数列的通项公式是( )图1­1A．a n＝2nB．a n＝2(n－1)C．a n＝2nD．a n＝2n－14．C 阅读题中所给的程序框图可知，对大于2的整数N，输出数列：2，2×2＝22，2×22＝23，2×23＝24，…，2×2N－1＝2N，故其通项公式为a n＝2n.5．E5，L1执行如图1­1所示的程序框图，如果输入的x，y∈R，那么输出的S的最大值为( )图1­1A ．0B ．1C ．2D ．35．C 题中程序输出的是在⎩⎪⎨⎪⎧x ＋y ≤1，x ≥0，y ≥0的条件下S ＝2x ＋y 的最大值与1中较大的数．结合图像可得，当x ＝1，y ＝0时，S ＝2x ＋y 取得最大值2，2>1，故选C.3．L1 阅读如图1­1所示的程序框图，运行相应的程序，输出S 的值为( )图1­1A ．15B ．105C ．245D ．9453．B 第1次循环，i ＝1，T ＝3，S ＝1×3； 第2次循环，i ＝2，T ＝5，S ＝1×3×5； 第3次循环，i ＝3，T ＝7，S ＝1×3×5×7.执行完后，这时i 变为4，退出循环，故输出S ＝1×3×5×7＝105.11．L1 若某程序框图如图1­3所示，当输入50时，则该程序运行后输出的结果是________．图1­311．6 第一次运行，S ＝1，i ＝2；第二次运行，S ＝4，i ＝3；第三次运行，S ＝11，i ＝4；第四次运行，S ＝26，i ＝5；第五次运行，S ＝57，i ＝6，此时S >n ，输出i ＝6.5．L1 执行如图1­1所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )图1­1A ．s >12B ．s >35C ．s >710D ．s >455．C 第一次循环结束，得s ＝1×910＝910，k ＝8；第二次循环结束，得s ＝910×89＝45，k ＝7；第三次循环结束，得s ＝45×78＝710，k ＝6，此时退出循环，输出k ＝6.故判断框内可填s >710.L2 基本算法语句 L3 算法案例L4 复数的基本概念与运算1．L4 复平面内表示复数i(1－2i)的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限1．A i(1－2i)＝2＋i ，其在复平面内对应的点为(2，1)，位于第一象限．2．L4、A2 已知i 是虚数单位，a ，b ∈R ，得“a ＝b ＝1”是“(a ＋b i)2＝2i ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 2．A 由a ，b ∈R ，(a ＋b i)2＝a 2－b2＋2ab i ＝2i, 得⎩⎪⎨⎪⎧a 2－b 2＝0，2ab ＝2，所以⎩⎪⎨⎪⎧a ＝1，b ＝1或⎩⎪⎨⎪⎧a ＝－1，b ＝－1.故选A.1．L4 设z ＝10i3＋i ，则z 的共轭复数为( )A ．－1＋3iB ．－1－3iC ．1＋3iD ．1－3i1．D z ＝10i 3＋i ＝10i （3－i ）（3＋i ）（3－i ）＝10（1＋3i ）10＝1＋3i ，根据共轭复数的定义，其共轭复数是1－3i.1．L4 设i 是虚数单位，z －表示复数z 的共轭复数．若z ＝1＋i ，则z i＋i ·z －＝( )A ．－2B ．－2iC ．2D ．2i1．C 因为z ＝1＋i ，所以z i＋i ·z －＝(－i ＋1)＋i ＋1＝2.9．L4 复数⎝ ⎛⎭⎪⎫1＋i 1－i 2＝________．9．－1 ⎝ ⎛⎭⎪⎫1＋i 1－i 2＝⎣⎢⎡⎦⎥⎤（1＋i ）2（1－i ）（1＋i ）2＝⎝ ⎛⎭⎪⎫2i 22＝－1.1．L4 复数z ＝(3－2i)i 的共轭复数z 等于( )A ．－2－3iB ．－2＋3iC ．2－3iD ．2＋3i1．C 由复数z ＝(3－2i)i ＝2＋3i ，得复数z 的共轭复数z ＝2－3i. 2．L4 已知复数z 满足(3＋4i)z ＝25，则z ＝( ) A ．－3＋4i B ．－3－4i C ．3＋4i D ．3－4i2．D 本题考查复数的除法运算，利用分母的共轭复数进行求解． 因为(3＋4i)z ＝25，所以z ＝253＋4i ＝25（3－4i ）（3－4i ）（3＋4i ）＝3－4i.1．L4 i 为虚数单位，⎝ ⎛⎭⎪⎫1－i 1＋i 2＝( )A ．－1B ．1C ．－iD ．i1．A ⎝ ⎛⎭⎪⎫1－i 1＋i 2＝－2i 2i ＝－1.故选A.1．L4 满足z ＋i z＝i(i 为虚数单位)的复数z ＝( )A.12＋12iB.12－12i C ．－12＋12i D ．－12－12i 1．B 因为z ＋i z ＝i ，则z ＋i ＝z i ，所以z ＝i i －1＝i （－1－i ）（i －1）（－1－i ）＝1－i 2. 1．L4 z －是z 的共轭复数，若z ＋z －＝2，(z －z －)i ＝2(i 为虚数单位)，则z ＝( )A ．1＋iB ．－1－iC ．－1＋iD ．1－i1．D 设z ＝a ＋b i(a ，b ∈R )，则z －＝a －b i ，所以2a ＝2，－2b ＝2，得a ＝1，b ＝－1，故z ＝1－i.2．L4 设复数z 满足(z －2i)(2－i)＝5，则z ＝( )A ．2＋3iB ．2－3iC ．3＋2iD ．3－2i2．A 由(z －2i)(2－i)＝5，得z －2i ＝52－i，故z ＝2＋3i. 2．L4 （1＋i ）3（1－i ）2＝( ) A ．1＋i B ．1－iC ．－1＋iD ．－1－i2．D （1＋i ）3（1－i ）2＝（1＋i ）2（1＋i ）（1－i ）2＝2i （1＋i ）－2i＝－1－i. 2．L4 设复数z 1，z 2在复平面内的对应点关于虚轴对称，z 1＝2＋i ，则z 1z 2＝( )A ．－5B ．5C ．－4＋iD ．－4－i2．A 由题知z 2＝－2＋i ，所以z 1z 2＝(2＋i)(－2＋i)＝i 2－4＝－5.1．L4 已知a ，b ∈R ，i 是虚数单位，若a －i 与2＋b i 互为共轭复数，则(a ＋b i)2＝( )A ．5－4iB ．5＋4iC ．3－4iD ．3＋4i1．D 因为a －i 与2＋b i 互为共轭复数，所以a ＝2，b ＝1，所以(a ＋b i)2＝(2＋i)2＝3＋4i.故选D.11．L4 复数2－2i 1＋i＝________． 11．－2i 2－2i 1＋i ＝2（1－i ）2（1＋i ）（1－i ）＝－2i. 1．L4 i 是虚数单位，复数7＋i 3＋4i ＝( )A ．1－iB ．－1＋iC.1725＋3125i D ．－177＋257i 1．A 7＋i 3＋4i ＝（7＋i ）（3－4i ）（3＋4i ）（3－4i ）＝25－25i 32＋42＝1－i.L5 单元综合2． 已知复数z ＝3＋4i ，z 表示复数z 的共轭复数，则⎪⎪⎪⎪⎪⎪z i ＝( ) A. 5 B ．5 C. 6 D ．6 2．B 因为|z|＝|z|＝5，所以⎪⎪⎪⎪⎪⎪z i ＝5. 4． 已知复数z 的共轭复数z ＝1＋2i(i 为虚数单位)，则z 在复平面内对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．D 由题意知，z ＝1－2i ，故其所对应的点(1，－2)在第四象限．9． 运行如图G12­2所示的程序框图，则输出k 的值是( )图G12­2A ．4B ．5C ．6D ．79．A 运行程序框图可知，输出k 的值为4.10． 运行如图G12­3所示的程序框图，若输出的S ＝120，则判断框内应为( )图G12­3A ．k ＞4?B ．k ＞5?C ．k ＞6?D ．k ＞7?10．B ∵S ＝1，k ＝1；k ＝2，S ＝4；k ＝3，S ＝11；k ＝4，S ＝26；k ＝5，S ＝57；k ＝6，S ＝120.故选B.12． 若z ＝sin θ－35＋i ⎝⎛⎭⎪⎫cos θ－45是纯虚数，则tan θ的值为( ) A.34 B.43 C ．－34 D ．－4312．C 由题意知sin θ＝35，cos θ≠45，所以cos θ＝－45，所以tan θ＝－34.14． 如图G12­7所示的四个程序框图都是为了计算S ＝1＋13＋15＋17＋19的值，其中，错误的算法是( )图G12­714．C 根据程序框图，易知选项A ，B ，D 正确；对于选项C ，由该框图可知当i ＝1时，S ＝1；当i ＝7时，S ＝1＋13＋15＋17，程序结束，不符合题意．。

山东省2014届理科数学一轮复习试题选编38：算法初步一、选择题 1 ．（山东省潍坊市2013届高三第一次模拟考试理科数学）运行右面框图输出的S 是254,则①应为（ ）A ．n ≤5B ．n ≤6C ．n ≤7D ．n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C ． 2 ．（2013年山东临沂市高三教学质量检测考试理科数学）执行如图所示的程序框图,输出的S 值为（ ）A ．4B ．32 C．23D ．-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C ．3 ．（山东省济宁市2013届高三第一次模拟考试理科数学 ）如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是（ ）A ．i≥3B ．i≥4C ．i≥5D ．i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D ．4 ．（山东省泰安市2013届高三第二次模拟考试数学（理）试题）已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是（ ）A ．11?n ≤B ．10?n ≤C ．9?n ≤D ．8?n ≤【答案】C 5 ．（山东省临沂市2013届高三5月高考模拟理科数学）执行如图所示的程序框图,输出的结果是（ ）A ．11B ．12C ．13D ．14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C ． 6 ．（山东省泰安市2013届高三第一轮复习质量检测数学（理）试题）若程序框图如图所示,则该程序运行后输出k 的值是（ ）A ．4B ．5C ．6D ．7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B ． 7 ．（山东省济南市2013届高三4月巩固性训练数学（理）试题）定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. （ ）A ．-2B ．-1C ．0D ．2【答案】D 8 ．（山东省济宁市2013届高三4月联考理科数学）左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7．98．6 3 89．3 9 8 8 4 1 5 10．3 1 11．4 （ ）A ．7B ．8C ．9D ．10【答案】D9 ．（山东省滨州市2013届高三第一次（3月）模拟考试数学（理）试题）执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为（ ）A ．1B ．2C ．3D ．4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C ．10．（山东省德州市2013届高三第二次模拟考试数学（理）试题）执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为（ ）A ．17B ．16C ．10D ．9【答案】C 11．（山东省2013届高三高考模拟卷（一）理科数学）执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为（ ）A ．5,1B ．30,3C ．15.3D ．30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12．（山东省德州市2013届高三3月模拟检测理科数学）如图所示,程序框图运行后输出k 的值是（ ）A ．4B ．5C ．6D ．7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B ． 13．（山东省菏泽市2013届高三第二次模拟考试数学（理）试题）阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是（ ）A ．i>5?B ．i>6?C ．i>7?D ．i>8?【答案】A14．（山东省兖州市2013高三9月入学诊断检测数学(理)试题）右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 （ ）A ．10>iB ．10<iC ．11>iD ．11<i【答案】A15．（山东省莱钢高中2013届高三4月模拟检测数学理试题 ）若右边的程序框图输出的S 是254,则条件①可为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤【答案】C16．（山东省枣庄市2013届高三3月模拟考试数学（理）试题）如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是（ ）A ．3B ．4C ．5D ．6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B ． 17．（山东省莱芜五中2013届高三4月模拟数学（理）试题）执行如图所示的程序框图,则输出的结果为（ ）A ．2B ．1C ．21 D ．1-【答案】C 18．（山东省凤城高中2013届高三4月模拟检测数学理试题 ）阅读如图所示的程序框图,运行相应的程序,则输出的结果是（ ）ABC．D．【答案】A19．（山东省文登市2013届高三3月二轮模拟考试数学（理））右面的程序框图中,若输出S 的值为126,则图中应填上的条件为（ ） A ．5n ≤ B ．6n ≤C ．7n ≤D ．8n ≤【答案】B 20．（2012年山东理）(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为（ ）C ．4D ．5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B ．21．（山东省枣庄市2013届高三4月（二模）模拟考试数学(理)试题）右图是某算法的程序框图,则程序运行后输出的结果是（ ）A ．6B ．27C ．124D ．168【答案】B 22．（山东省潍坊市2013届高三第二次模拟考试理科数学）运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为（ ）A ．14t ≥B ．18t ≥C ．14t ≤D ．18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B ．23．（山东省济南市2013届高三3月高考模拟理科数学）阅读右边的程序框图,运行相应的程序,输出的结果为（ ）A ．1311B ．2113C ．813D ．138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D ． 24．（山东省夏津一中2013届高三4月月考数学（理）试题）如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是（ ）A ．2012i ≤B ．i >2012C ．1006≤iD ．i >1006【答案】A 25．（山东省青岛即墨市2013届高三上学期期末考试数学（理）试题）如果执行下面的程序框图,输出的S=110,则判断框处为（ ）A ．10<k ?B ．11≥k ?C ．10≤k ?D ．11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C ．26．（山东省莱芜市莱芜二中2013届高三4月模拟考试数学（理）试题）右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C27．（山东威海市2013年5月高三模拟考试数学（理科））一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 （ ）A ．1－B ．1C ．1或5D ．1－或1【答案】 B ． 二、填空题 28．（2013届山东省高考压轴卷理科数学）执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29．（2013山东高考数学（理））执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30．（山东省济南市2013届高三上学期期末考试理科数学）已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31．（山东省德州市2013届高三上学期期末校际联考数学（理））执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32．（2011年高考（山东理））执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33．（山东省烟台市2013届高三3月诊断性测试数学理试题）执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34．（山东省菏泽市2013届高三5月份模拟考试数学（理）试题）执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35．（山东省淄博市2013届高三复习阶段性检测（二模）数学（理）试题）执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36．（2010年高考（山东理））执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-（）,此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37．（山东省济南市2012届高三3月高考模拟题理科数学（2012济南二模））如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38．（山东省莱芜市莱芜十七中2013届高三4月模拟数学（理）试题）执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39．（山东省青岛市2013届高三第一次模拟考试理科数学）某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40．（2009高考(山东理)）执行右边的程序框图，输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。