MTALAB机器人工具箱知识分享

Matlab Robotic Toolbox工具箱学习笔记（一）软件：matlab2013a工具箱：Matlab Robotic Toolbox v9.8Matlab Robotic Toolbox工具箱学习笔记根据Robot Toolbox demonstrations目录，将分三大部分阐述：1、General(Rotations,Transformations,Trajectory)2、Arm(Robot,Animation,Forwarw kinematics,Inversekinematics,Jacobians,Inverse dynamics,Forward dynamics,Symbolic,Code generation)3、Mobile(Driving to apose,Quadrotor,Braitenberg,Bug,D*,PRM,SLAM,Particle filter) General/Rotations%绕x轴旋转pi/2得到的旋转矩阵(1)r = rotx(pi/2);%matlab默认的角度单位为弧度，这里可以用度数作为单位(2)R = rotx(30, 'deg') * roty(50, 'deg') * rotz(10, 'deg');%求出R等效的任意旋转变换的旋转轴矢量vec和转角theta(3)[theta,vec] = tr2angvec(R);%旋转矩阵用欧拉角表示，R = rotz(a)*roty(b)*rotz(c)(4)eul = tr2eul(R);%旋转矩阵用roll-pitch-yaw角表示，R = rotx(r)*roty(p)*rotz(y) (5)rpy = tr2rpy(R);%旋转矩阵用四元数表示（6）q = Quaternion(R);%将四元数转化为旋转矩阵(7)q.R;%界面,可以是“rpy”，“eluer”角度单位为度。

matlab中robotics toolbox的函数解说1. PUMA560的MATLAB仿真要建立PUMA560的机器人对象，首先我们要了解PUMA560的D-H参数，之后我们可以利用Robotics Toolbox工具箱中的link和robot函数来建立PUMA560的机器人对象。

其中link函数的调用格式：L = LINK([alpha A theta D])L =LINK([alpha A theta D sigma])L =LINK([alpha A theta D sigma offset])L =LINK([alpha A theta D], CONVENTION)L =LINK([alpha A theta D sigma], CONVENTION)L =LINK([alpha A theta D sigma offset], CONVENTION)参数CONVENTION可以取‘standard’和‘modified’，其中‘standard’代表采用标准的D-H参数，‘modified’代表采用改进的D-H参数。

参数‘alpha’代表扭转角，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’代表横距，参数‘sigma’代表关节类型：0代表旋转关节，非0代表移动关节。

另外LINK还有一些数据域：LINK.alpha %返回扭转角LINK.A %返回杆件长度LINK.theta %返回关节角LINK.D %返回横距LINK.sigma %返回关节类型LINK.RP %返回‘R’(旋转)或‘P’(移动)LINK.mdh %若为标准D-H参数返回0，否则返回1LINK.offset %返回关节变量偏移LINK.qlim %返回关节变量的上下限 [min max]LINK.islimit(q) %如果关节变量超限，返回 -1, 0, +1LINK.I %返回一个3×3 对称惯性矩阵LINK.m %返回关节质量LINK.r %返回3×1的关节齿轮向量LINK.G %返回齿轮的传动比LINK.Jm %返回电机惯性LINK.B %返回粘性摩擦LINK.Tc %返回库仑摩擦LINK.dh return legacy DH rowLINK.dyn return legacy DYN row其中robot函数的调用格式：ROBOT %创建一个空的机器人对象ROBOT(robot) %创建robot的一个副本ROBOT(robot, LINK) %用LINK来创建新机器人对象来代替robotROBOT(LINK, ...) %用LINK来创建一个机器人对象ROBOT(DH, ...) %用D-H矩阵来创建一个机器人对象ROBOT(DYN, ...) %用DYN矩阵来创建一个机器人对象2．变换矩阵利用MATLAB中Robotics Toolbox工具箱中的transl、rotx、roty和rotz可以实现用齐次变换矩阵表示平移变换和旋转变换。

MATLAB机器学习工具箱的使用方法1. 引言在现代科技发展的背景下，机器学习在各个领域中的应用越来越广泛。

而MATLAB作为一款功能强大的数学软件，其机器学习工具箱为用户提供了丰富的算法和工具，方便快捷地进行机器学习任务。

本文将详细介绍MATLAB机器学习工具箱的使用方法，帮助读者更好地利用这个工具箱进行数据分析、模型训练和结果评估等任务。

2. 数据预处理在进行机器学习任务之前，首先需要对数据进行预处理。

MATLAB机器学习工具箱提供了多种数据预处理的方法和函数，如数据清洗、特征选择、数据变换等。

可以使用`preprocess`函数对数据进行缺失值处理，使用`featureselect`函数进行特征选择，或者使用`datapreprocessing`函数进行数据变换。

通过这些预处理的方法，可以使得数据更好地适用于后续的机器学习算法。

3. 特征工程特征工程是机器学习中一个重要的环节，它的目的是将原始数据转换为能够更好地反映问题特点的特征。

MATLAB机器学习工具箱提供了丰富的特征工程方法和函数，如特征提取、特征转换和特征选择等。

可以使用`featureextract`函数对原始数据进行特征提取，使用`featuretransform`函数进行特征转换，或者使用`featureselect`函数进行特征选择。

这些方法和函数的灵活使用可以帮助用户更好地理解数据并选择合适的特征。

4. 模型选择与训练在进行机器学习任务的过程中，选择适合问题的机器学习模型是非常重要的。

MATLAB机器学习工具箱提供了多种常见的机器学习模型，如线性回归、决策树、支持向量机等。

可以使用`fitmodel`函数来选择和训练机器学习模型。

用户可以根据具体的问题需求选择合适的模型，并通过调整模型参数来优化模型性能。

5. 模型评估与调优在完成模型的训练之后，需要对模型的性能进行评估和调优。

MATLAB机器学习工具箱提供了多种模型评估的方法和函数，如交叉验证、ROC曲线分析、精确度和召回率等。

[原创]强大的MATLAB机器人工具箱Matlab
强大的MATLAB机器人工具箱Matlab_Robotic_Toolbox_v9.10及教程
下载地址：
Matlab_Robotic_T oolbox_v9.10是一个功能强大的机器人工具箱，包含了机器人正、逆向运动学，正、逆向动力学，轨迹规划等等，其中的可视化仿真使得学习抽象的机器人学变得相对直观、好理解。

学习这个工具箱，对理解机器人学很有帮助。

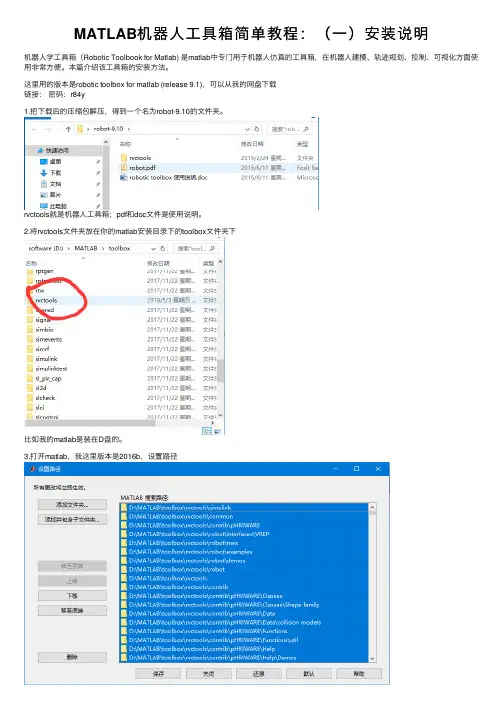
工具箱的安装：将Matlab_Robotic_T oolbox_v9.10.rar解压后，放在matlab的安装目录下，最好是放在toolbox文件夹里，利用matlab的工具栏的setpath,将文件夹Matlab_Robotic_T oolbox_v9.10\rvctools设置为matlab的搜索目录，在command window输入“startup_rvc”，安装工具箱。

最后，你可以在command window输入“ver”，查看机器人工具箱是否已经安装成功了。

command window会列出所有的工具箱，其中Robotics Toolbox已经包含在里面。

安装成功！！。

• 数字和模拟滤波器设计、应用及仿真 • 谱分析和估计 • FFT、DFT等变换 • 参数化模型
学科前沿最新的工具箱
模糊控制逻辑工具箱 友好的交互设计界面，自适应神经-
模糊学习、聚类以及Sugeno推理。 神经网络工具箱
神经网络系统具有集体运算的能力 和自适应的学习能力。具有很强的容错 性和鲁棒性，善于联想、综合和推广。
A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900]; Aeq=[]; beq=[]; vlb=[0;0;0;0;0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)
Genetic Algorithm and Direct Search Toolbox
• 是针对 MATLAB 优化处理算法的扩展， 它在 MATLAB 和 Optimization Toolbox 的基础上，提供遗传算法和直接搜索的 基本功能。
• 使用遗传算法工具箱的两种方法： 1. 直接在命令窗口使用函数。
• Spline Toolbox——样条工具箱 • Statistics Toolbox——统计工具箱 • Symbolic Math Toolbox——符号数学工具箱 • Simulink Toolbox——动态仿真工具箱 • Virtual Reality Toolbox——虚拟现实工具箱 • Wavelet Toolbox——小波工具箱
c:\matlab\toolbox\matlab • matlab主工具箱是任何版本的matlab都
不可缺少的。

MATLAB的机器学习工具箱使用教程机器学习是当今科技领域的热门话题，它的应用范围广泛，从自动驾驶到语音识别，无所不在。

而MATLAB作为一款功能强大的数学软件，其机器学习工具箱提供了丰富的函数和算法，可以帮助用户快速构建和训练机器学习模型。

本文将为大家介绍MATLAB的机器学习工具箱的使用方法和一些实用技巧。

一、数据准备在使用MATLAB的机器学习工具箱之前，首先需要准备好数据集。

数据集是机器学习模型的基础，它包含了训练样本和对应的标签。

在MATLAB中，可以使用csvread()函数读取CSV格式的数据文件，并将其转换为矩阵形式。

例如，假设我们有一个名为data.csv的数据文件，其中包含了1000个样本和10个特征，可以使用以下代码读取数据：```matlabdata = csvread('data.csv');```读取数据后，可以使用size()函数查看数据的维度，以确保数据读取正确。

同时，还可以使用plot()函数绘制数据的分布情况，以便更好地了解数据的特征。

二、数据预处理在构建机器学习模型之前，通常需要对数据进行预处理，以提高模型的性能和稳定性。

常见的数据预处理方法包括特征缩放、特征选择、数据平衡等。

特征缩放是指将数据的特征值缩放到相同的尺度范围内，以避免某些特征对模型的影响过大。

MATLAB提供了scale()函数可以实现特征缩放。

例如，可以使用以下代码对数据进行特征缩放：```matlabscaled_data = scale(data);```特征选择是指从原始数据中选择出最具有代表性的特征，以减少模型的复杂度和计算开销。

MATLAB提供了featureSelection()函数可以实现特征选择。

例如，可以使用以下代码对数据进行特征选择：```matlabselected_data = featureSelection(data);```数据平衡是指通过增加或减少样本数量，使得不同类别的样本数量相等，以避免模型对某些类别的偏见。

matlab 机器人工具箱动力学参数作为一款广泛应用于机器人控制领域的软件，MATLAB提供了许多有用的工具，包括机器人工具箱。

该工具箱是MATLAB和Simulink中用于机器人建模和控制的一系列函数和工具的集合。

在机器人的实时运动控制中，了解并正确设置机器人动力学参数非常重要。

因此，本文将用以下步骤来阐述如何设置机器人的动力学参数。

第一步：下载并安装机器人工具箱在MATLAB中，我们可以使用 add-on 栏或从MathWorks网站上下载机器人工具箱。

可从MATLAB的添加功能工具箱中直接下载或导航到网站中下载。

将下载的工具箱安装到MATLAB中后，可以开始了解和使用其中的函数。

第二步：选择合适的机器人模型机器人工具箱提供了许多现有的机器人模型，包括SCARA（选择性遵从装配机器人臂）、PUMA（程序升级管理局，一个六自由度连杆机器人）和Stäubli TX90（六自由度机器人）。

对于不同的机器人，动力学参数也是不同的。

因此我们需要先选择正确的机器人模型。

第三步：了解机器人动力学参数了解机器人的动力学参数对于实时控制机器人至关重要。

动力学参数通常包括连接杆长度、质量、惯性和摩擦力。

这些参数都影响机器人的实时运动，通过具体的物理计算，可以计算机器人的实际运动结果。

第四步：设置机器人的动力学参数机器人工具箱中提供了函数用于设置机器人模型的动力学参数。

例如，在设置机器人模型的惯性张量时，可以使用`inertia(m,I,c)’ 函数。

其中，m 是质量，I 是惯性张量矩阵，c 是惯性张量相对于机器人惯性坐标系的中心。

第五步：测试机器人模型设置完机器人模型的动力学参数后，我们需要对其进行测试以确认参数设置是否正确。

可以使用机器人工具箱中的模拟功能模拟机器人的运动或使用机器人模型进行真实操作，如搬运或拧紧物体。

总结：正确设置机器人模型的动力学参数是机器人实时控制的重要部分。

机器人工具箱中提供了许多有用的函数和工具帮助我们完成这一任务。

MATLAB机器学习工具箱应用指南第一章：介绍MATLAB机器学习工具箱MATLAB机器学习工具箱是一款强大且广泛使用的软件工具，用于开发和部署机器学习模型。

它提供了丰富的功能和算法，可应用于数据预处理、特征选择、模型训练和评估等各个方面。

本章将介绍MATLAB机器学习工具箱的主要特点和使用场景。

第二章：数据预处理在机器学习任务中，数据预处理是非常重要的一步。

MATLAB机器学习工具箱提供了丰富的功能和算法来处理原始数据。

例如，你可以使用数据清洗工具来处理缺失值和异常值。

此外，你还可以使用特征缩放工具将数据归一化，以提高模型的性能。

本章将详细介绍MATLAB机器学习工具箱中的数据预处理功能和使用方法。

第三章：特征选择特征选择是机器学习中的关键步骤，可以帮助减少特征空间的维度并提高模型的性能。

MATLAB机器学习工具箱提供了多种特征选择算法，如相关系数、方差选择和基于树的方法等。

本章将介绍这些算法的原理和使用方法，并结合实例演示如何在MATLAB环境下进行特征选择。

第四章：模型训练与评估MATLAB机器学习工具箱支持多种机器学习算法，包括支持向量机、神经网络、决策树等。

本章将重点介绍这些算法的原理和使用方法，并结合实例演示如何使用MATLAB进行模型训练和评估。

此外，你还可以通过交叉验证等技术来评估模型的性能和泛化能力。

第五章：模型部署与应用完成了模型训练和评估后，下一步就是将模型部署到实际应用中。

MATLAB机器学习工具箱提供了丰富的功能和接口，可用于模型导出、部署和集成。

你可以将训练好的模型部署到MATLAB生产服、Python环境或者嵌入式设备中。

此外，你还可以使用MATLAB Compiler将模型转换为可执行文件，以供其他用户使用。

第六章：实战案例分析本章将通过几个实战案例来展示MATLAB机器学习工具箱的应用。

例如，你可以使用工具箱中的算法来预测股票市场的趋势，或者通过图像分类算法来识别手写数字。

机器人学工具箱robotictoolbookformatlab是matlab中专门用于机器人仿真的工具箱在机器人建模轨迹规划控制可视化方面使用非常方便
MATLAB机 器 人 工 具 箱 简 单 教 程 ： （ 一 ） 安 装 说 明
机器人学工具箱（Robotic Toolbook for Matlab) 是matlab中专门用于机器人仿真的工具箱，在机器人建模、轨迹规划、控制、可视化方面使 用非常方便。本篇介绍该工具箱的安装方法。 这里用的版本是robotic toolbox for matlab (release 9.1)，可以从我的网盘下载 链接： 密码：r84y 1.把下载后的压缩包解压，得到一个名为robot-9.10的文件夹。
rvctools就是机器人工具箱；pdf和doc文件是使用说明。 2.将rvctools文件夹放在你的matlab安装目录ቤተ መጻሕፍቲ ባይዱ的toolbox文件夹下
比如我的matlab是装在D盘的。 3.打开matlab，我这里版本是2016b，设置路径
保存并关闭。 4.运行rvctools文件夹下的startup_rvc.m文件，安装完成。

matlab机器人工具箱的安装和使用心得体会
matlab机器人工具箱通过安装使用后得知它是一个功能强大的数学软件，但是正被微积分的计算缠身，听说有一个高级的计算器当然高兴，以后可以偷懒了，当然现在不能偷懒。

听说关于自动化的计算特别复杂，如果有一种软件能帮忙解题，那是一种极大的解脱，有益于缩短研究时间。

目前我只知道有三种数学软件，都是国外的，没有国内的，差距挺大的。

matlab学起来挺顺手的，比c语言简单。

但是深入学习的时候却困难重重，因为很多知识都没有学习，就算知道那些函数，也没有什么用处。

老师布置的作业难度大，写一篇实验，大一什么都不会，写一篇这种论文谈何容易。

最多也就会一些数值计算、符号计算、简单绘图，根本不会什么实验。

学习matlab体会最多的是这个软件的功能强大，好多数学题都被轻易的解出。

但是有一点遗憾，不知是我不会用，还是它没个功能，已知空间的电荷分布，求空间的电场分布。

其中电场分布是无法用函数表达式表示。

我知道计算机肯定可以实现，但是这个软件能不能实现就不知道了，我看过许多资料，但是在这方面没有提到相关信息。

总之，这个matlab机器人工具箱功能强大，不知什么时候国内才有类似的软件。

matlab机器人工具箱工作空间边界曲线提取
MATLAB机器人工具箱为机器人仿真和分析提供了一套完整的解决方案。

若要在MATLAB中使用机器人工具箱来提取工作空间边界曲线，您需要进行以下步骤：
1.导入机器人模型：首先，您需要将机器人模型导入到MATLAB中。

这通常
涉及使用robotics.loadRobot函数来加载机器人描述文件。

2.设置工作空间：定义机器人的工作空间。

这通常是一个三维的欧几里得空
间，其范围定义了机器人的最大移动范围。

3.生成轨迹：使用MATLAB中的轨迹规划工具（例如
robotics.TrajectoryGenerator）生成机器人的轨迹。

这些轨迹描述了机器人从起始点到目标点的运动。

4.碰撞检测：使用工具箱中的碰撞检测功能，您可以确定哪些轨迹点或路径
与环境中的障碍物相交或接近相交。

5.提取边界曲线：基于碰撞检测的结果，您可以提取出机器人的工作空间边
界曲线。

这些曲线通常代表机器人在工作空间中移动时可能遇到的障碍物
边界。

6.可视化结果：使用MATLAB的绘图功能，您可以将提取的边界曲线可视
化，以便更好地理解机器人的工作空间限制。

具体的代码实现将取决于您的具体需求和机器人工具箱的版本。

如果您需要更详细的代码示例或帮助，建议查阅MATLAB机器人工具箱的官方文档或相关的技术论坛。

机器人PUMA560 的MATLAB 仿真要建立PUMA560 的机器人对象，首先我们要了解PUMA560 的D-H 参数，之后我们可以利用Robotics Toolbox 工具箱中的link 和robot 函数来建立PUMA560 的机器人对象。

其中link 函数的调用格式：L = LINK([alpha A theta D])L =LINK([alpha A theta D sigma])L =LINK([alpha A theta D sigma offset])L =LINK([alpha A theta D], CONVENTION)L =LINK([alpha A theta D sigma], CONVENTION)L =LINK([alpha A theta D sigma offset], CONVENTION)参数CONVENTION 可以取‘standard’和‘modified’，其中‘standard’代表采用标准的D-H 参数，‘modified’代表采用改进的D-H 参数。

参数‘alpha’代表扭转角，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’代表横距，参数‘sigma’代表关节类型：0 代表旋转关节，非0 代表移动关节。

另外LINK 还有一些数据域：LINK.alpha %返回扭转角LINK.A %返回杆件长度LINK.theta %返回关节角LINK.D %返回横距LINK.sigma %返回关节类型LINK.RP %返回‘R’(旋转)或‘P’(移动)LINK.mdh %若为标准D-H 参数返回0，否则返回1LINK.offset %返回关节变量偏移LINK.qlim %返回关节变量的上下限[min max]LINK.islimit(q) %如果关节变量超限，返回-1, 0, +1LINK.I %返回一个3×3 对称惯性矩阵LINK.m %返回关节质量LINK.r %返回3×1 的关节齿轮向量LINK.G %返回齿轮的传动比LINK.Jm %返回电机惯性LINK.B %返回粘性摩擦LINK.Tc %返回库仑摩擦LINK.dh return legacy DH rowLINK.dyn return legacy DYN row其中robot 函数的调用格式：ROBOT %创建一个空的机器人对象ROBOT(robot) %创建robot 的一个副本ROBOT(robot, LINK) %用LINK 来创建新机器人对象来代替robotROBOT(LINK, ...) %用LINK 来创建一个机器人对象ROBOT(DH, ...) %用D-H 矩阵来创建一个机器人对象ROBOT(DYN, ...) %用DYN 矩阵来创建一个机器人对象利用MATLAB 中Robotics Toolbox 工具箱中的transl、rotx、roty 和rotz 可以实现用齐次变换矩阵表示平移变换和旋转变换。

MATLAB在机器人控制中的使用教程导言：机器人控制是现代工业和科研中的重要领域。

MATLAB作为一种强大的计算工具，提供了丰富的功能和工具箱，可以在机器人控制中发挥重要作用。

本文将介绍MATLAB在机器人控制中的使用教程，并深入探讨其中的关键概念和技术。

一、MATLAB中的机器人建模1. 机器人建模的概念和意义在机器人控制中，建模是实现各种控制算法的基础。

机器人建模的目的是将机器人的动力学特性抽象为数学模型，以方便控制算法的开发和仿真验证。

MATLAB提供了机器人工具箱（Robotics Toolbox），其中包括了常见的机器人模型和动力学模型，方便用户进行建模和分析。

2. 刚体变换和坐标系机器人建模中重要的概念之一是刚体变换和坐标系。

刚体变换描述了一个物体在三维空间中的平移和旋转，它们的组合可以描述机器人的末端执行器在空间中的位置和姿态。

MATLAB中的Homogeneous Transformations（齐次变换矩阵）提供了一种便捷的方式来表示刚体变换和坐标系之间的关系。

3. 建模示例以一个简单的二自由度机械臂为例，介绍如何在MATLAB中建立机器人模型。

首先，需要定义机器人的连接方式和几何结构，包括关节类型、关节限制等。

然后，根据机械结构确定机器人的运动学方程和动力学方程。

最后，结合机器人工具箱提供的函数，可以快速地生成机器人模型，并进行运动学和动力学分析。

二、MATLAB中的机器人控制1. 机器人运动学分析机器人运动学是研究机器人运动和位置的学科，是机器人控制的重要组成部分。

MATLAB提供了丰富的运动学函数和工具箱，可以帮助用户进行机器人的正向和逆向运动学分析。

通过正向运动学，可以根据给定的关节角度计算出末端执行器的位置和姿态。

通过逆向运动学，可以根据给定的末端执行器的位置和姿态计算出关节角度。

2. 机器人轨迹规划与插补轨迹规划是指在给定起始点和目标点的情况下，生成机器人的轨迹，使得机器人在指定时间内平稳地从起始点运动到目标点。

matlab机器人工具箱matlabrobotics_toolbox_demoMATLAB ROBOTTOOLrtdemo演示目录一、rtdemo机器人工具箱演示 (2)二、transfermations坐标转换 (2)三、Trajectory齐次方程 (8)四、forward kinematics 运动学正解 (12)四、Animation 动画 (18)五、Inverse Kinematics运动学逆解 (23)六、Jacobians雅可比---矩阵与速度 (32)七、Inverse Dynamics逆向动力学 (45)八、Forward Dynamics正向动力学 (52)一、rtdemo机器人工具箱演示>> rtdemo%二、transfermations坐标转换% In the field of robotics there are many possible ways of representing% positions and orientations, but the homogeneous transformation is well% matched to MATLABs powerful tools for matrix manipulation. %% Homogeneous transformations describe the relationships between Cartesian% coordinate frames in terms of translation and orientation.% A pure translation of 0.5m in the X direction is represented bytransl(0.5, 0.0, 0.0)ans =1.0000 0 0 0.50000 1.0000 0 00 0 1.0000 00 0 0 1.0000%% a rotation of 90degrees about the Y axis byroty(pi/2)ans =0.0000 0 1.0000 00 1.0000 0 00 0 0 1.0000%% and a rotation of -90degrees about the Z axis by rotz(-pi/2) ans =0.0000 1.0000 0 0-1.0000 0.0000 0 00 0 1.0000 00 0 0 1.0000%% these may be concatenated by multiplication t = transl(0.5, 0.0, 0.0) * roty(pi/2) * rotz(-pi/2)t =0.0000 0.0000 1.0000 0.5000-1.0000 0.0000 0 00 0 0 1.0000%% If this transformation represented the origin of a new coordinate frame with respect% to the world frame origin (0, 0, 0), that new origin would be given byt * [0 0 0 1]'ans =0.50001.0000pause % any key to continue%% the orientation of the new coordinate frame may be expressed in terms of% Euler anglestr2eul(t)ans =0 1.5708 -1.5708%% or roll/pitch/yaw anglestr2rpy(t)ans =-1.5708 0.0000 -1.5708pause % any key to continue%% It is important to note that tranform multiplication is in general not% commutative as shown by the following examplerotx(pi/2) * rotz(-pi/8)ans =0.9239 0.3827 0 0-0.0000 0.0000 -1.0000 0-0.3827 0.9239 0.0000 00 0 0 1.0000rotz(-pi/8) * rotx(pi/2)ans =0.9239 0.0000 -0.3827 0-0.3827 0.0000 -0.9239 00 1.0000 0.0000 00 0 0 1.0000%%pause % any key to continueecho off三、Trajectory齐次方程% The path will move the robot from its zero angle pose to the upright (or% READY) pose.%% First create a time vector, completing the motion in 2 seconds with a% sample interval of 56ms.t = [0:.056:2];pause % hit any key to continue%% A polynomial trajectory between the 2 poses is computed using jtraj()%q = jtraj(qz, qr, t);pause % hit any key to continue%% For this particular trajectory most of the motion is done by joints 2 and 3,% and this can be conveniently plotted using standard MATLAB operationssubplot(2,1,1)plot(t,q(:,2))title('Theta')xlabel('Time (s)');ylabel('Joint 2 (rad)')subplot(2,1,2)plot(t,q(:,3))xlabel('Time (s)');ylabel('Joint 3 (rad)')pause % hit any key to continue%% We can also look at the velocity and acceleration profiles. We could% differentiate the angle trajectory using diff(), but more accurate results% can be obtained by requesting that jtraj() return angular velocity and% acceleration as follows[q,qd,qdd] = jtraj(qz, qr, t);%% which can then be plotted as beforesubplot(2,1,1)plot(t,qd(:,2))title('Velocity')xlabel('Time (s)');ylabel('Joint 2 vel (rad/s)')subplot(2,1,2)plot(t,qd(:,3))xlabel('Time (s)');ylabel('Joint 3 vel (rad/s)')pause(2)% and the joint acceleration profiles subplot(2,1,1) plot(t,qdd(:,2))title('Acceleration')xlabel('Time (s)');ylabel('Joint 2 accel (rad/s2)')subplot(2,1,2)plot(t,qdd(:,3))xlabel('Time (s)');ylabel('Joint 3 accel (rad/s2)')pause % any key to continueecho off四、forward kinematics 运动学正解% Forward kinematics is the problem of solving the Cartesian position and% orientation of a mechanism given knowledge of the kinematic structure and% the joint coordinates.%% Consider the Puma 560 example again, and the joint coordinates of zero,% which are defined by qzqzqz =0 0 0 0 0 0%% The forward kinematics may be computed using fkine() with an appropropriate% kinematic description, in this case, the matrix p560 which defines% kinematics for the 6-axis Puma 560.fkine(p560, qz)ans =1.0000 0 0 0.45210 1.0000 0 -0.15000 0 1.0000 0.43180 0 0 1.0000%% returns the homogeneous transform corresponding to the last link of the% manipulatorpause % any key to continue%% fkine() can also be used with a time sequence of joint coordinates, or% trajectory, which is generated by jtraj()%t = [0:.056:2]; % generate a time vectorq = jtraj(qz, qr, t); % compute the joint coordinate trajectory %% then the homogeneous transform for each set of joint coordinates is given byT = fkine(p560, q);%% where T is a 3-dimensional matrix, the first two dimensions are a 4x4% homogeneous transformation and the third dimension is time.%% For example, the first point isT(:,:,1)ans =1.0000 0 0 0.45210 1.0000 0 -0.15000 0 1.0000 0.43180 0 0 1.0000%% and the tenth point isT(:,:,10)ans =1.0000 -0.0000 0 0.4455-0.0000 1.0000 0 -0.15000 0 1.0000 0.50680 0 0 1.0000pause % any key to continue%% Elements (1:3,4) correspond to the X, Y and Z coordinates respectively, and% may be plotted against timesubplot(3,1,1)plot(t, squeeze(T(1,4,:)))xlabel('Time (s)');ylabel('X (m)')subplot(3,1,2)plot(t, squeeze(T(2,4,:)))xlabel('Time (s)');ylabel('Y (m)')subplot(3,1,3)plot(t, squeeze(T(3,4,:)))xlabel('Time (s)');ylabel('Z (m)')pause % any key to continue%% or we could plot X against Z to get some idea of the Cartesian path followed% by the manipulator.%subplot(1,1,1)plot(squeeze(T(1,4,:)), squeeze(T(3,4,:)));xlabel('X (m)')ylabel('Z (m)')gridpause % any key to continueecho off四、Animation 动画clf%% The trajectory demonstration has shown how a joint coordinate trajectory% may be generatedt = [0:.056:2]'; % generate a time vectorq = jtraj(qz, qr, t); % generate joint coordinate trajectory%% the overloaded function plot() animates a stick figure robotmoving% along a trajectory.plot(p560, q);% The drawn line segments do not necessarily correspond to robot links, but% join the origins of sequential link coordinate frames.%% A small right-angle coordinate frame is drawn on the end of the robot to show% the wrist orientation.%% A shadow appears on the ground which helps to give some better idea of the% 3D object.pause % any key to continue。

M T A L A B机器人工具箱Robotic tool提供了一些如运动学，动力学和生成机器人轨迹的许多有用功能。

用这个工具箱进行仿真以及分析与真正的机器人得到实验结果是非常有用。

工具箱的优点是代码是一个相当成熟的算法，对于教学源代码是免费的。

该工具箱提供了机器人动力学正解和逆解，其次坐标转换所必需的三维位置和方向。

该工具箱可以计算任意结构机器人的正反运动学（用数值积分的方法，不是给出解析解）、正反动力学（反运动学采用的是递归牛顿欧拉方法，效率很高）、路径规划等；里面还有Puma560和Stanford机器人的实例。

1. PUMA560的MATLAB仿真要建立PUMA560的机器人对象，首先我们要了解PUMA560的D-H参数，之后我们可以利用Robotics Toolbox工具箱中的link和robot函数来建立PUMA560的机器人对象。

其中link函数的调用格式：L = LINK([alpha A theta D])L =LINK([alpha A theta D sigma])L =LINK([alpha A theta D sigma offset])L =LINK([alpha A theta D], CONVENTION)L =LINK([alpha A theta D sigma], CONVENTION)L =LINK([alpha A theta D sigma offset], CONVENTION)参数CONVENTION可以取‘standard’和‘modified’，其中‘standard’代表采用标准的D-H参数，‘modified’代表采用改进的D-H参数。

参数‘alpha’代表扭转角，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’代表横距，参数‘sigma’代表关节类型：0代表旋转关节，非0代表移动关节。

另外LINK还有一些数据域：LINK.alpha %返回扭转角LINK.A %返回杆件长度LINK.theta %返回关节角LINK.D %返回横距LINK.sigma %返回关节类型LINK.RP %返回‘R’(旋转)或‘P’(移动)LINK.mdh %若为标准D-H参数返回0，否则返回1LINK.offset %返回关节变量偏移LINK.qlim %返回关节变量的上下限 [min max]LINK.islimit(q) %如果关节变量超限，返回 -1, 0, +1LINK.I %返回一个3×3 对称惯性矩阵LINK.m %返回关节质量LINK.r %返回3×1的关节齿轮向量LINK.G %返回齿轮的传动比LINK.Jm %返回电机惯性LINK.B %返回粘性摩擦LINK.Tc %返回库仑摩擦LINK.dh return legacy DH rowLINK.dyn return legacy DYN row其中robot函数的调用格式：ROBOT %创建一个空的机器人对象ROBOT(robot) %创建robot的一个副本ROBOT(robot, LINK) %用LINK来创建新机器人对象来代替robot ROBOT(LINK, ...) %用LINK来创建一个机器人对象ROBOT(DH, ...) %用D-H矩阵来创建一个机器人对象ROBOT(DYN, ...) %用DYN矩阵来创建一个机器人对象2．变换矩阵利用MATLAB中Robotics Toolbox工具箱中的transl、rotx、roty和rotz可以实现用齐次变换矩阵表示平移变换和旋转变换。

matlab中机器人工具箱生成d-h参数机器人工具箱（Robotics Toolbox）是MATLAB中常用的一个工具箱，用于辅助机器人的建模、仿真、控制等应用。

其中，机器人的建模主要包括如何确定机器人的d-h参数。

在机器人工具箱中，可以通过函数来自动生成机器人的d-h参数，本文将介绍在MATLAB中机器人工具箱生成d-h参数，并对其进行详细讲解。

1. 基本介绍机器人的d-h参数，全名为Denavit-Hartenberg参数，是一种用于描述机器人关节之间的位置关系的标准方法。

通过确定机器人各关节之间的距离、长度、旋转角度等属性，可以建立机器人的运动模型，进而实现机器人的运动控制等功能。

在机器人工具箱中，可以通过直接设置机器人经d-h参数来实现机器人的建模。

针对机器人的d-h参数，机器人工具箱提供了两种方法来完成参数的确定：手动输入法和自动计算法。

下面我们将依次介绍这两种方法的具体实现过程。

2. 自动计算方法机器人工具箱中提供了一系列函数，可以通过直接调用这些函数来计算机器人的d-h 参数。

这些函数主要包括：- DHparameters：用于生成机器人的d-h参数矩阵- DHFactorization：用于分解机器人的d-h参数矩阵- DYNparameters：用于计算机器人的动力学参数- Link：用于创建机器人的链接对象下面我们将以机器人Puma560为例，介绍自动生成d-h参数的具体步骤。

（1）创建链接对象在MATLAB命令行窗口中，输入以下命令：>> L1 = Link('d',0,'a',0,'alpha',pi/2,'offset',0)上述命令的作用是创建一个名为L1的链接对象，用于描述机器人的第一关节。

其中，'d'表示链接对象相对前一关节坐标系在z方向上的偏移量，'a'表示链接对象相对前一关节坐标系在x方向上的偏移量，'alpha'表示链接对象相对前一关节坐标系的旋转角度，'offset'表示链接对象的初始位移。

（学习笔记）matlab机器人工具箱攻略一．旋转矩阵：（1）基本R = rotx(pi/2)R = roty(pi/2)R = rotz(pi/2)分别对X Y Z轴生成3*3的旋转矩阵R = rotx(30, 'deg')R = roty(30, 'deg')R = rotz(30, 'deg')可以改变输入的方式（2）姿态的叙述方法：1.Y-Z-Y欧拉角R = rotz(a)*roty(b)*rotz(c)eul2r(a,b,c)旋转矩阵反解出y-z-y欧拉角度的函数为tr2eul(R)2.x-y-z欧拉角R = rotx(r)*roty(p)*rotz(y)rpy2r（r,p,y）旋转矩阵反解出x-y-z欧拉角度的函数为tr2rpy(R)3.等效轴角坐标表示法把坐标系b看做原坐标a按向量V方向按右手方向旋转theta度旋转矩阵反解出等效轴角坐标表示的函数为[theta,V] = tr2angvec(R)由等效轴角坐标表示转换为旋转矩阵的函数R = angvec2r(theta, V)（记得把v做单位化的处理v = v / norm(v)）4.欧拉参数法表示（4元数）在等效轴角坐标表示法的基础上更进一步E1=Kx*sin（θ/2）;E2=Ky*sin（θ/2）;E3=Kz*sin （θ/2）;E4=cos(θ/2);求解4元数的函数为Quaternion(R)二．齐次变换矩阵4*4矩阵用于描述坐标系的位置和姿态1.平移算子transl(x, y, z)2.旋转算子trotx(pi/2)；troty(pi/2)；trotz(pi/2)3.各种表示下齐次矩阵的求解rpy2tr(roll, pitch, yaw, options) 求解x-y-z欧拉角变化对应的齐次矩阵 options：’deg’或不填angvec2tr(theta, V)求解等效轴角坐标表示的齐次矩阵eul2tr(phi, theta, psi, options）反解出Y-Z-Y欧拉角 options：’deg’或不填同样可以用tr2eul(t)反解出Y-Z-Y欧拉角tr2rpy(t)反解出x-y-z欧拉角[theta,vec] = tr2angvec(R);反解等效轴角坐标表示Quaternion(R) 反解4元数表示4.求出姿态的相关表示trprint(T, OPTIONS)可以表示出齐次矩阵的参数Options为：（1）'rpy' ； 'euler' ；'angvec' ；改变转换的方式为rpy,欧拉角，等效轴角坐标（2）'radian' ；改变显示的方式，和‘deg’功能相对。