西南交大物理实验期末试题题库-转动惯量

1. 物体的速度作为时间的函数显示在下图中，则在 A－E 图中，哪个最好地显示了物体受到的合力和 时间的关系：
密封装订线
姓名
学号
密封装订线
t
F
F
F
F
F
t
1(A)
t
2(B)
t
3(C)
t
4(D)
2. 若产生如图所示的自感电动势方向，则通过线圈的电流是：
(A) 恒定向右
(B) 恒定向左
(C) 增大向左
(D) 增大向右
、
k
表示）。
5．（本小题 2 分）一个带电为 Q 的空腔导体，其内部无其他带电体，则电荷将分布于空腔导体的 ___________________(选填：内表面；外表面；导体体内；内表面和外表面)。
学号
密封装订线
班级
密封装订线
第1页共7页
6．（本小题 2 分）在均匀磁场中放置一半径为 R 的半圆形导线，电流强度为 I，导线两端连线与磁感
S
B t

d
S
②
_________________________
④
二、判断题（每小题 2 分，共 16 分。请将表示正确的符号：T，表示错误的符号：F，填入相应 题号后的括号内。填入其它符号和其它位置处答案不得分）
1．（ 2．（
3．（ 4．（ 5．（ 6．（
7．（ 8．（
）一对大小相同、方向相反的作用力，所做的功也一定相消为零。 ）花样滑冰运动员以一只脚为轴旋转，当她两臂收拢时, 则绕轴转动角动量减小，转动角速度
为 l 、截面积为 S，质量为 m 的棒，且这根棒安放在运动方向上，则乙测得此棒的密度为
。
2．（本小题 2 分）有一边长为 a 的正方形平面，在其中垂线上距中心 O 点 1 a 处， 2

分别为 m1 、 m2 相对于地的加速度。以竖直向下为正方向。 和 a2
m2 m1
f
a2
以地球为参考系，分别对 m1 、 m2 和一段轻绳应用牛顿运动定律：
m1 g T m1 a1 m2 g f m2 a2 f T
又由相对加速度公式
1 2 3
（ 4）
T
a 2 a1 a2
V0 －2 V
(B) (D)
2 ( V 0 －V) 2 (V － V 0 )
(C) 2 V－ V0
解：设小球质量为 m，碰撞后速度为 V1 ，车质量为 M，碰撞后速度为 V 2。 完全弹性碰撞，碰撞前后，机械能守恒； 忽略外力作用，碰撞前后动量守恒，即有 移项得
mV0 MV mV1 MV2 mV1 V0 M V V2
©西南交大物理系_2013_02
《大学物理 AI》作业
No.02 动量、动量守恒定律
班级 ________ 学号 ________ 姓名 _________ 成绩 _______
一、判断题： （用“T”和“F”表示） [ F ] 1． 在匀速圆周运动中，质点的动量守恒。 解：因为动量是矢量，在匀速圆周运动中，动量的大小不变，方向时时刻刻在变化。 [ F ] 2． 物体运动方向与作用在物体上的合外力方向相同。 反例：抛体运动。 [ F ] 3． 物体所受摩擦力的方向与物体运动的方向相反。
4. 假设一个乒乓球和一个保龄球向你滚来。都具有相同的动量，然后你用相同的力将两 只球停住，比较停住两只球所用的时间间隔 [ B ] (A) 停住乒乓球所用的时间间隔较短 (B) 停住两只球所用的时间间隔相同 (C) 停住乒乓球所用的时间间隔较长 (D) 条件不足，不能确定 解：根据动量定理： I 也相同。 5．在 t = 0 时刻，一个大小恒定的力 F 开始作用在一正在外层空间沿 x 轴运动的石块上。 石块继续沿此轴运动。对 t >0 的时刻，下面的哪一个函数有可能表示石块的位置： [ B ]

西南交通大学大物A作业解析西南交大物理系_2013_02《大学物理AI 》作业角动量角动量守恒定律班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题：（用“T ”和“F ”表示）[ F ] 1．如果一个刚体所受合外力为零，其合力矩一定为零。

[ F ] 2．一个系统的动量守恒，角动量一定守恒。

[ T ] 3．一个质点的角动量与参考点的选择有关。

[ F ] 4．刚体的转动惯量反映了刚体转动的惯性大小，对确定的刚体，其转动惯量是一定值。

[ F ] 5．如果作用于质点的合力矩垂直于质点的角动量，则质点的角动量将不发生变化。

二、选择题:1．有两个半径相同、质量相等的细圆环A 和B 。

A 环的质量分布均匀，B 环的质量分布不均匀。

它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ，则[ C ] (A) A J >B J(B) A J(D) 不能确定A J 、B J 哪个大2．绕定轴转动的刚体转动时, 如果它的角速度很大, 则[ D ] (A) 作用在刚体上的力一定很大 (B) 作用在刚体上的外力矩一定很大(C) 作用在刚体上的力和力矩都很大 (D) 难以判断外力和力矩的大小3．一个可绕定轴转动的刚体, 若受到两个大小相等、方向相反但不在一条直线上的恒力作用, 而且力所在的平面不与转轴平行, 刚体将怎样运动[ C ] (A) 静止 (B) 匀速转动 (C) 匀加速转动 (D) 变加速转动4．绳的一端系一质量为m 的小球, 在光滑的水平桌面上作匀速圆周运动. 若从桌面中心孔向下拉绳子, 则小球的[ A ] (A) 角动量不变 (B) 角动量增加(C) 动量不变 (D) 动量减少5．关于力矩有以下几种说法：(1) 对某个定轴而言，内力矩不会改变刚体的角动量 (2) 作用力和反作用力对同一轴的力矩之和必为零(3) 质量相等，形状和大小不同的两个刚体，在相同力矩的作用下，它们的角加速度一定相等在上述说法中，[ B ] (A) 只有(2)是正确的 (B) (1)、(2)是正确的(C) (2)、(3)是正确的 (D) (1)、(2)、(3)都是正确的6. 一圆盘正绕垂直于盘面的水平光滑固定轴O转动，如图射来两个质量相同、速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度ω [ C ] (A) 增大 (B) 不变(C) 减小 (D) 不能确定三、填空题:1．如图所示的俯视图表示5个同样大小的力作用在一个正方形板上，该板可以绕其一边的中点P 转动。

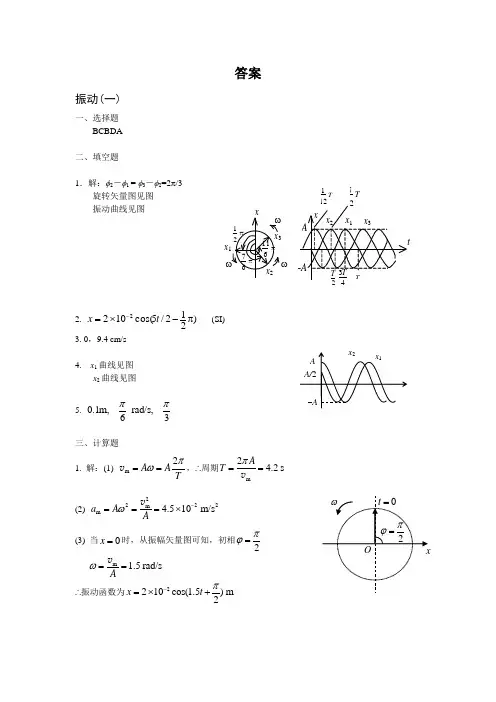
答案振动(一)一、选择题BCBDA二、填空题1．解：φ2－φ1 = φ3－φ2=2π/3旋转矢量图见图 振动曲线见图2. )212/5cos(1022π-⨯=-t x (SI)3. 0，9.4 cm/s4. x 1曲线见图x 2曲线见图5. 0.1m ,rad/s,63ππ三、计算题1. 解：(1) m 2A ATπω==v ，∴周期m2 4.2s A T π==v(2) 2222m m 4.510m/s a A Aω-===⨯v(3) 当0x =时，从振幅矢量图可知，初相2πϕ=m 1.5r a d /sAω==v ∴振动函数为2210cos(1.5)m 2x t π-=⨯+TT1T 5ω x12T 1212. 解：弹簧劲度系数 260 2.010N /m 0.3F k x===⨯ 静止时弹簧伸长量为 0249.80.196m 2.010m g x k⨯===⨯(1) 设向下为正方向，则 0ϕ= （若设向上为正方向，则 ϕπ=）；0.1mA =7.07r a d /sω== 振动函数为 0.1cos(7.07)m x t =(2) 物体在平衡位置上方5cm （即0.05m ），此时弹簧的净伸长为 00.050.1960.050.146m l x =-=-=弹簧对物体的拉力 2000.14629.2N F kl ==⨯=(3) 5cm 是振幅之半，物体从平衡位置到振幅之半所需最短时间是112T ，2T πω=∴10.074s 126t T πω===3．解：(1) 容器中每滴入一油滴的前后，水平方向动量值不变，而且在容器回到O 点滴入下一油滴前， 水平方向动量的大小与刚滴入上一油滴后的瞬间后的相同。

依此，设容器第一次过O 点油滴滴入前的速度为v ，刚滴入第个油滴后的速度为v ′,则有 v v '+=)(nm M M ① 3分系统机械能守恒 2202121v M kl = ② 2分22)(2121v '+=nm M kx③ 2分由①、②、③、解出0)/(l nm M M x +=2分(2) 时间间隔( t n +1-t n )应等于第n 滴油滴入容器后振动系统周期T n 的一半．k nm M T t t t n n n n /)(211+==-=∆+π 3分4．解：由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒， ∴ T = 8 s ， ν = (1/8) s -1， ω = 2πν = (π /4) s -1 3分 (1) 以AB 的中点为坐标原点，x 轴指向右方．t = 0时， 5-=x cm φcos A =t = 2 s时， 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零，所以φ = -3π/4或5π/4（如图） 2分 25c o s/==φx A cm 1分∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) 1分 (2)速率 )434s i n (41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时，质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 1分5*．解：令θ 为杆和竖直线之间的夹角．运动方程为：θθθθc o s s i n s i n 21/d d 222kL MgL t J --= 3分θ 很小时，sin θ ≈θ ，cos θ ≈1所以：0/d d )21(222=++tJ kL MgL θθ 2分上式中231ML J =是杆绕其一端的转动惯量，所以0/d d 31)21(22=++tML Lk Mg θθ可知杆作角谐振动，并得到 )2/()2(3ML kL Mg +=ω2分)2(322/2kL Mg ML T +π=π=ω 1分振动(二)一、选择题ADDBB二、填空题 1．T /8，3T /8 2．222/2T mA π3．动能曲线见图 势能曲线见图 机械能曲线见图4．0.02 5．0三、计算题1.解：设小球的质量为m ，则弹簧的劲度系数 0/l mg k =．选平衡位置为原点，向下为正方向．小球在x 处时，根据牛顿第二定律得T220d /d )(t x m x l k mg =+- 将 0/l mg k = 代入整理后得0//d d 022=+l gx t x∴ 此振动为简谐振动，其角频率为． 3分 π===1.958.28/0l g ω 2分设振动表达式为 )c o s (φω+=t A x由题意： t = 0时，x 0 = A=2102-⨯m ，v 0 = 0，解得 φ = 0 1分∴ )1.9c o s (1022t x π⨯=- 2分2．解一：(1) 取平衡位置为原点，向下为x 正方向．设物体在平衡位置时弹簧的伸长量为∆l ，则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0，则0)(0=+-+∆x l k mg F解得F = kx 02分 由题意，t = 0时v0 = 0；x = x 0 则 02020)/(x x A =+=ωv 2分又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k =∴ 444.0)/4(22=π==A T m kA F N 1分 (2) 平衡位置以下1 cm 处： )()/2(2222x A T -π=v 2分 221007.121-⨯==vm E K J 2分2222)/4(2121x T m kxE p π=== 4.44³10-4J 1分解二：(1) 从静止释放，显然拉长量等于振幅A （5 cm ），kA F = 2分2224νωπ==m m k ，ν = 1.5 Hz 2分 ∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kAE J 2分当x = 1 cm 时，x = A /5，E p 占总能量的1/25，E K 占24/25． 2分∴ 21007.1)25/24(-⨯==E E K J ， 41044.425/-⨯==E E p J 1分3．解：(1) 选地心为x 坐标原点，向上为x 轴正方向．质量为m 的物体在地球内部距地心为x 处受到的地心引力为232/)3/4(/x m x G x G M m F ρπ-=-=3/4x Gm ρπ-= 3分由牛顿第二定律得 xm x Gm =π-3/4ρ， 03/4=π+x G xρ 1分 令 3/420ρωG π=， 则 020=+x x ω． 显然物体作简谐振动． 2分(2) 2/10)/3(4/32/2ρρωG G T π=ππ=π=已知 G = 6.67³10-11 N ²m 2²kg -2，ρ = 5.5³103 kg/m 3代入上式 T = 5.07³103 s 2分 物体从地面落到地心的时间 t = T /4 = 1.27³103 s 2分4．解：选平板位于正最大位移处时开始计时，平板的振动方程为 t A x π=4c o s (SI)t A xπ4c o s π162-= (SI) 1分 (1) 对物体有 x m N mg =- ① 1分 t A mg xm mg N ππ+=-=4cos 162 (SI) ②物对板的压力为 t A mg N F ππ--=-=4cos 162 (SI)t ππ--=4c o s 28.16.192 ③ 2分 (2) 物体脱离平板时必须N = 0，由②式得 1分 04c o s 162=ππ+t A mg (SI) Aq t 2164cos π-=π 1分若能脱离必须 14cos ≤πt (SI) 即221021.6)16/(-⨯=π≥g A m 2分5．解：依合振动的振幅及初相公式可得 φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++=m21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t g π+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI) 1分波动（一）一、选择题CBDCD 二、填空题1．φλ+π-/2Lλk L ± ( k = 1，2，3，…) λ)12(21+±k L ( k = 0, 1，2，…)2．1cos x y A t u ωϕ⎡+⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦3. ]4/)/(cos[11π+-=u L t A y ω；uL L )(21+ω4. ]2)2(2cos[π-+-π=ux t uA y λ]2)2(2c o s [π+-π=t uA y P λ5．0.2cos m 22p y t ππ⎛⎫=-⎪⎝⎭三、计算题1. 解：反射波在x 点引起的振动相位为 π+π--+π-=+21)55(4x t t φωπ-π+π+=10214x t 3分反射波表达式为)10214cos(01.0π-π+π+=x t y (SI) 2分或 )214c o s (01.0π+π+=x t y (SI)2．解： λxu t A y -π=2c o s = -0.01 m 1分1.0,2d d ===t x ty v 0)2s i n (2=-ππ-=λλxut uA 2分22d d ty a =)2c o s ()2(2λλxut uA -ππ-= = 6.17³103m/s 22分3．解：用旋转矢量解此题，如图可得A为代表P 点振动的旋转矢量. 210)cos sin 3(21-⨯-=t t y P ωω210)]cos()21cos(3(21-⨯π++π-=t t ωω)3/4c o s (1012π+⨯=-t ω (SI)． 3分波的表达式为：]2/234c o s [1012λλω-π-π+⨯=-x t y )312c o s (1012π+π-⨯=-λωxt (SI) 2分4．解：从y －x 波形图中可知 40m,A λ==由振幅矢量图可知 ,2P Q πϕϕπ=-=)由20m/s u =可得 2s,rad/s T uλωπ==∴=0.2cos()m20.2cos()mP Q y t y t ππππ∴=-=+5．解：(1) 由y －x 曲线可知160m λ=。

大学物理实验试题
【学生姓名】
【学号】
【实验题目】刚体转动
【试题】
利用扭摆测量塑料圆柱的转动惯量。
年月日
物体 名称
质量 m （kg）
金属载 ╱
物盘
几何尺寸 （10－2m）
╱
周期（s）
Ti
Ti
转动惯量理论值 （10－2kgm2）
转动惯量实验值 (10－2kgm2）
╱
I0
=
I1¢T02 T12 - T02
测量次数 位置(mm) 波长(mm)
1
2
3
4
5
6
7
8
9
10
43.980 52.749 61.365 70.139 78.833 87.525 96.252 104.875 113.658 122.312
要求：1、利用逐差法计算出声速，要有详细的数据处理过程； 2、计算实验值与理论值的百分误差。
成 绩： 主考教师：
宽度（mm） 22.80 22.78 22.82
D仪
0.05
0.01
要求：写出刀口间距 d、横梁的宽度 b、横梁的厚度 a 的标准表达式
(1)d : uA =
厚度（mm） 0.960 0.962 0.958
0.005
uB =
u=
(2)b : uA = uB = u=
(3)a : uA = uB = u=
，(mg)i 和
Dzi
对应）
4a bDzi
成 绩： 主考教师：
【学生姓名】
大学物理实验试题
【学号】
年月日
【实验题目】杨氏模量（梁弯曲法）
【试题】
已知刀口间距，宽度，厚度的测量值，分别求出它们的不确定度.(刀口间距用米尺测量，

i
Hale Waihona Puke 系统内所有质点对同一参考点角动量的矢量和
pp i p i 2 cr i r2 mi ri
rc mi vi ri mi vc vi rc mi vi ri mi vc ri mi vi
i
L自旋
L轨道
L
L轨道
L自旋
6
3. 定轴转动刚体的角动量
转轴 z 角速度 刚体上任一质点 mi
mi 绕
z
o
转动 平面

vi
转轴与其转动平面交点
mi 对 o 的角动量： Lio ri mi vi
大小：Lio ri mi vi mi ri 2 Lio 方向：沿 2 即 Lio mi ri
同学们好！
1
§5.1
一、角动量
角动量
转动惯量 力矩
问题：将一绕通过质心的固定轴转动的圆盘视为一 个质点系，则由于该系统质心速度为零，所以，系 统总动量为零，系统有机械运动，总动量却为零？ 说明不宜用动量来量度转动物体的机械运动量。 引人与动量
p 对应的角量
—— L 角动量
1. 质点的角动量 大小：
J r 2 dm x 2 dm
L m1 3 2 2 m x dx x L L L 3 2
12
m 1 L3 L3 1 2 m L 12 L 3 8 8
(2) 轴过一端端点
dm
o
x
L
x
J r dm x dm
y
Jz Jx J y
16
练习

dl
r
dθ θ
解：取离轴线距离相等的点的集合 为积分元
R
d S = 2πrd l = 2πRsinθ ⋅ Rdθ
o
m
m σ= 4πR 2
1 d m = σ d S = m sin θ d θ 2 1 2 2 d J = r d m = ( R sin θ ) d m = mR 2 sin 3θ d θ 2
mgs 解得：a = ( m + 1 M )l 2
x
又： a = rβ s = x1 − x2
第四节 角动量守恒定律
例: 一半径为R、质量为 M 的转台，可绕通过其中心 的竖直轴转动, 质量为 m 的人站在转台边缘，最初人 和台都静止。若人沿转台边缘跑一周 (不计阻力)，相 对于地面，人和台各转了多少角度？ 思考： 1.台为什么转动？向什么方向 转动？ 2.人相对转台跑一周，相对于 地面是否也跑了一周？ 3.人和台相对于地面转过的角 度之间有什么关系？
A M r o x2 s
m
B
解：在地面参考系中，建立如图 x 坐标系，设绳两端坐标分别为x1， x2，滑轮半径为 r , 有：
l = A A′ + AB + B B ′ = x1 + x 2 + π r
B′
s = x1 − x 2
A′
x1 x
m AB
m m m A = m AA′ = ⋅ x1 = ⋅π r l l m m B = mBB′ = ⋅ x2 l
J=
∫
dJ =
∫
0
R
2 mr 4dr 2 2 = mR 3 R 5
例4. 一长为 L 的细杆，质量 m均匀分布，求该杆对垂直 于杆，分别过杆的中点、一端端点和距端点L/4处的轴的 转动惯量。 解:(1)轴过中点

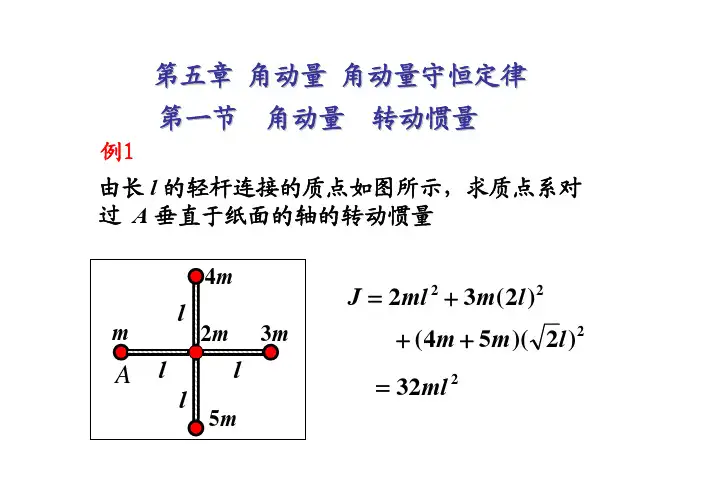
1、质量分别为m和2m的两个质点，用长为的轻质细杆相连，系统绕过质心且与杆垂直的轴转动，其中质量为m的质点的线速度为，，则系统对质心的角动量为( )A.mlB .20m/3D .3ml正确答案A2、一刚体以e=60r/min绕Z轴匀速转动( o沿着转轴正方向)如果某时刻，刚体上点P的位置矢量r=(m)+(4m)j+(5m)，则该时刻P的速度为( )A .v=(94.1m/0)i+025 6mfs)j-(7m/s)kB. v=(-25.1m/(s)+(8.8m]a)jC. r=(-23m/2)i -(188m/9)jD.￥=G1.4m[s)正确答案：B3.三个质量相等的物体A、B、C紫靠起置于光滑水平面上，如下图，若A C分别受到水平力和R的作用( 月>只)，则A对B的作用力大小( )A. F₁-F₂B. 2F₁/3+F₂/3C .2F₁/3－F₂/3D.F₁/3+2F₂/3正确答案:B4、物体自高度相非同的A点沿不同长度的光滑斜面自由下滑，如下图所示，斜面倾角多大时，物体滑到斜面底部的速率最大( )A.30。

B.45。

C. 60。

D.各倾角斜面的速率相等。

正的答案:D5. 用铁锤将一铁钉击入木板，设铁钉受到的阻力与其进入木板内的深度成正比，若铁锤两次击钉的速度相同第一次将铁钉击入板内1x10²m，则第二次能将钉继续击入木板的深度为( )正确答案:D6.试指出当曲率半径p*0时，下列说法中哪一种是正确的( )A: 在圆周运动中，加速度的方向一定指向圆心B: 匀速率圆周运动的速度和加速度都恒定不变C:物体作曲线运动时速度方向定在运动轨道的切线方向，法线分速度恒等于零因此法问加速度也一定等于零D:物体作曲线运动时，一定有加速度加速度的法向分量一定不等于零正确答案:D7、可以认为，地球是一个匀角速转动的非惯性系，因此通常所说的物体的重力实际上是地球引力和地球自转引起的惯性离心力的合力，由此可见，重力和地球的引力两者无论大小，方向都不相同，那么两者大小相差最多的，应该是( )A.在赤道上B. 在南北极C. 在纬度450处D. 在纬度600处正确答案:A8、一个轻质弹簧竖直悬挂，原长为，今将质量为m的物体挂在弹簧下端，同时用手托住重物缓慢放下，到达弹簧的平衡位置静止不动，在此过程中，系统的重力势能减少而弹性势能增加，则有( )A.减少的重力势能大于增加的弹性势能B .减少的重力势能等于增加的弹性势能C.减少的重力势能小于增加的弹性热能D.条件不足，无法确定正确答案:A9、1mol刚性双原子分子理想气体当温度为T时,其内能为( )A: 3RT/2B: 3KT/2C: SRT/2D: 5RT/2正确答案:C10、电场的环路定理王i-说明了静电场是( )A: 无源场B: 在闭合回路中各点的电场强度为零C.有源场D: 电场是闭合场正确答案:C11、物体质量为m，水平面的滑动摩擦因数为u，今在力F作用下物体向右方运动，如下图所示，欲使物体具有最大的加速度值，则力F与水平方向的夹角应满足( )A .cosθ=1B .sinθ=1C. tgθ=μD. ctgθ=μ正确答案:C12、已知氢气与氧气的温度相同.请判断下列说法哪个正确?( )A: 氧分子的质量比氧分子大，所以氧气的压强定大于氢气的压强B: 氧分子的质量比氢分子大，所以氧气的密度一定大于氢气的密度C: 氧分子的质量比氢分子大，所以氢分子的速率一定比氧分子的速率大. D: 氧分子的质量比氢分子大，所以氢分子的方均根速率-定比氧分子的方均根速率大.正确答案:D13、若在某个过程中，一定量的理想气体的内能E随压强P的变化关系为一直线，如下图所示(其延长线过E-P图的点)，则该过程为( )A .等温过程B.等压过程C .绝热过程D.等体过程。

“转动惯量测定”实验（一）判断题1、（）转动惯量测定实验：由于g﹥﹥a（g和a分别表示重力加速度和砝码下落的加速度），所以实验中忽略了a。

2、（）转动惯量测定实验：由于遮光片的初始位置．．．．与测量的时间数据有关，因此需将遮光片的初始位置设定在转台的某一光电传感器处。

3、（）转动惯量测定实验：实验可以证明，圆环的转动惯量与砝码质量．．．．有关。

4、（）转动惯量测定实验：实验中忽略了转台转轴所受摩擦力矩的影响。

5、（）“转动惯量测定”实验中，未考虑滑轮的摩擦力矩和滑轮质量的影响。

6、（）转动惯量测定实验：由于遮光片的初始角速度．．．．．与测量的时间数据有关，因此需将遮光片的初始位置设定在某一光电传感器处。

7、（）转动惯量测定实验：实验可以证明，两金属圆柱体构成的转动系统其转动惯量与塔轮半径．．．．有关。

（二）填空题1、“转动惯量测定”实验中，通过改变的距离证明刚体的转动惯量与其质量分布有关。

2、“转动惯量测定”实验中，如果测得空台转动惯量J=11.18×10-3kgm2，在不加外力矩的情况下，角加速度β=-0.043/s2，估计转轴摩擦力矩的数量级为 Nm。

3、转动惯量测定实验：电脑计时器测量的时间间隔是从到所经历的时间。

4、“转动惯量测定”实验中，过改变圆柱体到转轴的距离证明刚体的转动惯量与有关。

（三）选择题1、转动惯量实验中的间接测量量是：A）角加速度 B）时间C）圆柱体和圆盘的直径、质量 D）光电门输出的脉冲数12E ）转动惯量2、转动惯量实验中，转台不水平会导致 。

A ）绳上张力难与转轴保持垂直B ）转轴的摩擦力不稳定C ）计时不准确D ）光电门与遮光片发生碰撞3、转动惯量实验中，①忽略了转台所受摩擦力矩的影响，②不考虑滑轮的摩擦力矩和滑轮质量的影响。

这两种说法中：A ）①正确，②错误B ）①错误，②正确C ）①和②都正确D ）①和②都错误4、转动惯量实验中，电脑计时记录的是砝码从最高点下落到地面所经历的时间。

误差理论＿05 出题：物理实验中心 用误差限 0.10mm 的钢直尺测量钢丝长度，11 次的测量数据为：（单位：mm） 45.8、25.8、25.7、25.5、25.6、25.8、 25.6、25.5、25.4、25.7、25.6。钢丝的测量结果为(D) A) l =25.62 0.04 m B) l =27.4 2.1 m C) l =25.62 m 0.06 m D) l =25.6 0.1 m
( xi x )2 n ( n 1)
A)
B) uA2i uB2i
2
f
C)

xi
uxi

ai
D) 3
误差理论＿17 出题：物理实验中心 以下表述中错误的是(B) 正常测量数据的标准 S 有可能为零 系统误差指的是在测量过程中其值保持不变的那部分误差 最小二乘法原理适用于任意的曲线 使用逐差法的前提是自变量与因变量之间满足线性关系
误差理论＿14 出题：物理实验中心
某同学测量物理量 L 后写出的最终结果表达式为：L=12.003 0.006。该式(C)
完全正确 有一处错误 有两处错误 有三处错误
误差理论＿15 出题：物理实验中心
对某物体的长度进行测量，得到结果：L=12.340 0.010 cm，则下面叙述中正确的是(D)
ux2

u
2 y
N n xi yi3 uN
C)
i1 n ，
n xi yi3 N 2
i1 n n 1
D)
N

x y3
uN
，

n xi yi3 N 2
i1 n n 1
误差理论＿04 出题：物理实验中心 下列测量结果正确的表示为（D） A) 重力加速度 g=9.78±0.044 B) v=343.24±2.553m/s C) E=1.34325V±2.00 mV D) I=1.3V±0.2 mA

2019西南交大大物AI作业03答案西南交大物理系_2019_02《大学物理AI》作业 No.03角动量角动量守恒定律一、判断题：（用“T”和“F”表示）[ F ] 1．如果一个刚体所受合外力为零，其合力矩一定为零。

解：合力为零，合力矩不一定为零。

反之亦然。

[ F ] 2．对于一个做直线运动的质点，其角动量一定为零。

解：L=r×p，其中r与参考点的选择密切相关，如果参考点在运动直线上，那么r与p的夹角为0或是π，此时角动量为0；如果参考点不在运动直线上，那么角动量就不为0。

角动量与参考点的选择密切相关。

[ T ] 3．刚体的转动惯量反映了刚体转动的惯性大小。

一般说来，同一刚体对不同转轴的转动惯量是不同的。

解：根据转动惯量的定义：J=2r∫dm知，上面叙述正确。

KGGGGG[ F ] 4．一物体正在绕固定光滑轴自由转动，它受热或遇冷时，角速度均变大。

解：当一物体正在绕固定光滑轴自由转动时，其对轴的合力矩为0，所以对轴的角动量守恒。

而当物体受热或遇冷时，它的转动惯量就会增大或减小，角动量还要保持守恒，那么就只有其角速度变小或变大。

所以上述说法错误。

[ F ] 5．如果作用于质点的合力矩垂直于质点的角动量，则质点的角动量将不发生变化。

GGdLGGGG解：根据M=,如果M⊥L，即是dL⊥L,只要一个物理量的增量垂直于它本身，那么这个增量就只改变它的方dt向，不改变它的大小。

如：旋进。

二、选择题:1．有两个半径相同、质量相等的细圆环A和B。

A环的质量分布均匀，B环的质量分布不均匀。

它们对通过环心并与环面垂直的轴的转动惯量分别为JA和JB，则 [ C ] (A) JA>JB(C) JA=JB(B) JA(D) 不能确定JA、JB哪个大解：对于圆环，转动惯量为J=r2dm=R2dm，设细圆环总质量为M，无论质量分布均匀与否，都有dm=M，∫∫∫所以JA=JB=RM 选C2. 均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，如图所示。

2003〜2004学年第二学期八理论力学（AID期终试题02级土木（80学时类）用（一）.概念题（每小题4分，共5小题）1.已知均质三角板A3D的质量为m ,且有OA // O X B, OA = O X B = r, CM的角速度为则三角板A3D的动量p的大小为（）。

①p = mra）,作用在质心，方向水平向左；②p =，作用在质心，方向垂直于。

A ；③p = mnysin。

，作用在质心，方向垂直于OA。

④p = mrm，作用在质心，方向水平向右；2.已知刚体的质量为对z轴的转动惯量为人，又知刚体质心C到两相互平行的轴Z'、Z之间的距离分别为。

、b,贝U刚体对Z'轴的转动惯量人为（）。

①J z' = J z— m（a2—）；②人=</：—彻+ 人j；③ J = J z + m{a2 +Z?2）；④ J = J - + m（a2 ~b2\,3.质量为m、长为Z的均质杆A3,以角速度切绕A轴转动，而物块A以速度D作水平运动，则杆A3在图示位置的动能为（）o①T=-^mu2 + -^ml2a）2 -\-—mulco.19 i j 2 2 i r\②T= — mv co + —mulco . □2 6 3c③T=~mu2 + ^ml2co2—mulcD.121/2 2 1 ,④T=~mu — a） -o2 3 64.均质圆盘绕。

轴转动，某瞬时其角速度、角加速度如图所示。

圆盘上虚加惯性力系向。

点简化的如下结果中，正确的为（）。

①图（a）；②图（b）；③图（c）；④图（d）。

题4图5.重为P、长为Z的均质杆A3放置如图。

设各处光滑，在A点处的水平力E作用下而保持平衡，9 = 60。

，今给A点一向右的虚位移&X,则由虚位移原理所建立的虚功方程为（）。

① P V35X/6 - Fdx =0 ；③ P V38X/2-F5X=0；④ P8x-F8xgp o Fgn（二）.电皎车提升一质量为农=lkg的物体，其中电皎车半径r2 =0.5mo在齿轮1上作用一矩为M=60kN・m的常力偶。

EBC EDA A
S BC S DA
2. 理想气体的卡诺循环 1） 正循环效率 等温过程：
1 2 Q1 A1 M M

RT1ln V3 V4
V2 V1
34
| Q2 |

RT2 ln
绝热过程：
23 T1V2 1 T2V3 1
V2 V3 V1 V4
4 1
3
一个实际的过程如果进行的很缓慢可以近似看做准静态过程。 4.非准静态过程：中间状态不是平衡态，整个过程不能用状态参量描述。 例如：气体自由膨胀过程压强不均匀，高温到低温温度不均匀。 5.等值过程: 状态参量值始终不变的过程统称为等值过程。例如：等压，等体， 等温。 热力学系统的平衡状态和准静态过程可以用相图（状态参量作为坐标轴）表示， 相图中每一个相点代表系统的一个平衡状态， 任一曲线代表系统经历的一个准静 态过程（平衡过程） 。 例如：P-V、V-T、P-T、E-P、E-T 等，但只有 P-V 相图中曲线下面积值才是该准 静态过程的功值。下图为等压、等体和等温过程在 P-V 相图中的表示。
9
2 1
Q1 A1 M
M

RT1ln V3 V4
V2 V1
43
Q2

RT2 ln
绝热过程：
3 2 T1V2 1 T2V3 1
V2 V3 V1 V4
M 1 4 T1V1
1
T2V4
1
w
Q2 Q2 A Q1 Q2 M RT ln V2 M RT ln V3 2 1 V1 V4
-1
R=8.31J•mol (普适常量或摩尔气体常量) k= =1.38×10-23J·K-1(玻尔兹曼常量)

43.求图示系统的稳态响应.
题43解：
k k m X1 F0 k k m jc X 0 , 2 k k k m 1 k m jc k k m jc k k m
为J. 设 t = 0 时摆角向右最大为 0.
求 振动周期和振动方程. 解 M mgh sin J
mgh sin 0 J 5时, sin mgh 0 J mgh J T 2 J mgh 0 cosω t 振动方程
39. 图所示系统中，质量为M用弹簧 k 连结于活动支点0， 质量M与点O 都限于在同一水平方向作直线运动设点 0 的运动规律已知为x0 a(t ) 。在质量M上悬挂一物理摆， 摆重为mg ，其重心C至悬挂点的距离为 l ，摆绕其重心 轴的迴转半径为 。求系统的运动方程.
题39解：
1 1 1 2 2 2 2 1 m x 1 lx 2 cos x2 lx 2 sin x2 m 2 x 2 T Mx 2 2 2 1 1 2 2 1 m 2lx 1 x 2 cos x2 (l 2 2 ) x 2 M m x 2 2 1 U mgl (1 cos x2 ) k ( x1 x0 ) 2 2 ml M m k M ,K 2 2 ml m ( l ) mgl
3. 截面为s 的U 形管中有适量液体,总长为l, 质量为
m, 密度为 , 求液面上下振动的频率(不计摩擦)
y y
解（一） 设t 时刻，右边液面的位移为y ，左边液面 的位移为-y ，系统的势能为 ySyg
机械能为

第五章 角动量 角动量守恒定律5-1 选择题：（1）一质点作匀速率圆周运动时，（A ）它的动量不变，对圆心的角动量也不变。

（B ）它的动量不变，对圆心的角动量不断改变。

（C ）它的动量不断改变，对圆心的角动量不变。

（D ）它的动量不断改变，对圆心的角动量也不断改变。

[C] 解：质点作匀速率圆周运动时，其速度大小虽不变，但速度方向不断改变，故其动量不断改变。

而该质点对圆心角动量大小不变，方向始终垂直于圆轨道平面，指向也不变。

（2）已知地球的质量为m ，太阳的质量为M ，地心与日心的距离为R ，引力常数为G ，则地球绕太阳作圆周运动的轨道角动量为（A ）GMR m （B ）RGMm（C ）R G Mm（D ）RGMm 2 [A] 解：由万有引力定律和牛顿第二定律有R v m RmM G 22=得地球绕日运动速率RGM v =由角动量定义得GMR m mvR L ==（3）一刚体以每分钟60转绕Z 轴做匀速转动（ω沿z 轴正方向），设某时刻刚体上一点P 的位置矢量为k j i r 543++=，其单位为“m 102-”，若以“12s m 10--⋅”为速度单位，则该时刻P 点的速度为：（A ）k j i v 0.1576.1252.94++= （B ）j i v 8.181.25+-= （C ）j i v 8.181.25--=（D ）k v 4.31= [B] 解：刚体转动平面与转轴垂直，所以P 点速度无z 分量。

由题意，作出P 的位矢，可知该时刻P 点速度的x 分量为负而y 分量为正，故答案（B ）正确。

（4）均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的？（A ）角速度从小到大，角加速度从大到小。

（B ）角速度从小到大，角加速度从小到大。

（C ）角速度从大到小，角加速度从大到小。

大物实验网上答题答案(已分类)测定刚体的转动惯量1对于转动惯量的测量量，须要考量b类不确认度。

在烛焰实验中，振动周期的b类不确认度必须挑（）a.b.c.d.d13在测刚体的转动惯量实验中，需要用到多种测量工具，下列测量工具中，哪一个是不会用到的()a.游标卡尺b.千分尺c.天平d.秒表c测量刚体的转动惯量14在扭摆实验中，为了测得圆盘刚体的转动惯量，除了测得圆盘的振动周期外，还要加入一个圆环测振动周期。

加圆环的作用是（）a.减小测量误差b.做测量结果对比c.消除计算过程中的未知数d.验证刚体质量的影响c测量刚体的转动惯量15转动惯量是刚体转动时惯性大小的量度，是表征刚体特性的一个物理量。

转动惯量与物体的质量及其分布有关，还与（）有关a.转轴的位置b.物体转动速度c.物体的体积d.物体转动时的阻力a测量刚体的转动惯量16在测转动惯量仪实验中，以下不需要测量的物理量是（）a.细绳的直径b.绕绳轮直径c.圆环直径d.圆盘直径a测定刚体的转动惯量17在烛焰实验中，并使圆盘搞角谐振动，角度无法少于（），但也无法太小。

a.90度b.180度c.360度d.30度b测量刚体的转动惯量测定空气的比热容比2如图，实验操作的正确顺序应该是：a.关闭c2，打开c1，打气，关闭c1，打开c2b.关闭c1，打开c2，打气，关闭c1，关闭c2c.关闭c2，打开c1，打气，关闭c2，打开c1d.打开c2，关闭c1，打气，打开c1，关闭c2a18数字电压表u1，u2与气压p1，p2的关系式为：a.p1=p0+u1/2;p2=p0+u2/2b.p1=p0-u1/2;p2=p0-u2/2c.p1=p0+u1;p2=p0+u2d.p1=p0-u1;p2=p0-u2a测定空气的比热容比19本实验测量的物理量就是：a.cvb.cpc.cv/cpd.cp/cvd测定空气的比热容比20cv指的是a.等压比热容b.容比热容c.温比热容d.上都不对b测量空气的比热容比21cp所指的就是a.等温比热容b.容比热容c.温比热容d.上都不对a测定空气的比热容比夫兰克-赫兹实验3参考夫兰克-赫兹实验原理图，以下定义恰当的就是：a.在阴极k和第二栅极(帘栅极)g2之间靠近阴极k存在第一栅极g1(图中未画出)，g1和k之间加有正向电压ug1，主要用以清除空间电荷对阴极发射电子的影响，提高阴极发射电子的能力；b.g2、k间有正向快速电压ug2k（缩写ug2），经ug2快速而存有一定能量的电子主要就是在g1、g2空间与氩原子出现相撞互换能量；c.在g2与屏极a之间加有反向的拒斥电压ug2a，其作用是挑选能量大于eug2a的电子，从而冲过拒斥电压形成通过电流计的屏极电流；d.以上表述均正确。

NO.3 角动量和刚体定轴转动班级 姓名 学号 成绩一、选择1.体重、身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端．他们从同一高度由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是 [ C ] (A)甲先到达． (B)乙先到达．(C)同时到达． (D)谁先到达不能确定．2.如图所示，A 、B 为两个相同的绕着轻绳的定滑轮．A 滑轮挂一质量为M 的物体，B 滑轮受拉力F ，而且F ＝Mg ．设A 、B 两滑轮的角加速度分别为βA 和βB ，不计滑轮轴的摩擦，则有 [ C ] (A) βA ＝βB ． (B) βA ＞βB ．(C) βA ＜βB ． (D) 开始时βA ＝βB ，以后βA ＜βB ．参考：2A Mgr Mr J β=+，BMgrJβ= 3.如图所示，一质量为m 的匀质细杆AB ，A 端靠在光滑的竖直墙壁上，B 端置于粗糙水平地面上而静止．杆身与竖直方向成θ角，则A 端对墙壁的压力大小[ B ] (A) 为41mg cos θ． (B) 为21mg tg θ(C) 为mg sin θ． (D) 不能唯一确定．4.如图所示，一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转，初始状态为静止悬挂．现有一个小球自左方水平打击细杆．设小球与细杆之间为非弹性碰撞，则在碰撞过程中对细杆与小球这一系统 [ C ] (A) 只有机械能守恒． (B) 只有动量守恒．(C) 只有对转轴O 的角动量守恒． (D) 机械能、动量和角动量均守恒．5.一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度ω [ C ] (A) 增大． (B) 不变． (C) 减小． (D) 不能确定． 参考：角动量守恒 ，而J 变大，故ω 变小。

6．已知地球的质量为m ，太阳的质量为M ，地心与日心的距离为R ，引力常数为G ，则地球绕太阳作圆周运动的轨道角动量为：[ A ]（A ）m GMR ； （B ）R GMm ；（C ）Mm RG ； （D ）R GMm 2。