当前位置：文档之家 › 7-第七章 应力状态分析 强度理论

7-第七章 应力状态分析 强度理论

  • 格式：doc
  • 大小：1.19 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

第七章+应力应变分析+强度理论

第七章+应力应变分析+强度理论
Chapter7 Analysis of Stress and Strain Failure Criteria
(Analysis of stress-state and strain-state)
§7-1 应力状态概述 (Introduction of stress-state)
一、应力状态的概念 (Concepts of stresses-state)
σ1 ≥ σ 2 ≥ σ 3
(Analysis of stress-state and strain-state)
三、应力状态的分类 （The classification of stresses-state）
1.空间应力状态（Triaxial stress-state or three-dimensional stress-state ） 三个主应力σ1 ,σ2 ,σ3 均不等于零 2.平面应力状态（Biaxial stress-state or plane stress-state） 三个主应力σ1 ,σ2 ,σ3 中有两个不等于零 3.单向应力状态（Uniaxial stress-state or simple stress-state） 三个主应力 σ1 ,σ2 ,σ3 中只有一个不等于零
x
− 62.5
σ3
因为 σx < σy ，所以 α0= 27.5°与σmin对应
σx −σ y 2 ⎧σ max σ x + σ y ⎧ 26MPa 2 ) + τ xy = ⎨ = ± ( ⎨ 2 2 ⎩ − 96MPa ⎩σ min σ 1 = 26MPa , σ 2 = 0, σ 3 = −96MPa
1.求单元体上任一截面上的应力（Determine the stresses on any inclined plane by using stress-circle） 从应力圆的半径 CD 按方位角α的转向转动2α得到半径CE. 圆周上 E 点的坐标就依次为斜截面上的正应力σα 和切应力τα.

材料力学第七章 应力状态

材料力学第七章 应力状态

主平面的方位：
tan
2a0
2 xy x
y
主应力与主平面的对应关系： max 与切应力的交点同象限
例题：一点处的平面应力状态如图所示。
已知 x 60MPa， xy 30MPa, y 40MPa, a 30。
试求（1）a 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解：（1）a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
在二向应力状态下，任意两个垂直面上，其σ 的和为
一常数。
证明： a
x y

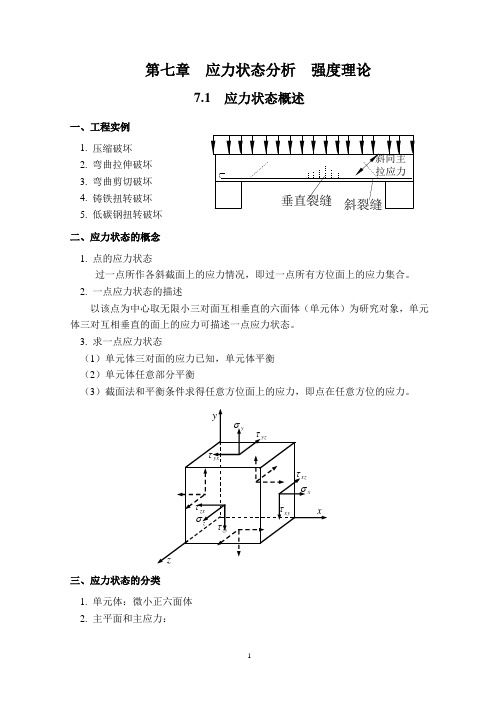
7-第七章 应力状态分析 强度理论.

7-第七章 应力状态分析 强度理论.

第七章应力状态分析强度理论7.1 应力状态概述一、工程实例1. 压缩破坏2. 弯曲拉伸破坏3. 弯曲剪切破坏4. 铸铁扭转破坏5. 低碳钢扭转破坏二、应力状态的概念1. 点的应力状态过一点所作各斜截面上的应力情况，即过一点所有方位面上的应力集合。

2. 一点应力状态的描述以该点为中心取无限小三对面互相垂直的六面体（单元体）为研究对象，单元体三对互相垂直的面上的应力可描述一点应力状态。

3. 求一点应力状态（1）单元体三对面的应力已知，单元体平衡（2）单元体任意部分平衡（3）截面法和平衡条件求得任意方位面上的应力，即点在任意方位的应力。

三、应力状态的分类1. 单元体：微小正六面体2. 主平面和主应力：主平面：无切应力的平面主应力：作用在主平面上的正应力。

3. 三种应力状态单项应力状态：三个主应力只有一个不等于零，如A 、E 点 二向应力状态：三个主应力中有两个不等于零，如B 、D 点 三向应力状态：三个主应力都不等于零四、应力状态分析的方法 1.解析法2. 图解法7.2应力状态分析的解析法一、解析法图示单元体，已知应力分量x σ、y σ、xyτ和yx τ。

xxx（一）任意截面上的正应力和切应力：利用截面法，考虑楔体bef 部分的平衡。

设ef 面的面积为dA ， ∑=0F n 0sin )Asin (cos )sin A (cos )cos A (sin )cos A (A =-+-+αασααταασαατσαd d d d d y yx x xy∑=0F tsin )Asin (cos )sin A (sin )cos A (cos )cos A (A =++--ααταασαασαατταd d d d d yx y x xy根据切应力互等定理： y x xy ττ=三角函数关系：22cos 1cos 2αα+=，22cos 1sin 2αα-=，∂=cos sin 22sin αα解得：ατασσσσσα2sin 2cos 22x x xy yy--++=（7-1）ατασστα2cos 2sin 2x xy y+-= （7-2）（二）主应力即主平面位置将式（8-1）对取一次导数，并令其等于零可确定正应力的极值和所在平面的位置。

材料力学-应力状态分析

材料力学-应力状态分析

+
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意： 的正负号， 注意：1）σx 、σy 、τx 和 α的正负号， 2） 公式中的切应力是τx ，而非τy， 而非 的正负号。 3） 计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中， 已知圆轴直径d=100mm， 轴向拉 例 ： 图示圆轴中 ， 已知圆轴直径 ， 力 F=500kN，外力矩Me=7kNm。求 C点α = 30°截 ， 外力矩 。 点 ° 面上的应力。 面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa

第七章_应力状态和强度理论

第七章_应力状态和强度理论

第 1 页/共 4 页第七章 应力状态和强度理论7-3 横截面上 AF =σ α截面上 αστασσσαα2sin 22cos 22=+=，强度条件 ][432sin 2][)2cos 1(2σατσασαα≤=≤+=A F A F ，等价于 ][2sin 342)2cos 1(2max σαασ≤⎭⎬⎫⎩⎨⎧⋅+=A F A F e ，由0=ασd d e，并比较︒=0α或︒60的e σ，得使e σ最小的角度︒=60α 7-7 内力 m kN M ⋅-=2.7，kN F s 10-=应力 MPa I Myz 55.10==σ，MPa bI S F z z s 88.0*-==τ 主应力 MPa 62.1022221=+⎪⎭⎫⎝⎛+=τσσσ，MPa 073.022223-=+⎪⎭⎫⎝⎛-=τσσσ主平面方位 ︒=⇒=-=74.4167.022tan 00αστα7-8(d) MPa MPa x y x 50200-=-==τσσ，， ︒=45α截面上：MPaMPax yx yy102cos 2sin 2402sin 2cos 22=+-==--=αταστατασσσαα主应力：MPa x y y4122221=+⎪⎪⎭⎫ ⎝⎛+=τσσσ， MPa x y y6122223-=+⎪⎪⎭⎫ ⎝⎛-=τσσσ主平面方位：︒=⇒=--=34.39522tan 00ασταyx7-15(a) MPa z 50=σ——为主应力，另两个主应力由下列应力决定 MPa MPa MPa x y x 403070-===τσσ，，MPa MPa x y x yx x y x yx 3.5227.94222222=+⎪⎪⎭⎫ ⎝⎛--+=''=+⎪⎪⎭⎫ ⎝⎛-++='τσσσσστσσσσσ主应力 MPa MPa MPa z 3.5507.94321=''===='=σσσσσσ，， 最大切应力 MPa 7.44231max =-=σστ7-16(a) MPa MPa MPa 105070321＝，＝，＝σσσ A 点：MPa MPa A A 2030==τσ，在2σ与3σ决定的应力圆上使切使劲达极值7-18 立方体边长 a ＝20mm不计摩擦，各面上的应力为主应力顶面 MPa aF3523-=-=σ，侧面021<=σσ 主应变021==εε，又)]([13211σσνσε+-=EMPa 151321-=-==⇒σννσσ7-21 k 处截面上的内力： e M laM =，l M F e s =应力： bhFb I S F s z z s 230*==＝，τσ︒=45α方向即为主应力方向第 3 页/共 4 页τστσ-==31，主应变 )(131451νσσεε-==︒E由上可得 ︒+=45)1(32ενElbhM e7-22 钢球各点应力状态相同 MPa 14321-===σσσ体应变 )(21321σσσνθ++-=E体积改变 3101054.6m V V -⨯==∆θ7-23 MPa MPa MPa z y x 403070-===σσσ，，MPaMPax y x y x x y x y x 28.54)(21)(2172.944)(21)(212222=+--+=''=+-++='τσσσσστσσσσσ主应力 MPa MPa MPa 28.55072.94321==σσσ，＝， []3213232221/99.12)()()(61m m kN Ev d ⋅=-+-+-+=σσσσσσν7-24 平面应力状态 MPa MPa x y x 15015===τσσ，，主应力 MPa MPa x x x27.9027.242232221-===+⎪⎭⎫ ⎝⎛+=σστσσσ，， 按第一强度理论：][11t r σσσ<= 按第二强度理论：][59.26)(3212t r MPa σσσνσσ<=+-= 满意强度条件。

第七章 应力状态、应变分析和强度理论

第七章 应力状态、应变分析和强度理论

§7-3 平面应力状态分析－－解析法
二、 正应力极值
1 1 ( x y ) ( x y ) cos 2 xy sin 2 2 2 d ( x y ) sin 2 2 xy cos 2 d
设α＝α0 时，上式值为零，即
2
1 0, 2 0, 3 0
1 0, 2 0, 3 0
§7-1 应力状态的概念
3、三向（空间）应力状态 三个主应力1 、2 、3 均不等于零
2 1
3 1
3 2
1 0, 2 0, 3 0
§7-1 应力状态的概念
仅在微体四侧面作用应力，且 应力作用线均平行于微体的不 受力表面－平面应力状态
1
1
1
1
3
3
1 0, 2 0, 3 0
1 0, 2 0, 3 0
§7-1 应力状态的概念 2、二向（平面）应力状态 三个主应力1 、2 、3 中有两个不等于零
3 2 3 2
3
2
1
3
1
1
1
1 0, 2 0, 3 0
Ft 0
dA ( x dAcos )cos ( x dAcos )sin ( y dAsin )sin ( y dAsin )cos 0
§7-3 平面应力状态分析－－解析法
一、任意斜截面上的应力公式 已知： x , y , x , y , dA 求： ，
sin 2 xy cos 2
2 xy 2 ( 50) tan 2 0 1 x y 40 60 2 0 45 135

y =60 MPa xy = -50MPa =-30°

应力状态理论与强度理论

应力状态理论与强度理论

D，承受内压 p 作用。
FN
A
p D2
p 4
p Dt
pD 4t
1
2
pD 4t
3 p 0
实例四 圆杆受扭转和拉伸共同作用
m
P
P
m
FN 4 P
A pd2
T 16m Wt p d 3
按工程应用传统观念，判断构件强度取 决于危险点的应力状态。
危险点是怎样达到破坏的呢？
在什么方向最容易破坏呢？
剪应力（应力单位为MPa）。
20
40
50 30
解：
max 30 20
min
2
30 + 20 2 2
+ 402
52.2 MPa
42.2
1 52.2MPa
20
2 50MPa
40
3 42.2MPa
max
1
3
2
47.2MPa
30
50
例6、求图示应力状态的主应力和
最大剪应力（应力单位MPa）。
第七章 应力状态理论与强度理论
本章重点 1、应力状态的概念 2、如何建立一点处的应力状态 3、平面应力状态分析 4、广义胡克定律 5、强度理论的概念 6、四种主要强度理论及其应用
问题的提出：
铸铁
低碳钢
思考：塑性材料拉伸时为什么会出现滑移线？
低碳钢
铸铁
思考：为什么脆性材料扭转时沿45º螺旋面断开？
P
解：刚性凹座是不变形的
Nx
Nz Ny
Nx
Ny
x y 0
Nx
x
1 E
x
(
y
+ z )
0
y

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

工程力学(材料力学部分第七章)

工程力学(材料力学部分第七章)

4 主应力及应力状态的分类
主应力和主平面
切应力全为零时的正应力称为主应力；
主应力所在的平面称为主平面；
主平面的外法线方向称为主方向。
主应力用1 , 2 , 3 表示 (1 2 3 ) 。
应力状态分类
单向应力状态
11
应力状态分类
单向应力状态 二向应力状态(平面应力状态)
三向应力状态(空间应力状态)
D点
由 y 40, yx 60
D'点
画出应力圆
52
圆心坐标
OC x y 80 (40)
2
2
20
半径
R
x
2
y
2
2 xy
80 (40) 2
(60)2
84.85 85
2
53
圆心坐标 OC 20
半径
R 85
1 OA1 OC R
E
105 MPa
3 OC R
65 MPa
D (x ,xy)
x y
2
R 1 2
x y
2
4
2 xy
38
3 应力圆上的点与单元体面上的应力的对应关系 (1) 点面对应
应力圆上某一点 的坐标值对应着 单元体某一方向面上的正应力和切应力。
39
(1) 点面对应
应力圆上某一点的坐 标 值对应着单元体某 一方向面上的正应力 和切应力。
D点对应的面与E点 对应的面的关系
主应力。
从半径CD转到CA1 的角度即为从x轴转
到主平面的角度的
两倍。
44
主应力 即为A1, B1处的正应力。
max min
x
y
2
x
2

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2

材料力学课件——应力状态理论和强度理论

材料力学课件——应力状态理论和强度理论

Me B
Me
B Me/Wn
P Me
C Me
C
第二节 二向应力状态下斜截面上的应力
目的 — 用一点某个微元上的应力表示其它
无限多微元上的应力 伴随结果
•应力极值 — 主应力状态 •从一个斜截面的应力构造一个单元体的应力
• 分析方法：1 解析法
•
2 图解法
二向应力状态下斜截面上的应力（续）
正应力符号规定
τα M τβ
σβ (c)
cos2
1
2
sin 2
cos2
1 sin 2
2
应力状态理论（续）
P
B
A
max A
max
M W
y
y
B
B
My
I
QS
Ib
应力状态理论（续）
P
P
A
A P/A
a) 一对横截面，两对纵截面
b)横截面，周向面，直径面 各一对
c) 同b)，但从上表面截取
应力
要指明
哪一点？
•那个面在
• 在哪一个面上？
哪个方位？
• 一点的应力状态：过一点不同方向面上应力的集合
•
称之为这一点的应力状态
•
State of the Stresses of a Given
Point
应力状态理论（续）
三向（空间）应力状态
Three-Dimensional State of Stresses
第七章 应力状态理论和强度理论
Theory of Stress State and Intensity
第一节 第二节 第三节 第四节 第五节 第六节 第七节 第八节

第七章：应力状态、强度理论

第七章：应力状态、强度理论

s
2 2
s
2 3
2 s1s 2
s 3s 2
s1s 3 )
1 t 2 0 (t )2 2 0 0 t (t ))
2E
s1
1 t 2
E
G
E
21
)
§7–6 强度理论及其相当应力
强度理论：是关于“材料发生强度破坏或失效”的假设
材料的破坏形式： ⑴ 脆性断裂 如铸铁在拉伸和扭转时的突然断裂 ⑵ 塑性屈服 如低碳钢在拉伸和扭转时明显的塑性变形
sx
t 绕研究对象顺时针转为正；
y
txy
逆时针为正。
Ox
图1
s
sx
y
sy
ttxy
Ox 图2
设：斜截面面积为dA，由分离体平衡得：
Fn 0
n s dA (t xydAcos )sin (s xdAcos ) cos t (t yxdAsin ) cos (s ydAsin )sin 0
容器表面用电阻应变片测得环向应变 t =350×10-6，若已知容器平均 直径D=500 mm，壁厚=10 mm，容器材料的 E=210GPa，=0.25
试求:1.导出容器横截面和纵截面上的正应力表达式； 2.计算容器所受的内压力。
s1 sm
p p
p
x
l
图a
D
y
xp
AO
B
解：容器的环向和纵向应力表达式 1、轴向应力:(longitudinal stress) 用横截面将容器截开，受力如图b所示,根据平衡方程
第七章 应力状态和强度理论
§7–1 概述 §7–2 平面应力状态的应力分析.主应力 §7–3 空间应力状态的概念
§7–4 复杂应力状态下的应力 -- 应变关系 ——（广义虎克定律）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章应力状态分析强度理论7.1 应力状态概述一、工程实例1. 压缩破坏2. 弯曲拉伸破坏3. 弯曲剪切破坏4. 铸铁扭转破坏5. 低碳钢扭转破坏二、应力状态的概念1. 点的应力状态过一点所作各斜截面上的应力情况，即过一点所有方位面上的应力集合。

2. 一点应力状态的描述以该点为中心取无限小三对面互相垂直的六面体（单元体）为研究对象，单元体三对互相垂直的面上的应力可描述一点应力状态。

3. 求一点应力状态（1）单元体三对面的应力已知，单元体平衡（2）单元体任意部分平衡（3）截面法和平衡条件求得任意方位面上的应力，即点在任意方位的应力。

三、应力状态的分类1. 单元体：微小正六面体2. 主平面和主应力：主平面：无切应力的平面主应力：作用在主平面上的正应力。

3. 三种应力状态单项应力状态：三个主应力只有一个不等于零，如A 、E 点 二向应力状态：三个主应力中有两个不等于零，如B 、D 点 三向应力状态：三个主应力都不等于零四、应力状态分析的方法 1.解析法2. 图解法7.2应力状态分析的解析法一、解析法图示单元体，已知应力分量x σ、y σ、xyτ和yx τ。

xxx（一）任意截面上的正应力和切应力：利用截面法，考虑楔体bef 部分的平衡。

设ef 面的面积为dA ， ∑=0F n 0sin )Asin (cos )sin A (cos )cos A (sin )cos A (A =-+-+αασααταασαατσαd d d d d y yx x xy∑=0F tsin )Asin (cos )sin A (sin )cos A (cos )cos A (A =++--ααταασαασαατταd d d d d yx y x xy根据切应力互等定理： y x xy ττ=三角函数关系：22cos 1cos 2αα+=，22cos 1sin 2αα-=，∂=cos sin 22sin αα解得：ατασσσσσα2sin 2cos 22x x xy yy--++=（7-1）ατασστα2cos 2sin 2x xy y+-= （7-2）（二）主应力即主平面位置将式（8-1）对取一次导数，并令其等于零可确定正应力的极值和所在平面的位置。

令0αα=时，0d d =ασα 即：yx xy xy y x σσταατασσασα--==⎥⎦⎤⎢⎣⎡+--=22tan 02cos 2sin 22d d 000 将0α和ο900+α代入（8-1），求出最大及最小的正应力为：22min max )2(2xy y x yx τσσσσσσ+-±+=⎭⎬⎫ （三）最大切应力及其作用平面的位置将式（8-2）对α取一次导数，并令其等于零可确定切应力的极值和它所在平面的位置。

令1αα=时，0d d =ατα即： xy y x τσσα22tan 1-= 22min max )2(xy y x τσσττ+-±=⎭⎬⎫ 所以有：22201παα+=，401παα+=即最大和最小切应力所在平面与主平面的夹角为ο45 例题1. 如图a 所示受力杆件内单元体各面上的应力分量。

试用解析法求出单元体在ο30=α倾斜面上的应力，主应力的大小并确定主平面的方位。

解：（1） 斜截面上的应力如图a ，有：MPa 50x =σ，MPa 100y -=σ，MPa 70xy -=το30=α所以，axy y y MP 1.7360sin 7060cos 2100502100502sin 2cos 22x x 30=-++-=--++=οοοατασσσσσa xy yMP 3060cos 7060sin 2100502cos 2sin 2x 30=-++-=οοοατασστ （2）主应力及主平面的方向MPa 6.127MPa 6.77)2(222min max -=+-±+=⎭⎬⎫或xy y x yx τσσσσσσ 主应力为MPa 6.771=σ，MPa 02=σ，MPa 6.1273-=σσο5.b)ya)933.010050)70(222tan 0=+-⨯=--=yx xyσστα（3）主平面位置为ο5.210=α或ο5.1110=α，即主平面外法线与x 轴的夹角为ο5.21或ο5.111（见图b ），该单元体是主单元体。

2. 已知圆轴直径d=15mm ，在外力偶m N 100M ⋅=e 作用下，发生扭转。

试分析圆轴表面上A 点的应力状态，并分析铸铁试件受扭时的破坏现象。

解：（1）A 点处横截面上的切应力为MPa 97.150m)015.0(14.3m N 1001616M W M 333e P T =⨯⋅⨯===d πτ 在A 点周围截取单元体，单元体各面上的应力如图b ，ττσσ===xy ,0y x 所以，150.97MPa )2(222min max ±=±=+-±+=⎭⎬⎫ττσσσσσσxy y x yx （2）主应力为MPa 97.150,0,MPa 97.150321-===σσσ-∞→--=y x xyσστα22tan 0主平面位置为：σ a)οο4590200-=-=αα 或οο135270200-=-=αα（3）由上分析可知，圆轴扭转时表面上各点均处于纯剪切应力状态，而且各点m ax σ所在的平面连成一个倾角为ο45的螺旋面，由于铸铁抗拉强度低，试件将沿这一螺旋面上因抗拉能力不足而发生断裂破坏。

二、主应力迹线σ311τ梁在横力弯曲时，除横截面上、下两边缘各点均处于单向拉伸或压缩外，横截面其他各点处的正应力就不是主应力。

现利用应力圆来确定这些点处主应力的数值和主平面的位置。

如图a ，表示一个受均布荷载q 作用的矩形截面梁，在梁的某一横截面m-n 上，围绕2、4两点各取出一个单元体。

设此横截面上的剪力和弯矩都是正值，则此二单元体各面上的应力状态如b 图所示。

单元体的x 平面是梁的横截面。

其上的正应力y I ZM x =σ和切应力b Z *ZQ xy I S F =τ。

单元体的y 平面是梁的水平纵截面，其上的0y =σ，xy τ和y x τ等值反号。

根据这些已知应力，就可以作出相应的应力圆。

求出梁截面上一点主应力方向后，把其中一个主应力的方向延长与相邻横截面相交，求出交点的主应力后，再将其延长线与下一个相邻横截面相交，依次类推，所做出的折线。

折线上任一点的切线方向表示该点的主应力方向。

梁内任意一点的主应力的表达式为：22x 1)2(2xyx τσσσ++= 22x3)2(2xyxτσσσ+-=由上式知，梁内任意一点处的两个主应力必然一个为拉应力，另一个为压应力，两者的方向任意垂直。

所以在梁的xy 平面内可以绘制两组正交的曲线，在一组曲线上每一点处切线的方向是该点处主应力1σ（拉应力）的方向，而在另一组曲线上每一点处切线的方向则为主应力3σ（压应力）的方向。

这样的曲线称为梁的主应力迹线，前者称为主应力1σ迹线，后者则称为主应力3σ迹线。

如图实线表示主应力1σ迹线，虚线表示主应力3σ迹线。

由于主拉应力的存在，混凝土抗拉强度不足而沿着所在的主平面的方向开裂。

在梁跨中的底部，主拉应力1σ方向是水平或接近水平的，所以裂隙方向是垂直的。

在两端主拉应力1σ方向是倾斜的，所以裂隙也是与主应力正交而倾斜。

正因为这样，在钢筋混凝土受弯构件中，主要承受拉力的钢筋应大致按照主应力1σ迹线来配置排列，以承担梁内各点处的最大拉应力。

7.3 应力状态分析的图解法一、应力圆方程由式（7-1）（7-2）可知在二向应力状态下，在法向倾角为α的斜截面上的正应力与切应力均为α的函数。

现消去α，则有，ατασσσσσα2sin 2cos 22x x xy yy --=+-ατασστα2cos 2sin 2x xy y+-=以上两式等号两边平方，然后相加，得2xy 2x 22x 22τσστσσσαα+-=++-）（）（y y以横坐标表示σ，以纵坐标表示τ，上式时一个以ασ和ατ为变量的圆周方程，圆心的横坐标为2x yσσ+；纵坐标为零。

圆的半径为2xy2x 2τσσ+-）（y。

这一圆周称为应力 圆。

又称摩尔应力圆，简称摩尔圆。

二、应力圆的作法以图a 所示单元体为例说明应力圆的做法。

先建立τσ-直角坐标系，按一定比例尺量取横坐标x OA σ=， xy AD τ=,先确定D 点（见图B ）。

量取y OB σ=，xy D B τ='，确定D '，根据前节符号规定，y x τ为负，所以D 点与D '点分别位于横坐标的上下边。

连接D 、D '与横坐标交于C 点。

以C 点为圆心，CD 为半径作圆，显然圆心C 的纵坐标为零，横坐标为2OB OA 21OD x y σσ+=+=）（，所以，C 点即是应力圆的圆心。

圆半径22x 22)2(AD CA CD xyy τσσ++=+=。

所以，图b 所作的xyτy xτ ,0)三、应力圆的应用（一）二向应力状态单元体与应力圆的对应关系1. 点面对应 应力圆上某一点的坐标值对应着单元体某一截面上的正应力和切应力值。

2. 二倍角对应 单元体上任意两个斜截面的外法线之间的夹角若为α，则对应在应力圆上代表该斜截面上应力的两点之间的圆弧所对应的圆心角必为α2。

3. 转向对应 应力圆半径旋转时，半径端点的坐标随之改变，对应地，单元体上斜截面的法线亦沿相同方向旋转，才能保证斜截面上的应力与应力圆上半径端点的坐标相对应。

（二）确定单元体斜截面上的应力根据以上的对应关系，可以从作出的应力圆确定单元体内任意斜截面那个的应力值。

注意上图a 、b ，若求法线n 与x 轴夹角为逆时针α角的斜截面的应力ασ、ατ，则在应力圆上，从D 点也按逆时针方向沿圆周转到E 点，且使DE 弧所对应的圆心角α2，则E 点的坐标就代表以n 为法线的斜面上的应力ασ、ατ。

证明：⎪⎪⎭⎪⎪⎬⎫+=+=-+=++=αααααααααααα2sin 2cos CE 2cos 2sin CE )22(sin CE OF 2sin 2cos CE 2cos 2cos CE OC )22(cos CE OC OF 000000因为CD CE =2CA 2cos CD 2cos CE x 00yσσαα-===xy ταα===AD 2sin CD 2sin CE 00所以 ασατασσσσ=-++-=2sin 2cos 22OF x x xy yyασατασσ=+-=2cos 2sin 2FE x xy y这就是式（7-1）（7-2），证毕。

（三）主应力的数值和主平面的方位由于应力圆上1A 点的横坐标（正应力）最大，纵坐标（切应力）等于零，所以1A 代表最大主应力，即：11max A OC OA C +==σ同理，1B 点表示最小正应力，即：11min CB -OC OB ==σ。