概率论与数理统计浙大版概述
- 格式:pps
- 大小:698.50 KB
- 文档页数:37


![[工学]浙大概率论与数理统计课件免费.ppt](https://uimg.taocdn.com/9182d0c752d380eb63946db8.webp)

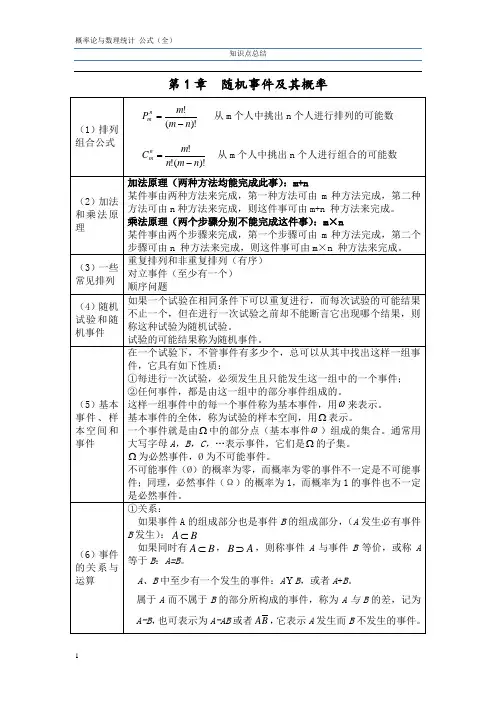






浙大第5版概率论与数理统计
《浙大第5版概率论与数理统计》是浙江大学统计学系编写的一本概率论与数理统计教材,是浙大统计学系著名的课程教材之一。
该书的作者是严立华、赵学功和赵旭阳等。
该教材主要包含了概率论和数理统计的基本内容,内容丰富、系统性强,适合作为本科生和研究生的教材使用。
书中既包含了基础理论,如概率空间、随机变量、概率分布等,也包含了一些应用领域的内容,如参数估计、假设检验等。
该教材的特点之一是对概念解释清晰、推导严格,在讲解概率论与数理统计的基本理论时,注重理论的抽象性和应用性的统一性,以便学生能够更好地掌握和应用相关的知识。
此外,该书还包含了大量的例题和习题,方便学生巩固和加深对知识的理解。
总体来说,《浙大第5版概率论与数理统计》是一本深入浅出、全面系统的教材,适合统计学和相关专业的学生学习和参考。
§3.2 二维 r.v.的条件分布,2,1,,),(====j i p y Y x X P ij j i 设二维离散型 r.v. ( X ,Y )的分布若)(1>===∑∞=∙j ij i i p x X P p 则称 ∙====i iji j i p p x X P y Y x X P )(),(为在 X = x i 的条件下, Y 的条件分布律,2,1=j )(i j x X y Y P ===记作二维离散 r.v.的条件分布律若,0)(1>===∑∞=∙i ij j j p y Y P p 则称 jij j j i p p y Y P y Y x X P ∙====)(),(为在 Y = y j 的条件下X 的条件分布律,2,1=i )(j i y Y x X P ===记作类似乘法公式)()(),(i j i j i x X y Y P x X P y Y x X P ======)()(j i j y Y x X P y Y P ====或,2,1,=j i类似于全概率公式),()(11∑∑∞=∞======j j i j ij i y Y x X P p x X P )()(1j j j i y Y P y Y x X P ====∑∞=,2,1=i ),()(11∑∑∞=∞======i j i i ij j y Y x X P p y Y P )()(1i i i j x X P x X y Y P ====∑∞=,2,1=j例1把三个球等可能地放入编号为 1, 2, 3 的三个盒子中, 每盒可容球数无限. 记X 为落入 1 号盒的球数, Y 为落入 2 号盒的球数,求(1) 在Y = 0 的条件下,X 的分布律;(2) 在X = 2 的条件下,Y 的分布律.解 先求联合分布,)()(),(i X j Y P i X P j Y i X P ======ji j ji i i i C C ----⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=333321213231;3,2,1,0;3,,0=-=i i j 其联合分布与边缘分布如下表所示XYp ij 0 1 2 3 0 1 23 27127127127191912710 0919109191920p i•278278929294941p • jX )0(==Y i X P 0 1 2 38/18/38/18/3将表中第一行数据代入得条件分布)0()0,()0(======Y P Y i X P Y i X P 27/8)0,(===Y i X P 3,2,1,0=i (1)Y)2(==X j Y P 0 12/12/1(2) 当 X = 2 时,Y 只可能取 0 与 1. 将表中第三列数据代入下式)2(==X j Y P ,9/2),2(j Y X P ===1,0=j 得Y 的条件分布解 例2 已知一射手每次击中目标概率为 p ( 0 < p < 1 ), 射击进行到击中两次为 止. 令 X 表示首次击中目标所需射击次数, Y 表示总共射击次数. 求的联 合分布律、条件分布律 和 边缘分布律. ),(Y X ,)(~p G X 由题设知 故 X 与Y 的边缘分布律分别为,)1(1--m p p ==)(m X P ,2,1=m ),2(~p P Y )(n Y P =,3,2=n ,)1()1(22---=n p p n22)1(--=n p p )()(m X n Y P m X P ==== ,3,2;1,,2,1=-=n n m ),2,1;,2,1( ++==m m n m 的联合分布律为),(Y X 11)1()1(----⋅-=m n m p p p p ),(n Y m X P ==律为)(),()(n Y P n Y m X P n Y m X P ======1,,2,1-=n m 11)1()1()1(2222-=---=--n p p n p p n n 当 时, X 的条件分布),3,2( =n n Y =)(),(m X P n Y m X P ====1122)1()1()1(-----=--=m n m n p p p p p p,2,1++=m m n )(m X n Y P ==律为当 时, Y 的条件分布 ),2,1( =m m X =二维连续型随机变量的条件分布和条件密度()i j P X x Y y ==当X 连续时, 条件分布不能用 来定义, 因为 ,()0i j P X x Y y ==≡()P X x Y y ≤=来定义.而应该用)(),()(y Y y y P y Y y y x X P y Y y y x X P ≤<∆-≤<∆-≤=≤<∆-≤xy - ∆yy)()(),(),(y y F y F y y x F y x F Y Y ∆--∆--=[][])()()()(),(),(y y F y y F y y x F y y x F Y Y ∆--∆-∆--∆-=∆y设 0>y ∆xy -∆yy dyy dF y y x F Y )(),(∂∂=)(),(y f du y u f Y x⎰∞-=连续连续,0)(),(≠y f y x f Y )(def.y Y x X P =≤=[][])()()()(),(),(lim0y y F y y F y y x F y y x F YY y ∆--∆-∆--∆-+→∆若 f (x,y ) 在点(x, y ) 连续, f Y (y )在点 y 处连续且 f Y (y ) > 0, 则称dyy dF yy x F Y )(),(∂∂)(),(y f du y u f Y x⎰∞-=⎰∞-=xY du y f y u f )(),(为Y = y 时,X 的条件分布函数, 记作()X Y F x y 定义 ⎰∞-=xY du y f y u f )(),(类似地, 称 ⎰∞-=yX dv x f v x f )(),(为X = x 的条件下Y 的条件分布函数;()Y X F y x (,)()X f x y f x =为 X = x 的条件下Y 的条件 p.d.f.)(x y f X Y (,)()Y f x y f y =称为 Y = y 的条件下 X 的条件 p.d.f. )(y x f Y X 称注意y 是常数, 对每一 f Y (y ) >0 的 y 处, 只要),(x y F X Y )(x y f X Y 相仿论述. 0)()()(),(>=x f x y f x f y x f X X Y X 0)()()(>=y f y x f y f Y Y X Y ),(y x F Y X )(y x f Y X 仅是 x 的函数,类似于乘法公式:符合定义的条件, 都能定义相应的函数.类似于全概率公式⎰⎰∞+∞-∞+∞-==dy y f y x f dy y x f x f Y Y X X )()(),()(⎰⎰∞+∞-∞+∞-==dxx f x y f dx y x f y f X X Y Y )()(),()(类似于Bayes 公式)(),(y f y x f Y =)(y x f Y X )()()(y f x f x y f Y X X Y =)(),(x f y x f X =)(x y f X Y )()()(x f y f y x f X Y Y X =例3 已知(X,Y )服从圆域 x 2 + y 2 ≤ r 2 上的均匀分布,求 ),(y x f Y X ).(x y f X Y r解 ⎪⎩⎪⎨⎧<+=其他,0,1),(2222r y x ry x f π⎰∞+∞-=dy y x f x f X ),()(r x r dy r x r x r <<-⎰-+--,122222π22xr -∙22x r --∙ x⎪⎩⎪⎨⎧<<--=其他,0,2222r x r r x r π-r 其他,0=同理,⎰∞+∞-=dxy x f y f Y ),()(⎪⎩⎪⎨⎧<<--=其他,0,2222r y r r y r π边缘分布不是均匀分布!)(),(y f y x f Y =)(y x f Y X 当 – r < y < r 时,⎪⎩⎪⎨⎧-<<---=其他,0,21222222y r x y r y r 22yr --∙∙22yr -y— 这里 y 是常数,当Y = y 时,()2222,~yr y r U X ---)(),(x f y x f X =)(x y f X Y 当 – r < x < r 时,⎪⎩⎪⎨⎧-<<---=其他,0,21222222x r y x r x r — 这里 x 是常数,当X = x 时,()2222,~xr x r U Y ---22xr -∙ 22xr --∙ x例4 已知 ()ρσμσμ;,;,~),(222211N Y X 求 )(y x fYX 解)(y x f Y X )(),(y f y x f Y =222222222121212122)(2)())((2)()1(2122121121σμσμσσμμρσμρσπρσπσ--⎥⎦⎤⎢⎣⎡-+-------=y y y x x e e⎥⎦⎤⎢⎣⎡------=)()()1(21212211221121μσσρμρσρσπy x e 同理,)(x y f X Y ⎪⎭⎫ ⎝⎛--+)1(),(~2221122ρσμσσρμx N ⎪⎭⎫ ⎝⎛--+)1(),(~2212211ρσμσσρμy N )(y x f Y X例5 设⎩⎨⎧≤≤≤≤=其他,010,0,8),(y y x xy y x f 求 )(y x f Y X )(,x y f X Y 解11⎪⎩⎪⎨⎧≤≤=⎰其他,010,8)(1x xydy x f xX ⎩⎨⎧≤≤-=其他,010),1(42x x x1 1 ⎩⎨⎧≤≤=⎰其他,010,8)(0y xydx y f yY ⎩⎨⎧≤≤=其他,010,43y y 当0 < y < 1 时,)(y x f Y X )(),(y f y x f Y =y⎪⎩⎪⎨⎧≤≤=其他,00,22yx yx 当0 < x < 1 时,11x )(),(x f y x f X =)(x y f X Y ⎪⎩⎪⎨⎧≤≤-=其他,01,122y x x y例6 已知)(x y f X Y ⎪⎩⎪⎨⎧≤≤-=其他,01,122y x x y ⎩⎨⎧≤≤-=其他,010),1(4)(2x x x x f X 求 ⎪⎭⎫ ⎝⎛=<<≥+2132),5.0(),1(X Y P Y P Y X P解 11)()(),(x f x y f y x f X X Y =当f X (x ) > 0 时,即 0 < x < 1 时,⎩⎨⎧≤≤=其他,01,8y x xy 当f X (x ) = 0 时,f (x,y ) = 0 故⎩⎨⎧≤≤≤≤=其他,010,0,8),(y y x xy y x fx + y =1)1(≥+Y X P )5.0(<Y P 1 1 0.5⎰⎰-=yy xydx dy 115.0865=1 10.5⎰⎰=21008yxydx dy 161=⎪⎭⎫ ⎝⎛=<2132X Y P 1 1 0.5 32⎰∞-⎪⎭⎫ ⎝⎛=3221dy y f X Y ()⎰-=322125.012dy y ⎰=322138dy y 277=876.6⨯=脚印长度身高算出罪犯的身高. 这个公式是 公安人员根据收集到的 罪犯脚印,通过公式由脚印估计罪犯身高 如何推导出来的?显然,两者之间是有统计关系的,故X 设一个人身高为 ,脚印长度为 .Y 由于影响人类身高与脚印的随机因素是大量的、相互独立的,且各因素的影响又是微小的,可以叠加的. 故),(Y X 应作为二维随机变量来研究. 由中心极限定理知可以近似看 ),(Y X .);,,,(222211ρσσu u N 成服从二维正态分布ρσσ;,;,222211u u 其中参数因区域、 民族、生活习惯的不同而有所变化 , 但它们都能通过统计方法而获得.密度为现已知罪犯的脚印长度为 , 要 y 估计其身高就需计算条件期望 , 条件 )(),()|(|y f y x f y x f Y Y X =的密度函数, 因此 ))1(),((2212211ρσσσρ--+u y u N 这正是正态分布 )()|(2211u y u y Y X E -+==σσρ}2)(exp{]})())((2)([)1(21exp{.12222222222212122122212σσσσρσρρσπσσπu y u y u y u x u x ---+-------= 如果按中国人的相应参数代入上式,即可得出以脚印长度作自变量的身高近似公式.作业 P.133习题三16 17设随机变量 Z 服从参数为 1 的指数分布,引入随机变量:⎩⎨⎧>≤=⎩⎨⎧>≤=21201110Z Z Y Z Z X 求 ( X , Y ) 的联合分布律和联合 第8周 问 题分布函数.。