数学：7.5三角形的内角和(第1课时)教案(苏科版七年级下)

江苏省灌南县实验中学七年级数学下册《三角形的内角和》教案苏科版一、教学目标：1.通过将多边形分割成三角形，从而探索出多边形内角和的计算公式，并能进行应用.2.经历操作、探索等活动，提高分析问题、解决问题的水平，提升从不同角度思考问题的能力.二、教学重难点：理解多边形的内角和公式的推导过程，体会化归思想.三、教学过程：【预习交流】1.预习课本P27到P28，记下你的疑惑.2.在△ABC中，如果∠A=2∠B=3∠C，则△ABC是（按角分）三角形.3.如图是一个五角星，则∠A+∠B+∠C+∠D+∠E=° 3题图 4题图4. 如图，∠A+∠B+∠C+∠D+∠E=°5.直角三角形的两个锐角平分线所夹的钝角= °6.在△ABC中，∠A－∠B＝36°，∠C＝2∠B，则∠A＝，∠B＝，∠C＝.7.一个零件的形状如图中阴影部分．按规定∠A应等于90º，∠B、∠C应分别是29º和21º，检验人员度量得∠BDC＝141º，就断定这个零件不合格．你能说明理由吗？8.如图，已知△ABC中，已知∠B＝65°，∠C＝45°，AD是B C边上的高，AE是∠BAC 的平分线，求∠DAE的度数.【点评释疑】1. 课本P27议一议.结论：n边形的内角和为（n-2）·180°.2. 课本P28想一想.3.应用探究（1）一个多边形的内角和是2340°，求它的边数.（2）一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？（3）一个五边形截去一个角后，求剩下的多边形的内角和.（4）一个多边形，除去一个内角外，其余各内角的和为2750°，求这个多边形的边数.（5）如图，求∠1＋∠2＋∠3＋∠4的度数．。

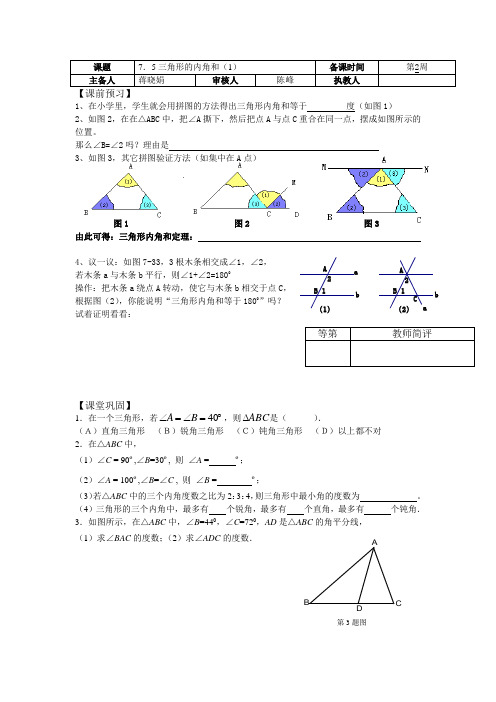
课题 7．5三角形的内角和（1） 备课时间第2周 主备人 蒋晓娟 审核人陈峰执教人1、在小学里，学生就会用拼图的方法得出三角形内角和等于 度（如图1）2、如图2，在在△ABC 中，把∠A 撕下，然后把点A 与点C 重合在同一点，摆成如图所示的位置。

那么∠B=∠2吗？理由是 3、如图3，其它拼图验证方法（如集中在A 点）图1 图2 图3由此可得：三角形内角和定理：4、议一议：如图7-33，3根木条相交成∠1，∠2，若木条a 与木条b 平行，则∠1+∠2=1800 操作：把木条a 绕点A 转动，使它与木条b 相交于点C ， 根据图（2），你能说明“三角形内角和等于1800”吗？试着证明看看：【课堂巩固】1．在一个三角形，若︒=∠=∠40B A ，则ABC ∆是（ ）．（Ａ）直角三角形 （Ｂ）锐角三角形 （Ｃ）钝角三角形 （Ｄ）以上都不对 2．在△ABC 中，（1）∠C = 90º,∠B =30º, 则 ∠A = º； （2）∠A = 100º,∠B =∠C , 则 ∠B = º；（3）若△ABC 中的三个内角度数之比为2：3：4，则三角形中最小角的度数为 。

（4）三角形的三个内角中，最多有 个锐角，最多有 个直角，最多有 个钝角． 3．如图所示，在△ABC 中，∠B =440，∠C =720，AD 是△ABC 的角平分线， （1）求∠BAC 的度数；（2）求∠ADC 的度数．等第 教师简评ABCD第3题图A B a b (2)1221(1)b aC B A【课后巩固】1、（1）三角形的3个内角和等于； （2）直角三角形的两个锐角 ； （3）三角形的一个外角等于 ．2、若△ABC 中的三个内角度数之比为2：3：4，则相应外角之比为 ．3、如图，在△ABC 中，外角∠DBA ＝78º，∠A ＝36º，求∠C 和∠ABC 的大小．4．如图，在△ABC 中，BE 、CD 相交于点E ．（1）∠1是哪一个三角形的外角？ ∠2是哪一个三角形的外角？ （2）如果∠A ＝2∠ACD ＝76º，∠2＝143º．试求∠1和∠DBE 的度数．5． 如图，△ABC 中，∠ABC 和∠ACB 的平分线交于点O ， (1)若∠ABC =60°，∠ACB =80°，求∠BOC 的度数； (2) 若∠A =70°, 求∠BOC 的度数． (3)若∠BOC =120°, 求∠A 的度数．6、(选做题)．已知：如图，△ABC 中，∠B 的平分线和△ABC 的外角平分线交于点D ，∠A =90°．求∠D 的度数．等第 教师简评第3题图21ABD E 第4题图第5题OCBA第6题图DEC BAA BA B1、操作一下：在下图中，连接AC ，把四边形ABCD 分成 个三角形。

图4312DC BA EF 7.5三角形的内角和（1）学习目标：通过操作活动认识“三角形的内角和是180°”，推出“直角三角形的两锐角互余”与“三角形的一个外角等于和它不相邻的两个内角的和”. 并会简单运用. 学习过程：一、三角形的内角和是180°1．如图1，先将三角形纸片一角折向其对边，使顶点落在对边上，折线与对边平行；然后把另外两角相向对折，使其顶点与对折角的顶点相嵌合，可得：三角形3个内角的和等于 .2. 阅读课本第25页“议一议”，改编为：如图2，请说明在△ABC 中，∠BAC +∠B +∠C =180°的理由.过△ABC 的顶点A 画DE ∥BC ，延长BA 到F . ∵DE ∥BC ，∴∠B =∠1(两直线平行，同位角相等)，∠C =∠2(两直线平行，内错角相等).又∵∠BAC +∠2+∠1=180°（平角定义）， ∴∠BAC +∠B +∠C =180°（等量代换） 3. 课本第26页做一做第1题. 做在书上. 4. 阅读课本第25页例题.二、认识“直角三角形的两个锐角互余”1. 课本第26页做一做第2题. 做在书上. 注：直角三角形ABC 可以写成Rt △ABC . 在Rt △ABC 中，如果∠C =90°，那么∠A +∠B = °.2. 如图3，在△ABC 中，已知∠ACB =90°，AD 是AB 边上的高. 那么在Rt △ABC 中，∠B 与∠ 互余； 在Rt △BDC 中，∠B +∠ =90°； 在Rt △ADC 中，∠A +∠ =90°.三、认识“三角形的一个外角等于与它不相邻的两个内角的和” 1. 阅读课本第26页“试一试”. 三角形的一边与另一边的 所组成的角，叫做三角形的外角. 三角形的一个外 角等于 的和.2. 如图4，AF 、BD 、CE 分别是边BA 、CB 、AC 的延长线.∠ABD = ∠ +∠ ；∠BCE = ∠ +∠ ；∠CAF = ∠ +∠ . 3. 如图5，∠ADE 是△ 的外角，∠ADE =∠ +∠ ； ∠3是△ 的外角，∠3 = ∠ +∠ ；∠ADB 可以是△ 的外角，也可以△ 的外角，∠ADB =∠ +∠ ，或∠ADB =∠ +∠ . 四、解决问题A (B) (C)图1F E21ABCD图2DCBA图34EA BCD213图51．课本第27页练一练第1题.解：图① ∵∠BCD =∠A +∠B （三角形的一个外角等于与它不相邻的两个外角的和），∴112= x +65，解得x =57.图②∵ ∠C =90°，∴∠A +∠ABC = 90°（直角三角形的两个锐角互余）， ∴ x +（x 10）= 90，解得x =50.又∵ ∠ABE =∠C +∠A （三角形的一个外角等于与它不相邻的两个外角的和）， ∴ y =x90，即y =50+90=140.课本第27页练一练第2题改编：(1) 三角形的3个内角中，最多有 个直角；最多有 个钝角；至少有 个锐角. (2) 直角三角形的外角中最大的度数是 °.直角三角形的外角可能是锐角吗？ . 为什么？解释一：因为直角三角形的3个内角中有1个直角与2个锐角，那么与直角相邻的外角一定是直角，与锐角相邻的外角一定是钝角，所以直角三角形的外角中不可能有锐角. 解释二：假设直角三角形的外角中有1个锐角，那么与这个锐角相邻的内角一定是钝角，即这个三角形的3个内角中有1个直角及1个钝角，而1个直角与1个钝角的和一定大于180°，与“三角形3个内角和等于180°”相矛盾，所以直角三角形的外角不可能是锐角. 课本第27页练一练第3题. 如图6，AD 是角平分线，∠EAC =∠B ，那么∠ADE 与∠DAE 相等吗？为什么？分析：(1)在图中将相等的角用不同的弧线表明；(2) 条件中∠EAC =∠B ，那么要求的∠ADE 与∠EAC 或∠B 有何关系？那么要求的∠DAE 与∠EAC 或∠B 有何关系？(3) ∠ADE 是哪个三角形的外角？ 解：∠ADE =∠DAE∵AD 是角平分线，∴∠1=∠2（角平分线定义）.又∵∠ADE =∠ +∠ （三角形的一个外角等于与它不相邻的两个外角的和）， ∠DAE =∠ +∠ ， ∴∠ADE =∠DAE （等量代换）.EC213图6。

1
、知道三角形内角之间的关系，直角三角形的两个内角互余 2、知道三角形外角的意义以及外角和内角之间的关系 3、能运用相关结论进行有关的推理和计算；
教学重点：1、探索三角形3个内角之间的关系以及三角形外角的性质 教学难点：灵活使用相关结论，理性思维的培养 教学过程： 【预习导学】
1、在小学里，学生就会用拼图的方法得出三角形内角和等于 度（如图1）
2、如图2，在在△ABC 中，把∠A 撕下，然后把点A 与点C 重合在同一点，摆成如图所示的位置。

那么∠B=∠2吗？理由是
3、如图3，其它拼图验证方法（如集中在A 点）
图1 图2 图3
由此可得：三角形内角和定理：
4、议一议：如图
7-33，3根木条相交成∠1，∠2
，
若木条a 与木条b 平行，则∠1+∠2=1800 操作：把木条a 绕点A 转动，使它与木条b 相交于点C ， 根据图（2），你能说明“三角形内角和等于1800”吗？
试着证明看看：
【合作交流】
例1、 如图，AC 、BD 相交于点O ，∠A 与∠B 的和等于 ∠C 与∠D 的和吗？为什么？
做一做：
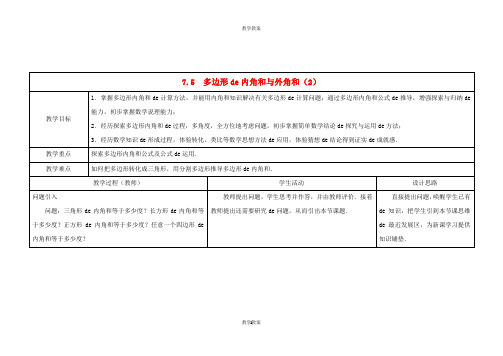
1、根据图填空。

A B a b (2)
1
221(1)b a
C B A
（1）n= ; (2) x= ; (3) y= .
【精讲释疑】
2、在直角三角形ABC中，∠C=90 º，∠A与∠B的和为多少度？
由此得到一个结论：。

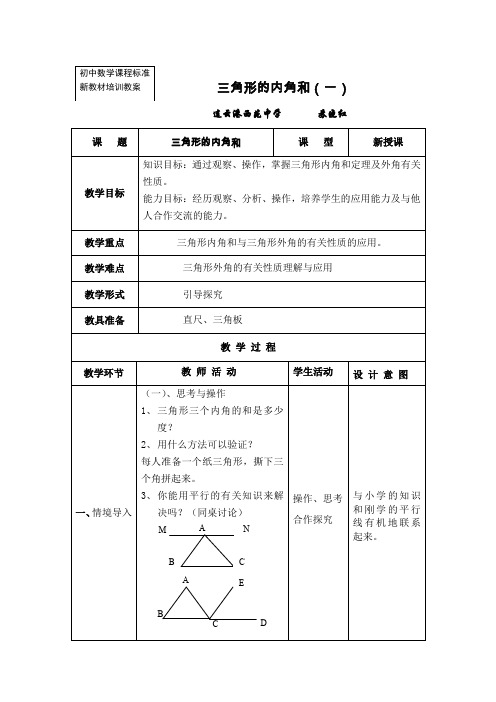
CB A NM 数学初一下苏科版7.5三角形的内角和(第1课时)教案学习目标 知识与技能：1.了解三角形3个内角之间的关系及外角有关性质2.能有条理的进行表达，过程与方法：通过观看、操作，掌握三角形内角和定理情感、态度与价值观：经历观看、分析、操作，培养学生的应用能力及与他人合作交流的能力。

学习重点 三角形内角和与三角形外角的有关性质的应用 学习难点 三角形外角的有关性质理解与应用教学流程预习 导航 1.三角形三个内角的和是多少度？ 三角形三个内角的和是 2.用什么方法能够验证？3.剪出一个纸三角形，撕下三个角拼起来。

合 作 探 究【一】新知探究 〔一〕三角形的内角和用平行的有关知识来说明三角形的内角和是180° 〔1〕如图，过点A 作直线MN ∥BC ， 因为MN ∥BC ，因此∠B ＝，∠C ＝因为∠MAB ＋∠BAC ＋∠NAC ＝180°，因此∠B ＋∠BAC ＋∠C ＝180° 〔2〕书P ２５议一议aba'b a21213(1) (2)CB AB A由图〔1〕a ∥b ，可得∠1＋∠2＝180°，假设将木条a 绕点A 转动，使它与b 相交于点C ，得图〔2〕，因为a ′和b 平行，那么∠1＋〔∠2＋∠3〕＝180°，∠ACB ＝∠3，因此∠1＋〔∠2＋∠ACB 〕＝180°，即△ABC 的内角和为180°。

〔二〕直角三角形锐角的性质 〔1〕、依照图形填空n=x=〔2〕、在直角三角形中ABC 中，∠C=90归纳：直角三角形的两个锐角互余。

〔三〕三角形的外角把⊿ABC 的边AB 延长，得到∠CBD 。

度量∠A 、∠C 和∠CBD 的度数。

∠A+∠C+∠1=∠CBD+∠1=你能发明∠A+∠C 与∠CBD 的大小关系吗？像如此，三角形的一边与另一边的延长线所组成的角，叫做三角形的外角。

结论：三角形的一个外角等于。

教学准备1. 教学目标知识技能①了解三角形内角和定理及证明方法.②运用三角形内角和定理决问题.过程方法①通过动手拼图、观察猜想、推理等数学活动，探索三角形内角和定理的证明，让学生经历从感性认识到理性说明的过程，发展合情推理能力和语言表达能力.②通过三角形内角和定理的证明与应用过程，让学生体会“转化”的思想方法、以及用方程思想解几何问题的方法。

提高应用意识、发展思维的多样性，培养解题能力．情感态度通过小组探讨展示，观察、推理、应用等活动，发展学生的合作互助意识，培养学生学数学的热情，及说理能力.2. 教学重点/难点重点三角形内角和定理的证明及应用.难点添加辅助线证明三角形内角和定理.3. 教学用具4. 标签教学过程活动1：复习引入想一想：(课件)三角形三个内角的和是多少? 用什么方法可以验证？活动2 动手实验拼一拼：（课件）将双层三角形纸片上的一个△ABC的两个内角剪下，拼到第三个角的顶点处，你有几种拼合方法？活动3 探究证法说一说：（课件）(1) 观察，经过拼合你能发现什么？会得出什么结论？（2）你能不能用数学知识从理论上来说明：三角形三个内角的和等于180°？活动4 证明结论证一证谁来说一说证明过程？已知：已知：△A B C.求证：∠A +∠B +∠C =180°定理：三角形三个内角的和等于思路总结（课件）添加辅助线的技巧；平行线转移角的作用，从而内角和转化成平角或两平行线下的同旁内角。

活动5 定理应用A. 比一比，赛一赛 (课件)(1)在△ABC中,∠A=35°,∠B=45°，则∠C= _____(2)在△ABC中,∠A =30°∠B=∠C,则∠B = _____(3)在△ABC中，∠A:∠B:∠C=1:2:3则△ABC是 _______三角形(4)∠A+∠B+∠C+∠D+∠E+∠F =____B.解决问题教材第73页例1如图：C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80°方向，C岛在B 岛的北偏西40°方向．从C岛看A、B两岛的视角∠ACB是多少度？C练一练教材第74页1,2活动6 小结与作业回顾小结（课件）谈一谈:通过本节课的学习，你有哪些收获？作业：教材76页1、3题课后再探索:1、一个三角形最多有几个直角？为什么？2、一个三角形最多有几个钝角？为什么？3、一个三角形最多有几个锐角？最少有几个锐角？板书课题定理三角形三个内角的和等于180°已知:△ABC求证:∠A+∠B+∠C=180°证明:。

多边形的内角和教学目的1、通过“剪一剪”“拼一拼”使学生直观地感受三角形内角和为18002、探索并了解多边形的内角和与外角和公式及其运用。

3、发展学生空间观念，推理能力和有条理地表达能力。

教学重难点：1、探索三角形3个内角之间的关系以及三角形外角的性质。

2、由三角形3个内角之间的关系得到直角三角形的性质：直角三角形的两个内角互余。

教学方法：引导探索法，讲练结合，探索交流。

教学过程：一、探索我们小学的时候曾经说过三角形的内角和是180度，但是你知道为什么吗？如图：三角形ABC ，你能说明∠A+∠B+∠C 为什么等于180度吗二、灵活应用1、 已知，在△ABC 中，∠A ＝40°，∠B ＝∠C ，求∠C 的度数．2、如图5，AD 、BC 相交于点O ，∠A ＝50°，∠B ＝32°，∠C ＝45°，求∠D 的度数．AC B A CBBAOC D（图5）3、在△ABC中，若∠A＋∠B＝90°，则△ABC一定是__________三角形．4、在△ABC中，若∠A∶∠B∶∠C＝2∶3∶4，求∠A、∠B、∠C的度数．5、直角三角形的两个锐角____________________三、探索二能否通过此方法计算五边形、六边形、七边形、…、n边形的内角和呢？（大胆尝试！再填写下表）结论：n边形的内角和等于.四、灵活应用1. 四边形的内角和是________，五边形的内角和是________，六边形的内角和是__________，2.多边形的内角和可能是（）A．810°B．540°C．180°D．605°3. 下列各角不是多边形的内角的是（）A．1800 B．5400 C．19000 D．108004.一个十边形所有内角都相等，它的每一个内角等于.5.一个多边形的边数每增加1，它的内角和就增加________。

6．如果四边形有一个角是直角，另外三个角的度数比是2：3：4，那么这三个内角的度数分别是多少？7、一个多边形，除去一个内角外，其余各内角的和为2750°，求这个多边形的边数。