下载文档原格式
编译原理-第5章-习题与答案2第五章习题5-1 设有文法G[S]：S→A/ A→aA∣AS∣/(1) 找出部分符号序偶间的简单优先关系。
(2) 验证G[S]不是简单优先文法。
5-2 对于算符文法G[S]：S→E E→E-T∣T T→T*F∣F F→-P∣P P→(E)∣i(1) 找出部分终结符号序偶间的算符优先关系。
(2) 验证G[S]不是算符优先文法。
5-3 设有文法G′[E]：E→E1 E1→E1+T1|T1 T1→T T→T*F|F F→(E)|i其相应的简单优先矩阵如题图5-3所示，试给出对符号串（i+i）进行简单优先分析的过程。
题图5-3 文法G′[E]的简单优先矩阵5-4 设有文法G[E]：E→E+T|TT→T*F|FF→(E)|i其相应的算符优先矩阵如题图5-4所示。
试给出对符号串（i+i）进行算符优先分析的过程。
题图5-4 文法G[E]的算符优先矩阵5-5 对于下列的文法，试分别构造识别其全部可归前缀的DFA和LR(0)分析表，并判断哪些是LR(0)文法。
(1) S→aSb∣aSc∣ab(2) S→aSSb∣aSSS∣c(3) S→A A→Ab∣a5-6 下列文法是否是SLR(1)文法？若是，构造相应的SLR(1)分析表，若不是，则阐明其理由。
(1) S→Sab∣bR R→S∣a(2) S→aSAB∣BA A→aA∣B B→b(3) S→aA∣bB A→cAd∣ε B→cBdd∣ε5-7 对如下的文法分别构造LR(0)及SLR(1)分析表，并比较两者的异同。
S→cAd∣b A→ASc∣a5-8 对于文法G[S]:S→A A→BA∣ε B→aB∣b(1) 构造LR(1)分析表；(2) 给出用LR(1)分析表对输入符号串abab的分析过程。
5-9 对于如下的文法，构造LR(1)项目集族，并判断它们是否为LR(1)文法。
(1) S→A A→AB∣ε B→aB∣b(2) S→aSa∣a第5章习题答案25-1 解：(1) 由文法的产生式和如答案图5-1(a)所示的句型A／／a／的语法树，可得G中的部分优先关系如答案图5-1(b)所示。
第7 题证明下述文法G[〈表达式〉]是二义的。
〈表达式〉∷=a|(〈表达式〉)|〈表达式〉〈运算符〉〈表达式〉〈运算符〉∷=+|-|*|/答案：可为句子a+a*a 构造两个不同的最右推导:最右推导1 〈表达式〉=>〈表达式〉〈运算符〉〈表达式〉=>〈表达式〉〈运算符〉a=>〈表达式〉* a=>〈表达式〉〈运算符〉〈表达式〉* a=>〈表达式〉〈运算符〉a * a=>〈表达式〉+ a * a=>a + a * a最右推导2 〈表达式〉=>〈表达式〉〈运算符〉〈表达式〉=>〈表达式〉〈运算符〉〈表达式〉〈运算符〉〈表达式〉=>〈表达式〉〈运算符〉〈表达式〉〈运算符〉a=>〈表达式〉〈运算符〉〈表达式〉* a=>〈表达式〉〈运算符〉a * a=>〈表达式〉+ a * a=>a + a * a第8 题文法G[S]为：S→Ac|aB A→ab B→bc该文法是否为二义的？为什么？答案：对于串abc(1)S=>Ac=>abc (2)S=>aB=>abc即存在两不同的最右推导。
所以，该文法是二义的。
或者：对输入字符串abc，能构造两棵不同的语法树，所以它是二义的。
第9 题考虑下面上下文无关文法：S→SS*|SS+|a(1)表明通过此文法如何生成串aa+a*，并为该串构造语法树。
(2)G[S]的语言是什么？答案：(1)此文法生成串aa+a*的最右推导如下S=>SS*=>SS*=>Sa*=>SS+a*=>Sa+a*=>aa+a*(2)该文法生成的语言是：*和+的后缀表达式，即逆波兰式。
第10 题文法S→S(S)S|ε(1) 生成的语言是什么？(2) 该文法是二义的吗？说明理由。
答案：（１）嵌套的括号（２）是二义的，因为对于（）（）可以构造两棵不同的语法树。
第11 题令文法G[E]为：E→T|E+T|E-T T→F|T*F|T/F F→(E)|i证明E+T*F 是它的一个句型，指出这个句型的所有短语、直接短语和句柄。
编译原理第三版课后习题答案编译原理是计算机科学中的一门重要课程，它研究的是如何将高级程序语言转换为机器语言的过程。
而《编译原理》第三版是目前被广泛采用的教材之一。
在学习过程中，课后习题是巩固知识、提高能力的重要环节。
本文将为读者提供《编译原理》第三版课后习题的答案，希望能够帮助读者更好地理解和掌握这门课程。
第一章：引论习题1.1：编译器和解释器有什么区别？答案：编译器将整个源程序转换为目标代码，然后一次性执行目标代码；而解释器则逐行解释源程序，并即时执行。
习题1.2：编译器的主要任务是什么？答案：编译器的主要任务是将高级程序语言转换为目标代码，包括词法分析、语法分析、语义分析、中间代码生成、代码优化和目标代码生成等过程。
第二章：词法分析习题2.1：什么是词法分析？答案：词法分析是将源程序中的字符序列划分为有意义的词素（token）序列的过程。
习题2.2：请给出识别下列词素的正则表达式：（1）整数：[0-9]+（2）浮点数：[0-9]+\.[0-9]+（3）标识符：[a-zA-Z_][a-zA-Z_0-9]*第三章：语法分析习题3.1：什么是语法分析？答案：语法分析是将词法分析得到的词素序列转换为语法树的过程。
习题3.2：请给出下列文法的FIRST集和FOLLOW集：S -> aAbA -> cA | ε答案：FIRST(S) = {a}FIRST(A) = {c, ε}FOLLOW(S) = {$}FOLLOW(A) = {b}第四章：语义分析习题4.1：什么是语义分析？答案：语义分析是对源程序进行静态和动态语义检查的过程。
习题4.2：请给出下列文法的语义动作：S -> if E then S1 else S2答案：1. 计算E的值2. 如果E的值为真，则执行S1；否则执行S2。
第五章：中间代码生成习题5.1：什么是中间代码？答案：中间代码是一种介于源代码和目标代码之间的表示形式，它将源代码转换为一种更容易进行优化和转换的形式。
第五章习题解答5.1 设一NDPDA识别由下述CFG定义的语言，试给出这个NDPDA的完整形式描述。
S→SASCS→εA→AaA→bC→DcDD→d5.2 消除下列文法的左递归：① G[A]:A→BX∣CZ∣WB→Ab∣BcC→Ax∣By∣Cp② G[E]:E→ET+∣ET–∣TT→TF*∣TF/FF→(E)∣i③ G[X]:X→Ya∣Zb∣cY→ Zd∣Xe∣fZ→X e∣Yf∣a④ G[A]:A→Ba|Aa|cB→Bb|Ab|d5.3 设文法G[<语句>]：<语句>→<变量>: = <表达式>|if<表达式>then<语句>|if<表达式>then<语句>else<语句> <变量>→i<表达式>→<项>|<表达式>+<项><项>→<因子>|<项>*<因子><因子>→<变量>|′(′<表达式>′)′试构造该文法的递归下降子程序。
5.4 设文法G[E]：E→ TE'E'→ + E∣εT→ FT'T'→ T∣εF→ PF'F'→ *F∣εP→ (E)∣ a∣^①构造该文法的递归下降分析程序；②求该文法的每一个非终结符的FIRST集合和FOLLOW集合；③构造该文法的LL（1）分析表，并判断此文法是否为LL（1）文法。
5.5 设文法G[S]：S→ SbA∣aAB→ SbA→ Bc①将此文法改写为LL（1）文法；②求文法的每一个非终结符的FIRST集合和FOLLOW集合；③构造相应的LL（1）分析表。
5.6 设文法G[S]：S→ aABbcd∣εA→ ASd∣εB→ SAh∣eC∣εC→ Sf∣Cg∣εD→ aBD∣ε①求每一个非终结符的FOLLOW集合；②对每一个非终结符的产生式选择，构造FIRST集合；③该文法是LL（1）文法。
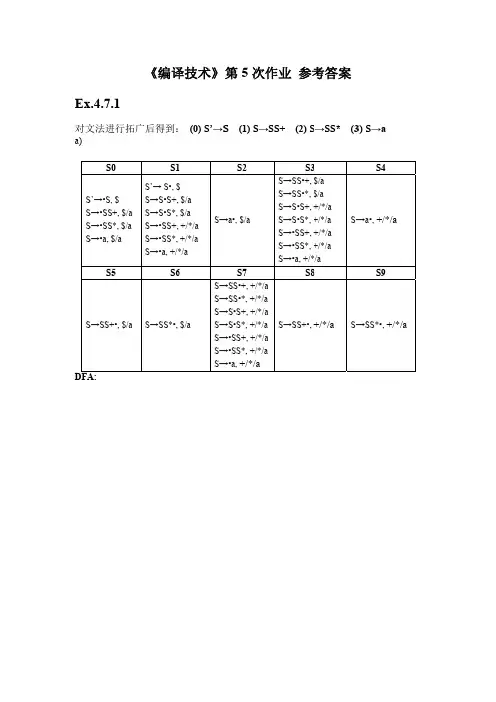
第五章语法制导翻译及中间代码生成5.1说明属性文法与属性翻译文法有何异同?5.2考虑下面的属性文法：Z →sXattribution:Z.a=X.c;X.b=X.a；Z.p=X.b；Z →t Xattribution：X.b=X.d;Z.a=X.b;X →uattribution:X.d=1;X.c=X.d;X →Vattribuion:X.c=2;X.d=X.c;(1) 上述文法中的属性哪些是继承的?哪些是综合的?(2) 上述文法中的属性依赖是否出现了循环?5.3为什么说S属性文法一定是L属性文法?反之结论亦正确吗?5.4将下列中缀式改写为逆波兰式。
(1) -A*(B+C)↑(D-E)(2) ((a*d+c)/d+e)*f+g(3) a+x≤4∨(C∧d*3)(4) a∨b∧c+d*e↑f(5) s=0; i=1;while (i＜=100) {s+=i*i; i++;}5.5将下列后缀式改写为中缀式。
(1) abc*+(2) abc-*cd+e/-(3) abc+≤a0＞∧ab+0≠a0∧∨(4) ab＜p1 BZ xab-c↑= p2 BR gh=↑↑p1p25.6设已给文法G［E］：E →E+T | -T | TT →T*F | FF →P ↑F | PP →(E) | i试设计一个递归下降分析器，要求此分析器在语法分析过程中，将所分析的符号串翻译成后缀式。
5.7设已给布尔表达式文法G［Z］：Z →EE →T{∨T}T →F{∧F}F → F | (E) | b试设计一个递归下降分析器，它把由G［Z］所描述的布尔表达式翻译为四元式序列。
5.8(1) 利用54节所给的属性翻译文法将赋值语句：X=A*(B+C)+D翻译成四元式序列，给出语法制导的翻译过程。
(2) 利用55节所给的属性翻译文法将布尔表达式：A∧(B∨(C∨D F))翻译成四元式序列，给出语法制导的翻译过程。
(3) 利用56节所给的属性翻译文法将语句：while A＜C∧B＞0 doif A=1 then C∶=C+1else while A＜=D do A∶=A+2翻译成四元式序列，给出语法制导的翻译过程。
《编译原理》习题参考答案（六）第五章5.4 为下列类型写类型表达式：(a) 指向实数的指针数组，数组的下标从1到100。
(b) 两位数组（即数组的数组），他的行下标从1到10，列下标从1到20。
(c) 函数，他的定义域是从整数到整数的指针的函数，它的值域是从一个整数和一个字符组成的纪录。
Solution:(a) array ( 1 . . 100 , pointer ( real ) )(b) array ( 1 . . 10 , array ( 1 . . 20 , type ) )(c) ( integer →pointer(integer) )→record((i : integer) * ( c : char )) 假定作为值域的记录类型的两个域分别叫i和c。
5.6 下列文法定以字面常量表的表。
符号的解释和图5.2文法的那些相同，增加了类型list，它表示类型T的元素表。
→ D ; EP→ D ; D | id : TD→ list of T | char | integerTE→ ( L ) | literal | num | id→ E , L | EL写一个类似5.3节中的翻译方案，以确定表达式( E )和表( L )的类型。
P→ D ; ED→ D ; DD→ id : T { addtype ( id.entry , T.type ) }T→ char { T.type := char }T→ integer { T.type := integer }T→ list of T1 { T.type := list ( T1.type ) }E→ literal { E.type := char }E→ num { E.type := integer }E→ id { E.type := lookup ( id.entry ) }E→ ( L ) { E.type := list ( L.type ) }L→E{L.type:=E.type}L→ E , L1 { L.type := if L1.type = E.type then E.typeelse type_error }5.16 对下面的每对表达式，找出最一般的合一代换：(a) α1 → ( α2 →α1 )(b) array ( β1 ) → ( pointer( β1 ) →β2 )(c) γ1 →γ2(d) δ1 →(δ1 →δ2 )Solution:S(α1) = array ( β1 ) S(α2) = pointer ( β1 ) S(β2) = array ( β1 ) (a)(c):S(γ1) = α1 S(γ2) = α2 → α1 (a)(d):S(α1) = S(α2) = S(δ1) = S(δ2) = α (b)(c):S(γ1) = array ( β1 ) S(γ2) = pointer ( β1 ) → β2 (b)(d): 无 (c)(d):S(γ1) = δ1 S(γ2) = δ1 → δ25.17 仿效例5.5，推到下面map 的多态类型: map: ∀ α . ∀ β . ( ( α → β ) * list ( α ) ) → list ( β ) map 的ML 定义是 fun map ( f , l ) = if null ( l ) then nilelse cons ( f ( hd ( l ) ) , map ( f , tl ( l ) ) );在这个函数体中，内部定义的标识符的类型是： null : ∀α . list (α ) → boolean ; nil : ∀α . list (α ) ;cons : ∀α . ( α * list (α ) ) → list (α ) ;hd:∀α . list (α ) →α;∀α . list (α ) → list (α ) ;tl:Solution:行定型断言代换规则(1) f : α( Exp Id )(2) l : β( Exp Id )(3) map : γ( Exp Id )(4) map ( f , l ) : δγ = ( α * β ) →δ(Exp Funcall)(5) null : list (α0) → boolean ( Exp Id ) 和( Type Fresh )(6) null ( l ) : boolean β = list (α0) (Exp Funcall)(7) nil : list (α1) ( Exp Id ) 和( Type Fresh )(8) l : list (α0) 由（2）可得(9) hd : list (α2) →α2( Exp Id ) 和( Type Fresh )(10) hd ( l ) : α0α2 = α0(Exp Funcall)(11) f ( hd ( l ) ) : α3α = α0→α3( Exp Id )(12) f : α0→α3由（1）可得(13) tl : list (α4)→ list (α4) ( Exp Id ) 和( Type Fresh )(14) tl ( l ) : list (α0) α4 = α0(Exp Funcall)(15) map : ((α0→α3)*list(α0))→δ由（3）可得(16) map ( f , tl ( l ) ) : δ(Exp Funcall)(17) cons : α5 * list(α5) → list(α5) ( Exp Id ) 和( Type Fresh ) (18) cons (…) : list (α3) α5 = α3 , δ=list(α3) (Exp Funcall)(19) if : boolean *α6 * α6→α6( Exp Id ) 和( Type Fresh )(20) if (…) : list (α1) α6 = α1 , α3 = α1(Exp Funcall)(21) match : α7 *α7 →α7( Exp Id ) 和( Type Fresh ) (22) match (…) : list (α1) α7 = list (α1) (Exp Funcall)至此有map : ( (α0→α1)*list(α0) )→list(α1)所以map : ∀α . ∀β . ( ( α→β ) * list ( α ) ) → list ( β )5.18 假定类型名link和cell如5.5节那样定义，下面的表达式中，那些结构等价？那些名字等价？(a) link(b) pointer ( cell )(c) pointer ( link )(d) pointer ( record ( ( info : integer ) * ( next : pointer ( cell ) ) ) ) Solution:(a)、(b)、(d)结构等价，无名字等价。
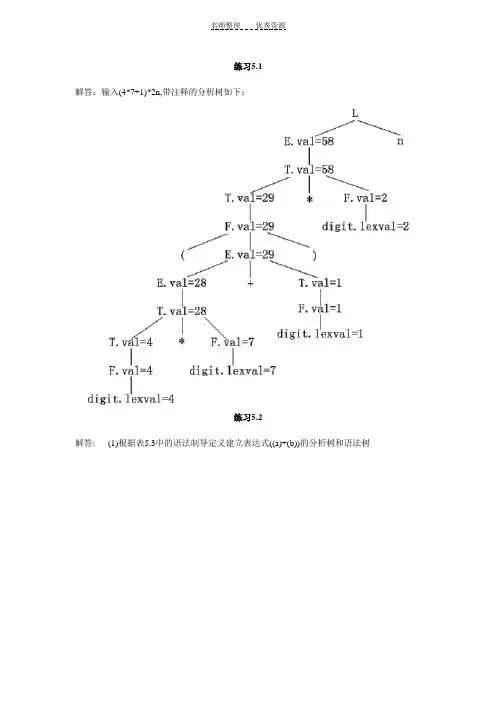
练习5.1解答：输入(4*7+1)*2n,带注释的分析树如下：练习5.2解答: (1)根据表5.3中的语法制导定义建立表达式((a)+(b))的分析树和语法树(2)根据图5.17的翻译模式构造((a)+(b))的分析树和语法树练习5.3解答:设置下面的函数和属性：expr1||expr2:把表达式expr2拼写在表达式expr1后面。
deletep(expr):去掉表达式expr左端的‘（’和右端的‘)’。
E.expr,T.expr,F.expr:属性变量，分别表示E，T，F的表达式。
E.add,T.add,F.add,属性变量，若为true，则表示其表达式中外层有‘＋’号，否则无‘＋’号。
E.pmark,T.pmark,F.pmark,属性变量，若为true，表示E,T,F的表达式中左端为‘（’，右端是‘）’。
语法制导定义如下：产生式语义规则E -> E1 +T if(T.pmark==true)THEN E.expr=E1.expr||'+'||deletep(T.expr) ELSE E.expr:=E1.expr||'+'||T.expr;E.add:=true;E.pmark:=false;E -> T if(T.pmark==true)THEN E.expr:=deletep(T.expr)ELSE E.expr:=T.expr;E.add:=T.add;E.pmark:=false;T -> T1*F T.expr:=T1.expr||'*'||F.expr; T.add:=false;T.pmark:=false;T -> F T.expr:=F.expr; T.add:=F.add;T.pmark:=F.pmark;F -> (E) if(E.add==false)THEN BEGINF.expr:=E.expr;F.add:=false;F.pmark:=false;ENDELSE BEGINF.expr:='('||E.expr||')';F.add:=true;F.pmark:=true;END;F -> id F.expr:=id.lexval;F.add:=false;F.pmark:=false;练习5.4解答: (1)语法制导定义如下：产生式语义规则E -> E1+T if(E1.type==int) AND (T.type==int) THEN E.type:=intELSE E.type:=real;E -> T E.type:=T.type;T -> num T.type:=int;T -> num.num T.type:=real;(2)设E.pf和T.pf分别是E和T的前缀形式，||是两个字符串的连接，语法制导定义如下：产生式语义规则E -> E1+T if(E1.type==int) AND (T.type==int)THEN E.type:=intELSE BEGINE.type:=real;if(E1.type==int) AND (T.type==real)THEN E1.pf:='inttoreal'||E1.pfELSE if(E1.type==real)AND(T.type==int)THEN T.pf:='inttoreal'||T.pfEND;E.pf:='+'||E1.pf||T.pf;E -> T E.type:=T.type; E.pf:=T.pf;T -> num T.type:=int; T.pf:=int.lexval;T ->num.numT.type:=real; T.pf:=real.lexval;练习5.5解答: (1)用综合属性决定s.val的语法制导定义：产生式语义规则S -> L S.val:=L.val;S ->L1.L2S.val:=L1.val+L2.val*L2.p;L -> B L.val:=B.val; L.p:=2-1;L -> L1B L.val:=L1.val*2+B.val; L.p:=L.p*2-1;B -> 0 B.val:=0;B -> 1 B.val:=1;注：L.p表示恢复L.val的因子。
第五章自顶向下语法分析方法1．对文法G[S]S→a|∧|(T)T→T,S|S(1)给出(a,(a,a))和(((a,a),∧,(a)),a)的最左推导。
(2)对文法G，进行改写，然后对每个非终结符写出不带回溯的递归子程序。
(3)经改写后的文法是否是LL(1)的？给出它的预测分析表。
(4)给出输入串(a,a)#的分析过程，并说明该串是否为G的句子。
解：(1) (a,(a,a))的最左推导为S→(T)→(T,S)→(S,S)→(a,(T))→(a,(T,S))→(a,(S,a))→(a,(a,a))(((a,a),∧,(a)),a)的最左推导为S→(T)→(T,S)→(S,a)→((T),a)→((T,S),a)→((T,S,S),a)→((S,∧,(T)),a)→(((T),∧,(S)),a) →(((T,S),∧,(a)),a)→(((S,a),∧,(a)),a)→(((a,a),∧,(a)),a)(2)由于有T→T,S的产生式，所以消除该产生式的左递归，增中一个非终结符U有新的文法G/[S]:S→a|∧|(T)T→SUU→，SU|ε分析子程序的构造方法对满足条件的文法按如下方法构造相应的语法分析子程序。
(1) 对于每个非终结号U，编写一个相应的子程序P(U)；(2) 对于规则U::=x1|x2|..|xn,有一个关于U的子程序P(U),P(U)按如下方法构造：IF CH IN FIRST(x1) THEN P(x1)ELSE IF CH IN FIRST(x2) THEN P(x2)ELSE ......IF CH IN FIRST(xn) THEN P(xn)ELSE ERROR其中，CH存放当前的输入符号，是一个全程变量；ERROR是一段处理出错信息的程序；P(xj)为相应的子程序。
(3) 对于符号串x=y1y2...yn;p(x)的含义为：BEGINP(y1);P(y2);...P(yn);END如果yi是非终结符，则P(yi)代表调用处理yi的子程序；如果yi是终结符，则P(yi)为形如下述语句的一段子程序IF CH=yi THEN READ(CH) ELSE ERROR即如果当前文法中的符号与输入符号匹配，则继续读入下一个待输入符号到CH中，否则表明出错。
(4) 如果文法中有空规则U::=EPSILON,则算法中的语句IF CH IN FIRST(xn) THEN P(xn)ELSE ERROR改写为：IF CH IN FIRST(xn) THEN P(xn)ELSE IF CH IN FOLLOW(U) THEN RETURNERROR(5) 要分析一个OrgStr,应在该串的后面加上一个串括号'#',并从子程序P(S)(S为文法的开始符号)开始，如果中途没有产生错误，并且最后CH='#',则说明OrgStr串合法，否则该串不合法。
对每个非终结符写出不带回溯的递归子程序如下：char CH;//存放当前的输入符号void P_S()//非终结符S的子程序{if(CH==’a’) READ(CH);//产生式S→aelse if(CH==’^’) READ(CH);//产生式S→^else if(CH==’(’)//产生式S→(T){READ(CH);P_T();IF (CH==’)’) THEN READ(CH) else ERROR}else ERR;}void P_T()//非终结符S的子程序{if(IsIn(CH,FIRST_SU)) //FIRST_SU为T→SU的右部的FIRST集合{P_S();P_U();}}void P_U()//非终结符U的子程序{if(CH==’,’)//产生式U→，SU{READ(CH);P_S();P_U();}else//产生式U→ε{if(IsIn(CH,FOLLOW_U)) //FOLLOW_U为U的FOLLOW集合return ;else ERR;}}(3)判断文法G/[S]是否为LL(1)文法。
各非终结符的FIRST集合如下：FIRST(S)={a,∧,（}FIRST(T)=FIRST(S)={a,∧,（}FIRST(U)={，,ε}各非终结符的FOLLOW集合如下：FOLLOW(S)={#} ∪ FIRST(U) ∪ FOLLOW(T) ∪ FOLLOW(U)={#,，,)}FOLLOW(T)={)}FOLLOW(U)=FOLLOW(T)={)}每个产生式的SELECT集合如下：SELECT(S→a)={a}SELECT(S→∧)={∧}SELECT(S→(T))={(}SELECT(T→SU)=FIRST(S)={a,∧,（}SELECT(U→，SU)={，}SELECT(U→ε)=FOLLOW(U)={)}可见，相同左部产生式的SELECT集的交集均为空，所以文法G/[S]是LL(1)文法。
文法G/[S]的预测分析表如下：(5)给出输入串(a,a)#的分析过程2．对下面的文法G：E→TE/E/→+E|εT→FT/T/→T|εF→PF/F/→*F/|εP→(E)|a|b|^(1)计算这个文法的每个非终结符的FIRST集和FOLLOW集。
(2)证明这个方法是LL(1)的。
(3)构造它的预测分析表。
(4)构造它的递归下降分析程序。
解：（1）计算这个文法的每个非终结符的FIRST集和FOLLOW集。
FIRST集合有：FIRST(E)=FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^};FIRST(E/)={+,ε}FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^};FIRST(T/)=FIRST(T)∪{ε}={(,a,b,^,ε};FIRST(F)=FIRST(P)={(,a,b,^};FIRST(F/)=FIRST(P)={*,ε};FIRST(P)={(,a,b,^};FOLLOW集合有：FOLLOW(E)={),#};FOLLOW(E/)=FOLLOW(E)={),#};FOLLOW(T)=FIRST(E/)∪FOLLOW(E)={+,),#};//不包含εFOLLOW(T/)=FOLLOW(T)=FIRST(E/)∪FOLLOW(E)={+,),#};FOLLOW(F)=FIRST(T/)∪FOLLOW(T)={(,a,b,^,+,),#};//不包含εFOLLOW(F/)=FOLLOW(F)=FIRST(T/)∪FOLLOW(T)={(,a,b,^,+,),#};FOLLOW(P)=FIRST(F/)∪FOLLOW(F)={*,(,a,b,^,+,),#};//不包含ε(2)证明这个方法是LL(1)的。
各产生式的SELECT集合有：SELECT(E→TE/)=FIRST(T)={(,a,b,^};SELECT(E/→+E)={+};SELECT(E/→ε)=FOLLOW(E/)={),#}SELECT(T→FT/)=FIRST(F)={(,a,b,^};SELECT(T/→T)=FIRST(T)={(,a,b,^};SELECT(T/→ε)=FOLLOW(T/)={+,),#};SELECT(F→PF/)=FIRST(P)={(,a,b,^};SELECT(F/→*F/)={*};SELECT(F/→ε)=FOLLOW(F/)={(,a,b,^,+,),#};SELECT(P→(E))={(}SELECT(P→a)={a}SELECT(P→b)={b}SELECT(P→^)={^}可见，相同左部产生式的SELECT集的交集均为空，所以文法G[E]是LL(1)文法。
(3)构造它的预测分析表。
文法G[E]的预测分析表如下：(4)构造它的递归下降分析程序。
对每个非终结符写出不带回溯的递归子程序如下：char CH;//存放当前的输入符号void P_E()//非终结符E的子程序{if(IsIn(CH,FIRST_TEP)) //FIRST_TEP为E→TE/ 的右部的FIRST集合，产生式E→TE/{P_T();P_EP();}else ERR;}void P_EP()//非终结符E/的子程序{if(CH==’+’) //产生式E/→+E{READ(CH);P_E();}else//产生式E/→ε{if(IsIn(CH,FOLLOW_EP)) //FOLLOW_EP为E/的FOLLOW集合return ;else ERR;}}void P_T()//非终结符T的子程序{if(IsIn(CH,FIRST_FTP)) //FIRST_ FTP为T→FT/ 的右部的FIRST集合，产生式T→FT/ {P_F();P_TP();}else ERR;}void P_TP()//非终结符T/的子程序{if(IsIn(CH,FIRST_T)) //FIRST_T为产生式T/→T的右部的FIRST集合，产生式T/→T {P_T();}else//产生式T/→ε{if(IsIn(CH,FOLLOW_TP)) //FOLLOW_TP为T/的FOLLOW集合return ;else ERR;}}void P_F()//非终结符F的子程序{if(IsIn(CH,FIRST_PFP)) //FIRST_PFP为F→PF/ 的右部的FIRST集合，产生式F→PF/ {P_P();P_FP();}else ERR;}void P_FP()//非终结符F/的子程序{if(CH==’*’) //产生式F/→*F/{READ(CH);P_FP();}else//产生式F/→ε{if(IsIn(CH,FOLLOW_FP)) //FOLLOW_FP为F/的FOLLOW集合return ;else ERR;}}void P_P()//非终结符P的子程序{if(CH==’(‘){READ(CH);P_E();if(CH==’)’) READCH(C H);elseERR;}else if(CH==’a’) READ(CH);else if(CH==’b’) READ(CH);else if(CH==’^’) READ(CH);else ERR;}3．已知文法G[S]：S→MH|aH→LSo|εK→dML|εL→eHfM→K|bLM判断G是否是LL（1）文法，如果是，构造LL（1）分析表。
解：首先求各非终结符的FIRST集合：FIRST(S)={a}∪FIRST(M)∪FIRST(H)={a}∪{b,d,ε}∪{e,ε}={a,b,d,e,ε};FIRST(H)=FIRST(L)∪{ε}={e,ε};FIRST(K)={d,ε};FIRST(L)={e};FIRST(M)=FIRST(K)∪{b}={b,d,ε};然后求非终结符的FOLLOW集合：FOLLOW(S)={o,#}FOLLOW(H)=FOLLOW(S)∪{f}={f,o,#}FOLLOW(K)=FOLLOW(M)=FIRST(H)∪FOLLOW(S)={e,o,#};//不包含εFOLLOW(L)=FIRST(S)∪{o}∪FOLLOW(K)∪FIRST(M)∪FOLLOW(M)={a,b,d,e,o,#}∪FOLLOW(M)={a,b,d,e,o,#};//不包含εFOLLOW(M)=FIRST(L)∪FIRST(H)∪FOLLOW(S)={e,o,#}//不包含ε最后求各产生式的SELECT集合：SELECT(S→MH)=(FIRST(MH)-{ε})∪FOLLOW(S)={b,d,e}∪{o,#}={b,d,e,o,#};SELECT(S→a)={a}SELECT(H→LSo)={e}SELECT(H→ε)=FOLLOW(H)={f,o,#}SELECT(K→dML)={d}SELECT(K→ε)=FOLLOW(K)={e,o,#}SELECT(L→eHf)={e}SELECT(M→K)=(FIRST(K)-{ε})∪FOLLOW(M)={d,e,o,#}SELECT(M→bLM)={b}可见，相同左部产生式的SELECT集的交集均为空，所以文法G[S]是LL(1)文法。
