第八章自动控制原理第二版

自动控制原理第二版课后答案(孟庆明)目录第一章 (1)第二章 (2)第三章 (5)第四章 (15)第五章 (18)第六章 (27)1-1（略） 1-2（略） 1-3 解：受控对象：水箱液面。

被控量：水箱的实际水位 h c 执行元件：通过电机控制进水阀门开度，控制进水流量。

比较计算元件：电位器。

测量元件：浮子，杠杆。

放大元件：放大器。

工作原理：系统的被控对象为水箱。

被控量为水箱的实际水位 h 。

给定值为希望水位 h （与电位器设定 c r 电压 u r 相对应，此时电位器电刷位于中点位置）。

当 h c = h r 时，电位器电刷位于中点位置，电动机不工作。

一但 h c ⎺ h r 时，浮子位置相应升高（或降低），通过杠杆作用使电位器电刷从中点位置下移（或上移），从而给电动机提供一定的工作电压，驱动 电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值 h r 。

水位自动控制系统的职能方框图1-4 解：受控对象：门。

执行元件：电动机，绞盘。

放大元件：放大器。

受控量：门的位置 测量比较元件：电位计工作原理：系统的被控对象为大门。

被控量为大门的实际位置。

输入量为希望的大门位置。

当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动， 使大门向上提起。

同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开 门开关自动断开。

反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。

开(闭)门门实际 仓库大门自动控制开（闭）的职能方框图1-5 解：系统的输出量：电炉炉温 给定输入量：加热器电压 被控对象：电炉第一章放大元件：电压放大器，功率放大器，减速器比较元件：电位计 测量元件：热电偶 职能方框图： 2-1 解：对微分方程做拉氏变换：♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s ) X 5 (s ) ♦♠TsX 4 (s ) = X 3 (s )♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s ) ♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥3 5 绘制上式各子方程的方块图如下图所示：(s)3(s)5(s)K 1K 3C (s ) / R (s ) = ， Ts 3 + (T + 1)s 2+ s + K K 1 3第二章C (s ) / N 1 (s ) = C (s ) / R (s ) ，K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解：对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )]♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s ) ♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图：⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s )N (s ) =0 2-3 解：（过程略） C (s ) 1 C (s ) =G 1 + G 2 (a)=R (s ) ms 2 + fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) = G 2 + G 1G 2 C (s ) = G 1 G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 ：（1）求 C/R ，令 N=0G (s ) =K 1K 2 K 3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3 求 C/N ，令 R=0，向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3 s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n1 K K Ts2 + s + K K K s 1 +3 2 K 1 2 31Ts + 1 s（2）要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n= 0Ts 2 + s + K K K 1 2 3K n sG (s ) = nK 1K 22-5 解：（a ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触，可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（2）有两条前向通道，且与两条回路均有接触，所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1（3）闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5（b ）（1）系统的反馈回路有三个，所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触，可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1（2）有四条前向通道，且与三条回路均有接触，所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1（3）闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解：用梅逊公式求，有两个回路，且接触，可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ，可得C (s ) = G 1G 2G 3 + G 2G 3C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s ) (1 + G 2 )G 3C(s ) = 1⋅ (1 + G 1G 2G 3 + G 2 )= 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s ) =1 + G2 G 2G3 E (s ) = C (s ) =G 2G 3 G 1G 2G 3 R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2E(s ) = C (s )(1 + G 2 )G 3 E (s )= C (s )= = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )103-1 解：（原书改为 G (s ) =）0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) =C (s ) = K G (s )1 + 10K H = R (s ) 0 1 + G (s )K 0.2s + 1H1 + 10K H要使过渡时间减小到原来的 0.1 倍，要保证总的放大系数不变，则：（原放大系数为 10，时 间常数为 0.2）10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9 ♠ H 1 + 10K = 10 ♥ H3-2 解：系统为欠阻尼二阶系统（书上改为“单位负反馈……”，“已知系统开环传递函数”）⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1第三章解得：⎤n = 33.71 ⎩ = 0.358所以，开环传递函数为：1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解：（1） K = 10s 1时：100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得：⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 （2） K = 20s 1 时：200 G (s ) = s 2+ 10s⎤ 2 = 200 n2⎩⎤n = 10解得：⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论，K 增大，超调增加，峰值时间减小。

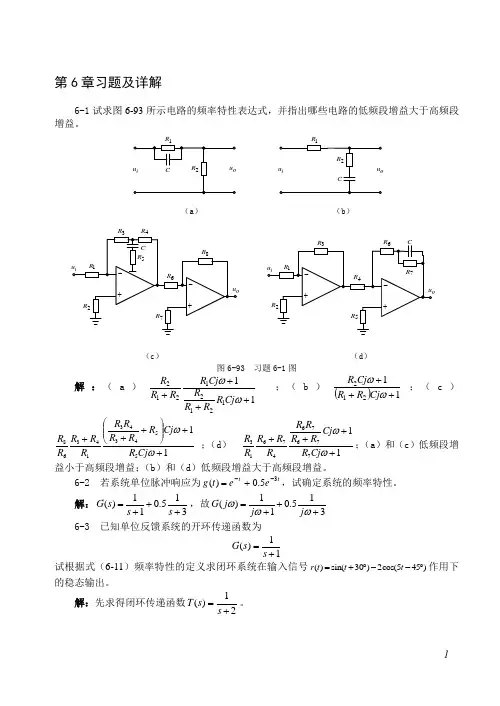
第6章习题及详解6-1 试求图6-93所示电路的频率特性表达式，并指出哪些电路的低频段增益大于高频段增益。

（a ） （b ）R R（c ） （d ）图6-93 习题6-1图解：（a ）1112121212++++ωωCj R R R R Cj R R R R ；（b ）()11212+++ωωCj R R Cj R ；（c ）1155434314368++⎪⎪⎭⎫ ⎝⎛+++ωωCj R Cj R R R R R R R R R R ；（d ） 117767647613++++ωωCj R Cj R R R R R R R R R ；（a ）和（c ）低频段增益小于高频段增益；（b ）和（d ）低频段增益大于高频段增益。

6-2 若系统单位脉冲响应为t t e e t g 35.0)(--+=，试确定系统的频率特性。

解：315.011)(+++=s s s G ，故315.011)(+++=ωωωj j j G 6-3 已知单位反馈系统的开环传递函数为11)(+=s s G 试根据式（6-11）频率特性的定义求闭环系统在输入信号()sin(30)2cos(545)r t t t =+︒--︒作用下的稳态输出。

解：先求得闭环传递函数21)(+=s s T 。

（1）1=ω，447.055211)1(==+=j j T ，︒-=-=∠56.2621arctan )1(j T 。

（2）5=ω，186.02929251)5(==+=j j T ，︒-=-=∠20.6825arctan )5(j T 。

故)2.1135cos(372.0)44.3sin(447.0)(︒--︒+=∞→t t t y t 。

6-4 某对象传递函数为s e Ts s G τ-+=11)( 试求：(1) 该对象在输入()sin()u t t ω=作用下输出的表达式，并指出哪部分是瞬态分量； (2) 分析T 和τ增大对瞬态分量和稳态分量的影响；(3) 很多化工过程对象的T 和τ都很大，通过实验方法测定对象的频率特性需要很长时间，试解释其原因。

《自动控制原理》（第2版）习题答案1第2章2-1 （1）t e t ett23sin 3123cos122--+- （2）6 + 3t（3）)334(322+++---t t e e t t （4）t t ωωωsin 1132-2-2 （1）2351853tt e e --+-（2）t e 2-（3）t e a b t ae n t nnn t n n ωωζωωζωζωsin cos --++（4）t a Aa t a A e b a A atωωωωωωωsin cos 222222++++⎪⎭⎫ ⎝⎛++- 2-3 （a ）)()()(2110f f ms f s X s X i ++=（b ）212110)()()(k k s k k f fsk s X s X i ++=2-4 （a ）)()()(t u t kx t xm =+ （b ）)()()(2121t u t x k k k k t x m =++ 2-5 （a ）)()()()()(2212121t u R dt t du C R R t u R R dt t du CR R r r c c +=++ （b ）)()()()()()(22121221t u R t u R R dt t du C R R L dt t u d LC R r c c c =++++ 2-6 252312)14(100)()(2+++=s s s s R s C 2523125231210)()(22++++⋅=s s s s s R s E 2-7 t t e e t c 2241)(--+-= 2-8 )1)(2(23)(+++=s s s s G t t e e t h ---=24)(22-9 （a ）1)(1)()(32213+++⋅-=s R R C s CR R R s U s U r c （b ）13221)()()(R R R s R CR s U s U r c ++-= 2-10 （a ）))((1)()(432121G G G G G G s R s C -+++=（b ）)(1)1()()(21221H H G G G s R s C -++=（c ）331311321332123113211)()(H G H G H G G G G H G G H G G H G G G G s R s C ++++++=2-11 （a ）32211)()(G G G G s R s C ++=（b ）H G H H G s R s C 111)1()()(+--=（c ）121223121)()()(H G G H G G G G s R s C +++=2-12 （a ）))((1)1()()(23111232123111134321H G H G H H G G G H G H G H G G G G G G s R s C --++++++=))((1)1(1)()(2311123212311123423H G H G H H G G G H G H G H H G G H G s R s E --++++-+⋅=（b ）21212121312)()(G G G G G G G G s R s C ++-++-= 21212131)1(1)()(G G G G G G s R s E ++-+⋅=2-13 （a ）12121211)()(H G G G G G G s R s C ++= 121211211)1(1)()(H G G G G H G G s R s E +++⋅=12121231211)1(1)()(H G G G G G G H G G s D s C ++++⋅-=12121231211)1(1)()(H G G G G G G H G G s D s E ++-+⋅= （b ）434242143421)()(G G G G G G G G G G G s R s C ++++= 434242111)()(G G G G G G G s R s E ++-=434241)()(G G G G G s D s C ++= 434241)()(G G G G G s D s E ++-=32-14 （a ）))((1)(23113343321231134321H G H G H G G H G G G H G H G G G G G G s G -+++-++=（b ）3541432326543211)(H G G H G G H G G G G G G G G s G +-+=（c ） 15.1 （d ）))((1)1()(ch af ehgf ch gb af gb ed abcd s G +----++=45σ % = 56.2% t p = 1.006 t s = 63-13 0 < K < 0.75 3-14 （1）0（2）1 3-16 （1）∞ ∞6分离点：d = -0.8857（4） 渐近线：σa = -1 ϕa = ± 60︒，180︒与虚轴的交点：K = 3 s = ± j1.414分离点：d = -0.423 根迹图略（5） 渐近线：σa = -2/3 ϕa = ± 60︒，180︒与虚轴的交点：K = 4 s = ± j1.414（6）渐近线：σa = -1.5 ϕa = ± 45︒，± 135︒起始角：ϕ1 = -63.4︒根迹图略 （7）（8）894-9 零度根轨迹。

自动控制原理第二版课后习题参考答案2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+=(b) ()()141112+⋅-=Cs R R R s U s U (c)()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i 2-8 (a)()()()()3113211G H G G G G s R s C +++=(b)()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b)()()()1221211222112++++=s C R C R C R s C R C R R s R s C 2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()⎪⎭⎫ ⎝⎛++-=-=-t e t t c s n t n n nn 21222,1ωωωωω()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 32220220222001200=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。

第八章非线性控制系统分析l、基本内容和要求（l）非线性系统的基本概念非线性系统的定义。

本质非线性和非本质非线性。

典型非线性特性。

非线性系统的特点。

两种分析非线性系统的方法——描述函数法和相平面法。

（2）谐波线性化与描述函数描述函数法是在一定条件下用频率特性分析非线性系统的一种近似方法。

谐波线性化的概念。

描述函数定义和求取方法。

描述函数法的适用条件。

（3）典型非线性特性的描述函数（4）用描述函数分析非线性系统非线性系统的一般结构。

借用奈氏判据的概念建立在奈氏图上判别非线性反馈系统稳定性的方法，非线性稳定的概念，稳定判据。

（5）相平面法的基本概念非线性系统的数学模型。

相平面法的概念和内容。

相轨迹的定义。

（6）绘制相轨迹的方法解析法求取相轨迹；作图法求取相轨迹。

（7）从相轨迹求取系统暂态响应相轨迹与暂态响应的关系，相轨迹上各点相应的时间求取方法。

（8）非线性系统的相平面分析以二阶系统为例说明相轨迹与系统性能间的关系，奇点和极限环的定义，它们与系统稳定性及响应的关系。

用相平面法分析非线性系统，非线性系统相轨迹的组成。

改变非线性特性的参量及线性部分的参量对系统稳定性的影响。

2、重点（l）非线性系统的特点（2）用描述函数和相轨迹分析非线性的性能，特别注重于非线性特性或线性部分对系统性能的影响。

8-1非线性控制系统分析1研究非线性控制理论的意义实际系统都具有程度不同的非线性特性，绝大多数系统在工作点附近，小范围工作时，都能作线性化处理。

应用线性系统控制理论，能够方便地分析和设计线性控制系统。

如果工作范围较大，或在工作点处不能线性化，系统为非线性系统。

线性系统控制理论不能很好地分析非线性系统。

因非线性特性千差万别，无统一普遍使用的处理方法。

非线性元件(环节)：元件的输入输出不满足(比例+叠加)线性关系，而且在工作范围内不能作线性化处理(本质非线性)。

非线性系统：含有非线性环节的系统。

非线性系统的组成：本章讨论的非线性系统是，在控制回路中能够分为线性部分和非线性部分两部分串联的系统。