第一讲 四则运算

挑战练习题
总结词：挑战高难度，培 养解决复杂问题的能力
100-(30/6)*4=？
7+9*3/2=？
(3+4)*5/6=？
(8*5)/4+3=？
(10/5)+(6*3)=？
05
四则运算的常见错误及纠正方 法
加法常见错误及纠正方法
总结词
进位不准确
总结词
忽略小数点
详细描述
在进行加法运算时，学生常常会因为进位不准确而导致结 果错误。纠正方法包括加强进位规则的理解和练习，使用 计数器或画图等方式辅助理解。
03
04
购物时计算找零和总价。
计算时间和速度。
解决日常生活中的各种问题， 如计算工资、计算路程等。
在科学、工程、经济等领域中 也有广泛应用。
02 四则运算的基本规则
加法规则
总结词
加法交换律和结合律
详细描述
加法交换律指的是加法满足交换性质，即a+b=b+a；加法结合律指的是加法满 足结合性质，即(a+b)+c=a+(b+c)。
详细描述
在进行小数乘法运算时，学生可能会忽略小数点 的位置和乘法规则，导致结果错误。纠正方法包 括强调小数乘法的规则和注意事项，通过实例和 练习来加深理解。
除法常见错误及纠正方法
总结词
除数误解为被除数
详细描述
总结词
学生在进行除法运算时，有时 会将除数误解为被除数，导致 计算结果错误。纠正方法包括 强调除数和被除数的概念和区 别，通过实例和练习来加深理 解。
01
03
详细描述：在减法运算中，学生有时会忽略负数的存 在，导致结果错误。纠正方法包括强调负数的概念，

C 语言程序设计第一讲四则运算程序举例：<1>长方形的长与宽分别为 25,12求周长?main(){printf(“%d\n”,(25+12)*2);}<2>求23*5的积是多少?main(){ printf(“%d”,23*5);}<3>求(1/2+1/3+1/4)*(1/5+1/6)的值。

main(){float a,b,c;a=1/2.0+1/3.0+1/4.0;b=1/5.0+1/6.0;c=a*b;printf(“c=%f \n”,c);}<4>巳知圆的半径是7.6求圆的周长?main() /*主函数.程序从这里开始*/{float a,r; /*定义单精度实型变量*/r=7.6; s=2*3.14*r; /*進行运算*/printf(“%f \n”,s); / *打印周长*/}<5>打印字符串:This is a book.main(){printf(“This is a book.”);}<6>打印小队旗.main(){printf(“A\n”);pri ntf(“I*\n”);printf(“I***\n”);printf(“I*****\n”);printf(“I\n”);printf(“I\n”);printf(“I\n”);}注: ①任何程序都以main()开头.②:任何程序都有函数体.用{}括起来.程序语法解释<1> 什么是程序?程序是为做一件亊预先写岀的符合逻辑的详细计划或工作过程。

<2> 什么是函数？是可以完成某一工作的程序模块.有接受任务与数据,并执行任务,返回结果的功能<3> 什么是函数体？在一对括号”{ }”里面的内容称为函数体.<4> 什么是C语言的语句?语句是实现函数功能的最小功能单元.函数体内,毎行由分号结束的都是语句.<5> 函数体一般由三部分组成:{①定义变量部分.②数据处理部分.③输岀结果部分.}<6> 在程序3中:哪是定义变量的语句?哪些是数据处理的语句?哪一行是输岀结果的语句?<7>定义变量类型与输岀格式必须相匹配:①int →%d ②long→%ld ③float→%f④double→%lf⑤char→%c ⑥char→%s<8> 算术运算符与赋値运算符的介绍:①”( )” 括号运算符.②”+ +” ; ”――”自增加1,自减减1③“*”;”/”;”%”乘除运算符 .④“+”;”-“加减运算符 .⑤“=”赋值运算符.运算符优先级别:①→②→⑶→④→⑤.而赋值运算符⑥优先级别最低.<9> 什么是变量?程序中可以攺变的量叫变量..在C语言中变量必须先定义后使用. 定义方法如下:①int a , b; /*定义a, b为整型变量.*/②float c ,d; /*定义为单精度实型变量.*/③long e, f; /*定义e ,f为长整型变量*/.④double;g,h; /*定义为双精度实型量*/注:变量名要用小写字母表示(待详讲).<10>为什么要先定义变量类型．．．．．．．再使用?因它关系到为变量分配内单元数及取数范围.如定义不正确,会影响数据运算的正确性.<11> 各种类型变量佔内存的宇节数:①char占1个字节.②int占2个字节.③long占4个字节④float占4个字节⑤double占8个字节.<12> 各种类型变量的取数范围:①char: - 128←→127②int: -32768←→32767③long:-2147483648←→2147483647④float:3.4e-38←→3.4e+38⑤double:1.7e-308←→1.7+308程序实例:已知a=5000,b=200求a*b的积main(){ int a,b,c;a=5000;b=200;c=a*b;printf(“c=%d\n”,c);}运行结果是错误的.上面的程序作如下修攺:main(){long a,b,c;a=5000;b=200;c=a*b;prinnf(“c=%ld\n”,c);}运行结果是正确的.观察襾个程序,为什么结果一个错一个正确?一:赋值语句（各种赋值形式）赋值语句由赋值表达式加一个分号构成.例如:a=2+3*6;是一个赋值语句.其中“=”不是等号而是赋值运算符.作用是將2+3*6的得数20送给変量a.二:输岀语句 (程序3为例)printf(“c=%f\n”,c);是输岀语句,作用是向屏幕输岀结果.printf是保留字.在括号中有双引号和旡双引号两部分,用逗号隔开.其中: “c=”是原样输岀.”\n”是光标換行.输岀时,%f是变量c中的数值的位置．．．．．,“f”要求用实数形式输岀.并自动带6位小数.怎样输入程序并运行程序⑴点击相对应图标(TC)进入C语言集成环境.⑵在编辑窗口输入源程序(在上面大窗口).⑶按”F9”査检程序是否有语法错误.⑷按”Ctrl+F9”运行程序.⑸按”Alt+F5”察看运行结果.注:⑴要想输入第二个源程序,必须删除第一个程序后,再进行第二个源程序的输入.⑵如未见光标可按F6.按F6光标可以在上下窗口中来回移动.如发现有光带复盖菜单请按“Esc”键,即可去掉复盖的光带.存盘的方法⑴第一次存盘时,按F2会出现NONAME.C,删除此名再键入新程序名如:a1.c 回车即可.⑵程序修攺后,如再次存盘时,直接按f2则自动存盘.⑶如果想调岀已存盘的程序,可按F3.找到程序名回车即可.编程与上机练习题<1>求(64+5×4)+(85―5×13)的值.<2>求(1/2+1/3+1/4)+45*(23/111)的值.<3>已知某学生的平时成绩为95分,考试成绩为87.75分,求总评分.并保留一位小数.(总评分=平时分×40%+考分×60%)<4>求90,76,89三数和与平均数.<5>求127除以36的啇及余数.<6>打印平行四边形(大小自定).三: 键盘输入语句编程实例:巳知苹果2.5元一斤,香蕉2元一斤,请为售货员编一个自动收款程序.main(){float a,b,p,x,s; /*定义为实型変量*/a=2.5;b=2; /*两物品单价*/scanf(“%f%f”,&p,&x); /*输入斤数*/s=a*p+b*x; /*求应付款*/printf(“s=%.2f\n”,s); /*输出*/}本例的语法解释:⑴scanf(“%f%f”,&p,&x);是键盘输入语句.它在程运行过程中,输入两个数据到变量p和x所对应内存单元中.<2>在键盘输入语句中,変量前面要加地址符.用逗号隔开两个変量….<3>printf(“s=%.2f”,s);语句中的”%.2f”是要求用保留両位小数的实数形式输岀.⑷键盘输入语句输入数据的方法:(以买苹果4斤,香蕉2.5斤为例:)运行:输入: 4 2.5 ↙s=15.00若键盘输入语句改为:scanf(“%f, %f”, &p, &x);再次运行:输入: 4,2.5↙s=15.00注:特别注意键盘输入时的不同方法.注:如果不买其中一项,则此项输入0.四:条件分支语句编程实例:输入成绩,如>=60分,则打印”pass”,如<60分,则打印”fail”.<方法一>main(){float a;scanf(“%f”,&a);if(a<60)printf(“a=% .1f→fail\n”,a);if(a>59)printf(“a=% .1f→pass\n”,a);}运行: 再次运行:45 ↙ 80 ↙a= 45.0→ fail a=80.0→ pass方法二:main(){float a;scanf(“%f”,&a);if(a<60.0)printf(“a=%.1f→fail”,a);else printf(“a=% .1f→pass”,a);}运行: 再次运行:50 ↙ 80a=50.0→fail a=80.0→pass本例的语法解释:<1>分支语句有两种格式:.否则不执行后面的语句,语句可以是一条语句,也可以是多条语句.如果是多条语句时,必须用花括号括起来,构成一个复合语句.行语句.如果(表达式)为假时,执行语句2, 执行完后顺序执行下一条语句. 同理:语句1和语句2可以是一行语句,也可是复合语句．．．．.．五条件运算符:( ？：)编程实例:键盘输入任意大小两亇整数,打印大数.main(){int a,b; scanf(“%d%d”,&a,&b);printf(“max=%d\n”,a>b ? a:b);}运行: 再次运行:24 15 ↙9 26 ↙max=24 max=26本例的语法解释:⑴在printf(“max=%d\n”,a>b ? a:b);中,a>b ? a : b 是条件运算符的实际应用.其意是如果a>b为真时打印a ,为假时则打b.⑵当if～else结构中是表达式语句时,就可用条件运算符” ? : ”来编程.上机注意亊项:⑴在上机编程旡特别要求时,都用小写字母⑵输入源程序时,要在”英文狀态”下输入.⑶在使用键盘输入语句时,要在变量前加地址符”&”.多个变量之间用逗号隔开。

=在3括0-号26里面，也要先算二级、然后算一级。
这 =4是21过5＋渡3期64，5教÷师81要告诉学生，没有算的一些步骤都要抄下来，直到计算结束多强调几次后,没 有人错掉。
重点3 一这道是四 过则渡运期算，的教算师式要并告不诉一学定生有，四没种有运算算的符一号些，步一骤般都指要由抄两下个来或，两直个到以计上算运结算束符多号强及调括几号次，后合,没并有成人一错个掉数。的运算。
0和1 在=4括40号+（里2面40，－也1要6）先＝算4二40级＋、22然4后算一级。
因=4数× 因数 =积
71133除－以（2168加5上6÷383的2）和
在除法里，0不能做除 这和是= 过加渡数期+，加教数师要告诉学生，没有算的一些步骤都要抄下来，直到计算结束多强调几次后,没 有人错掉。
=816240-6÷0 32＋730
=1和4 任何数相乘都的任何数。
这 （是2）过7渡8与期5，2教的师和要乘告以诉它学们生的，差没，有积算是的多一少些？步骤都要抄下来，直到计算结束多强调几次后,没 有人错掉。
2783+÷3（2×263+-6308）的算式用文字表达是（ ）。
从=43560）。
=440+240-16 =440+（240－16） ＝440＋224 =664
对策：学生以前算惯了小括号里只 有一步的算式， 这种题目后要把 小括号里的题都算完后，才能把括
号去掉，否则要一直抄下来。
归纳总结
如果只有加和减或者 01
只有乘和除，从左往
右计算。
四则运算应当
如果有括号，要先算括
注意的地方：
重点2
1
4
2
3
整数加法：

六年级奥数第1讲：四则混合运算[例1] 计算2002×（2.3×47+2.4）÷（2.4×47-2.3）点拨：运用乘法分配律，从简到繁，是为了最后的简。

解答：原式 =2002×（2.4×47-0.1×47+2.4）÷（2.4×47-2.3） = 2002×（2.4×47-2.3）÷（2.4×47-2.3）=2002[试一试1] 计算37.5×21.5×0.112+35.5×12.5×0.112 （答案：140）[例2] 计算:（2+3.15+5.87）×（3.15+5.87+7.32）- （2+3.15+5.87+7.32）×（3.15+5.87）点拨：某些数据重复出现时，用字母代替，可简化运算。

解答：设2+3.15+5.87=A，2+3.15+5.87+7.32=B，则原式 =A×（B-2）-B×（A-2）= AB-2A-AB+2B=2(B-A)=2×[(2+3.15+5.87+7.32)-(2+3.15+5.87)]=2×7.32=14.64[试一试2] 计算: （答案：12002） (1+12 +13 + … +12000 + 12001 )×( 12 +13 + … + 12001 + 12002)[例3] 计算999...99 × 888...88 ÷ 666 (66)2002个9 2002个8 2002个6点拨：不要被大数吓倒，结合数据特点化简。

解答：原式 =3×333...33 ×4× 222...22 ÷ 666 (66)2002个3 2002个2 2002个6= 3×4×111...11 × 666...66 ÷ 666 (66)2002个1 2002个6 2002个6=3×444 (44)2002个4=133 (332)2001个3[试一试3] 计算99999×22222 + 33333×33334 （答案：3333300000）[例4] 计算999…99×999…99 + 1999…99计算结果的末尾有多少个连续的零？ 2002个9 2002个9 2002个9点拨：运用乘法分配律将乘法运算转化为减法运算。

第一讲分小四则混合运算一、数的互化1.小数化成分数：原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。

2.分数化成小数：用分母去除分子。

能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。

3.一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。

4.小数化成百分数：只要把小数点向右移动两位,同时在后面添上百分号。

5.百分数化成小数：把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。

6.分数化成百分数：通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。

7.百分数化成小数：先把百分数改写成分数,能约分的要约成最简分数。

二、数的整除1.把一个合数分解质因数,通常用短除法。

先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。

2.求几个数的最大公约数的方法是：先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的最大公约数。

3.求几个数的最小公倍数的方法是：先用这几个数(或其中的部分数)的公约数去除,一直除到互质(或两两互质)为止,然后把所有的除数和商连乘求积,这个积就是这几个数的最小公倍数。

4.成为互质关系的两个数：1和任何自然数互质;相邻的两个自然数互质;当合数不是质数的倍数时,这个合数和这个质数互质;两个合数的公约数只有1时,这两个合数互质。

三、约分和通分1.约分的方法：用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止。

2.通分的方法：先求出原来的几个分数分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。

四、性质和规律1.商不变的规律商不变的规律：在除法里,被除数和除数同时扩大或者同时缩小相同的倍数,商不变。

第一讲速算与巧算之四则运算一．加、减法速算与巧算：凑整法：凑整法就是将算式中的数分成若干组，使每组的运算结果都是整十、整百、整千……的数，再将各组的结果相加。

凑整法主要分为：⑴移数凑整法，⑵借数凑整法，⑶拆数凑整法，⑷找“基准数”法，⑸分组凑整法；例1.（一）同学们是不是很简单啦，都来试试吧！⑴34+53+66 ⑵679+27+321 ⑶63+294+37+54+6=34+66+53 =679+321+27 =63+37+294+6+54=100+53 =1000+27 =100+300+54=153 =1027 =454解析：同学们还记加法中的朋友数吗？1+9，2+8，3+7，4+6，5+5；通过运用移数凑整法（带号搬家）将朋友数组合在一起；（二）下面这道题的所有加数都是很有特点的，仔细观察，快速计算，其实并不难199999+19999+1999+199+19=200000-1+20000-1+2000-1+200-1+20-1=200000+20000+2000+200+20-5=222220-5=222215解析：此题采用借数凑整法，通过借加、还减的思想将加数转化成整数。

另外，此题还可拆小数补大数：199999+19999+1999+199+19=200000+20000+2000+200+19-4=222200+15=222215（补） 28+208+2008+20008+200008=20+8+200+8+2000+8+20000+8+200000+8=20+200+2000+20000+200000+5×8=222220+40=222260解析：此题采用拆数凑整法，通过拆减、补加的思想将加数转化成整数。

（三）计算： 801+802+805+798+807+808+795=7×800+1+2+5-2+7+8-5=5600+16=5616解析：观察发现这个几个数比较接近于同一个整数（800），所以选择这个整数（800）为“基准数”，把多加的数减去，把少加的数加上，称为找“基准数”法；（补） 100-99-98+97+96-95-94+93+…+4-3-2+1=（100-99-98+97）+（96-95-94+93）+…+（4-3-2+1）=0+0+…+0=0解析：此题采用分组凑整法，典型的分组有：⑴ + - - + ，⑵ - + + -，连续的自然数或等差数列结果等于0.观察发现此算式中恰好包含 + - - + = 0，则将100个数分成4个1组，每组结果为0，整体也为0，但需要注意的是，并不是没到题目都能正好分完，同学们在做题的时候要注意数字的个数.注：凑整看“数字”，分组看“符号”；二．乘法速算与巧算：⑴乘法交换律：两个数相乘，交换两个数的位置，其积不变，即：a×b=b×a⑵乘法结合律：三个数相乘，可以先把前两个数相乘后，再与后一个数相乘；或先把后两个相乘后，再与前一个数相乘，乘积不变，即：a×b×c=（a×b）×c=a×（b×c）⑶乘法分配律：两个数之和（或差）与数相乘，可用此数先分别乘和（或差）中的各数，然后再把这两个积相加（或减），即：（a+b）×c=a×c+b×c或（a-b）×c=a×c-b×c。

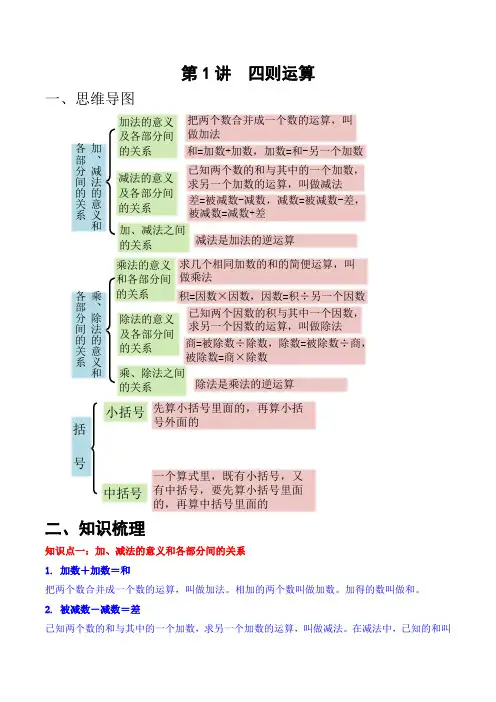
第1讲 四则运算一、思维导图加法的意义及各部分间的关系把两个数合并成一个数的运算，叫做加法减法的意义及各部分间的关系加、减法之间的关系减法是加法的逆运算已知两个数的和与其中的一个加数，求另一个加数的运算，叫做减法加、减法的意义和各部分间的关系和=加数+加数，加数=和-另一个加数差=被减数-减数，减数=被减数-差，被减数=减数+差乘法的意义和各部分间的关系求几个相同加数的和的简便运算，叫做乘法除法的意义及各部分间的关系乘、除法之间的关系除法是乘法的逆运算已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法乘、除法的意义和各部分间的关系积=因数×因数，因数=积÷另一个因数商=被除数÷除数，除数=被除数÷商，被除数=商×除数先算小括号里面的，再算小括号外面的 括号一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的小括号中括号 二、知识梳理知识点一：加、减法的意义和各部分间的关系1. 加数＋加数＝和把两个数合并成一个数的运算，叫做加法。

相加的两个数叫做加数。

加得的数叫做和。

2. 被减数－减数＝差已知两个数的和与其中的一个加数，求另一个加数的运算，叫做减法。

在减法中，已知的和叫做被减数。

减法是加法的逆运算。

3. 各部分间的关系（1）加法各部分间的关系：和＝加数＋加数；加数＝和－另一个加数。

（2）减法各部分间的关系：差＝被减数－减数；减数＝被减数－差；被减数＝减数＋差。

知识点二：乘、除法的意义和各部分间的关系1.求几个相同加数的和的简便运算，叫做乘法。

积=因数×因数2.除法是已知两个因数的积和其中的一个因数求另一个因数的运算。

因数=积÷另一个因数3.除法是乘法的逆运算。

商=被除数÷除数，除数=被除数÷商，被除数=商×除数知识点三：括号算式中有小括号时，要先算小括号里面的。

知识点四：解决租船问题的策略先计算哪种船的租金便宜，就考虑先租这种船，如果船没坐满，就再进行调整，考虑租另一种船。

小学数学三年级第一讲四则运算学生版第1讲四则运算一内容概述学习加减法运算中的各种计算技巧，例如凑整、带着符号搬家、加减相消、数的分拆与合并等等;掌握加减法运算中添、去括号的法则，并借此简化运算。

典型问题兴趣篇1(计算:(1)15+21+25+19;(2)70+63+81+37+30+19(2(计算:(1)17+19+234+21+183+26;(2)(1+11+21+31)+(9+19+29+39)(3(计算:(1)35+121-35-21;(2)152-19-13+19+223-32(4(计算:(1)25-(25-14)-(14-7);(2)57-(50-28)+(44-28)-(57-26)(5(计算:(1)199+99+9;(2)9+98+397+247(6(计算:(1)321-199;(2)456-197-98(7(请大家先不要动笔，看能不能把下面的题目直接口算出来:(1)2580-2547;(2)1596-1296;(3)365+97;(4)365-97(8(计算:(1)150-85-15;(2)1450-375-203-625(9. 计算:(1)38+83-55;(2)(235+523+352)-(111+333+555)(10(计算:(1)11-10+9-8+7-6+5-4+3-2+1;(2)100+102-104+106-108+110-112+114-116+118(拓展篇1(计算:(1)51+62+49+38;(2)64+127+129+23+71+136(2(计算:(1)2+13+224+3330+6670+676+87+8;(2)73+119+231+69+381+17(3(计算:(1)82-29-22+259;(2)375-138+247-175+139-237(4(计算:(1)162-(162-135)-(35-19);(2)163-(50-18)-(153-76)+(124-18)(5(计算:(1)999+599+199;(2)3996+449+98+9(6(计算:(1)1365-598;(2)1206-199-297-398(7(请大家先不要动笔，看能不能把下面的题目直接口算出来: (1)93570-93534; (2)45235-38235;(3)465+197; (4)465-197(8(计算:(1)280-24-76-65-35;(2)267-162+84-38-147+116(9(计算:(1)267-136+36-167;(2)325-251-34+151-66(10((1)在加法算式中，如果一个加数增加10，另一个加数减少5，两数的和如何变化?(2)在减法算式中，如果被减数增加15，差减少8，那么减数应如何变化?11(计算:(1)246+462+624-888;(2)125-24+251-240+512-402(12(计算:(1)21-20+19-18+17-16+15-14+13-12+11;(2)12+23-34+45-56+67-78+89-78+67-56+45-34+23+12(超越篇1. 计算下面4个算式:1+2+1，1+2+3+2+1,1+2+3+4+3+2+1,1+2+3+4+5+4+3+2+1(观察这4个算式的结果，并找出规律，再用这个规律求出下面算式的结果: 1+2+3+4+…+19+20+19+…+4+3+2+1(2. 计算:364-(476-187)+213-(324-236)-150(3. 如图1-1，教室里有4个书柜，每个书柜里都有4格书，图中标明了每格内书的册数. 一天，老师问小悦和冬冬:“不许用加法计算，你们马上回答，这4个书柜里，哪一个书柜里的书多一些?”两个人看了看书柜上标出的数，想了想齐声说:“4个书柜里的书同样多!”老师高兴地说:“完全正确!”请你说一说他们是怎样想的?4(计算:3355+4466+9977-3366-4477-9955(5. 已知1234+2345+3456+4567+5678-6543-5432-4321的计算结果是984(请问:1244+2355+3466+4577+5688-6513-5412-4311的计算结果是多少?6(如图1-2，除第一行外，每个圆圈中的数都等于它上面两个圆圈中数的和，请计算最下面的圆圈中应填的数(7(如图1-3，老师将9个数写在一个九宫格里，让同学们选数，每个同学可以从中选5个数来求和(小悦选的5个数的和是120，冬冬选的5个数的和是111(如果两人选的数中只有一个是一样的，这个数是多少?8(计算:8457-(7630-4578)+(7845-3076)-(6307-5784)-763(。

第1讲 四则运算例1、1÷（2÷3）÷（3÷4）÷（4÷5）…÷（4010÷4011）÷（4011÷4012）例2、2006×20052006－2005×20062005=例3、2005－2004+2003－2002+…+3－2＋1= 。

例4、2006+200.6+20.06+2.006+994+99.4+9.94+0.994= 。

例5、计算：=⨯1111111112140120052005 。

例6、=++++199908191990990191919303031919202191个个 。

例7、49.2492492÷1.23123123＝( )。

例8、设,716151,4131++=+=b a 则在a 与b 中，较大的数是 。

例9、设,103102,102101,101102,100101====d c b a 则a ，b ，c ，d 这四个数中，最大的数是 ，最小的数是 。

第1讲 练习1、8.1×1.3－8÷1.3+1.9×1.3+11.9÷1.3= 。

2、在113,72,31中，最小的数是 。

3、若c b a c b a ,,,111111111,1111111,11111则===中最大的数是 ，最小的数是 。

4、两个自然数的乘积是72，72除以这两个自然数的差，所得的商等于其中一个自然数，这个商是 。

5、一个数被7除，余数是3，该数的3倍被7除，余数是 。

6、一个数除以39，商和余数相同，这个数最大是 。

7、有一个不等于1的正整数，除1773，1888，1957，2003，得到相同的余数，则这个正整数是 。

8、请将下列四个自然数用四则运算符号连接成一个综合算式，使结果等于24，（可以交换位置，可以加括号，一个数只能用一次）①2，3，5，7列式： =24②4，5，7，8列式： =249、将一个分数的分子加1与将该分数的分子和分母同时加2所得的结果相同，这个分数是。

第1讲四则运算案例1：已知鸡和兔共有15只，共有40只脚，问鸡和兔各有多少只？算法：假设鸡和兔训练有素，吹一声哨，它们抬起一只脚，40－15＝25，再吹一声哨，它们又抬起一只脚，25－15＝10，这时的鸡就一屁股就坐在了地上，兔还有2只脚立着，所以10÷2＝5（只），那么鸡的数量为15－5＝10（只），你能列出综合算式吗？教法说明：引导学生通过具体的实例，来列出综合算式，并且回顾运算顺序。

参考答案：兔子：（40－15－15）÷2＝（25－15）÷2＝5（只）鸡：10－5＝5（只）案例2：先说出下面各题的运算顺序，再计算。

（1）42＋6×（12－4）（2）42＋6×12－4教法说明：相同的数据，相同的运算符号，不同的运算顺序需要引导学生找到不同，进而准确的计算运算结果。

参考答案：（1）先算减法，再算乘法，最后算加法（2）先算乘法，再从左往右计算（1）42＋6×（12－4）（2）42＋6×12－4＝42＋6×8 ＝42＋72－4＝42＋48 ＝114－4＝90 ＝110例题1：用递等式计算（1）28＋172×88－78 （2）（28＋172）×88－78（3）（28＋172）×（88－78）（4）[28＋（172－88）] ×78教法说明：先让学生观察四个算式，说一说先计算哪一步，最后归纳总结四则运算的顺序：（1）没有括号的算式：先乘除，后加减（同级运算按从左到右依次计算）（2）有括号的算式：先算括号内的，再算括号外的（先算圆括号里的，再算方括号里的）参考答案：（1）28＋172×88－78 （2）（28＋172）×88－78＝28＋15136－78 ＝200×88－78＝15138－78 ＝17600－78＝15060 ＝17522（3）（28＋172）×（88－78）（4）[28＋（172－88）] ×78＝200×10 ＝[28＋84]×78＝2000 ＝112×78＝8736试一试：用递等式计算（1）28＋624×88－78 （2）（28＋624）×88－78（3）（28＋624）×（88－78）（4）[28＋（624－88）] ×78参考答案：（1）54862；（2）57298；（3）65200；（4）44304例题2：巧算（1）997×7＋21 （2）27×43＋85×73＋27×42教法说明：首先要让学生理解乘法的分配率。

的体重的8倍。这头牛的体重是多少千克？
就是求把5600平均分成8份，求一份是多少， 用除法计算。
5600 ÷ 8 = 700 (千克) 答：这头牛重700千克。
2. 根据乘、除法各部分间的关系,写出另外两 个算式。
17×42=714
714÷17＝42 714÷42＝17
208×67=1393 13936÷208=67
4.
被除数÷＝除商数×＝除商数....+.. 余数
被除数 除数
商
余数
225
21
10
15
420
18
23
6
478
36
13
10
除数＝（被除数–余数）÷商
5.计算下面各题，并利用乘、除法各部分间 的关系进行验算。
48×27= 1296
48
27
× 257 验 × 458
336 算 216
1
96
1 028
1296
③ 数。
替换为 ① − ② = × − ÷
综合算式
×− ÷=
11.
进入知识宫的密码是
，
请破译密码。
14+82− = 87
密码是
。
×6+10 = 58 =9
14+82− = 87
96 96−87=9
11.
进入知识宫的密码是
，
请破译密码。
14+82− = 87 密码是 9898 。
×6+10 = 58 =9 =8
89×❀=356 ❀÷20=35
❀×18=774 29×❀=928
672÷❀=24 858÷❀=39
89×❀ = 356 ❀× 18 = 774 672÷❀ = 24

一、整数四则运算定律（1） 加法交换律：a b b a +=+（2） 加法结合律：()()a b c a b c ++=++ （3） 乘法交换律：a b b a ⨯=⨯（4） 乘法结合律：()()a b c a b c ⨯⨯=⨯⨯（5） 乘法分配律：()a b c a b a c ⨯+=⨯+⨯；()b c a b a c a +⨯=⨯+⨯ （6） 减法的性质：()a b c a b c --=-+ （7） 除法的性质：()a b c a b c ÷⨯=÷÷；（8） 除法的“左”分配律：()a b c a c b c +÷=÷+÷；()a b c a c b c -÷=÷-÷，这里尤其要注意，除法是没有“右”分配律的，即()c a b c a c b ÷+=÷+÷是不成立的！ 备注：上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用．二、 加减法中的速算与巧算速算巧算的核心思想和本质：凑整。

常用的思想方法总结如下：（1） 分组凑整法．把几个互为“补数”的减数先加起来，再从被减数中减去，或先减去那些与被减数有相同尾数的减数．“补数”就是两个数相加，如果恰好凑成整十、整百、整千……，就把其中的一个数叫做另一个数的“补数”．（2） 加补凑整法．有些算式中直接凑整不明显，这时可“借数”或“拆数”凑整．三、乘法凑整思想核心：先把能凑成整十、整百、整千的几个乘数结合在一起，最后再与前面的数相乘，使得运算简便。

例如：425100⨯=，81251000⨯=，520100⨯=理论依据：乘法交换律：a ×b=b ×a 乘法结合律：(a ×b) ×c=a ×(b ×c) 乘法分配律：(a+b) ×c=a ×c+b ×c知识点拨第一讲 整数四则混合运算的简便运算积不变规律：a ×b=(a ×c) ×(b ÷c)=(a ÷c) ×(b ×c)四、乘、除法混合运算的性质⑴商不变性质：被除数和除数乘（或除）以同一个非零数，其商不变．即： ()()()()0a b a n b n a m b m m ÷=⨯÷⨯=÷÷÷≠ ，0n ≠⑵在连除时，可以交换除数的位置，商不变．即：a b c a c b ÷÷=÷÷⑶在乘、除混合运算中，被乘数、乘数或除数可以连同运算符号一起交换位置（即带着符号搬家）．例如：a b c a c b b c a ⨯÷=÷⨯=÷⨯⑷在乘、除混合运算中，去掉或添加括号的规则去括号情形：①括号前是“×”时，去括号后，括号内的乘、除符号不变．即()()a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷ ②括号前是“÷”时，去括号后，括号内的“×”变为“÷”，“÷”变为“×”．即()()a b c a b c a b c a b c ÷⨯=÷÷÷÷=÷⨯ 添加括号情形：加括号时，括号前是“×”时，原符号不变；括号前是“÷”时，原符号“×”变为“÷”，“÷”变为“×”．即()()()()a b c a b c a b c a b c a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷ ⑸两个数之积除以两个数之积，可以分别相除后再相乘．即 ()()()()()()a b c d a c b d a d b c ⨯÷⨯=÷⨯÷=÷⨯÷ 上面的三个性质都可以推广到多个数的情形．一、加法【例1】：278+463+22+37举一反三：732+580+268二、减法【例2】：2871-299例题精讲举一反三：（1）157-99 （2）363-199 （3）968-599三、连减（5种）【例3】：528－53－47举一反三：（1）489－134－76 （2）470－254－46 （3）545－167－133【例4】：496－（296＋144）举一反三：（1）675－（175＋89）（2）466－（66＋125）（3）354－（154＋77）【例5】：496－（144＋296）举一反三：（1）675－（89＋175）（2）466－（125＋66）（3）354－（77＋154）【例6】：528－72－28举一反三：（1）489－77－389 （2）465－267－65 （3）545－167－145【例7】：824－224－176－124举一反三：（1）643－164－133－243 （2）487－187－139－61 （3）545－167－145四、乘法分配律（8种）【例8】：计算：125×（80＋32）（24＋40）×25举一反三：（1）125×（64＋80）（2）（80＋32）×125 （3）（16＋32）×25【例9】：（1）125×（100－8）（2）（125－40）×8举一反三：（1）125×（100－48）（2）（100－16）×25【例10】：（1）117×56＋117×44举一反三：（1）269×26＋74×269 （2）521×65＋35×521 （3）126×72＋126×12＋126×16【例11】：125×69－125×61举一反三：（1）25×127－25×119 （2）365×251－365×151（3）156×59－156×27－156×22 （4）137×97－44×137－137×43【例12】：45×102举一反三：（1）25×44 （2）125×168 （3）125×18【例13】：36×99举一反三：（1）45×98 （2）125×92 （3）35×99【例14】：（1）81＋9×391 （2）9＋9×999 （3）99＋9×99【例15】：（1）9×107－63 （2）6×108－48 （3）134×101－134五、连除（2种）【例16】：1250÷25÷5举一反三：（1）2000÷125÷8 （2）1280÷16÷8 （3）1300÷5÷20（4）840÷5÷8 （5）1700÷25÷4 （6）4800÷50÷2【例17】：630÷（63×5）举一反三：（1）780÷（78×2）（2）1250÷（125×5）（3）6300÷（63×5）六、四则混合运算(1)（24＋24）÷24×24 （2）24＋24÷24×24 （3）16＋4－16＋4 （4）（16＋4）－（16＋4）（5）25×6÷25×6 （6）120－（72＋48）÷24（7）45＋55÷5－20 （8）12×（280－80÷4）（9）218＋324÷18×5（10）（488＋32×5）÷12 （11）4500÷（170－60×2）（12）（28＋41）÷（92÷4）（13）80＋320÷4－30 （14）18×（420－320÷20）（15）48－2×8÷8×2 （16）480÷（144－960÷8）（17）120＋480÷（43－28）（18）（273＋562）÷5－96 （19）4500÷（150－40×3）（20）812÷（532－36×14）（21）（12＋12）÷12×12（22）625÷（54－522÷18）（23）17＋13－17＋13 （24）60－15×7÷15×7 （25）12×（289－84÷4）（26）218＋702÷18×5 （27）45000÷（150－40×3）（28）（77＋38）÷（92÷4）（29）58－28×2＋40 （30）56×4－175÷5（31）（73－59）×（6＋13）（32）（85－40）÷（15÷3）（33）71－17×7÷17×7课堂检测：（1）43×202 （2） 59×299 （3） 134×51-51×34 （4） 7200÷36 （5）68×32—784÷56 （6）3000÷125÷8 （7）98×35 （8） 960×46÷48 （9）480×46÷48 （10）302×99+302 （11）756+483-556（12）230×54+540×77 （13）887×25-87×25 （14）（825+25×8）×4（15）325-225÷5+145 （16）35×102 （17）498+（201-154）（18）125×89×8 （19）428×78+572×78 （20）8800÷（25×88）（21）3600÷50÷2（22）25×（20+4）容易出错类型（共五种类型）600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷（25×8）。

第一讲四则运算四年级知识小屋：1、四则运算加法、减法、乘法和除法统称四则运算2、四则混合运算的运算顺序在四则混合运算里，加法和减法叫做第一级运算，乘法和除法叫做第二级运算。

四则混合运算的顺序是：同级运算、从左到右依次计算，含有两级的运算，先算第二级，后算第一级，算式里有括号，要先算括号里面的，后算括号外面的。

3、解决问题的步骤和方法：（1）弄清题意，从题目中找出已知量和所求问题。

（2）分析已知量和所求问题之间的数量关系。

（3）确定先算什么，后算什么，并列式解答。

（4）写出答语。

基本范例：例1：（1）48+18×10－6 （2）48+18×（10－6）例2、四（1）班图书柜里有科技书和文艺书共560本，其中文艺书是科技书的3倍，文艺书和科技书各有多少本？例3、王芳今年18岁，王芳的爸爸今年51岁，问几年前王芳爸爸的年龄是王芳的4倍？例4、一队解放军叔叔过河去执行任务，如果每条船坐6人，则还多16人，如果每条船坐8人，则还差4人，问有多少条船？解放军叔叔有多少人？基本练习：1、计算下面各题（273+562）÷5－96 （28+35）×（92÷4）2、解决问题（1）学校组织6个植树小组，每组有18人，共植树540棵，平均每人植树多少棵？（2）小明集了76张邮票，小方集的邮票是小明的一半，他们两人一共集了多少张邮票？快乐大本营：想一想河岸边按照1棵桃树、2棵梨树、3棵苹果树种下去，问第100棵是什么树？奥林匹克攀登：1、有两篮鸡蛋，第一篮有56个，第2篮有20个，如果每次从第一篮里拿出3个鸡蛋放入第二篮里，至少拿多少次，使两个篮里的鸡蛋同样多？2、星星小学新盖一座教学楼，每上一层楼要走24个台阶，杨丽到教室去要走72个台阶，问杨丽的教室在几楼？3有五个数，它们的平均数是138，把这些数按从小到大的顺序排列起来，那么前三个数的平均数是127，后三个数的平均数是148，求当中的一个数。

2240÷（600÷15）－15 =2240÷40－15 =56－15 =41(天）
答：还要加工41天才能完成任务。
亮亮读一本童话书，前6天每天读12页， 后4天每天读18页才读完．这本童话书 一共有多少页?
12×6＋18×4 =72＋72 =144（页） 答：这本童话书一共有144页。
工程队修一条路，已经修了150千米， 剩下的恰好是修了的一半，剩下的要 在5天内修完，平均每天应修多少千米
=50＋4×60 =50＋240 =290 =150÷50 =3
330÷(65－50)
=330÷15 =22
128－6×8÷16
=128－48÷16 =128－3 =125
例：1、45与15的商，再加上84 与12的商，和是多少？
45÷15＋84÷12 =3＋7 =10
2、78与42的和，除以5，商 78＋42）÷5 是多少？ （ =120÷5
=24
3、12与15的积，减去
540
除以9的商，差是多少？
12×5－540÷9 =60－60 =0
30除600的商的一半是多少？
600÷30÷2 =20÷2 =10
小结： 1.审题找关键词 2.确定最后一步（看尾、题意） 3.正确使用括号 4.灵活计算
例.小迪的爸爸一月份交电话费82元， 二月份交了117元，他想将本季度电 话费控制在平均每月90元，那么他三 月份用电费是多少元？ 90×3－82－117 =270－82－117 =188－117 =71(元） 答：爸爸三月份用电费是71元.
你来当小法官 1、8+2-8+2=0 （ ×） 2、在算式中，括号有改变运算顺序 的作用 （ √ ） 3、25×4÷25×4=1 （× ） 4、72×3+72÷3中，乘、除法可同时 进行运算 （ √ ） 5、（ 18×5）+（36÷2）去掉括号后， 结果不变 （ √ ）

2024年人教版数学四升五暑假衔接培优精讲练过关讲义（知识梳理+易错精讲+真题拔高卷）第1讲四则运算与运算律知识点01：.加、减法的意义和各部分间的关系1.加、减法的意义（1）把两个数合并成一个数的运算，叫做加法。

在加法中，相加的两个数叫做加数，加得的数叫做和。

（2）已知两个数的和与其中的一个加数，求另一个加数的运算，叫做减法。

在减法中，已知的和叫做被减数，减号后面的数叫做减数，减得的数叫做差。

（3）减法是加法的逆运算。

2.加、减法各部分间的关系（1）加法各部分间的关系：和=加数+加数，加数=和一另一个加数。

（2）减法各部分间的关系：差=被减数一减数，减数=被减数差，被减数=减数+差。

（3）由加、减法各部分间的关系，我们可以根据一个加法算式写出两个减法算式，也可以根据一个减法算式写出一个加法算式和一个减法算式。

知识点02：.乘、除法的意义和各部分间的关系1.乘、除法的意义（1）求几个相同加数的和的简便运算，叫做乘法。

在乘法中，相乘的两个数叫做因数，乘得的数叫做积。

（2）已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法。

在除法中，已知的积叫做被除数，其中一个因数叫做除数，求出的另一个因数叫做商。

（3）除法是乘法的逆运算。

2.乘、除法各部分间的关系（1）乘法各部分间的关系：积=因数×因数因数=积÷另一个因数（2）除法各部分间的关系：商=被除数÷除数除数=被除数÷商被除数=商×除数3.有关0的运算（1）一个数加上0，还得原数；一个数减去0，还得原数；被减数等于减数，差是0；一个数和0相乘，仍得0； 0除以一个非0的数，还得0。

（2）注意：0不能作除数。

知识点03：括号1.四则运算我们学过的加、减、乘、除四种运算统称四则运算。

2.有括号的混合运算的顺序（1）一个算式里，有小括号的要先算小括号里面的，再算小括号外面的。

（2）一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的。

第一讲 整数四则混合运算的简便运算知识点拨1、整数四则运算定律（1） 加法交换律：（2） 加法结合律：（3） 乘法交换律：（4） 乘法结合律：（5） 乘法分配律：；（6） 减法的性质：（7） 除法的性质：；（8） 除法的“左”分配律：；，这里尤其要注意，除法是没有“右”分配律的，即是不成立的！备注：上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用．2、加减法中的速算与巧算速算巧算的核心思想和本质：凑整。

常用的思想方法总结如下：（1） 分组凑整法．把几个互为“补数”的减数先加起来，再从被减数中减去，或先减去那些与被减数有相同尾数的减数．“补数”就是两个数相加，如果恰好凑成整十、整百、整千……，就把其中的一个数叫做另一个数的“补数”．（2） 加补凑整法．有些算式中直接凑整不明显，这时可“借数”或“拆数”凑整．三、乘法凑整思想核心：先把能凑成整十、整百、整千的几个乘数结合在一起，最后再与前面的数相乘，使得运算简便。

例如：，，理论依据：乘法交换律：a×b=b×a乘法结合律：(a×b) ×c=a×(b×c)乘法分配律：(a+b) ×c=a×c+b×c积不变规律：a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)四、乘、除法混合运算的性质⑴商不变性质：被除数和除数乘（或除）以同一个非零数，其商不变．即：，⑵在连除时，可以交换除数的位置，商不变．即：⑶在乘、除混合运算中，被乘数、乘数或除数可以连同运算符号一起交换位置（即带着符号搬家）．例如：⑷在乘、除混合运算中，去掉或添加括号的规则去括号情形：①括号前是“×”时，去括号后，括号内的乘、除符号不变．即 ②括号前是“÷”时，去括号后，括号内的“×”变为“÷”，“÷”变为“×”．即添加括号情形：加括号时，括号前是“×”时，原符号不变；括号前是“÷”时，原符号“×”变为“÷”，“÷”变为“×”．即⑸两个数之积除以两个数之积，可以分别相除后再相乘．即上面的三个性质都可以推广到多个数的情形．例题精讲一、加法【例1】：278+463+22+37举一反三：732+580+268二、减法【例2】：2871-299举一反三：（1）157-99 （2）363-199 （3）968-599三、连减（5种）【例3】：528－53－47举一反三：（1）489－134－76 （2）470－254－46 （3）545－167－133 【例4】：496－（296＋144）举一反三：（1）675－（175＋89）（2）466－（66＋125）（3）354－（154＋77）【例5】：496－（144＋296）举一反三：（1）675－（89＋175）（2）466－（125＋66）（3）354－（77＋154）【例6】：528－72－28举一反三：（1）489－77－389 （2）465－267－65 （3）545－167－145【例7】：824－224－176－124举一反三：（1）643－164－133－243 （2）487－187－139－61 （3）545－167－145四、乘法分配律（8种）【例8】：计算：125×（80＋32）（24＋40）×25举一反三：（1）125×（64＋80）（2）（80＋32）×125 （3）（16＋32）×25【例9】：（1）125×（100－8）（2）（125－40）×8举一反三：（1）125×（100－48）（2）（100－16）×25【例10】：（1）117×56＋117×44举一反三：（1）269×26＋74×269 （2）521×65＋35×521 （3）126×72＋126×12＋126×16【例11】：125×69－125×61举一反三：（1）25×127－25×119 （2）365×251－365×151（3）156×59－156×27－156×22 （4）137×97－44×137－137×43【例12】：45×102举一反三：（1）25×44 （2）125×168 （3）125×18【例13】：36×99举一反三：（1）45×98 （2）125×92 （3）35×99【例14】：（1）81＋9×391 （2）9＋9×999 （3）99＋9×99【例15】：（1）9×107－63 （2）6×108－48 （3）134×101－134五、连除（2种）【例16】：1250÷25÷5举一反三：（1）2000÷125÷8 （2）1280÷16÷8 （3）1300÷5÷20（4）840÷5÷8 （5）1700÷25÷4 （6）4800÷50÷2【例17】：630÷（63×5）举一反三：（1）780÷（78×2）（2）1250÷（125×5）（3）6300÷（63×5）六、四则混合运算(1)（24＋24）÷24×24 （2）24＋24÷24×24 （3）16＋4－16＋4（4）（16＋4）－（16＋4）（5）25×6÷25×6 （6）120－（72＋48）÷24（7）45＋55÷5－20 （8）12×（280－80÷4）（9）218＋324÷18×5（10）（488＋32×5）÷12 （11）4500÷（170－60×2）（12）（28＋41）÷（92÷4）（13）80＋320÷4－30 （14）18×（420－320÷20）（15）48－2×8÷8×2（16）480÷（144－960÷8）（17）120＋480÷（43－28）（18）（273＋562）÷5－96 （19）4500÷（150－40×3）（20）812÷（532－36×14）（21）（12＋12）÷12×12（22）625÷（54－522÷18）（23）17＋13－17＋13 （24）60－15×7÷15×7（25）12×（289－84÷4）（26）218＋702÷18×5 （27）45000÷（150－40×3）（28）（77＋38）÷（92÷4）（29）58－28×2＋40 （30）56×4－175÷5（31）（73－59）×（6＋13）（32）（85－40）÷（15÷3）（33）71－17×7÷17×7课堂检测：（1）43×202 （2）59×299 （3） 134×51-51×34 （4）7200÷36（5）68×32—784÷56 （6）3000÷125÷8 （7）98×35 （8） 960×46÷48（9）480×46÷48 （10）302×99+302 （11）756+483-556（12）230×54+540×77 （13）887×25-87×25 （14）（825+25×8）×4（15）325-225÷5+145 （16）35×102 （17）498+（201-154）（18）125×89×8（19）428×78+572×78 （20）8800÷（25×88）（21）3600÷50÷2（22）25×（20+4）容易出错类型（共五种类型）600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷（25×8）。

先把前两个数相加，或者先把后两个数相加，和不变。 这叫做加法结合律。
乘法结合律
先把前两个 数相加，或 者先把后两 个数相加， 和不变。这 叫做乘法结 合律。
如果用字母a、b表示两个加数， 则可以写成：
(a×b) ×c＝a× (b×c)
a×(b+c) ＝ a×b+a×c
如果用字母a、b表示两个加数， 则可以写成：
两个数的和与一个数相乘，可以先 把它们与这个数分别相乘，再相加， 这叫做乘法分配律。
(a+b) ×c＝a×c+b×c
01
减法的运算性质:
02
除法的运算性质:
○ a ÷ b ÷ c = a ÷(b × c) ○ a － b － c = a －(b ＋ c)
加强练习,巩固所学知识
1.用简便方法计算下面各题。
125 × 48
52 × 101
=125 × 8 × 6
=1000 × 6 =6000 =52 × （100 ＋ 1） =52 × 100 ＋ 52 =5200 ＋ 52 =5252
自我检测
（1）填空。
①有括号的运算式题里的运算顺序是先算（括号里面的
），
如果括号里既有加减法，有乘除法，先算（ 乘法
四则运算和简便运算
学习目的:
经过本节课的学习， 大家不仅要掌握四则 运算的顺序；并且要 掌握它们的运算定律, 并且利用运算定律进 行解决相关的数学问 题。
运算定律
加法的运算定 律
如果用字母a、b表示两个加数，则 可以写成：
两个加数交换位置，和不变，这叫 做加法交换律。
a+b＝b+a
(a+b)+c＝a+(b+c) 如果用字母a、b、c表示 三个加数，则可以写成：