频域法滞后校正

实验五 控制系统的频域法校正设计姓名： 学号：一、实验题目题1.设有一单位反馈系统的开环传函为)5.0(08.0)(0+=s s s G ，试用频率特性法设计一个超前校正装置，以满足下列性能指标：kv ≥8，相位裕量为50°。

题2.设有一单位反馈系统的开环传函为)5.0(08.0)(0+=s s s G ，试用频率特性法设计一个滞后控制器，使得kv ≥4，相位裕量为50°。

二、实验目的利用控制系统设计的频域法设计控制器，以改变原系统的频域特性图，使之达到预定的性能指标要求。

掌握串联超前校正和串联滞后校正两种设计方法。

三、实验过程与结果题1：1、设超前控制器传函为)1(11)(>++=a TsaTs K s G c ，根据稳态误差要求确定开环增益K 。

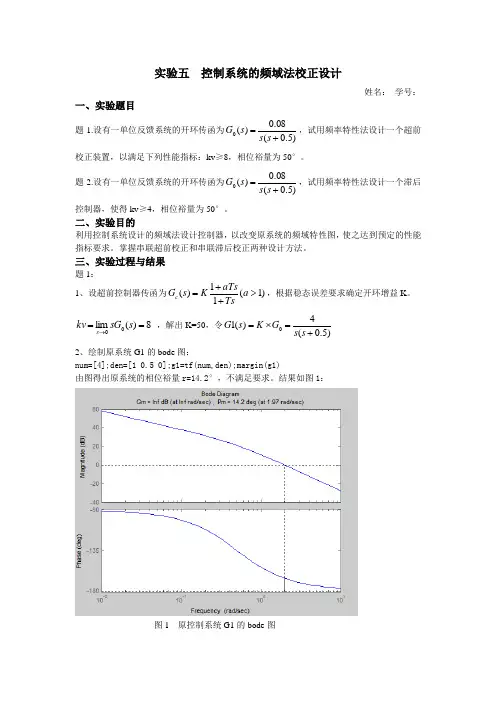
8)(lim 00==→s sG kv s ，解出K=50，令)5.0(4)(10+=⨯=s s G K s G 2、绘制原系统G1的bode 图：num=[4];den=[1 0.5 0];g1=tf(num,den);margin(g1)由图得出原系统的相位裕量r=14.2°，不满足要求。

结果如图1：图1 原控制系统G1的bode 图3、求所需超前角fai ：fai=50°-14.2°+5°=40.8°4、计算a:fai=40.8*pi/180;a=(1+sin(fai))/(1-sin(fai))得出a = 4.77075、求m ω:a=4.7707;10*log10(a)=6.7858在0db 线下10lga=6.7858处作水平线，与原系统G1的bode 图幅频特性曲线的交点对应的w 值即为m ω，由图知m ω=2.93，结果如图2：图2 作图解m ω6、求T ：wm=2.93;T=1/(wm*sqrt(a))运行得到T=0.1563，因此超前控制器为ss s G c 156.01744.0150)(++⨯= 7、校验性能指标：num=[4];den=[1 0.5 0];g1=tf(num,den);nc=[0.744 1];dc=[0.156 1];gc=tf(nc,dc);g=g1*gc;bode(g1);hold on;bode(gc);hold on;bode(g);legend('g1','gc','g')原系统g1的bode 图，超前控制器gc 的bode 图，校正后系统g 的bode 图如图3：图3 校验校正后系统性能指标由图知相位裕量为50.5°，满足要求。

系统的滞后超前频域法校正1 设计目的通过课程设计熟悉频域法分析系统的方法原理。

通过课程设计掌握滞后-超前校正作用与原理。

通过在实际电路中校正设计的运用，理解系统校正在实际中的意义。

2设计任务控制系统为单位负反馈系统，开环传递函数为G(s)=180/[s(s/6+1)(s/2+1)],设计校正装置，使系统满足下列性能指标：相角裕量45+-3度；幅值裕量不低于10db；调节时间不超过3s.3 具体要求1）使用MATLAB进行系统仿真分析与设计，并给出系统校正前后的MATLAB仿真结果，同时使用Simulink仿真验证。

2）使用EDA工具EWB搭建系统的模拟实现电路，分别演示并验证校正前和校正后的效果。

3）在实验箱上搭建实际电路，验证系统设计结果。

4 设计原理概述校正方式的选择。

按照校正装置在系统中的链接方式，控制系统校正方式分为串联校正、反馈校正、前馈校正和复合校正4种。

串联校正是最常用的一种校正方式，这种方式经济，且设计简单，易于实现，在实际应用中多采用这种校正方式。

串联校正方式是校正器宇受控对象进行串联链接的。

本设计按照要求将采用串联校正方式进行校正。

校正方法的选择。

根据控制系统的性能指标表达方式可以进行校正方法的确定。

本设计要求以频域指标的形式给出，因此采用基于Bode图的频域法进行校正。

几种串联校正简述。

串联校正可分为串联超前校正、串联滞后校正和滞后-超前校正等。

超前校正的目的是改善系统的动态性能，实现在系统静态性能不受损的前提下，提高系统的动态性能。

通过加入超前校正环节，利用其相位超前特性来增大系统的相位裕度，改变系统的开环频率特性。

一般使校正环节的最大相位超前角出现在系统新的穿越频率点。

滞后校正通过加入滞后校正环节，使系统的开环增益有较大幅度增加，同时又使校正后的系统动态指标保持原系统的良好状态。

它利用滞后校正环节的低通滤波特性，在不影响校正后系统低频特性的情况下，使校正后系统中高频段增益降低，从而使其穿越频率前移，达到增加系统相位裕度的目的。

一 问题描述已知单位反馈控制系统的开环传递函数为：0100()(0.11)(0.011)G s s s s =++设计滞后校正装置，使校正后系统满足：v K ＝100，c ω=5, σ％≤40％二 设计过程和步骤1、根据给定静态误差系数的要求，确定系统的开环增益K ；则 K=1002、根据确定的K 值，画出未校正系统的伯德图，并给出相应的相位裕量和增益裕度。

增益调整后系统的开环频率特性为：0()G ω=1)1)(0.01j (0.1j 100++ωωωj0100000()(10)(100)G s s s s =++在MATLAB 命令窗口键入以下命令即得未校正系统的伯德图： G0=zpk([ ],[0 -10 -100],100000); bode(G0) hold on margin(G0)未校正系统的伯德图如图1所示。

键入以下命令得未校正系统的相位裕量1γ： [Gm,Pm,Wcg,Wcp]=margin(0G ) Gm=1.1000 %增益裕度 Pm=1.5763 %相位裕度 Wcg=31.6228 %相位交接频率 Wcp=30.1454 %幅值交接频率0s 0100lim lim (0.11)(0.011)v s K sG sKs s s →→===++图1 未校正系统的伯德图Pm=1γ=1.5763︒3、由以上可知相位裕量不满足要求，则在对对数相频特性曲线上找这样一个频率点，要求在该频率处的开环频率特性的相角为εγ++︒-=Φ180以这一频率作为校正后系统的剪切频率c ω式中γ 为系统所要求的相位裕量，ε是考虑到因迟后网络的引入，在剪切频率c ω处产生的相位迟后量，一般取︒︒=15~5ε。

根据高阶系统频域指标与时域指标的关系： 谐振峰值：10.83 1.2()0.07111.070.09c s s G s ss ++==++超调量：%0.160.4(1)r M σ=+-根据题目要求取%σ的极限值即%σ=40%，则求得r M =1.6.由此可求得γ=38.68.取︒=15ε,再由εγ++︒-=Φ180可以算得Φ=-126.32在该点处的相频所对应的频率c ω=6.39≥51s -满足要求。

实验7 系统校正设计：频率法滞后校正一.实验目的对于给定的控制系统，设计满足频域性能指标的校正装置，并通过仿真结果验证设计的正确性。

二.实验步骤1.在Windows界面上用鼠标双击matlab图标，即可打开MATLAB 命令平台。

2.键入命令simulink，打开结构图设计界面。

3.建立时域仿真的结构图文件“mysimu.m”。

给定结构图如图19所示。

图19 SIMULINK仿真结构图4.结构图单元参数设置。

用鼠标器双击任何一个结构图单元即激活结构图单元的参数设置窗口，完成结构图单元的参数设置。

5.仿真参数设置。

用鼠标选择主菜单的“Simulation”选项，选择“Simulation Parameter”选项，打开仿真参数设置窗口，完成仿真参数设置。

6.仿真操作。

选中“simulation”菜单项中的选项“start”即启动系统的仿真。

（或者使用工具栏上的启动按钮。

）三.实验要求1.原系统的波得图。

no=[10];do=[0.5 1 0];syso=tf(no,do);margin(syso);grid求出静态速度误差系数k v0.相位裕度γc0和开环截止频率ωc0；（可以人工计算。

）2.作原系统结构图时域仿真。

求出阶跃响应曲线，记录未校正系统的时域性能M p和t s，并记录下所选择的仿真参数；也可以由命令行执行如下。

no=[10];do=[0.5 1 0];syso=tf(no,do);sysc=feedback(syso,[1]);step(sysc)3. 设计滞后校正装置G c (s)，实现希望的开环频域性能k v>20，γc >45°，ω c>1 rad/s4. 按照滞后校正装置G c (s)的参数，修改结构图的校正单元参数，进行新的时域仿真，作出阶跃响应曲线，记录校正后系统的时域性能指标M p和t s。

四.实验报告要求1. 作出滞后校正装置G c (s)的波得图；2. 分析滞后校正装置的作用特点；3.讨论滞后校正装置对于阶跃响应过渡时间t s的影响。

系统的滞后频域校正法
系统的滞后频域校正法是一种基于频域分析的控制系统校正方法，其主要目的是消除系统的滞后响应，提高系统的稳定性和响应速度。

步骤：
1.进行频域分析，得到系统的频率响应曲线，可以使用频率响应函数或传递函数进行分析。

2.确定系统的滞后频率ωH，即始终滞后于输入信号的最高频率。

3.在滞后频率的左侧选择一个频率ωa，使得系统的相位延迟角φ(ωa)为-π/4。

4.根据滞后频率和ωa之间的差异，计算相位补偿角δ。

5.应用相位补偿器，将补偿角δ加到系统的传递函数中，以消除系统在滞后频率处的相位延迟。

6.检查校正后的频率响应曲线，确保相位延迟角在滞后频率
处为零。

注意事项：
1.在选择频率ωa时，应该尽可能选择靠近滞后频率但又远离系统的干扰频率。

2.应该检查校正后的频率响应曲线，并根据需要进行调整，以达到最佳的系统性能。

3.在进行相位补偿时，应该小心使用带通滤波器等滤波器，以避免引入不必要的相位延迟。

自动控制原理课程设计题目：基于频率法的滞后校正理论设计班级：自动化091班姓名：XXXX学号：200908436指导教师：XXXX设计时间：2019.1.2—2019.1.6连续定常系统的频率法滞后校正一、目的1.掌握用频率特性法分析自动控制系统动态特性的方法；2.研究串联滞后校正装置对系统的校正作用；3.设计给定系统的滞后校正环节，并实验验证校正环节的正确性。

二、问题描述已知单位反馈控制系统的开环传递函数为设计滞后校正装置，使校正后系统满足：三、基于频率法的滞后校正器理论设计用频率法对系统进行滞后校正的步骤为：1.由该系统的开环传递函数可知其为I 型系统，则1100-==s K K ν （3.1）2.未较正系统的伯德图如图1所示。

由该图可见，未校正系统的相位裕量0γ=︒58.1。

又因%40%σ≤，故由公式 10.160.4(1)40sin σγ︒︒︒︒=+-= （3.2） 可得校正后系统的相位裕量γ ≥38.68︒。

3.由于0γ不满足相位裕量要求，则在对数相频特性曲线上找这样一个频率点，要求在该频率处的开环频率特性的相角为式中，γ为系统所要求的相位裕量，ε是考虑到因迟后网络的引入，在剪切频率c ω处产生的相位迟后量，取ε=ο5，则由未校正系统的bode 图可得则59.8=c ω1-s ，这一频率作为校正后系统的剪切频率c ω。

图1 未校正系统的伯德图4.未校正系统在c ω处的幅值L(c ω)，于是得20lg β=L(c ω)，则β=8.85.选择滞后校正网络的转折频率2ω=1/T =c ω/5=1.718，则另一个转折频率为1ω=1/βT =0.195,则滞后校正网络的传递函数为6.校正后系统的伯德图如图2所示，此时校正后系统的开环传递函数为=)(s G )195.0)(10)(100()718.1(64.11363++++s s s s s 由公式可解得由公式（3.2）可得校正后系统的相位裕量γ ≥38.68︒,因此γ不满足相位裕量的要求。

目录摘要 (1)引言 (2)1 滞后-超前校正设计目的和原理 (2)1.1滞后-超前校正设计目的 (2)1.2滞后-超前校正设计原理 (2)2 滞后-超前校正的设计过程 (4)2.1校正前系统的参数 (4)2.1.1 用MATLAB绘制校正前系统的伯德图 (4)2.1.2 用MATLAB求校正前系统的幅值裕量和相位裕量 (5)2.1.3 用MATLAB绘制校正前系统的根轨迹 (6)2.1.4 对校正前系统进行仿真分析 (7)2.2滞后-超前校正设计参数计算 (8)ω (8)2.2.1 选择校正后的截止频率c2.2.2确定校正参数β、2T和1T (8)2.3滞后-超前校正后的验证 (9)2.3.1 用MATLAB求校正后系统的幅值裕量和相位裕量 (9)2.3.2 用MATLAB绘制校正后系统的伯德图 (10)2.3.3 用MATLAB绘制校正后系统的根轨迹 (11)2.3.4 用MATLAB对校正前后的系统进行仿真分析 (12)结束语 (14)参考文献 (15)用MATLAB进行控制系统的滞后－超前校正设计摘要自动控制技术的应用日益广泛，除了在国防、空间科技等尖端领域里成为不可或缺的重要技术之外，在机电工程、冶金、化工、轻工、交通管理、环境保护、农业等领域中，自动控制技术的作用也日显突出。

自动控制技术的运用大大提高了劳动生产率和产品质量，同时，也改善了劳动条件，在改善人类的居住环境和提高生活质量方面也发挥了非常重要的作用。

今天的社会生活中，自动化装置已经无所不在，为人类文明进步做出了重要的贡献。

自动控制系统的课程设计是检验我们学过知识扎实程度的好机会，也让我们的知识体系更加系统，更加完善。

在不断学习新知识的基础上得到了动手能力的训练，启发创新思维及独立解决实际问题的能力，提高设计、装配、调试能力。

关键词：滞后超前校正伯德图 MATLAB 校正参数引言如果系统设计要求满足的性能指标属频域特征量，则通过采用频域校正方法。

频域法滞后超前校正任务书介绍频域法滞后超前校正是一种常用于信号处理和控制系统中的技术。

通过对信号在频域上的分析，可以对信号进行滞后或超前校正，以达到信号调节和优化的目的。

本文将详细介绍频域法滞后超前校正的原理、方法和应用。

原理频域法滞后超前校正的原理是基于信号在频域上的特征。

信号可以通过傅里叶变换将其表示为频域上的幅度和相位信息。

在信号处理和控制系统中，我们常常需要调节信号的相位和幅度来实现系统的稳定性和性能优化。

方法频域法滞后超前校正有多种方法，下面将介绍其中几种常用的方法：1. 增益校正法增益校正法是一种通过调整幅度来校正信号的方法。

通过频域分析，可以确定信号在不同频率上的增益特性。

对于需要增加信号幅度的情况，可以通过增加系统的增益来实现。

而对于需要降低信号幅度的情况，则可以通过减小系统的增益来实现。

增益校正法在控制系统中经常被使用，例如PID控制器中的增益调节。

2. 相位校正法相位校正法是一种通过调整相位来校正信号的方法。

信号的相位与信号在频域上的延迟有关。

在频域分析中，可以确定信号在不同频率上的相位特性。

通过改变信号的相位，可以实现信号的滞后或超前校正。

相位校正法在信号处理和通信系统中广泛应用，例如音频处理中的相移校正。

3. 混合校正法混合校正法是一种将增益和相位校正相结合的方法。

通过频域分析，可以确定信号在不同频率上的增益和相位特性。

根据信号调节的需求，可以在不同频率范围内采用不同的校正方法。

混合校正法在实际应用中常常被使用，例如音频系统中的均衡器。

应用频域法滞后超前校正广泛应用于信号处理和控制系统中，下面将介绍几个常见的应用场景：1. 音频系统校正在音频系统中，频域法滞后超前校正常常被用于音频信号的均衡和优化。

通过对音频信号在频域上的分析，并根据音频系统的特性和需求，可以对信号的幅度和相位进行调节，以实现声音的更好的效果和逼真性。

2. 控制系统优化在控制系统中，频域法滞后超前校正可以用于调节控制器的增益和相位，以提高系统的稳定性和响应速度。