2008年江苏省无锡市中考数学试卷及答案及答案

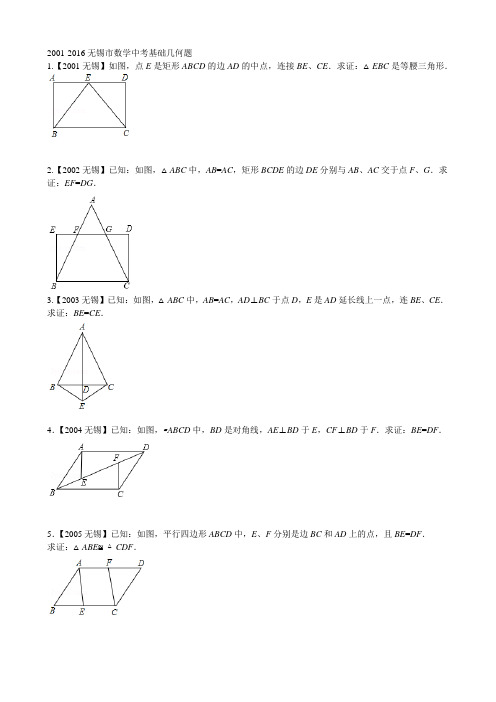
2001-2016无锡市数学中考基础几何题1.【2001无锡】如图，点E是矩形ABCD的边AD的中点，连接BE、CE．求证：△EBC是等腰三角形．2.【2002无锡】已知：如图，△ABC中，AB=AC，矩形BCDE的边DE分别与AB、AC交于点F、G．求证：EF=DG．3.【2003无锡】已知：如图，△ABC中，AB=AC，AD⊥BC于点D，E是AD延长线上一点，连BE、CE．求证：BE=CE．4．【2004无锡】已知：如图，▱ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F．求证：BE=DF．5．【2005无锡】已知：如图，平行四边形ABCD中，E、F分别是边BC和AD上的点，且BE=DF．求证：△ABE≌△CDF．6．【2006无锡】已知：如图，平行四边形ABCD中，∠BCD的平分线交AB于E，交DA的延长线于F．求证：AE=AF．7．【2007无锡】如图，已知四边形ABCD是菱形，点E，F分别是边CD，AD的中点．求证：AE=CF．8．【2007无锡】如图，AB是⊙O的直径，P A切⊙O于A，OP交⊙O于C，连BC．若∠P=30°，求∠B的度数．9．【2008无锡】如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．10．【2008无锡】如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．（1）求证：四边形AECD是菱形；（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．11．【2009无锡】如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC上，且四边形AEFD是平行四边形．（1）AD与BC有何等量关系，请说明理由；（2）当AB=DC时，求证：平行四边形AEFD是矩形．12．【2010无锡】在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km 处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．（1）求该轮船航行的速度（保留精确结果）；（2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．13．【2011无锡】如图，在▱ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．求证：BE=DF．14．【2012无锡】如图，在▱ABCD中，点E在边BC上，点F在BC的延长线上，且BE=CF．求证：∠BAE=∠CDF．15．【2013无锡】如图，在Rt△ABC中，∠C=90°，AB=10，sin∠A=，求BC的长和tan∠B的值．16．【2014无锡】如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．17．【2014无锡】如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．（1）若∠B=70°，求∠CAD的度数；（2）若AB=4，AC=3，求DE的长．18．【2015无锡】已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：（1）∠AEC=∠BED；（2）AC=BD．19．【2015无锡】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．（1）求BD的长；（2）求图中阴影部分的面积．20．【2016无锡】已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．【解答】解：∵P A切⊙O于A，AB是⊙O的直径，∴∠P AO=90°，∵∠P=30°，∴∠AOP=60°，∴∠B=∠AOP=30°．1.【解答】证明：∵ABCD是矩形，∴∠A=∠D=90°，AB=CD．∵E是AD中点，∴AE=DE．∴△ABE≌△DCE．∴BE=CE．∴△BEC是等腰三角形．2.【解答】证明：∵四边形EBCD为矩形，∴∠E=∠EBC=∠BCD=∠D=90°，EB=DC．又∵AB=AC，∴∠ABC=∠ACB．∴∠FBE=∠GCD．∴△EFB≌△DGC．∴EF=DG．3.【解答】证明：证法1：∵AB=AC，AD⊥BC，∴BD=DC．（2分）∴AD为BC的中垂线．（4分）∴BE=EC．（6分）证法2：∵AB=AC，AD⊥BC，∴∠BAE=∠CAE．（2分）在△ABE与△ACE中，，∴△ABE≌△ACE（SAS）．（4分）∴BE=CE．（6分）4.【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD．∵AB∥CD，∴∠ABE=∠CDF．又∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°．∴△ABE≌△CDF．∴BE=DF．5.【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD，∠B=∠D（2分）在△ABE和△CDF中，∴△ABE≌△CDF．6.【解答】证明：在平行四边形ABCD中，∵AB∥DC，AD∥BC，∴∠AEF=∠DCE，∠F=∠BCE．∵CE平分∠DCB，∴∠DCE=∠BCE，∴∠F=∠AEF，∴AE=AF．7.【解答】证明：∵ABCD是菱形，∴AD=CD，∵E，F分别是CD，AD的中点，∴DE=CD，DF=AD，∴DE=DF，又∵∠ADE=∠CDF，∴△AED≌△CFD（SAS），∴AE=CF．8.【解答】解：∵P A切⊙O于A，AB是⊙O的直径，∴∠P AO=90°，∵∠P=30°，∴∠B=∠AOP=30°．9.【解答】证明：∵矩形ABCD中，AB∥CD，（2分）∴∠BAF=∠AED．（4分）∵BF⊥AE，∴∠AFB=90°．∴∠AFB=∠D=90°．（5分）∴△ABF∽△EAD．（6分）10.【解答】（1）证明：∵AB∥CD，即AE∥CD，又∵CE∥AD，∴四边形AECD是平行四边形．∵AC平分∠BAD，∴∠CAE=∠CAD，又∵AD∥CE，∴∠ACE=∠CAD，∴∠ACE=∠CAE，∴AE=CE，∴四边形AECD是菱形；（2）解：△ABC是直角三角形．证法一：∵E是AB中点，∴AE=BE．又∵AE=CE，∴BE=CE，∴∠B=∠BCE，∵∠B+∠BCA+∠BAC=180°，∴2∠BCE+2∠ACE=180°，∴∠BCE+∠ACE=90°．即∠ACB=90°，∴△ABC是直角三角形．证法二：连DE，由四边形AECD是菱形，得到DE⊥AC，且平分AC，设DE交AC于F，∵E是AB的中点，且F为AC中点，∴EF∥BC．∠AFE=90°，∴∠ACB=∠AFE=90°，∴BC⊥AC，∴△ABC是直角三角形．11.【解答】（1）解：AD=BC．理由如下：∴四边形ABED和四边形AFCD都是平行四边形．∴AD=BE，AD=FC，又∵四边形AEFD是平行四边形，∴AD=EF．∴AD=BE=EF=FC．∴AD=BC．（2）证明：∵四边形ABED和四边形AFCD都是平行四边形，∴DE=AB，AF=DC．∵AB=DC，∴DE=AF．又∵四边形AEFD是平行四边形，∴平行四边形AEFD是矩形．12.【解答】解：（1）∵∠1=30°，∠2=60°，∴△ABC为直角三角形．∵AB=40km，AC=km，∴BC===16（km）．∵1小时20分钟=80分钟，1小时=60分钟，∴×60=12（千米/小时）．（2）能．理由：作线段BR⊥AN于R，作线段CS⊥AN于S，延长BC交l于T．∵∠2=60°，∴∠4=90°﹣60°=30°．∵AC=8（km），∴CS=8sin30°=4（km）．∴AS=8cos30°=8×=12（km）．又∵∠1=30°，∴∠3=90°﹣30°=60°．∵AB=40km，∴BR=40•sin60°=20（km）．∴AR=40×cos60°=40×=20（km）．易得，△STC∽△RTB，所以=，，解得：ST=8（km）．所以AT=12+8=20（km）．∵19.5＜AT＜20.5故轮船能够正好行至码头MN靠岸．13.【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD，∠ABE=∠CDF，又已知∠BAE=∠DCF，∴△ABE≌△DCF，∴BE=DF．14.【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠B=∠DCF，在△ABE和△DCF中，，∴△ABE≌△DCF（SAS），∴∠BAE=∠CDF．15.【解答】解：在Rt△ABC中，∠C=90°，AB=10，sinA===，∴BC=4，根据勾股定理得：AC==2，则tanB===．16.【解答】证明：△ABC中，∵AB=AC，∴∠DBM=∠ECM，∵M是BC的中点，∴BM=CM，在△BDM和△CEM中，，∴△BDM≌△CEM（SAS），∴MD=ME．∴∠ACB=90°，又∵OD∥BC，∴∠AEO=90°，即OE⊥AC，∠CAB=90°﹣∠B=90°﹣70°=20°，∠AOD=∠B=70°．∵OA=OD，∴∠DAO=∠ADO===55°∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°；（2）在直角△ABC中，BC===．∵OE⊥AC，∴AE=EC，又∵OA=OB，∴OE=BC=．又∵OD=AB=2，∴DE=OD﹣OE=2﹣．18. ∴∠AEC=∠ECD，∠BED=∠EDC，∵CE=DE，∴∠ECD=∠EDC，∴∠AEC=∠BED；（2）∵E是AB的中点，∴AE=BE，在△AEC和△BED中，，∴△AEC≌△BED（SAS），∴AC=BD．19.【解答】解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∵BC=6cm，AC=8cm，∴AB=10cm．∴OB=5cm．连OD，∵OD=OB，∴∠ODB=∠ABD=45°．∴∠BOD=90°．∴BD==5cm．（2）S阴影=S扇形﹣S△OBD=π•52﹣×5×5=cm2．20.【解答】证明：∵四边形ABCD是正方形，∴AD=CD，∠DAB=∠C=90°，∴∠FAD=180°﹣∠DAB=90°．在△DCE和△DAF中，，∴△DCE≌△DAF（SAS），∴DE=DF．。

江苏省无锡市中考数学试卷一．选择题（共10小题）1．（无锡）﹣2的相反数是（）A． 2 B．﹣2 C．D．考点：相反数。

专题：探究型。

分析：根据相反数的定义进行解答即可．解答：解：由相反数的定义可知，﹣2的相反数是﹣（﹣2）=2．故选A．点评：本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．2．（无锡）sin45°的值等于（）A．B．C．D． 1考点：特殊角的三角函数值。

分析：根据特殊角度的三角函数值解答即可．解答：解：sin45°=．故选B．点评：此题比较简单，只要熟记特殊角度的三角函数值即可．3．（无锡）分解因式（x﹣1）2﹣2（x﹣1）+1的结果是（）A．（x﹣1）（x﹣2）B． x2C．（x+1）2D．（x﹣2）2考点：因式分解-运用公式法。

分析：首先把x﹣1看做一个整体，观察发现符合完全平方公式，直接利用完全平方公式进行分解即可．解答：解：（x﹣1）2﹣2（x﹣1）+1=（x﹣1﹣1）2=（x﹣2）2．故选：D．点评：此题主要考查了因式分解﹣运用公式法，关键是熟练掌握完全平方公式：a2±2ab+b2=（a±b）2．4．（无锡）若双曲线y=与直线y=2x+1的一个交点的横坐标为﹣1，则k的值为（）A．﹣1 B． 1 C．﹣2 D． 2考点：反比例函数与一次函数的交点问题。

专题：计算题。

分析：将x=1代入直线y=2x+1，求出该点纵坐标，从而得到此交点的坐标，将该交点坐标代入y=即可求出k的值．解答：解：将x=﹣1代入直线y=2x+1得，y=﹣2+1=﹣1，则交点坐标为（﹣1，﹣1），将（﹣1，﹣1）代入y=得，k=﹣1×（﹣1）=1，故选B．点评：本题考查了反比例函数与一次函数的交点问题，知道交点坐标符合两函数解析式是解题的关键．5．（无锡）下列调查中，须用普查的是（）A．了解某市学生的视力情况B．了解某市中学生课外阅读的情况C．了解某市百岁以上老人的健康情况D．了解某市老年人参加晨练的情况考点：全面调查与抽样调查。

2008年江苏省常州市中考数学试卷注意事项：1.全卷共8页，28题，满分120分，考试时间120分钟.2.用蓝色或黑色钢笔、圆珠笔直接答在试卷上.3.答卷前将密封线内的项目填写清楚,并将座位号填写在试卷规定的位置上.4.考生在答题过程中,不得使用任何型号的计算器,若试题计算结果没有要求取近似值,则计算结果取精确值(保留根号和π).1. -3的相反数是_______,-12的绝对值是________,2-1=______. 2. 点A(-2,1)关于y 轴对称的点的坐标为___________,关于原点对称的点的坐标为________. 3. 如图,在△ABC 中BE 平分∠ABC,DE ∥BC,∠ABE=35°,则∠DEB=______°,∠ADE=_______°. 4. 已知一组数据为5,6,8,6,8,8,8,则这组数据的众数是_________,平均数是_________.5. 已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm 2,扇形的圆心角为______°. 6. 过反比例函数(0)ky k x=>的图象上的一点分别作x 、y 轴的垂线段,如果垂线段与x 、y 轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.7. 已知函数22y x x c =-++的部分图象如图所示,则c=______,当x______时,y 随x 的增大而减小.8. 若将棱长为2的正方体切成8个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为3的正方体切成27个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为n(n>1,且为整数)的正方体切成n 3个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍. 9. 下列实数中,无理数是【 】B.2πC.13D.1210.,则x 的取值范围是【 】一.填空题(本大题每个空格1分,共18分,把答案填在题中横线上)二.选择题(在每小题给出的四个选项中,只有一项最符合题目要求,把符合要求的选项的代号填在题后的【 】内,每小题2分,共18分)_4>-5 <-5 ≠-5 ≥-511.若反比例函数1kyx-=的图象在其每个象限内,y随x的增大而减小,则k的值可以是【】B.312.在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的【】A.方差B.平均数C.频率分布D.众数13.顺次连接菱形各边中点所得的四边形一定是【】A.等腰梯形B.正方形C.平行四边形D.矩形14.如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是【】A. B. C. D.15.如图,在△ABC中,若DE∥BC,ADDB=12,DE=4cm,则BC的长为【】A.8cmB.12cmC.11cmD.10cm16.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为【】A. B. D. 4（第15题）（第16题）（第17题）17.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法: 【】(1)他们都骑行了20km;(2)乙在途中停留了;(3)甲、乙两人同时到达目的地;(4)相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有个个个个18.(本小题满分10分)化简:12⎛⎫⎪⎝⎭(2)211111a aa a+---+g19.(本小题满分8分)解方程(组)(1)245x yx y+=⎧⎨-=⎩(2)2133xx x-=--20.(本小题满分6分)为了解九年级女生的身高(单位:cm)情况,某中学对部分九年级女生身高进行了一次测量 , 所得数据整理后列出了频数分布表,并画了部分频数分布直方图(图、表如下):（第20题）根据以上图表,回答下列问题:(1)M=_______,m=_______,N=_______,n=__________;(2)补全频数分布直方图.21.（本小题满分6分）小敏和小李都想去看我市举行的乒乓球比赛,但俩人只有一张门票.小敏建议通过摸球来决定谁去欣赏,他的方法是:把1个白球和2个红球放在一只不透明的袋子中(这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录下颜色后三.解答题(本大题共2小题,共18分,解答时应写出演算步骤)四.解答题(本大题共2小题,共12分,解答时应写出文字说明或演算步骤)放袋中并搅匀,再从中任意摸出1个球.如果两次都摸出相同颜色的球,则小敏自己去看比赛,否则小李去看比赛.问小敏的这个方法对双方公平吗?请说明理由. 22. (本小题满分7分)已知:如图,AB=AD,AC=AE,∠BAD=∠CAE. 求证:AC=DE.23. 已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED. 求证:AE 平分∠BAD.24. (本小题满分6分)五.解答题(本大题共2小题,共14分,解答时应写出证明过程)五.画图与探究(本大题共2小题,共14分)已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD 的顶点都在格点上.(1) 在所给网格中按下列要求画图:① 在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD 各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);② 将四边形ABCD 沿坐标横轴翻折180°,得到四边形A ’B ’C ’D ’,再将四边形A ’B ’C ’D ’绕原点O 旋转180°,得到四边形A ”B ”C ”D ”; (2)写出C ”、D ”的坐标;(3)请判断四边形A ”B ”C ”D ”与四边形ABCD 成何种对称?若成中心对称,请写出对称中心;若成轴对称,请写出对称轴.(第24题)25. 如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图．．．,并写出它们的周长.26. (本小题满分8分)如图,港口B 位于港口O 正西方向120海里外,小岛C 位于港口O 北偏西60°的方向.一艘科学考察船从港口O 出发,沿北偏东30°的OA 方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B 出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C 用1小时装补给物资后,立即按原来的速度给考察船送去.(1) 快艇从港口B 到小岛C 需要多少时间?(2) 快艇从小岛C五.解答题(本大题共3小题,共26分,解答时应写出文字说明、证明过程或演算步骤)27. (本小题满分7分)2008年5月12日四川汶川地区发生级特大地震.举国上下通过各种方式表达爱心.某企业决定用p 万元援助灾区n 所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n 所学校的捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a 都是正整数)根据以上信息，解答下列问题： (1)写出p 与n 的关系式；(2)当p=125时，该企业能援助多少所学校？(3)根据震区灾情，该企业计划再次提供不超过20a 万元的捐款,按照原来的分配方案援助其它学校.若a 由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?28. 如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点. (1) 求点A 的坐标;(2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.。

x x=12时止，全国共接受国内外社会各界捐赠的抗万元，这个数据用科学记数法可表示为．80，则∠（第10题）60，则∠（第12题）A．B．C．D．80到OCD△45，则∠55Ｂ．45Ｃ．40Ｄ．35．下列事件中的必然事件是（）60(1+-4(2)x+，其中（第16题）（第18题）3，4，5，6的正方体骰子掷一，小晶赢；点数之和等于7．小红赢；问他们两人谁获胜的概率大？请你用“画树状图”或40．40”，那么图151260；以P半径作圆．设点A运动了t秒，求：（1）点C的坐标（用含t的代数式表示）；（2）当点A在运动过程中，所有使P与菱形OABC的边所在直线相切的t的值．28．（本小题满分8分）一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）图1 图2 图3 图421(2)2)2x += (1)(54)-=．解法一：矩形90， ···················BF AE ⊥90，∴∠ABF ∴△∽△··············解法二：矩形90． ······90，90EAD ∠，∴∠）AB CD ∥，又CE AD ∥·········································AC 平分BAD ∠，， ················又AD CE ∥，∴∠ACE ∴∠=∠∴四边形AECD （2）证法一：E 是AB 又AE CE =，BE ∴=180B BCA BAC ∠+∠+∠， ······∴∠．180，9090，∴△DE，则E是AB∴⊥BC AC22．解：列表如下：P（和为评分说明：得1分．23．解：（1又0m≤≤400间板房可安置灾民m=当300PE x ∥轴，设E 点坐标为点EF x ⊥轴，E PE x ∴=33317)(3)2222P P Px x EF x --⎛⎫=++= ⎪⎝⎭， ···········2=-，12P x =，当0y =时，3x =-， 1OA =+1602OD OC +∴==3(160=）①当P 与OC 相切时（如图cos30OP ，3132∴，4分）②当P与OA，即与⊥作PE OC33=cos302③当P与AB所在直线相切时（如图⊥，∴PF OC3(130+93t=-∴=93t130215=2个这种装置可以达到预设的要求．3分）（图案设计不唯一）的O去覆盖边长为设O经过A，，O与ADAE=，这说明用两个直径都为31的圆不能完，则31全覆盖正方形ABCD。

某某省某某市北塘区2008届中考数学模拟试卷（二）1、本试卷满分130分，考试时间为120分钟.2、卷中除要求近似计算的结果取近似值外，其余各题均应给出精确结果.一、细心填一填（本大题共有13小题，18空，每空2分，共36分．请把结果直接填1、23-的倒数是_________；25的平方根是_________． 2、分解因式：=-x x 43_________．3、为了保证某某居民能喝上健康安全的自来水，某某市将“长江引水”工程作为市政府2366000000元，这个数据用科学记数法表示为_________元．4、函数1+=x xy 中，自变量x 的取值X 围是_________； 函数12-=x y 中，自变量x 的取值X 围是_________．5、正十边形的一个外角为_________°．6、已知近视眼镜的度数y 与镜片焦距x 成反比例，若250度的近视眼镜片的焦距为，则与x 之间的函数关系是_________．7、某商品在“五一”节期间进行促销活动，该商品进价为500元，标价750元．若要打5%，则最低可打_________折．8、如图，已知AB ∥CD ，直线EF 分别交AB 、CD 于点E 、F ，EG 平分∠BEF ．若∠1=50°，9、如图，AB 是⊙O 的直径，若AC =4，∠DAB =_________．10则中位数在哪个分数段内_________；若在该班中随机抽取1人，恰好获得35分的学_________．11、已知圆锥母线长为5cm ，侧面积是210cm π，则底面圆的半径为_________cm ． 12、一个等腰梯形的高恰好等于这个梯形中位线，_________． 13、如图，一个动点在第一象限内及x 轴、y 轴上运动， 在第一分钟，它从原点运动到（1，0），第二分钟， A B C D EF G 12第8题图 第9题图从（1，0）运动到（1，1），而后它接着按图中箭头 所示在与x 轴,y 轴平行的方向来回运动，且每分钟运 动1个单位长度．当动点所在位置分别是（5，5）时， 所经过的时间是_______，在第1002分钟后，这个动 点所在的位置的坐标是_________．二、精心选一选（本大题共7小题，每小题3分，共21分. 在每小题所给出的四个选项中，只有一项是正确的.把所选项前的字母代号填在题后的括号内. 只要你掌握概念，认真思考，相信你一定会选对！）14、已知点P 的坐标为（-1，2），则点P 关于x 轴的对称点 Q 的坐标为 （ ）A ．（2，-1）B ．（-1，-2）C ．（1，2）D ．（1，-2）15、下列运算正确的是 （ ）A ．1535a a a =⋅ B ．235a a a =- C ．()1025a a =- D ．236a a a =÷16、在下列四个图形中，哪一个不是．．中心对称图形 ( )17、下列各图中，每个正方形网格都是由四个边长为1的小正方形组成的，其中阴影部分面25的是（ ）18、下列事件比较容易用普查方法调查的是 （ ） A ．了解某某市民的年人均收入 B ．了解某校初三学生数学模拟考试成绩 C ．了解某某市中小学生的近视率 D ．了解“五一”黄金周来锡的流动人口 19、如图所示是正六棱柱的三视图，则它的表面积．．．为 （ ） A ．60 B ．36 C ．60312+A ． C ． A ．B ．C ．D ． 5cm场____________某某号…不…………要…………答…………题…………………………D ．6036+20、直角梯形ABCD 中（如图1），动点P 从B 点出发，由B →C →D →A 沿边运动，设点P 运动的路程为x ，△ABP 的面积为y .如果关于x 函数y 的图象如图2，则△ABC 的面积为 （ ）A ．10B ．16C ．18D ．32三、认真答一答（本大题共7小题，满分53分. 解答需写出必要的文字说明、演算步骤或证明过程. 只要你积极思考, 细心运算, 你一定会解答正确的!）21、(本小题满分8分)（1）计算：()11560tan 2-+︒--（2）解分式方程： 2223--=-x xx图1 图222、(本小题满分6分)已知：如图，点O 为平行四边形ABCD 的对角线BD 的中点，直线EF 经过点O ，分别交BA 、DC 的延长线于点E 、F ．求证：AE =CF ．23、(本小题满分6分)甲、乙两人利用分别标有数字1，2，3的三X 卡片玩游戏．游戏规则：先将三X 卡片洗匀后，背面朝上放在桌面上．随机地抽取一X 卡片，该卡片上的数字作为十位上的数字；放回后再抽取一X 卡片，该卡片上的数字作为个位上的数字，如果组成的两位数是“奇数”，则甲赢，如果组成的两位数是“偶数”，则乙赢．你认为这个游戏公平吗？试利用树状图分析．如果不公平，请你设计一个公平的游戏规则．24、(本小题满分6分)某中学团委会为研究该校学生的课余活动情况，采取抽样调查的方法，从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制了如下的两幅不完整的统计图（如图所示），请你根据图中提供的信息解答下列问题：（1）在这次研究中，一共调查了________名学生； （2）“其它”在扇形图中所占的圆心角是________度； （3）补全频数分布直方图．A B C EFO 50人数25、(本小题满分9分)如图1，△ABC 是直角三角形，将△ABC 补成矩形，使△ABC 的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．那么符合条件的矩形可以画2个（即矩形ABCD 和矩形AEFB ）（1）设图1中矩形ABCD 和矩形AEFB 的面积为1S 和2S ，则1S ________2S ；（2）如图2，△ABC 为锐角三角形（AB AC BC >>），按文中要求把它补成矩形． ①请画出尽可能多符合条件的矩形；②这些矩形面积是否相等？如果不相等，哪个矩形的面积最大？A B C 图1ABC EF ② 图2 阅读运动娱乐其它20%40%ABC A B CA B C A B C （备用图）① A B C D③这些矩形周长是否相等？如果不相等，哪个矩形的周长最大？26、(本小题满分10分)如图，抛物线c bx x y ++-=2与x 轴分别交于A （1，0）、B （3，（1）求这条抛物线解析式；（2）设点P 在该抛物线上滑动，若使△PAB 面积为1，这样的点P 有几个？并求所有满足P 点的坐标；（3）设抛物线交y 轴于点C ，在该抛物线对称轴上一是否存在点M ，使得△MAC 的周长最M 的坐标；若不存在，请说明理由．27、(本小题满分8分)长江边上的A 港距B 港约300千米（A 港在上游，B 港在下游），满载物资的货船从B 港出发在A 港卸货后，再空载返回B 港．它离开B 港的路程随时间的变化关系如图所示．若货船满载时，速度比空载时在静水中的速度少5千米/小时．（1）求长江水流速度及货船空载时在静水中的速度；0 20 30 40 300 s (千米)t (小时)（2）此船在距离A港90千米的时候，接到警报，将有强对流天气影响航道安全，预报再过4小时此段航道将有暴风雨，为了安全，货船必须在4小时之内进入A港避风．现决定从A 港派出一艘大马力动力拖轮，从A港出发，顺流而下，遇到货船后，将其快速拖到A港．动力拖轮拖着货船在静水中的速度，是它们分别在静水中速度的平均值．动力拖轮在静水中速度是40千米/小时．问：能否在规定时间内将货船拖到A港？请说明理由．四、实践与探索（本大题共有2小题，满分20分. 只要你开动脑筋，大胆实践，勇于探28、(本小题满分10分)如(图1)，在直角梯形ABCD中，∠D＝∠C＝90°，AB＝4，BC＝6，AD＝8. 点P、Q同时从A点出发，分别作匀速直线运动，其中点P沿AB、BC向终点C运动，速度为每秒2个单位，点Q沿AD向终点D运动，速度为每秒1个单位．当这两点中有一个点到达自己的终点时，另一个点也停止运动，设这两点从出发开始运动了t秒．(1)动点P与Q哪一个先到达自己的终点？此时t为何值？(2)如（图2），当0＜t＜2时，求证：以PQ为直径的圆与AD相切．(3)以PQ为直径的圆能否与CD相切？若有可能，求出t的值或t的取值X围；若不可能，请说明理由．（图1）（图2）ABCD（备用图）29．(本小题满分10分)把两个全等的直角三角板ABC 和EFG 叠放在一起，使三角板EFG 的直角顶点G 与三角板ABC 的斜边中点O 重合，其中∠B ＝∠F ＝30°，斜边AB 和EF 长均为4．(1)当 EG ⊥AC 于点K ，GF ⊥BC 于点H 时（如图①），求GH :GK 的值； (2)现将三角板EFG 由图①所示的位置绕O 点沿逆时针方向旋转，旋转角α满足条件：0°＜α<30°（如图②），EG 交AC 于点K ，GF 交BC 于点H ，GH :GK 的值是否改变？证明你发现的结论；(3)在（2）的情况下，连接HK ，在上述旋转过程中，设GH =x ，△GKH 的面积为y ，求y 与x 之间的函数关系式，并写出自变量x 的取值X 围；(4)三角板EFG 由图①所示的位置绕O 点逆时针旋转一周，是否存在某位置使△BFG 是等腰三角形，若存在，请直接写出相应的旋转角α(精确到0.1°)；若不存在，说明理由．E E (备用图)(图①) (图②) A［参考答案］一、细心填一填（每空2分，共36分）1、32-；5± 2、()()22-+x x x 3、910366.2⨯ 4、1-≠x ；21≥x 5、36 6、x y 100= 7、7 8、65 9、60；8 10、32-34分；9411、2 12、外切 13、30分钟；（21，31）二、精心选一选（每小题3分，共21分）14、B 15、C 16、C 17、D 18、B 19、C 20、B 三、认真答一答 21、（1）()11560tan 2-+︒--1321+-=————————3’ 323-=————————4’ （2）2223--=-x xx ()x x --=223————————1’ x x --=423————————2’7=x ————————3’经检验： 7=x 是原方程的解————————4’ 22、证明：是平行四边形ABCDCD AB CD AB =∴，//————————1’ CDO ABO ∠=∠∴————————2’ 在BOC ∆和DOF ∆中 ⎪⎩⎪⎨⎧∠=∠=∠=∠DOF BOE DOBO CDO ABO DOF BOE ∆≅∆∴————————4’ DF BE =∴————————5’ CF AE =∴————————6’23、不公平。

数学试题節1页（其8页）总 分誉分人検分人2008年无锡市:级鑫学爲;考试数学试题三四19202122 232425262728得分呑分人核分人注虑事项J ・本试参擋分】JU 分•考试时徇为120分算. 2.卷中1*3［求近似计算的结果取近似值外•其僉各理均应给出轉*结果.得分界卷人复核人一4心填一孙：本大题共有12小ft.15空•蒔空2分. 共30分•谄把结聚直接填生题中的炭拔上.>_______ ・ 2•分解因式上?_场. _____________________ •3•设一元二7rr3・O 的两个整诫分别为彳和事一_ 5 •卫■ __ 4 •截至S/1 30日12时止•全国共接蚩1M 内外林会鋅界钳甜的抗翼救灾款物合“约3 990 000 力元•这个tt»W 科学记数浓町表泾为 ________________ 万元. 5•硕散，■斗中fl«» r 的取的范隔是I沟数y*虫丹中白变址乂的取值范圈堆 ______________ .6・若反tt 例函敷y =令的图象蛭过点—2）•机 的他为 ___________ ・ 7.射击色动员一次射击练习的成绩尺（单位，环•这m 员这次射击戍绝的半均数是 ________ 环. 8. 五边形的內角和为 _________ 二9. 如图・（加一（兀・/〃一 JW ••则/ A （.>L> ■ _ ： 10. 如屬・CDI AU TE •若ZH-OO •■则Z 八- _________ \ 11. 已如平贡上四点 A （0,0>.«（10.0）.C （10.S>.D<0.6）.i!£^ 丿=心一3 材 42 均四边形ABCD 分攻血积相绞的州刨分・则期的值为 _____ .】2•巳施，如图.边任为Q 的iI-AABC 内冇 边长为d 的内丧正ADEF •训 . •（■ 2趣）A（® I2S ）傅分评泄人震権人13.计算亏活的结果为二■科心迭一迭（本大腿共有6小越•毎小& 3分•共18分•在毎小题洽岀的四个违项中•只有一项蹩止的的. 请把正确述从前的字□代的括号内」A.bB.aC ・114•不等式一 ^x>l 的解集是A.z>—*B. x>—2C. x< —2D. x<—y15 •下面何个图案中•是轴对廉图形但不是錠转对称图形的是16.如图•△OAB 绕点O 迄时tt 放转80°到△OCD 的位5£ •已知ZAOB=45SP1ZAOD 尊于 .............................. ()A. 55*R45°0 4()6D ・35・17•下列耶件中的必然寧件是 ............................... (> A. 2008年夾运会在北京学行B. —打开HA 视机就看到奥运圣火传逆的腐IKC. 2凶8勺奥运会开粵弍当天，北京的天气時朗D. 全世界均在门天看到北京奥运会开幕式的实况宜鳴18.如图•枳F.G 、H 分别为正方形A BCD 的边AB .BC.CD.DA 上的点•且AE= BF=a ；^ DHAH. W1 Hfl 中阴的部分的曲枳与止方J&ABCD 的面枳之比为 ................................... ()A? B — C 丄D ~入 59 2 5三、认真答一答I A 人题共自8小题，共64分.解答需写出必妥的文字说明，演算步異或证明过 程・)得分评卷人复枝人19•解答F 列各逆(本題有3小&•第⑴、⑵小题毎题5 分・策0〉小题3分.共13分・〉⑴计花 J12 +【一3|-2um«r +（_i+谑）.(2、先化简•再求似瓷兰F G 亠2)・口中 %(3)如民绘曲6个相口的正方形拼成的图形•谄你称貝中•个王方形 移妙到合适的位置•使它与另5个正方形储拼成一个正方体的表 血憑JI 图.(讷在图中将耍移动的那个it 方形涂黑•并曲出仔动后 tfiiF.h 形)A. B. C.DD《弟16題)数学试题第3页（共8刀〉22.（本小题肉分G 分〉小晶和小红玩怫骰子游戏•毎人将一个各而分別标 冇1.2.3.4.5.6的正方体诫子梅一次•把两人濟殍的点 数相加•并为定’点数之和等于6•小品fib 虚数之和等丁 7■小红廉；点数Z FflSfK 它故•两人不分胜负•何他们啟人谁获牲的槪净大？甘你用甜状闱••哎••列表'•的方法加以分忻说叨・20•（車小趣拂分6分》如图•巳知K 足笼形ABCD 的边CD 上一成・BF 丄AF 干F.试说明:&・42廿3少沁）・得分评堂人复核人21•（本小题淸分7分〉如庵・lffl 边形A BCD 中■力R 〃「“・A 「平分N HAD.（2） 若点EJSAB 的中点▼试判斷AABC 的形状，并说明理由.分评卷人复核人（1） 求证：四边形人ECD 是菱形・23•〈本小题清分6分〉小明所4学校初二学生漳合素质评定分A.IXCJ〉四个等第•为广了解评定情况•小耳随机训査了初三30〈】〉请在F面给出縫囹中JH1出这30名学生综合索质评定導第的頻数条形统汁图，并计算其中等第达到良好以上（含良好〉的頻率.（2）已知初三学生学号足从3001开始•按由小列大顺序排列的连績整敷•请你计算这30 名学生孚号的中位数•并运用中位数的知识来估计这次初三学生评定等第达到良好以上（含良好）的人敕.24.（4；小题满分8分）已知一个三角老的两条边长分别是lcm和2cm,- 个内角为40°.助圈1価出一个浏足題设条件的三角形$（2）你趁否还能倚岀既滿足题设条件■又与（1）中所抽的三角形不全等的三角形？若能■请你柱图1的右边用.尺规作图'作岀所冇这样的三角形■若不施•请说圈刖由.⑶如果将题设条件改为•三角妙的两条边K分别是3cm和4g —个内角为40"•那么满足这一条件•且彼此不全等的三角殄共有_______________________ 个.友情提用L请在你s«ffi中标出已知倉的龙敏和已知边巧长应•必尺规作刃■不委求药作決，但要保您作图浪迹・分评它人复俵人学号30033008301230163024302K301230483068307S 箒第A C B C D B A B B A 学号3079SOS83091S1043116311831223136314431M 等第B B B c A C B A~h B 学号3I5C31633172318F319381993201S20«32109229C L A B L8B C C B B得分评卷人复核人•数学试割豹4贞（共8页）25.(本小越满分9分｝在・5・12大地点”尖民安蛍工作中•菓企业接到一 批生产甲种板W 24000m 1和乙神飯材12(XK)m :的任务• (1》已知诛企认安排140人宅产这胡幹板材•毎人毎天牝生产甲种板材30rn 戒乙种板材20m 2. IS],应分別安挣多少人生产屮和板材和Z •神板材•才施确保他们用相冋的时同完成各自 的生产任务？〈2》某灾民安迂点计划用谏金业宝产的这推板材菸建A.B 两种型号的板房人400间，在 搭中•按宏际需宴调运这两种板材•已知建一问A 型板房和一钊B 型仮房所需械材及 俺安H 的人数如下表所示，«分悴卷人复核人数宁试题第5页＜Jt8 1JO何；这《00何板房竝多能安址參少灾民?《】〉求这条范物线的两数关系式s26.（本小题満分9分〉已知楸物线y-a/—+ 它的对称仙相交十点A〈1 •一4）.与y帕交于C•与T轴正半紬交于B.〈2）设直线AC交工抽丁D•。

某某省各市06-08年中考数学试卷大汇编----规律探索及阅读理解题（习题及答案）一、填空题1．（08某某）如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动，行走2008厘米后停下，则这只蚂蚁停在点．2．（08宿迁）对于任意的两个实数对),(b a 和),(d c ，规定：当d b c a ==,时，有),(b a =),(d c ；运算“⊗”为：),(),(),(bd ac d c b a =⊗；运算“⊕”为：),(),(),(d b c a d c b a ++=⊕．设p 、q 都是实数，若)4,2(),()2,1(-=⊗q p ，则_______),()2,1(=⊕q p ．3．（08某某）如图，用锤子以相同的力将铁钉垂直钉入木块，随着铁钉的深入，铁钉所受的阻力也越来越大。

当铁钉未进入木块部分长度足够时，每次钉入木块的铁钉长度是前一次的21。

已知这个铁钉被敲击3次后全部进入木块（木块足够厚），且第一次敲击后，铁钉进入木块的长度是2cm ，若铁钉总长度为acm ，则a 的取值X 围是_____________.二、选择题1．(2007某某)一个机器人从数轴原点出发，沿数轴正方向。

以每前进3步后退2步的程序运动。

设该机器人每秒钟前进或后退1步，并且每步的距离是1个单位长，x n 表示第n 秒时机器人在数轴上的位置所对应的数。

给出下列结论：⑴33x =；⑵51x =；⑶103104x x <；⑷20072008x x <。

其中，正确结论的序号是（ ） A ．⑴、⑶B ．⑵、⑶C ．⑴、⑵、⑶D ．⑴、⑵、⑷2．(2007某某)按右边33⨯方格中的规律，在下面4个符号中选择一个填入方格左上方的空格内（ ）3．(2007某某)如图，小明作出了边长为的第1个正△A 1B 1C 1，算出了正△A 1B 1C 1的面积。

然后分别取△A 1B 1C 1的三边中点A 2、B 2、C 2，作出了第2个正△A 2B 2C 2，算出了正△A 2B 2C 2的面积。

ABCDOE ABy xO 2008年无锡市江南中学中考数学模拟考试注意事项：1．本试卷满分130分，考试时间为120分。

2．卷中除要求近似计算的结果取近似值外，其余各题均应给出精确结果。

一、细心填一填（本大题共有12小题，15空，每空2分，共30分．请把结果直接填在题中的横线上．只要你理解概念，仔细计算，相信你一定会填对的！） 1．-2的相反数是 ，16的平方根是 ． 2．分解因式：32b b a - = ．3．设一元二次方程0252=+-x x 的两个实数根分别为1x 和2x ，则12x x += . 4．据中新社报道：2010年我国粮食产量将达到540000000千克，，用科学记数法表示这个粮食产量为 千克 5．函数31+=x y 中自变量x 的取值范围是 ， 函数23y x =-中自变量x 的取值范围是 ．6．反比例函数xmy -=的图象经过点)2,1(-，则m 的值为 ．7．不等式组⎩⎨⎧-≥-03012x ＞x 的解集是 ． 8． 梯形ABCD 的上底AD=5cm ，中位线长为7cm ，则下底BC= cm.9. 如图,AB 是⊙O 的直径,弦CD⊥AB 于E,AB=20cm,CD=16cm,则OE= cm ．（第9题） （第11题） （第12题）10．小明过生日时，戴上了漂亮的圆锥形“寿星帽”，已知该帽的母线长是25cm ，底面圆半径是10cm ，则这个帽子是用面积为 cm 2的扇形纸版做成的．（结果用π表示）11．如图，在直角坐标系中，点Ａ在y 轴上，△OAB 是等腰直角三角形，斜边OA=2，将△OAB 绕点O 逆时针旋转90°得△OA 'B '，则点A '的坐标为 ；点B '的坐标为 ．12．如图，对面积为s 的△ABC 逐次进行以下操作：第一次操作，分别延长AB 、BC 、CA 至点A 1、B 1、C 1,使得A 1B=2AB ，B 1C=2BC ，C 1A=2CA ，顺次连接A 1、B 1、C 1，得到△A 1B 1C 1，记其面积为S 1；第二次操作，分别延长A 1B 1、B 1C 1、C 1A 1至点A 2、B 2、C 2，使得A 2B 1=2A 1B 1，B 2C 1=2B 1C 1，C 2A 1=2C 1A 1，顺次连接A 2、B 2、C 2，得到△A 2B 2C 2，记其面积为S 2；…；按此规律继续下去，可得到△A 5B 5C 5，则其面积S 5= ．二、精心选一选（本大题共有7小题，每小题3分，共21分．在每小题给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填在题后的括号内．只要你掌握概念，认真思考，相信你一定会选对的！）13．下列计算正确的是 （ ） A. 632x x x =⋅ B.ab b a 532=+ C.123=-a a D. ()632a a =14．下面与3是同类二次根式的是 （ ）Ａ．912Ｃ．18Ｄ．13-15．下列图案中既是轴对称图形又是中心对称图形的是 ( )(A) (B) (C) (D)16．已知两圆的半径分别为3和4，圆心距为7，则两圆的位置关系是 （ ） Ａ．相交Ｂ．内切Ｃ．外切Ｄ．内含17．如图1放置的一个机器零件，若其主视图为图2，则其俯视图是 （ ） 18．一道围栏是由宽的柱子和2米长的链子组成(链子的长度看作是两根柱子之间的距离),如果围栏的起点与终点均为柱子,下面各数中不可能是围栏长度的是 ( )Ａ．m Ｂ． m Ｃ．m Ｄ.m19．如图，直角梯形ABCD 中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E 由B 沿折线BCD 向点D 移动,EM⊥AB 于M,EN ⊥AD 于N.设BM=x,矩形AMEN 的面积为y,那么y 与x 之间的函数关系的图象大致是 ( )三、认真答一答（本大题共有8小题，共59分．解答需写出必要的文字说明、演算步骤或证明过程．只要你积极思考，细心运算，你一定会解答正确的！） 20．（本题共2小题，第⑴小题4分，第⑵小题6分，满分10分） ⑴ 计算：01)2008(545cos 2)21(π-⨯+︒--⑵ 化简：)2)(1(31+---x x x x ，并选一个你喜欢的x 值代入求值．图1 图2 A ． B ． C ． D ．OCDBAABCD E F 21．（本小题满分7分）如图，已知E 、F 是平行四边形ABCD 的对角线AC 上的两点，AE=CF. 求证：DF ∥BE.22．（本小题满分6分） 如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,若⊙O 的半径r=23,AC=2,求cosB 的值. 23．（本小题满分6分）在学习勾股定理时，我们学会运用图（I ）验证它的正确性：图中大正方形的面积可表示为2()a b +，也可表示为2142c ab +⨯，即2()a b +=2142c ab +⨯,推出勾股定理222a b c +=，这种根据图形可以简单直观推论或验证数学规律和公式的方法，简称“无字证明”．⑴ 请你用图（II ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形全等）．⑵ 请你用（III ）提供的图形进行组合，用组合图形的面积表达式验证：222()2x y x xy y +=++⑶ 请你设计图形的组合,用其面积表达式验证：pq qx px x q x p x +++=++2))((24．（本小题满分7分）小明对本班同学上学的交通方式进行了一次调查，他根据采集的数据，绘制了下面的统计图1和图2．请你根据图中提供的信息，解答下列问题： ⑴ 计算本班骑自行车上学的人数，补 全图1的统计图；⑵ 在图2中，求出“乘公共汽车” 部分所对应的圆心角的度数； ⑶观察图1，你能得出哪些结论？ （只要求写出一条）．（图1） （图2）25．（本小题满分6分）如图，有四张编号为①、②、③、④的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．⑴ 从中随机抽取一张，抽到的卡片是眼睛的概率是多少？⑵ 从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．26．（本小题满分9分）2007年5月，第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． ⑴ 哪个队先到达终点？乙队何时追上甲队？ ⑵ 在比赛过程中，甲、乙两队何时相距最远？ ② ① ③ ④AB CMFOα 图①图②27．（本小题满分8分）如图①、②，图①是一个小朋友玩“滚铁环”的游戏，铁环是圆形的，铁环向前滚动时，铁环钩保持与铁环相切．将这个游戏抽象为数学问题：如图②，已知铁环的半径为5个单位(每个单位为5cm)，设铁环中心为Ｏ，铁环钩与铁环相切点为Ｍ，铁环与地面接触点为Ａ，∠ＭＯＡ＝α，且sin α＝53． (1)求点Ｍ离地面ＡＣ的高度ＢＭ(单位：厘米)；(2)设人站立点Ｃ与点Ａ的水平距离ＡＣ等于11个单位，求铁环钩ＭＦ的长度(单位：厘米)．A C DE F四、实践与探索（本大题共2小题，满分20分．只要你开动脑筋，大胆实践，勇于探索，你一定会成功！） 28．（本小题满分10分）已知：等腰直角三角形纸片ABC ，∠C=90°，BC=AC ．将纸片折叠使点A 总是落在BC 边上,记为点D,EF 为折痕(如图).⑴ 当△DEF 是以∠EDF 为顶角的等腰三角形时,试判断△DCF 的形状,并说明理由;⑵ 在BC 边上是否存在点D,使折叠后所得的△DEF 与△DEB 相似?若存在,请求出相似比;若不存在,请说明理由.数学参考答案一、细心填一填（本大题共有12小题，15空，每空2分，共30分） 1．2；±4 2．))((b a b a b -+3．5 4．×1085．23;3≥-≠x x 6． 2 7．321x ＜≤ 8．9 9．6 10．250π 11．（-2，0）；（-1，1） 12．195s二、精心选一选（本大题共有7小题，每题3分，共21分）13．D 14. B 15. A 16. C 17. D 18. C 19.A 三、认真答一答（本大题共8题，满分59分.） 20．（4分+6分）（1）原式152222⨯+⨯-= ……………………………………………（2＇） =2-1+5=6 …………………………………………（4＇） （2）原式)2)(1(3)2(+--+=x x x x …………………………………………………………（2＇）Bxy y 2xy x 2yy yy x xx xqx pq px x 2xx p q px x q23)2)(1()3)(1(++=+-+-=x x x x x x ……………………………………………………（4＇）X 可以取不等于1且不等于-2的任意数代入求值 ……………………………（6＇） 21．（7分）证明： 在平行四边形ABCD 中，AB=CD, AB ∥CD ∴∠DCF=∠BAE ∵AE=CF∴CDF ABE ∆≅∆ ……………………………………………（4＇）∴∠BEA =∠DFC ………………………………………………（5＇） ∴∠DFA=∠BEC ∴ DF ∥BE ……………………（7＇） 22．（6分）解：∵AD 是⊙O 的直径 ∴∠ACD=90° …………………………………………（1＇）∵r=23∴AD=2r=3 ...................................................（2＇） 在Rt △ACD 中，∠ACD=90° ∴522=-=AC AD CD (3)） ∴cosD=35=AD CD ……………………………………………（4＇） ∵∠D=∠B ∴cosB= cosD 35=…………………………………………（6＇） 23．（6分）（1）设直角三角形的两直角边为a 、b ，斜边为c （a>b ） 则22)(214b a ab c S -+⨯==正方形 ∴ 222c b a =+ ……………………………………………（2＇）（2）……………………………………………（4＇）(3)……………………………………………（6＇）24．（7分）（1） 骑自行车人数 ：14÷28％-14-12-8=16 （人） ……………………（2＇） 图略 ……………………………………………（4＇）（2）28％×360°° ……………………………………………（6＇） （3）略 ……………………………………………（7＇） 25．（6分）(1)P （抽到眼睛）=2142=， (2)） (2) ① ② ③ ④② ③ ④ ① ③ ④ ① ② ④ ① ② ③……（4＇） ∴P （贴法正确）=61122= (6)） 26．（9分）解：(1)乙队先到达终点. ……………………………………………（1＇）对于乙队，x ＝1时，y ＝16，所以y ＝16x ，……………………………………………（2＇） 对于甲队，出发1小时后，设y 与x 关系为y ＝kx ＋b ， 将x ＝1，y ＝20和x ＝2.5，y ＝35分别代入上式得：⎩⎨⎧+=+=bk bk 5.23520 解得：y ＝10x ＋10 ……………………………………………（3＇） 解方程组⎩⎨⎧+==101016x y x y 得：x ＝35，……………………………………………（5＇）∴在出发1小时40分钟后即上午10点40分时乙队追上甲队. ………………（6＇）（2）1小时之内，两队相距最远距离是4千米， ………………（7＇） 乙队追上甲队后，两队的距离是16x －(10x ＋10)＝6x －10，当x 为最大，即x ＝1635时，6x －10最大，此时最大距离为6×1635－10＝3.125＜4，所以比赛过程中，甲、乙两队在出发后1小时即上午10时相距最远 ………………… ……（9＇） 27．（8分）解：过M 作与AC 平行的直线,与OA 、FC 分别交于H 、N 。

无锡市中考数学试卷一、选择题（本大题共10小题,每小题3分,共30分．在每小题所给出的四个选项中,只有一项是正确的,请用2B 铅笔把答题卡上相应的选项标号涂黑） 1．2-的值等于（ ▲ ） A ．2B ．-2C ．2±D ．2答案：A解析：负数的绝对值是它的相反数，所以｜－2｜＝2，选A 。

2．函数y=1-x ＋3中自变量x 的取值范围是（ ▲ ）A ．x ＞1B ．x ≥1C ．x ≤1D ．1≠x 答案：B解析：由二次根式的意义，得：x －1≥0，所以，x ≥1，选B 。

3.方程0321=--xx 的解为 （ ▲）A ．2=xB ．2-=xC ．3=xD ．3-=x答案：C解析：去分母，得：x －3（x －2）＝0，即x －3x ＋6＝0，解得：x ＝3，经检验x ＝3是原方程的解，选C ＞4.已知一组数据：15,13,15,16,17,16,14,15，则这组数据的极差与众数分别是（ ▲）A ．4,15B ．3,15C ．4,16D ．3,16答案：A解析：极差为：17－13＝4；数据15出现的次数最多，故众数为15，选A 。

5.下列说法中正确的是 （ ▲）A ．两直线被第三条直线所截得的同位角相等B ．两直线被第三条直线所截得的同旁内角互补C ．两平行线被第三条直线所截得的同位角的平分线互相垂直D ．两平行线被第三条直线所截得的同旁内角的平分线互相垂直 答案：D解析：A 、B 都漏掉关键词“平行”，应该是“两条平行直线”，故错；两平行直线被第三条直线所截得的同位角的平分线互相平行，不垂直，故C 错；由两直线平行，同旁内角互补，及角平分线的性质，可得D 是正确的。

6．已知圆柱的底面半径为3cm ，母线长为5cm ，则圆柱的侧面积是 （ ） A ．30cm 2 B ．30πcm 2 C ．15cm 2 D ．15πcm 2 答案：B解析：圆柱侧面展开图为长方形，长为圆柱的底面圆周长：6π，因此，侧面积为S ＝6π⨯5＝30πcm 27．如图，A 、B 、C 是⊙O 上的三点，且∠ABC =70°，则∠AOC 的度数是 （ ） A ．35° B ．140° C ．70° D ．70°或140° 答案：B解析：同弧所对圆周角是它所对圆周角的一半，所以，∠AOC ＝2∠ABC ＝140°，选B 。