模糊因素影响下的框架结构的有限元分析

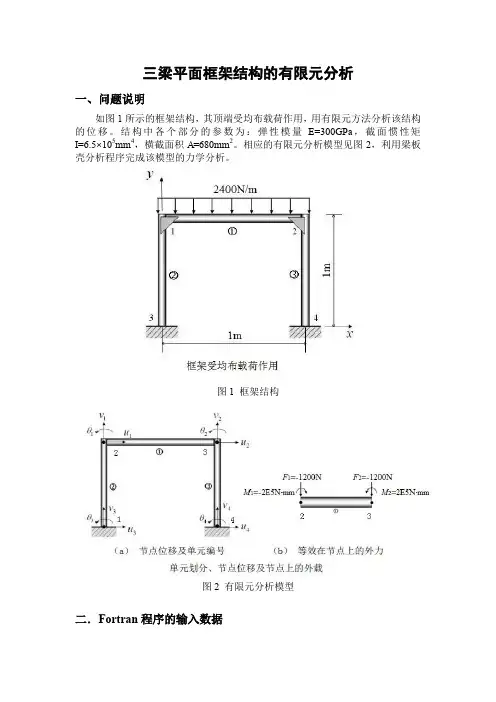
三梁平面框架结构的有限元分析一、问题说明如图1所示的框架结构，其顶端受均布载荷作用，用有限元方法分析该结构的位移。

结构中各个部分的参数为：弹性模量E=300GPa，截面惯性矩I=6.5×105mm4，横截面积A=680mm2。

相应的有限元分析模型见图2，利用梁板壳分析程序完成该模型的力学分析。

图1框架结构图2有限元分析模型二．Fortran程序的输入数据（1）Facile.11 4 3 6 0 12 42 1 11 1 11 3 51 2 2 3 3 40 0 0 0 1000 01000 1000 0 1000 0 0（2）Facile.2111 211 1111 0 0 0 1 03E5 1.6E5680 6.5E5 6.5E5 6.5E50 0（3）Facile.312 41 02 03 04 05 06 0 19 0 20 0 21 0 22 023 0 24 08 -1200 12 -200000 14 -1200 18 200000输出的数据文件为：Facile7和Facile8，其中各节点位移结果在文件Facile8中。

三．计算结果各节点的位移计算结果见表1。

四．Ansys分析结果Ansys计算结果如下图所示，图3为节点x方向的位移云图，图4为节点y 方向的位移云图，图5为节点转角云图。

图3 节点x方向的位移图4 节点y方向的位移图5 节点转角各节点的位移值见表2。

五．结果对比通过对比表1和表2中的数据可以发现，Fortran程序与Ansys分析的结果十分接近。

预应力混凝土框架结构抗震性能有限元分析的开题
报告
一、选题的依据
预应力混凝土结构是一种具有优异抗震性能的结构形式，预应力混
凝土框架结构因具有梁柱节点预应力优势，具有高抗震性能，因此在工
程建设中得到了广泛应用。

如何提高预应力混凝土框架结构的抗震性能，已成为结构工程领域中的一个重要研究课题。

二、研究目的和意义
本研究旨在探究预应力混凝土框架结构的抗震性能及其影响因素，
并通过有限元模拟分析方法进行数值模拟。

在研究中，将探究预应力混
凝土框架结构在地震载荷下的滞回曲线、耗能能力、稳定性等抗震性能
指标，以及节点预应力对抗震性能的影响。

本研究对于提高预应力混凝
土结构在地震灾害中的抵御能力具有一定的理论意义和工程应用价值。

三、研究内容和方法
本研究主要内容包括：采用ANSYS有限元软件建立预应力混凝土框架结构有限元模型，通过地震波输入进行动力时程分析，分析在地震作
用下框架结构的状态变化及其抗震性能。

同时，分析节点预应力对结构
抗震性能的影响，通过有限元分析得出节点预应力的最优预应力值。

四、预期成果
通过本研究，可对预应力混凝土框架结构的抗震性能及节点预应力
优势进行更深入的了解。

同时，通过有限元模拟分析方法得出的结果，
可为工程实践提供参考，提高工程结构在地震灾害中的抵御能力。

03
结果优化
如果结果不满足设计要求，需要对有 限元模型进行优化设计，如改变梁的 截面尺寸、增加支撑等。
THANKS
谢谢您的观看
结构静力学的求解方法
解析法
解析法是通过数学方法求解结构在静载荷作用下的响应的求解方法。它通常 适用于具有简单几何形状和载荷条件的结构，如梁、板、壳等。
数值法
数值法是一种通过数值计算方法求解结构在静载荷作用下的响应的求解方法 。它通常适用于具有复杂几何形状和载荷条件的结构，如飞机、汽车等。
结构静力学的基本假设和简化
问题描述和基本方程
问题描述
弹性地基梁是支撑在弹性地基上的梁，受到垂直荷载的作用。该问题可描述为求 解地基反力和梁的挠度。
基本方程
该问题的基本方程包括梁的平衡方程、几何方程和物理方程。这些方程描述了梁 在受力后的变形和应力分布情况。
利用有限元法进行每个单元之间通过节点相连。每个节点具有三个自由度：沿 x、y、z方向的移动。
系统方程的建 立
将所有单元的平衡方程 和变形协调方程组合起 来，得到整个结构的系 统方程。
求解系统方程
利用数值方法（如高斯 消元法）求解系统方程 ，得到每个节点的位移 和应力。
结果分析和讨论
01
结果输出
输出每个节点的位移、应力、应变和 弯矩等结果。
02
结果评估
根据输出结果，对框架结构的强度、 刚度和稳定性进行评估，判断是否满 足设计要求。
连续性假设
结构静力学的基本假设是结构的材料是连续的， 即结构的内部没有空隙和缺陷。
各向同性假设
结构静力学的基本假设是结构的材料是各向同性 的，即结构的各个方向具有相同的材料性质。
均匀性假设
结构静力学的基本假设是结构的材料是均匀的， 即结构的各个部分具有相同的材料性质。

梁表面弯曲 拉应力 安全！ 安全！
MX MN
最大拉应力 远小于150MPa
Y X 1.868 SHOW WALL STATIC ANALYSIS
-.302789 Z
4.04
8.382 6.211 10.553
12.725 14.896
17.067 19.239
模拟地震显示屏冲击力上拉加载
1
ELEMENTS U F CP ACEL
梁连接螺钉的力学处理
连接螺栓
显示墙框架
• 采用Ansys中的 MPC135连接单元专门 模拟螺钉的连接行为 • 根据实际情况约束连接 部分的移动自由度，但 旋转自由度不加限制 • 螺钉连接的点之间可以 耦合成零距离
RotX,RotY,Rot Z无约束 无
UX,UY, UZ约束
刚性杆，中间杆 距可以为极限小
最大处
MN
MX
Z Y X
小于150Mpa 安全！
13.133 6.586 19.68 SHOW WALL STATIC ANALYSIS
.038678
26.227 32.774
39.321 45.868
52.415 58.961
螺钉拉力分析
1
LINE STRESS STEP=1 SUB =1 TIME=1 ITENSZ JTENSZ MIN =-1167 ELEM=628 MAX =1167 ELEM=27
XXXXXXX有限公司
显示墙框架结构体有限元分析
作者：XXX XXXXX大学电子与电气工程学院
建立有限元模型之特点
• 在地震等冲击条件下，对于m（行）Xn （列）的显示单元进行受力有限元模拟。 • 建立的力学模型应能适应不同的mXn组合， 自动约束加载，自动网格产生。 • 该力学模型能够适应不同的螺钉布置位置， 并能够增加或删减螺钉 • 输出结果可以输出铝型材的截面最大弯曲 应力，端面空间应力与力矩（包含并等效 了螺钉部位的拉力）

１概述
模拟Ｐ △曲线
近 年来 ， 国 内外 众多 学 者 的很 多 研 究 和设 计 规 范 中关 于剪 力 墙 结构 设 计 的相 关 规定 表 明 ， 剪 Ｚ 力 墙 结 构 的抗 震 性 能与 多 种 因素 有关 ， 荷 载 分 布 （ 如截面剪跨 比、 轴压 比） 、 几何 尺 寸 （ 如高宽 比 、 截 面形 状 ） 、 材 料 强度 （ 如混凝土的强度 、 各个 部 １ ５ ＊ 位 的 配筋 形 式 和强 度 ） 。框 剪 结 构 结合 了框 架结 构 和剪 力 墙 结 构 ， 在 研 究 上 比剪 力 墙结 构 更 为 复 杂， 关 于框 架 一 剪 力 墙 结 构 整 体 的抗 震 性 能 的影 响 因素 的研究 很 少 。 文 章 通过 有 限元 分 析 软件 从 结 构材料性 能人手 ， 探讨 这些 因素是否对框架一 剪 力 墙 力 学性 能 产 生影 响 。 （ ａ ） Ｒ Ｃ１ （ ｂ） Ｒ Ｃ２ ２有 限元软件介绍及试件概要 图２ Ｒ Ｃ １ 和Ｒ Ｃ ２在 水平 往 复加 载下 的荷 载 一 相 对 变形 角 曲线 东 京 大学 混 凝 土研 究 室 开 发 的 钢 筋 混 凝 土 ３ ． １模 拟 结果 对 比分析 结 构 物 的分 析 程 序 ＷＣ Ｏ Ｍ Ｄ基 于 混 凝 土 相 关 的 许 多 实 验 和 理 论 验 如图 １ 所示 ， 在 单调 加 载条 件 下 ， 通过荷载一 相 对 变 形 角 曲线 可 证结果 ， 运用高精度 的构成规则 ， 可高精度地进行生成裂缝的各类 以看 出 Ｒ Ｃ ２的承 载 力也 有 所 提 高 ， Ｒ Ｃ ２的 刚度要 比 Ｒ Ｃ １ 大些 。Ｒ Ｃ １ 钢 筋 混凝 土 结 构物 的二 维非 线 性动 力 分 析， 静力 分 析 。 二者 的延 性相 差 不 大 。其 他 相 关 的研 究 表 明 在 本 软 件 主要 是 针对 钢 筋 混凝 土 而 设 计 ， 特 别 是其 在 混 凝 土 实验 的最 大 位移 略大 些 ， 室研 究 出的混 凝 土 本构 关 系模 型成 果 显 著 ， 其 准 确度 不 仅 考 虑 了 日 合理的配箍下 ， 使用高强度混凝土 的剪力墙将提高由 区混凝土所 使 用 高 强 度 混凝 土 有 助 于提 高 构 件 的开 本在 内 ，而且 也 包 含考 虑 了其 他 海 外 国 家混 凝 土 本 构关 系 的情 况 ， 产 生 的抗 剪 承 载力 。此外 ， 裂荷载 ， 减少 裂 缝 宽度 。 因此 文 章 选用 ＷＣ Ｏ ＭＤ模 拟 分 析 。 如 图 ２所示 ， 在 水平 往 复 加 载条 件 下 ， 通 过 荷 载一 相 对 变形 角 曲 ２ ． １模 型设 置 Ｒ Ｃ ２的刚 度 相对 于 Ｒ Ｃ １ 有 所 提 高 。Ｒ Ｃ ２的承 载 力也 有 为 了探讨 混 凝 土 强度 对 装 配式 框 一 剪 结 构体 系 的 受力 性 能 的影 线 可 以看 出 ， 但不 是 很 明显 。Ｒ１ 的最 大 位 移 略 大些 ， 二 者 的 延性 变 化 不 响，建立一个一榀双层单跨的装配式框架一 剪力墙结构的有 限元数 所 提 高 ， 值 模 拟 进 行 对 比 分 析 。 在 有 限 元 软 件 中 建 立 试 件 模 型 ，取 边 长 大 。 ３ ． ２ 其 他 各 因素 对混 凝 土 框架 一 剪 力墙 力学 性 能 的影 响 １ ０ ０ ｍ ｍ 的正 方 形为 一 个 网格 的大小 ， 由此 建 立有 限元模 型 。 综 上可 以看 出 ，混凝 土强 度 对 框 剪结 构 的 力学 性 能 产 生影 响 ， 为 了研 究 混 凝 土强 度 的差 异 是 否 对 试件 的力 学 性 能 造成 影 响 ， 还 有 以下 因 素会 对 框 剪 结 构 所以我们在模 拟时需要输入模拟的不同部 位的混凝土抗压强度值 另根 据 其他 文 献 提供 的研究 结 果 表 明 ， 即 可 。在 设 置 时 ， 在保 证 其 他 条 件 相 同的 情 况 下 ， Ｒ Ｃ １ 与Ｒ Ｃ ２的墙 的力 学性 能 有影 响 ： 剪 力墙 厚 度 ： 在 其他 参数 保 持 不 变 的情 况 下 ， 随着 剪 力 墙 厚 度 的混 凝 土强 度 值 有差 别 ， Ｒ Ｃ １ 的采 用 Ｃ ３ ０ ， Ｒ Ｃ ２采用 Ｃ ４ ０ 。 的增加 ， 屈 服 位 移逐 渐 降 低 。 ２ ． ２ 加 载方 式 轴压 比： 在 其他 参 数 保 持 不 变 的情 况下 ， 随 着 结 构 的轴 压 比 的 （ １ ） 单调 加 载 屈服 位 移 显著 增 加 。 （ ２ ） 水 平 往 复加 载模 拟 的加 载 制 度 分 两 阶段 进 行 ， 第 一 阶 段 是 提 高 ， 纵筋配筋率 ： 在 其 他 参 数 保 持 不 变 的情 况 下 ， 随 着 剪 力 墙 纵 筋 在 两 个小 柱 头 顶 面 中心处 各 施 ７ ２ ０ ｋ Ｎ 的轴压 力 ， 第 二 阶段 在 试 件 顶 框 剪 构件 屈 服 位 移略 有增 加 。 层梁 跨 中的 钢板 中心 处 ， 施加 水 平 方 向的循 环 往 复 力 。设 置 每 个 分 配 筋率 的提 高 ， 剪跨 比： 大 量 的研 究 结 果 表 明 ， 剪 跨 比是 影 响 框 剪 结 构抗 剪 承 析 步 加载 （ 或 卸载 ） 位移 为 ０ ． ３ ｌ ｍ ｍ， 每 级进 行 两 个 往 复循 环 加 载 ， 直 载力 、 破 坏 形态 、 延 性 及 耗 能性 能 的重 要 因素 之 一 。 到试 件 最 终 破坏 。 ４结 束 语 ３模拟结果分析及其他影 响因素 框架 一 剪 力墙 结 构 的抗 震 设计 中 ，连 接节 点 的优 化 设 计 固 然重 通 过 ＷＣ Ｏ Ｍ Ｄ对 有 限元 模 型用 两 种 加 载方 式 加 载 （ 单 调 加 载 和 但 是材 料 及 尺寸 作 为结 构 的 重 要属 性 ， 它 的优 化 需 要 更 多 的研 水 平 往 复加 载 ） ，再 将试 件 的 荷载 一 位 移 曲线 及 荷载 一 相对变形角曲 要， 最 大程 度 线 进 行 比较 ， 从 混 凝 土 的强 度 人手 ， 分 析 并 讨论 其 对 框 架 一 剪 力 墙 结 究 和关 注 。在设 计 中要 综 合 考 虑经 济 性 和 安 全性 的需求 ， 地 优化 结 构 ， 从 而使 结 构 在地 震 作用 下 发 挥最 大 的效 能 。 不足 的 是 ， 还 需要 收 集更 多 的试验 结 果来 分 析 各参 数 对 框架 一 剪 力 墙 结构 的影 响， 从 而提 出方便 实 际 工程 应 用 的结 论 。 硝： 、 ．

ABAQUS混凝土损伤塑性模型的静力性能分析一、本文概述混凝土作为一种广泛使用的建筑材料，在土木工程中占据了重要地位。

然而，混凝土在受力过程中会出现损伤和塑性变形，这对其静力性能产生显著影响。

为了更深入地理解混凝土的力学行为，并对工程实践提供指导，本文将对ABAQUS中的混凝土损伤塑性模型进行详细分析。

本文首先简要介绍了混凝土材料的特性以及其在工程中应用的重要性。

接着，阐述了混凝土在受力过程中的损伤和塑性变形的机制，为后续分析提供理论基础。

随后，重点介绍了ABAQUS中的混凝土损伤塑性模型，包括模型的基本假设、控制方程以及参数的选取。

在此基础上，本文通过实例分析了该模型在静力性能分析中的应用，包括模型的建立、加载过程以及结果的后处理。

本文旨在通过理论分析和实例验证，展示ABAQUS混凝土损伤塑性模型在静力性能分析中的有效性和实用性。

通过本文的研究，读者可以对混凝土的力学行为有更深入的理解，并掌握使用ABAQUS进行混凝土静力性能分析的方法。

这对于提高混凝土结构设计的准确性、优化施工方案以及保证工程安全具有重要意义。

二、混凝土损伤塑性模型理论混凝土作为一种复杂的多相复合材料，其力学行为受到内部微观结构、加载条件以及环境因素等多重影响。

在静力性能分析中，混凝土表现出的非线性、弹塑性以及损伤特性使得对其行为进行准确模拟成为一项挑战。

ABAQUS软件中的混凝土损伤塑性模型（Concrete Damaged Plasticity Model）旨在提供一种有效的工具，用以描述混凝土在静载作用下的力学响应。

混凝土损伤塑性模型是一种基于塑性理论和损伤力学的本构模型，它结合了塑性应变和损伤因子来描述混凝土的力学行为。

在模型中，损伤被视为一种不可逆的退化过程，通过引入损伤变量来反映材料内部微裂缝的扩展和累积。

这些损伤变量在加载过程中逐渐增大，导致材料的刚度降低和承载能力下降。

该模型通过引入两个独立的损伤变量，分别模拟混凝土在拉伸和压缩状态下的损伤演化。

钢框架结构的优化设计研究一、本文概述随着现代建筑技术的不断发展，钢框架结构作为一种重要的建筑形式，已经广泛应用于各类建筑项目中。

然而，在追求建筑美观和实用性的如何优化钢框架结构的设计，以降低成本、提高结构性能、确保安全稳定，已成为当前建筑领域亟待解决的问题。

本文旨在探讨钢框架结构的优化设计研究，通过对钢框架结构的受力性能、稳定性、经济性等关键因素的分析，寻求最佳的设计方案，以期为钢框架结构的未来发展提供理论支持和实践指导。

具体而言，本文将从以下几个方面展开研究：介绍钢框架结构的基本概念和特点，阐述优化设计的重要性和必要性；分析钢框架结构的受力性能和稳定性，探讨不同设计参数对结构性能的影响；再次，结合经济因素，研究如何在满足结构性能要求的前提下，降低材料消耗和工程造价；通过实际案例分析和模拟计算，验证优化设计的可行性和有效性。

通过本文的研究，期望能够为钢框架结构的优化设计提供一套系统、科学的方法论，为建筑工程师在实际工程中提供有益的参考和借鉴，推动钢框架结构在建筑设计中的广泛应用和优化发展。

二、钢框架结构的优化设计理论钢框架结构作为现代建筑的重要支柱，其优化设计理论在提升结构性能、提高经济效益和满足建筑功能需求等方面具有深远意义。

优化设计理论的核心在于通过合理的设计手段，使钢框架在满足安全、稳定和经济的前提下，实现最佳的性能表现。

在钢框架结构的优化设计中，首要考虑的是结构的承载能力和稳定性。

这要求设计者在结构选型、材料选择、截面尺寸确定等方面进行全面考量。

通过先进的计算方法和设计软件，对结构在各种荷载工况下的受力性能进行精确分析，从而确保结构的安全性和稳定性。

优化设计还需要注重结构的经济性。

在满足结构性能的前提下，通过合理的材料使用、截面优化、节点设计等手段，降低结构成本，提高经济效益。

随着绿色建筑和可持续发展的理念日益深入人心，优化设计还需考虑结构的环保性和可持续性，例如采用可再生材料、优化能源利用等。

考虑初始缺陷影响的空间钢框架结构稳定分析的新方法的开题报告题目：考虑初始缺陷影响的空间钢框架结构稳定分析的新方法背景：钢结构在建筑工程中应用越来越广泛，特别是在高层建筑中。

结构的稳定性是一个重要的设计考虑因素，因为稳定性失效将导致严重的后果。

在实际工程中，存在许多因素会影响结构的稳定性，例如几何和物理非线性、材料不均匀性、渐进挠度等。

其中，初始缺陷是一种常见的因素。

许多先前的研究研究了结构稳定性的不同方面，但只有少数考虑了初始缺陷的影响。

在实际结构中，有许多情况下会存在初始缺陷，例如在切割、钻孔和焊接等加工过程中，都有可能导致结构缺陷，而这些缺陷对结构稳定性的影响必须得到考虑。

研究目标：该研究旨在开发一种新的方法，以考虑结构中的初始缺陷对稳定性的影响。

研究将采用数值模拟和实验方法，针对典型的空间钢框架结构进行分析。

研究内容：1.基于初始缺陷的空间钢框架结构数值模拟采用非线性有限元分析方法，考虑不同大小和位置的初始缺陷，对典型空间钢框架结构进行数值模拟，以评估缺陷对结构稳定性的影响。

在模拟中，将使用开源有限元软件Abaqus。

2.实验验证在实验室中进行空间钢框架结构的制造和测试，以验证数值模拟结果的准确性。

特别是注意不同初始缺陷对结构稳定性的影响，以便与数值模拟结果进行比较。

3. 结合数值模拟和实验结果进行分析和优化根据数值模拟和实验结果，分析各种类型的缺陷，并据此优化空间钢框架结构的设计方法，以使其更好的抵抗初始缺陷的影响。

预期结果：该研究将产生一种新方法，可用于分析空间钢框架结构中的初始缺陷对结构稳定性的影响。

研究还将提供一些有关优化结构设计的建议，以在初始缺陷存在时提高结构的稳定性。

这对于工程师更好地理解不同因素对结构稳定性的影响，从而更好地设计、构造和维护结构具有重要意义。

钢筋混凝土框架结构的有限元分析[摘要]利用ANSYS软件建立一榀三层框架模型，对该结构模型进行非线性有限元分析，得出框架结构在一定荷载作用下的破坏特征。

【关键词】ANSYS；框架；非线性1、框架尺寸和材料参数框架模型为单跨三层结构，跨度和层高尺寸见图1，结构选用混凝土等级为C30，梁柱截面尺寸及配筋情况见图2。

钢筋及砼强度设计值通过查阅《混凝土结构设计规范》取得。

2、分离式建模采用link8，Solid65单元分别模拟钢筋和混凝土，保护层厚度取2cm。

ANSYS 中对模型的网格划分方法有映射网格划分和自由网格划分两种。

自由网格划分对于单元形状没有限制，并且没有特定的准则，映射网格划分对单元形状有限制。

且须满足特定规则，映射面网格只包含四边形和三角形单元，映射体网格只包含六面体单元，映射网格具有规则的形状，明显成排的单元，如果要用这种网格类型，须将模型划分成相当规则的体和面，但映射网格有利于结点数据的储存，使得计算速度快耗时少。

由于框架几何形状比较规则，采用映射划分网格，单元均采用六面体划分网格，单元最小尺寸为2cm（见图3）。

为避免加载点砼出现局部破坏而影响计算结果，在加载点设置垫块并将集中荷载等效为垫块区域均布荷载。

3、有限元计算与结果分析一次性施加竖向荷载，在左侧柱顶分步逐级施加水平右向荷载（加载图参见图1），图4、图5分别为开裂裂缝图和破坏裂缝图，结构开始出现裂缝时的荷载为6KN，钢筋屈服荷载为36KN，结构破坏荷载58KN。

当荷载加至6KN时，梁端最先出现裂缝，然后裂缝向梁中间延伸，随着梁端裂缝的增长增多，柱子底部出现水平裂缝和拉裂裂缝，裂缝不断增多并向上延伸，当荷载加至36KN时，梁端钢筋开始屈服，标志着结构从弹性阶段开始过度到弹塑性阶段，由于顶梁比第一、二层梁截面尺寸和配筋小，顶梁裂缝最多破坏最严重，当荷载加至58KN时，梁端纵筋和柱底纵筋达到极限强度，梁柱节点区域出现许多裂缝，以致整个结构彻底破坏而计算停止。

Ｓ ｔ ｅ ｅ ｎ ａ ｃ ｋ ｅ ｒ ｓ 等 【 ７ 将 传 统 的 模 型 修 正 方 法 进 行 了扩 展， 考 虑 了试验 不确 定 性 ， 将 结构 各 阶频率 的试 验 方
差 作为 目标 函数 中各 模态 项 次 的权 系 数 ， 采 用 最 小 二 乘法 对 结 构 的待 修 正参 数 进 行 了识 别 ， 但 其 修 正
Ｇｏ ｌ ｌ ｅ ｒ 等 。 １ 基 于 贝 叶斯 方 法 ， 结 合 某 航 空 结 构 的模
作 者简介 ： 陈 学前 （ １ ９ ７ ５ ． ） ， 男， 四川 中江县人 ， 硕士 ， 目前从
事 结 构 动 力 学研 究 。
态 实验 数据 ， 对 模 型 中的不确 定参 数进 行 了升 级 ， 建
一
位 虚拟 材 料 弹 性 模 量 的不 确 定 性 。这 样 ， 组合 梁 结
构 中 的两 个 不确 定 性 源 在其 有 限 元模 型 中表现 为 ３ 个 不确 定 性 参 数 ， 可 以通 过校 准 层 次 子 结构 的模 态 试验结 老 行 识别。各子结构的有限 己 模型如图２ 所示。
Ｆ ｉ ｎ ｉ ｔ ｅ Ｅｌ ｅ ｍｅ ｎ ｔ Ｍｏ ｄ ｅ ｌ ｉ ｎ ｇ ａ ｎ ｄ Ｖａ ｌ ｉ ｄ ａ ｔ ｉ ｎ ｇ ｏ ｆ
Ｓ ｔ ｒ ｕ ｃ ｔ ｕ ｒ ａ ｌ Ｕｎ ｃ ｅ ｒ ｔ ａ ｎｔ ｉ ｙ Ｆａ ｃ ｔ ｏ ｒ ｓ
ＣＨＥＮ Ｘｕ ｅ — ｑ ｉ ａ ｎ ＸＩ Ａ ０ Ｓ ｈｉ － ｆ ｕ ＬＩ Ｕ Ｘｉ ｎ． ｅ Ｉ ７
收稿 日期： ２ ０ １ ２ ． １ ２ — １ ３ ； 修改 日期： ２ ０ １ ２ — １ ２ ． ３ ０
项 目基 金 ： 国家 自然 科 学基 金委 员会 一 中 国工 程 物 理 研 究 院 联 合基 金 ＮＳ Ａ Ｆ （ 基金编号： １ ０ ８ ７ ６ １ ０ ０ ） ； 中 国工 程 物 理 研 究 院重 点 基 金

有限元法在框架优化设计中的应用【摘要】钢筋混凝土框架结构是我国目前各种建筑类型中使用最普遍的结构形式之一。

本文就结构优化理论的发展进程，利用有限元法的分析功能对框架结构进行优化设计，为结构优化分析在实际工程中的应用，节省建筑材料和降低造价，探索一条新的解决问题的途径。

【关键词】有限元；框架；优化设计有限元法是利用计算机进行运算的一种数值分析方法，它的主要内容包括两部分：一是结构单元分析，即分析杆件单元的力学特性，其二是结构分析，也就是将众多离散的单元集合成全结构单元计算模型，再根据计算模型列出全结构模型的矩阵方程。

建筑框架结构形式主要采用梁柱杆件等刚接组合而成为空间体系，它的主要特点是：①约束条件多：从杆件局部尺寸约束到全结构强度刚度约束，从构件单元约束到全结构体系约束，从正常使用状态下的弹性约束到极限状态下弹塑性约束等多特点、多种类的约束条件大大增加了优化方法的难度；②变量参数多：框架结构的构件尺寸、截面类型、受力特征等都可能成为优化设计的变量，再加上框架结构构件超静定受力条件复杂，且相互影响较多，一定程度上导致优化工作量的大量增加。

本文利用框架结构杆件截面尺寸作为离散变量，把数学规划法和有限元结构分析法相结合，对框架结构进行优化设计。

1.实体结构的简化要求正常使用情况下框架结构的受力变形是以弯曲变形为主，本文以框架结构的体积作为目标函数，把结构的截面尺寸做为变量参数。

通过施加内外作用力求得各个构件的内力，随后对构件截面进行优化设计。

为了详细说明优化方法的特点，先要对框架结构做一些简化：（1）设定适宜的配筋率：在框架结构中，钢筋的影响是非常大的，因此在目标函数中一定要考虑钢筋的影响，为了简化工作量，我们把构件截面设定适宜的配筋率。

本文中结构截面均取2.5%的配筋率。

（2）调整参数变量的优化步幅：优化的步幅决定了离散变量最优解偏离精确度的程度，参数变量寻优的速度也和优化步幅的大小有关，因此在寻优过程中各参数步幅必须可调。

１９ （２ ：１１ ． ９ ３ １ ）１－５
其 中， 为材料性质和加载方式等因素决定 的常数 。 ｍ
［］ ３ 沈祖 炎， 董 宝 ， 曹文衔 ． 结构损 伤 累积 分析 的研 究现状 和存
在的问题 ［］ 同济大学学报 ，９７ ２ ：３ —４ ． Ｊ． １９ （ ） １５１０
同时 ， 国对 压力容 器用钢 的研究 表 明， 美 低周疲 劳 寿命 依赖 于整体应变 ｅ， 而不只是塑性应变 ｅ， 由下式确 定 ：
维普资讯
・
７ ・ ０
第３ ３卷 第 ｌ ２期 ２０ ０ ７年 ４ 月
山 西 建 筑
Ｓ ＨＡＮＸＩ ＡＲＣＨＩ ＴＥＣｒＵＲＩ
Ｖｏ ． ３ Ｎｏ １ １３ ． ２ Ａｐ ． ２ ７ ｒ ００
文章编号 ： ０ ．８ ５２ ０ ）２ ０ ００ １ ９６ ２ （０ ７ １ — ７ —３ ０ ０
中 图分 类 号 ： Ｕ３ １４ Ｔ １ ． 文献标识码 ： Ａ
１ 概述
超长框架 的裂缝 问题一直是结构设计 、 施工 以及工程科研人
２ １ 结构 平 面布置 ．
多层框架结构温度应 力计算 较为 复杂 ， 据文献 ［ ］ 根 １ 的计算
在温度 应力作用下 ， 内剪 力与柱高 的三次方成 反 比。即 柱 员最 为关心 的重大问题 ， 而建筑物运行期 间温度应 力对此类裂缝 理论 ： 温度 应力 衰减越快 ， 而可 以把 一个多层 从 的贡献尤难把握 ， 目前现有文献 已对此进 行了多方面研究 。钢筋 离地基 的约束面越远 ， 框架结构简化 为两层计 算。对于顶 层 ， 虑到楼 板受太 阳辐射 ， 考 混凝土超长框架结 构属 于高次超静定结构 ， 温度作 用下三维尺度 将结 构顶 部亦 可简 化 为顶部 两层 计 效应究竟如何不得 而知 ， 另外 由于钢 筋混凝 土 的非 线性 ， 因此从 对结构也会 产生 内力变 化 ， 基础和地 下室 假定 不变 形。文 中对 五层框 架进 行 了简单试 般 的平面角度去分析 显然不合 理 ， 中主要从空 间着手 ， 文 利用 算 ，

工 程
管 理
Ｓ ＩＯ Ｏ ＮＥ＆ＴＣＮＬＧ Ｅ ＥＨＯ ＯＹ
匪圆
模 糊 因素 影 响 下 的框 架 结 构 的有 限 元分 析
龙 强
（ 辽宁工 程技术 大学 辽 宁阜新 １ ３ ０ ） ０ ０ ２ 摘 要： 针对工程 中存在参数 不确定性 问题 ， 用模糊数 学方法 ， 采 通过 区间函数在模 糊有限元 中的应 用， 其转化 为模糊 信息熵 ， 而使得 将 从 模糊 问题 转化 为用概率方 法进行 分析 ， 在建立桁 架模 型进行 有限 元分析 中说 明该方法解 决 了模糊数和模糊 值函数运算基 于扩张原理 中存
＝
（ ， ） ， 女 ｌ
（ ，ｔ ） ｐ ， ｌ
Ｕ ＝“， ，） ｝ （ ＝… ｒ ，（ ｉ“ ￡ ｌ ｉ Ｌ ， ， ２…， ， Ｊ ） 、
＝
ｎ 结 构 自 由度 数 。 为 对 模 糊 平 衡 方 程 （ ） 不 同 的 水 平 截 １作 集 ， 可 得 到 一 列 系 数 为 区 间 的 线 性 方 就 一系 程组 。
ｌ ，．， 。．【 ， ＿ ］ 【， 。［ ．．， ‘］Ｉ ， １ ｋ】 ， ］．生 【
【 】 Ｐ， 【 】 Ｐ，
一
ｌ ｋ］ ｋ］， ｋ］ ， ｆ ２【 ２ 【 ｌ ｌ ［ １ ， … ， ， ， ｎ
上 式 可 简 记 为
Ｕ＝ｆ ｆ
Ｅ ＝ ．５ ０ Ｅ ＝ ． ５ ０ 节点 ８ 中力为５ ０ １ ０ ７Ｅ ，２ １２ Ｅ 。 集 ． ０Ｎ 对 于 信 息 本质 上是 随机 的 ， 可以 采 用 非 Ｘ １ 。 用信 息 熵 的转 化 方 法 可 将 模 糊 变 量 转 决 定 论 的 统 计 方 法 来 处 理 。 用 统 计 力学 采 则 中 “ ” 个 词 ， 出 了用 信 息 熵 对 概 率 信 换 为 等 效 的正 态 随 机 变 量 。 其 变 异 系数 熵 这 提 Ｖ ＝ ０． ５。 ０９ 息 进行 度量 的方 式 ， 这 类熵 称 为 概 率 熵 把 … 再 采 用 Ｍｏ ｔ －Ｃａ ｌ 法 求 解结 构 节 点 ｎｅ ｒｏ 信 息论 中 则把 它 作 为随 机 变 量 无 约 束程 内 样 ０ 编 度 的 一 种 度 量 。 可 以 看 作 对 参数 不 确 定 位 移 、 力 的 统 计 特 征 ， 本 数 ８ ０。 写 熵 Ｉ ＡＢ ｘ ｍｐ ｅ 。 性 的 一 种 度 量 。 确定 性 越 大 ， 就 越 大 。 不 熵 的ＭＡＴ 程序 为ｅ ａ ｌ２ 将 自编程 序 ａ ｓｓ 其 对 于 连 续 随机 变 量 Ｘ， 概 率熵 定义 如 ￣ ｎ ｙ 运 算 结 果 的 对 比 。 中随 机 变量 取 其 的 是 它 的 均 值 。 出 节 点 位 移 的 方 差 都 是 看 下 ： ０． ０ ７， 主 要 是 与 随 机 变 量 为 有 关 ， Ｏ０ 这 而 Ｈ ＝一Ｉ （） ｐｘｄ ｘｌ （）ｘ ｐ ｎ （ 通 过 结 构 的 有 限 元 计算 得 出 节 点 位 移 ， ６ ） 参 随 着 对 信 息 理 解 的 不 断 深 入 ， 们 注 数 的 随 机 性 决 定 了 位移 的 随 机 性 ， 人 因此 用 意 到 信 息并 非 必 然 具 有 概 率 的 性 质 。 许 Ｍｏ ｔ －Ｃ ｒｏ 在 ｎ ｅ ａ ｌ 方法 得 出 的 节点 位 移 统计 特 多场 合 下 ， 能 不 存 在 统 计 意 义 下的 概 率 ， 征 都具 有 相 同 的 方 差 ， 就 是 说 当 结 构 的 可 也 比 如 某 些 “ 验 ” 能 重 复 进 行 ， 此 无 法 随 机性 因 素 ， 有 限 元 计 算 结 果 中 得 到 反 试 不 因 在 用 概 率 理 论 来 描 述 这 类试 验 。 但是 ， 们 『 映 。 ｎ ｅ ａ ｌ 方法 与ａ ｓ ｓ 人 乃 Ｍｏ ｔ —Ｃ ｒｏ ｎ ｙ 运算 结 果对 能 从 试 验 中获 取 信 息 ， 就 说 明 应 该 存 在 比 ， 这 反映 出节 点位 移 有 差 距 ， 方面 存 在 计 一 着 一 类 “ 概 率 信 息 ” 而 “ 糊 信 息 ” 是 算 误差 ； 非 ， 模 则 另一 方 面Ｍｏ ｔ － ａ ｌ 方法 主要 反 ｎｅ Ｃ ｒ ｏ 种 重 要 的 非 概 率 信 息 。 模 糊 信 息 也 应 映 了节 点 统 计 特 征 ， 样 本 较 大 的 情 况 下 对 在 该 可 以 用 信 息 熵 来 度 量 ， 们 把 这 种 用 来 可 以 反 映结 构 响 应 ，ｎ ｙ 的运 算 反 映 了 变 我 ａｓｓ 度 量 模 糊 信 息 的 熵 称 为 模 糊 熵 ， 是 对 模 量 主值 的运 动情 况 ， ｎ ｅ Ｃ ｒ 方法 可 以 它 Ｍｏ ｔ — ａ ｌ ｏ 糊 集 所 含 模 糊 性 大 小 的一 种 度 量 。 代 表ａ ｓ ｓ ｎ ｙ 的运 算 结 果 。 在 保 证 熵 不 变 的 前 提 下 ， 以 将 模 糊 可 变 量 转 换 为 随 机 变 量 。 换 的 原 则 是 随 机 ４ 结语 转 在 模 糊 分 析 中 ， 糊 数 和 模 糊 值 函 数 模 变量的 等效熵等 于原来模糊 变量的熵 ， 即 运 算 都 是 基 于 扩 张 原 理 的 形 式 给 出的 ， 存 满 足 下 式 使 Ｇ’ （） 在 遍 历 性 的 困 难 ， 得 模 糊 方 程 的 求 解 变 ’ 得 异 常 困难 。 利 用 模 糊 有 限 元 和 信 息 熵 而 在 这 里 我 们讨 论 将 模 糊 变 量 转 换 为等 方 法 可 以有 效 解 决 模 糊 数 和 模 糊值 函数 的 效 的 正 态 随 机 变 量 ， 为 正 态 分 布 是 工 程 因 解 析 表 达 问题 ， 得 模 糊 分 析 计 算 得 到 简 使 中 最 常 见 的 随 机 变 量 分 布 形 式 。 论 上 是 理 化 ， 克 服 模 糊 运 算 的 一 个 有 效 工具 。 是 可 以 将 模 糊 变 量 转变 为任 意 我们 所 期 望 的 分布 。 参考文献 假 设 模 糊 变 量 Ｙ的 隶 属 函数 为 ｆｙ） 经 （ ， ［】吕恩琳 ． １ 结构 模 糊 有 限 元平 衡 方 程 的 一 等 效转 换后 成 为 正 态 随 机 变 量 ｘ。 ｘ的 均 值 种新 解 法【］应 用 数学 和 力 学 ， ９ ７ １ Ｊ． １ ９ ， ８ ｍ ， 准 差 为 。。 设 等 效 正 态 随 机 变 量 ｘ 标 假 （ ： ４）９～ １ ３． 的 均 值 ｍ等于 不 考 虑 该 变 量 模 糊 性 时 变 量 ［］郭 书 祥 ， 震 宙 ． 间 有 限 元静 力控 制 ２ 吕 区 的 值 。 以 得 到ｘ的概 率 熵 为 ： 可 方 程 的 一种 迭 代解 法 ［ 西北 工 业 大 学 Ｊ． Ｊ 学 报 ， ０ ２， ０ １ ： １ ｌ ７ ２ ０ ２ （ ） １ ４～ １ ． Ｈ ＝Ｉ（ ２ ） ｎ √ Ｐ （） ８ ［】郭 嗣 琮 ， 刚 ． 息 科 学 重 的 软 计 算 方 ３ 陈 信 法【 ． 阳： Ｍ］ 沈 东北 大 学 出版 社 ， ０ ． ２ ０１ ３ 实例分 析 ［】郭嗣 琮 ． 于 结 构 元理 论 的 模 糊数 学 分 ４ 基 在 框 架 结 构 中 ， 凝 土 采 用 ｃ２ ， 轴 混 ５其 析 原理 ［ ］沈 阳 ： 北 大学 出版 ， ０ ４． Ｍ ． 东 ２０ 心 抗 压 强度 设计 值ｆ ＝ｌ ５ ｍｍｓ 抗 拉 强 ［】汪 培 庄

多层建筑结构设计中框架结构的问题分析与处理多层建筑结构设计中，框架结构是一种常见的结构形式，其稳定性和安全性直接关系到建筑物的使用寿命和安全性。

在实际的设计与建造过程中，框架结构也会面临一些问题和挑战，需要合理分析和有效处理。

本文将针对多层建筑结构设计中框架结构的问题进行分析与处理，并提出相应的解决方案。

一、框架结构的问题分析1. 水平荷载作用下的稳定性问题在多层建筑中，由于外界环境的影响以及建筑本身的荷载等因素，建筑结构会受到水平方向的力的作用，如风荷载、地震荷载等。

这些水平荷载对框架结构的稳定性会产生一定影响，如果不合理设计或施工不规范，则容易导致结构发生侧移、倾斜甚至倒塌的危险。

2. 纵向荷载作用下的承载能力问题除了水平荷载外，建筑结构还会受到纵向方向的荷载作用，包括建筑物自身重力荷载、使用荷载等。

如果框架结构的承载能力不足，会导致结构变形过大，甚至发生破坏，影响建筑物的使用安全性。

3. 建筑结构与非结构构件的协调问题在实际建筑中，除了框架结构外，还有大量的非结构构件，如幕墙、内墙、屋面等，这些构件与框架结构之间需要进行协调和配合，以保证整个建筑结构的稳定性和安全性。

由于设计与施工中的误差以及材料的不均匀性等因素，会导致结构与非结构构件之间的协调出现问题，从而影响建筑物整体结构的稳定性。

4. 结构材料的选择与性能问题框架结构在设计中所选用的结构材料的性能直接关系到结构的稳定性和安全性。

不同的结构材料具有不同的力学性能、耐久性和抗震性能，而且在实际使用中还需要考虑到材料的施工工艺等因素。

结构材料的选择与性能问题是框架结构设计中需要重点关注的问题之一。

1. 结构稳定性分析与优化设计对于框架结构在水平和纵向荷载作用下的稳定性问题，可以通过有限元分析等手段对结构进行全面稳定性分析，找出结构的弱点和不足之处，并针对性地进行优化设计。

在结构柱的设计中可以采用加强加固的设计手段，提高结构的承载能力和抗侧移能力。

外加载荷条件下框架结构的有限元分析
张贺;王建楹;尹恩华
【期刊名称】《机械工程与自动化》
【年(卷),期】2024()1
【摘要】以某高铁接触网参数测量装备车体框架为分析对象,运用三维软件建立实体三维模型,并通过ANSYS对车体框架进行在外加载荷状态下的静力学分析,探究车体框架在外加载荷工况下的受力特性。

通过静力学分析,得知车体框架的选型满足强度和刚度设计要求。

最后根据结构的实际受载情况,对车体框架进行了预应力条件下的模态分析,通过对前6阶模态振型云图分析,得知了车体框架结构的低阶固有频率范围,为驱动电机的选型及对结构的进一步优化提供了参考。

【总页数】3页(P92-94)
【作者】张贺;王建楹;尹恩华
【作者单位】中船重工海为郑州高科技有限公司
【正文语种】中文
【中图分类】TP391.7
【相关文献】
1.立式玻璃钢贮罐水压静载荷条件下的有限元分析
2.热载荷条件下TiO2薄膜热应力有限元分析
3.面载荷工况条件下三维有限元分析下颌第一磨牙的应力情况
4.多种冲击载荷条件下的人体肋骨骨折有限元分析
因版权原因，仅展示原文概要，查看原文内容请购买。

第３ ０卷增
刊
辽 宁工程技 术 大 学学报 （自然科 学版 ）
Ｊ ｕ ｎ ｌ ｆ ａ ｎ ｎ ｅｈ ｉａ ｉｅｓｔ （ ｔ ｒｌ ｃｅ ｃ ｏ ｒ ａ ｏ ｉｇＴ ｃ ｎ ｃ ｌ ｏ Ｌｉ Ｕｎｖ ｒｉ ｙ Ｎａｕ ａ ｉｎ ｅ） Ｓ
２ １ 年 ５月 ０１
Ｍａ Ｖ ２０ｌ １
ቤተ መጻሕፍቲ ባይዱ转化为模糊信息熵 ， 从而使得模 糊问题转化 为用概率方法进行分析 ， 在建立桁架模 型进行有 限元分析 中说 明该方
法 解 决 了基 于 扩 张 原 理 的 模 糊 数 和 模 糊 值 函 数运 算存 在 的遍 历 性 网难 ，是 解 决工 程 模 糊 问题 有 效 途 径 。 关键 词 ：框 架 结 构 ；模 糊 有 限 元 ； 数 值 模 拟 ；模 糊熵 中 图分 类号 ：Ｔ ７ ｕ３５ 文献 标 识 码 ：Ａ
［ ｛ ＝ ） （） １ 式 中 ， 【 是 模糊 刚度矩 阵，［ 是模 糊位 移 向 阚
统计 的办法 外 ，这种 不确 定性 问题 也属 于模 糊数 学
范 畴 。吕恩琳解 决 了区 间数方 程组 解 的定义 与结 构
量， ｝ 是模糊 载荷 向量 。当采用 Ｌ Ｒ型模 糊数 作模 — 糊 信 息 的 描 述 和 处 理 时［ ， ， ） 的 元 素 均 为 ［ 中
Ｆｉｉ ｌｍ ｅ ｔ ｎ ｌｓｓ ｆ ｒ ｓ ｍ ｃｕ ｅｗｉ ｚ ｙｐ ｒ ｍｅｅｓ ｎ ｔ ｅｅ ｎ ａｙ ｉ ｏ ｓ ｔ ｔ ｒ ｔ ｆ ｚ ａａ ｔｒ ｅ ａ ｔ ｅ ｓ ｈ ｕ
ＭＡＹ ｎｕ ｎ ａ ｊ ａ ，ＧＡ Ｌ ａ ｈ ｉ ｏ ｉｎ ａ
（ ｉｉＲ ｏ ｏ ｅ ｈ ｉａ ｐ ｒｍｅ ｔＳｎ ｍａＥ ｅｇ ｎ ｅｖ ｔ ｎＬ ｄ， ｉｎ ｉ ０ ４ ０ Ｃ ｉａ Ｃ ｖｌ ｏ ｍ ｆ ｃ ｎｃ ｌ ａ ｔ ｎ， ｉｏ ｎ ｒ ｙＣｏ ｓｒ ａｉ ｔ．Ｔａ ｊ ３ ０ ０ ， ｈｎ ） Ｔ Ｄｅ ｏ ｎ

第38卷第3期2006年6月 南　京　航　空　航　天　大　学　学　报Jou rnal of N an jing U n iversity of A eronau tics &A stronau ticsV o l .38N o.3　Jun .2006动力学有限元模型的模糊评估张安平　王　轲(南京航空航天大学航空宇航学院,南京,210016)摘要:由于结构动力学有限元模型的评估具有主观性,本文将模糊数学有关理论应用于动力学有限元模型的评估,提出了一种动力学有限元模型的一致性模糊综合评估方法。

评估中将动力学模型计算振型、频率与试验结果相比较,通过建立模型的评判对象因素集、评价集和权重集,寻找隶属函数,构造模糊关系矩阵,完成有限元模型的模糊综合评估。

该方法不仅能界定有限元模型是否可用,还能对多个模型进行排队选优。

文中算例表明了该方法对单个模型评估准确,并能从多个模型中选出最优者。

关键词:结构动力学;综合评估;模糊数学;模态;有限元中图分类号:TB 12 文献标识码:A 文章编号:100522615(2006)0320367206　基金项目:航空科技预研基金(102010603.2)资助项目。

　收稿日期:2005204201;修订日期:2005205211　作者简介:张安平,男,硕士研究生,1979年9月生;王轲(联系人),男,副教授,硕士生导师,E 2m ail :W angk @nuaa .edu .cnFuzzy Eva lua tion of D ynam ics F i n ite Elem en tM odelZ hang A np ing ,W ang K e(Co llege of A ero space Engineering ,N an jing U n iversity of A eronau tics &A stronau tics ,N an jing ,210016,Ch ina )Abstract :D ue to the evaluati on of structu ral dynam ics fin ite elem en t m odel having the facto r of sub jec 2tivity ,the related theo ry of fuzzy m athem atics is u sed to evaluate the dynam ic fin ite elem en t m odel .A k ind of con sistency fuzzy com p rehen sive evaluati on m ethod fo r the dynam ic fin ite elem en t m odel is p re 2sen ted .Calcu lated shap es and frequencies of the dynam ics m odel are com p ared w ith that of the exp eri 2m en tal resu lts du ring the evaluati on .B y setting up facto r sets ,evaluati on sets and pow er sets ,iden tify 2ing the m em bersh i p functi on and con structing fuzzy relati on m atrix ,the fuzzy com p rehen sive evaluati on is fu lfilled .T he m ethod confirm s w hether the fin ite elem en t m odel is u sab le o r no t ,and select the best one am ong several m odels .T he exam p le show s that the m ethod is accu rate in evaluating one m odel and can select the best one from several m odels .Key words :structu ral dynam ics ;com p rehen sive evaluati on ;fuzzy m athem atics ;m ode ;fin ite elem en t引 言工程中所使用的有限元模型都是经结构简化得到的,通常检验建模准确性最好的方法是与试验结果相比较。