基于Matlab Simulink的直线ISG发动机起动力换向策略研究
- 格式:pdf
- 大小:334.07 KB
- 文档页数:6

基于MATLABSIMULINK的插床导杆机构运动学和动力学分析1基于MATLABSIMULINK的插床导杆机构运动学和动力学分析1插床导杆机构是一种常用于工业自动化中的机构,用于实现工件的夹持和定位。
该机构包括固定在机床上的床身、在床身上滑动的导轨和固定在导轨上的插块。
插块通过导杆与导轨相连,从而可以在导轨上沿水平方向移动。
在这个系统中,我们感兴趣的是插块的运动学和动力学分析。
首先,我们将利用MATLABSIMULINK的建模工具箱来建立插床导杆机构的运动学模型。
运动学模型描述了机构中各个部件的运动关系。
我们可以使用MATLABSIMULINK的基本几何构件,如块、源和终端等,来建立导杆机构的运动学模型。
假设我们已经测量了导杆的长度和导块的位置,并且我们还知道导杆与导轨之间的摩擦系数。
我们可以使用MATLABSIMULINK的代数运算器来计算导块的位移和速度。
在动力学分析中,我们可以利用MATLAB SIMULINK的自动求解器来求解导块在机构中的力学方程。
这些力学方程可以通过牛顿第二定律得到,即F=ma,其中F是力,m是质量,a是加速度。
我们可以使用MATLABSIMULINK的物理系统建模工具箱来建立机械系统的动力学模型。
该工具箱包含了众多应用于机械系统的物理模块,如质量、弹簧和阻尼器等。
通过建立机械系统的动力学模型,我们可以确定导块在机构中所受的力和扭矩。
对于这个系统,我们可以进一步使用MATLABSIMULINK的力学仿真工具来模拟导块在机构中的运动。
在仿真过程中,我们可以改变不同的系统参数,如导杆的长度和导块的质量,以研究它们对机构性能的影响。
此外,我们还可以模拟不同的工作条件,如不同的工件质量和工件的夹持力。
综上所述,基于MATLABSIMULINK的插床导杆机构的运动学和动力学分析提供了一个强大的工具,用于研究机构的运动性能和设计优化。
通过使用MATLABSIMULINK的建模和仿真功能,我们可以更好地理解和改进机构的性能。

基于MATLAB/SIMULINK的插床导杆机构运动学和动力学分析杨启佳1,徐承妍2,李滨城1(1. 江苏科技大学机械工程学院,江苏镇江212003)(2. 华东师范大学软件学院,上海200062)摘要:在对插床导杆机构进行分析的基础上,运用MATLAB/SIMULINK软件对其进行运动学分析和动力学分析,并将分析结果可视化,为应用MA TLAB/SIMULINK对其它机构进行分析提供了借鉴。
关键词:导杆机构;MA TLAB/SIMULINK;运动学分析;动力学分析中图分类号:TH112.1 文献标志码: AKinematic and dynamic analysis of leader mechanism of slotting machine based on MATLAB/SIMULINKYang Qi-jia,Xu Cheng-yan,Li Bin-Cheng(School of Mechanical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China) ( Software Engineering Institute, East China Normal University , Shanghai 200062, China)Abstract: Based on the analysis of leader mechanism of slotting machine, kinematic and dynamic analysis of leader mechanism was analyzed by software MA TLAB/SIMULINK. The analysis results were made visual. The content of this paper can provide a reference to the analysis of other mechanisms by MA TLAB/SIMULINK.Key words:leader mechanism; MA TLAB/SIMULINK; kinematic analysis; dynamic analysis连杆机构因其承载能力大、润滑性好、加工容易、可靠性好等优点被广泛地应用于机械各领域。

基于MATLAB/SIMULINK的混合动态模拟线性步进电机Szabó Loránd1 – Ioan-Adrian Viorel2 – Józsa János3摘要:直线电机的主要优点是,他们不把电能转换为旋转运动,而直接转换为线性运动。
发动机的电枢负载直接耦合,提供了另外几个优势的性能,高速度,高精度,无隙,高刚度,快速响应和时间稳定。
在这种情况下,它是对新型的高性能混合线性直接驱动步进电机的模块化的一种研究。
用MATLAB / Simulink ®环境对计算机模拟得到的结果仿真,并对电机的配置进行研究。
1.引言线性电机由旋转音圈电机和负荷直接刚性连接的。
不用的有滚珠、齿轮、皮带、和滑轮。
所有这些创造出优势是简单、高效、定位精度。
特别是加速度,可以显著的从这些旋转的直线运动发动机和传统的转换发动机比较中看出。
通过一些众所周知的文献和广泛的利用中也发现了线性步进电动机的一些缺点。
在任何一个位置原动机中的一个极都会引起很大的破坏力,减少了切向力。
这种方式,其总体的效率是降低了。
此外磁通量通过原动机和在两个电枢之间两极的滚筒通过引起了很强的法向力之间的吸引力。
最大的法向力是上述两个相同电极发生破坏力所产生的。
为了消除这些不足,提出了一种模块化混合式直线步进电动机。
这种电动机的横截面图已经给出了(图1)。
电机的先行者的讨论是建立了四个独立的模块,被四分之一的XX所取代。
每个模块有两个磁极,永久磁铁和线圈的命令。
该命令线圈放在核心分支平行于永久磁铁。
模块的两极间距在仿佛一极的牙齿与牙齿的排列方式压板,比另一极的牙齿也与滚筒的牙齿对齐。
滚筒是等距离的,从高渗透冷轧钢板制作任何长度的齿列。
在两个转子的齿结构具有相同音高的罚款牙齿。
空气轴承系统维护所需的两个转子之间的航空期间动议人的旅行沿着滚筒的差距,在低分辨率提供直,僵硬,齿轮,自由运动,保证了电机的寿命几乎无限像古典混合线性步进电机,这种电机的变体也正在变磁阻组合原则和永磁电动机运行[4]。

车辆工程基于MATLAB的动力性仿真分析及优化设计程序n=linspace(600,4000,100); %均分计算指令,600最低转速,4000最高转速,均分为100等分r=0.367;i0=5.83;nt=0.85;G=3880*9.8;f=0.013;CDA=2.77;If=0.218;Iw1=1.798;Iw2=3.598;m=3880;L=3.2;a=1.947;hg=0.9;ig=[6.09,3.09,1.71,1.00]; %输入已知参数ua1=0.377*r*n/i0/ig(1);ua2=0.377*r*n/i0/ig(2);ua3=0.377*r*n/i0/ig(3);ua4=0.377*r*n/i0/ig(4); %各转速各挡位下的速度Tq=-19.313+295.27*(n/1000)-165.44*(n/1000 ).^2+40.874*(n/1000).^3-3.8445*(n/1000).^ 4; %从600~4000rpm油拟合公式计算发动机转距Ft1=Tq*i0*ig(1)*nt/r;Ft2=Tq*i0*ig(2)*nt/r;Ft3=Tq*i0*ig(3)*nt/r;Ft4=Tq*i0*ig(4)*nt/r; %从600~4000rpm各挡位的驱动力Ff=G*f;ua=linspace(0,200,100);Fw=CDA*ua.*ua/21.15; %空气阻力plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua,F f+Fw); %画出各挡位的Ua-Ft,及Ua-Ff+Ft xlabel('ua/ km/h');ylabel('F/N'); %标注横纵轴title('汽车驱动力-行驶阻力平衡图'); %标注图形题目gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gt ext('Ft4'),gtext('Ff+Fw'); %给每根线条添加符号legend('Ft1','Ft2','Ft3','Ft4','Ff+Fw');%标注图例umax=max(ua4);disp('汽车最高车速=');disp(umax);disp('km/h');imax=tan(asin(max((Ft1-(Ff+Fw))/G))); %最大爬坡度的公式disp('汽车最大爬坡度=');disp(imax); %输出最高车速,与最大爬坡度的结果n=600:1:4000; %600最低转速,4000最高转速,相邻数组间隔1r=0.367;i0=5.83;eff=0.85;f=0.013;CdA=2.77;m=3880;g=9.8; %输入已知参数G=m*g;Ttq=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4 ;%从600~4000rpm油拟合公式计算发动机转距for ig=[6.09,3.09,1.71,1.00]Ua=0.377*r*n/ig/i0; %各转速各挡位下的速度Pe=Ttq.*n/9550; %各转速下的功率plot(Ua,Pe);hold on; %使当前轴及图形保持而不被刷新,准备接受此后将绘制的图形,多图共存endUa=0:0.1:max(Ua);Pf=G*f*Ua/3600; %滚动阻力Pw=CdA*Ua.^3/76140; %空气阻力plot(Ua,(Pf+Pw)/eff);title('汽车的功率平衡图'),xlabel('Ua/(km/h)'),ylabel('P/kw'); %画出汽车的功率平衡图gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gt ext('Ft4'),gtext('(Pf+Pw)/nt');legend('Ⅰ','Ⅱ','Ⅲ','Ⅳ','Pf+Pw/nt');n=600:1:4000; %600最低转速,4000最高转速,相邻数组间隔r=0.367;i0=5.83;nt=0.85;f=0.013;CdA=2.77;m=3880;g=9.8; %输入已知参数G=m*g;Ttq=-19.313+295.27*n/1000-165.44*(n/1000) .^2+40.874*(n/1000).^3-3.8445*(n/1000).^4 ;%从600~4000rpm油拟合公式计算发动机转距for ig=[6.09,3.09,1.71,1.00] Ua=0.377*r*n/ig/i0;Ft=Ttq*i0*ig*nt/r;Fw=CdA*Ua.^2/21.15;D=(Ft-Fw)/G %汽车动力因子公式plot(Ua,D); %画出汽车动力特性图hold on; %使当前轴及图形保持而不被刷新,准备接受此后将绘制的图形,多图共存endf=0.0076+0.000056*Ua %滚动阻力与速度之间的关系plot(Ua,f); %画出速度与滚动阻力图title('汽车动力特性图'), %给图加题目xlabel('Ua/(km/h)'),ylabel('D');gtext('Ⅰ'),gtext('Ⅱ'),gtext('Ⅲ'),gtext('Ⅳ'),gtext('f');legend('Ⅰ','Ⅱ','Ⅲ','Ⅳ','f');n=600:10:4000; %600最低转速,4000最高转速,相邻数组间隔10m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[6,09 3.09 1.71 1.00];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598; %输入已知参数Tq=-19.313+295.27*(n/1000)-165.44*(n/1000 ).^2+40.874*(n/1000).^3-3.8445*(n/1000).^ 4;%从600~4000rpm油拟合公式计算发动机转距Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r; %各转速各挡位下的驱动力ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0; %各挡位各转速下的速度Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;Fw4=CDA*ua4.^2/21.15; %不同速度下的空气阻力Ff=G*f;deta1=1+(Iw1+Iw2)/(m*r^2)+(If*ig(1)^2*i0^ 2*nT)/(m*r^2);deta2=1+(Iw1+Iw2)/(m*r^2)+(If*ig(2)^2*i0^ 2*nT)/(m*r^2);deta3=1+(Iw1+Iw2)/(m*r^2)+(If*ig(3)^2*i0^ 2*nT)/(m*r^2);deta4=1+(Iw1+Iw2)/(m*r^2)+(If*ig(4)^2*i0^ 2*nT)/(m*r^2); %不同挡位下的汽车旋转质量换算系数a1=(Ft1-Ff-Fw1)/(deta1*m);ad1=1./a1;a2=(Ft2-Ff-Fw2)/(deta2*m);ad2=1./a2;a3=(Ft3-Ff-Fw3)/(deta3*m);ad3=1./a3;a4=(Ft4-Ff-Fw4)/(deta4*m);ad4=1./a4; %各挡位下的加速度plot(ua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4); title('汽车的加速度倒数曲线');xlabel('ua(km/h)'); ylabel('1/a)'); %作汽车加速度倒数曲线gtext('1/a1'),gtext('1/a2'),gtext('1/a3') ,gtext('1/a4');legend('1/a1','1/a2','1/a3','1/a4');n=600:10:4000;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[6.09 3.09 1.71 1.00];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598; %输入已知参数Tq=-19.313+295.27*(n/1000)-165.44*(n/1000 ).^2+40.874*(n/1000).^3-3.8445*(n/1000).^ 4;%从600~4000rpm油拟合公式计算发动机转距Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r; %各转速各挡位下的驱动力ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0; %各挡位各转速下的速度Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;Fw4=CDA*ua4.^2/21.15; %不同速度下的空气阻力Ff=G*f;i1=asin((Ft1-Ff-Fw1)/G);i2=asin((Ft2-Ff-Fw2)/G);i3=asin((Ft3-Ff-Fw3)/G);i4=asin((Ft4-Ff-Fw4)/G); %不同档位下的坡度plot(ua1,i1,ua2,i2,ua3,i3,ua4,i4);title('汽车的爬坡度图');xlabel('ua/(km*h^-1)');ylabel('i/%'); %作汽车的坡度图gtext('Ⅰ'),gtext('Ⅱ'),gtext('Ⅲ'),gtext('Ⅳ');m=3880;g=9.8;r=0.367;nt=0.85;f=0.013;CdA=2.77;i0=5.83;pg=7.1; %汽油的重度取7.1N/Lig=[6.09 3.09 1.71 1];n=600:1:4000;n0=[815 1207 1614 2012 2603 3006 3403 3804]; B00=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B10=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B20=[72.379 36.657 14.524 7.0035 4.4763 2.8593 2.9788 0.71113];B30=[-5.8629 -2.0553 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]; B40=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568]; %输入已知参数B0=spline(n0,B00,n);B1=spline(n0,B10,n);B2=spline(n0,B20,n);B3=spline(n0,B30,n);B4=spline(n0,B40,n); %使用三次样条插值,保证曲线的光滑连续ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0; %求出发动机转速范围内对应的3、4档车速Pe3=(m*g*f*ua3/3600+CdA*ua3.^3/76140)/0.8 5;Pe4=(m*g*f*ua4/3600+CdA*ua4.^3/76140)/0.8 5; %发动机功率for i=1:1:3401 %用拟合公式求出各个燃油消耗率b3(i)=B0(i)+B1(i)*Pe3(i)+B2(i)*Pe3(i).^2+ B3(i)*Pe3(i).^3+B4(i)*Pe3(i).^4;b4(i)=B0(i)+B1(i)*Pe4(i)+B2(i)*Pe4(i).^2+ B3(i)*Pe4(i).^3+B4(i)*Pe4(i).^4;%插值得出对应速度的燃油消耗率endQ3=Pe3.*b3./(1.02.*ua3.*pg);Q4=Pe4.*b4./(1.02.*ua4.*pg); %3.4挡等速百公里燃油消耗量plot(ua3,Q3,ua4,Q4);title('最高档与次高档等速百公里油耗曲线'); %画出最高档与次高档等速百公里油耗曲线xlabel('ua(km/h)'); ylabel('百公里油耗(L/100km)');gtext('3档'),gtext('4档');。

matlab simulink 动力学问题动力学问题是指研究物体运动、运动规律和动力学关系等方面的问题。
在工程领域中,动力学问题广泛运用于机械设计、控制系统设计、车辆动力学、机器人运动控制等方面。
Matlab Simulink是一款基于图形模型的设计与仿真环境,可以用于解决动力学问题。
Simulink提供了一种直观的、图形化的方式,允许用户将复杂的系统划分为多个模块,并通过信号连接这些模块,从而构建整个系统的模型。
用户可以在模型中定义系统的数学公式、边界条件、初始条件等,并基于这些模型进行仿真、分析和优化。
在动力学问题中,常常用到的公式包括牛顿第二定律、动量定理、角动量定理、能量守恒定律等。
以机械系统为例,当我们考虑一个物体受到外力作用时的运动情况时,可以利用牛顿第二定律来描述物体的运动规律。
根据牛顿第二定律,物体受力的大小与所受的加速度成正比,反方向与加速度相同。
因此,在Matlab Simulink中,我们可以通过建立物体的模型,在模型中加入受力的作用,并通过求解运动方程来得到物体的运动状态。
例如,考虑一个简单的弹簧振子系统,该系统由一个质量为m的物体和一个弹簧组成。
弹簧的劲度系数为k,物体受到地球引力的作用。
我们可以建立如下的模型来描述该系统的动力学问题:-建立物体的动力学方程:F = m*a,其中a表示物体的加速度,F表示作用在物体上的合力。
合力包括地球引力和弹簧的作用力,分别由mg和-kx表示,其中g表示地球的重力加速度,x表示弹簧的位移量。
-通过求解动力学方程,可以得到物体的加速度,进而得到物体的速度和位移。
在Simulink中,我们可以通过建立一个模块化的系统模型,将这些步骤一一对应地实现。
具体步骤如下:1.在Simulink中创建一个新模型。
2.在模型中添加一个纵向布局的框架,用于容纳其他模块。
3.添加一个输入信号,用于控制模型的运行时间。
4.添加一个数学运算模块,用于计算物体受力大小。
作者简介:赵立邺(1985-),男,硕士,研究方向:风电建模、风电并网。
收稿日期:2011-01-06基于Matlab/Simulink 直驱式永磁风力发电系统的建模与仿真赵立邺,孟镇(沈阳农业大学信息与电气工程学院,沈阳110161)摘要:直驱式风力发电系统不需要电励磁、噪声小、维护费用低、控制简单,在风力发电系统中越来越受到欢迎。
在Matlab/Simulink 环境下,建立了直驱式永磁同步发电机的风力发电系统仿真模型,模型通过对风速、风力机、永磁同步发电机、全功率变流器进行理论分析实现模型搭建,最终建成整个风力发电系统模型。
仿真结果表明,系统能够在不同风速下稳定运行,最终输出的电压波形近似正弦,谐波含量小。
关键词:直驱;永磁同步发电机;Matlab/Simulink ;仿真中图分类号:TM315文献标识码:A文章编码:1672-6251(2011)02-0030-03Modeling and Simulation of Direct-driver Permanent Wind PowerSystem Based on Matlab/SimulinkZHAO Liye,MENG Zhen(Information and Electric Engineering College of Shenyang Agricultural University,Shenyang 110161)Abstract:Direct -drive wind power generation systems become popular with the advantages of without the need for electricity excitation,low noise,low maintenance costs,simple control,etc.Based on Matlab/Simulink,the wind power system simulation model with Direct -drive permanent magnet synchronous generator was established in this paper.In the model of wind power generation system,by the analysis of the wind speed,wind turbines and permanent magnet synchronous generator,the whole power converters,the wind power generation system model was developed.Simulation results showed that the system can run in the stable way under different wind speeds,and the final output voltage waveform was approximate to sine with small harmonic content.Key words:direct-drive;permanent magnet synchronous generator;Matlab/Simulink;simulation农业网络信息AGRICULTURE NETWORK INFORMATION·研究与开发·2011年第2期风能作为一种无污染、可持续发展的能源越来越受到人类的重视。
基于VB和Matlab的光杆起升系统的动力学仿真
王二化;刘宏伟;孙新国
【期刊名称】《制造业自动化》
【年(卷),期】2009(031)006
【摘要】本文建立了光杆起升系统的动力学模型,并对其进行仿真计算.给出了起升系统的各阶固有频率及相应的主振型,给出了开始起升工况下起升系统各部件的载荷曲线、最大动载和动载系数,分析了各输入参数对动载系数的影响.以上理论分析,能为光杆起升系统的优化设计提供一定的理论依据.
【总页数】4页(P116-119)
【作者】王二化;刘宏伟;孙新国
【作者单位】南阳理工学院,南阳,473004;南阳理工学院,南阳,473004;南阳理工学院,南阳,473004
【正文语种】中文
【中图分类】TH113
【相关文献】
1.基于ADAMS和Matlab的大口径舰炮发射系统动力学仿真 [J], 侯健;樊龙龙;可学为
2.基于MATLAB和ADAMS发动机曲轴系统动力学仿真 [J], 武建新;李华强;庞茂盛
3.基于MSC-ADAMS的某型起升机构建模及起升工况动力学仿真 [J], 郭晓松;许倍榜
4.基于MATLAB/SIMULINK的单缸柴油机活塞曲轴系统动力学仿真 [J], 李同杰;王娟;孙启国
5.基于MATLAB对变频起重机起升机构动力学仿真与研究 [J], WANG Dahui;ZHAO Bin;LIU Yong;TANG Fuchun;YE Dingwu
因版权原因,仅展示原文概要,查看原文内容请购买。
28北京,2009年10月 A P C联合学术年会论文集基于M a t l a b/S i m u l i n k的直线I S G/发动机起动力换向策略研究王 哲,叶晓倩,邓 俊(同济大学,上海,200092)摘要:直线发动机舍弃了曲柄连杆机构,减少了发动机的摩擦损失,具有高效、轻量、低排放等特点。
与直线ISG相结合的直线ISG/发动机是一种可应用于串联式混合动力汽车的新型动力装置。
本文对一台直线ISG/发动机的起动过程进行了分析。
针对起动力换向模式,提出了两种可行方案,并通过Matlab/Simulink动力学仿真研究了不同起动模式下系统的运行特性,最终提出了优化方案。
结果表明:起动力的精确换向是直线ISG/发动机起动控制的关键;结合速度跟踪式仿真结果的变换向点位置跟踪起动模式不仅易于实现,且具有能量利用率高的特点。
主题词:直线ISG/发动机;Matlab/Simulink;起动过程;换向策略1 前言与传统发动机相比,直线发动机的最大特点是省去了用于刚性连接的曲柄连杆机构,通过液、电等介质实现“柔性”输出,从而避免传统内燃机中曲轴和轴承所消耗的大量摩擦热,以及由于曲柄滑块机构所引起的侧向力而造成的活塞上的摩擦[1]。
与直线ISG相结合的直线ISG/发动机是一种可应用于串联式混合动力汽车的新型动力装置,具有效率高、比功率大、结构紧凑、燃料适用性强等特点。
1998年,美国Sandia国家实验室开发了一种与直线发电机有机结合的内燃发电机,采用均质充量压燃的燃烧方式,实现了高效、轻量、有害气体排放低,并可适用于多种燃料[2]。
美国西弗吉尼亚大学试制了可用于混合动力汽车的自由活塞发动机/发电机系统,并对二冲程压燃直喷式样机的运动过程进行了热力学、动力学仿真[3]。
澳大利亚悉尼潘柏股份有限公司开发的潘柏系统(Pempek Systems)是一种新型的混合式引擎驱动发电机,加装该系统的串联式混合电力汽车的市内交通耗油量为传统汽车的四分之一,有效减少了有害废气的排放[4]。
在系统的起动研究方向,韩国Kyungnam大学对一台二冲程自由活塞发动/发电机样机的起动方式做了研究。
起动工况下,三相永磁直线电机向活塞组件提供推力,电磁推力的大小与方向由PWM逆变器通过控制电机的输入电流来进行调控[5]。
马来西亚Teknologi PETRONAS大学则提出了一种利用永磁无刷直流电机的方波电流控制,使活塞组件往复运动从而实现起动的方法。
该研究在进行起动力方向控制时,使起动力方向始终与活塞组件运动方向一致[6]。
美国西弗吉尼亚大学的混合动力车用直线发动机系统在样机试验初期阶段采用了定起动力换向频率的开环控制方案,研究结果表明,该系统在换向频率为20Hz的起动力作用下可实现成功起动[7]。
在我国,自由活塞技术尚处于起步阶段。
目前,浙江大学流体传动及控制国家重点实验室正致力于液压式自由活塞发动机的研究[8]。
在直线ISG/发动机系统的研究方向,有哈尔滨工业大学、上海交通大学与同济大学正在开展相关课题。
本文在前期研究的基础上,以直线ISG/发动机起动过程为研究对象,通过Matlab/ Simulink仿真分析,为该系统选出较为合适的起动力换向控制方案。
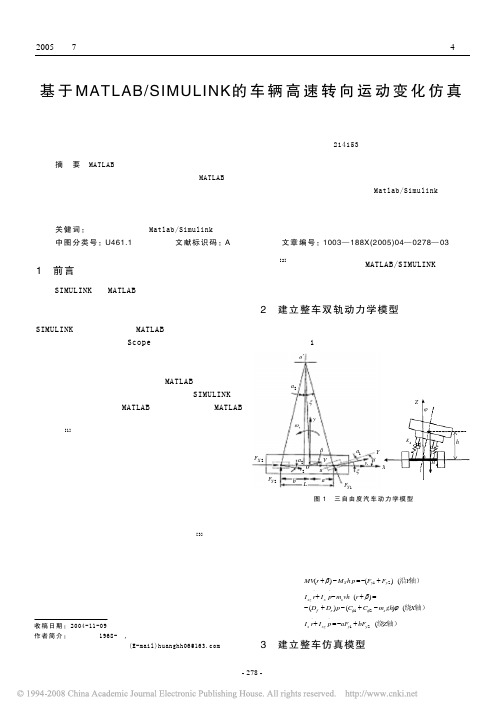
2直线I S G/发动机系统简介本文所研究的直线ISG/发动机系统结构如图1所示,它由两大部分组成:①直线发动机部分,包括:活塞、气缸、连杆轴、火花塞等;②直线ISG部分,包括:动子轴、动子永磁体,动子背铁、定子铁芯和定子线圈。
其中,发动机连杆轴与直线ISG的动子轴相集成,作为系统的活塞组件。
资助项目:上海市科委资助项目(08DZ1207700),上海市重点学科建设项目(B303)作者简介:王哲(1963-),男,教授,研究方向:汽车现代设计方法与理论Email: zhe.wang@北京,2009年10月 王哲等:基于Matlab/Simulink 的直线ISG/发动机起动力换向策略研究 29图1 双活塞对置式直线发动/发电机系统示意图 1—气缸 2—连杆轴 3—定子铁芯 4—活塞 5—火花塞 6—线圈 7—永磁体 8—动子背铁当系统处于起动工况时,直线ISG 作为电动机向活塞组件提供其所需的起动推力,拖动活塞组件往复运动,直至满足点火要求,混合气点燃,系统进入正常运行状态。
当系统正常运行时,左右两气缸内的可燃混合气轮流做功,推动活塞组件作直线往复运动。
同时,固定于活塞组件上的动子永磁体将产生运动的磁场,使布置于动子外部的定子线圈中产生感应电流,输出电能。
3 直线I S G /发动机起动过程的描述3.1 直线发动机的起动条件由于直线发动机的特殊结构型式,它的正常起动除了必须满足传统发动机对混合气准备以及起动转速的一般要求之外,还须具备以下特殊条件:1) 确保活塞组件在起动过程中能够获得足够的压缩比。
对于直线发动机来言,由于不受曲柄连杆机构的机械约束,其活塞组件的上下止点位置均不固定。
因此在起动过程中,不仅需保证足够高的起动运动频率,还必须确保活塞组件能够被拖动到合适的上止点位置,以获得足够的压缩比与缸内压力,从而使直线发动机成功点火起动。
2) 进行精确起动力换向控制的必要性。
由于在起动过程中直线发动机若要在左右两缸内将可燃混合气准备完毕,至少需要经历三个冲程[9]。
因此,在起动第一行程便拖动活塞组件至预定上止点位置的做法不仅对直线ISG 的工作能力提出了很高的要求,也是完全没有必要的。
故对直线发动机的起动过程做如下设想:令活塞组件在起动过程中做若干次循环的往复直线运动,使其行程在各循环中逐渐增加,直至达到合适的压缩比位置,满足混合气体的燃烧条件。
这就需要起动力能够适时地在直线发动机起动过程的各冲程间进行换向。
这也意味着直线ISG 的精确换相控制是起动控制的关键。
3.2 起动过程动力学模型图3 活塞组件的受力分析图直线ISG/发动机在起动过程中的受力情况如图3所示。
忽略扫气腔压力差的影响,活塞组件所受到的作用力包括电磁推力F e 、两缸气体压力差ΔF p (即起动压缩阻力)以及活塞组件与气缸间的摩擦力F f (即起动摩擦阻力)。
根据牛顿第二定律,可得到质量为m 的活塞组件的动力学模型如下:f p e F F F dt xd m −∆+=2 (1) ()()[]2D t p t p F r l p π⋅−=∆ (2)其中p l (t)和p r (t)分别为左右两缸内的气体压力,D 为缸径。
4 直线I S G /发动机起动过程仿真为实现系统起动过程中适时、精确的换向控制,下面提出两种较典型的直线发动机起动力换向策略。
4.1 速度跟踪模式速度跟踪换向模式是通过对电机动子的速度信号进行控制算法,来实现直线ISG 电磁力方向控制的方法。
这里采用ECU 在活塞组件的速度零点时刻发出起动力换向指令的控制策略。
直线ISG/发动机的起动过程的Matlab/ Simulink 动力学模型如图4所示。
其中,起动力大小|FE |为该模式下仿真程序的输入参数,即起动控制参数。
北京,2009年10月 王哲等:基于Matlab/Simulink 的直线ISG/发动机起动力换向策略研究30图4 速度跟踪模式动力学仿真模型图5给出了|FE |=135N 的起动工况下活塞组件的速度/位移曲线。
图6、7分别为活塞组件的位移&电磁力/时间曲线与速度&电磁力/时间曲线。
图5 |F E |=135N 时活塞组件的速度/位移曲线图6 |F E |=135N 时活塞组件的位移&电磁力/时间图图7 |F E |=135N 时活塞组件的速度&电磁力/时间图从图中可以看出,速度跟踪模式下,直线发动机的起动运动具有如下特点:① 起动过程中,活塞组件的位移/时间曲线近似于正弦分布,且频率、幅值随时间明显逐渐增大(图5、6)。
可见,速度跟踪式起动过程是直线发动机逐渐积累起动能量的过程。
该起动能量来自于起动蓄电池,能量以活塞组件动能以及发动机气缸内气体压缩能的形式积累储存。
② 起动力换向频率与活塞组件的往复运动频率相同。
由图7可看出,活塞组件的运动方向始终与起动力方向相一致。
这就表明:电磁起动力在整个起动过程中始终对活塞组件作正功,即蓄电池所提供的电能完全用于拖动发动机活塞组件起动,除直线ISG 效率损失外,理论上无电能的浪费。
4.2 位置跟踪模式位置跟踪换向模式是通过对电机动子的位置信号进行控制算法,来实现直线ISG 电磁力方向控制的一种方法。
该模式下,ECU 根据活塞组件在各个行程中是否到达起动力换向位置来判断换向时刻。
起动力换向点xp n (n为行程数)的合理设置是位置跟踪式起动控制的关键。
在起动过程中,换向点的位置可以始终保持不变,也可以根据不同行程进行不同的设计。
在此,首先对固定换向点的位置跟踪模式进行研究。
浙江大学流体传动及控制国家重点实验室所研制的液压自由活塞发动机便采用了固定换向点的位置跟踪模式来进行起动力换向控制[10]。
图8给出了该模式下直线ISG/发动机的起动过程动力学模型。
该模式下所需设定的起动控制参数包括起动力大小|FE |及起动力换向位置xp 。
图8 位置跟踪模式动力学仿真模型下面我们以|FE |=182N 、xp =15mm 时的起动工况为例,考察位置跟踪模式下直线ISG/发动机的起动特点:① 图9给出了该起动工况下直线发动机活塞组件的位移&电磁力/时间曲线。
可以看出,起动过程中活塞组件的运动曲线近似于正弦分布,且尽管所定义的各行程起动力换向位置相同,活塞组件的运行频率北京,2009年10月 王哲等:基于Matlab/Simulink 的直线ISG/发动机起动力换向策略研究 31及行程长度仍随时间逐渐增大。
与速度跟踪模式不同的是,位置跟踪式对活塞组件在起动各行程中的左右极限位置均有明确的要求,这是由起动力换向判断的定义所决定的。
倘若因为起动力过小或换向位置设计不当而造成活塞组件的左右止点达不到某一下限,即起动力换向位置,则起动力无法成功实现换向。
图10给出了起动第一行程中起动力换向失败时活塞组件的运动情况。
该工况下,活塞组件的极限位置为14.5mm ,未达到换向位置xp =15mm 的要求。
此时,活塞组件在电磁起动力的作用下做衰减振动,直线发动机起动失败。
由于位置跟踪模式对起动第一行程的行程长度就有一定的要求,因此相比速度跟踪模式,该模式通常需要更大的起动力来保证起动成功。
图9 |F E |=182N 、x p =15m m 时活塞组件的位移&电磁力/时间曲线图10 起动力换向失败工况(|F E |=175N 、x p =15m m )② 图11为活塞组件的速度&电磁力/时间曲线。
可以发现,位置跟踪模式下,活塞组件的运动换向点即速度零点一般滞后于起动力的换向时刻。