欧拉函数积性公式证明

欧拉函数（总结）定义欧拉函数ϕ(n)是不超过n且和n互质的正整数的个数。

欧拉函数φ(n)的作⽤就是转化，从⽽简化运算（⼩性质：n的所有质因⼦之和=eular(n)*n/2);下⾯直观地看看欧拉函数：n123456789101112131415φ(n)11224264641041268定理定理1 算术函数f如果满⾜对于任意两个互质的正整数m和n，均有f(mn)=f(m)f(n)，就称f为积性函数（或乘性函数）。

如果对于任意两个正整数m和n，均有f(mn)=f(m)f(n)，就称为完全积性函数。

定理2 若m、n互质，ϕ(mn)=ϕ(m)ϕ(n)，所以欧拉函数是积性函数。

因为mn互质，和m互质的数乘上和n互质的数就会和mn互质。

定理3欧拉函数的两种求法#include<iostream>using namespace std;int phi[100011];int eular(int n){//求⼀个数的欧拉值int res=n;if(n==1)return 1;for(int i=2;i<=n;i++){if(n%i==0){res=res/i*(i-1);while(n%i==0)n/=i;}}return n>1?res/n*(n-1):res;}void eularplus(int n){//求多个数的欧拉值for(int i=1;i<=n;i++)phi[i]=i;for(int i=2;i<=n;i++){if(phi[i]==i){for(int j=i;j<=n;j+=i)phi[j]=phi[j]/i*(i-1);}}}int main(){int n;scanf("%d",&n);printf("%d\n",eular(n));eularplus(n);for(int i=1;i<=n;i++)printf("%d ",phi[i]); printf("\n");return 0;}// 15// 8// 1 1 2 2 4 2 6 4 6 4 10 4 12 6 8。

高中数学120·同步辅导·选修2-2高中数学·北师大版2016年11月1欧拉公式的证明与应用【欧拉公式】公式：简单多面体的顶点数V 、面数F 及棱数E 之间有关系：2=-+E F V 。

【欧拉公式的证明】方法1：（利用几何画板）逐步减少多面体的棱数，分析E F V -+先以简单的四面体ABCD 为例：（分析法）去掉一个面，使它变为平面图形，四面体顶点数V 、棱数E 与剩下的面数1F 变形后都没有变。

因此，要研究2=-+E F V ，只需去掉一个面变为平面图形，证11=-+E F V ；（1）去掉一条棱，就减少一个面，E F V -+1不变。

依次去掉所有的面，变为“树枝形”。

（2）从剩下的树枝形中，每去掉一条棱，就减少一个顶点，E F V -+1不变，直至只剩下一条棱。

以上过程E F V -+1不变，则11=-+E F V ，所以加上去掉的一个面，2=-+E F V 。

对任意的简单多面体，运用这样的方法，都是只剩下一条线段。

因此公式对任意简单多面体都是正确的。

方法2：计算多面体各面内角和设多面体顶点数V ，面数F ，棱数E 。

剪掉一个面，使它变为平面图形（拉开图）,求所有面内角总和α∑；一方面，在原图中利用各面求内角总和。

设有F 个面，各面的边数为1n ,2n ，…，F n ，各面内角总和为：]180)2(180)2(180)2[(21︒⋅-++︒⋅-+︒⋅-=∑F n n n α︒⋅-+++=180)2(21F n n n F ︒⋅-=︒⋅-=360)(180)22(F E F E （1）另一方面，在拉开图中利用顶点求内角总和。

设剪去的一个面为n 边形，其内角和为︒⋅-180)2(n ，则所有V 个顶点中，有n 个顶点在边上，n V -个顶点在中间。

中间n V -个顶点处内角和为︒⋅-360)(n V ，边上的n 个顶点处的内角和︒⋅-180)2(n 。

则多面体各面的内角总和：︒⋅-=︒⋅-+︒⋅-+︒⋅-=∑360)2(180)2(180)2(360)(V n n n V α（2）由(1)(2)得：︒⋅-=︒⋅-360)2(360)(V F E ，所以2=-+E F V .【欧拉公式的意义】（1）数学规律：公式描述了简单多面体中顶点数、面数、棱数之间特有的规律；（2）思想方法创新：定理发现证明过程中，观念上，假设它的表面是橡皮薄膜制成的，可随意拉伸；方法上将底面剪掉，化为平面图形（立体图→平面拉开图）。

欧拉函数证明过程
欧拉函数,也称为phi函数或欧拉指标函数,是一个重要的数论函数,它用于统计小于或等于一个给定的正整数n,并且与n互素的正整数的个数。

欧拉函数的定义如下:
φ(n) = |{k ∈ Z+|1 ≤ k ≤ n, gcd(k, n) = 1}|
其中,|A|表示集合A的基数,Z+表示正整数集合,gcd(k, n)表示k和n 的最大公约数。

下面我们来证明欧拉函数的一个重要性质:
对于任意两个互质的正整数m和n,有φ(mn) = φ(m)φ(n)。

证明过程如下:
1. 先证明对于任意正整数n,有φ(n) = n∏p|n(1 - 1/p),其中p为n的不同素因子。

证明:对于n = ∏p_i^k_i,其中p_i为不同的素数,k_i为对应的指数。

每个p_i^k_i有p_i^(k_i-1)(p_i-1)个与它互质的正整数(详见"互质数的计数方法"),因此φ(n) = ∏(p_i^k_i - p_i^(k_i-1)) = n∏(1 - 1/p_i)。

2. 对于两个互质的正整数m和n,可以分解为m = ∏p_i^k_i,n = ∏q_j^l_j,其中p_i和q_j为不同的素数。

那么:
φ(mn) = mn∏p_i,q_j(1 - 1/(p_i*q_j)) = mn∏p_i(1 - 1/p_i)∏q_j(1 - 1/q_j) = mφ(m)nφ(n)/(mn)
= φ(m)φ(n)
这就证明了φ(mn) = φ(m)φ(n)。

欧拉函数及其证明欧拉函数定义：phi(n) = 1到n中与n互质的数的个数 有公式：　phi(n) = n* ∏ ( 1 - 1/pi ) 其中p为n的所有质因⼦,每个质因⼦只算⼀次下⾯是证明：1. 当n为质数，显然phi(n) = n-12. 当n=p^k ，其中p为素数 与n不互质的数必定有p因⼦，把p提出来 于是不互质的数有{ p*1, p*2, p*3, ......, p*p^(k-1) } 于是互质的数即phi(n) = p^k - p^(k-1) = p^k * ( 1 - 1/p )3. 当n= (x^a)*(y^a), 其中x和y为不相同的素数 有phi(n*m)=phi(m)*phi(n) , 当m和n互质 证明这个之前先证明 ( {1, 2, 3, 4, ....n } , {1, 2, 3, 4, ...... m }) 与 {1, 2, 3, 4, ...... m*n } ⼀⼀对应 (m,n互质) ①从m*n到（m,n）的唯⼀性 m*n中的x， x%m和x%n有唯⼀值 ②从(m,n)到 m*n的唯⼀性 设从m中取x，x%m=r 则x对应m*n中的f可能值为 {r, m+r, 2m+r, 3m+r, .... (n-1)*m+r } 这n个数组成了n的完全剩余系 因为这n个数两两之间的差值可表⽰为 k* m (k<n) 则（k*m）%n=0不成⽴（ k<n , ⽽gcd(m,n)=1 即 m不提供n的因⼦） 即每个数对n取模两两不同，则组成n的完全剩余系 因此假设再从n中取y，（x，y）可唯⼀确定⼀个m*n中的值 （似乎适⽤于中国剩余定理）可拓展到多维，即多个互质量 再看，（当m和n互质）只要x与m互质且x与n互质则x与m*n互质 任何与m互质的数x除以m的余数即（x%m）也必然与m互质，反之也如此 所以从（1...n）和（1...m）分别取x与n互质，y与m互质，则会唯⼀对应⼀个m*n中的值f 与m*n互质 ⽽每个与（1...m*n）互质的值 f 都会唯⼀对应⼀个（1...n）中与n互质的x和⼀个（1...m）中与m互质的y 所以phi(m*n) = phi(m) * phi(n) ， (m，n互质) 证明完毕那么这样，对于要求欧拉值的n，将他因数分解成 pi^ai, ⽽ phi(pi^ai )= pi^ai ( 1 - 1/pi )再将pi相乘得到n，就可以得出公式 phi(n) = n* ∏ ( 1 - 1/pi )代码：long long eular(long long n) {long long ans = n;for(int i = 2; i*i <= n; i++) {if(n % i == 0) {ans −= ans/i;while(n % i == 0)n /= i;}}if(n > 1)ans −= ans/n;return ans;}从证明可以看出，欧拉函数是⾮完全积性函数所以可以⽤线性筛来O(n) 预处理值bool check[maxn];int phi[maxn];int prime[maxn];int tot;//素数的个数void phi_and_prime_table(int n) {memset(check,false,sizeof(check));phi[1] = 1;tot = 0;for(int i = 2; i <= n; i++) {if( !check[i] ) {prime[tot++] = i;phi[i] = i-1;}for(int j = 0; j < tot; j++) {if(i * prime[j] > n)break;check[i * prime[j]] = true;if( i % prime[j] == 0) {phi[i * prime[j]] = phi[i] * prime[j];break;} else {phi[i * prime[j]] = phi[i] * (prime[j] - 1);}}}}性质：考虑gcd，假设i与n的gcd为g，那么有g|n , gcd(n/g,i/g)=1。

欧拉公式的运用及余元公式的证明1.欧拉公式的定义)0,0()1(),()0()(111010>>-⎰=B >⎰=Γ----+∞q p dx x xq p dxe x q p x ααα欧拉公式的几个基本变形：函数Γ)1(令2y x =, 就有)0(2)(212010>⎰=⎰=Γ--+∞--+∞ααααdy e y dx e x y x令py x =, 则有)0,0()(1010>>⎰=⎰=Γ--+∞--+∞p dy e y p dx e x py x ααααα特别地当21=α时，有π=Γ)21(且有)()1(αααΓ=+Γ 函数B )2(令ϕ2cos =x 就有ϕϕϕπd q p p q 121220cos sin 2),(--⎰=B令yyx +=1，则有 dy y y q p qp p +-∞++⎰=B )1(),(1欧拉积分间的联系：)()()(),(q p q p q p +ΓΓΓ=B )0,0(>>q p2.余元公式的证明余元公式：)sin()1,(ππa a a =-B对dt t ta a B a a a a a110)1()1,()1()(,10---⎰=-=-ΓΓ<<令xt +=11，则 x x dx x x x x dt t t a a a a a+⎰=+++⎰-=-⎰-∞--∞--1)1(1)1()11()1(10210110 dx xx dx x x a a +⎰++⎰=-∞-111111当10<<x 时，由幂级数理论可得()10111-+∞=-∑-=+k a kk a x x x 此级数在[]t ,ε其中10<<<t ε上一致收敛，故可在[]t ,ε上逐项积分，从而dx x dx xk a k k tk a k kt101)1()1(-+∞=-+∞=∑∑-⎰=-⎰εε=()()k a k a kk t ka ++∞=-+-∑ε110 ()()k a kk k a k k k a t k a +∞=+∞=+--+-=∑∑ε111100 （1） 因级数()ka kk t ka +∞=+-∑110的收敛半径为1，且1,0=t 时级数均收敛，由阿贝尔定理知： ()ka kk t ka +∞=+-∑110在[]1,0上一致收敛，故有 ()()ka kk kk t +-=-∑∑∞=∞=→111lim 001同理有()011lim 0=+-+∞=→∑+k a kk ka εε 在（1）式中，令+→→0,1εt 便有:=+⎰-dx xx a 1110()ka kk +-∑∞=110对得令tx dx xx a 1,111=+⎰-∞+dx x x a +⎰-∞+111==+⎰--dt tta 11)1(10()ak kk -+-∑∞=1110综上可得：=-ΓΓ)1()(a a dx x x a +⎰-∞+110=dx xxdx x x a a +⎰++⎰-∞+-1111110 ()k a kk +-=∑∞=110+()a k kk -+-∑∞=1110=+a1)11()1(0ka k a k k --+-∑∞= （2） 再由)cos(ax 在],[ππ-的Fourier 级数展式有)cos(ax =+aax 1[sin π())11(11ka k a kk -++-∑∞=)]cos(kx , ],[ππ-∈x 令0=x 可得+=aa 1)sin(ππ())11(11ka k a kk -++-∑∞= 从而由（2），（3）知余元公式成立。

欧拉函数欧拉函数直接计算公式 欧拉函数的定义: E（N）= ( 区间[1,N-1] 中与 N 互质的整数个数). 对于积性函数 F（X*Y），当且仅当 GCD（X，Y）= 1 时， F（X*Y） = F（X）* F（Y） 任意整数可因式分解为如下形式： 其中( p1, p2 ... pk 为质数, ei 为次数 )　 所以 因为欧拉函数 E（X）为积性函数，所以 对于，我们知道因为pi 为质数，所以 [ 1, pi-1 ] 区间的数都与 pi 互质 对于区间[ 1, ] ，共有个数，因为只有⼀个质因⼦， 所以与约数⼤于1 的必定包含质因⼦，其数量为　所以 ⼜ E（N）为积性函数，所以可得： ⼜因为其中( p1, p2 ... pk 为质数, ei 为次数 )　 但是此计算公式，除法过多，所以计算速度较慢 在程序中利⽤欧拉函数如下性质，可以快速求出欧拉函数的值 ( P为N的质因⼦ ) 若(N%P==0 && (N/P)%P==0) 则有:E(N)=E(N/P)*P; 若(N%P==0 && (N/P)%P!=0) 则有:E(N)=E(N/P)*(P-1);直接计算欧拉函数值代码：View Code#include<stdio.h>#include<string.h>#include<stdlib.h>#include<math.h>typedef long long LL;LL Eular( LL x ){if( x == 0 ) return0;LL res = 1, t = x;for(LL i = 2; i <= (LL)sqrt(1.*x); i++){if( t%i == 0 ){res *= (i-1);t /= i;while( t%i ==0 ){res *= i;t /= i;}}if( t == 1 ) break;}if( t > 1 ) { res *= (t-1); }return res;}int main(){LL x;while( scanf("%lld", &x) != EOF)printf("%lld\n", Eular(x) );return0;}关于欧拉函数其他的证明⽅式： 证明过程如下： 1. 容易想到：当n为素数时，PHI(n) = n - 1。

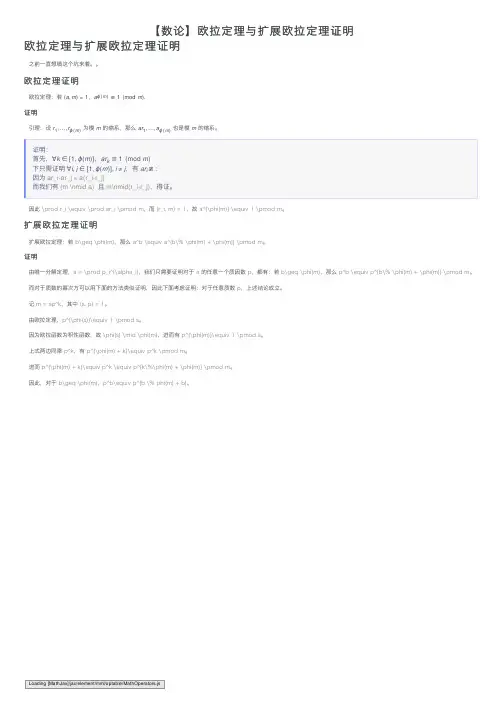
【数论】欧拉定理与扩展欧拉定理证明欧拉定理与扩展欧拉定理证明之前⼀直想填这个坑来着。

欧拉定理证明欧拉定理：若 (a,m)=1，aϕ(m)≡1(mod m).证明引理：设 r1,…,rϕ(m)为模 m的缩系，那么 ar1,…,aϕ(m) 也是模 m的缩系。

证明：⾸先，∀k∈[1,ϕ(m)]，ar k≡1(mod m)下只需证明∀i,j∈[1,ϕ(m)],i≠j，有ar i≢：因为ar_i-ar_j = a(r_i-r_j)⽽我们有(m \nmid a) 且m\nmid(r_i-r_j)，得证。

因此 \prod r_i \equiv \prod ar_i \pmod m，⽽ (r_i, m) = 1，故 a^{\phi(m)} \equiv 1 \pmod m。

扩展欧拉定理证明扩展欧拉定理：若 b\geq \phi(m)，那么 a^b \equiv a^{b\% \phi(m) + \phi(m)} \pmod m。

证明由唯⼀分解定理，a = \prod p_i^{\alpha_i}，我们只需要证明对于 a的任意⼀个质因数 p，都有：若 b\geq \phi(m)，那么 p^b \equiv p^{b\% \phi(m) + \phi(m)} \pmod m。

⽽对于质数的幂次⽅可以⽤下⾯的⽅法类似证明，因此下⾯考虑证明：对于任意质数 p，上述结论成⽴。

记 m = sp^k，其中 (s, p) = 1。

由欧拉定理，p^{\phi(s)}\equiv 1 \pmod s。

因为欧拉函数为积性函数，故 \phi(s) \mid \phi(m)，进⽽有 p^{\phi(m)}\equiv 1 \pmod s。

上式两边同乘 p^k，有 p^{\phi(m) + k}\equiv p^k \pmod m。

进⽽ p^{\phi(m) + k}\equiv p^k \equiv p^{k\%\phi(m) + \phi(m)} \pmod m。

一、引言在数学及许多分支中都可以见到很多以欧拉命名的常数、公式和定理。

在数论中，欧拉定理（Euler Theorem ，也称费马-欧拉定理或 欧拉函数定理）是一个关于同余的性质。

欧拉定理得名于瑞士数学家 莱昂哈德·欧拉，该定理被认为是数学世界中最美妙的定理之一，欧拉定理实际上是 费马小定理的推广.二、内容在数论中， 欧拉定理,（也称 费马--欧拉定理）是一个关于同余的性质。

欧拉定理表明，若n,a 为正整数，且n,a 互质，则： () 1( )n amod n ϕ≡. 1.知识准备：（1）欧拉函数 ：欧拉函数是数论中很重要的一个函数，欧拉函数是指：对于一个正整数 n ，小于 n 且和 n 互质的正整数（包括1）的个数，记作 φ(n) .（2）完全余数集合：定义小于 n 且和 n 互质的数构成的集合为 Zn ，称呼这个集合为 n 的完全余数集合。

显然 |Zn| ＝φ(n) 。

其中，“ |A |”表示这个集合中元素的个数，比如A=｛a,b} 则|A|=2.（3）有关性质：①对于素数 p ，φ(p) = p -1 。

②对于两个不同素数 p ， q ，它们的乘积 n = p * q 满足 φ(n) = (p -1) * (q -1). 因为Zn = {1, 2, 3, ... , n - 1} - {p, 2p, ... , (q - 1) * p} - {q, 2q, ... , (p - 1) * q} ， 则 φ(n) = (n - 1) - (q - 1) - (p - 1) = (p -1) * (q -1) ＝φ(p) * φ(q) .2.证明方法：证明：( 1 ) 首先证明下面这个命题：对于集合Zn = {x1, x2, ..., xφ(n)} ， S = {a*x1(mod n),a*x2(mod n),...,a*xφ(n)(mod n)} ，其中xi(i=1,2,…φ(n))是不大于n 且与n 互素的数，即n 的一个化简剩余系，或称简系，或称缩系)，则Zn = S .1) 由于a,n 互质，xi 也与n 互质，则a*xi 也一定于n 互质，因此 任意xi ，a*xi(mod n) 必然是Zn 的一个元素2) 对于Zn 中两个元素xi 和xj ，如果xi ≠ xj 则a*xi(mod n) ≠ a*xj(mod n)，这个由a 、n 互质和消去律可以得出。

欧拉函数（Euler_Function）⼀、基本概述在数论，对正整数n，欧拉函数varphi(n)是少于或等于n的数中与n互质的数的数⽬。

此函数以其⾸名研究者欧拉命名，它⼜称为Euler's totient function、φ函数、欧拉商数等。

⼆、计算公式三、基本性质欧拉函数⽤希腊字母φ表⽰,φ(N)表⽰N的欧拉函数.对φ(N)的值,我们可以通俗地理解为⼩于N且与N互质的数的个数(包含1).欧拉函数的⼀些性质:1.对于素数p, φ(p)=p-1，对于对两个素数p,q φ（pq）=pq-1欧拉函数是积性函数,但不是完全积性函数.证明：函数的积性即：若m,n互质,则φ(mn)=φ(m)φ(n).由“m,n互质”可知m,n⽆公因数,所以φ(m)φ(n)=m(1-1/p1)(1-1/p2)(1-1/p3)…(1-1/pn)·n(1-1/p1') (1-1/p2')(1-1/p3')…(1-1/pn'),其中p1,p2,p3...pn为m的质因数,p1',p2',p3'...pn'为n的质因数,⽽m,n⽆公因数,所以p1,p2,p3...pn,p1',p2',p3'...pn'互不相同,所以p1,p2,p3...pn,p1',p2',p3'...pn'均为mn的质因数且为mn质因数的全集,所以φ(mn)=mn(1-1/p1)(1-1/p2)(1-1/p3)…(1-1/pn)(1-1/p1') (1-1/p2')(1-1/p3')…(1-1/pn'),所以φ(mn)=φ(m)φ(n).即φ(mn)=φ(n)*φ(m)只在(n,m)=1时成⽴.2.对于⼀个正整数N的素数幂分解N=P1^q1*P2^q2*...*Pn^qn.φ(N)=N*(1-1/P1)*(1-1/P2)*...*(1-1/Pn).3.除了N=2,φ(N)都是偶数.4.设N为正整数,∑φ(d)=N (d|N).四、求欧拉函数1、埃拉托斯特尼筛求欧拉函数观察欧拉函数的公式，。

欧拉公式的证明
1欧拉公式
欧拉公式是18世纪数学家著名的欧拉提出的一条著名公式，公式如下：
$$\scr{V}-\scr{E}+\scr{F}=2$$
这公式定义的是`多边形的顶点数`减去`边数`加上`面数`等于2的公式。

它的意义是，如果一个平面图形的顶点数-边数+面数=2，那么这个图形将是一个封闭的封闭多边形图形。

2欧拉公式的证明
对于欧拉公式的证明，就是要证明一个封闭多边形图形，即一个环状图形，它的顶点数减去边数加上面数等于2。

给定一个封闭多边形图形，假设它包含v顶点，e边，f面，则按照绘图准则，有:
v-e+f=2
为了证明这个公式，先来看一下一个特殊情况，如果我们有一个三角形，则它有3个顶点，3条边和1个面，这时候，注意这个三角形是封闭的一个环，那么令v=3，e=3，f=1，原式如下:
V-E+F=3-3+1=2
根据上述特殊情况，说明了如果我们有一个封闭多边形，那么它的顶点数减去边数加上面数，等于2。

而当多边形更大一些时，比如四边形，有4个顶点，4条边，1个面，类似的，令v=4，e=4，f=1，原式如下：
V-E+F=4-4+1=2
所以，按照上述演示，当任何一个封闭多边形的顶点数减去边数加上面数，都等于2，就证明了欧拉公式有效。

结论
从上述演示来看，欧拉公式在封闭多边形的情况下是有效的，即多边形的顶点数减去边数加上面数等于2。