下载文档原格式
五年级数学上册全册教案(人教版)第一章：小数乘法教学目标：1. 理解小数乘法的意义，掌握小数乘法的基本运算方法。
2. 能够正确进行小数乘法的计算。
教学内容：1. 小数乘法的意义和运算方法。
2. 小数乘法的计算法则。
教学步骤：1. 引入小数乘法的概念，通过实际例题让学生理解小数乘法的意义。
2. 讲解小数乘法的运算方法，引导学生进行实际计算。
3. 总结小数乘法的计算法则，让学生能够独立进行计算。
教学评价：1. 通过课堂练习，检查学生对小数乘法的理解程度。
2. 通过课后作业，评估学生小数乘法的计算能力。
第二章：小数除法教学目标：1. 理解小数除法的意义，掌握小数除法的基本运算方法。
2. 能够正确进行小数除法的计算。
教学内容：1. 小数除法的意义和运算方法。
2. 小数除法的计算法则。
1. 引入小数除法的概念，通过实际例题让学生理解小数除法的意义。
2. 讲解小数除法的运算方法，引导学生进行实际计算。
3. 总结小数除法的计算法则，让学生能够独立进行计算。
教学评价：1. 通过课堂练习，检查学生对小数除法的理解程度。
2. 通过课后作业，评估学生小数除法的计算能力。
第三章：分数乘法教学目标：1. 理解分数乘法的意义，掌握分数乘法的基本运算方法。
2. 能够正确进行分数乘法的计算。
教学内容：1. 分数乘法的意义和运算方法。
2. 分数乘法的计算法则。
教学步骤：1. 引入分数乘法的概念，通过实际例题让学生理解分数乘法的意义。
2. 讲解分数乘法的运算方法，引导学生进行实际计算。
3. 总结分数乘法的计算法则，让学生能够独立进行计算。
教学评价：1. 通过课堂练习，检查学生对分数乘法的理解程度。
2. 通过课后作业，评估学生分数乘法的计算能力。
第四章：分数除法1. 理解分数除法的意义，掌握分数除法的基本运算方法。
2. 能够正确进行分数除法的计算。
教学内容：1. 分数除法的意义和运算方法。
2. 分数除法的计算法则。
教学步骤：1. 引入分数除法的概念，通过实际例题让学生理解分数除法的意义。
北师大版五年级数学上册小数点乘除讲解小数点乘除是五年级数学上册中的一个重要内容，下面将对它进行详细讲解。
首先，我们先来回顾一下小数点的基本概念和相关规则。
小数点是用来表示数的大小和位置的符号，它位于数的右边，表示数的整数部分和小数部分的分界线。
在小数点的左边是整数部分，右边是小数部分。
在小数运算中，我们需要掌握小数的加减乘除四则运算规则。
1.小数点的乘法：当两个小数相乘时，先按普通乘法计算出积，然后将积的小数点位置确定下来。
具体步骤如下：a.先将两个乘数的小数点去掉，按整数相乘计算出积；b.将积的小数点位置确定下来。
小数点的位置等于两个乘数的小数位数之和；c.将确定了小数点位置的积结果加上小数点。
例如：计算0.5 × 0.3。
a.先将0.5和0.3的小数点去掉，得到5 × 3 = 15；b. 0.5有一个小数位，0.3有一个小数位，小数位数之和为2，所以小数点位置在1的位置上；c.将15转化为小数，既得0.15。
所以0.5 × 0.3 = 0.15。
2.小数点的除法：当两个小数相除时，先确定商的整数部分，然后将商的小数部分按要求计算出来。
具体步骤如下：a.先将被除数和除数的小数点去掉，按整数相除计算出商；b.将商的小数部分计算出来。
计算方法有两种情况：-如果商是一个有限小数，那么将被除数的小数点向左移动和除数的小数位数相同的位置；-如果商是一个循环小数，那么将被除数的小数点向左移动，一直到商中出现重复的数字为止，并在重复的数字上方加上一对括号。
例如：计算0.47 ÷ 0.06。
a.先将0.47和0.06的小数点去掉，得到47 ÷ 6 = 7余5；b. 5是一个有限小数，所以将小数点向左移动两位得到0.83。
所以0.47 ÷ 0.06 = 7.83。
通过以上的讲解，我们对小数点的乘除运算应有了更清楚的理解。
但在实际运算中，还需要注意以下几个问题：1.确定小数点位置时，要注意两个乘数或被除数中小数部分的位数是否相同，不同的话需要进行补零操作。
五年级上学期小数乘除法（第一、三单元）知识点整理1、小数乘法一、规律1、积的扩大缩小规律：1）在乘法里，一个因数不变，另外一个因数乘几（0除外），积也乘几。
一个因数不变，另外一个因数除以几（0除外），积也除以几。
2）在乘法里，一个因数乘10，另外一个因数乘100，积乘1000（10×100）。
3）在乘法里，一个因数除以10，另外一个因数除以几100，积除以1000（10×100）。
以上两个变化规律为举例子2、积不变规律：（这个要与商不变的规律做个比较）在乘法里，一个因数乘几（0除外），另外一个因数除以几（0除外），积不变。
6.25×37=625×0.37 625×0.37=0.0625×37003、商不变的规律：（这个要与积不变的规律做个比较）在除法里，被除数和除数同时乘或者除以一个相同的数（0除外），商不变。
6.25÷37 = 625÷3700 62500÷3700= 625÷374、商变化规律被除数乘几，除数不变，商就乘几。
被除数除以几（0除外），除数不变，商就除以几。
被除数不变，除数乘几，商就除以几。
被除数不变，除数除以几（0除外），商就乘几。
二、1、小数乘整数计算方法：1）先把小数扩大成整数2）按整数乘法法则计算出积3）看被乘数有几位小数点，就从积的右边起数出几位点上小数点。
若积的末尾有0可以去掉2、小数乘小数的计算方法：1）先把小数扩大成整数2）按整数乘法乘法法则计算出积3）看积中有几位小数从积的右边起数出几位，点上小数点。
如果乘得的积的位数不够，要在前面用0补足。
3、计算结果发现小数末尾有0的，要先点小数点，再把0去掉。
顺序不可调换。
4、积的小数位数等于两个因数的小数位数之和。
5、小数点的位移规律：把一个小数扩大10倍、100倍、1000倍、……只要把小数点向右移动一位、两位、三位……位数不够时，要用“0”补足。
课题小数的乘除法讲义教学目标1、经历将整数乘整数转化为小数乘整数的过程，体会转化的思想2、感受小数乘法在生活中的广泛应用重点☆小数乘整数、小数乘小数的计算方法难点☆小数点的处理问题12知识梳理小数乘整数计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。
小数乘小数计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小 小数乘法 数，就从积的右边起数出几位点上小数点。
规律：一个数（0除外）乘大于1的数，积比原来的数大；一个数（0除外）乘小于1的数，积比原来的数小。
小数除以整数的计算方法：小数除以整数，按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除，商0，点上小数点。
如果有余数，要添0再除。
除数是小数的除法：先将除数和被除数扩大相同的倍数，使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。
小数除法 注意：如果被除数的位数不够，在被除数的末尾用0补足。
在实际应用中，小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数，求出商的近似数。
除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。
②除数不变，被除数扩大，商随着扩大。
③被除数不变，除数缩小，商扩大。
循环小数：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小 数叫做循环小数。
循环节：一个循环小数的小数部分，依次不断重复出现的数字。
如6.3232……的循环节是32。
小数部分的位数是有限的小数，叫做有限小数；小数部分的位数是无限的小数，叫做无限小数。
小数分类 按整数部分：纯小数（如：0.324 86.0 ） 带小数（如：13.6 92.14 ） 有限小数 纯循环小数（如：53.0 642.6 ） 无限循环小数按小数部分 无限小数 混循环小数（如：293.4 92.14 ） 无限不循环小数小数四则运算顺序跟整数是一样的。
人教版五年级数学上册1-4单元知识点第一单元小数乘法重、难点：小数乘以整数，确定积的小数点位置的方法（看因数中一共有几位小数，就从积的右边起数出几位，点上小数点）积的近似数：计算后如需保留几位小数的，先看需保留的后一位，如果≥5，则向前进一位，如果＜5，则要舍去。
最后用“≈”连乘、乘加、乘减：在小数混合运算中，运算方法和整数乘法一样，乘法的运算规律也适用于小数中。
一个数（0除外）乘以一个大于1的数，积比原来的数大。
一个数（0除外）乘以一个大于1的数，积比原来的数小。
必考点：列竖式计算小数乘法（积保留几位小数）小数乘法混合运算易错点：在列竖式计算的过程中小数点位置的确定。
第2单元小数除法重、难点：小数除以整数：商的小数点要和被除数的小数点对齐（如果有余数，应在被除数的末尾添上0再除）除数为小数，要把除数转换成整数（除数和被除数同时扩大相同的倍数），转化为除数是整数的形式商的近似数：方法和积的近似数一样无限小数：无限不循环小数和无限循环小数（循环节的确定和标注）小数乘除混合运算：在小数混合运算中，运算方法和整数混合一样，运算规律也适用于小数中。
一个数（0除外）除以一个大于0的数，商大于被除数一个数（0除外）除以一个小于0的数，商小于被除数必考点：列竖式计算小数除法（商的近似数）小数乘除混合运算从一列数中挑出有限小数、无限小数、循环小数、无限小数易错点：列竖式计算除法中小数点位置的确定、无限循环小数也是无限小数第3单元观察物体能从不同的位置认定物体。
给出从一个位置看到的物体形状，想象从其相对位置看到的形状。
第4单元简易方程重、难点：用字母表示数、方程的定义、解方程（根据等式的性质）必考点：判断一个式子是不是方程、解方程易错点：在解方程过程中未知数移项中容易出错。
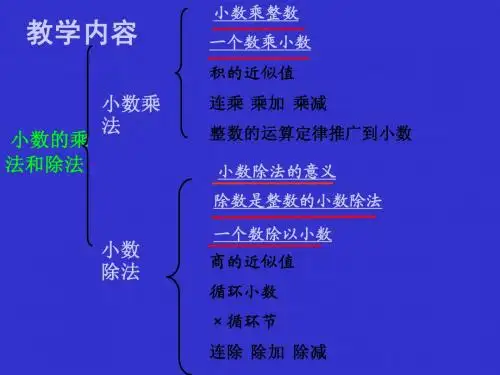
五年级数学上册全册教案(人教版)第一章：小数乘法1.1 教学目标让学生掌握小数乘法的基本运算方法。
培养学生解决实际问题的能力。
1.2 教学内容小数乘法的意义和运算规则。
小数乘法的竖式计算方法。
小数乘法的应用题。
1.3 教学步骤引入小数乘法的概念，通过实际例子讲解小数乘法的意义和运算规则。
演示小数乘法的竖式计算方法，让学生跟随老师一起完成计算。
提供一些应用题，让学生运用小数乘法进行计算和解决问题。
1.4 练习题完成一些小数乘法的计算题。
解决一些实际问题，运用小数乘法进行计算。
第二章：小数除法2.1 教学目标让学生掌握小数除法的基本运算方法。
培养学生解决实际问题的能力。
2.2 教学内容小数除法的意义和运算规则。
小数除法的竖式计算方法。
小数除法的应用题。
2.3 教学步骤引入小数除法的概念，通过实际例子讲解小数除法的意义和运算规则。
演示小数除法的竖式计算方法，让学生跟随老师一起完成计算。
提供一些应用题，让学生运用小数除法进行计算和解决问题。
2.4 练习题完成一些小数除法的计算题。
解决一些实际问题，运用小数除法进行计算。
第三章：分数的加减法3.1 教学目标让学生掌握分数加减法的基本运算方法。
培养学生解决实际问题的能力。
3.2 教学内容分数加减法的意义和运算规则。
分数加减法的竖式计算方法。
分数加减法的应用题。
3.3 教学步骤引入分数加减法的概念，通过实际例子讲解分数加减法的意义和运算规则。
演示分数加减法的竖式计算方法，让学生跟随老师一起完成计算。
提供一些应用题，让学生运用分数加减法进行计算和解决问题。
3.4 练习题完成一些分数加减法的计算题。
解决一些实际问题，运用分数加减法进行计算。
第四章：几何图形的认识4.1 教学目标让学生掌握常见几何图形的特征和性质。
培养学生观察和描述几何图形的能力。
4.2 教学内容常见几何图形的名称和特征。
几何图形的大小和位置关系。
几何图形的对称性。
4.3 教学步骤介绍常见几何图形的名称和特征，让学生观察和描述这些图形。
复习：小数的加减法
一、复习导入
1、说说小数加减法的计算法则。
2、比一比，看谁算得又对又快。
6.35+3.29= 8.63-3.97=
7.06+2.83= 8.5-0.9=
二、探究新知
1、计算示例
8.2+9.416=
（1）和上一例题有什么不同？
（2）位数不同的小数加减法怎样计算？
（3）为什么要小数点对齐呢？
（4）百分位上怎样计算？这里为什么可以添0？根据是什么？
（5）在小数加减法中，要想直接相加减，这两个数字得什么相同啊？
2、验证结果是否正确，怎么办？
（1）独立验算，说一说验算的方法。
（2）小结：小数的加减法的验算和整数加减法的验算方法一样的。
3、计算小数加减法要注意些什么？
(1)小数点对齐，也就是把相同数位上的数对齐。
(2)按照整数加减法的计算方法进行计算，最后在得数的相应位置上点上小数点。
(3)得数的小数部分末尾有0，一般要把0去掉。
三、巩固练习：
1.口算:
2.6+0.4＝5-0.2 ＝0.74-6.4 ＝0.37+0.63 ＝0.48+0.29 ＝1-0.89 ＝5.8+2＝ 4.3-1.6 ＝3-2.3 ＝2.计算:
① 4.2+15.6＝
②13+7.1＝
③ 3.96+6.04＝① 4.03-1.97＝
②24.8-18.2＝
③10-9.05＝
小数的乘法
0.5 6 ……两位小数 0.5 6
×0.0 4 ……两位小数→× 0.0 4
2 2 4 ……四位小数 0.0 2 2 4
乘得的积的小数位数不够时，要在前面用0补足，再点小数点。
讨论：
①小数乘小数，我们首先怎样想？
（把两个因数的小数点去掉，转化为整数乘法（整数乘法右对齐）。
）
②怎样得到正确的积？
（因数扩大到它的几倍，积就缩小到它的几分之一。
）
③积的小数位数和两个因数的小数位数有什么关系？能举例说明吗？
（因数中一共有几位小数，积就有几位小数；积的小数位数不够时，要在前面用O补足。
）
总结出来就是“1看、2算、3数、4点”。
练习：
1.不计算，说一说下列各题的积有几位小数。
2.3×0.4 0.08×0.9 7.3×0.06
9.1×0. 03 0.25×0.23 45.9×3.5
一个数（0除外）乘大于1的数，积比原来的数大。
一个数（O除外）乘小于1的数，积比原来的数小。
小数的除法
（1）小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。
如果除到末尾仍有余数，要添0再继续除。
（2）被除数比除数大的，商大于1。
被除数比除数小的，商小于1。
（3）计算除数是小数的除法，先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也向右移动几位，数位不够的要添0补足；再按照除数是整数的小数除法进行计算。
（4）一个数（0除外）除以1，商等于原来的数。
一个数（0除外）除以大于1的数，商比原来的数小。
一个数（0除外）除以小于1的数，商比原来的数大。
（5）A除以B=A÷B；A除B=B÷A；A去除B=B÷A；A被B除=A÷B。
（小数加减乘除混合运算）
4×25=100，8×125=1000，A×B+A×C=A×（B+C）
加法结合律：（a+b）+c=a+（b+c）
乘法交换律：a×b=b×a
乘法法结合律：（a×b）×c=a×（b×c）
减法的性质：a―b―c = a ―（b＋c）
除法的性质：
a÷b÷c=a÷（b×c）a÷c+b÷c=(a+b)÷c a÷c-b÷c=(a-b)÷c
1、简便计算：
2.5×
3.2×12.5 6.3÷1.4
2.5×2.4 15.32×4＋4.68÷0.25
2.55×1.5＋1.5＋6.45×1.5 2.95×101-2.95
3.12＋3.12×9915÷(0.15×0.4)
2.55×1.5＋1.5＋6.45×1.57
3.8－1.64－13.8－5.36
6.75－(0.9＋3.75)2
7.38－5.34＋2.62－4.66
35.72－4.9－(5.72＋5.1)0.73-0.25-0.73+0.25
5.3+0.1+5.3-0.1 12.7-4.8-5.2
2、实际应用
1、用8元钱可以买5千克苹果，1元钱可以买（）千克苹果，买1千克苹果需要（）元钱。
2、某地的海水1千克含盐0.03千克，100克海水含盐
（）克。
3、1千克香蕉3.2元，购买800克需（）元，4.48元可以买（）千克。
4、一拖拉机0.45小时耕地0.072公顷，这种拖拉机平均每小时耕地（）公顷，耕地1公顷需要（）小时。
5、18、王师傅2.5小时生产40个零件，平均每小时生产
（）零件，平均生产1个零件需
（）小时。
6、兔子0.5小时可以跑22.5千米，兔子每小时跑（）千米，它跑1千米需（）小时
7、1种钢丝0.25米重0.2千克，1千克长（）米。
8、10吨海水可以晒出0.85吨盐,50吨海水可以晒出
()吨盐,
要晒出1.7吨盐,需要()吨海水
4、小数乘除法专题训练
（列竖式计算）
32.6×12 5.05×36 24.3×6.8 2.16××0.78 0.21×4.05 5.09×0.48 21.6×7.32 241.6÷0.2
4.68÷1.2 0.98÷0.35 19.5÷7.5 540.6÷
5.3 0.032÷1.6 0.675÷2.7 60.8÷0.76
6.8÷0.16
0.306÷0.15 4.85÷0.25 78.6÷11（商用循环小数表示）
认识位置
一．学习探究
自学教材P19例1，完成下面的练习。
（1）行与列的意义：通常我们把竖排叫做（），横排叫做（）。
（2）从情境图可以看出张亮在第（）列，第（）行；王艳同学在第（）列，第（）行；赵雪同学在第（）列，第（）行。
（3）如果用（2，3）表示张亮同学的位置，王艳同学的位置可表示为（，），赵雪同学的位置可表示为（，），周明同学的位置可表示为（，）。
温馨提示：
1.确定第几列一般从左往右数，确定第几行一般是从前往后数。
2.用数对表示物体位置的方法：用“（）”把代表列数和行数的数或字母括起
来，用逗号把代表列数、行数的数或字母隔开（列数，行数）。
二．巩固
学习教材P3页例2
（1）用数对表示图上已有场馆所在位置。
用（3，0）表示大门的位置，熊猫馆可表示为（，），大门和熊猫馆在同一（）上；大象馆可表示为（，），海洋馆可表示为（，），大象馆和海洋馆在同一（）上。
（先用数对表示各场馆的位置，在观察每个数对的特点）
（2）根据所给数对，在平面图上标出相应场馆的位置（想一想每一处在第几列和第几行的交点处）
飞禽馆（1，1）
猩猩馆（0，3）
狮虎山（4，3）
鹰山（4，1）
（3）由上面的图和数对可以看出：在同一平面图上，两个数对的后一个数相同，表明这两个数对表示的位置在同一（），如果两个数对的前一个数相同，表明这两个数对表示的位置在同一（）。
三．达标检测
1．想一想，填一填。
（1）小红和小军在同一个教室上课，小红的座位在第二列，第四行，简记为（2，4）；小军的位置简记为（3，5），则小军在该教室的位置是第（）
列，第（）行。
（2）电影票上的“4排9号”，记做（9，4），则7排11号记做（）。
（3）学校组织看电影，小刚在8排3号，许明在7排3号，秦月在9排3号，小文在8排1号。
则小刚的前面是（），后面是（）。
2．看图填空。
（1）请标出棋盘中每个棋子的位置。
（2）在棋盘上画出“象”到（2，4）和“马”到（7，9）的具体位置。
