材料力学讲解作业
- 格式：doc
- 大小：6.85 MB
- 文档页数：22
下载文档原格式
合集下载
材料力学作业参考题解(2)PPT学习教案
FN1 F gA1x
混凝土柱各段危险截面分别为柱中截 面和柱 底截面 ，其轴 力分别 为：
FN2 F gA1l1 gA2 (x l1)
FN1max F gA1l1
FN 2max F g( A1l1 A2l2 ) (受压)
由强度条件：
FN max [ ]
A
A1
F [ ] gl1
2.242m
m
第7页/共40页
2-12 图示接头，由两块钢板用四个直径相同 的钢铆 钉连接 而成。 已知载 荷F=80kN， 板宽b=80mm， 板厚δ =10mm，铆 钉直径 d =16mm，许 用切应 力[ τ ]=100MPa，许用挤压应力[σbs]=300MPa,许 用拉应 力[σ]=170MPa 。试校核接头的强度。(提示：设 每个铆 钉受力 相同)
FB
220 4 220 8
M B (F ) 0 FAy
12
220kN
M A(F) 0
FB
220 4 220 8 12
220kN
求杆AC和CD的轴力：
由A点的平衡条件：
FNAC
FAy cos45
2 220 311.13kN
(拉 )
由C点的平衡条件：
FNCD FNAC cos45 220kN
:bs : [ ]:[bs ]:[ ] 90: 240:120 3:8: 4
其中：
Fs F
A dh
bs
Fb Abs
(D2
F d2)/4
d 2 (D2
F /d2
1) / 4
FN A
F d 2
/
4
则有：
d3
d
h
4h 4
3
《材料力学》第2章 轴向拉(压)变形 习题解讲解
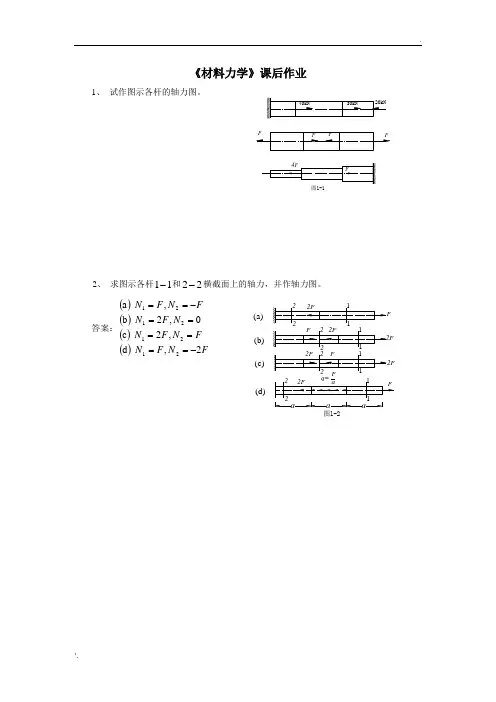
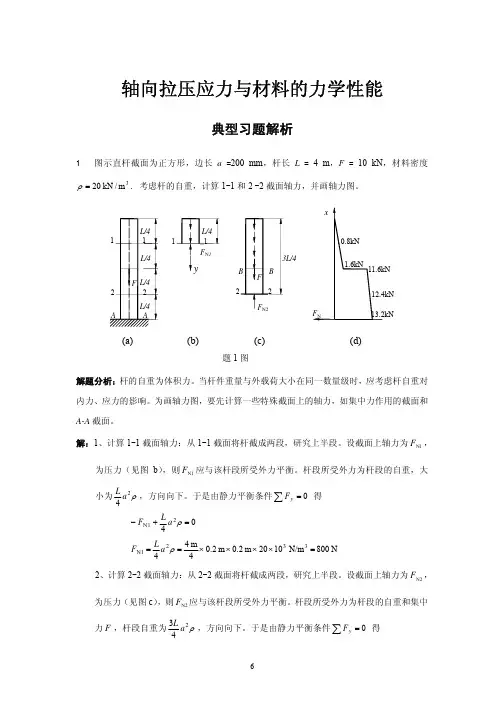
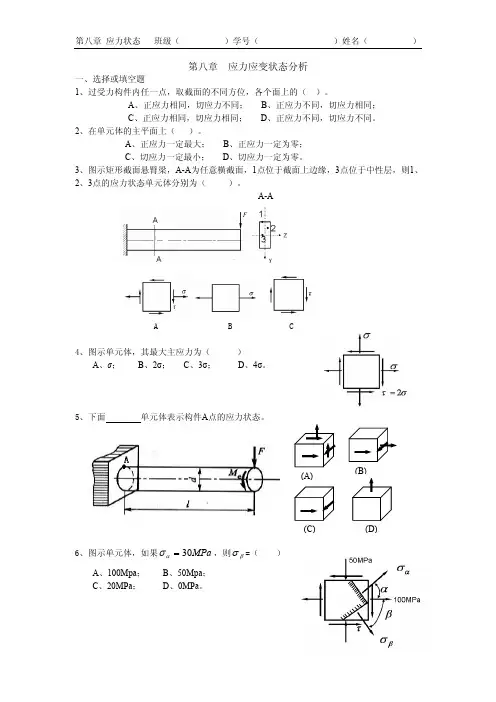
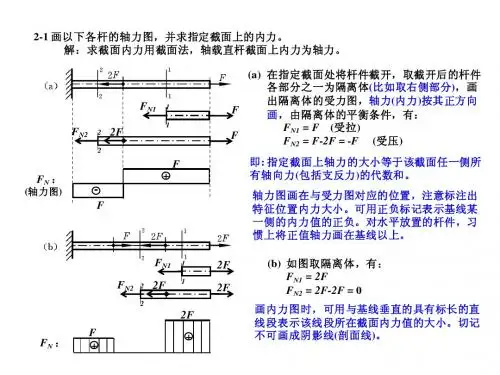
第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。
由平衡条件可知：②以C节点为研究对象，其受力图如图所示。
由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。
荷载，材料的密度，试求墩身底部横截面上的压应力。
解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。
解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
材料力学作业
材料力学作业 Prepared on 22 November 20202-4 木架受力如图所示，已知两立柱横截面均为100m m ×100mm 的正方形。
试求：（1）绘左、右立柱的轴力图；（2）求左、右立柱上、中、下三段内横截面上的正应力。
解：（1）求立柱各节点的受力为了求出ACEG 立柱（左立柱）和BDFH 立柱（右立柱）中的内力和应力，首先对各杆受力进行分析如下图2-4a 所示，并求出数值。
取AB 为研究对象，由平衡方程∑=0)(F m A，0211=⨯'-⨯BF F ①∑=0Y ，01=-'+'F F F B A②联合①和②解得，KN F F B A5='='。
又由牛顿第三定律得，KN F F AA 5='=，KN F FB B 5='=。
同理可得，KN F F CC 9='=，KN F FD D 3='=；KN F FE E 4='=，KNF F F F 12='=。
（2）绘左、右立柱的轴力图取左立柱（ACEG 立柱）为研究对象。
采用截面法，画受力图如图2-4b 所示,求得 )(5KN F N A AC -=-=；)(1495KN F F N C A CE -=--=--=；)(10495KN F F F N E C A EG -=+--=+--=。
同理又取右立柱（BDFH 立柱）为研究对象。
采用截面法求得)(5KN F N B BD -=-=；)(235KN F F N D B BD -=+-=+-=；)(141235KN F F F N F D B FH -=-+-=-+-=。
画轴力图如图左立柱所示和如图右立柱所示。
（3）求左、右立柱上、中、下三段内横截面上的正应力由轴向拉压正计算公式AN=σ应力得，左立柱上、中、下正应力：MPa mm N A N AC 5.010********3-=⨯⨯-==左上σ； MPa mm N A N CE 4.1100100101423-=⨯⨯-==左中σ； MPa mmN A N EG 1100100101023-=⨯⨯-==左下σ。
材料力学课后作业
31、如图示，设q、a均为己知。求：各梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
32、如图示，设q、a均为己知。求：梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
33、如图示，设q、a均为己知。求：梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
《材料力学》课后作业
1、试作图示各杆的轴力图。
2、求图示各杆 和 横截面上的轴力，并作轴力图。
答案：
3、 求图示阶梯状直杆横截面 、 和 上的轴力，并作轴力图。如横截面面积 ， ， ，求各横截面上的应力。
答案：
4、 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个 的等边角钢。已知屋面承受集度为 的竖直均布荷载。求拉杆 和 横截面上的应力。
40、割刀在切割工件时，受到F=1KN的切削力作用，割刀尺寸如图所示，若割刀的许用弯曲正应力〔σ〕=200MPa。试校核割刀的弯曲正应力强度。
答案：σmax=200MPa
41、图示为一承受纯弯曲的铸铁梁，其截面为⊥形，材料的拉伸和压缩许用应力之比
〔σ+〕/〔σ-〕=1/4。求水平翼板的合理宽度b。
答案：b=510mm
答案：σA=σD=-163.5MPaσB=38.8 MPaσC=58.8 MPa
38、矩形截面的悬臂梁受集中力和集中力偶作用，如图所示。试求Ⅰ-Ⅰ截面和固定端Ⅱ-Ⅱ截面上A、B、C、D四点处的正应力。
答案：I-I截面：σA=-7.41MPaσB=4.94MPaσC=0σD=7.41MPa
I-I截面：σA=9.26MPaσB=-6.18MPaσC=0σD=-9.26MPa
和弯矩方程绘制剪力图和弯矩图。
32、如图示，设q、a均为己知。求：梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
33、如图示，设q、a均为己知。求：梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
《材料力学》课后作业
1、试作图示各杆的轴力图。
2、求图示各杆 和 横截面上的轴力，并作轴力图。
答案：
3、 求图示阶梯状直杆横截面 、 和 上的轴力，并作轴力图。如横截面面积 ， ， ，求各横截面上的应力。
答案：
4、 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个 的等边角钢。已知屋面承受集度为 的竖直均布荷载。求拉杆 和 横截面上的应力。
40、割刀在切割工件时，受到F=1KN的切削力作用，割刀尺寸如图所示，若割刀的许用弯曲正应力〔σ〕=200MPa。试校核割刀的弯曲正应力强度。
答案：σmax=200MPa
41、图示为一承受纯弯曲的铸铁梁，其截面为⊥形，材料的拉伸和压缩许用应力之比
〔σ+〕/〔σ-〕=1/4。求水平翼板的合理宽度b。
答案：b=510mm
答案：σA=σD=-163.5MPaσB=38.8 MPaσC=58.8 MPa
38、矩形截面的悬臂梁受集中力和集中力偶作用，如图所示。试求Ⅰ-Ⅰ截面和固定端Ⅱ-Ⅱ截面上A、B、C、D四点处的正应力。
答案：I-I截面：σA=-7.41MPaσB=4.94MPaσC=0σD=7.41MPa
I-I截面：σA=9.26MPaσB=-6.18MPaσC=0σD=-9.26MPa
材料力学典型例题与详解(经典题目)
G = [σ ]A(l) − F
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大
材料力学作业(8-11)
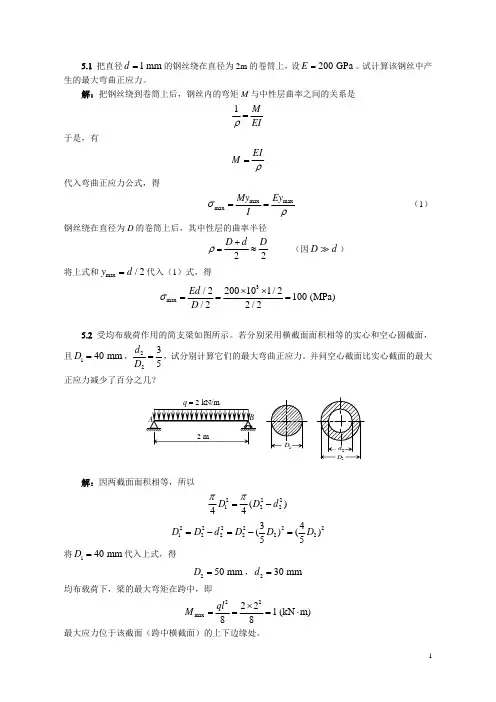
第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点，取截面的不同方位，各个面上的（ ）。
A 、正应力相同，切应力不同；B 、正应力不同，切应力相同；C 、正应力相同，切应力相同；D 、正应力不同，切应力不同。
2、在单元体的主平面上（ ）。
A 、正应力一定最大；B 、正应力一定为零；C 、切应力一定最小；D 、切应力一定为零。
3、图示矩形截面悬臂梁，A-A 为任意横截面，1点位于截面上边缘，3点位于中性层，则1、2、3点的应力状态单元体分别为（ ）。
A-AA B C4、图示单元体，其最大主应力为（ ）A 、σ；B 、2σ；C 、3σ；D 、4σ。
5、下面 单元体表示构件A 点的应力状态。
6、图示单元体，如果MPa 30=ασ，则βσ=（ ） A 、100Mpa ； B 、50Mpa ； C 、20MPa ； D 、0MPa 。
(C)7、图示单元体应力状态，沿x 方向的线应变εx 可表示为（ ）A 、Eyσ； B 、)(1y x E μσσ−；C 、)(1x y E μσσ− ；D 、Gτ。
8、图示应力圆对应于单元体( )。
9、已知单元体及应力圆如图所示，σ1所在主平面的法线方向为( )。
A 、n 1；B 、 n 2；C 、n 3；D 、n4。
二、计算题1、已知应力状态如图所示，试用解析法计算图中指定截面上的正应力和切应力。
2、试画图示应力状态的三向应力圆，并求主应力、最大正应力和最大切应力。
3、边长为20mm的钢立方块置于刚性模中，在顶面受力F=14kN作用。
已知材料的泊松比为0.3，求立方体各个面上的正应力。
4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m，Q=120 kN。
试绘出截面上1、2、3、4各点的应力状态单元体，并求其主应力。
第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下，水管中的水会受冻而结冰。
根据低温下水管和冰所受力情况可知（ ）。
A 、冰先破裂而水管完好；B 、水管先破裂而冰完好；C 、冰与水管同时破裂；D 、不一定何者先破裂。
材料力学作业题解_第5-9章
5.1 把直径 d = 1 mm 的钢丝绕在直径为 2m 的卷筒上， 设 E = 200 GPa 。 试计算该钢丝中产 生的最大弯曲正应力。 解：把钢丝绕到卷筒上后，钢丝内的弯矩 M 与中性层曲率之间的关系是
1
ρ
于是，有
=
M EI EI
M=
代入弯曲正应力公式，得
ρ
σ max =
Mymax Eymax = I ρ
空心圆截面比实心圆截面最大正应力减少了
5.4 矩形截面悬臂梁如图所示，已知 l = 4 m ， 确定此梁横截面的尺寸。 解：梁的最大弯矩发生在固定端处，其值为
b 3 = ， q = 10 kN/m ， [σ ] = 10 MPa 。试 h 5
q A
l
M max =
梁的强度条件
1 2 1 ql = ×10 × 42 =80 (kN ⋅ m) 2 2 M 80 ×106 = = ≤ [σ ] 1 2 W bh 6
m
n
8
m
22
n
13
发生，应加以比较，方可决定割刀内的最大正应力。 n-n 截面
2.5
4
1 WI = × 2.5 × 132 =70.4 (mm3 ) 6
M I = 1× 103 × 8=8 ×103 (N ⋅ mm)
σI =
n-n 截面
M I 8 ×103 = = 114 (MPa ) WI 70.4
− = σ max
C 截面
+ σ max =
10 × 106 ×158 = 26.3 (MPa)<[σ t ]=40 MPa 60.1× 106 10 × 106 × (230 − 158) = 12 (MPa)<[σ c ]=160 MPa 60.1×106
1
ρ
于是，有
=
M EI EI
M=
代入弯曲正应力公式，得
ρ
σ max =
Mymax Eymax = I ρ
空心圆截面比实心圆截面最大正应力减少了
5.4 矩形截面悬臂梁如图所示，已知 l = 4 m ， 确定此梁横截面的尺寸。 解：梁的最大弯矩发生在固定端处，其值为
b 3 = ， q = 10 kN/m ， [σ ] = 10 MPa 。试 h 5
q A
l
M max =
梁的强度条件
1 2 1 ql = ×10 × 42 =80 (kN ⋅ m) 2 2 M 80 ×106 = = ≤ [σ ] 1 2 W bh 6
m
n
8
m
22
n
13
发生，应加以比较，方可决定割刀内的最大正应力。 n-n 截面
2.5
4
1 WI = × 2.5 × 132 =70.4 (mm3 ) 6
M I = 1× 103 × 8=8 ×103 (N ⋅ mm)
σI =
n-n 截面
M I 8 ×103 = = 114 (MPa ) WI 70.4
− = σ max
C 截面
+ σ max =
10 × 106 ×158 = 26.3 (MPa)<[σ t ]=40 MPa 60.1× 106 10 × 106 × (230 − 158) = 12 (MPa)<[σ c ]=160 MPa 60.1×106
材料力学作业参考题解(1)
2F
q=F/a
F + FN ：
2F
2-2 图示杆件由两根木杆粘接而成。欲使其在受拉时，粘接面上的正应力为其切应力的 倍， 图示杆件由两根木杆粘接而成。欲使其在受拉时，粘接面上的正应力为其切应力的2倍 试问粘接面的位置应如何确定？ 试问粘接面的位置应如何确定？
解：本题实质上是要考察斜截面上的应力。由斜截面应力公式，有： 本题实质上是要考察斜截面上的应力。由斜截面应力公式，
2-4图示实心圆钢杆 和AC在A点作用有铅垂向下的力 图示实心圆钢杆AB和 在 点作用有铅垂向下的力 点作用有铅垂向下的力F=35kN。已知杆 和AC的直径分别 图示实心圆钢杆 。 已知杆AB和 的直径分别 点在铅垂方向的位移。 为d1=12mm和d2=15mm，钢的弹性模量 和 ，钢的弹性模量E=210GPa。试求 点在铅垂方向的位移。 。试求A点在铅垂方向的位移 解：求各杆内力，如图取A点为对象，由平衡条件，有： 求各杆内力，如图取 点为对象，由平衡条件， 点为对象
AAB =
F [σ ] sin θ
ABC =
F cosθ [σ ] sin θ
要求结构的总重量为最小即结构总体积最小，其体积为： 要求结构的总重量为最小即结构总体积最小，其体积为：
V = AAB ⋅ l AB + ABC ⋅ l BC =
令：
F l F cosθ Fl 1 cosθ ⋅ + ⋅l = + [σ ] sin θ cosθ [σ ] sin θ [σ ] sin θ cosθ sin θ
取A1=0.664m2 柱底固定，则柱顶位移值等于柱的伸缩量， 柱底固定，则柱顶位移值等于柱的伸缩量，可用叠加原理计算
2 FNi dx Fl1 ρgl12 ( F + ρgA1l1 )l2 ρgl2 ∆ A = ∆l = ∑ ∆li = ∑ ∫ = + + + li EA EA1 2 E EA2 2E i 1000 × 103 ×12 2.25 × 103 × 9.8 × 12 × 12 = + 9 20 × 10 × 0.576 2 × 20 ×109 (1000 + 2.25 × 9.8 × 0.576 × 12) ×103 × 12 2.25 ×103 × 9.8 × 12 ×12 + + = 2.242mm 20 ×109 × 0.664 2 × 20 × 109
材料力学讲解作业
材料力学讲解作业Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】作下图所示梁的剪力图和弯矩图。
2m1m1mm1kN 2kN2kN 2kNA BCD梁分三段，AB 、BC 为空荷载段，CD 段为均布荷载段，均布荷载q=2kN/2m=1kN/m 。
A ，B ，D 三处剪力有突变，说明有集中力作用，在A 截面有向上集中力2kN ，在B 截面有向下集中力2kN ，在D 截面有向上集中力2kN 。
荷载图如图 (b)。
根据荷载图作弯矩图，如图 (c)所示。
如下图所示机构中，1,2两杆的横截面直径分别为cm d 101= ，cm d 202= ，P=10kN 。
横梁ABC ，CD 视为刚体。
求两杆内的应力。
p DCBA122m2m1.5m1m1mCD 杆的D 支座不受力，CD 杆内也不受力，所以p 可视为作用于ABC 杆的C 端。
取ABC 为受力体，受力图如图(b)所示。
MPaMPa A N MPaMPa A N kN N kN N 7.6310204103203.12710104101020210162222623111=⨯⨯⨯⨯===⨯⨯⨯⨯====--πσπσ，如图所示的阶梯形圆轴，直径分别为cm d 41=,cm d 72=。
轮上三个皮带轮，输入功率为kW N 171=，kW N 132=，kW N 303=。
轴的转速为n=200r/min ，材料的许用剪应力[τ]=60MPa 。
试校核其强度。
1计算各轮处的扭转外力偶矩。
mkN m kN m m kN m kN n N m m kN m kN n N m ⋅=⋅⨯=⋅=⋅⨯=⋅=⋅⨯==433.12003055.9621.02001355.9255.9812.02001755.9155.9321(c)(b)kN m 31图3 传动轴可简化为图3(b)，⑦扭矩图如图3(c)。
AD 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TAD 6.64104168126311max BC 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TBC 3.211071614326322max AD 段的单位长度扭转角为[]θπθ>=⨯⨯⨯⨯⨯⨯==-m mGI M p TAD /1.23/104108018032812842911BC 段的单位长度扭转角为[]θπθ<=⨯⨯⨯⨯⨯⨯==-m m GIp MINC/44.0/1074108018032143222829由此可知轴的强度与刚度都不够。
材料力学部分作业解析新精品文档
E I2 4160Nm 2， 由钢杆CD相连接。CD杆
的 l 5 m ， A 3 1 4 0 m 2 ， E 2G 00 。 Pa
若F=50kN，试求悬臂梁AD在D点的挠度。
解：这是个一次超静定问题。将CD杆拆除，使系统 成为两个悬臂梁和一个受轴向拉伸的杆，如图所 示。设BE梁长 l 1 ，在C点的挠度 C 等于AD梁的挠 度 D与CD杆的伸长量 l 之和，即：
Pa2.88MPa
max min
22 2.88 2.8820.8325MPa
2 2
2 2
（2）试用第三强度理论校核轴的强度。
• 解：这是一个弯扭组合问题，砂轮轴的受力图和 内力图如下所示：
砂轮承受的扭矩：T 95P 4 9 95 4 39 N m 2.5 0 N m
n 14 00
磨削力：F zD T /2 2 2 .5 .0 5 /0 2 1N 6 ,F 4 y 3 F z 4N 92
• 2-48 在图示结构中，1、2两杆的抗拉刚度同为
E1A1, 3杆为E3A3。3杆的长度为l ，其中 为加
工误差。试求3杆装入AC位置后，1、2、3三杆的 内力。
解：这是个典型的装配应力问题。将3杆装配入AC
位置后，杆1、2受拉，杆3受压，杆1、2的结点A
和3的A’点在A1处结合，A1点的受力如图所示。 因结构和载荷均对称，所以FN1=FN2，
由角应变的定义可知，在B点处的角应变为：
AB'C
2
2
2arctanOOBA'
2
2arctan12102.003
2.5104rad
第二章 拉伸、压缩与剪切
• 2-14 图示拉杆沿斜面m-m由两部分胶合而 成。设在胶合面上许用拉应力[]100MPa,
的 l 5 m ， A 3 1 4 0 m 2 ， E 2G 00 。 Pa
若F=50kN，试求悬臂梁AD在D点的挠度。
解：这是个一次超静定问题。将CD杆拆除，使系统 成为两个悬臂梁和一个受轴向拉伸的杆，如图所 示。设BE梁长 l 1 ，在C点的挠度 C 等于AD梁的挠 度 D与CD杆的伸长量 l 之和，即：
Pa2.88MPa
max min
22 2.88 2.8820.8325MPa
2 2
2 2
（2）试用第三强度理论校核轴的强度。
• 解：这是一个弯扭组合问题，砂轮轴的受力图和 内力图如下所示：
砂轮承受的扭矩：T 95P 4 9 95 4 39 N m 2.5 0 N m
n 14 00
磨削力：F zD T /2 2 2 .5 .0 5 /0 2 1N 6 ,F 4 y 3 F z 4N 92
• 2-48 在图示结构中，1、2两杆的抗拉刚度同为
E1A1, 3杆为E3A3。3杆的长度为l ，其中 为加
工误差。试求3杆装入AC位置后，1、2、3三杆的 内力。
解：这是个典型的装配应力问题。将3杆装配入AC
位置后，杆1、2受拉，杆3受压，杆1、2的结点A
和3的A’点在A1处结合，A1点的受力如图所示。 因结构和载荷均对称，所以FN1=FN2，
由角应变的定义可知，在B点处的角应变为：
AB'C
2
2
2arctanOOBA'
2
2arctan12102.003
2.5104rad
第二章 拉伸、压缩与剪切
• 2-14 图示拉杆沿斜面m-m由两部分胶合而 成。设在胶合面上许用拉应力[]100MPa,
材料力学作业题解
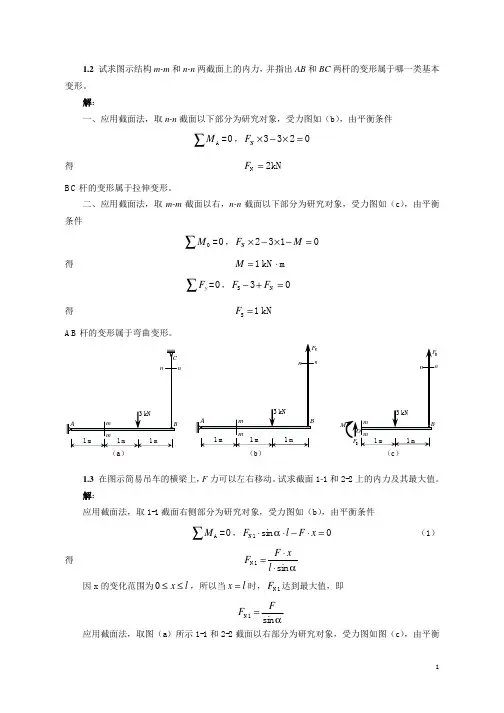
（a ）（b ）O SF M（c ）1.2 试求图示结构m-m 和n-n 两截面上的内力，并指出AB 和BC 两杆的变形属于哪一类基本变形。
解：一、应用截面法，取n-n 截面以下部分为研究对象，受力图如（b ），由平衡条件A=0M∑，N 3320F ×−×=得 N 2kN F =BC 杆的变形属于拉伸变形。
二、应用截面法，取m-m 截面以右，n-n 截面以下部分为研究对象，受力图如（c ），由平衡条件O=0M∑，N 2310F M ×−×−=得 1 kN m M =⋅=0yF ∑，SN 30FF −+=得 S 1 kN F = AB 杆的变形属于弯曲变形。
1.3 在图示简易吊车的横梁上，F 力可以左右移动。
试求截面1-1和2-2上的内力及其最大值。
解：应用截面法，取1-1截面右侧部分为研究对象，受力图如（b ），由平衡条件A=0M∑，N1sin 0F l F x α⋅⋅−⋅= （1）得 N1sin F xF l α⋅=⋅因x 的变化范围为0x l ≤≤，所以当x l =时，N1F 达到最大值，即N1sin FF α=应用截面法，取图（a ）所示1-1和2-2截面以右部分为研究对象，受力图如图（c ），由平衡（a ）（b ）F （c ）条件=0xF ∑，N2N1cos 0FF α−⋅= （2） =0yF ∑，S2N1sin 0FF F α−+⋅= （3）O=0M∑，N12sin ()0F l x M α⋅⋅−−= （4）解以上各式，得N2cot /F x F l α=⋅⋅，S2(1/)F x l F =−，2()/M l x F x l =−⋅当x l =时，N 2达到最大值，即N2max cot F F α=⋅当0x =时，F S2达到最大值，即S2max F F =当/2x l =时，M 2达到最大值，即2max /4M F l =⋅1.4 拉伸试样上A ，B 两点间的距离l 称为标距。
材料力学作业参考题解扭转
17.76MPa [ ]
（3）如图取坐标系，有：
T (x) m0 x
AB
l T (x) dx
m0
0 GI p
GI p
l
xdx
m0l 2
M 0l
0
2GI p 2GI p
32 389.9 40
0.064 [1
(5 /
6)4 ]
0.148弧度
8.48
3-16 如图所示，将空心圆杆（管）A套在实心圆杆B旳一端。两杆在同一横截面处有一直径 相同旳贯穿孔，但两孔旳中心线构成一β角，目前杆B上施加扭力偶使之扭转，将杆A和B旳 两孔对齐，装上销钉后卸去所施加旳扭力偶。试问两杆横截面上旳扭矩为多大？已知两杆旳 极惯性矩分别为 IpA和 IpB，且材料相同，切变模量为G。
620.7 16
0.043
49.4MPa [ ]
max 2
TDB W pDB
1432.4 16
0.073
21.3MPa [ ]
max
TAC GI pAC
180
80
32 620.7
109
180
0.044
1.77 / m [ ]
该轴满足强度与刚度要求
3-13 已知钻探机钻杆旳外径D=60mm，内径d=50mm，功率P=7.35kW，转速n=180r/min，钻 杆入土深度l=40m，材料旳G=80GPa，[ τ ]=40MPa。假设土壤对钻杆旳阻力沿长度均匀分布， 试求：（1）单位长度上土壤对钻杆旳阻力矩；（2）作钻杆旳扭矩图，并进行强度校核； （3）A、B两截面旳相对扭转角。
d 4
d 8
32 100 103
8 0.13
127MPa
材料力学作业解答
材料力学作业解答1.弹簧的力学行为弹簧是一种具有弹性的材料，它可以在受力时发生弹性形变，并且能够恢复到原始形状。
弹簧的力学行为可以通过胡克定律来描述。
根据胡克定律，弹簧的形变与施加在它上面的力成正比，即F=k*x，其中F是施加在弹簧上的力，k是弹簧的弹性系数，x是弹簧的形变量。
2.弹簧的应变能和弹性势能当弹簧被拉伸或压缩时，它会储存一定量的应变能。
弹簧的应变能可以通过下式计算：U=(1/2)*k*x^2，其中U是弹簧储存的应变能，k是弹簧的弹性系数，x是弹簧的形变量。
3.伸长弹簧的应变能假设一个弹簧的弹性系数为k，它被拉伸或压缩x长度。
根据胡克定律，施加在弹簧上的力可以通过F = k * x计算得到。
通过积分力在形变路径上的关系，可以得到弹簧的应变能。
假设初始长度为L，拉伸后的长度为L+x，则弹簧的伸长应变能可以计算如下：U = ∫[0, L+x] F(x)dx = ∫[0, x] k * x dx = (1/2) k * x^24.剪切应力和剪切应变剪切应力是作用于物体上的横截面内的剪切力与该横截面上的面积之比。
剪切应变是物体在受到剪切应力时产生的形变。
剪切应力和剪切应变之间的关系可以通过剪切弹性模量来描述。
剪切弹性模量G可以通过下式计算：G=τ/γ，其中τ是剪切应力，γ是剪切应变。
5.弯曲应力和弯曲应变弯曲应力是作用于物体上的弯曲力与该物体的横截面想对距离之比。
弯曲应变是物体在受到弯曲应力时产生的形变。
弯曲应力和弯曲应变之间的关系可以通过弯曲弹性模量来描述。
弯曲弹性模量E可以通过下式计算：E=σ/ε，其中σ是弯曲应力，ε是弯曲应变。
6.斯特拉因准则斯特拉因准则描述了材料在达到破坏点之前的应力和应变行为。
根据斯特拉因准则，当材料达到其屈服点时，应力和应变之间的关系可以通过单一的线性方程来描述。
这个线性方程表明了在屈服点之前，应力与应变之间的比例关系。
7.杨氏模量和泊松比杨氏模量是一种描述材料刚度的量度，它可以表示应力与应变之间的比例关系。
《材料力学》第2章 轴向拉(压)变形 习题解讲解
第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。
由平衡条件可知：②以C节点为研究对象，其受力图如图所示。
由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。
荷载，材料的密度，试求墩身底部横截面上的压应力。
解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。
解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
材料力学全部习题解答讲解
1 2 R2
3
2
（b）
yc =
ydA
A
=
A
b 0
y ayndy b ayndy
=
n n
1 2
b
0
26
Iz =
y2dA
A
Iy =
z2dA
A
解： 边长为a的正方截面可视为由图示截面和一个半 径为R的圆截面组成，则
Iz
=I（za）
I（zR）=
a4 12
2R 4
0
FN A
10103 N 1000 106 m2
10MPa
由于斜截面的方位角 450
得该截面上的正应力和切应力分别为
45
0 cos2 10106 cos2 450 pa 5MPa
0 sin 2 1 10106 sin 900 pa 5MPa
2
18
解：1.求预紧力 由公式l FNl 和叠加原理，故有
EA
l
l1
l2
l3
Fl1 EA1
Fl2 EA2
Fl3 EA3
4F
E
l1 d12
l2 d22
l3 d32
由此得 F
El
18.65kN
4
l1
d
2 1
l2
d
2 2
l3
根据式
tan 2 2I y0z0
I z0 I y0
解得主形心轴 y 的方位角为 a =
3.计算主形心惯性矩
材料力学作业及答案
二、 杆件受力如图所示，计算 BC 段的轴力时分离体的最佳取法是（ ）
【A】
【B】
【C】
【D】 解：正确答案为【D】； 【A】 分离体上不能带有支座，因为支座处的支反力要影响分离体的平衡（如下图所示），
因此必须将支座去除，用相应的支反力取而代之； 【B】 用截面法计算轴力时，不要在集中力作用点上取截面，因为此处的受力比较复杂，
为了保险起见，建议大家用 的公式来计算线应变。从这个公式可以看出，当材料相同的时， E
线应变的变化规律与正应力的变化规律相同，正应力发生变化的截面上，线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成，已知材料的容重为 ，弹性模量为 E，则
解：正确答案为【A】。 [B]问题出在分子上的 3，在用胡克定律计算变形时分子上要用轴力，而不能用杆件上作用的外力。 [C]这是一个常见的错误，很多同学会仿照对变形进行分段累加的算法来计算线应变，要注意变形有累 加意义，即一段杆件的总的变形量等于每个分段变形量的代数和；但是线应变指的是在一个很小的范围 内杆件的变形程度，可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时，这段杆件 各个横截面上的线应变都是相等的，你可以笼统地说这段杆件的线应变是多少，但是当两段杆件的轴力 不同时，只能说两段杆件的线应变个各是多少，而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变，即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶，在第 一段上是一个速度，在第二段上是另一个速度，显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时，不能像本选项那样将两段杆件连在一起，一次性计算线应变，必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下，这个截面上的轴力 是不确定的，在材料力学中绘制出来的集中力作用截面附近的轴力图，如下图所示， 此时只需要求出集中力作用截面左右两条线代表的轴力值即可，因此，应该在集中 力作用截面的左右两侧取计算截面。，而不要把计算截面取在集中力的作用截面上。
【A】
【B】
【C】
【D】 解：正确答案为【D】； 【A】 分离体上不能带有支座，因为支座处的支反力要影响分离体的平衡（如下图所示），
因此必须将支座去除，用相应的支反力取而代之； 【B】 用截面法计算轴力时，不要在集中力作用点上取截面，因为此处的受力比较复杂，
为了保险起见，建议大家用 的公式来计算线应变。从这个公式可以看出，当材料相同的时， E
线应变的变化规律与正应力的变化规律相同，正应力发生变化的截面上，线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成，已知材料的容重为 ，弹性模量为 E，则
解：正确答案为【A】。 [B]问题出在分子上的 3，在用胡克定律计算变形时分子上要用轴力，而不能用杆件上作用的外力。 [C]这是一个常见的错误，很多同学会仿照对变形进行分段累加的算法来计算线应变，要注意变形有累 加意义，即一段杆件的总的变形量等于每个分段变形量的代数和；但是线应变指的是在一个很小的范围 内杆件的变形程度，可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时，这段杆件 各个横截面上的线应变都是相等的，你可以笼统地说这段杆件的线应变是多少，但是当两段杆件的轴力 不同时，只能说两段杆件的线应变个各是多少，而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变，即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶，在第 一段上是一个速度，在第二段上是另一个速度，显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时，不能像本选项那样将两段杆件连在一起，一次性计算线应变，必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下，这个截面上的轴力 是不确定的，在材料力学中绘制出来的集中力作用截面附近的轴力图，如下图所示， 此时只需要求出集中力作用截面左右两条线代表的轴力值即可，因此，应该在集中 力作用截面的左右两侧取计算截面。，而不要把计算截面取在集中力的作用截面上。
材料力学作业参考解答
2-2（b）答：
2-3答：以B点为研究对象，由平面汇交力系的平衡条件
2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2；
解：（1）分析整体，作示力图
：
（2）取部分分析，示力图见（b）
：
（3）分析铰E，示力图见（c）
：
2-3求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。
解：（1）求①、②杆轴力
由平衡方程可以求出:
（2）求杆的变形
（压缩）
（拉伸）
（压缩）
（3）由几何关系： （下降）
2-9答：任一截面上轴力为F，由
得面积为
伸长量为
2-11图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB杆所需的直径。
：
（2）由强度条件求
2-14图示AB为刚性杆，长为3a。A端铰接于墙壁上，在C、B两处分别用同材料、同面积的①、②两杆拉住，使AB杆保持水平。在D点作用荷载F后，求两杆内产生的应力。设弹性模量为E，横截面面积为A。
解：
1．本题为超静定问题，
见图(a),设AB杆产生角位移 ，则
，
2．由Hooke定律：
由平衡条件可知：
所以B,C截面相对位移为
3-1试作下列各杆的扭矩图。
3-2一直径d=60mm的圆杆，其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面上1，2，3点处的切应力和最大切应变，并在此三点处画出切应力的方向。(G=80GPa)。
解：横截面上切应力大小沿半径线性分布，方向垂直半径
2-3答：以B点为研究对象，由平面汇交力系的平衡条件
2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2；
解：（1）分析整体，作示力图
：
（2）取部分分析，示力图见（b）
：
（3）分析铰E，示力图见（c）
：
2-3求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。
解：（1）求①、②杆轴力
由平衡方程可以求出:
（2）求杆的变形
（压缩）
（拉伸）
（压缩）
（3）由几何关系： （下降）
2-9答：任一截面上轴力为F，由
得面积为
伸长量为
2-11图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB杆所需的直径。
：
（2）由强度条件求
2-14图示AB为刚性杆，长为3a。A端铰接于墙壁上，在C、B两处分别用同材料、同面积的①、②两杆拉住，使AB杆保持水平。在D点作用荷载F后，求两杆内产生的应力。设弹性模量为E，横截面面积为A。
解：
1．本题为超静定问题，
见图(a),设AB杆产生角位移 ，则
，
2．由Hooke定律：
由平衡条件可知：
所以B,C截面相对位移为
3-1试作下列各杆的扭矩图。
3-2一直径d=60mm的圆杆，其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面上1，2，3点处的切应力和最大切应变，并在此三点处画出切应力的方向。(G=80GPa)。
解：横截面上切应力大小沿半径线性分布，方向垂直半径
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作下图所示梁的剪力图和弯矩图。
2m1m1mm1kN 2kN2kN 2kNA BCD梁分三段，AB 、BC 为空荷载段，CD 段为均布荷载段，均布荷载q=2kN/2m=1kN/m 。
A ，B ，D 三处剪力有突变，说明有集中力作用，在A 截面有向上集中力2kN ，在B 截面有向下集中力2kN ，在D 截面有向上集中力2kN 。
荷载图如图 (b)。
根据荷载图作弯矩图，如图 (c)所示。
如下图所示机构中，1,2两杆的横截面直径分别为cm d 101= ，cm d 202= ，P=10kN 。
横梁ABC ，CD 视为刚体。
求两杆内的应力。
p DCBA122m2m1.5m1m1mCD 杆的D 支座不受力，CD 杆内也不受力，所以p 可视为作用于ABC 杆的C 端。
取ABC 为受力体，受力图如图(b)所示。
MPaMPa A N MPaMPa A N kN N kN N 7.6310204103203.12710104101020210162222623111=⨯⨯⨯⨯===⨯⨯⨯⨯====--πσπσ，如图所示的阶梯形圆轴，直径分别为cm d 41=,cm d 72=。
轮上三个皮带轮，输入功率为kW N 171=，kW N 132=，kW N 303=。
轴的转速为n=200r/min ，材料的许用剪应力[τ]=60MPa 。
试校核其强度。
1计算各轮处的扭转外力偶矩。
mkN m kN m m kN m kN n N m m kN m kN n N m ⋅=⋅⨯=⋅=⋅⨯=⋅=⋅⨯==433.12003055.9621.02001355.9255.9812.02001755.9155.9321 (c)(b)kN m 31图3传动轴可简化为图3(b)，⑦扭矩图如图3(c)。
AD 段的最大剪应力为 []τπτ>=⨯⨯⨯==-MPa Pa W M T TAD 6.64104168126311max BC 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TBC 3.211071614326322max AD 段的单位长度扭转角为[]θπθ>=⨯⨯⨯⨯⨯⨯==-m mGI M p TAD /1.23/104108018032812842911BC 段的单位长度扭转角为[]θπθ<=⨯⨯⨯⨯⨯⨯==-m m GIp MINC/44.0/1074108018032143222829由此可知轴的强度与刚度都不够。
如图8所示的结构，由Q235刚制成，[σ] =160MPa ，斜撑杆外径D=45mm ，内径d=36mm ，3=st n ，斜撑杆的1001=λ，6.612=λ，中长柱的MPa cr )12.1304(λσ-=，试由压杆的稳定计算，确定结构的许用载荷[P]。
利用平衡关系，确定斜撑杆BD 的压力与P 的关系，即P N P N M BD o BD A 2202145sin 0==⨯-⨯=∑，，由于杆长m l 414.1=，惯性半径mm D d D i 41.14142=⎪⎭⎫⎝⎛+=，长度系数1=μ，所以 9801441.0414.11=⨯==ilμλ因为12λλλ≤≤，故BD 属于中长杆。
()()kNN d D A P MPaMPa b a cr cr cr cr 11110)3645(410619441949812.130462222=⨯-⨯⨯⨯=-===⨯-=-=-ππσσλσ 代入稳定安全系数计算式，有BDcrst N P n =即 []kN kN n P P stcr 1332211122=⨯==作图 6所示梁的剪力图和弯矩图。
图6求支反力：qa R qa R D A 4741==， qa R Q A A 41== AB 段内无荷载，为水平线，B 点集中力偶矩对剪力无影响，因此BC 段剪力都为水平，且4qaR Q BC BA ==。
CD 段内剪力为斜直线，截距为qa 2。
D 处剪力有突变，大小为D R 。
AB 段空载荷，弯矩图为斜直线。
但B 处有集中力偶作用，弯矩有突变，应分左、右两个截面计算。
在截面24a q a R M A BA ==,右截面2245qa qa a R M A Bc =+=。
图1BC 段，弯矩图应是斜直线。
CD CB M qa M ==223，即连接BC M 及CB M 。
CD 段为二次抛物线，但该段有0=Q 的点——E 点，离C 截面距离为a q Q CD 41/=，23249qa M E =。
连接C ，E ，D 的弯矩值(用下半圆曲线)。
可得弯矩图。
直径相同的铸铁圆截面直杆，可设计成图 7中（a ）、（b ）两种结构的形式，问哪种结构所承受的载荷P 大大多少°°p p60aABCABC6图7由于杆件材料、截面形状相同，并且为铸铁，属于脆性材料，抗压性能优于抗拉性能，因此比较两种结构的拉应力与P的关系。
图2(a)中的AC杆受拉，取A 点为受力体，受力图如图2(c)。
()t bσ为拉伸的强度极限。
令12)(PANtbAC==σ，则()21AP t bσ=图(b)中AB杆受拉，取A点为受力体，受力体如图2(d)。
令()32PANtbAB==σ，()APtbσ32=，所以12PP〉，即图(b)承受载荷P大。
又()()323212==AAPPtbtbσσ所以图(b)承受的荷载P是图(a)承受的荷载P的32倍。
图23、简支梁承受均布载荷作用，如图 8 所示。
若采用两种截面面积相等的实心和空心圆截面，D1=40mm, α=d2/D2=3/5。
试分别计算其最大的正应力，空心截面比实心截面的最大正应力减小了百分之几图8图3(1)几何尺寸。
依题意两种截面面积相等，即)1(4)(44222222221απππ-=-=D d D D所以 mm mm D D 505314012212=⎪⎭⎫ ⎝⎛-=-=αmm D d 305322==(2)最大正应力。
因简支梁受均布载荷作用，故最大弯矩： m kN m N ql M ⋅=⋅⨯⨯==182)102(8232max 实心截面3231D W z π= ()MPa Pa W M z 15904.01013233max max =⨯⨯==πσ 空心截面[]432'132απ-=D W z()MPa Pa W Mz6.93)531(05.010132433max 'max=⎥⎦⎤⎢⎣⎡-⨯⨯==πσ最大正应力发生在梁中间截面的上、下边缘。
(3)最大正应力的比较。
空心截面比实心截面的最大正应力减小了%1.411596.93159max 'max max =-=-σσσ图9所示结构，AB 为工字截面梁，其横梁面面积为22610mm A =，抗弯截面模量为3310141mm W z ⨯=。
已知AB 、CD 杆材料相同，其中E=160GPa ，稳定安全系数5.2=stn ，1001=λ，校核结构是否安全。
图9AB 、CD 杆的内力和变形形式：AB 杆承受拉弯变形，m kN M kN N AB ⋅==215210max ， CD 杆位压杆，kN N CB 220=所以，结构的安全性包括AB 杆的强度问题和CD 杆压杆的稳定性。
(1) AB 梁的强度问题：[]σσ<=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯=+=--MPa Pa W M A N 1561014110215101.2610210max 6343max 故AB 梁的强度足够。
(2) CD 杆压杆的稳定性113303.0411λμλ>=⨯⨯==il故CD 杆为细长杆。
()kN N l EI P cr 5.78)11(6403.010320024222=⨯⨯⨯⨯⨯⨯==ππμπ 工作安全系数5.277.23.285.78>===CD cr w N P n 故CD 杆的稳定性也满足要求。
所以，整个结构是安全的。
三根圆截面压杆，直径均为d=160mm ，材料为A3钢（E=206Gpa, 240s Mpa σ=,200p Mpa σ=，304, 1.12a Mpa b Mpa ==），三杆两端均为铰支，长度分别为123,,l l l ，且123245l l l m ===。
试求各杆的临界压力。
1μ=，三根杆的柔度分别为：可见：1杆适用欧拉公式，2杆适用经验公式，3杆适用强度公式。
1125l i μλ'==262.5l i μλ''==331.25li μλ'''==1100λ==257sa bσλ-==()2211225364cr cr E d F A KN ππσλ==='222()47104cr cr d F A a b KNπσλ''==-=23348234cr cr sd F A KNπσσ===一铸铁圆柱的直径为40mm ，其一端固定，另一端受到315 的力偶矩作用。
若该铸铁材料的许用拉应力为MPa t 30][=σ，试根据强度理论对圆柱进行强度校核。
解：圆柱表面的切应力最大，即：Mpa d T W T t 25)16//(/3max max max ===πτ圆柱表面首先破坏，其上任一点的应力状态为纯剪切，见图3。
进行应力分析可得：MPa 252520020022min max ±=+⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫σσ∴ MPa 251=σ，02=σ， MPa 253-=σ由第一强度理论有：[]t MPa σσ≤=251， 满足强度条件。
25MPa图3所示。
（2）B 处的挠度为0，即：由叠加法得,见图（d ）：铸铁压力机框架，立柱横截面尺寸如图所示，材料的许用拉应力[t]＝30MPa ，许用压应力[c]＝120MPa 。
试按立柱的强度计算许可载荷F 。
已知， ，。
F F3501501505050z1z 1y ymm750=z 47mm 1031.5⨯=y I F350)()(=+=By F B F B B y y y EIFa a a EI a F y F B 314)29(6)2()(32-=--=EIa F y By F B By 38)(3=03831433=+-EIa F EI Fa By F F By 47=（1）立柱横截面的内力（2）立柱横截面的最大应力（3）求压力F()Pa 66710151031.5075.0104253530max .F FF AF I Mz Ny t =⨯+⨯⨯⨯=+=---σFF N =()()N.m 10425107535033--⨯=⨯+=F F M ()Pa 93410151031.5125.0104253531max .F FF AF I Mz Ny c =⨯-⨯⨯⨯=-=---σ[]t t F σσ≤=667max .[]N4500066710306676=⨯=≤t F σ[]c c F σσ≤=934max .许可压力为：某传动轴设计要求转速n = 500 r / min ，输入功率N 1 = 500马力， 输出功率分别 N 2 = 200马力及 N 3 = 300马力，已知：G =80GPa ，[ ]=70M Pa ，[]=1º/m ，试确定：①AB 段直径 d 1和 BC 段直径 d 2 ②若全轴选同一直径，应为多少 ③主动轮与从动轮如何安排合理解：（1）计算外力偶矩据扭转强度条件：，，[]N128500934101209346=⨯=≤c F σ45000N 45kNF ≤=5040N 1 N 3 N 2 ACB7024(N m)N m n =⋅max max []t T W ττ=≤316t W d π=T –可得：由扭转刚度条件：可得：综上所述，可取：(2) 当全轴取同一直径时，(3) 轴上扭矩的绝对值的越小越合理，所以，1轮和2轮应该换位。