重庆市第八中学2021届高三上学期阶段性测试数学试题

重庆八中高2021级高三（上）第一次月考试题数学（理科）本试卷满分150分，考试时间120分钟一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个备选项中，只有一项是符合题目要求的．1．已知集合(){}22,2,,A x y xy x y =+<∈∈Z Z ，则A 中元素的个数为 A ．3 B ．4 C ．5 D ．6 2．已知复数()211i z i -=+，（其中i 为虚数单位），则z 的虚部为 A ．-1 B ．1 C ．-i D ．i3．若1m n >>，a =，()1lg lg 2b m n =+，lg 2m n c +⎛⎫= ⎪⎝⎭，则 A ．a b c <<B ．c a b <<C ．b a c <<D ．a c b <<4．在ABC 中，已知a =b =60A =︒，则ABC 的面积为A ．34+B ．34-C ．4D 5．下面几种推理中是演绎推理的为A ．高三年级有30个班，1班55人，2班56人，三班57人，由此推测各班都超过55人B ．猜想数列112⨯，123⨯，134⨯，…的通项公式为()()*11n a n n n =∈+N C ．半径为r 的圆的面积2S r π=，则单位圆的面积S π=D ．由等差数列的性质，推测等比数列的性质6．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的值不可能为A ．2B ．3C ．4D ．57．某几何体的三视图如图所示，其中网格纸上的小正方形的边长为1，则该几何体的体积为A ．223B ．203C ．6D ．16 8．已知()1n x -展开式中第4项与第10项的二项式系数相等，则奇数项的系数和为A ．112B ．112-C ．132D ．132- 9．已知α为锐角，()3sin 155α-︒=，则()cos 215α+︒= A．50- B．50 C．50- D．5010．某市政府为加强数学科学研究，计划逐年加大研发资金投入．已知市政府1979年全年投入研发资金100万元，2019年全年投入研发资金500万元，若每年投入的研发资金的增长率相同，则该市政府2020年全年投入的研发资金约为（ ）万元．（本题中增长率0.1x <，可用自然对数的近似公式：()ln 1x x +≈，参考数据：ln5 1.6≈）A ．510B ．520C ．530D ．540 11．已知实数x ，y 满足()2221x y +-=的最大值为A ．12B ．2C ．1D ．712．如图，矩形ABCD 中，2AB AD ==E 为边AB 的中点，将ADE 沿直线DE 翻折成1A DE ．在翻折过程中，直线1A C 与平面ABCD 所成角的正弦值最大为A ．4B ．6C ．14D ．5二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中的横线上．13．函数()f x =______________． 14．如图，茎叶图表示甲、乙两名篮球运动员在五场比赛中的得分（均为整数），其中一个数字模糊不清，则甲的平均得分高于乙的平均得分的概率为______________．15．已知正ABC 的边长为2，PQ 为ABC 内切圆O 的一条直径M 为ABC 边上的动点，则MP MQ ⋅的取值范围为______________．16．已知点P 为椭圆2214x y +=上的任意一点，点1F ，2F 分别为该椭圆的左、右焦点，则1221sin sin PF F PF F ∠+∠的最大值为______________．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求做答．（一）必考题：共60分．17．（本小题满分12分）设数列{}n a 的前n 项和为n S ，已知11a =，121n n a S +=+，*n ∈N ．（1）求通项公式n a ；（2）设()()()*111n n n n a b n a a +=∈++N ，数列{}n b 的前n 项和为n T ，求证：14n T <． 18．（本小题满分12分）重庆八中为了普及环保知识，增强学生的环保意识在全校组织了一次有关环保知识的竞赛．经过初赛、复赛，高二年级代表队和高一年级代表队（每队3人）进入了决赛，规定每人回答一个问题，答对为本队赢得100分，答错得0分．假设高二年级代表队中每人答对的概率均为34，高一年级代表队中3人答对得概率分别为45，34，23，且各人回答正确与否相互之间没有影响，用X 表示高一年级代表队的总得分．（1）求X 的分布列和数学期望；（2）求两队总得分之和等于300分且高二年级获胜的概率．19．（本小题满分12分）如图，在四棱锥P ABCD -中，底面ABCD 为正方形，AP ⊥平面CDP ，已知2AP DP ==，Q 为线段DP 的中点．（1）求证：//BP 平面ACQ ；（2）求二面角C BQ P --的平面角的余弦值．20．（本小题满分12分）设函数()1e xf x x-=，若()()12f x f x t ==（其中12x x <）． （1）求实数t 的取值范围；（2）证明：()21221x f x f x ⎛⎫>⎪-⎝⎭． 21．（本小题满分12分）已知点F 为抛物线()2:20C y px p =>的焦点．点()()2,20A m m m >在C 上，点D 在x 轴上（位于点F 右侧），直线AF ，AD 分别交C 于另一点B ，E ，点G 在线段FD 上且0GA GB GE ++=．（1）求抛物线C 的方程；（2）设BFG ，ADG 的面积分别为BFG S，ADG S ，求BFG ADG S S 的表达式()f m 及()f m 的取值范围． （二）选考题：共10分．请考生在22，23题中任选一题作答．如果多做，则按所做的第一题计分．22．（本小题满分10分）在直角坐标系中，已知曲线C 的参数方程为13cos 3sin x y ββ=+⎧⎪⎨=⎪⎩，（β为参数），以原点为极点，x 轴正半轴为极轴建立极坐标系，直线1l 的极坐标方程为θα=，直线2l 的极坐标方程为2πθα=+．（1）写出曲线C 的极坐标方程； （2）设1l 与曲线C 交于P ，Q 两点，2l 与曲线C 交于M ，N 两点，求四边形PMQN 面积的取值范围．23．（本小题满分10分） 己知函数()11,f x x x x =+--∈R ．（1）求不等式()1f x ≥的解集；（2）若方程()f x a x -=有三个实数根，求实数a 的取值范围．。

2021届重庆市第八中学高三上学期适应性月考数学（文）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合0,1,2,3A =，301x B x x ⎧-⎫=⎨⎬-⎩⎭≤，则A B ⋂=（ ）A ．1,2B ．1,2,3C ．2.3D ．22.复数()()2234i R z a a a =-+-∈的实部与虚部相等，且z 在复平面上对应的点在第三象限，则a =（ ） A ．1 B ．2 C ．1或2 D ．1-3.函数()sin 0,0,2y A x A πωϕωϕ⎛⎫=+ ⎪⎝⎭＞＞＜的部分图象如图1所示，则（ ）A ．3sin 26y x π⎛⎫=- ⎪⎝⎭B ．3sin 23y x π⎛⎫=- ⎪⎝⎭C ．3sin 6y x π⎛⎫=- ⎪⎝⎭D ．3sin 3y x π⎛⎫=- ⎪⎝⎭4.直三棱柱111ABC A B C -中，AB BC ⊥，12AB BC AA ===，则该三棱柱的外接球的表面积为（ ） A ．4π B ．8π C.12π D ．323π5.已知直线40x y ++=被圆22220x y x y a ++-+=所截得弦长为2，则实数a 的值为（ ） A ．1- B ．4- C.7- D ．10-6.已知直线3y x =-与两坐标轴围成的区域为1Ω，不等式组3,0,2y x x y x -⎧⎪⎨⎪⎩≤≥≥所形成的区域为2Ω，现在区域1Ω中随机放置一点，则该点落在区域2Ω的概率是（ ） A ．14 B ．13 C.12 D ．237.某几何体的三视图如图2所示，则该几何体的体积为（）A．123π+ B．136π C.73πD．52π8.已知直线l过点()0,1，且倾斜角为6π，当此直线与抛物线24x y=交于A，B时，AB=（）A．163B．16 C.8 D．16339.阅读如图3所示的程序框图，运行相应的程序，则程序运行后输出的结果为（）A．8 B．9 C.10 D．1110.已知函数()12log,02,12,2,2x xf xx x⎧⎪⎪=⎨⎪-+⎪⎩＜≤＞且()2f a=，则()2f a+=（）A．12B．14C.58D．7811.设当x θ=时，函数()3sin 4cos f x x x =+取得最小值，则sin θ=（ ） A ．35 B ．45 C.35- D ．45-12.设函数()211121x f x x+⎛⎫=+⎪+⎝⎭，则使得()()()21122f x f x f x -+-＜成立的x 的取值范围是（ ） A ．1,13⎛⎫ ⎪⎝⎭ B ．()1,1,3⎛⎫-∞⋃+∞ ⎪⎝⎭ C.11,33⎛⎫- ⎪⎝⎭ D ．11,,33⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知向量()22,2a =，()0,2b =，(),2c m =，且()2a b c +⊥，则实数m = ．14.若双曲线()221024x y a a -=＞的一条渐近线过点()2,1，则a = ． 15.ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若3cos 5A =-，1sin 2C =，1c =，则ABC ∆的面积为 ．16.重庆好食寨鱼火锅底料厂用辣椒、花椒等原材料由甲车间加工水煮鱼火锅底料，由乙车间加工麻辣鱼火锅底料.甲车间加工1吨原材料需耗费工时10小时，可加工出14箱水煮鱼火锅底料，每箱可获利80元；乙车间加工1吨原材料需耗费工时6小时，可加工出8箱麻辣鱼火锅底料，每箱可获利100元.甲、乙两车间每天总获利最大值为 元．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （本小题满分12分）已知n a 是递增的等差数列，1a ，2a 是函数()21021f x x x =-+的两个零点. （1）求数列n a 的通项公式；（2）记3n n n b a =⨯，求数列n b 的前n 项和n S . 18. （本小题满分12分）发改委10月19日印发了《中国足球中长期发展规划（2016-2050年）重点任务分工》通知，其中“十三五”校园足球普及行动排名第三，为了调查重庆八中高一高二两个年级对改政策的落实情况，在每个年级随机选取20名足球爱好者，记录改政策发布后他们周平均增加的足球运动时间（单位：h ），所得数据如下：高一年级的20位足球爱好者平均增加的足球运动时间： 1.6 3.4 3.7 3.3 3.8 3.2 2.8 4.2 2.5 4.5 3.5 2.5 3.3 3.7 4.0 3.9 4.1 3.6 2.2 2.2 高二年级的20位足球爱好者平均增加的足球运动时间： 4.2 2.8 2.9 3.1 3.6 3.4 2.2 1.8 2.3 2.7 2.6 2.4 1.5 3.5 2.1 1.9 2.2 3.7 1.5 1.6（1）分别计算两组数据的平均数，从计算结果看，哪个年级政策落实得更好？ （2）根据两组数据完成图4的茎叶图，从茎叶图简单分析哪个年级政策落实得更好？ 19. （本小题满分12分）如图5所示，四边形ABCD 是边长为2的正方形，四边形BDFE 是平行四边形，点M ，N 分别是BE ，CF 的中点.（1）求证：MN ∥平面ABCD ；（2）若ABE ∆是等边三角形且平面ABE ⊥平面ABCD ，记三棱柱E ABF -的体积为1S ，四棱锥F ABCD -的体积为2S ，求12S S 的值. 20. （本小题满分12分）已知椭圆()2222:10x y C a b a b+=＞＞的长轴是圆224x y +=的一条直径，且右焦点到直线230x y +-=的距离（1）求椭圆C 的标准方程；（2）是否存在直线():l y kx m k R =+∈与椭圆C 交于A ，B 两点，使得22OA OB OA OB +=-成立？若存在，求出实数m 的取值范围；若不存在，请说明理由. 21. （本小题满分12分） 设函数()()3x f x k x e x =---.（1）当1k =时，求()f x 在()()0,0f 处的切线方程； （2）若()0f x ＜对任意0x ＞恒成立，求整数k 的最大值.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. （本小题满分10分）选修4-4：坐标系与参数方程已知圆O 和圆C 的极坐标方程分别为2ρ=和4sin ρθ=，点P 为圆O 上任意一点． （1）若射线OP 交圆C 于点Q ，且其方程为3πθ=，求PQ 的长；（2）已知32,2D π⎛⎫⎪⎝⎭，若圆O 和圆C 的交点为A ，B ，求证：222PA PB PD ++为定值．23. （本小题满分10分）选修4-5：不等式选讲 若0a ＞，0b ＞且223ab a b =++． （1）求2a b +的最小值；（2）是否存在a ，b 使得22417a b +=？并说明理由．2021届重庆市第八中学高三上学期适应性月考数学（文）试题参考答案一、选择题1-5:CACCC 6-10:BBABD 11、12：CB 【解析】1.{}13B x x =＜≤，{}2,3A B ∴⋂=，故选C .2.由题意2234a a-=-，解得1a=或2，当2a=时，22iz=+，它在复平面上对应的点在第一象限，不符合题意，舍去，所以1a=，故选A.3.24362 Tπππ=-=，2Tπ∴=，2Tπω=，又,06π⎛⎫⎪⎝⎭为“五点法”的第一个点，则06πϕ+=，6πϕ=-，sin6y xπ⎛⎫∴=-⎪⎝⎭，故选C.4.设D，1D分别为AC，11A C的中点，则1DD的中点O为球心，球的半径223R CD OD=+=，故表面积为2412S Rππ==，故选C.5.圆的方程为()()22112x y a++-=-，圆心为()1,1-，由22114122a⎛-++⎫+=-⎪⎝⎭得7a=-，故选C.6.如图1所示，OAB∆对应的区域为1Ω，OBC∆对应的区域为2Ω，所以该点落在区域2Ω的概率13OBCOABSPS∆∆==，故选B.7.该几何体由一个圆柱和半个圆锥构成，2211131211236Vπππ=⨯⨯+⨯⨯⨯⨯=，故选B.8.直线3:1l y=+与24x y=联立得24340x-=，643∆=，故21211611333AB k x x=+⋅-=+=，故选A.9.当1i=时，1lg12S=-＞；当2i=时，1lg13S=-＞；当3i=时，1lg14S=-＞……当9i=时，1lg110S==-，故输出9i=，故选B.10.（1）当2a＞时，()1212f a a=-+＜，不成立；（2）当02a＜≤时，()12log2f a a==，则14a=或4a=（舍），所以()9197224248f a f⎛⎫+==-⨯+=⎪⎝⎭，故选D.11.()()343sin4cos5sin cos5sin55f x x x x x xϕ⎛⎫=+=+=+⎪⎝⎭，其中4sin5ϕ=，3cos5ϕ=，由()()5sin5fθθϕ=+=-得()sin1θϕ+=-，所以22kπθϕπ+=-+，k Z∈，22kπθϕπ=--+，k Z∈，所以3 sin sin2sin cos225kππθϕπϕϕ⎛⎫⎛⎫=--+=--=-=-⎪ ⎪⎝⎭⎝⎭，故选C.12.由解析式可知，()f x为偶函数且在[)0,+∞上单调递减，则()()()2112221f x f x f x-+-=-，所以()()()()()()()()()2112222122121f x f x f x f x f x f x f x f x f x-+-⇔-⇔-⇔-⇔＜＜＜＜()222212121213x x x x x x x-⇔-⇔-⇔＞＞＞＜或1x＞，故选B.二、填空题13.3- 14.4 15.83625-16.60800【解析】13.()222,6a b+=，由()20a b c+⋅=得22620m+=，所以3m=-.14.渐近线方程为2y xa=±，故41a=，所以4a=.15.22sincRC==，则482sin255a R A==⨯=，又()sin sin sin cos cos sinB AC A C A C=+=+=4331433525210-⎛⎫⨯+-⨯=⎪⎝⎭，118433836sin12251025S ac B--∴==⨯⨯⨯=.16.设甲车间加工原材料x吨，乙车间加工原材料y吨，甲、乙两车间每天获利为z元，则0,0,70,106480,x yx yx y⎧⎪+⎨⎪+⎩≥≥≤≤目标函数1120800z x y=+，作出可行域，如图2所示.当1120800z x y=+对应的直线过直线70x y+=与106480x y+=的交点A时，目标函数1120800z x y=+取得最大值.由70,106480x yx y+=⎧⎨+=⎩得15,55,xy=⎧⎨=⎩故max1120158005560800z=⨯+⨯=，即甲、乙两车间每天总获利最大值为60800元.三、解答题17.解：（1）函数()21021f x x x =-+的两个零点为3，7， 由题意得13a =，37a =.()()213353213213n n n S n n -=⨯+⨯++-⨯++⨯， ()()23133353213213n n n S n n +=⨯+⨯++-⨯++⨯，两式相减得()()()()23111292333213939213n n n n n S n n +++-=+⨯+++-+⨯=+--+⨯，所以13n n S n +=⨯.18.解：（1）设高一年级所得数据的平均数为x ，高二年级所得数据的平均数为y . 由记录数据可得 ()11.6 3.4 3.7 3.3 3.8 3.22.8 4.2 2.5 4.53.5 2.5 3.3 3.74.0 3.9 4.1 3.6 2.2 2.220x =⨯+++++++++++++++++++3.3=，()14.2 2.8 2.9 3.1 3.6 3.4 2.2 1.8 2.3 2.7 2.6 2.4 1.5 3.5 2.1 1.9 2.2 3.7 1.5 1.620y =⨯+++++++++++++++++++2.6=，由以上计算结果可得x y ＞，因此可看出高一年级政策落实得更好. （2）由记录结果可绘制如图3所示的茎叶图：从以上茎叶图可以看出，高一年级的数据有710的叶集中在茎3，4上，而高二年级的数据有710的叶集中在茎1，2上，由此可看出高一年级政策落实得更好.19.（1）证明：如图4，取DF 的中点H ，连接MH ，NH ， 点N ，H 分别是CF ，DF 的中点，NH CD ∴∥. EBDF 是平行四边形，且点M ，H 是BE ，DF 的中点， MH BD ∴∥，又MH NH H ⋂=，BD CD D ⋂=，所以平面MNH ∥平面ABCD ， 又MN ⊂平面MNH ，MN ∴∥平面ABCD.（2）解：法一：DF BE ∥，DF ⊄平面ABE ，BE ⊂平面ABE ， DF ∴∥平面ABE ，1=E ABF F ABE D ABE E ABD S V V V V ----∴===，又EF BD ∥，EF ⊄平面ABCD ，BD ⊂平面ABCD ， EF ∴∥平面ABCD ，2122F ABCD E ABCD E ABD S V V V S ---∴====，1212S S ∴=. 法二：DF BE ∥，DF ⊄平面ABE ，BE ⊂平面ABE ，DF ∴∥平面ABE ,平面EAB ⊥平面ABCD ，DA AB ⊥，平面EAB ⋂平面ABCD AB =， DA ∴⊥平面EAB ，11123=3233E ABF D EAB EAB S V V S DA --∴==⋅⋅==， EF BD ∥，EF ⊄平面ABCD ，BD ⊂平面ABCD ， EF ∴∥平面ABCD ，又平面EAB ⊥平面ABCD ，∴点F 到平面ABCD 的距离等于E 到AB的距离，即h =113F ABCD ABCD S V S h -∴==⋅⋅=， 1212S S ∴=. 20.解：（1）由已知24a =， 解得2a =，c =，所以1b =，椭圆C 的标准方程为2214x y +=.（2）假设存在这样的直线.由22,1,4y kx m x y =+⎧⎪⎨+=⎪⎩得()222418440k x kmx m +++-=， ()2216410k m ∆=-+＞，()*设()11,A x y ，()22,B x y ，则122841kmx x k +=-+，21224441m x x k -=+，()()1212y y kx m kx m =++()221212k x x km x x m =+++ ()22222224484141k m k m m k k -=-+++ 222441m k k -=+， 由22OA OB OA OB +=-得0OA OB ⋅=，即12120x x y y +=， 故22454k m =-，代入()*式得m -＜m 21.解：（1）当1k =时，()1x f x xe '=--， 则()01f '=-，()02f =-，所以()f x 在()()0,0f 处的切线方程为()()210y x --=-⨯-， 即20x y ++=.（2）()30x k x e x ---＜对任意0x ＞恒成立3x x k x e+⇔+＜对任意0x ＞恒成立 min 3x x k x e +⎛⎫⇔+ ⎪⎝⎭＜， 令()()30xx h x x x e +=+＞，则 ()221x x xx e x h x e e ----'=+=. 令()2x x e x ϕ=--，则()10x x e ϕ'=-＞，()x ϕ∴在()0,+∞上单调递增，又()130e ϕ=-＜，3237022e ϕ⎛⎫=- ⎪⎝⎭＞， ∴存在031,2x ⎛⎫∈ ⎪⎝⎭使得()00x ϕ=，其中()h x 在()01,x 上单调递减，在()0,x +∞上单调递增， ()()0000min 3x x h x h x x e +∴==+， 又()00x ϕ=，即0020x e x --=，002x e x ∴=+，()()0000000min 00331122x x x h x h x x x x x x e ++∴==+=+=++++， 031,2x ⎛⎫∈ ⎪⎝⎭，0512,2x ⎛⎫∴+∈ ⎪⎝⎭，0110,22x ⎛⎫∈ ⎪+⎝⎭， ()00112,32x x ∴++∈+， k Z ∈，2k ∴≤，k ∴的最大值为2.22.（1）解：把3πθ=代入4sinρθ=得到Q 点的极径4sin 3Q πρ==， 而点P 的极径为2P ρ=，所以2Q P PQ ρρ=-=.（2）证明：联立2ρ=和4sin ρθ=解得52,6A π⎛⎫ ⎪⎝⎭，2,6B π⎛⎫ ⎪⎝⎭，32,2D π⎛⎫⎪⎝⎭，其直角坐标为()A ，)B，()0,2D -，圆O 的直角坐标方程为224x y +=.则(()(()()22222222211224PA PB PD x y x y x y ++=+-+-+-+++=. 23.解：（1）由条件知()21230a b b -=+＞，12b ＞.所以2321b a b +=-，23422212262121b a b b b b b ++=+=-++=--≥. 当且仅当212b -=，即32b =，3a =时取等，所以2a b +的最小值为6. （2）因为22224269222a b a b ++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭≥≥，当且仅当32b =，3a =时取等， 所以22418a b +≥，故不存在a ，b 使得22417a b +=.。

2021届重庆市第八中学高三上学期入学考试数学文科试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试时间120分钟第I 卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．sin(150)-的值为A ．12-B ．12C ． D2．已知命题:,20x p x R ∀∈>，命题:,sin cos q x R x x ∃∈+> A ．命题p q ∨是假命题 B ．命题p q ∧是真命题 C ．命题()p q ∧⌝是真命题D ．命题()p q ∨⌝是假命题3．已知函数221,1(),1x x f x x ax x ⎧+<⎪=⎨+≥⎪⎩，若[](0)4f f a =，则实数a 等于A ．12B ．45C ．2D ．94．已知1sin cos 2x x -=，则sin 2x = A ．34B ．34-C ．12-D ．125．2()ln f x ax bx x =++在点(1,(1))f 处的切线方程为42y x =-，则b a -= A ．1-B ．0C ．1D ．2 6．在ABC ∆中，,,a b c 为角,,A B C 的对边，若6A π=，3cos 5B =，8b =，则a = A ．403 B ．10 C ．203D ．5 7．已知()sin()(0,0,)f x A x A x R ωϕω=+>>∈，则“()f x 在1x =处取得最大值”是“(1)f x +为偶函数”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 8．下图可能是下列哪个函数的图象 A ．1xy x =+B ．ln x y x=C ．2(2)x y x x e =-D ．22||y x x =-9．将函数sin()(0,||)y x ωϕωϕπ=+><的图象向右平移6π个单位，再将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）所得的图象解析式为sin y x =，则sin()y x ωϕ=+图象上距离y 轴最近的对称轴方程为A ．6x π=-B ．3x π=C ．12x π=-D ．12x π=10．某几何体的三视图如图所示，则该几何体的体积可以是 A ．4483π+B ．482π+C ．8483π+D ．483π+11．在ABC ∆中，60B =，AC 2AB BC +的最大值为A ．B ．C ．D ．12．设直线y t =与曲线2(3)y x x =-的三个交点分别为(,)A a t 、(,)B b t 、(,)C c t ，且a b c <<，现给出如下结论：①abc 的取值范围是(0,4)；②222a b c ++为定值；③c a -有最小值无最大值。

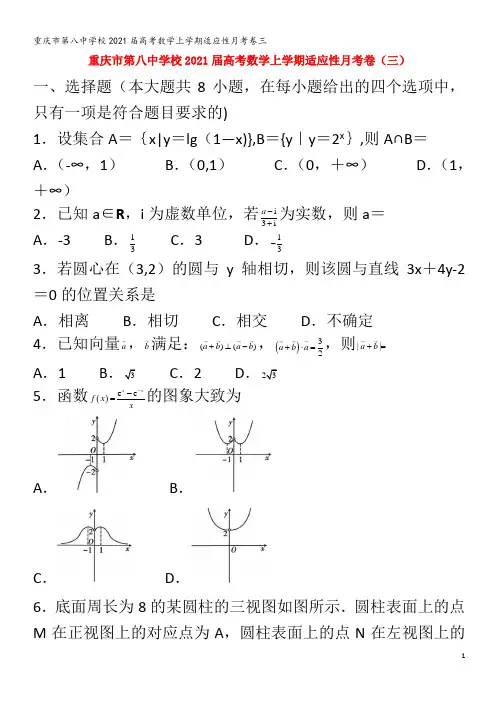
重庆市第八中学校2021届高考数学上学期适应性月考卷（三）一、选择题（本大题共8小题，在每小题给出的四个选项中，只有一项是符合题目要求的)1．设集合A ＝｛x|y ＝lg （1—x)},B ＝{y ｜y ＝2x ｝,则A∩B ＝A ．（-∞，1）B ．（0,1）C ．（0，＋∞）D ．（1，＋∞）2．已知a ∈R ，i 为虚数单位，若i 3i a -+为实数，则a ＝A ．-3B ．13C ．3D ．13-3．若圆心在（3,2）的圆与y 轴相切，则该圆与直线3x ＋4y-2＝0的位置关系是A ．相离B ．相切C ．相交D ．不确定 4．已知向量a ，b 满足：()()a b a b +⊥-，()32a b a +⋅=，则||a b +=A ．1B ．3C ．2D ．235．函数()e e xxf x x --=的图象大致为A ．B ．C ．D ．6．底面周长为8的某圆柱的三视图如图所示．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B,在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为13，则该圆柱的体积为A ．24πB ．32πC ．48πD ．192π7．已知抛物线C ：y 2＝4x 的准线l 与x 轴的交点为D ，过F （1,0）的直线与C 的一个交点为A ，与准线l 相交于点B ，若2FA BF =，则三角形BDF 的面积为A 5B ．5C ．42D ．58．已知α，β满足2sin 2sin 23αβ+=，且()1sin 3αβ+=，则()cos αβ-=A ．13B ．12C ．34D ．1二、选择题(本大题共4小题，在每小题给出的选项中，有多项是符合题目要求的．）9．函数f （x ）=Asin(2x+φ）在π0,6⎡⎤⎢⎥⎣⎦上是单调函数的一个充分条件是A ．A ＞0,π3ϕ=B ．A ＞0，π3ϕ=- C ．A ＜0，π3ϕ= D ．A ＜0,π3ϕ=-10．设a ＞0，b ＞0，a ＋2b ＝1,则A ．ab 的最大值为18B ．a 2＋4b 2的最小值为12C ．12a b+的最小值为8 D ．2a ＋4b 的最小值为2211．已知双曲线C ：22221x y a b -=（a ＞0，b ＞0)5，右焦点为F ，过F 的直线l 与C 的两条渐近线的交点分别为A ，B,且与其中一条渐近线垂直，△OAB 的面积为163（O 为坐标原点）,则A ．直线l 与C 的左、右两支各有一个交点B ．C 的焦距为410C ．点O 到直线l 的距离为42D ．若P 为C 右支上一点,则｜PF ｜的最小值为16212．设f'（x)是函数f （x ）（x ∈R ）的导函数,若对任意x ∈R ，都有2f （x ）＋xf'（x ）＞0,则下列说法一定正确的是 A ．4f （2）＞f(1） B ．f （x)为增函数 C ．f （x ）没有零点 D ．f （x)没有极值点 三、填空题 13．62x x ⎛⎫+ ⎪⎝⎭展开式中的常数项为________．14．已知{a n ｝是各项均为正数的等比数列，a 1＝6，若2a 5，a 3，3a 4成等差数列，则a 2＝________．15．某人设计一项单人游戏，规则如下:先将一棋子放在如图所示正方形ABCD （边长为1个单位）的顶点A 处，然后通过抛掷一枚质地均匀的硬币来确定棋子的走向，若硬币正面朝上，则沿正方形的边按逆时针方向行走1个单位，若硬币反面朝上，则沿正方形的边按顺时针方向行走1个单位，一直循环下去．则某人抛掷4次硬币后棋子恰好又回到点A 处的概率为________．16．如图，过原点O 的直线AB 交椭圆C ：22221x y a b +=（a ＞b ＞0）于A ，B 两点,过点A 分别作x 轴、AB 的垂线AP ，AQ 分别交椭圆C 于点P ，Q ，连接BQ 交AP 于一点M,若3AM 4AP =，则椭圆C 的离心率是________．四、解答题(解答应写出文字说明、证明过程或演算步骤） 17．在①2asinC=3csin2A ；②3bcosA —acosC=ccosA;③π53sin 28cos 2A A⎛⎫+-= ⎪⎝⎭．这三个条件中任选一个,补充在下面问题中的横线处，并解答．问题：△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若△ABC 222a =________，求b ＋c ．注：如果选择多个条件分别解答，按第一个解答计分． 18．S n 为数列{a n }的前n 项和．已知a n ＞0，2n2S n na a =+．(1）求｛a n }的通项公式; （2）设2na nb=，求m ，k(m ，k ∈N *）的值，使得b m ＋1＋b m ＋2＋..。

重庆八中高2021级高三（上）阶段性检测（5）数 学 试 题一、选择题：本题共8小题，每小题5分，共40分. 在每小题给出的选项中，只有一项符合题目要求.1．设集合{|11}A x x =-，N 为自然数集，则A N = A ．{1} B ．{0，1} C ．{1-，1} D ．{1-，0，1} 2．已知i 是虚数单位，1(1)0()a i a R +->∈，复数2z a i =-，则1||=zA ．15B ．5C ．5D ．53．已知a R ∈，则“01a <<”是“x R ∀∈，2210ax ax ++>”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“”和阴爻“”，如图就是一重卦．如果某重卦中有3个阳爻，3个阴爻，则它可以组成( )种重卦． A ．6B ．15C ．20D ．15．在ABC △中，AD 为BC 边上的中线，E 为AD 的中点，则BE = A ．3144AB AC - B ．1344AB AC - C ．3144AB AC -+D ．3144AB AC + 6．将曲线()cos2y f x x =上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移4π个单位长度，得到曲线cos2y x =，则()6π=f A ．1B ．1-C ．3D ．3-7．已知ln ,1()(2),1x x f x f x k x ⎧=⎨-+<⎩，若函数()1y f x =-恰有一个零点，则实数k 的取值范围是A ．(1,)+∞B ．[1，)+∞C ．(,1)-∞D ．(-∞，1]8．已知直线1:0()l kx y k R +=∈与直线2:220l x ky k -+-=相交于点A ，点B 是圆22(2)(3)2x y +++=上的动点，则||AB 的最大值为 A ．32B ．52C ．522+D ．322+二、选择题：本题共4小题，在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对得3分，选错不得分.9．某特长班有男生和女生各10人，统计他们的身高，其数据（单位：cm ）如下面的茎叶图所示，则下列结论正确的是A ．女生身高的极差为12B ．男生身高的均值较大C ．女生身高的中位数为165D ．男生身高的方差较小10．在正方体1111ABCD A B C D -中，N 为底面ABCD 的中心，P 为线段11A D 上的动点（不包括两个端点），M 为线段AP 的中点，则 A ．CM 与PN 是异面直线 B ．存在P 点使得//PN 平面11CC D D C ．平面PAN ⊥平面11BDD BD ．过P ，A ，C 三点的正方体的截面一定是等腰梯形11．在平面直角坐标系xOy 中，抛物线2:2(0)C y px p =>的焦点为F ，准线为l ．设l 与x 轴的交点为K ，P 为C 上异于O 的任意一点，P 在l 上的射影为E ，EPF ∠的外角平分线交x 轴于点Q ，过Q 作⊥QM PF 于M ，过Q 作QN PE ⊥交线段EP 的延长线于点N ，则 A ．||||PE PF =B ．||||PF QF =C ．||||PN MF =D ．||||PN KF =12．如图所示，一座小岛距离海岸线上最近的P 点的距离是2km ，从P 点沿海岸正东12km 处有一个城镇．假设一个人驾驶的小船的平均速度为3/km h ，步行的速度为5/km h ，时间t （单位：)h 表示他从小岛到城镇的时间，x （单位：)km 表示此人将船停在海岸处距P 点的距离．设24u x x =++，24v x x =+-，则A ．函数()v f u =为减函数B ．15432t u v --=C ．当 1.5x =时，此人从小岛到城镇花费的时间最少D ．当4x =时，此人从小岛到城镇花费的时间不超过3h 三、填空题（本题共4小题，每小题5分，共40分）13．()512x -展开式中按x 的升幂排列的第3项是_________________. 14．若3tan 4α=，则2cos 2sin 2αα+=___________________．15．已知1F 为双曲线22221(0,0)x y a b a b-=>>的左焦点，P 是双曲线右支上一点，线段1PF 与以该双曲线实轴为直径的圆相切于线段1PF 的中点，则该双曲线的离心率为___________________．16．已知数列{}n a 满足：对任意*n ∈N ，(0,)2n a π∈，且13a π=，1()()n n f a f a +='，其中()tan f x x =，则使得121sin sin sin 10k a a a ⨯⨯⋯⨯<成立的最小正整数k 为___________________． 四、解答题：本题共6小题，满分70分. 17．（10分）在ABC △中，5cos 13A =-，4cos 5B =． （1）求sinC 的值；（2）设5BC =，求ABC ∆的面积. 18．（12分）已知等比数列{}n a 满足1a ，2a ，31a a -成等差数列，且134a a a =；等差数列{}n b 的前n 项和2(1)log 2nn n a S +=．求：（1）n a ，n b ； （2）数列{}n n a b 的前项和n T ． 19．（12分）如图，在四棱锥P ABCD -中，23AD =，3AB =，3AP =，//AD BC ，AD ⊥平面PAB ，90APB ∠=︒，点E 满足2133PE PA PB =+．（1）证明：PE DC ⊥；（2）求二面角A PD E --的余弦值．20．（12分）2017年11月河南省三门峡市成功入围“十佳魅力中国城市”，吸引了大批投资商的目光，一些投资商积极准备投入到“魅力城市”的建设之中．某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中．项目一：天坑院是黄土高原地域独具特色的民居形式，是人类“穴居”发展史演变的实物见证．现准备投资建设20个天坑院，每个天坑院投资0.2百万元，假设每个天坑院是否盈利是相互独立的，据市场调研，到2020年底每个天坑院盈利的概率为(01)p p <<，若盈利则盈利投资额的40%，否则盈利额为0．项目二：天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区．据市场调研，投资到该项目上，到2020年底可能盈利投资额的50%，也可能亏损投资额的30%，且这两种情况发生的概率分别为p 和1p -．（1）记X （单位：百万元）为投资项目一盈利额，求()E X （用p 表示）； （2）试以项目盈利的期望为依据，针对以上两个投资项目，请你为投资公司选择一个项目，并说明理由．21．（12分）设中心在原点O ，焦点在x 轴上的椭圆C 过点1)2A ，F 为C 的右焦点，F 的方程为221104x y +-+=． （1）求C 的方程；（2）若直线:(0)l y k x k =>与动圆O 相切，与F 交于M 、N 两点，与C 交于P 、Q 两点，其中M 、P 在第一象限，记O 的面积为()S k ，求(||||)()NQ MP S k -取最大值时，直线l 的方程． 22．（12分）已知函数21()ln 2f x x ax =+，a R ∈．（1）讨论()f x 的单调性；（2）若不等式1()2x f x e e a <-+对(1,)x ∀∈+∞恒成立，求a 的取值范围．1 2 3 4 5 6 7 8 9 10 11 12 BCAC CDB CABBCDABD AC13141516 240x642552986．解：曲线()cos2y f x x =上各点的横坐标伸长到原来的2倍，纵坐标不变，得到：1()cos 2y f x x =，再把得到的曲线向右平移4π个单位长度，得到：1()cos()cos2284y f x x x ππ=--=， 所以221()2(cos sin )2cos()2842(cos sin )f x x x x x x ππ-==-=++．设128x t π-=，解得24x t π=+， 所以()2cos(2)2cos(2)2sin 2442f t t t t πππ=++=+=-．所以()2sin 2f x x =-．所以3()2()36f π=⨯-=-，另解：将曲线cos2y x =向左平移4π个单位长度，再将其横坐标压缩到原来的12倍，纵坐标不变，可得到曲线()cos2sin 4()2sin 2()36y f x x x f x x f π==-⇒=-⇒=-。

2021届重庆市第八中学高三上学期阶段性测试数学试题一、单选题1．与角2021︒终边相同的角是（ ） A ．221° B ．2021-︒C ．221-︒D ．139︒【答案】A【解析】根据终边相同的角相差360的整数倍，逐个判断即可. 【详解】2021360=5︒÷余221，故A 正确，B 、 C 、 D 中的角均不与角2021︒终边相同.故选：A . 【点睛】本题考查了终边相同角的概念，考查了简单的计算，属于概念题，本题属于基础题. 2．已知i 为虚数单位，若21m ii++是纯虚数，则实数m 的值为（ ） A ．12B ．2C ．﹣2D ．12-【答案】C【解析】利用复数代数形式的乘除运算化简，再由实部为0且虚部不为0列式求解． 【详解】 解：2(2)(1)221(1)(1)22m i m i i m mi i i i ++-+-==+++-是纯虚数， ∴202202m m +⎧=⎪⎪⎨-⎪≠⎪⎩，即2m =-．故选：C ． 【点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念，属于基础题．3．我们处在一个有声世界里，不同场合，人们对声音的音量会有不同要求．音量大小的单位是分贝（dB ），对于一个强度为I 的声波，其音量的大小η可由如下公式计算：10lg II η=（其中0I 是人耳能听到的声音的最低声波强度），则60dB 的声音强度1I 是50dB 的声音强度2I 的（ ）A ．76倍 B ．7610倍C ．10倍D ．7ln 6倍【答案】C【解析】由题设中的定义，将音量值代入010Ilg I η=，计算出声音强度1I 与声音强度2I 的值，再计算出即可求出倍数 【详解】解：由题意，令106010I lgI =，解得，61010I I =⨯，令25010I lg I =，解得，52010I I =⨯， 所以1210I I = 故选：C ． 【点睛】本题考查对数的计算与对数性质在实际中的应用，熟练掌握对数运算性质是解答的关键，属于基础题.4．小涛、小江、小玉与本校的另外2名同学一同参加《中国诗词大会》的决赛，5人坐成一排，若小涛与小江、小玉都相邻，则不同坐法的总数为（ ） A ．6 B ．12 C ．18 D ．24【答案】B【解析】首先将小涛与小江、小玉捆绑在一起，其中小涛在小江与小玉之间，再与其他两个人全排列，按照分步乘法计算原理计算可得； 【详解】解：将小涛与小江、小玉捆绑在一起，与其他两个人全排列，其中小涛位于小江、小玉之间，按照分步乘法计算原理可得323212A A ⋅=故选：B 【点睛】本题考查捆绑法解决排列组合问题，属于基础题.5．德国数学家莱布尼茨是微积分的创立者之一，他从几何问题出发，引进微积分概念.在研究切线时认识到，求曲线的切线的斜率依赖于纵坐标的差值和横坐标的差值，以及当此差值变成无限小时它们的比值，这也正是导数的几何意义．设()f x '是函数()f x 的导函数，若()0f x '>，且对1x ∀，2x R ∈，且12x x ≠总有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭，则下列选项正确的是（ ）A ．()()()π2f f e f <<B ．()()()2πf f e f '''<<C ．()()()()1212f f f f <-'<'D ．()()()()2211f f f f ''<-<【答案】D【解析】由()0f x '>，得()f x 在R 上单调递增，并且由()f x 的图象是向上凸，进而判断选项. 【详解】由()0f x '>，得()f x 在R 上单调递增，因为2e π>>，所以()()()2f f e f π>>，故A 不正确；对1x ∀，2x R ∈，且12x x ≠，总有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭，可得函数的图象是向上凸，可用如图的图象来表示，由()f x '表示函数图象上各点处的切线的斜率，由函数图象可知， 随着x 的增大，()f x 的图象越来越平缓，即切线的斜率越来越小， 所以()()()2f f e f π'''<<，故B 不正确；()()()()212121AB f f f f k --==-，表示点()()1,1f 与点()()22f ,连线的斜率，由图可知()()21AB f k f ''<<，所以D 正确，C 不正确. 故选：D . 【点睛】本题考查以数学文化为背景，导数的几何意义，根据函数的单调性比较函数值的大小，属于中档题型. 6．函数())2ln1f x x kx =+的图象不可能是（ ）A ．B ．C ．D ．【答案】C【解析】假设函数为奇函数和偶函数时，分别根据图象求得k 的值，即可得答案； 【详解】因为A 、B 选项中，图像关于原点对称， 所以()f x 为奇函数，()()0f x f x +-=， 即))22ln1ln10,x kx x kx +++=()()22222ln 1ln1,10x k x k x+-=-=，所以1k =±．当()1,k f x =的图像为选项A ；当()1,k f x =-的图像为选项B ．而C 、D 选项中，图像关于y 轴对称， 所以()f x 为偶函数，()()f x f x =-， 即))22ln1ln1,0x kx x kx kx +=+=，所以0k =．当()0,0k f x =≥，故()f x 的图像为选项D ，故()f x 的图像不可能为C ． 故选：C ． 【点睛】本题考查根据函数的解析式选择函数的图象，考查函数与方程思想、数形结合思想，考查逻辑推理能力、运算求解能力.7．已知函数()3ln f x x m x =+在区间[]2,3上不是单调函数，则m 的取值范围是（ ） A ．(),81-∞- B ．()24,-+∞C ．()81,24--D ．()81,-+∞【答案】C【解析】求得()()32330m x mf x x x x x+'=+=>，然后分0m ≥,0m <两种情况讨论，得到()f x 的单调性，然后可建立不等式求解. 【详解】由()3ln f x x m x =+可得()()32330m x mf x x x x x+'=+=>，当0m ≥时，()0f x '≥，()f x 在()0,∞+上单调递增，不满足题意；当0m <时，由()0f x '>得x >，由()0f x '<得0x <<所以()f x 在⎛ ⎝上单调递减，在⎫+∞⎪⎪⎭上单调递增， 要使得函数()3ln f x x m x =+在区间[]2,3上不是单调函数，则有23<<，解得：8124m -<<-. 故选：C【点睛】本题考查的是利用导数研究函数的单调性，考查了分类讨论的思想.8．已知函数()f x 对任意x ∈R 都有()()()422f x f x f ++=，()1y f x =-的图象关于点()1,0对称，则()20201f +=（ ） A ．0 B ．2-C ．1-D ．1【答案】D【解析】由()1y f x =-的图象关于点()1,0对称有()f x 关于点(0,0)对称：()f x 是奇函数；函数()f x 对任意x ∈R 都有()()()422f x f x f ++=，即(0)0f =且(2)0f =可证()f x 是周期函数，进而利用奇函数、周期性即可求()20201f +的值【详解】()1y f x =-的图象关于点()1,0对称，知：()f x 关于点(0,0)对称即()f x 在x ∈R 上是奇函数，故有()()f x f x -=-且(0)0f = ∴由()()()422f x f x f ++=，有：(0)(4)2(2)(4)(0)2(2)f f f f f f +-=⎧⎨+=⎩可得(2)0f =∴(4)()((4)4)(4)()f x f x f x f x f x +=-⇒++=-+= ∴()(8)f x f x =+，即()f x 是周期为8的函数 而(2020)(82524)(4)f f f =⨯+=，又(4)0f = ∴()202011f += 故选：D 【点睛】本题考查了判断抽象函数的奇偶性、周期性，利用奇偶性和周期性求函数值，注意()1y f x =-的图象关于点()1,0对称即是()f x 关于点(0,0)对称，奇函数()f x 在x ∈R 上都有意义即有(0)0f =等奇函数的性质应用9．已知log x a y =，log y b x =，y c x =，x d y =，其中x 、y 为正数且1x ≠，1y ≠，则（ ）A ．对任意的x 和y ，都有c d ≠B ．存在x 和y ，使得a b =C ．a ，b ，c ，d 中大于1的数有奇数个D ．存在x 和y ，使得a b c d <<< 【答案】B【解析】应用特殊值法：2x y ==有c d =、a b =且a ，b ，c ，d 中大于1的数有偶数个；2,3x y ==有b a c d <<<，3,2x y ==有a b d c <<<，由此即可判断选项正误 【详解】由x 、y 为正数且1x ≠，1y ≠，若令2x y ==，则1a b ==，4c d == ∴根据选项中描述，知：A 、C 错误，B 正确 当x y ≠时，分类讨论如下若x y <：2,3x y ==，有322839c d ==<==，而32log 21log 32b a =<<=<，即b a c d <<<若x y >：3,2x y ==，同理有a b d c <<<，故D 错误 故选：B 【点睛】本题考查了对数、指数比较大小，利用特殊值法排除错误选项即可二、多选题10．下列函数中，既是偶函数又是区间(0,)+∞上增函数的有（ ） A ．||2x y -= B ．23y x =C ．21y x =-D ．3y x =【答案】BC【解析】根据偶函数的定义，f （﹣x ）＝f （x ）进行判断，再根据解析式判断单调性； 【详解】A 、令||()2x y f x -==，则f （﹣x ）＝||2x --＝||2x -＝f （x ），为偶函数，但在（0，+∞）上，2xy -=是减函数，故错误；B 、令23()y f x x ==，f （﹣x ）＝2233()x x =-，是偶函数，且在区间(0,)+∞上是增函数，故B 正确；C 、令2()1y f x x ==-，f （﹣x ）＝（﹣x ）2+1＝x 2+1＝f （x ），且在区间(0,)+∞上是增函数，故C 正确；D 、令3()y f x x ==，f （﹣x ）＝3()x -＝﹣x 3＝﹣f （x ），是奇函数，故D 错误； 故选BC ． 【点睛】此题主要考查函数的奇偶性，偶函数的性质，关键是对基本初等函数的性质要熟悉，是基础题；11．若()2345501234512a a x a x a x a x a x x =+++-++，则下列结论中正确的是（ ） A ．01a =B ．123452a a a a a ++++=C ．50123453a a a a a a -+-+-=D ．0123451a a a a a a【答案】ACD【解析】根据赋值法，分别令0x =，1x =，1x =-，可判断ABC ；根据二项展开式的通项公式，判断出对应项系数的正负，即可判断D 选项. 【详解】因为()2345501234512a a x a x a x a x a x x =+++-++，令0x =，则5011a ==，故A 正确；令1x =代入()2345501234512a a x a x a x a x a x x =+++-++，得0123451a a a a a a =+++++-，所以12345012a a a a a a ++++=--=-，故B 错； 令1x =-代入()2345501234512a a x a x a x a x a x x =+++-++，得01253453a a a a a a =-+-+-，故C 正确；因为二项式()512x -的展开式的第1r +项为15(2)r r rr T C x +=-， 所以当r 为奇数时，5(2)r rC -为负数；即0i a <（其中i 为奇数），所以0123450123451a a a a a a a a a a a a -+-+-=+++++=-；故D 正确. 故选：ACD. 【点睛】本题主要考查二项式定理的应用，熟记二项式定理，灵活运用赋值法求解即可，属于常考题型.12．若方程22131x y t t +=--所表示的曲线为C ，则下面四个选项中正确的是（ ）A ．若13t <<，则C 为椭圆B ．若C 为椭圆，且长轴在y 轴上，则12t << C ．若C 为双曲线，则3t >或1t <D ．若C 是双曲线，则其离心率有1e <<【答案】CD【解析】根据选项逐个分析可得答案，选项A 中2t =时，曲线C 为圆；选项B 可得23t <<；选项C 可得3t >或1t <；选项D 可得1e <<【详解】对于选项A ，当2t =时，曲线C 化为221x y +=，此时C 为圆，故A 不正确； 对于选项B ，若C 为椭圆，且长轴在y 轴上，则130t t ->->，解得23t <<，故B 不正确；对于选项C ，若C 为双曲线，则()()310t t --<，解得3t >或1t <，故C 正确；对于选项D ，若C 是双曲线，则3t >或1t <，当3t >时， ()224221,211t e t t -==-∈--，此时离心率1e <<当1t <时， ()242221,233t e t t -==+∈--，此时离心率1e <<故D 正确. 故选：CD. 【点睛】本题主要考查曲线方程的识别，明确各类曲线方程的特点是求解本题的关键，侧重考查数学运算的核心素养.三、填空题13．已知()π,2πα∈，3tan 4α=-，则cos α=______． 【答案】45. 【解析】根据同角三角函数的关系，直接计算即可. 【详解】由()π,2πα∈，且3tan 4α=-， 可知α在第四象限，可取在终边上一点为(4,3)-， 由任意角三角函数公式4cos 5x r α==， 故答案为：45. 【点睛】本题考查了同角三角函数的关系以及计算，在计算正余弦和正切函数互化时，可以利用任意角三角函数终边上的点进行计算，属于简单题.14．已知一个扇形的周长为8cm ，则当该扇形的半径r =__________cm 时，面积最大. 【答案】2【解析】首先设出扇形的半径和弧长，建立关系式，结合二次函数的图象与性质求解最值即可. 【详解】设扇形的半径为r ，弧长为l ，则28rl ，扇形的面积为()2118222rl r r r =-=-24(2)4r r +=--+， 所以当2r时，面积最大为4.故答案为2 【点睛】该题考查的是有关扇形的面积的最值的问题，涉及到的知识点有扇形的周长，扇形的面积，二次函数的最值，属于简单题目.15．已知点P 是抛物线24y x =上动点，且点P 在第一象限，F 是抛物线的焦点，点A的坐标为()1,0-，当PFPA取最小值时，直线AP 的方程为______．【答案】10x y -+=【解析】由()1,0A -在准线上，过抛物线上点P 作PD 垂直与准线，得到cos PDPAF PA=∠，得出 PAF ∠最大时即过点A 的直线与抛物线相切，设出切线方程为(1)y k x =+，结合判别式，即可求解. 【详解】由题意，抛物线的方程24y x =可得焦点(1,0)F ，()1,0A -在准线上，过抛物线上的点P 作PD 垂直与准线交于D 点， 由抛物线的定义，可得PF PD =，在PAD △中，cos cos PDDPA PAF PA=∠=∠， 所以PDPA最小时，则cos PAF ∠最小，此时PAF ∠最大， 而PAF ∠最大时即过点A 的直线与抛物线相切， 设过()1,0A -与抛物线相切的直线方程为(1)y k x =+，联立方程组2(1)4y k x y x=+⎧⎨=⎩，整理得2440y y k -+=，则24()440k∆=--⨯=，解得1k =±， 又由点P 在第一象限，所以1k =，所以直线AP 的方程为1y x =+，即10x y -+=.故答案为：10x y-+=.【点睛】本题主要考查了抛物线的定义及标准方程，以及直线与抛物线的位置关系的应用，其中解答中熟记抛物线的几何性质和直线与抛物线的位置关系是解答的关键，着重考查推理与运算能力.16．函数()f x对于任意x∈R，均满足()()2f x f x=-，()3,0132,0x xf xx x⎧≤≤=⎨+<⎩，若存在实数a，b，c，()d a b c d<<<满足()()()()f a f b f c f d===，则()()2b ac d--+的取值范围是______．【答案】8,19⎡⎤⎢⎥⎣⎦【解析】首先得到函数的对称性，从而求出函数解析式、画出函数图象，根据对称性可得b a d c-=-，令t b a d c=-=-，则24,33t⎡⎫∈⎪⎢⎣⎭，再根据二次函数的性质计算可得；【详解】解：由函数()f x对于任意x∈R，均满足()(2)f x f x=-，可知()f x的对称轴方程为1x=．因为()3,0132,0x xf xx x⎧≤≤=⎨+<⎩，所以()()33,0132,02,1283,2x xx xf xx xx x⎧≤≤⎪+<⎪=⎨-≤≤⎪⎪->⎩函数图象如图所示：因为存在实数a ，b ，c ，()d a b c d <<<, 满足()()()()01f a f b f c f d ≤===<,332(01)a b b +=≤<,所以b a d c -=-，令t b a d c =-=-， 则3212,10,[0,1)33t b a b b t b b =-=-++'=-+≥∈恒成立， 所以24,33t ⎡⎫∈⎪⎢⎣⎭， 所以()()()()282211,19b a c d t t t ⎡⎤--+=-+=--+∈⎢⎥⎣⎦故答案为：8,19⎡⎤⎢⎥⎣⎦【点睛】本题考查函数方程的综合应用，函数的对称性的应用，属于中档题.四、解答题17．已知tan 3α=，求值： （1）cos sin cos sin αααα-+（2）23π2sin 3sin sin 2ααα⎛⎫+-⎪⎝⎭． 【答案】（1）12-；（2）910【解析】（1）分子、分母同除cos α，将弦化切，再代入计算可得；（2）由诱导公式及22sin cos 1αα+=，将弦化切，再代入计算可得； 【详解】解：（1）因为tan 3α= 所以cos sin 1tan 131cos sin 1tan 132αααααα---===-+++（2）23π2sin 3sin sin 2ααα⎛⎫+-⎪⎝⎭22sin 3sin cos ααα=-2222sin 3sin cos sin cos ααααα-=+ 222tan 3tan 1tan ααα-=+ 22233391103⨯-⨯==+ 【点睛】本题考查同角三角函数的基本关系的应用，属于基础题. 18．已知函数()xf x e ax =-，a R ∈，e 是自然对数的底数．（1）若函数()f x 在1x =处取得极值，求()f x 的单调区间： （2）记函数()f x 在区间0,1上的最小值为()h a ，求()h a ．【答案】（1）函数()f x 在(,1)-∞上单调递减，在(1,)+∞上单调递增；（2）()()[)(]ln ,1,,,1,,1a a a a e h a e a a e a ⎧-∈⎪=-∈+∞⎨⎪∈-∞⎩【解析】（1）先求出导函数()'f x ，再利用()20f '=即可求出a 的值，从而求出()f x 的单调区间．（2）求出导函数()'f x ，通过讨论a 的范围，求出函数()f x 的单调区间，从而求出函数()f x 的最小值即可． 【详解】解：（1）函数()xf x e ax =-，x ∈R ，()x f x e a '∴=-，函数()f x 在1x =处取得极值，()10f '∴=，a e ∴=，()x f x e e '∴=-，当(,1)x ∈-∞时，()0f x '<，函数()f x 单调递减；当(1,)x ∈+∞时，()0f x '>，函数()f x 单调递增，综上可得，函数()f x 在(,1)-∞上单调递减，在(1,)+∞上单调递增；（2）()xf x e a '=-，①当0a 时，()0f x '>恒成立，即函数()f x 在[0，1]上单调递增，∴函数()f x 在[0，1]上的最小值为()(0)1f h a ==，②当0a >时，令()0f x '=得到ln x a =，若ln 0a ，即01a <时，在[0，1]上，()0f x '>，函数()f x 在[0，1]上单调递增，∴函数()f x 在[0，1]上的最小值为()(0)1f h a ==，若ln 1a ，即a e 时，在[0，1]上，()0f x '<，函数()f x 在[0，1]上单调递减，∴函数()f x 在[0，1]上的最小值为()()1e a h a f ==-，若0ln 1a <<，即1a e <<时，在[0，ln )a 上，()0f x '<，在(ln a ，1]上，()0f x '>，即函数()f x 在[0，ln )a 上单调递减，在(ln a ，1]上单调递增，∴函数()f x 在[0，1]上的最小值为()()ln ln h a f a a a a ==-，综上所述，()()[)(]ln ,1,,,1,,1a a a a e h a e a a e a ⎧-∈⎪=-∈+∞⎨⎪∈-∞⎩【点睛】本题主要考查了利用导数研究函数的单调性和最值，属于中档题．19．如图，四棱台1111ABCD A B C D -中，底面ABCD 是菱形，1CC ⊥底面ABCD ，且BAD ∠=60°，1114CD CC C D ===，E 是棱1BB 的中点.（1）求证：1AA BD ⊥；（2）求直线1AA 与平面11A EC 所成线面角的正弦值. 【答案】（1）证明见解析；（2）6735. 【解析】（1）由1C C ⊥底面ABCD ，得1C C BD ⊥，再由底面ABCD 是菱形，得BD AC ⊥，利用直线与平面垂直的判定可得BD ⊥平面1AC C ，进一步得到1BD AA ⊥；（2）设AC 交BD 于点O ，依题意，11//AC OC 且11AC OC =，得到1A O ⊥底面ABCD ．以O 为原点，OA 、OB 、1OA 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系．求出平面11EA C 的一个法向量与1AA 的坐标，再由两向量所成角的余弦值求解直线1AA 与平面11A EC 所成线面角的正弦值． 【详解】（1）因为1CC ⊥底面ABCD ，所以1CC BD ⊥ 因为底面ABCD 是菱形，所以BD AC ⊥ 又1ACCC C =，所以BD ⊥平面1AC C又由四棱台1111ABCD A B C D -知，1A ，A ，1C ，C 四点共面 所以1BD AA ⊥（2）如图，设AC 交BD 于点O ，依题意，11//AC OC 且11AC OC =， 11//AO CC ∴，且11AO CC =， 又由已知1CC ⊥底面ABCD ，得1A O ⊥底面ABCD ．以O 为原点，OA 、OB 、1OA 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，如图设AC 交BD 于点O ，依题意，11//AC OC 且11=AC OC ，所以11=AO CC 则()23,0,0A =，()10,0,4A =，()123,0,4C =-，()0,2,0B =， 由1112A B AB =，得()13,1,4B - 因为E 是棱1BB 中点，所以33,,222E ⎛⎫- ⎪ ⎪⎝⎭所以133,222EA ⎛⎫=- ⎪ ⎪⎝⎭，()1123,0,0AC=-，()123,0,4AA =- 设(),,n x y z =为平面11EA C 的法向量则111230332022n AC x n EA x y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩，取3z =，得()0,4,3n = 设直线1AA 与平面11A EC 所成线面角为θ，则1167sin AA n AA nθ⋅==⋅所以直线1AA 与平面11A EC 67【点睛】本题考查空间中直线与直线、直线与平面、平面与平面位置关系的判定及其应用，考查空间想象能力与思维能力，考查利用空间向量求解空间角，是中档题．20．某市2017年房地产价格因“棚户区改造”实行货币化补偿，使房价快速走高，为抑制房价过快上涨，政府从2018年2月开始采用实物补偿方式（以房换房），3月份开始房价得到很好的抑制，房价渐渐回落，以下是2018年2月后该市新建住宅销售均价的数据：（1）研究发现，3月至7月的各月均价y （百元/平方米）与月份x 之间具有较强的线性相关关系，求y （百元价格/平方米）关于月份x 的线性回归方程ˆˆˆybx a =+； （2）用ˆi y表示用（1）中所求的线性回归方程得到的与i x 对应的销售均价的估计值，3月份至7月份销售均价估计值ˆi y与实际相应月份销售均价i y 差的绝对值记为i ξ，即ˆi i i yy ξ=-，1,2,3,4,5i =．现从5个数据1ξ，2ξ，3ξ，4ξ，5ξ中任取2个，记取到的2个数据和为η，求η的分布列和数学期望E η．注意几点：①可供选择的数据511984iii yx ==∑，521135i i x ==∑；②参考公式：回归方程系数公式1221ˆni ii nii x y nxybxnx ==-=-∑∑，ˆˆay bx =-； 【答案】（1）ˆ 1.688yx =-+（2）见解析 【解析】（1）由表格中的数据，求得5x =80y =，根据公式求得ˆ 1.6b=-，进而得到ˆ88a=，即可求得y 关于x 的回归方程． （2）利用（1）中的回归方程，求得12346ˆˆˆˆˆ83.2,81.6,8078.4,768,.yy y y y =====，得到随机变量i ξ的值，进而求得η的可能取值为0.2,0.4,0.6,0.8，求出相应的概率，列出分布列，利用公式，即可求解数学期望． 【详解】（1）由表格中的数据，可得3456755x ++++==8382807877805y ++++==，所以2198455801.613555ˆb-⨯⨯==--⨯，则80 1.588ˆ6a=+⨯=， 所以y 关于x 的回归方程ˆ 1.688yx =-+． （2）利用（1）中的回归方程ˆ 1.688yx =-+，可得1122334456ˆˆˆˆˆ3,83.2,4,81.6,5,806,78.4,7,76,.8x yx y x y x y x y ==========，所以123450.2,0.4,0,0.4,0.2ξξξξξ=====， 所以η的可能取值为0.2,0.4,0.6,0.8， 则2521(0.2)5P C η===，2533(0.4)10P C η===， 2542(0.6)5P C η===，2511(0.8)10P C η===， 所以随机变量η的分布列为：期望1321120.20.40.60.851051025E η=⨯+⨯+⨯+⨯=． 【点睛】本题主要考查了回归直线方程的求解，以及离散型随机变量的分布列与数学期望的计算，其中解答中认真审题，求得随机变量的取值，准确计算相应的概率是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题．21．在直角坐标系内，点A ，B 的坐标分别为()2,0-，()2,0，P 是坐标平面内的动点，且直线PA ，PB 的斜率之积等于14-.设点P 的轨迹为C . （1）求轨迹C 的方程；（2）某同学对轨迹C 的性质进行探究后发现：若过点()1,0且倾斜角不为0的直线l 与轨迹C 相交于M ，N 两点，则直线AM ，BN 的交点Q 在一条定直线上.此结论是否正确？若正确，请给予证明，并求出定直线方程；若不正确，请说明理由.【答案】（1）()22104x y y +=≠；（2）正确，证明见解析，直线4x =. 【解析】（1）设点P 的坐标为(),x y ，利用直接法，列方程即可求解.（2）根据题意，可设直线MN 的方程为：1x my =+，将直线与椭圆方程联立，整理可得()224230m y my ++-=，利用韦达定理可得12224my y m +=-+，12234y y m =-+，直线AM 的方程与直线BN 的方程，直线AM ，BN 的交点()00,Q x y 的坐标满足：()()()2100122222y x x x y x ++=⋅--，整理可得04x =，即证.【详解】（1）设点P 的坐标为(),x y ，由1224y y x x ⋅=-+-，得2244y x =-，即()22104x y y +=≠. 故轨迹C 的方程为：()22104x y y +=≠（2）根据题意，可设直线MN 的方程为：1x my =+，由22114x my x y =+⎧⎪⎨+=⎪⎩，消去x 并整理得()224230m y my ++-= 其中，()222412416480m m m ∆=++=+>. 设()11,M x y ，()22,N x y ，则12224m y y m +=-+，12234y y m =-+. 因直线l 的倾斜角不为0，故1x ，2x 不等于2±（1y ，2y 不为0）， 从而可设直线AM 的方程为()1122y y x x =++①， 直线BN 的方程为()2222y y x x =--②， 所以，直线AM ，BN 的交点()00,Q x y 的坐标满足：()()()2100122222y x x x y x ++=⋅--而()()()()2121122121212123321y x y my my y y y x y my my y y +++==---()()2122121123239344433344m m y m m y m m m m m y y m -⎛⎫+-- ⎪--+++⎝⎭===---+-+， 因此，04x =，即点Q 在直线4x =上. 所以，探究发现的结论是正确的. 【点睛】本题主要考查轨迹的求法、直线与椭圆的位置关系等基础知识；考查运算求解能力和创新意识；考查化归与转化等思想方法，属于中档题.22．已知()()2121ln 1f x x x k x x x ⎛⎫=-+--+ ⎪⎝⎭，其中k ∈R ，()()1f xg x x =-． （1）当1k =时，求()g x 的单调区间，并证明：()0f x ≥；（2）若对任意的0x >且1x ≠时，()0f x <恒成立，求实数k 的取值范围． 【答案】(1) 增区间为()0,1和()1,+∞，无减区间，证明见解析；(2) (],1-∞-. 【解析】(1)代入1k =，求出()12ln g x x x x=+-，通过导数即可求出单调区间.由单调性求()g x 的取值范围，分()0,1x ∈，1x =，()1,x ∈+∞三种情况求()f x 的取值范围，即可证明.(2) 令()212ln x h x x k x-=+⋅，令()22x kx x k ϕ=++，通过讨论1k ≤-，0k ≥，10k -<<三种情况，结合二次函数的性质，求出函数的单调性，从而判断不等式是否能恒成立. 【详解】(1)当1k =时，()()2112ln x f x x x x ⎛⎫-=-+ ⎪⎝⎭，定义域为()0,∞+，则()()12ln ,01f x g x x x x x x=+-=>-且1x ≠，则()22110g x x x '=++>，所以()g x 在()0,1和()1,+∞上单调递增，即增区间为()0,1和()1,+∞. 当1x =时，2ln1110+-=，当()0,1x ∈时，()0g x <，当()1,x ∈+∞时，()0g x >，第 1 页 共 6 页 由()()()1f x x g x =-，则当()0,1x ∈时，()0f x >，当()1,x ∈+∞时，()0f x >， 当1x =时，()0f x =，综上所述，()0f x ≥.(2) ()()2112ln x f x x x k x ⎛⎫-=-+⋅ ⎪⎝⎭，令()212ln x h x x k x -=+⋅， 可知()10h =，()222,0kx x k h x x x++'=>，令()22x kx x k ϕ=++， 当1k ≤-时，由二次函数的性质可得()0h x '≤，()h x 单调递减，又()10h =， 所以当()0,1x ∈时，()0h x >，当()1,x ∈+∞时，()0h x <，可知此时()0f x <成立；当0k ≥时，由二次函数的性质可得()0h x '>，则()h x 单调递增，又()10h =， 所以当()0,1x ∈时，()0h x <，当()1,x ∈+∞时，()0h x >，可知此时()0f x ≤不恒成立；当10k -<<时，由()10,ϕ>()22x kx x k ϕ=++对称轴11x a=->， 那么()x ϕ在区间11,a ⎛⎫- ⎪⎝⎭上大于0，即()0h x '>在11,a ⎛⎫- ⎪⎝⎭恒成立， 所以()h x 在11,a ⎛⎫- ⎪⎝⎭上单调递增，此时()()10h x h >=，则()0f x >不符合题意. 综上所述，实数k 的取值范围为(],1-∞-.【点睛】本题考查了利用导数求函数的单调性，考查了运用导数解决恒成立问题.本题第一问的关键是对()g x 进行化简整理.。