圆周等分尺寸计算(钻孔)
- 格式:xls
- 大小:20.50 KB
- 文档页数:2

利用宏程序在FAUNC数控系统中加工圆周等分孔,
在半径为100mm的圆周上铣削8个深10mm直径为17mm的等分孔,第一孔的起始角度为15度。
O0001(程序号)
T10M6(调用直径为10的铣刀)
G90G54(坐标G54)
G43H10G0Z200(刀长补正)
S600M3(转速600和转向)
G0Z100(安全距离Z100)
#1=8.5(均布孔半径)
#2=11(刀补号D11-R5.2)
#3=45(孔之间角度)
#4=10(沉孔深度)
#5=15(均布孔起始角度)
#7=10(刀补号D10-R5)
#8=100(均布圆半径)
N10#9=COS[#5]*#8(孔X坐标值)
……(完整程序请查阅《金属加工(冷加工)》2013年第9期)
……
G3I-#1(逆时针插补铣圆)
G0Z100(快速拔刀到Z100)
G40X0Y0(取消刀补)
#5=#5+#3(每次递增45度)
IF﹝#5LT#11﹞GOTO10(当#5小于360度时循环N10)
G0Z200(快速拔刀至Z200)
M9(切削液停止)
M5(主轴停止)
M30(程序结束)
以上程序不仅适合360度范围内圆周等分沉孔,对于任何角度内圆周等分沉孔也一样适合,只不过是
适合,只不过是对#11的赋值不一样而已。
希望此宏程序对大家的工作能有所帮助和启发。

等分三个孔距计算公式在工程设计和制造中,经常会遇到需要将一个物体等分成若干个相等的部分的情况。
这种情况在机械加工、建筑设计、电子制造等领域都会经常遇到。
其中,等分三个孔距计算是一个常见的问题,特别是在机械加工中。
在本文中,我们将介绍等分三个孔距的计算公式,并且给出一个实际的例子来说明如何应用这个公式。
等分三个孔距的计算公式可以用来计算在一个物体上等分三个孔的距离。
假设我们需要在一个长度为L的物体上等分三个孔,我们可以使用以下的公式来计算每个孔的距离:d = L / 4。
其中,d表示每个孔的距离,L表示物体的长度。
这个公式的推导过程可以通过简单的几何推导来得到。
假设我们将物体等分成四个部分,那么每个部分的长度就是L / 4。
因此,每个孔的距离也就是L / 4。
现在让我们来看一个实际的例子来说明如何应用这个公式。
假设我们需要在一个长度为20厘米的木板上等分三个孔,我们可以使用上面的公式来计算每个孔的距离。
根据公式,每个孔的距离就是20 / 4 = 5厘米。
因此,我们可以在这个木板上分别标出距离两个孔5厘米的位置,然后就可以准确地将三个孔等分在这个木板上了。
除了上面介绍的简单的情况,有时候我们也会遇到一些更复杂的情况。
比如,有时候我们需要在一个物体上等分三个孔,但是这个物体的长度不是一个整数,而是一个小数。
在这种情况下,我们可以使用下面的公式来计算每个孔的距离:d = (L 2t) / 3。
其中,d表示每个孔的距离,L表示物体的长度,t表示孔的直径。
这个公式的推导过程可以通过简单的代数推导来得到。
假设我们将物体等分成三个部分,其中每个孔的直径都占据了一部分的长度,那么每个部分的长度就是(L 2t) / 3。
因此,每个孔的距离也就是(L 2t) / 3。
在实际应用中,我们可以根据具体的情况来选择合适的公式来计算每个孔的距离。
如果物体的长度是一个整数,那么我们可以使用第一个公式来计算每个孔的距离;如果物体的长度是一个小数,那么我们可以使用第二个公式来计算每个孔的距离。
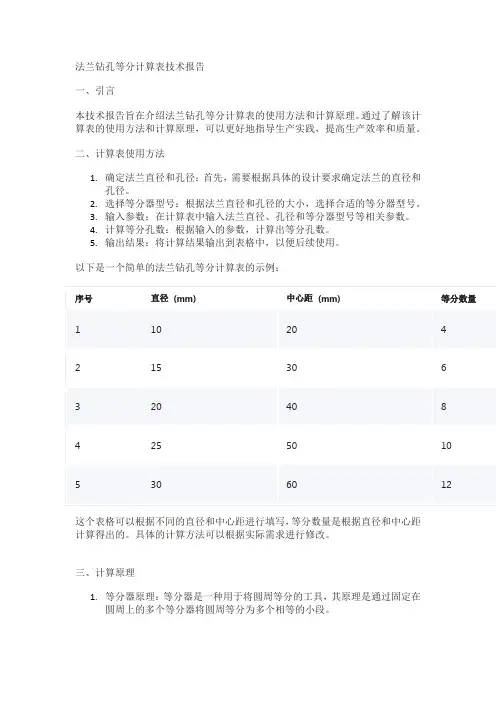
法兰钻孔等分计算表技术报告一、引言本技术报告旨在介绍法兰钻孔等分计算表的使用方法和计算原理。
通过了解该计算表的使用方法和计算原理,可以更好地指导生产实践,提高生产效率和质量。
二、计算表使用方法1.确定法兰直径和孔径:首先,需要根据具体的设计要求确定法兰的直径和孔径。
2.选择等分器型号:根据法兰直径和孔径的大小,选择合适的等分器型号。
3.输入参数:在计算表中输入法兰直径、孔径和等分器型号等相关参数。
4.计算等分孔数:根据输入的参数,计算出等分孔数。
5.输出结果:将计算结果输出到表格中,以便后续使用。
以下是一个简单的法兰钻孔等分计算表的示例:这个表格可以根据不同的直径和中心距进行填写,等分数量是根据直径和中心距计算得出的。
具体的计算方法可以根据实际需求进行修改。
三、计算原理1.等分器原理:等分器是一种用于将圆周等分的工具,其原理是通过固定在圆周上的多个等分器将圆周等分为多个相等的小段。
2.圆周率原理:在等分计算中,圆周率是一个重要的参数。
圆周率是一个常数,它表示圆的周长与直径之比。
通过圆周率,可以将圆的周长等分为多个相等的小段,从而确定等分孔数。
3.几何公式:在计算过程中,需要使用一些几何公式,如圆的周长公式、直径公式等。
通过这些公式,可以方便地计算出等分孔数。
四、注意事项1.在使用计算表时,应确保输入的参数准确无误。
2.在计算过程中,应注意精度问题,避免出现误差。
3.在实际生产中,应根据具体情况选择合适的等分器型号和参数设置。
4.在使用过程中,应注意安全问题,避免出现意外事故。
五、结论本技术报告介绍了法兰钻孔等分计算表的使用方法和计算原理。
通过了解该计算表的使用方法和计算原理,可以更好地指导生产实践,提高生产效率和质量。
在实际应用中,应注意安全问题和使用精度问题,以确保生产过程的顺利进行。

圆法兰孔等分三孔计算公式在工程设计和制造中,圆法兰是一种常见的连接元件,它通常用于连接管道、阀门和设备。
在一些特定的情况下,需要在圆法兰上开设多个孔,而且这些孔需要等分。
本文将介绍圆法兰孔等分三孔的计算公式,帮助工程师和制造人员更好地进行设计和制造。
首先,我们需要了解圆法兰的基本结构和参数。
圆法兰通常由两部分组成,即法兰盘和法兰圈。
法兰盘是圆形的,有一定的厚度,用于连接管道或设备;而法兰圈则是用来连接法兰盘和螺栓的。
在法兰盘上开设孔洞时,需要考虑孔的数量和位置,以确保连接的稳固和平衡。
接下来,我们将介绍圆法兰孔等分三孔的计算公式。
假设圆法兰的直径为D,我们需要在圆法兰上开设三个等分孔,那么每个孔的位置可以通过以下公式计算:孔1的位置,θ1 = 0°。
孔2的位置,θ2 = 120°。
孔3的位置,θ3 = 240°。
其中,θ表示角度,以圆心为原点,逆时针方向为正方向。
根据上述公式,我们可以得到三个孔的位置。
在实际操作中,可以使用角度标尺或者传感器来确定孔的位置,确保准确性。
除了孔的位置,我们还需要计算孔的直径。
通常情况下,孔的直径取决于连接的螺栓和螺母的尺寸,以确保螺栓能够穿过孔并与螺母配合。
在设计中,需要考虑螺栓的直径、孔的间距和孔的直径之间的关系,以确保连接的稳固和可靠。
在实际操作中,我们还需要考虑一些其他因素,例如孔的加工工艺、孔的表面处理和孔的位置误差。
在加工过程中,需要使用合适的工艺和设备来确保孔的质量和精度;在表面处理中,需要考虑孔的防锈和防腐蚀处理;在位置误差方面,需要使用精密的测量设备来确保孔的位置准确。
总之,圆法兰孔等分三孔的计算公式可以帮助工程师和制造人员更好地进行设计和制造。
在实际操作中,我们需要综合考虑孔的位置、孔的直径和其他因素,以确保连接的稳固和可靠。
希望本文对大家有所帮助,谢谢阅读!。

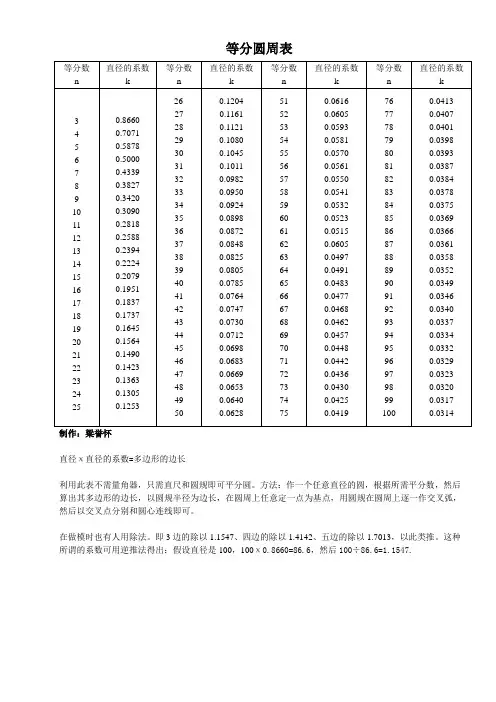
圆的等分系数圆的等分系数也叫等分圆周直径系数!是已知圆的直径,求圆内接正n边形边长时,所利用到的一个参数。
中文名圆的等分系数意义等分圆周直径系数公式AB=k*d目的求圆内接正n边形边长目录1 计算公式2 数表计算计算公式设圆的直径为d,圆内接正n边形,等分系数为:k则:正n边形的边长a=k*d这里的k根据n的取值不同,有不同的对应值!数表计算下面给出圆的等分系数表:1--0.000002--1.000003--0.866034--0.707115--0.587796--0.500007--0.433888--0.382689--0.3420210--0.3090211--0.2817312--0.2588213--0.2393214--0.2225215--0.2079116--0.1950917--0.1837518--0.1736519--0.1645920--0.15643(其中前面的数字就是n的取值,后面的为取值为n的时候系数k的取值!)下面补充下上面系数表的算法问题:以求内接正n边形的边长为例子!依然设圆的直径为d,等分系数为k,我们来探讨下k的取值!每条边对应的角度为:2π/n然后求每条边的长度,实际就是求边所在的弦的长度!选取任意一条边AB,那么连接该边两个端点AB与圆心O,得到<AOB=2π/n 延长AO交圆于C,连接CB,得到直角三角形CAB,其中:<ACB=<AOB/2=π/n则所求的AB的长度为:AB=AC*sin<ACB=d*sin(π/n)而AB=k*d因此k=sin(π/n)。

圆周等分计算范文圆周等分是指将圆分成n等分的过程,其中n是一个整数。
这个问题可以用以下几个步骤来解决:计算圆周的长度,然后将长度除以n,就可以得到每个等分的长度。
接下来,我们将逐步解释每个步骤的具体计算方法。
为了计算圆周的长度,我们需要知道圆的半径。
如果已知圆的直径d,可以使用公式r=d/2来计算半径。
如果已知圆的面积A,可以使用公式r=√(A/π)来计算半径。
我们可以根据这些方法计算圆周的长度,然后得出每个等分的长度。
假设我们要将圆等分成n份,我们需要将圆周的长度除以n来得到每个等分的长度。
例如,如果圆周的长度为L,我们可以得到每个等分的长度l=L/n。
下面是一个具体的例子,说明如何计算圆周的长度和等分的长度。
假设我们有一个圆的直径为d=10厘米,我们想要将圆等分成5份。
首先,我们需要计算圆周的长度。
根据之前提到的公式C=2πr,我们可以得到圆周的长度C=2π(10/2)=2π*5=10π≈31.4159厘米(保留小数点后四位)。
这个方法同样适用于其他情况,如已知圆的面积来计算圆周的长度。
只需根据给定的信息使用相应的公式来计算半径,然后再使用公式C=2πr来计算圆周的长度。
需要注意的是,不是所有的圆周等分都具有整数长度。
有时候,圆周的长度无法被等分的份数整除,这种情况下每个等分的长度将会是一个无限不循环的小数。
如果需要确定等分的具体长度,可以使用近似值或者将结果保留到足够的小数位数。
总结起来,圆周等分的计算可以通过以下步骤来完成:1.根据已知的圆的直径或面积计算半径。
2.使用公式C=2πr计算圆周的长度。
3.将圆周的长度除以需要等分的份数,得到每个等分的长度。
希望这些解释能够帮助您理解圆周等分的计算方法。
如果还有其他问题,请随时提问。

圆周等分系数表圆周等分系数表是一种数学概念,它是指将一个圆周等分为若干份,每份所占的角度等于360°(一周)÷若干份。
它是可逆的,如果一个角的圆周等分系数是x,那么2x的那个角的圆周等分系数是2x,以此类推a x的那个角的圆周等分系数是ax。
圆周等分系数用在测定圆周上物体的角度,也用来测量圆心的角度,以便为圆作图。
常见的圆周等分系数也可以用来表示正多边形的顶点之间的角度,正多边形的圆周等分系数与这个正多边形的边数有关。
以下是常见的圆周等分系数表:1. 一边:12. 两边:23. 三边:34. 四边:45. 五边:56. 六边:67. 七边:78. 八边:89. 九边:910. 十边:1011. 十一边:1112. 十二边:1213. 十三边:1314. 十四边:1415. 十五边:1516. 十六边:1617. 十七边:1718. 十八边:1819. 十九边:1920. 二十边:2021. 二十一边:2122. 二十二边:2223. 二十三边:2324. 二十四边:2425. 二十五边:2526. 二十六边:2627. 二十七边:2728. 二十八边:2829. 二十九边:2930. 三十边:3031. 三十一边及以上:每个正多边形的圆周等分系数可以由其拥有的边数来计算。
圆周等分系数表是有用的数学概念,有助于我们了解圆周上各个角度的大小,也有助于我们给圆上的物体定位,从而更好地掌握圆周的绘图,我们可以应用圆周等分系数表来测量多边形的每个角落,而且在测量圆周上物体位置时,我们也可以用到圆周等分系数表。

圆的等分系数表
圆的等分系数
圆的等分系数也叫等分圆周直径系数!是已知圆的直径,求圆内接正n边形边长时,所利用到的一个参数。
中文名圆的等分系数意义等分圆周直径系数公式AB=k*d目的求圆内接正n边形边长目录
1 计算公式
2 数表计算
计算公式
设圆的直径为d,圆内接正n边形,等分系数为:k
则:正n边形的边长a=k*d
这里的k根据n的取值不同,有不同的对应值!
数表计算
下面给出圆的等分系数表:
1--0.00000
2--1.00000
3--0.86603
4--0.70711
5--0.58779
6--0.50000
7--0.43388
8--0.38268
9--0.34202
10--0.30902
11--0.28173
12--0.25882
13--0.23932
14--0.22252
15--0.20791
16--0.19509
17--0.18375
18--0.17365
19--0.16459
20--0.15643
(其中前面的数字就是n的取值,后面的为取值为n的时候系数k的取值!)
下面补充下上面系数表的算法问题:
以求内接正n边形的边长为例子!依然设圆的直径为d,等分系数为k,我们来探讨下k的取值!
每条边对应的角度为:2π/n
然后求每条边的长度,实际就是求边所在的弦的长度!选取任意一条边AB,那么连接该边两个端点AB与圆心O,得到
则所求的AB的长度为:AB=AC*sin<="" p="">
而AB=k*d
因此k=sin(π/n)。

圆周开孔率
1.什么是圆周开孔率
圆周开孔率是指圆形物体表面上所开孔洞在整个圆周上所占比例的大小。
通常用百分比来表示,是材料开孔性能的一个重要参数。
2.圆周开孔率的计算方法
圆周开孔率的计算方法比较简单,是通过对圆形表面上的孔洞数目进行统计,并将孔洞周长累加后除以圆周长度得到的。
公式如下:圆周开孔率=(∑孔洞周长)/(π×D)×100%
其中,D为圆形物体的直径。
3.圆周开孔率的影响因素
圆周开孔率的大小取决于很多因素,包括制造工艺、材料本身的性质、环境温度等等。
一般来说,开孔率越高,材料的韧性和强度就越低,也容易受到外界影响而出现裂纹、折断等现象。
4.圆周开孔率的应用
圆周开孔率的重要性在于其可以直接反映材料的透气性、过滤性和过渡性能。
在某些特定领域中,如制造过滤器、筛网、电子元件、风扇叶片等,开孔率的大小对产品的质量和使用效果有直接的影响。
5.总结
圆周开孔率在材料工程中有着重要的应用价值,可以帮助制造者评价材料的透气性、过滤性和过渡性能,提高产品质量。
因此,在材料制造的过程中,需要严格控制圆周开孔率的大小,以保证制造出来的产品能够满足使用要求。