下载文档原格式
六、聚类分析（一）概述1.聚类分析的目的根据已知数据，计算样本或者变量之间亲疏关系的统计量（距离或相关系数）。
根据某种准则（最短距离法、最长距离法、中间距离法、重心法），使同一类内的差别较小，而类与类之间的差别较大，最初达到的就是将样本或变量分成若干类。
2.聚类分析的分类3.距离与相似性为了对样本或者变量进行分类，就需要研究样本之间的关系，最常用的方法有两个。
（二）系统聚类1.系统聚类的步骤距离的具体定义及计算方式计算n各样本两两之间的距离将距离接近的数据依次合并为一类，再计算，再合并 画聚类图，解释类与类之间的关系2.亲疏程度度量方法3.系统聚类的分类4.SPSS操作及实例SPSS采用的是凝聚法。
案例：根据30个省的23个主要行业的平均工资情况，通过聚类分析来判断哪些地区平均工资水平高。
SPSS操作及结果：打开SPSS上方菜单栏中的分析->分类->系统聚类选择变量->勾选统计量->在绘制里选择树状图和冰柱图勾选方法（通常使用组间联接）->度量区间->选择标准化方式（全距从0到1）下图为近似矩阵表，标注了相关系数，数值越大，距离越接近下图为聚类分析结果表，第一类表示这是聚类分析的第几步，第二三列表示该步中那几个样本或者小类聚成一类，第四列表示距离，第五六列表示本步骤中参与的是个体还是小类（0表示样本，非0表示第n步生成的小类），第七列表示本步骤的聚类结果将在以下第几步中用到。
下面是冰柱图和树状图的结果，根据树状图可以看出，如果分为三类的话，第一类包括北京上海，第二类包括天津、广东、浙江、江苏、西藏，剩下的归为一类。
（三）快速聚类(适合大样本聚类)1.快速聚类的步骤指定聚类数目K确定K个初始类的中心（自定义或者根据数据中心初步确定）根据距离最近的原则进行分类根据新的中心位置，重新计算每一记录距离新的类别中心的的距离，并重新分类重复步骤4，直到达到标准2.SPSS操作及实例打开SPSS上方菜单栏中的分析->分类->K-均值聚类选择变量->勾选统计量->定义变量值选择迭代次数->选项（勾选初始聚类中心、每个个案的聚类信息）->定义变量值->保存（勾选聚类成员、聚类中心距离）下图为输出的初始聚类中心下图为最终距离中心，第一类平均工资最高，第二类次之，第三类最低下图为每个聚类中的案例数和聚类成员。
各地区各行业工资水平的分析(2009年数据)小组成员：张艺伟、赵月、陈媛、邹莉、朱海龙、曾磊、胡瑛、候银萍1.研究背景及意义1.1 研究背景工资水平是指一定区域和一定时间内劳动者平均收入的高低程度。
生产决定分配，只有经济发展才能提供更多的可分配的社会产品，因此一个地区的工资水平在一定程度上反映了其经济发展的水平。
1.2 研究意义1. 通过多元统计分析方法，探究一个地区的工资水平与其经济发展水平之间的内在联系。
2. 将平均工资水平划分为3类，分析哪些地区、哪些行业的工资水平较高，可以为大学生就业提供宏观上的方向指引。
2.数据来源与描述2.1 数据来源——《中国劳动统计年鉴─2010》（URL：/Navi/YearBook.aspx?id=N2011010069&floor=1###）主编单位：国家统计局人口和就业统计司，人力资源和社会保障部规划财务司出版社：中国统计出版社简介：《中国劳动统计年鉴─2010》是一部全面反映中华人民共和国劳动经济情况的资料性年刊。
本刊收集了2009年全国和各省、自治区、直辖市、香港特别行政区、澳门特别行政区的有关劳动统计数据。
本书资料的取得形式主要有国家和部门的报表统计、行政记录和抽样调查。
2.2 数据描述本数据集记录了全国31个省市（港、澳、台除外）的工资状况，各省市分别记录了其23个主要行业的平均工资水平，这23个主要行业包括：企业、事业、机关、金融业、制造业、建筑业、房地产业、农林牧渔业等等，具体数据格式参见图-0。
图-03.分析方法及原理3.1 通过描述统计分析方法，判断哪些行业平均工资水平较高描述统计分析方法主要是从基本统计量（诸如均值、方差、标准差、极大/小值、偏度、峰度等）的计算和描述开始的，并辅助于SPSS提供的图形功能，能够把握数据的基本特征和整体的分布特征。
在本案例中，通过比较不同行业（诸如企业、事业、机关、建筑业、制造业……）工资的均值、极大/小值，可以从总体上判断哪些行业的平均工资水平较高，哪些行业的较低。
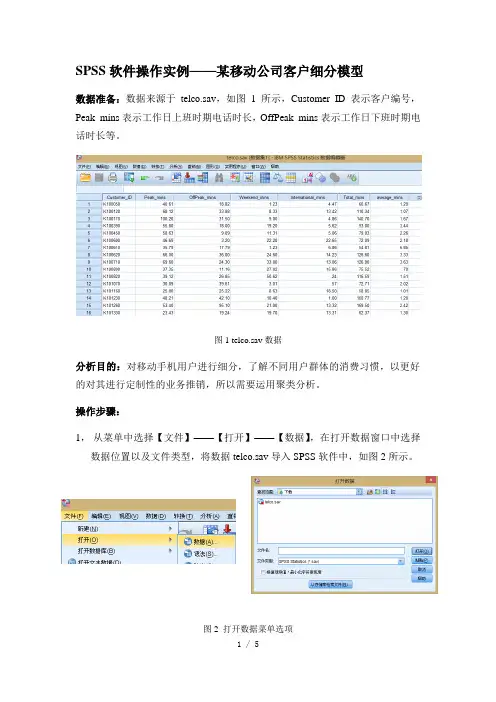
SPSS软件操作实例——某移动公司客户细分模型数据准备：数据来源于telco.sav，如图1所示，Customer_ID表示客户编号，Peak_mins表示工作日上班时期电话时长，OffPeak_mins表示工作日下班时期电话时长等。
图1 telco.sav数据分析目的：对移动手机用户进行细分，了解不同用户群体的消费习惯，以更好的对其进行定制性的业务推销，所以需要运用聚类分析。
操作步骤：1，从菜单中选择【文件】——【打开】——【数据】，在打开数据窗口中选择数据位置以及文件类型，将数据telco.sav导入SPSS软件中，如图2所示。
图2 打开数据菜单选项2，从菜单中选择【分析】——【描述统计】——【描述】，然后在描述性窗口中，将需要标准化的变量选到右边的“变量列表”，勾选“将标准化得分另存为变量”，点确定，如图3所示。
图3 数据标准化3，从菜单中选择【分析】——【分类】——【K-均值聚类】，在K-均值聚类分析窗口中将标准化之后的结果选入右边“变量列表”，客户编号选入“个案标记依据”，聚类数改为5。
点击迭代按钮，在迭代窗口将最大迭代次数改为100，点击继续。
点击保存按钮，在保存窗口勾选“聚类成员”、“与聚类中心的距离”，点击继续。
点击选项按钮，在选项窗口勾选“ANOV A表”、“每个个案的聚类信息”，点击继续。
点击确定按钮，运行聚类分析，如图4所示。
图4 聚类分析操作结果分析表1 最终聚类中心聚类1 2 3 4 5Zscore: 工作日上班时期电话时长 1.60559 -.78990 .61342 -.33584 .37303 Zscore: 工作日下班时期电话时长.46081 -.58917 -.49365 1.18873 -.29014 Zscore: 周末电话时长-.14005 -.15010 .35845 -.02375 -.40407 Zscore: 国际电话时长 1.68250 -.64550 .04673 .02351 -.04415 Zscore: 总通话时长 1.62690 -.94040 .41420 .10398 .21627 Zscore: 平均每次通话时长-.06590 -.14835 -.05337 -.14059 4.87718由最终聚类中心表可得最终分成的5个类它们各自的均值。
各地区各行业工资水平的分析(2009年数据)小组成员：张艺伟、赵月、陈媛、邹莉、朱海龙、曾磊、胡瑛、候银萍1.研究背景及意义1.1 研究背景工资水平是指一定区域和一定时间内劳动者平均收入的高低程度。
生产决定分配，只有经济发展才能提供更多的可分配的社会产品，因此一个地区的工资水平在一定程度上反映了其经济发展的水平。
1.2 研究意义1. 通过多元统计分析方法，探究一个地区的工资水平与其经济发展水平之间的内在联系。
2. 将平均工资水平划分为3类，分析哪些地区、哪些行业的工资水平较高，可以为大学生就业提供宏观上的方向指引。
2.数据来源与描述2.1 数据来源——《中国劳动统计年鉴─2010》（URL：/Navi/YearBook.aspx?id=N2011010069&floor=1###）主编单位：国家统计局人口和就业统计司，人力资源和社会保障部规划财务司出版社：中国统计出版社简介：《中国劳动统计年鉴─2010》是一部全面反映中华人民共和国劳动经济情况的资料性年刊。
本刊收集了2009年全国和各省、自治区、直辖市、香港特别行政区、澳门特别行政区的有关劳动统计数据。
本书资料的取得形式主要有国家和部门的报表统计、行政记录和抽样调查。
2.2 数据描述本数据集记录了全国31个省市（港、澳、台除外）的工资状况，各省市分别记录了其23个主要行业的平均工资水平，这23个主要行业包括：企业、事业、机关、金融业、制造业、建筑业、房地产业、农林牧渔业等等，具体数据格式参见图-0。
图-03.分析方法及原理3.1 通过描述统计分析方法，判断哪些行业平均工资水平较高描述统计分析方法主要是从基本统计量（诸如均值、方差、标准差、极大/小值、偏度、峰度等）的计算和描述开始的，并辅助于SPSS提供的图形功能，能够把握数据的基本特征和整体的分布特征。
在本案例中，通过比较不同行业（诸如企业、事业、机关、建筑业、制造业……）工资的均值、极大/小值，可以从总体上判断哪些行业的平均工资水平较高，哪些行业的较低。
3.2 通过聚类分析方法，判断哪些地区平均工资水平较高聚类分析是依据研究对象的个体特征，对其进行分类的方法，分类在经济、管理、社会学、医学等领域，都有广泛的应用。
聚类分析能够将一批样本（或变量）数据根据其诸多特征，按照在性质上的亲疏程度在没有先验知识的情况下进行自动分类，产生多个分类结果。
类内部个体特征之间具有相似性，不同类间个体特征的差异性较大。
在本案例中，我们将采用两种方法进行聚类分析：一种是系统聚类法，另一种是K-均值法（快速聚类法）。
3.2.1系统聚类法系统聚类法的基本原理：首先将一定数量的样本或指标各自看成一类，然后根据样本（或指标）的亲疏程度，将亲疏程度最高的两类进行合并，然后考虑合并后的类与其他类之间的亲疏程度，再进行合并。
重复这一过程，直到将所有的样本（或指标）合并为一类。
系统聚类分为Q型聚类和R型聚类两种：Q型聚类是对样本进行聚类，它使具有相似特征的样本聚集在一起，使差异性大的样本分离开来；R型聚类是对变量进行聚类，它使差异性大的变量分离开来，相似的变量聚集在一起，这样就可以在相似变量中选择少数具有代表性的变量参与其他分析，实现减少变量个数、降低变量维度的目的。
在本例中进行的是Q型聚类。
类与类之间距离的计算方法主要有以下几种：（1）最短距离法（Nearest Neighbor），是指两类之间每个个体距离的最小值；（2）最长距离法（Farthest Neighbor），是指两类之间每个个体距离的最大值；（3）组间联接法（Between-groups Linkage），是指两类之间个体之间距离的平均值；（4）组内联接（Within-groups Linkage），是指把两类所有个体之间的距离都考虑在内；（5）重心距离法（Centroid clustering），是指两个类中心点之间的距离；（6）离差平方和法（Ward法），同类样品的离差平方和应当较小，类与类之间的离差平方和应当较大。
3.2.2 K-均值法（快速聚类法）K-均值法（又称快速聚类法），是由MacQueen于1967年提出的，它将数据看成K维空间上的点，以距离作为测度个体“亲疏程度”的指标，并通过牺牲多个解为代价换得高的执行效率。
但是，K-均值法只能产生指定类数的聚类结果，而类数的确定离不开实践经验的积累。
快速聚类分析的基本思想是：首先按照一定方法选取一批凝聚点（聚心），再让样本向最近的凝聚点凝聚，形成初始分类，然后再按最近距离原则修改不合理的分类，直到合理为止。
因此，在快速聚类中，应首先要求用户自行给出需要聚成多少类，最终也只能输出关于它的唯一解。
快速聚类是一个反复迭代的分类过程，在聚类过程中，样本所属的类会不断调整，直到最终达到稳定为止。
4.实验操作与结果分析4.1 描述统计分析方法在数据编辑窗口的主菜单中选择“分析(A)”→“描述统计”→“描述性分析(D)”（如图-1），图-1打开如下对话框，将左侧框中的所有变量选入右侧框中，如图-2所示，单击“选项(O)”按钮，图-2在“选项”对话框中选择所需要分析的统计量，包括均值、标准差、极大值、极小值，如图-3所示。
图-3点击“确定”按钮之后，分析结果如下表-1所示：表-1描述统计量N 极小值极大值均值标准差企业31 22000 62046 30869.10 8680.069非农企业31 24788 62098 31787.84 8385.740事业31 25021 68371 35282.77 11732.956机关31 26668 74734 39085.10 13350.591农_林_牧_渔业31 8841 45925 19413.84 7964.071采矿业31 22846 66138 38030.74 11461.961制造业31 21242 48207 26453.74 5509.114电力_燃气及水的生产和供应业31 29605 86262 44113.10 14812.450建筑业31 16583 69131 25769.23 10063.993交通运输_仓储和邮政业31 25797 56955 35202.77 7353.178信息传输_计算机服务和软件业31 22347 105413 47303.87 18924.379批发和零售业31 16263 60260 26534.19 9705.925住宿和餐饮业31 13577 38040 19263.71 5071.244金融业31 31466 180816 62972.65 32341.917房地产业31 15993 57052 28447.45 8900.469输出结果分析：分析描述统计量的输出结果可知，平均工资水平较高的三个行业分别是金融业（62972.65元），信息传输_计算机服务和软件业（47303.87元），电力_燃气及水的生产和供应业（44113.10元）；平均工资水平较低的三个行业分别是住宿和餐饮业（19263.71元），农_林_牧_渔业（19413.84元），水利_环境和公共设施管理业（24446.45元）。
从极大值和极小值方面分析，在所有行业中，极大值最大的行业是金融业（180816元），极小值最小的行业是农_林_牧_渔业（8841元）。
4.2 聚类分析——系统聚类法在数据编辑窗口的主菜单中选择“分析(A)”→“分类(F)”→“系统聚类(H)”（如图-4所示），图-4弹出“系统聚类分析”对话框，将“地区”变量选入“标注个案(C)”中，将其他变量选入“变量框”中，如图-5所示。
在“分群”单选框中选中“个案”，表示进行的是Q型聚类。
在“输出”复选框中选中“统计量”和“图”，表示要输出的结果包含以上两项。
图-5单击“统计量(S)”按钮，在“系统聚类分析：统计量”对话框中选择“合并进程表”、“相似性矩阵”，如图-6所示，表示输出结果将包括这两项内容。
图-6单击“绘制(T)”按钮，在“系统聚类分析：图”对话框中选择“树状图”、“冰柱”，如图-7所示，表示输出的结果将包括谱系聚类图（树状）以及冰柱图（垂直）。
图-7单击“方法(M)”按钮，弹出“系统聚类分析：方法”对话框，如下图-8所示。
图-8“聚类方法(M)”选项条中可选项包括如图-9所示的几种方法，本例中选择“组间联接”：图-9“度量标准-区间(N)”选项条中可选项包括如图-10所示的几种度量方法，本例中选择“平方Euclidean距离”：图-10“转换值-标准化(S)”选项条中可选项包括如图-11所示的几种将原始数据标准化的方法，本例中选择“全局从0到1”：图-11输出结果分析：表-2显示的是用平方Euclidean距离计算的近似矩阵表，其实质是一个不相似矩阵，其中的数值表示各个样本之间的相似系数，数值越大，表示两样本距离越大。
表-2 近似矩阵表表-3显示的是聚类表，该表反映的是每一阶段聚类的结果，系数表示的是“聚合系数”，第2列和第3列表示的是聚合的类。
聚类表的具体说明可参照教材P91，此处不再赘述。
表-3 聚类表阶群集组合系数首次出现阶群集下一阶群集 1 群集 2 群集 1 群集 21 24 25 .076 0 0 52 18 20 .078 0 0 53 8 17 .081 0 0 64 12 16 .118 0 0 125 18 24 .138 2 1 96 8 23 .152 3 0 137 5 15 .153 0 0 108 4 28 .162 0 0 129 14 18 .173 0 5 1110 5 27 .191 7 0 1511 7 14 .198 0 9 1312 4 12 .213 8 4 1813 7 8 .223 11 6 1814 6 22 .226 0 0 1615 5 29 .272 10 0 1916 6 13 .288 14 0 1917 21 31 .322 0 0 2118 4 7 .341 12 13 2119 5 6 .352 15 16 2320 10 19 .379 0 0 2521 4 21 .381 18 17 2222 3 4 .450 0 21 2323 3 5 .532 22 19 2424 3 30 .736 23 0 2925 10 26 1.027 20 0 2626 10 11 1.229 25 0 2827 1 9 1.484 0 0 3028 2 10 1.766 0 26 2929 2 3 3.403 28 24 3030 1 2 11.285 27 29 0图-12是冰柱图，是反映样本聚类情况的图，如果按照设定的类数，在那类数的行上从左到右就可以找到各类所包含的样本。
