斜齿轮的参数及齿轮计算(携带)教学内容

课程设计斜齿轮一、教学目标本节课的学习目标包括知识目标、技能目标和情感态度价值观目标。

知识目标要求学生掌握斜齿轮的基本概念、类型和应用；技能目标要求学生能够通过实验和观察，了解斜齿轮的传动原理和计算方法；情感态度价值观目标要求学生培养对机械传动领域的兴趣和好奇心，提高学生的创新意识和实践能力。

二、教学内容本节课的教学内容主要包括斜齿轮的基本概念、类型和应用，斜齿轮的传动原理和计算方法，以及斜齿轮在实际工程中的应用案例。

首先，通过讲解和演示，使学生了解斜齿轮的基本概念和类型，引导学生掌握斜齿轮的工作原理和特点。

其次，通过实验和观察，让学生了解斜齿轮的传动原理和计算方法，提高学生的实践操作能力。

最后，通过分析实际工程案例，使学生了解斜齿轮在机械传动领域的重要应用，培养学生的创新意识和实践能力。

三、教学方法为了实现本节课的教学目标，采用多种教学方法相结合的方式进行教学。

首先，运用讲授法，向学生讲解斜齿轮的基本概念、类型和应用，使学生掌握斜齿轮的基本知识。

其次，运用讨论法，引导学生探讨斜齿轮的传动原理和计算方法，提高学生的思维能力和解决问题的能力。

然后，运用实验法，让学生观察和操作斜齿轮传动实验，增强学生的实践操作能力。

最后，运用案例分析法，分析实际工程案例，使学生了解斜齿轮在机械传动领域的重要应用。

四、教学资源为了支持本节课的教学内容和教学方法的实施，准备以下教学资源：教材、参考书、多媒体资料、实验设备等。

教材和参考书用于为学生提供丰富的学习材料，帮助学生掌握斜齿轮的基本知识和应用；多媒体资料用于为学生提供形象的视觉信息，增强学生的学习兴趣；实验设备用于开展斜齿轮传动实验，提高学生的实践操作能力。

通过充分利用这些教学资源，丰富学生的学习体验，提高学生的学习效果。

五、教学评估本节课的评估方式包括平时表现、作业和考试三个部分。

平时表现主要评估学生在课堂上的参与程度、提问回答和小组讨论的表现；作业主要评估学生对斜齿轮知识的掌握和应用能力；考试则全面考察学生对斜齿轮基本概念、传动原理和应用的理解。

齿轮机构 > 斜齿圆柱齿轮传动 > 斜齿轮的基本参数和几何尺寸计算
基本参数
法面参数: (垂直于螺旋线方向所作的截面称为法面)
端面参数: (垂直于齿轮轴线方向所作的截面称为端面)
法面参数与端面参数的换算关系
1)标准参数---------用滚齿法加工的斜齿轮, 其法面参数是标准值,即:
法面摸数m n符合国家规定的标准摸数系列表(GB/T1357-87).
法面压力角
法面齿顶高系数
法面顶隙系数2)端面参数计算--------在计算斜齿轮的几何尺寸时,常需用到的端面参数是:
端面模数:
端面压力角:
端面齿顶高系数:
端面顶隙系数:
斜齿圆柱齿轮端法面压力角的图形关系
3)斜齿轮的标准中心距公式
由此可知,在设计斜齿轮传动时,可以用改变螺旋角的办法来调节中心距的大小,使得凑中心距有多了一条途径。

例题
已知一对标准斜齿圆柱齿轮传动,
(1)试说明螺旋角取的理由(2)计算中心距和端面啮合角
解:(1)有两个理由:
A:为使斜齿轮传动时产生的轴向力不过大,取在8~20度范围内并取偏小的值B:为了把中心距凑成便于安装的整数(两轮齿数之和是99,而以)
(2)中心距
为:
啮合角为:。

斜齿轮参数计算
斜齿轮是一种常见的传动装置，其参数计算对于机械设计非常重要。

斜齿轮的设计需要考虑到多个因素，如齿轮的模数、压力角、齿数、齿宽等。

这些参数的选择对于传动效率、噪音、寿命等方面都有着直接的影响。

在斜齿轮的参数计算中，首先需要确定齿轮的模数。

模数是齿轮齿数与其分布圆直径的比值，是齿轮设计中的重要参数。

模数的选择需要根据传动的要求和实际应用来确定，一般来说，传动功率越大，模数也越大。

其次是压力角的确定。

压力角是齿轮齿廓与齿轮轴线的夹角，影响着齿轮的传动性能。

较常用的压力角有20度和14.5度两种。

压力角的选择需要根据具体的传动要求和齿轮的材料来确定。

齿数的选择也是斜齿轮参数计算中的重要一环。

齿数的多少直接影响着齿轮的传动比和传动效率。

一般来说，齿数越多，传动比就越大，但齿轮的制造难度也会增加。

因此，在确定齿数时需要综合考虑传动比和制造难度。

最后是齿宽的确定。

齿宽是指齿轮齿廓的宽度，直接影响着齿轮的载荷能力和传动效率。

齿宽的选择需要根据齿轮所承受的载荷和传动功率来确定。

通过对斜齿轮参数的合理选择和计算，可以使得齿轮传动具有较高
的传动效率、较低的噪音和较长的使用寿命。

同时，还可以根据实际需求对齿轮进行优化设计，以满足不同的工程要求。

斜齿轮参数的计算对于机械设计非常重要。

在进行参数计算时，需要综合考虑传动要求、材料特性和制造难度等因素，以确保齿轮传动的性能和可靠性。

只有在合理选择和计算参数的基础上，才能设计出优质的斜齿轮传动装置，满足工程需求。

斜齿轮的参数及齿轮计算斜齿轮是一种常见的传动装置，主要用于实现两个交叉轴之间的转动传递。

斜齿轮的参数与齿轮计算是设计斜齿轮传动所必备的基本步骤之一、本文将介绍斜齿轮的参数以及齿轮计算的相关知识，并详细解释如何进行齿轮设计与计算。

一、斜齿轮的参数1. 模数（Module）：模数是斜齿轮的一个重要参数，代表齿轮大圆与齿数之比。

模数一般以毫米为单位，常见的模数有0.5、1、1.5、2、2.5等。

模数越大，齿轮尺寸越大，传动能力越强。

2. 齿数（Number of Teeth）：齿数是指齿轮上的齿的数量，用N表示。

齿数决定了齿厚、齿宽等参数，可以根据传动比、模数和其他要求进行计算确定。

3. 压力角（Pressure Angle）：压力角是齿轮上任意一点的轮齿延长线与与该点处相切的准线之间的夹角。

常用的压力角有20°、14.5°、25°等，其中20°和25°的最常见。

选择合适的压力角可以提高齿轮传动的平稳性和效率。

4. 齿宽（Face Width）：齿宽是指齿轮上两相邻齿顶之间的距离。

齿宽大小应根据传递的转矩大小、使用环境等因素进行综合考虑与计算。

二、齿轮计算齿轮计算是根据给定的参数和需求，对齿轮的尺寸、传动比等进行计算和设计。

齿轮计算通常包括以下步骤：1.传动比计算：根据实际应用需求和设计要求，计算传动比。

传动比可以根据两个斜齿轮的齿数N1、N2来计算，传动比等于齿数比N2/N12.齿数计算：确定斜齿轮的齿数。

齿数一般根据传动比和模数来计算，可使用公式N=（Z1/Z2）*（Z2/Z1）。

3.齿轮尺寸计算：通过使用已知的参数，计算齿轮的尺寸。

齿轮尺寸计算包括齿顶高度、齿根高度、齿厚、齿槽宽度等。

4.齿轮间隙计算：齿轮间隙是两个齿轮啮合时齿顶与齿根之间的距离，用来保证齿轮运转时的正常啮合。

齿轮间隙的计算需要根据齿轮的尺寸和齿轮材料的热胀冷缩系数进行计算。

5.齿数修正：根据使用要求和实际制造条件，对齿数进行修正。

斜齿圆柱齿轮计算公式大全斜齿圆柱齿轮是一种常见的传动元件，广泛应用于机械设备中。

在齿轮计算中，需要掌握一些重要的公式，以下为大家介绍一些常用的斜齿圆柱齿轮计算公式。

一、基本参数计算公式1.齿比（传动比）：i=z2/z1，其中z1为小齿轮的齿数，z2为大齿轮的齿数。

2.传动比误差：δi=(i1-i2)/i1×100%，其中i1为理论传动比，i2为实际传动比。

3.中心距：a=(m1+m2)/2×cosα，其中m1、m2为两轮齿距离，α为齿轮锥角。

4.渐开线长度：L=π(m1+m2)/2×(z1+z2)/(2×cosα)。

5.公法线长度：LG=π(m1+m2)/2×(z1+z2)/(2×cosα×cosβ)，其中β为齿轮斜角。

二、齿形参数计算公式1.齿顶高：h1=m1+α×(1+εα)×(z1/2+1)，其中εα为齿顶圆偏差系数。

2.齿根高：h2=m1+α×(1+εα)×(z1/2-1)，其中εα为齿根圆偏差系数。

3.齿顶圆直径：d1=m1×z1/cosα，其中m1为模数。

4.齿根圆直径：d2=d1-2×h1，其中h1为齿顶高。

5.安全系数：K=Ys/ZE，其中Ys为击穿强度，ZE为齿展强度。

三、载荷参数计算公式1.齿面载荷：Ft=[2×T/(d1+d2)]×cosα，其中T为扭矩。

2.弯曲应力：σH=Ft×K1/b，其中K1为载荷分配系数。

3.接触应力：σZ=Ft×K2/(b×cosα)，其中K2为接触系数，b为齿宽。

以上为斜齿圆柱齿轮常用的计算公式，掌握这些公式能够更好地进行齿轮设计及计算。

在实际应用中，需要根据具体的情况灵活运用这些公式，以确保齿轮的可靠性和安全性。

斜齿轮设计计算过程斜齿轮是一种常见的传动装置，具有传递大转矩、平稳运转、精度高等优点，在各种机械设备中广泛应用。

斜齿轮的设计计算涉及到齿轮的基本几何参数、载荷计算、传动比选择等方面。

下面将详细介绍斜齿轮设计计算的过程。

一、齿轮的基本几何参数设计1.模数的选择：模数是斜齿轮设计的重要参数，它是齿轮齿数与分度圆直径之比。

根据所要传递的功率、速度和转矩大小，选择合适的模数。

通常，模数的选择与齿数有关，齿数多则模数小，齿数少则模数大。

2.齿数的确定：齿数与模数有关，一般模数越大，齿数越少。

齿数的确定是通过传动比和传动效率来选择的。

传动比是输入轴的转速与输出轴的转速之比，传动效率是指输入功率与输出功率之比。

3.齿轮齿宽的确定：齿轮齿宽的确定主要与所要传递的功率及轴向载荷有关。

齿宽一般比轴向载荷要大一些，通常为2-3倍。

4.齿轮齿数的选择：齿数的选择要注意齿轮尺寸、密度与传动比之间的关系，并根据啮合角、齿侧力系数等因素进行计算。

5.齿轮齿形修正：齿形修正是为了解决齿轮啮合中的啮合误差，提高传动效率和齿轮的寿命。

齿形修正一般采用弯曲齿形法。

二、载荷计算1.受力分析：首先需要确定齿轮在工作过程中所受的载荷类型和方向。

常见的载荷有径向力、轴向力和弯矩。

2.力的计算：根据齿轮传动的理论公式，计算齿轮所受的各个力的大小，并确定其作用点位置。

3.强度计算：根据齿轮所受载荷的大小和方向，采用材料的抗弯强度、接触强度等指标进行强度计算，判断齿轮的强度是否满足要求。

三、传动比选择根据所要传递的转速和转矩大小，选择合适的传动比。

一般情况下，传动比应选择为整数或近似值，以便于加工制造和传动装置的调整。

四、传动系统的优化设计在完成基本的几何参数设计和载荷计算后，可以对传动系统进行优化设计。

包括选取合适的传动方式、齿轮材料的选择、齿轮的热处理等。

五、齿轮加工制造根据已完成的设计计算结果，制定相应的加工工艺和技术要求，进行齿轮的加工制造。

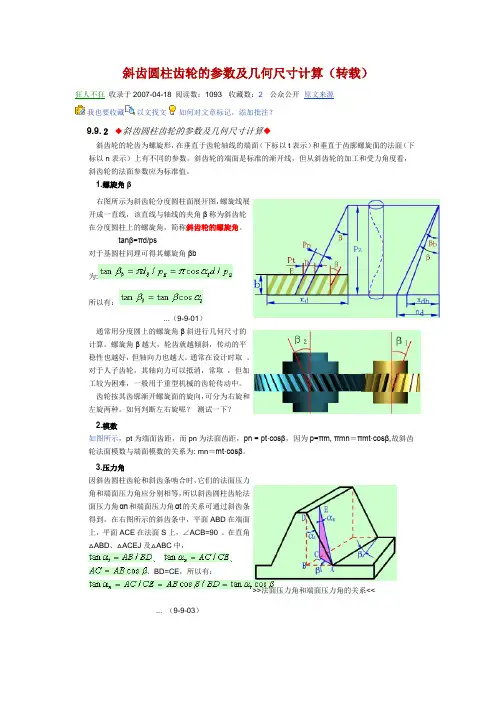
斜齿圆柱齿轮的参数及几何尺寸计算（转载）狂人不狂收录于2007-04-18 阅读数：1093 收藏数：2公众公开原文来源我也要收藏以文找文如何对文章标记，添加批注？9.9.２◆斜齿圆柱齿轮的参数及几何尺寸计算◆斜齿轮的轮齿为螺旋形，在垂直于齿轮轴线的端面（下标以t表示）和垂直于齿廓螺旋面的法面（下标以n表示）上有不同的参数。

斜齿轮的端面是标准的渐开线，但从斜齿轮的加工和受力角度看，斜齿轮的法面参数应为标准值。

1.螺旋角β右图所示为斜齿轮分度圆柱面展开图，螺旋线展开成一直线，该直线与轴线的夹角β称为斜齿轮在分度圆柱上的螺旋角，简称斜齿轮的螺旋角。

tanβ=πd/ps对于基圆柱同理可得其螺旋角βb为:所以有：...（9-9-01）通常用分度圆上的螺旋角β斜进行几何尺寸的计算。

螺旋角β越大，轮齿就越倾斜，传动的平稳性也越好，但轴向力也越大。

通常在设计时取。

对于人子齿轮，其轴向力可以抵消，常取，但加工较为困难，一般用于重型机械的齿轮传动中。

齿轮按其齿廓渐开螺旋面的旋向，可分为右旋和左旋两种。

如何判断左右旋呢？测试一下？2.模数如图所示，pt为端面齿距，而pn为法面齿距，pn = pt·cosβ，因为p=πm, πmn＝πmt·cosβ,故斜齿轮法面模数与端面模数的关系为: mn＝mt·cosβ。

3.压力角因斜齿圆柱齿轮和斜齿条啮合时，它们的法面压力角和端面压力角应分别相等，所以斜齿圆柱齿轮法面压力角αn和端面压力角αt的关系可通过斜齿条得到。

在右图所示的斜齿条中，平面ABD在端面上，平面ACE在法面S上，∠ACB=90°。

在直角△ABD、△ACEJ及△ABC中，、、、BD=CE，所以有：... （9-9-03）>>法面压力角和端面压力角的关系<<4.齿顶高系数及顶隙系数：无论从法向或从端面来看，轮齿的齿顶高都是相同的，顶隙也是相同的，即5.斜齿轮的几何尺寸计算：只要将直齿圆柱齿轮的几何尺寸计算公式中的各参数看作端面参数，就完全适用于平行轴标准斜齿轮的几何尺寸计算，具体计算公式如下表所示：名称符号公式分度圆直径 d d=m z=(m n/cosβ)z基圆直径d b d b=dcosαt齿顶高h a h a=h*an m n齿根高h f h f=(h*an+c*n)m n全齿高h h=ha+h f(2h*an+c*n)m n齿顶圆直径d a d a=d+2ha中心距 a a=(d1+d2)/2=m n(z1+z2)/2cosβ从表中可以看出，斜齿轮传动的中心距与螺旋角β有关。

斜齿圆柱齿轮的参数及几何尺寸计算（转载）狂人不狂收录于2007-04-18 阅读数：1093 收藏数：2公众公开原文来源我也要收藏以文找文如何对文章标记，添加批注？9.9.２◆斜齿圆柱齿轮的参数及几何尺寸计算◆斜齿轮的轮齿为螺旋形，在垂直于齿轮轴线的端面（下标以t表示）和垂直于齿廓螺旋面的法面（下标以n表示）上有不同的参数。

斜齿轮的端面是标准的渐开线，但从斜齿轮的加工和受力角度看，斜齿轮的法面参数应为标准值。

1.螺旋角β右图所示为斜齿轮分度圆柱面展开图，螺旋线展开成一直线，该直线与轴线的夹角β称为斜齿轮在分度圆柱上的螺旋角，简称斜齿轮的螺旋角。

tanβ=πd/ps对于基圆柱同理可得其螺旋角βb为:所以有：...（9-9-01）通常用分度圆上的螺旋角β斜进行几何尺寸的计算。

螺旋角β越大，轮齿就越倾斜，传动的平稳性也越好，但轴向力也越大。

通常在设计时取。

对于人子齿轮，其轴向力可以抵消，常取，但加工较为困难，一般用于重型机械的齿轮传动中。

齿轮按其齿廓渐开螺旋面的旋向，可分为右旋和左旋两种。

如何判断左右旋呢？测试一下？2.模数如图所示，pt为端面齿距，而pn为法面齿距，pn = pt·cosβ，因为p=πm, πmn＝πmt·cosβ,故斜齿轮法面模数与端面模数的关系为: mn＝mt·cosβ。

3.压力角因斜齿圆柱齿轮和斜齿条啮合时，它们的法面压力角和端面压力角应分别相等，所以斜齿圆柱齿轮法面压力角αn和端面压力角αt的关系可通过斜齿条得到。

在右图所示的斜齿条中，平面ABD在端面上，平面ACE在法面S上，∠ACB=90°。

在直角△ABD、△ACEJ及△ABC中，、、、BD=CE，所以有：... （9-9-03）>>法面压力角和端面压力角的关系<<4.齿顶高系数及顶隙系数：无论从法向或从端面来看，轮齿的齿顶高都是相同的，顶隙也是相同的，即5.斜齿轮的几何尺寸计算：只要将直齿圆柱齿轮的几何尺寸计算公式中的各参数看作端面参数，就完全适用于平行轴标准斜齿轮的几何尺寸计算，具体计算公式如下表所示：从表中可以看出，斜齿轮传动的中心距与螺旋角β有关。

斜齿轮的标准参数斜齿轮是一种常见的传动装置，其标准参数对于其正常运行和精准传动起着至关重要的作用。

在设计和选择斜齿轮时，必须严格遵循相关的标准参数，以确保其性能和可靠性。

本文将从模数、齿数、压力角、齿宽等几个方面介绍斜齿轮的标准参数。

首先，模数是斜齿轮的重要参数之一。

模数是齿轮齿数与齿轮直径的比值，通常用m表示。

斜齿轮的模数选择应根据传动功率、转速、工作环境等因素进行综合考虑。

一般来说，模数越大，齿轮的齿数就会相对较少，齿轮的强度和耐磨性也会增加。

而模数越小，齿轮的齿数就会相对较多，齿轮的精度和传动效率会提高。

因此，在选择斜齿轮的模数时，需要根据具体的使用要求进行合理的选择。

其次，齿数是斜齿轮的另一个重要参数。

齿数是指齿轮上的齿的数量，通常用z表示。

齿数的选择应考虑到传动比、传动精度、噪音和振动等因素。

一般来说，齿数较多的齿轮传动平稳，传动精度高，但制造成本和噪音会相对较高；而齿数较少的齿轮传动效率高，但传动精度和平稳性会相对较差。

因此，在选择斜齿轮的齿数时，需要综合考虑传动要求和实际情况，以达到最佳的传动效果。

压力角是斜齿轮的另一个重要参数。

压力角是齿轮齿廓上压力线与径向的夹角，通常用α表示。

常用的压力角有20°和14.5°两种。

较大的压力角有利于提高齿轮的承载能力和传动效率，但会增加齿轮的噪音和振动；而较小的压力角则具有较好的噪音和振动特性。

在实际应用中，需要根据具体的传动要求和工作环境选择合适的压力角。

最后，齿宽也是斜齿轮的重要参数之一。

齿宽是指齿轮齿面的宽度，通常用b表示。

齿宽的选择应根据齿轮的受力情况和传动功率进行合理的确定。

一般来说，齿宽较大可以提高齿轮的承载能力和传动效率，但会增加齿轮的制造成本和重量；而齿宽较小则具有较小的制造成本和重量，但承载能力和传动效率会相对较低。

因此，在选择斜齿轮的齿宽时，需要综合考虑传动要求和经济性，以达到最佳的设计效果。

综上所述，斜齿轮的标准参数包括模数、齿数、压力角和齿宽等几个方面，这些参数在斜齿轮的设计和选择过程中起着至关重要的作用。

斜齿轮计算公式大全斜齿轮是一种常见的传动装置，其计算公式涉及到许多参数和变量。

在工程设计和制造过程中，掌握斜齿轮计算公式是非常重要的。

本文将为大家详细介绍斜齿轮计算公式大全，希望能对大家有所帮助。

1. 基本参数。

在计算斜齿轮时，首先需要了解一些基本参数，包括模数、齿数、压力角、齿宽等。

这些参数将直接影响到斜齿轮的设计和计算。

模数是指齿轮齿数与齿轮直径的比值，通常用m表示。

齿数即为齿轮上的齿的数量，用z表示。

压力角是齿轮齿面上与基圆切线的夹角，用α表示。

齿宽即为齿轮齿面的宽度，用b表示。

2. 齿轮啮合传动比。

齿轮啮合传动比是指齿轮啮合时，从动齿轮齿数与动齿轮齿数之比。

在计算斜齿轮时，需要根据实际情况计算齿轮啮合传动比，以确定齿轮的设计参数。

3. 齿轮啮合角。

齿轮啮合角是指相邻两齿啮合时，它们的啮合线与轴线的夹角。

在斜齿轮的设计中，需要计算齿轮啮合角，以确定齿轮的啮合情况。

4. 齿轮啮合线速度。

齿轮啮合线速度是指齿轮啮合点上的线速度。

在设计斜齿轮时，需要计算齿轮啮合线速度，以确定齿轮的工作情况。

5. 齿轮啮合力。

齿轮啮合力是指齿轮啮合时所受的力。

在设计斜齿轮时，需要计算齿轮啮合力，以确定齿轮的强度和耐用性。

6. 齿轮啮合噪声。

齿轮啮合噪声是指齿轮啮合时产生的噪声。

在设计斜齿轮时，需要计算齿轮啮合噪声，以确定齿轮的工作环境。

7. 齿轮啮合温升。

齿轮啮合温升是指齿轮啮合时产生的温升。

在设计斜齿轮时，需要计算齿轮啮合温升，以确定齿轮的工作温度。

8. 齿轮啮合效率。

齿轮啮合效率是指齿轮啮合时的能量传递效率。

在设计斜齿轮时，需要计算齿轮啮合效率，以确定齿轮的能量传递情况。

总结。

斜齿轮计算公式涉及到许多参数和变量，包括基本参数、齿轮啮合传动比、齿轮啮合角、齿轮啮合线速度、齿轮啮合力、齿轮啮合噪声、齿轮啮合温升、齿轮啮合效率等。

在设计斜齿轮时，需要根据实际情况计算这些参数和变量，以确定齿轮的设计参数和工作情况。

希望本文所介绍的斜齿轮计算公式大全能对大家有所帮助。

斜齿圆柱齿轮的参数及几何尺寸计算斜齿圆柱齿轮的参数包括模数、齿数、压力角和齿顶高等。

其中，模数是一个重要的参数，表示单位齿数与齿轮圆直径的比值，通常用字母M表示。

模数的选择应考虑工作负荷、制造成本、齿轮尺寸等因素，一般常见的模数有0.5、1、1.5等。

齿数是指齿轮上的齿的数量，常用字母Z表示。

齿数的选择与传动比、工作负荷等因素有关，一般齿数较大时，传动平稳、传动比变化较小，但齿轮尺寸较大。

齿数的计算一般根据传动比和模数来确定。

压力角是齿轮齿面与齿轮轴线之间的夹角，通常用字母α表示。

压力角的选择主要考虑齿轮的强度和制造便利性。

一般常见的压力角为20°、14.5°等，通常应根据实际情况选择。

齿顶高是指从齿轮齿顶到基圆上的距离，通常用h_a表示。

齿顶高的计算一般根据齿小齿高、模数等来确定，可以通过以下公式计算：h_a=（2h+c）/m其中，h为齿小齿高，c为齿向厚度，m为模数。

而斜齿圆柱齿轮的几何尺寸计算主要包括齿顶圆直径、齿根圆直径、分度圆直径等。

这些尺寸的计算可以通过以下公式得出：齿顶圆直径：d_a=m*(Z+2)齿根圆直径：d_f=m*Z分度圆直径：d = m*Z/ cosα其中，d_a为齿顶圆直径，d_f为齿根圆直径，d为分度圆直径，m为模数，Z为齿数，α为压力角。

除了上述参数和几何尺寸的计算，还有齿廓曲线的计算，斜齿圆柱齿轮常用的齿廓曲线有圆弧形、渐开线形等。

在齿廓曲线的计算中，一般采用渐开线形齿廓，以保证齿轮传动的平稳性和齿面接触的均匀性。

综上所述，斜齿圆柱齿轮的参数和几何尺寸计算包括模数、齿数、压力角、齿顶高和齿廓曲线等。

这些计算是齿轮设计和制造中的重要部分，通过选取合适的参数和几何尺寸，可以保证齿轮传动的可靠性和传动效率。

齿轮各参数计算公式模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) （d为分度圆直径，z为齿数）齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上？13-2 一渐开线，其基圆半径r b＝40 mm，试求此渐开线压力角 ＝20°处的半径r和曲率半径ρ的大小。

13-3 有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径d a＝106.40 mm，齿数z=25，问是哪一种齿制的齿轮，基本参数是多少?13-4 两个标准直齿圆柱齿轮，已测得齿数z l＝22、z2＝98，小齿轮齿顶圆直径d al＝240 mm，大齿轮全齿高h＝22.5 mm，试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为z1＝19、z2＝81，模数m＝5 mm，压力角α＝20°。

若将其安装成a′＝250 mm的齿轮传动，问能否实现无侧隙啮合？为什么？此时的顶隙（径向间隙）C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮，其齿数z1＝21、z2＝66，模数m ＝3.5 mm，压力角α＝20°，正常齿。

试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。

13-7 已知一标准渐开线直齿圆柱齿轮，其齿顶圆直径d al＝77.5 mm，齿数z1＝29。

斜齿轮的标准参数斜齿轮是一种常见的传动装置，其标准参数对于其正常运转和传动效率起着至关重要的作用。

在设计和制造斜齿轮时，需要严格遵循相关的标准参数，以确保其性能和可靠性。

本文将对斜齿轮的标准参数进行详细介绍，包括模数、齿数、压力角、齿宽等内容。

首先，模数是斜齿轮的重要参数之一，它表示了齿轮齿数与直径的比值。

模数的选择直接影响着齿轮的传动比和传动效率。

一般来说，模数越大，齿轮的齿数就越少，齿轮的强度和承载能力就越大，但传动效率会降低。

相反，模数越小，齿轮的齿数就越多，传动效率会提高，但齿轮的强度和承载能力会降低。

因此，在选择模数时，需要综合考虑传动比、传动效率和齿轮的强度。

其次，齿数是斜齿轮的另一个重要参数，它直接影响着齿轮的传动比和传动效率。

一般来说，齿数越多，传动比就越大，传动效率就越高，但齿轮的强度和承载能力会降低。

相反，齿数越少，传动比就越小，传动效率就越低，但齿轮的强度和承载能力会提高。

因此，在确定齿数时，需要综合考虑传动比、传动效率和齿轮的强度。

压力角是斜齿轮的另一个重要参数，它表示了齿轮齿面上的压力方向与切向的夹角。

压力角的选择直接影响着齿轮的传动效率和噪音水平。

一般来说，较小的压力角可以提高传动效率，减小齿轮的损耗和噪音，但会降低齿轮的强度和承载能力。

相反，较大的压力角会提高齿轮的强度和承载能力，但会降低传动效率和增加噪音。

因此，在确定压力角时，需要综合考虑传动效率、噪音水平和齿轮的强度。

最后，齿宽是斜齿轮的另一个重要参数，它表示了齿轮齿面上的有效宽度。

齿宽的选择直接影响着齿轮的承载能力和传动效率。

一般来说，较大的齿宽可以提高齿轮的承载能力，但会降低传动效率。

相反，较小的齿宽会提高传动效率，但会降低齿轮的承载能力。

因此，在确定齿宽时，需要综合考虑齿轮的承载能力和传动效率。

综上所述，斜齿轮的标准参数包括模数、齿数、压力角和齿宽，它们是设计和制造斜齿轮时必须严格遵循的重要参数。

合理选择这些参数，可以确保斜齿轮具有良好的传动性能和可靠性，满足各种工程应用的需求。

斜齿圆柱齿轮的参数与几何尺寸计算斜齿轮的轮齿为螺旋形，在垂直于齿轮轴线的端面（下标以t表示）和垂直于齿廓螺旋面的法面（下标以n表示）上有不同的参数。

斜齿轮的端面是标准的渐开线，但从斜齿轮的加工和受力角度看，斜齿轮的法面参数应为标准值。

1.螺旋角β右图所示为斜齿轮分度圆柱面展开图，螺旋线展开成一直线，该直线与轴线的夹角β称为斜齿轮在分度圆柱上的螺旋角，简称斜齿轮的螺旋角。

tanβ=πd/ps对于基圆柱同理可得其螺旋角βb为:所以有：通常用分度圆上的螺旋角β斜进行几何尺寸的计算。

螺旋角β越大，轮齿就越倾斜，传动的平稳性也越好，但轴向力也越大。

通常在设计时取。

对于人子齿轮，其轴向力可以抵消，常取，但加工较为困难，一般用于重型机械的齿轮传动中。

齿轮按其齿廓渐开螺旋面的旋向，可分为右旋和左旋两种。

如何判断左右旋呢？测试一下？2.模数如图所示，pt为端面齿距，而pn为法面齿距，pn = pt·cosβ，因为p=πm, πmn＝πmt·cosβ,故斜齿轮法面模数与端面模数的关系为: mn＝mt·cosβ。

3.压力角因斜齿圆柱齿轮和斜齿条啮合时，它们的法面压力角和端面压力角应分别相等，所以斜齿圆柱齿轮法面压力角αn和端面压力角αt的关系可通过斜齿条得到。

在右图所示的斜齿条中，平面ABD在端面上，平面ACE在法面S上，∠ACB=90°。

在直角△ABD、△ACEJ与△ABC中，、、、BD=CE，所以有：法面压力角和端面压力角的关系4.齿顶高系数与顶隙系数：无论从法向或从端面来看，轮齿的齿顶高都是一样的，顶隙也是一样的，即5.斜齿轮的几何尺寸计算：只要将直齿圆柱齿轮的几何尺寸计算公式中的各参数看作端面参数，就完全适用于平行轴标准斜齿轮的几何尺寸计算，具体计算公式如下表所示：名称符号公式从表中可以看出，斜齿轮传动的中心距与螺旋角β有关。

当一对斜齿轮的模数、齿数一定时，可以通过改变螺旋角β的方法来凑配中心距。