降维状态观测器课件
- 格式:pdf
- 大小:1.45 MB
- 文档页数:25


降维观测器示例【例9.48】给定系统1122210011x x u x x -⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦,[]1210x y x ⎡⎤=⎢⎥⎣⎦设计此系统的降维观测器,使其极点配置在-5。
解 (1) 判定系统的可观测性 因为 1021C V CA ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦,0V ≠,因此系统可观测。
(2) 取非奇异线性变换矩阵为101011010Q -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦利用x Qx =将给定系统化为1122101120x x u x x -⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦,[]1201x y x ⎡⎤=⎢⎥⎣⎦待观测子系统的动态方程为1112222x x uz x x x y y=-+==+=+(3) 已知降维观测器的期望极点为-5,则其期望特征方程为50λ+=。
(4) 设观测器输出反馈系数为H ,降维观测器的特征方程为(1)10H H λλ---=++=(5) 对比(3)、(4)中的方程对应项系数,可得4H =。
(6) 实现先写出降维观测器的动态方程111ˆˆˆˆˆ(), xx u H z z z x =-+--= 应用本例(2)中的结果,上式可化为11ˆˆ548xx u y y =-+++ (9.222) ①变量变换法实现设1ˆ4xw y =+代入式(9.222),有 512w w u y =-+-其状态变量图如9.29所示。
图9.29变量变换法实现的降维状态观测器②结构变换法实现也可对式(9.222)直接应用结构变换法得降维观测器状态变量图如图9.30所示。
图9.30结构变换法实现的降维状态观测器1ˆxsw。

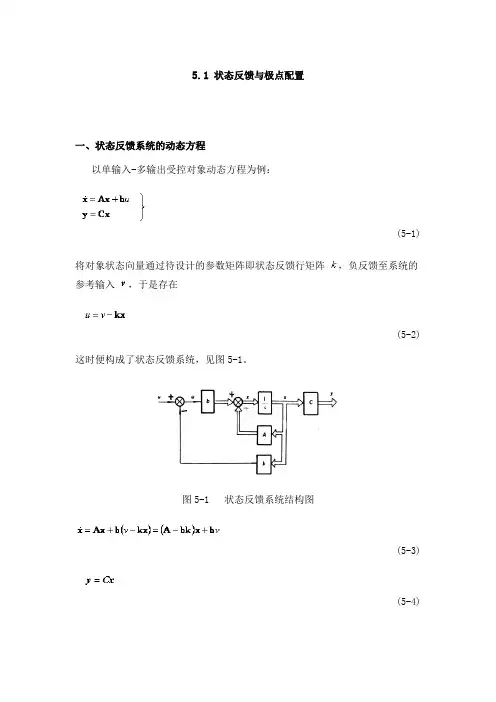
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。




状态观测器设计利用状态反馈实现闭环系统的极点配置,需要利用系统的全部状态变量。
然而系统的状态变量并不都是能够易于用物理方法量测出来的,有些根本就无法量测;甚至一些中间变量根本就没有常规的物理意义。
此种情况下要在工程上实现状态反馈,就需要对系统的状态进行估计,即构造状态观测器。
状态观测器,是一个在物理上可以实现的动态系统,它利用待观测系统的可以量测得到的输入和输出信息来估计待观测系统的状态变量,以便用该组状态变量的估计值来代替待观测系统的真实状态变量进行状态反馈设计,实现闭环系统极点的再配置。
1. 全维状态观测器当对象的所有状态均不可直接量测时,若要进行状态反馈设计,就需对全部状态变量进行观测。
这时构造的状态观测器,其阶次与对象的阶次相同,被称为全维状态观测器。
考虑如下n阶单输出线性定常离散系统(1)其中,A为n×n维系统矩阵,B为n×r输入矩阵,C为n×1维输出矩阵。
系统结构图如图1所示。
图1 全维状态观测器构造一个与受控系统具有相同参数的动态系统(2)当系统(1)与(2)的初始状态完全一致时,则两个系统未来任意时刻的状态也应完全相同。
但在实际实现时,不可能保证二者初始状态完全相同。
为此,应引入两个系统状态误差反馈信号构成状态误差闭环系统,通过极点配置使误差系统的状态渐趋于零。
由于原受控系统状态不可直接量测,故用二个系统的输出误差信号代替。
引入了输出误差的状态观测器状态方程为(3)其中,H为状态观测器的输出误差反馈系数矩阵,有如下形式定义状态估计误差为,用式(7.65)与(7.67)相减可得(4)即(5)通过式(5)可以看出,若选择合适的输出误差反馈矩阵H 使得状态估计误差系统(5)的所有极点均位于z平面单位圆内,则误差可在有限拍内趋于零,即状态估计值在有限拍内可以跟踪上真实状态,且极点越靠近原点状态估计误差趋于零的速度越快,反之越慢。
可见,能否逼近x(k)以及逼近速度是由H阵决定的。


线性系统理论的实验作业:1.找一个3阶单输入单输出系统;2.设计降维观测器(极点自己选);3.设计带降维观测器的状态反馈系统;4.讨论降维观测器极点配置和状态反馈极点的关系;5.画出状态变量及观测误差曲线。
一.给定系统u x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=011131413121211444x .[]x y 111=1.设计一个降维观测器使其极点为-3,-4.2.设计带观测器的状态反馈系统,使其极点为-1+j2,-1. 3.讨论降维观测器的极点和状态反馈极点的关系。
4.画出状态变量及观测误差随时间变化的曲线。
解:(1)构造坐标变换矩阵。
P=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡100010111L C [] 100010111 2 11Q Q Q P =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==-用线性变换PX =x —将系统变换成∑⎪⎪⎭⎫⎝⎛C BA ___,其中 []001C 010 01131111106 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----==-B P PA A 对于本例而言,降维观测器的的维数为n-p=2降维观测器期望特征多项式为127)4)(3()(f 2++=++=λλλλλ。
引入反馈阵⎥⎥⎦⎤⎢⎢⎣⎡=g gG 21__—得到降维观测器的特征多项式为g g 21211-1g --++λλ)(—比较两个多项式得:6g2 51-=-=g 可以得到降维观测方程:y6-5- 2u01-y 5460 6-16-1- ^^.^^⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=ωωωx 。
(为可以测量的,因为这里的的观测值或者是估计值为x1x2 2^x )执行以下的m 文件 >> A11=6;A22=[-1,-1;1,0]; A12=[0,-1]; A21=[-11;-13]; B1=0; B2=[-1;0]; V=[-3,-4];G=(acker(A22',A12',V))' Ahat=A22-L*A12Bhat=Ahat*G+A21-G*A11 Fhat=B2-G*B1 G =-5 -6Ahat =-1 -6 1 -6Bhat =60 54Fhat =-1 0因此降解观测器的增益矩阵G=⎥⎦⎤⎢⎣⎡--65,具有期望极点的降阶观测器为 y6-5- 2u01-y 5460 6-16-1- ^^.^^⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=ωωωx 。
状态反馈与状态观测器实验状态反馈与状态观测器一、实验目的1.自学全系列状态意见反馈布局极点的方法。
2.自学降维状态观测器的设计方法。
3.学习带有状态观测器的状态反馈系统的设计方法。
二、实验仪器1.el-at-ii型自动控制系统实验箱一台2.计算机一台三、实验建议1.1)用全状态反馈配置极点的方法,按给定的性能指标进行综合设计。
2)检验极点布局理论的正确性。
2.设计一个带有状态观测器的状态反馈系统。
四、实验前分析排序和设计已知被控系统如图所示:u10.05s+1x210.1sx1y图5-1被控系统结构图1、设计一个全状态反馈系统,闭环系统性能要求为ξ=0.707,ts≤0.2s.设计k阵,并图画出来尖萼电路图挑选适当元件参数。
2、假设x2不能直接测量,设计一个降维状态观测器将x2进行估计得到估计值,然后用2形成全系列状态意见反馈,并使闭环系统ξ=0.707,ts≤0.2s,并图画出来尖萼电路图挑选x1和x独以适当元件参数。
100k50k1uf1ufda1100k25k2-out650k2-out63100k+3+x2100k2-out6x1ad131k100k0-6out+321k0+1k100k01k0图5-2状态反馈系统演示电路图图5-3带有状态观测器的状态反馈系统模拟电路图五、实验步骤1.连接被测量典型环节的模拟电路。
电路的输入u1接a/d、d/a卡的da1输出,电路的输入u2接a/d、d/a卡的ad1输出。
检查有误后拨打电源。
2.启动计算机,在桌面双击图标[自动控制实验系统]运转软件。
3.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进行实验。
4.在实验课题下拉菜单中挑选实验二[二阶系统阶跃积极响应],具有状态观测器的状态反馈系统挑选实验五[状态意见反馈与状态观测器],鼠标单击该选项弹头出来实验课题参数窗口。
5.观测表明的波形记录最小市场汇率量mp和调节时间ts的数值和积极响应动态曲线,并与理论值比较。