四、灰度直方图是数字图像处理的重要工作。请简述灰度直方图规定化

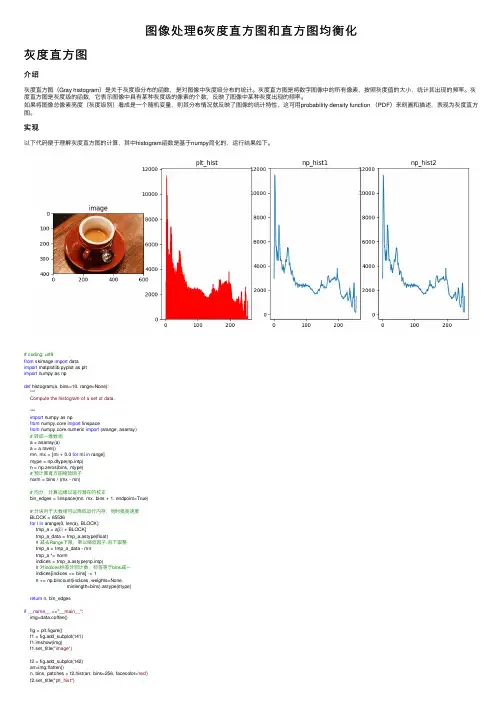
图像处理6灰度直⽅图和直⽅图均衡化灰度直⽅图介绍灰度直⽅图（Gray histogram）是关于灰度级分布的函数，是对图像中灰度级分布的统计。

灰度直⽅图是将数字图像中的所有像素，按照灰度值的⼤⼩，统计其出现的频率。

灰度直⽅图是灰度级的函数，它表⽰图像中具有某种灰度级的像素的个数，反映了图像中某种灰度出现的频率。

如果将图像总像素亮度（灰度级别）看成是⼀个随机变量，则其分布情况就反映了图像的统计特性，这可⽤probability density function （PDF）来刻画和描述，表现为灰度直⽅图。

实现以下代码便于理解灰度直⽅图的计算，其中histogram函数是基于numpy简化的，运⾏结果如下。

# coding: utf8from skimage import dataimport matplotlib.pyplot as pltimport numpy as npdef histogram(a, bins=10, range=None):"""Compute the histogram of a set of data."""import numpy as npfrom numpy.core import linspacefrom numpy.core.numeric import (arange, asarray)# 转成⼀维数组a = asarray(a)a = a.ravel()mn, mx = [mi + 0.0 for mi in range]ntype = np.dtype(np.intp)n = np.zeros(bins, ntype)# 预计算直⽅图缩放因⼦norm = bins / (mx - mn)# 均分，计算边缘以进⾏潜在的校正bin_edges = linspace(mn, mx, bins + 1, endpoint=True)# 分块对于⼤数组可以降低运⾏内存，同时提⾼速度BLOCK = 65536for i in arange(0, len(a), BLOCK):tmp_a = a[i:i + BLOCK]tmp_a_data = tmp_a.astype(float)# 减去Range下限，乘以缩放因⼦,向下取整tmp_a = tmp_a_data - mntmp_a *= normindices = tmp_a.astype(np.intp)# 对indices标签分别计数，标签等于bins减⼀indices[indices == bins] -= 1n += np.bincount(indices, weights=None,minlength=bins).astype(ntype)return n, bin_edgesif__name__ =="__main__":img=data.coffee()fig = plt.figure()f1 = fig.add_subplot(141)f1.imshow(img)f1.set_title("image")f2 = fig.add_subplot(142)arr=img.flatten()n, bins, patches = f2.hist(arr, bins=256, facecolor='red')f2.set_title("plt_hist")f3 = fig.add_subplot(143)hist, others = np.histogram(arr, range=(0, arr.max()), bins=256)f3.plot(others[1:],hist)f3.set_title("np_hist1")f4 = fig.add_subplot(144)hist, others = histogram(arr, range=(0, arr.max()), bins=256)f4.plot(others[1:], hist)f4.set_title("np_hist2")plt.show()关于bincount函数，可以参考Xurtle的博⽂https:///xlinsist/article/details/51346523bin的数量⽐x中的最⼤值⼤1，每个bin给出了它的索引值在x中出现的次数。

数字图像处理与模式识别实验目的打开一幅图像，进行直方图均衡化。

并将其灰度线性变化，将灰度线性拉伸。

实验准备实验之前，收集数字图像处理编程的相关资料，查阅C或Java关于本实验图像处理的相关类库和编程核心。

经过C和Java相关资料编程的比较，Java将图像处理的类封装的较完整，运用起来比C灵活方便。

以下是相关类库和实现操作的方法：import java.awt.image.*;import javax.imageio.*; //相关的图像处理类库和方法封装在两个包中//Java读取图像的方法BufferedImage newImage = ImageIO.read(new File(filePath));int width = newImage.getWidth(); //获得图像的像素宽度int height = newImage.getHeight(); //获得图像像素的长度//获得图像的色彩模型RGB分量ColorModel colorModel = ColorModel.getRGBdefault();int r = colorModel.getRed(currPixArray[k]);int g = colorModel.getGreen(currPixArray[k]);int b = colorModel.getBlue(currPixArray[k]); //分别获得图像的rgb分量PixelGrabber p = new PixelGrabber(image, 0, 0, width, height, array, 0, width); //将image图像像素值读入一位矩阵实验步骤算法实现RGB图像转灰度图由于数字图像的直方图均衡化和灰度的线性拉伸都是基于灰度图的算法实现，本框架中增加了由彩色图转灰度图的功能。

简单讲述下算法思想：将存储图像的一维矩阵像素点彩色分量用ColorModel类中的getRed(),getGreen()和getBlue()方法读取，按照(r * 0.3 + g * 0.59 + b * 0.11)公式计算灰度值。

一、课程设计目的（1）进一步掌握matlab的用法；（2）在实践中深入理解图像显示的方法；（3）学会用matlab对图像进行显示。

二、课程设计要求（1）根据题目，查阅有关资料，掌握图像显示技术；（2）学习MATLAB软件，掌握MATLAB各种函数的使用；（3）根据图像显示原理，运用MATLAB进行编程，仿真调制过程，记录并分析仿真结果；（4）形成设计报告。

三、设计方案一般情况下,如果图像的灰度分别集中在比较窄的区间,从而引起图像细节的模糊,为了使图像细节清晰,并使目标得到突出,达到图像增强的目的,可通过改善各部分亮度的比例关系,即通过直方图的方法来实现.直方图的方法是以概率论为基础的.常用的方法有直方图均衡化和直方图规定化.(1)直方图均衡化直方图均衡化又称直方图平坦化,是将一已知灰度概率密度分布的图像经过某种变换,变成一幅具有均匀灰度概率密度分布的新图像.其结果是扩展了像元取值的动态范围,从而达到增强图像整体对比度的效果.直方图均衡化的具体实现步骤如下:1）.列出原始图像的灰度级,-=Lfj1,,1,j2)．统计各灰度级的像素数目=L,-nj1,,,1j3).计算原始图像直方图各灰度级的频数=Lj=P(-fnn/,)11,,,fjj4).计算累积分布函数1,,,1,0,)()(0-==∑=L k j f P f C k j j f5).应用以下公式计算映射后的输出图像的灰度级，P 为输出图像灰度级的个数，其中INT 为取整符号1,,1]5.0)()[(min min max -=++-=P i g f C g g INT g i6).统计映射后各灰度级的像素数目 ni, i=0,1,…,k,…P-1.7). 计算输出直方图Pg(gi)=ni/n, i=0,1,…,P-1.8). 用fj 和gi 的映射关系修改原始图像的灰度级,从而获得直方图近似为均匀分布的输出图像(2) 直方图规定化直方图均衡化的优点是能自动增强整个图像的对比度,但它的具体增强效果不易控制,处理的结果总是得到全局的均衡化的直方图.实际工作中,有时需要变换直方图使之成为某个特定的形状,从而有选择地增强某个灰度值范围内的对比度,这时可采用比较灵活的直方图规定化方法.直方图规定化增强处理的步骤如下:令Pr （r ）和Pz （z ）分别为原始图像和期望图像的灰度概率密度函数。

(0.1) 灰度直方图不能表示出有某灰度级的像素在什么位置，也不能直接显示出图像内容，但是具有统计特征的直方图却能描述该图像的灰度分布特征，使人们从中得到诸如总体明亮程度、对比度、对象物的可分性等与图像质量有关的灰度分布概貌，成为一些处理方法的重要依据。

变换直方图使其达到较理想分布，能起到增强图像的效果。

面积为A 的连续图像f(x,y)经过数字化后，成为M 行N 列的数字图像f(m,n)。

一般而言在数字图像f(x,y)中取不同灰度值的像素数目是不同的。

直方图是用于表达图像灰度分布情况的统计图表。

其横坐标是灰度值r ，纵坐标是出现这个灰度值的概率密度p(r)(对连续图像f(x,y)而言)，或者出现这个灰度值的概率值p(r i )(对数字图像f(m,n))而言。

（1） 连续图像f(x,y)的直方图 0()()p()lim r A r r A r r r A →+-=⋅ 且有maxmin ()1r r p r dr =⎰（2） 数字图像f(m,n)的情况下，设图像像素的灰度值为r 0,r 1,…,r L-1,则概率p(r i )为：（i=0,1,…,L -1）且有 尽管灰度直方图不能表示出有某灰度级的像素在什么位置，更不能直接显示图像内容，但是具有统计特性的直方图却能描述该图像的灰度分布特性，使人们从中得到诸如总体明亮程度、对比度、对象物的可分性等于图像质量有关的灰度分布概貌，成为一些处理方法的重要依据。

imhist(I,N)函数绘制直方图。

其中N 表示长度，缺省值为256.Histeq(I,N)函数实现直方图均衡化，该命令对灰度图像I 进行变换，返回有N 级灰度的的图像J 。

N 的缺省值为64（当N 小于I 中灰度级数时，J 的直方图更为平坦）。

ＰＳ：直方图均衡化后，图像直方图趋于平坦化，且灰度间隔被拉大，从而有利于图像的分析和识别。

（理论上说直方图均衡化就是通过变换函数将原图的直方图调整为平坦的直方图，然后用此均衡直方图校正图像。

【数字图像处理】直⽅图的均衡与规定化很多情况下，图像的灰度级集中在较窄的区间，引起图像细节模糊。

通过直⽅图处理可以明晰图像细节，突出⽬标物体，改善亮度⽐例关系，增强图像对⽐度。

直⽅图处理基于概率论。

直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。

直⽅图均衡化可实现图像的⾃动增强，但效果不易控制，得到的是全局增强的结果。

直⽅图规定化可实现图像的有选择增强，只要给定规定的直⽅图，即可实现特定增强的效果。

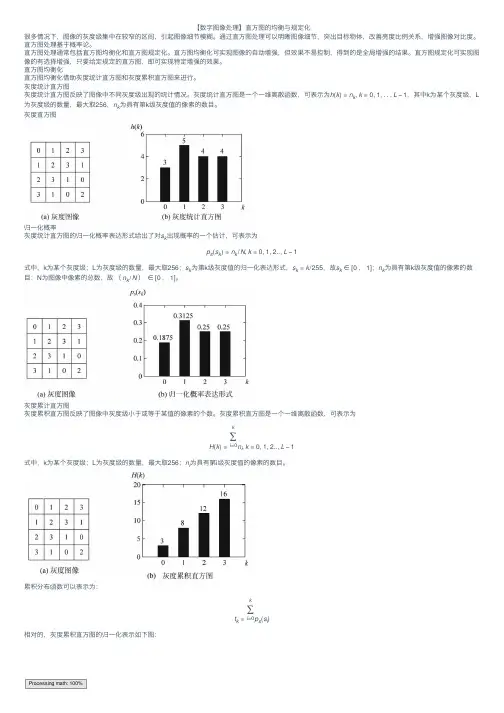
直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。

灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。

灰度统计直⽅图是⼀个⼀维离散函数，可表⽰为h (k )=n k ,k =0,1,...L −1，其中k 为某个灰度级，L 为灰度级的数量，最⼤取256，n k 为具有第k 级灰度值的像素的数⽬。

灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计，可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；s k 为第k 级灰度值的归⼀化表达形式，s k =k /255，故s k ∈[0，1]；n k 为具有第k 级灰度值的像素的数⽬；N 为图像中像素的总数，故（n k /N ）∈[0，1]。

灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。

灰度累积直⽅图是⼀个⼀维离散函数，可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；n i 为具有第i 级灰度值的像素的数⽬。

累积分布函数可以表⽰为：t k =k ∑i =0p s (s i )相对的，灰度累积直⽅图的归⼀化表⽰如下图：Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。

图像的点运算图像的点运算是图像处理中相对简单的技术，它主要用于改变一幅图像的灰度分布范围。

点运算通过一个变换函数将图像的像素一一转换，最终构成一幅新的图像。

由于操作对象是图像的一个个像素，故得名为“点运算”。

点运算的最大特点是输出像素值只与当前输入像素值有关。

点运算的图像处理过程可以用以下公式表示：g(x, y)=T[f(x, y)]其中f(x, y)表示输入图像，g(x, y)表示处理后的图像。

函数T 是对f的一种变换操作，在这里它表示灰度变换公式。

可以看到，对于点运算而言，最重要的是确定灰度变换公式。

变换公式一旦确定，点运算对于图像的处理效果就确定了。

本章研究的主要内容包括灰度直方图、线性变换、非线性变换、阈值变换、灰度拉伸及灰度均衡等。

若无特别说明，本章的点运算函数所针对的待处理对象即为8位灰度图。

■ 本章学习地图◆ 学会利用灰度直方图查看图像信息◆ 了解各种灰度变换公式◆ 掌握各种灰度变换的实现方法◆ 进一步了解各种点运算对于图像效果的影响9.1 灰度直方图本节介绍灰度直方图的相关概念和实现原理，它是提取图像信息的重要工具之一。

9.1.1 灰度直方图任何一幅图像都包含着丰富的图像信息，对于图像处理而言，如何提取这些信息并找出其中的特征就显得十分关键。

灰度直方图直观地显示了图像灰度分布的情况，这些信息在图像灰度变换等处理过程中显得十分重要。

在本章随后的内容中，也会经常通过直方图来分析变换后的图像效果。

图9-1显示一幅灰度图及它所对应的灰度直方图。

可以看到，灰度直方图是一个二维图。

从数学上来说，它描绘了图像各灰度值的统计特性，显示了各个灰度级出现的次数或概率。

从图形上来说，其横坐标表示图像的灰度值，取值范围是0到255。

其纵坐标则通过高度来表示出现次数的多少或者概率的高低。

在本章中，纵坐标表示像素出现的次数，最大值为该图像在0至 255阶灰度上分布像素出现次数的最大值。

图9-1 利用灰度直方图显示图像灰度分布需要说明的是，如果没有特别指出，在本章后续内容中的所有变换都是基于图9-1中左侧的图像进行的。

数字图像处理实验报告直方图匹配规定化直方图均衡化能够自动增强整个图像的对比度，但它的具体增强效果不容易控制，处理的结果总是得到全局均匀化的直方图。

实际上有时需要变换直方图，使之成为某个特定的形状，从而有选择地增强某个灰度值范围内的对比度。

这时可以采用比较灵活的直方图规定化。

一般来说正确地选择规定化的函数可以获得比直方图均衡化更好的效果。

所谓直方图规定化，就是通过一个灰度映像函数，将原灰度直方图改造成所希望的直方图。

所以，直方图修正的关键就是灰度映像函数。

直方图匹配方法主要有3个步骤（这里设M和N分别为原始图和规定图中的灰度级数，且只考虑N≤M的情况）：(1) 如同均衡化方法中，对原始图的直方图进行灰度均衡化：(2) 规定需要的直方图，并计算能使规定的直方图均衡化的变换：(3) 将第1个步骤得到的变换反转过来，即将原始直方图对应映射到规定的直方图，也就是将所有pf(fi)对应到pu(uj)去。

一、A图直方图规定B图Matlab程序:%直方图规定化clear allA=imread('C:\Users\hp\Desktop\A.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])C=imread('C:\Users\hp\Desktop\B.tif');%读入B图像imshow(C) %显示出来title('输入的B图像')%绘制直方图[m,n]=size(C); %测量图像尺寸D=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255D(k+1)=length(find(C==k))/(m*n); %计算每级灰度出现的概率，将其存入D中相应位置endfigure,bar(0:255,D,'g'); %绘制直方图title('B图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=D(j)+S1(i); %计算B灰度图累计直方图endendcounts=Bfigure,bar(0:255,counts,'r')title('A图像直方图 ')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:255if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:255if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+D(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('A规定B后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=C; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:255if T(k-1)<=C(i,j)&C(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('A规定B后图像')imwrite(PA,'guidinghua.bmp');二、用已知直方图规定A图规定灰度为[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zeros(1,49 ),0.2,zeros(1,49),0.1]Matlab程序：clear allA=imread('C:\Users\hp\Desktop\B.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=B(j)+S1(i); %计算原灰度图累计直方图endendcounts=[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zer os(1,49),0.2,zeros(1,49),0.1];%规定化直方图figure,bar(1:300,counts,'r')title('规定化直方图')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:256if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:256if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+B(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('规定化后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=A; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:256if T(k-1)<=A(i,j)&A(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('规定化后图像')imwrite(PA,'guidinghua.bmp');。

图像灰度变换、⼆值化、直⽅图1、灰度变换1）灰度图的线性变换Gnew = Fa * Gold + Fb。

Fa为斜线的斜率，Fb为y轴上的截距。

Fa>1 输出图像的对⽐度变⼤，否则变⼩。

Fa=1 Fb≠0时，图像的灰度上移或下移，效果为图像变亮或变暗。

Fa=-1，Fb=255时，发⽣图像反转。

注意：线性变换会出现亮度饱和⽽丢失细节。

2）对数变换t=c * log(1+s)c为变换尺度，s为源灰度，t为变换后的灰度。

对数变换⾃变量低时曲线斜率⾼，⾃变量⼤时斜率⼩。

所以会放⼤图像较暗的部分，压缩较亮的部分。

3）伽马变换y=(x+esp)γ,x与y的范围是[0,1]， esp为补偿系数，γ为伽马系数。

当伽马系数⼤于1时，图像⾼灰度区域得到增强。

当伽马系数⼩于1时，图像低灰度区域得到增强。

当伽马系数等于1时，图像线性变换。

4）图像取反⽅法1：直接取反imgPath = 'E:\opencv_pic\src_pic\pic2.bmp';img1 = imread(imgPath); % 前景图img0 = 255-img1; % 取反景图subplot(1,2,1),imshow(img1),title('原始图像');subplot(1,2,2),imshow(img0),title('取反图像');⽅法2：伽马变换Matlab：imadjust(f, [low_in, high_in], [low_out, high_out], gamma)[low_in, high_in]范围内的数据映射到 [low_out, high_out]，低于low的映射到low_out, ⾼于high的映射到high_out. imgPath = 'E:\opencv_pic\src_pic\pic2.bmp';img1 = imread(imgPath); % 前景图img0 = imadjust(img1, [0,1], [1,0]);subplot(1,2,1),imshow(img1),title('原始图像');subplot(1,2,2),imshow(img0),title('取反图像');2、⼆值化1）rgb2gray⼀般保存的灰度图是24位的灰度，如果改为8bit灰度图。

其中，n 表示图像中像素的总数，n k 是在图像中出现这种灰度级的次数，L 表示灰度级四、灰度直方图是数字图像处理的重要工作。

请简述灰度直方图规定化、 均衡化的基本原理。

并以分辨率为 5*4，图像的深度6bit 的图像为例，自举例说明直方图均衡化的计算过 程。

解答：数字图像的直方图是作为图像每一个灰度级的统计概率分布 ”它提供了图像灰度分布的 概貌，直方图增强技术正是利用修改给定图像直方图的方法来增强图像的 ，最后得到的图像 增强程度取决于我们所采用的直方图。

令变量 r 和S 分别代表图像增强前后的像素灰度级， 相应灰度级分布的概率密度分别为P (r)和P S (s) o为讨论方便，假设像素灰度值已经归一化在区间[0,1]，在灰度级坐标中r=0表示黑,r=1表示白。

对区间[0，1]内任一个r 值按变换函数：S = T(r)( 1)进行变换，T (r )满足两个条件：(1)单值单调递增函数；(2) 0 < T (r )< 1。

条件(1)使灰度级保持从黑到白的次序，条件( 2)保证映射变换后像素灰度值在允许的范围内。

从S 到r 的反变换为：r =T/(S ) , 0< s w 1 o和(2)o 由概率理论知，若P (r)和变换函数s = T(r)drP s (S )=[ P r (r) ]r»s)ds直方图增强技术就是通过变换函数 的外貌。

对于连续图像，变换函数为：rs=T(r) = 0 P(r)dr,0 <r <1此式右边为累积分布函数(CDF ，由该式对r 求导有:ds C 、 ——=P(r) dr代入(3)得到：(6)这说明，在变换后变量S 在定义域内,P s (s)是均匀概率密度。

在图像增强意义上，这 相当于像素的动态范围增加。

对于离散图像，灰度级r k 的概率值为:P r (r k )=nk ,0 <r k <1,k =0,1,2,•.…,L-1n(2)同样，规定变量s 也满足条件(1) 已知，r =T 」(s)是单值单调增加函数,则有:T (r )控制图像灰度级的概率密度函数而改变图像的数目，P r (r k )为第k 级灰度级的概率。

Unit 11、图像是对客观存在的物体的一种相似性的、生动的写真或描述。

2、图像处理的内容它是研究图像的获取、传输、存储、变换、显示、理解与综合利用的一门崭新学科。

根据抽象程度不同可分为三个层次：狭义图像处理、图像分析和图像理解。

Unit 21、图像数字化是将一幅画面转化成计算机能处理的形式——数字图像的过程。

它包括采样和量化两个过程。

像素的位置和灰度就是像素的属性。

2、将空间上连续的图像变换成离散点的操作称为采样。

采样间隔和采样孔径的大小是两个很重要的参数。

3、将像素灰度转换成离散的整数值的过程叫量化。

4、表示像素明暗程度的整数称为像素的灰度级（或灰度值或灰度）。

5、一幅大小为M×N、灰度级数为G的图像所需的存储空间，即图像的数据量，大小为M×N×g （bit）6、数字图像根据灰度级数的差异可分为：黑白图像、灰度图像和彩色图像。

7、对比度是指一幅图象中灰度反差的大小。

对比度=最大亮度/最小亮度8、清晰度由图像边缘灰度变化的速度来描述。

9、灰度直方图反映的是一幅图像中各灰度级像素出现的频率。

以灰度级为横坐标，纵坐标为灰度级的频率，绘制频率同灰度级的关系图就是灰度直方图。

10、简述灰度直方图的应用。

1）.数字化参数（判断量化是否恰当）。

2）. 边界阈值选取（确定图像二值化的阈值）。

3）. 利用直方图统计图像中物体的面积。

4）. 计算图像信息量H（熵）。

5）. 利用直方图分析图像的特性。

6）. 利用直方图进行图像增强。

11、对于任一像素（i，j），该像素周围的像素构成的集合{（i+p,j+q），p、q取合适的整数}，叫做该像素的邻域。

12、对输入图像IP（i,j）处理时，某一输出像素JP(i,j)值由输入图像像素（i,j)及其邻域N(IP(i,j))中的像素值确定。

这种处理称为局部处理。

13、在局部处理中，当输出值JP(i,j)仅与IP(i,j)有关，则称为点处理。

14、在局部处理中，输出像素JP(i,j)的值取决于输入图像大范围或全部像素的值，这种处理称为大局处理。

【数字图像处理】灰度直⽅图、直⽅图均衡化、直⽅图规定化灰度直⽅图 ⼀幅图像由不同灰度值的像素组成，图像中灰度的分布情况是该图像的⼀个重要特征。

图像的灰度直⽅图就描述了图像中灰度分布情况，能够很直观的展⽰出图像中各个灰度级所占的多少。

图像的灰度直⽅图是灰度级的函数，描述的是图像中具有该灰度级的像素的个数：其中，横坐标是灰度级，纵坐标是该灰度级出现的频率。

灰度直⽅图的计算公式如下：p(rk)=nk/MN其中，rk是像素的灰度级，nk是具有灰度rk的像素的个数，MN是图像中总的像素个数。

直⽅图均衡化 Histogram Equalization假如图像的灰度分布不均匀，其灰度分布集中在较窄的范围内，使图像的细节不够清晰，对⽐度较低。

通常采⽤直⽅图均衡化及直⽅图规定化两种变换，使图像的灰度范围拉开或使灰度均匀分布，从⽽增⼤反差，使图像细节清晰，以达到增强的⽬的。

直⽅图均衡化，对图像进⾏⾮线性拉伸，重新分配图像的灰度值，使⼀定范围内图像的灰度值⼤致相等。

这样，原来直⽅图中间的峰值部分对⽐度得到增强，⽽两侧的⾕底部分对⽐度降低，输出图像的直⽅图是⼀个较为平坦的直⽅图。

均衡化算法直⽅图的均衡化实际也是⼀种灰度的变换过程，将当前的灰度分布通过⼀个变换函数，变换为范围更宽、灰度分布更均匀的图像。

也就是将原图像的直⽅图修改为在整个灰度区间内⼤致均匀分布，因此扩⼤了图像的动态范围，增强图像的对⽐度。

通常均衡化选择的变换函数是灰度的累积概率，直⽅图均衡化算法的步骤：计算原图像的灰度直⽅图 P(Sk)=nknP(Sk)=nkn，其中nn为像素总数，nknk为灰度级SkSk的像素个数计算原始图像的累积直⽅图 CDF(Sk)=∑i=0knin=∑i=0kPs(Si)CDF(Sk)=∑i=0knin=∑i=0kPs(Si)Dj=L⋅CDF(Si)Dj=L⋅CDF(Si)，其中 DjDj是⽬的图像的像素，CDF(Si)CDF(Si)是源图像灰度为i的累积分布，L是图像中最⼤灰度级（灰度图为255）灰度直⽅图均衡化实现的步骤1.统计灰度级中每个像素在整幅图像中的个数2.计算每个灰度级占图像中的概率分布3.计算累计分布概率4.计算均衡化之后的灰度值5.映射回原来像素的坐标的像素值⽰例说明来看看通过上述步骤怎样实现的拉伸。

数字图像处理习题集1.图像的概念及分类学科定义：给定条件下被摄目标电磁波性质（反射、辐射、透射）的一种表现形式广义上：图像是对所表示物体的信息描述分类：1）、二值图像：图像中只能取值为0或1。

2）、灰度图像: 单色图像，只包含亮度信息。

3）、彩色图像：3波段单色图像，每波段代表不同颜色，通常为红色、绿色、蓝色。

2.决定图像质量的主要因素有哪些？被摄目标性质，成像的条件，干扰条件3.图像可用数学函数I= f (x, y, z, λ, t)表示，请解释函数中各参量的含义。

(x,y,z)为空间坐标，λ为波长，t为时间，I为光点的强度。

4.说明图像技术的层次，并叙述各层次的主要研究内容；图像技术包含三个层次:图像处理-从图像到图像的过程；利用计算机把原始图像（或图像信息）处理成期望图像（或图像信息）的过程。

图像处理是对图像进行分析、加工、和处理，使其满足视觉、心理以及其他要求的技术。

图像处理是信号处理在图像域上的一个应用。

图像分析－从图像到数据的过程；图像分析要求对图像中感兴趣的目标进行检测和测量，以获得它们的客观信息，从而帮助我们建立对图像的描述。

图像理解－图像解释与知识推理；以图像为对象，知识为核心，研究图像中有什么目标、目标之间的相互关系、图像是什么场景以及如何应用场景的一门技术。

5.简述图像处理的主要目的及主要处理技术；数字图像处理目的;改善图像质量;增强图像定位精度;提高信息传输效率;减少图像信息存贮容量;建立图像信息库1. 图像增强:2、图像复原3、几何处理:4、图像压缩与编码:5、图像重建:6、图像分割7、图像描述8、图像匹配6.什么是彩色三要素，解释各要素的含义；彩色三要素：亮度，色调和饱和度。

亮度，指彩色光作用于人眼时引起人眼视觉的明暗程度；色调，是一种颜色区别于另外一种颜色的特征。

饱和度，指色调的纯洁程度。

7.简述三基色原理；1) 自然界里的大多数彩色光可以分解为三种基色成份，而这三种基色也可以按一定比例混合得到不同的彩色光。

数字图像处理复习材料要点考试题型⼀、填空题（10分，10空）⼆、判断题（5分，5题）三、名词解释（15分，5题）图像，数字图像，数字图像处理，彩⾊图像，灰度图像，⾊度，采样，量化，灰度直⽅图，直⽅图均衡化，直⽅图规定化，图像增强，图像锐化，图像复原，图像滤化，中值滤波，均值滤波，数据压缩，⽆失真编码，⼏何畸变四、简答题（20分，4题）1.RGB,HIS模型2.视觉效应（判断，填空）3.图像复原（5.3 5.4 5.5 简答，名词解释）4.第六章5.7.2 边缘检测五、计算题（50分，5题）1.平移镜像错切（作业题）2.放⼤缩⼩（作业题）3.平滑，中值滤波，均值滤波（PPT）4.哈夫曼编码（参数计算，熵，效率，编码P148）5.均衡化（第四章P69 4.1）注意：看⼀下⼩波变换怎么⽤原理第⼀章绪论1.图像：对客观存在对象的⼀种相似性的、⽣动性的描述或写真。

2.模拟图像：空间坐标和明暗程度都是连续变化的、计算机⽆法直接处理的图像3.数字图像：空间坐标和灰度均不连续的、⽤离散的数字（⼀般整数）表⽰的图像（计算机能处理）。

是图像的数字表⽰，像素是其最⼩的单位。

4数字图像处理（Digital Image Processing）：利⽤计算机对数字图像进⾏（去除噪声、增强、复原、分割、特征提取、识别等）系列操作，从⽽获得某种预期的结果的技术。

（计算机图像处理）5.数字图像处理的特点（优势）：（1）处理精度⾼，再现性好。

（2）易于控制处理效果。

（3）处理的多样性。

（4）图像数据量庞⼤。

（5）图像处理技术综合性强。

6.数字图像处理的主要研究内容：（1）图像的数字化：如何将⼀幅光学图像表⽰成⼀组数字，既不失真⼜便于计算机分析处理；主要包括的是图像的采样与量化（2）图像的增强：加强图像的有⽤信息，消弱⼲扰和噪声（3）图像的恢复：把退化、模糊了的图像复原。

模糊的原因有许多种，最常见的有运动模糊，散焦模糊等（4）图像的编码：简化图像的表⽰，压缩表⽰图像的数据，以便于存储和传输。