全国通用六年级下册数学讲义 小升初专题--几何--立体几何之曲线型(一)(含答案)

第03讲 几何综合——曲线几何1：7个圆，半径分别是1、2、3、4、5、6、7，求阴影面积阴影面积为()()()22222221325476ππππ⨯+⨯-+⨯-+⨯-()()()1325476ππππ=⨯+⨯++⨯++⨯+28π=84=2：如图，直角三角形的三条边长度为，它的内部放了一个半圆，图中阴影部分的面积为多少？6,8,106S 阴影直角三角形半圆设半圆半径为，直角三角形面积用表示为：r r 610822r r r ⨯⨯+=又因为三角形直角边都已知，所以它的面积为，168242⨯⨯=所以，824r =3r =所以1249π=24 4.5π2S =-⨯-阴影3：如图，已知扇形的面积是半圆面积的34倍，则角的度数是________．BAC ADB CAB DCB A :设半圆的半径为1，则半圆面积为，扇形的面积为．ADB 21ππ122⨯=BAC π42π233⨯=因为扇形的面积为，所以，，得到，BAC 2π360n r ⨯22ππ23603n ⨯⨯=60n =即角的度数是60度．CAB 4：如图，已知三角形是边长为26厘米的正三角形，圆的半径为厘米．GHI O 15 ．求阴影部分的面积．90AOB COD EOF ∠=∠=∠=︒直接解决． 总阴影面积每块阴影面积(大弓形小弓形)．=3⨯=-3⨯ 关键在于大弓形中三角形的面积， 设为弧的中点，则可知是菱形，是正三角形，J GI GOIJ GOJ 所以，三角形的面积．GOI1152622=⨯⨯ 所以大弓形的面积：21115π1526322GJIS=⨯-⨯⨯ 235.597.5=- ．138= 小弓形的面积：．2211π1515176.625112.564.12542FJES=⨯-⨯=-= 所以，总阴影面积(平方厘米)．13864.1253221.625=-⨯=5：下图中，ABAD如图可知3，设大半圆半径为，小圆半径为，如右图，，EF =R r R EH =r HG EG ==根据勾股定理得，故大半圆面积等于小圆面积，由图可知222R r =S S S =-阴影小圆柳叶2)EHF EHF S SS =-- 小圆扇形（22EHF EHF S SS =-+ 小圆扇形2EHFS S S =-+ 小圆大半圆2EHFS = 332 4.5EF GH =⨯=⨯÷=6：某仿古钱币直径为厘米，钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图)．求钱币在桌面4上能覆盖的面积为多少？:将古钱币分成个部分，外部的个弓形的面积和等于大圆减去内接正方形，84中间的四个扇形的面积恰好等于内接正方形内的内切圆面积，所以总面积等于：．222444π224π6π810.84222⎛⎫⎛⎫⎛⎫-⨯+⨯÷⨯=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2(cm )7：如图中三个圆的半径都是5，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取)cm3.14:将原图割补成如图，阴影部分正好是一个半圆，面积为255 3.14239.25(cm )⨯⨯÷=8：求右图中阴影部分的面积．(取3)πA欲求图①中阴影部分的面积，可将左半图形绕B 点逆时针方向旋转180°，使A 与C 重合，从而构成如右图②的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积． 所以阴影部分面积为(平方厘米)．21110101010022π⨯⨯-⨯⨯=9：如图，边长为3的两个正方形BDKE 、正方形DCFK 并排放置，以BC 为边向内侧作等边三角形，分别以B 、C 为圆心，BK 、CK 为半径画弧．求阴影部分面积．()π 3.14=EE :根据题意可知扇形的半径恰是正方形的对角线，所以，r 223218r =⨯=如右图将左边的阴影翻转右边阴影下部，S S S =-阴影扇形柳叶1118π2(18π33)34=⨯-⨯-⨯183π8.58=-=10：如图，边长为12厘米的正五边形，分别以正五边形的5个顶点为圆心，12厘米为半径作圆弧，请问：中间阴影部分的周长是多少？()π 3.14=:如图，点是在以为中心的扇形上，所以，同理，则是正三角形，C B AB CB =CB AC =ABC ∆同理，有是正三角形．有，CDE ∆60ACB ECD ∠=∠= 正五边形的一个内角是，因此，1803605108-÷= 60210812ECA ∠=⨯-= 也就是说圆弧的长度是半径为12厘米的圆周的一部分，这样相同的圆弧有5个，AE 所以中间阴影部分的周长是．()122 3.1412512.56cm 360⨯⨯⨯⨯=11：ABCD 四个齿轮，直径分别是3、2、4、1.5，AB 共轴，问：C 转动一周时，重物被提起______语法第一练语法第二练语法第一练答案语法第一练答案。

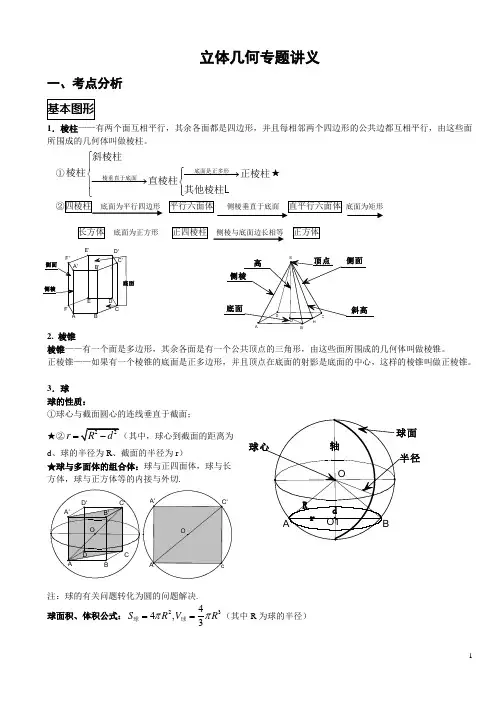
立体几何专题讲义一、考点分析1．棱柱——有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱★ 底面为矩形底面为正方形 侧棱与底面边长相等 2. 棱锥棱锥——有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

正棱锥——如果有一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥。

3．球球的性质：①球心与截面圆心的连线垂直于截面；★②r =d 、球的半径为R 、截面的半径为r ）★球与多面体的组合体：球与正四面体，球与长 方体，球与正方体等的内接与外切.注：球的有关问题转化为圆的问题解决. 球面积、体积公式：2344,3S R V R ππ==球球（其中R 为球的半径）1．求异面直线所成的角(]0,90θ∈︒︒：解题步骤：一找（作）：利用平移法找出异面直线所成的角；（1）可固定一条直线平移 另一条与其相交；（2）可将两条一面直线同时平移至某一特殊位置。

常用中位线平移法 二证：证明所找（作）的角就是异面直线所成的角（或其补角）。

常需要证明线线平行； 三计算：通过解三角形，求出异面直线所成的角；2求直线与平面所成的角[]0,90θ∈︒︒：关键找“两足”：垂足与斜足解题步骤：一找：找（作）出斜线与其在平面内的射影的夹角（注意三垂线定理的应用）； 二证：证明所找（作）的角就是直线与平面所成的角（或其补角）（常需证明线面垂直）；三计算：常通过解直角三角形，求出线面角。

3求二面角的平面角[]0,θπ∈解题步骤：一找：根据二面角的平面角的定义，找（作）出二面角的平面角； 二证： 证明所找（作）的平面角就是二面角的平面角（常用定义法，三垂线法，垂面法）； 三计算：通过解三角形，求出二面角的平面角。

俯视图二、典型例题1．_________________.第1题2.若某空间几何体的三视图如图2所示，则该几何体的体积是________________.第2题 第3题3．一个几何体的三视图如图3所示，则这个几何体的体积为 .4．若某几何体的三视图（单位：cm ）如图4所示，则此几何体的体积是 .第4题 第5题5．如图5是一个几何体的三视图，若它的体积是 a侧(左)视图 正(主)视图 3 俯视图6．已知某个几何体的三视图如图6，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 .第6题 第7题7.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm 8.设某几何体的三视图如图8（尺寸的长度单位为m ），则该几何体的体积为_________m 3。

表面积和体积专题一：表面积、体积（一）专题简析小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。

从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。

因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。

在解答立体图形的表面积问题时，要注意以下几点：（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。

（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。

反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。

（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。

若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。

专题精讲【例1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？【例2】把19个棱长为3厘米的正方体重叠起来，如图27-4所示，拼成一个立体图形，求这个立体图形的表面积。

图27—4【例3】把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体，拼成一个大长方体，这个大长方体的表面积最少是多少平方厘米？【例4】一个长方体，如果长增加2厘米，则体积增加40立方厘米；如果宽增加3厘米，则体积增加90立方厘米；如果高增加4厘米，则体积增加96立方里，求原长方体的表面积。

【例5】如图27-10所示，将高都是1米，底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体。

求这个物体的表面积。

专题过关1、把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？2、一堆积木（如图所示），是由16块棱长是2厘米的小正方体堆成的。

它们的表面积是多少平方厘米？3、将一个表面积为30平方厘米的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体。

第三节 立体图形小学梳理小学阶．段，我们主要学习的立体图形有长方体、正方体、圆柱、圆锥。

研究了各个立体图形的特征和表面积、体积的计算方法。

通过对物体的实际观察，使我们了解到从不同方向观察物体，所看到一、立体图形的特征 1、 长方体长方体有6个面，6个面一般都是长方形(也有可能相对的2个面是正方形)，长方体每一组相对的2个面形状相同、大小相等。

长方体有8个顶点、12条棱，每一组互相平行的4 条棱(相对的棱)的长度相等。

我们把相交于一个顶点的三条棱分别叫作这个长方体的长、宽、高。

2. 正方体正方体有6个面，6个面都是正方形，且面积相等。

正方体有8个顶点、l2条棱，12 条棱的长度相等。

有时我们也把正方体看成是长、宽、高都相等的长方体。

3、 圆柱圆柱由两个底面和一个曲面组成。

上、下两个底面是相等的两个圆，两个底面之间的距离叫作高，圆柱有无数条高。

把圆柱的侧面沿高展开后得到一个长方形(或正方形)，长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。

4、 圆锥圆锥有一个顶点、一个曲面和一个圆形的底面。

从顶点到底面圆心的距离就是圆锥的高，圆锥只有一条高。

二、立体图形的表面积 1. 表面积的意义一个立体图形所有面的面积的和叫作这个立体图形的表面积。

2. 表面积的计算方法(1) 长方体的表面积：长方体6个面的面积的和就是这个长方体的表面积。

长方体的表面积计算公式：:S=(ab+ah+b)×2(2) 正方体的表面积：正方体6个面的面积的和就是这个正方体的表面积。

正方体的表面积计算公式： S =6a²(3)圆柱的表面积：两个底面的面积与一个侧面面积的和就是这个圆柱的表面积。

圆柱的表面积计算公式： S 底=S N +S 底×2(其中 S N =Cℎ)进一法：在实际生产中，使用的材料都要比计算的结果多一些，因此，在保留得数的时候，即使被省略的尾数的最高位上的数是4或者比4小，都要向前一位进1。

【小升初培优专题】六年级下册数学-平面几何综合训练—曲线型（解析版）一、知识点1、圆周长：C＝πd＝2πr扩倍问题（1）：若圆的半径扩大到n倍，则直径扩大到n倍，周长扩大到n倍，面积扩大到n²倍扩倍问题（2）：若两个圆的半径比为n：m，则它们的直径比为n：m，周长比为n：m，面积比则为n²：m²构造圆在长方形中画一个最大的圆在长方形中画最大的半圆技巧：长的一半与宽比较，谁小谁是半径。

2、半圆周长：C＝πr＋d面积：πr²÷23、圆环＝大圆面积－小圆面积＝πR²－πr²圆环面积：S环4、扇形弧长：r nl π2360⨯=面积：2360r nS π=5、组合图形方中圆：正方形与圆面积之比为4：π圆中方：圆与正方形面积之比为π：2方中圆中方：大正方形面积是小正方形面积的2倍圆中方中圆：大圆面积是小圆面积的2倍割补法：重叠问题：整体减空白一、填空题。

（每道小题5分，共 40分）1. （1）一个圆的半经扩大到3倍，直径扩大到 倍；周长扩大到 倍；面积扩大到 倍。

【解答】3，3，9。

（2）大圆和小圆的半径比是3：2，它们的直径比是 ，他们的周长比是 ，它们的面积比是 。

【解答】3：2，3：2，9：4。

2. 在一个长10厘米、宽4厘米的长方形内画圆，圆的直径最大是 厘米，能画 个这样的圆且互不重叠。

【解答】如下图，4：2。

3. 如图，以B 、C 为圆心的两个半圆的直径都是3厘米，图中阴影部分的周长是 厘米。

【解答】如下图，半径为3÷2＝1.5（厘米），连接BP 与CP ，因为BC 、CP 、PB 均为半径，所以△BCP 是等边三角形，那么∠PBC ＝∠PCB ＝60（度），弧长PB ＝60＝弧长PC ＝36060×3.14×3＝1.57（厘米），阴影部分的周长为1.57＋1.57＋1.5＝4.64（厘米）。

2023年学校六班级小升初数学专项复习（12）——立体图形的分类及识别★★学学问问归归纳纳总总结结一、立体图形的分类及识别1.立体几何图形：从实物中抽象出来的各种图形，统称为几何图形，几何图形是数学争辩的主要对象之一．有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各个部分不都在同一平面内，它们是立体图形．由一个或多个面围成的可以存在于现实生活中的三维图形．点动成线，线动成面，面动成体．即由面围成体，看一个体最多看到立体图形实物三个面．2．常见立体几何图形及性质：（1）正方体：有8个顶点，6个面．每个面面积相等（或每个面都有正方形组成）．有12条棱，每条棱长的长度都相等．（正方体是特殊的长方体）（2）长方体：有8个顶点，6个面．每个面都由长方形或相对的一组正方形组成．有12条棱，相对的4条棱的棱长相等．（3）圆柱：上下两个面为大小相同的圆形．有一个曲面叫侧面．开放后为长方形或正方形或平行四边形．有很多条高，这些高的长度都相等．（4）圆锥：有1个顶点，1个曲面，一个底面．开放后为扇形．只有1条高．四周体有1个顶点，四周六条棱高．（5）直三棱柱：三条侧棱切平行，上表面和下表面是平行且全等的三角形．（6）球：球是生活中最常见的图形之一，例如篮球、足球都是球，球是由一个面所围成的几何体．例1：长方体有4个，正方体有4个，圆柱有5个，球有4个。

【分析】依据常见立体图形的特征及分类即可解答。

【解答】解：长方体有4个，正方体有4个，圆柱有5个，球有4个。

故答案为：4；4；5；4。

【点评】本题主要考查常见立体图形的特征及分类。

例2：填一填，圈一圈。

（1）一共有8个图形。

（2）排第6；排第7的是。

（3）如图的图形中有1个正方体，3个长方体，2个球和2个圆柱。

（4）圈出如图图形中简洁滚动的图形。

【分析】正方体：有8个顶点，6个面，每个面面积相等（或每个面都有正方形组成）；长方体：有8个顶点，6个面，每个面都由长方形或相对的一组正方形组成；圆柱：上下两个面为大小相同的圆形，有一个曲面叫侧面；球：球是生活中最常见的图形之一，例如篮球、足球都是球，球是由一个面所围成的几何体。

曲线型立体几何（一）一、圆柱和圆锥的基本特征1、圆柱的特征：（1）圆柱的两个底面是半径相等的两个圆（2）两个底面间的距离叫做圆柱的高（3）圆柱有无数条高，且高的长度都相等2、圆锥的特征：（1）圆锥的底面是一个圆（2）圆锥的侧面是一个曲面（3）圆锥只有一条高二、圆柱的表面积1、沿圆柱的高剪开，圆柱的侧面展开图是一个长方形（或正方形）。

2、圆柱的侧面积＝底面周长×高，用字母表示为：S侧＝Ch3、圆柱的侧面积公式的应用：（1）已知底面周长和高，求侧面积，可运用公式：S侧＝Ch（2）已知底面直径和高，求侧面积，可运用公式：S侧＝πdh（3）已知底面半径和高，求侧面积，可运用公式：S侧＝2πrh4、圆柱表面积的计算方法：如果用S侧表示一个圆柱的侧面积，S底表示底面积，d表示底面直径，r表示底面半径，h表示高，那么这个圆柱的表面积为：S表=S侧+ 2S底5、圆柱表面积的计算方法的特殊应用：（1）圆柱的表面积只包括侧面积和一个底面积的,例如无盖水桶等圆柱形物体。

（2）圆柱的表面积只包括侧面积的，例如烟囱、油管等圆柱形物体。

三、圆柱的体积1、圆柱的体积：一个圆柱所占空间的大小2、圆柱的体积＝底面积×高。

如果用V表示圆柱的体积，S表示底面积，h表示高，那么V＝Sh计算圆柱体积时，如果题中给出了底面积和高，可用公式：V ＝Sh 4、圆柱形容器公式的应用与圆柱体积公式的应用计算方法相同 四、、圆锥的体积 1.圆锥只有一条高2.圆锥的体积＝31×底面积×高如果用V 表示圆锥的体积，S 表示底面积，h 表示高，则字母公式为：31Sh3.圆锥体积公式的应用：求圆锥体积时，如果题中给出底面积和高这两个条件，可以直接运用“V=31Sh ”这一公式。

1、一个圆柱形水槽，里边盛满24升水，如果把一块与圆柱形水槽内部等底等高的圆锥形铁块放入水槽，此时水槽中还有多少水？2、一只皮球掉进一个盛有水的圆柱形水桶中，已知皮球的直径为12厘米，水桶的底面直径为60厘米，且皮球恰好有32的体积浸在水中，则皮球掉进水桶后，水桶的水面升高了多少厘米？（球的体积=r 343）3、自来水管的内半径是1厘米，水管内水的流速是每秒8厘米，一位同学去洗手，走时忘记关水龙头，10分钟后才被另一位同学发现并关上，问浪费了多少升水？4、一个圆柱的底面周长是一个圆锥的底面周长的32，而圆锥的高是圆柱高的52，则圆锥体积是圆柱体积的几分之几？1、压路机的滚筒是一个圆柱体，滚筒直径1.2米，长1.5米，现在滚筒向前滚动120周，被压路面的面积是多少？2、一个高10厘米的圆柱体，如果把它的高截短3厘米，它的表面积减少94.2平方厘米，则这个圆柱体的体积是多少立方厘米？3、把一个底面半径是9厘米的圆柱形木块沿底面直径竖直分成相同的两块，表面积增加了360平方厘米，则该圆柱的体积是多少立方厘米？（ 取3.14）4、把高为4厘米，底面直径为6厘米的圆柱体A 的侧面展开，再围成不同于A 的另一个圆柱体B ，则圆柱体B 的体积是多少？5、如图1 是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一个圆柱形铁块立方其中（圆柱形铁块的下底面完全落在乙槽底面上），现将甲槽的水匀速注入乙槽，甲、乙两个水槽中水的深度元y（厘米）与注水时间x（分钟）之间的关系如图2 所示，根据图像提供的信息，解答下列问题：（1）注水多长时间时，甲、乙两个水槽中水的深度相同？（2）若乙槽底面积为18 平方厘米（壁厚不计），求乙槽中铁块的体积；（3）若乙槽中铁块的体积为56 立方厘米，求甲槽底面积（壁厚不计）1、把一个圆柱体的底面平均分成若干个扇形，然后拼成一个近似的长方体，表面积增加了100平方厘米，圆柱体的高是10厘米，圆柱的侧面积是多少平方厘米？2、把一个底面直径是2分米、高是3分米的圆柱形容器注满水，现垂直轻轻插入一根底面积是0.6平方米、高是4分米的方钢，溢出水的体积是多少毫升？3、小明星期天请6名同学来家里做客，他选用一个长、宽、高分别为15厘米、12厘米、6厘米的长方体包装的饮料招待同学，给每个同学倒上一满杯，杯子的底面积为20平方厘米、高是8厘米。