停留时间分布及反应器的流动模型

连续反应器的停留时间分布及流动模型参数的测定连续反应器是化工过程中常用的反应器之一，其特点是进料和产物的连续流动，反应物在反应器中的停留时间是一个重要的参数。

停留时间分布及流动模型参数的测定对于反应器的设计、操作和优化具有重要意义。

停留时间分布是指进料从反应器的进口到出口所经历的时间。

在连续反应器中，每个分子或粒子在反应器中的停留时间可能不同，形成一定的分布。

停留时间分布的测定可以采用多种方法，其中较常用的是色谱法。

色谱法是一种基于成分浓度变化对时间的记录和分析的方法。

在连续反应器中，可以通过在进料中添加示踪剂，如某种色谱指示剂，来追踪反应物在反应器中的停留时间。

通过取样和分析，在不同时刻得到的浓度-时间曲线可以计算出停留时间分布。

流动模型参数的测定是指描述反应物在连续反应器中流动行为的参数。

常用的流动模型包括完全混合模型（CSTR）和分层流模型（PFR）。

完全混合模型假设反应物在反应器中快速均匀混合，适用于物理吸附、解离反应等。

分层流模型假设反应物在反应器中按照一定的流动方式进行，适用于化学反应、催化反应等。

流动模型参数的测定可以采用理论计算和实验测定结合的方法。

理论计算常用的方法包括理论模型的建立和数值模拟。

通过建立反应动力学模型和反应器流体力学模型，进行数值模拟，可以得到流动模型参数。

实验测定常用的方法包括加入示踪剂进行测定，如通过采样得到浓度-时间曲线，根据模型进行拟合，得到流动模型参数。

除了色谱法，还有其他一些测定停留时间分布和流动模型参数的方法。

例如，可以使用放射性示踪剂法，通过测量放射性示踪剂在反应器中的浓度变化，得到反应物的停留时间分布。

可以使用激光多普勒测速仪等仪器，测量流体在反应器中的速度分布，从而得到流动模型参数。

在连续反应器的设计和操作中，准确的停留时间分布和流动模型参数是非常重要的。

它们可以帮助确定最佳反应器尺寸和操作条件，提高反应器的效率和产物的质量。

因此，对于连续反应器的停留时间分布及流动模型参数的测定，需要选择合适的方法，并进行仔细的测量和分析。

实验报告课程名称： 化学反应过程远程实验 指导老师： 成绩：__________________实验名称： 连续均相反应器 实验类型：________________同组学生姓名：__________ 一、实验目的和要求（必填） 二、实验内容和原理（必填） 三、主要仪器设备（必填） 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析（必填） 七、讨论、心得一、实验目的1. 了解连续均相流动反应器的非理想流动情况及产生返混的原因；2. 了解有效扩散模型及多级混合流动模型的建立，及应用停留时间分布的测定，确定其有关参数E z 及N ；3. 掌握用阶跃示踪法测定停留时间分布的实验方法及数据处理。

二、实验原理在实际连续操作反应器内，由于短路、死区及漏液等原因，器内流体往往是偏离理想流动而造成不同程度的逆向混合（称返混）。

使得一批同时进入反应器的流体，在反应器内的停留时间不同，形成一个停留时间分布，所以常常利用停留时间的测定来分析器内的返混程度。

但应该指出，这两者并不一一对应的，即同样的停留时间分布可以由不同的流况而造成，因此不能把停留时间分布直接用于描述反应器内流况，而必须借助于较切合实际的流动模型，然后由停留时间分布的测定来确定其模型中的参数。

众所周知，流体在反应器内的停留时间是个随机过程，而E(t)，F(t)是常用的两个函数，其定义参见教材。

一般可用脉冲示踪法和阶跃示踪法求取： 脉冲示踪法：()E(t)C t C =(1)阶跃示踪法:1()()C t F t C =(2)式中：0Q C V ==示踪剂的脉冲量流体的流量C(t)——出口处示踪剂浓度C 1——进口处示踪剂浓度由此可见，若用脉冲示踪法，测定出口浓度变化曲线，即可得到E(t)函数，而用阶跃示踪法测定出口浓度曲线，可得到F(t)函数，其两者的关系为：()()dF t E t dt=(3)为了进行定量比较，引入随机函数的两个特征值——均值t 和方差2t σ。

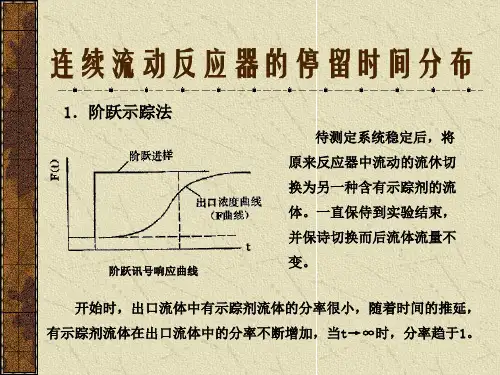
停留时间分布与反应器的流动模型在实际反应器中，流出反应器的反应物浓度的变化与流入反应器的浓度变化之间存在着一定的延迟。

这种延迟现象可以用停留时间来描述，即停留时间越长，反应物浓度的变化越大。

因此，停留时间分布的形态将直接影响反应物浓度和反应速率的分布。

关于停留时间分布的研究，可以采用物理实验方法和数学模型方法。

物理实验方法主要基于示踪剂法，通过在反应器中添加示踪剂，然后在反应物的进出口处进行测量，从而获得停留时间分布的数据。

示踪剂可以是稳定物质，也可以是具有明显性质差异的物质。

物理实验方法可以较为准确地获得停留时间分布的数据，但其工作量大且成本高。

数学模型方法则是通过建立数学方程来描述停留时间分布。

数学模型方法可以采用连续模型和离散模型两种方式。

连续模型是指将反应器内的流体视为连续介质，通过求解偏微分方程来描述流体在空间和时间上的分布。

而离散模型则是将反应器内的流体划分为离散的传输单元，通过求解离散的代数方程来描述传输单元之间的质量传递过程。

针对不同类型的反应器，可以采用不同的数学模型来描述停留时间分布。

例如，对于连续搅拌罐反应器，可以使用完全混合模型（CSTR model），假设反应器内的流体完全混合，从而得到均匀的停留时间分布。

而对于管式反应器，则可以使用两区模型（two-zone model），将管内的流体划分为两个区域，即分子在低速输运区域停留的时间较长，在高速输运区域停留的时间较短。

值得注意的是，停留时间分布对于反应器的性能有着重要的影响。

例如，在反应器中的流体停留时间分布较宽且对称时，反应物的转化率较高，反应速率较快。

而当停留时间分布较窄且偏斜时，反应物的转化率较低，反应速率较慢。

因此，在反应器设计和优化中，需要充分考虑停留时间分布对反应性能的影响，以实现高效的反应过程。

总之，停留时间分布是描述反应器内流体停留时间的概率分布函数。

在反应器设计和优化中，停留时间分布是一个重要的概念，对反应器的性能和反应物转化率等有着直接的影响。

停留时间分布与反应器的流动模型讲义停留时间分布（RTD）是描述流体在反应器内停留时间的分布情况。

它对于理解反应器的性能和效率至关重要。

通过分析停留时间分布，可以评估反应过程中各种反应物的浓度分布，从而优化反应器设计和操作。

在反应器中，流体进入并通过反应器。

然而，由于流体的动力学特性和反应器的几何形状，不同流体分子停留在反应器中的时间是不一样的。

停留时间分布图描述了流动物质的停留时间的概率分布。

停留时间分布可以通过数学模型来描述。

最常用的数学模型是以连续搅拌反应器（CSTR）为基础的模型。

CSTR是一种理想化的反应器类型，其中反应物在反应器中均匀分布，并以恒定的速率混合。

CSTR模型假设反应物的停留时间服从完美的指数分布。

另一个常用的模型是斑点流动模型（PFR）。

在PFR中，流体在反应器中形成了一系列的“斑点”，每个斑点代表一个流体分子，它们按照一定的速率顺序通过反应器。

PFR模型假设反应物的停留时间服从完美的单谷型分布。

PFR模型更适用于流体通过小直径管道或多孔介质的情况。

反应器的流动模型是利用数学模型描述反应物在反应器内的运动和行为，从而揭示反应过程中的动力学特性。

通过结合停留时间分布和流动模型，可以研究反应器中的物质传递、反应速率、混合程度等重要参数。

总结一下，停留时间分布和反应器的流动模型对于理解反应器的性能和优化设计非常重要。

它们可以帮助我们预测和改进反应过程中的各种流体动力学参数，从而提高反应器的效率和产量。

停留时间分布（RTD）与反应器的流动模型在化学工程领域具有广泛的应用。

通过分析停留时间分布和建立合适的流动模型，可以有效地揭示反应器内复杂流动与反应过程之间的关系，优化反应器设计和流程操作。

首先，停留时间分布是评估反应器性能的一个重要指标。

它反映了反应物在反应器内停留的时间分布情况。

对于快速反应，需要较短的停留时间，而对于缓慢反应，则需要较长的停留时间。

停留时间分布可以通过实验测量或数值模拟来获得。

第五章停留时间分布与反应器流动模型重点掌握：•停留时间分布的实验测定方法和数据处理。

•理想反应器停留时间分布的数学表达式。

•返混的概念。

•非理想流动模型（离析流模型、多釜串联模型和扩散模型）的模型假定与数学模型建立的基本思路，模型参数的确定。

•利用扩散模型和多釜串联模型的反应器计算。

深入理解：•停留时间分布的概念和数学描述方法。

•停留时间分布的数字特征和物理意义。

广泛了解：•流动反应器中的微观混合与宏观混合及其对反应器性能的影响。

停留时间分布与流动模型对于连续操作的反应器,组成流体的各粒子微团在其中的停留时间长短不一，有的流体微团停留时间很长，有的则瞬间离去，从而形成了停留时间的分布。

正如前面针对理想流动反应器的分析，停留时间分布的差异对反应系统的性能有很大影响，值得进一步深入探讨。

全混流和活塞流模型对应着不同的停留时间分布，是两种极端的情况，实际反应器中的流动状况介于上述两种极端情况之间。

本章将针对一般情况讨论停留时间分布及其应用问题，对于实际反应器的设计与分析非常必要。

具体内容包括：停留时间分布的概念与数学描述停留时间分布的统计分析理想流动反应器的停留时间分布非理想流动现象分析发几种常见的非理想流动模型非理想反应器设计与分析流动反应器中流体的混合及其对反应器性能的影响第一节停留时间分布一、举例说明停留时间及其分布•间歇系统：不存在RTD；•流动系统：存在RTD问题。

可能的原因有：•不均匀的流速（或流速分布）•强制对流•非正常流动-死区、沟流和短路等流动状况对反应的影响釜式和管式反应器中流体的流动状况明显不同，通过前面对釜式和管式反应器的学习，可以发现：•对于单一反应，反应器出口的转化率与器内的流动状况有关；•对于复合反应，反应器出口目的产物的分布与流动状况有关。

二、寿命分布和年龄分布区别在于：前者指反应器出口流出流体的年龄分布，而后者是反应器中流体的年龄分布。

三、系统分类系统有闭式系统和开式系统之分。

连续反应器是化工生产过程中常见的一种反应设备，其停留时间分布和流动模型参数的测定是对其性能进行评估和优化的重要步骤。

本文将就连续反应器的停留时间分布及流动模型参数的测定进行深入探讨，以期为相关领域的研究和实践提供有益的参考。

一、连续反应器的停留时间分布1. 理论基础：连续反应器的停留时间分布是指在反应器中参与化学反应的物质颗粒或分子所停留的时间在不同时间间隔内所占的比例。

它是影响反应器反应性能和产物分布的重要参数，也是评价反应器混合程度和性能优劣的重要依据。

2. 测定方法：常见的连续反应器停留时间分布的测定方法包括示踪剂法、直接测定法和间接测定法。

其中，示踪剂法是常用的一种方法，通过向反应器中加入示踪剂，并测定出口处的示踪剂浓度随时间的变化曲线，从而推导出停留时间分布的曲线。

3. 影响因素：连续反应器的停留时间分布受到很多因素的影响，如反应器结构形式、进料方式、搅拌强度等。

在测定过程中，需要考虑这些因素对停留时间分布的影响，以获得准确可靠的测定结果。

二、连续反应器的流动模型参数的测定1. 理论基础：流动模型参数是描述流体在连续反应器中运动规律的参数，它们包括流体的速度场、浓度场、温度场等。

测定这些参数可以揭示反应器内部流体运动的规律，为进一步优化反应器设计和操作提供依据。

2. 测定方法：常见的连续反应器流动模型参数的测定方法包括数值模拟方法、实验测定方法和经验公式法。

数值模拟方法是近年来发展较快的一种方法，通过建立流体力学模型，利用计算机进行模拟计算，可以较为准确地得到流体在反应器内的运动规律。

3. 应用实例：连续反应器的流动模型参数的测定方法已经得到了广泛的应用。

在工业生产中，通过测定反应器内部的流动参数，可以优化反应条件，提高反应效率和产物纯度，降低生产成本，具有重要的应用价值。

三、结语连续反应器的停留时间分布和流动模型参数的测定是重要的研究内容，对于提高反应器的反应性能、优化工艺条件具有重要的意义。

停留时间分布与流动模型分析摘要：停留时间分布和流动模型是交通流理论中的重要研究课题。

本文主要从停留时间分布和流动模型的概念、影响因素、应用以及未来研究方向等方面进行分析和探讨。

一、停留时间分布概述停留时间是指车辆在某一地点停留的时间长度，停留时间分布则是对车辆停留时间进行统计和描述的分布函数。

停留时间分布的研究对于交通规划和交通管理具有重要意义。

停留时间分布通常呈现出长尾分布的特点，即大多数车辆停留时间较短，而少数车辆具有较长的停留时间。

二、停留时间分布的影响因素1. 地点：不同地点的停留时间分布存在差异，主要因素包括地点的类型、功能、繁忙程度等。

2. 车辆特征：不同类型的车辆、不同的司机行为以及不同的出行目的都会对停留时间分布产生影响。

3. 外界因素：如交通状态、停车设施的供需关系、交通流量等都会对停留时间分布产生影响。

三、停留时间分布的应用1. 交通规划：通过对停留时间分布的研究可以了解不同地点的出行需求和停留行为，从而指导交通规划和交通设施的布局。

2. 交通管理：通过对停留时间分布的研究可以优化交通信号配时、调整道路限制措施等，从而提高道路通行能力和交通效率。

四、流动模型概述流动模型是对交通流动过程进行描述和分析的数学模型。

通过对流动模型的研究可以预测交通流量、交通拥堵现象以及交通干扰等情况。

五、流动模型的分类1. 宏观流动模型：主要通过对流量密度、平均速度等宏观指标进行建模和分析，常用的宏观流动模型包括Greenshields模型、Underwood模型等。

2. 微观流动模型：主要通过对车辆的运行过程进行建模和分析，在微观层面上研究车辆之间的相互作用，常用的微观流动模型包括Cellular Automaton模型、Car-Following模型等。

六、流动模型的应用1. 网络模拟：通过对流动模型进行网络模拟可以分析交通网络的拥堵情况、瓶颈位置以及交通干扰对整个网络的影响。

2. 交通控制：通过对流动模型的研究可以优化交通信号配时，提高交通网络的通行能力和交通效率。

停留时间分布与反应器的流动模型停留时间（residence time）是指流体在反应器中停留的平均时间，通常用时间单位表示。

它在反应器设计和操作中起着重要的作用，对反应器性能和产品质量有着直接影响。

此外，停留时间分布（residence time distribution）还可以用来描述流体在反应器中停留时间的分布情况。

停留时间分布与反应器的流动模型密切相关。

在反应器中，流体的流动通常遵循不同的模型，如完全混合模型、分层模型、或完全不混合模型等。

不同的流动模型会导致不同的停留时间分布。

完全混合模型是指在整个反应器内部，流体以均匀的速度混合和流动。

这意味着反应器内的任何一点，流体的特性都是相同的。

在完全混合模型中，停留时间分布是均匀的，即流体停留的时间是相等的，没有明显的梯度。

这种模型通常适用于小规模反应器或具有高速搅拌的大规模反应器。

分层模型是指在反应器中，流体分为不同的层次流动，形成不同的流速和混合程度。

在这种模型中，停留时间分布是不均匀的，不同位置的流体停留的时间不同。

通常，在底部和顶部的流体停留时间较长，而在中间位置的流体停留时间较短。

这种模型适用于某些特定的反应器类型，如换热塔或蓄能反应器。

完全不混合模型是指反应器中流体不进行混合，而是呈现分层的状态。

在这种模型中，停留时间分布是非常不均匀的，不同位置的流体停留时间差异非常大。

这种模型通常适用于某些特殊的反应器，如上升气流床反应器或固定床反应器。

为了更好地理解停留时间分布和反应器的流动模型，研究者通常使用流体动力学实验和数值模拟方法。

通过实验，可以测量反应器中不同位置的流体停留时间，进而推导出停留时间分布。

而数值模拟可以通过求解反应器内的流体运动方程，得到停留时间分布和流速分布等参数。

停留时间分布与反应器的流动模型对反应器的设计和运行具有重要意义。

在反应器设计中，需要选择合适的流动模型和控制参数，以满足反应物转化率和产品选择性的要求。

在反应器操作中，需要实时监测和控制停留时间分布，以确保反应器的稳定性和效率。