席位分配

席位分配问题是一个常见的实际问题，涉及到资源的分配和管理。

为了解决这个问题，我们可以使用数学建模的方法，通过建立数学模型来分析和优化席位的分配方案。

一、问题描述假设有一个大型会议，需要分配给不同的参与者席位。

每个参与者可能有不同的资格和需求，我们需要根据一定的规则来分配席位。

具体问题包括：1. 参与者数量和席位数量2. 参与者的资格和需求3. 席位分配的规则和标准二、数学建模为了解决席位分配问题，我们可以使用以下数学模型：1. 参与者集合P：表示所有的参与者。

2. 席位集合S：表示所有的席位。

3. 资格矩阵A：表示每个参与者的资格情况，每一行表示一个参与者，每一列表示一个资格类型（例如，专业、身份等）。

4. 需求矩阵D：表示每个参与者对席位的需求情况，每一行表示一个参与者，每一列表示一个席位类型（例如，地点、时间等）。

5. 分配规则R：表示席位的分配规则和标准，如按照资格优先、按照需求优先、按照公平分配等。

根据以上描述，我们可以建立如下的数学模型：目标函数：最小化席位浪费（即席位数与参与者需求之差）约束条件：1. 资格约束：每个参与者的资格必须满足分配规则的要求。

2. 需求约束：每个参与者所需席位类型必须得到满足。

3. 数量约束：总的席位数必须不超过总席位数量。

4. 可行性约束：分配的席位必须是有效的，即不存在冲突和重复的情况。

三、求解方法根据上述数学模型，我们可以使用以下方法进行求解：1. 枚举法：逐个尝试所有可能的席位分配方案，找到满足约束条件的方案。

这种方法需要大量的计算时间和空间，但在某些情况下可能找到最优解。

2. 优化算法：使用优化算法如遗传算法、粒子群算法等，通过不断迭代找到最优解。

这种方法需要一定的编程知识和技能，但通常能够快速找到满意的解。

3. 启发式算法：使用启发式算法如模拟退火、蚁群算法等，通过不断尝试找到满意解。

这种方法相对简单易行，但可能无法找到最优解。

4. 数学软件求解：使用专门的数学软件如Matlab、Python等，通过编程求解上述数学模型。

各类活动席位安排领导出席各类活动,（包括会见、会谈、会议、仪式、宴请等公务活动），都有一个席位安排要求，此类席位安排有其相对固定的模式,无论接待外宾和内宾,还是大型活动(会议)主席台的排位,按国际惯例,基本原则都是一样的,即"右首为尊"的原则.但也有特殊情况,在一些大型活动(会议)主席台座位的排位时,有时会沿用我国传统做法,即"左首为尊".现将目前常用各类活动席位安排分列如下供参考：1、宴请席位安排:首先需分清主人和客人的身份、职务、年龄等.然后,根据上述情况排席位,放席签.宴请时主位确定，如果只有一桌（圆桌）,通常是主人坐面对进门的上首,作为主陪，主要宾客坐主人右首.其他客人按职务或年龄大小依次分坐两边(见表一),但有时需从宴会所在房间实际情况考虑进行调整，如在国际会议中心四楼宴会厅，考虑观景方便，主位是安排在面对临江窗口的一侧;若主要宾客有夫人相随并有女主人作陪,则女主人面对主人坐,作为副陪,主宾夫人坐女主人右首,其他宾客则依次上下首交叉分坐两边（见表二）;若主要宾客无夫人相随,而主人方有多人作陪,则其中一人以"第二主人"身份,坐主人对面座位,作为副陪,其他客人席位坐法与上例一样（见表二）。

在具体安排时,往往为了方便交谈，在圆桌排位时经常将主方排名第二位的领导安排在第一主宾的右首即第三主人位置上。

如果是多桌,首先把主人和主要宾客、重要客人排到主桌上,其他几桌主陪人员座位面对主桌主人席位,其他客人依次而坐（见表三）。

2、长桌的席位安排：排法大体与圆桌要求相同.即面对门的为上首，作为主陪，主人的右首为主宾（见表四）.3、大型活动（会议）主席台席位安排：原则与宴请席位一样,但要求比较严格(见表5).在操作时,首先要求向有关部门了解清楚主席台就坐领导的具体身份,然后按"右首为尊",从中间座位开始,先右后左,按职务大小依次排列.目前,本市一般多采用“右首为尊”排位做法（见表五）。

中餐席位安排礼仪一、宾客身份：在中餐席位安排礼仪中，通常将宾客分为主宾、贵宾、宾客和配偶四个层次。

主宾一般是主办者或者主要负责人，贵宾是具有特殊身份地位或者职务地位的人士，宾客是一般参会人员，配偶则是主宾或者贵宾的配偶。

二、座位安排方式：1.圆桌座位安排：在圆桌座位安排上，主宾通常安排在桌子的正中央，贵宾和宾客按照重要性逆时针顺序均匀分布在主宾旁边，配偶则安排在对应的宾客身边。

2.长桌座位安排：在长桌座位安排上，主宾位于桌子的中间，贵宾坐在主宾旁边，宾客和配偶则从主宾两侧交替安排座位。

三、座位顺序：座位顺序的原则是根据宾客的社交地位和职务身份进行安排，遵循重要宾客靠近主宾或贵宾的原则。

一般来说，安排座位时应遵循以下几个原则：1.主宾应坐在最有面子的位置上，比如桌子的中央或最靠近舞台的位置。

2.贵宾应坐在主宾的旁边，根据职务地位或者社交地位的高低确定座位。

3.宾客按照重要性逆时针顺序均匀分布在主宾旁边，离主宾近的座位沾宴肩膀，离主宾远的座位沾宴脚趾。

4.配偶的座位则与对应的宾客保持一定的距离，以防止亲密关系的热度影响到整个宴会的秩序。

四、其他注意事项：1.座位的舒适性要考虑周到，避免将宾客安排在过于拥挤或者位置不佳的座位上。

2.座位安排还需要考虑宾客之间的关系，尽可能避免搁置有矛盾或者争议的人相邻。

3.座位安排应提前做好计划，并在宴会当天提前安排好，以避免临时混乱和困扰。

4.在座位安排时，可根据宾客的个人风格和喜好，为他们准备相应的名牌或者小礼物，以体现主办者的热情和细致服务。

总结起来，中餐席位安排礼仪是根据宾客身份、座位安排方式、座位顺序等因素来合理安排座位，既能展现主办者的尊贵待客礼仪，又能使每个宾客感到舒适和受尊重。

在实践中，还需要根据具体的场合和情况进行灵活调整，以达到最佳的效果。

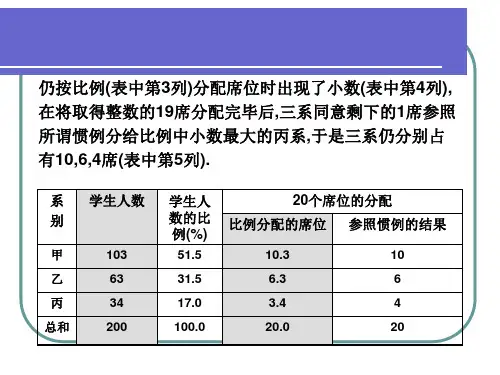
1 问题的假设与符号定义1.1问题的假设:1.席位是以整数计量的,并且为有限个,设为N个；2.每个系别有有限个人,席位是按各集体的人员多少来分配的；3．每个系别的每个人被选举都是等可能的；4．每个单位至少应该分配到一个名额,如果某个单位,一个名额也不应该分到的话,则应将其剔除在分配之外；5．在名额分配的过程中,分配是稳定的,不受任何其他因素所干扰.1.2符号的定义：n---－表示某系别的席位数（n1、n2、n3分别表示甲、乙、丙的席位数）；p----表示某系别的人数（p1、p2、p3分别表示甲、乙、丙的人数）；q-------表示总席位数；N-------表示总的席位人数.Q-------表示某单位的Ｑ值.3 问题的分析通常人们都是按照人数比例来进行分配的.当比例中有小数时,人们又按照惯例将多余的席位分给比例中小数最大者.我们能得出以下结论：公式：*pNqn/4 模型建立目标:建立公平的席位分配方案.4.1 引出绝对不公平值并给出相对不公平值:设A,B 两方人数分别为21,p p ；分别占有 1n 和2n 个席位,则两方每个席位所代表的人数分别为11n p 和 22n p. 我们称 2211n p n p -为.例：10,100,1202121====n n p p则22211=-n p n p ； 又 10,1000,10202121====n n p p 则22211=-n p n p 由上例可知,用绝对不公平程度作为衡量不公平的标准,并不合理,下面我们给出相对不公平值.①若 2211n pn p > 则称 11221222211-=-n p n p n p n p n p 为对A 的相对不公平值,记为 ),(21n n r A ；②若 2211n pn p < 则称 12112111122-=-n p n p n p n p n p 为对B 的相对不公平值 ,记为 ),(21n n r B .4.2给出相对公平的席位分配方案:如果，A B 两方分别占有1n 和2n 席,利用相对不公平值A r 和B r 讨论,当总席位增加1席时,应该分配给A 还是B.不妨设1122>p n p n ,即对A 不公平,当再分配一个席位时,有以下三种情况：I .当221>+11p pn n 时,这说明即使给A 增加1席,仍然对A 不公平,所以这一席显然应给A 方.II.当221<+11p pn n 时,这说明给A 增加1席,变为对B 不公平,此时对B 的相对不公平值为:21121211-1 ++=()(,)B p n r n n p n （3）III.当221>+11p pn n 时,这说明给B 增加1席,将对A 不公平,此时对A 的相对不公平值为:12122111-1 ++=()(,)A p n r n n p n （4）因为公平分配席位的原则是使相对不公平值尽可能小,所以如果121211+<+(,)(,)B A r n n r n n （5）则这1席给A 方,反之这1席给B 方.由(3)(4)可知,(5)等价于21222211<11++()()p p n n n n （6）不难证明上述的第I 种情况221>+11p pn n 也与(6)式等价,于是我们的结论是当(6)式成立时,增加的1席应给A 方,反之给B 方.若记:2, =1,21=+()i i i i p Q i n n则增加的1席给Q 值大的一方.4.3模型内部推广:上述方法可以推广到有m 方分配席位的情况.设第i 方人数为i p ,已占有i n 个席位.当总席位增加1席时,计算:2, =1,21=+()i i i i p Q i m n n ，，则增加的1席应分配给Q 值大的一方.这种席位分配的方法称为Q 值法.5 模型求解5.1下面用Q 值法讨论甲，乙，丙系分配20个席位的问题：先按照比例将整数部分的10席分配完毕n 1=10, n 2=6, n 3=3,.再用Q 值法分配第20席和第21席；分配第20席,计算得:Q1=96.4; Q2=94.5; Q3=96.3Q1最大,于是这1席应分给甲系.分配第21席,计算得:Q1=80.4;Q2=94.5;Q3=96.3;Q3最大,于是这1席应分给丙系.5.2现象分析及结果：根据Q值分配结果与假定情况一的现象,易得出:惯例分配总席位为21时,分配不公平,以至得出总席位数N增加一个,丙的席位数反而减少了一个的错误结论.6 模型评价●我们巧用绝对值,避免了分两种情况.从而简化了运算.●改进后的Q值法席位分配方案应用性推广,分配更公平.感谢您的支持与配合，我们会努力把内容做得更好！。

公平的席位分配问题席位分配在社会活动中经常遇到，如：人大代表或职工学生代表的名额分配和其他物质资料的分配等。

通常分配结果的公平与否以每个代表席位所代表的人数相等或接近来衡量。

符号设定：N ：总席位数 i n ：分配给第i 系席位数 （1,2,3i =分别为甲，乙，丙系）P ：总人数 i P ：第i 系数 （1,2,3i =分别为甲，乙，丙系）iQ ：第i 系Q 值 （1,2,3i =分别为甲，乙，丙系）Z ：目标函数方法一，比例分配法：即：某单位席位分配数 = 某单位总人数比例⨯总席位如果按上述公式参与分配的一些单位席位分配数出现小数,则先按席位分配数的整数分配席位,余下席位按所有参与席位分配单位中小数的大小依次分配之。

这种分配方法公平吗？由书上给出的案例，我们可以很清楚的知道该方法是有缺陷的，是不公平的。

方法二，Q 值法： 采用相对标准，定义席位分配的相对不公平标准公式：若2211n p n p >则称11221222211-=-n p np n p n p n p 为对A 的相对不公平值， 记为 ),(21n n r A ，若 2211n p n p < 则称 12112111122-=-n p n p n p n p n p 为对B 的相对不公平值 ，记为 ),(21n n r B 由定义有对某方的不公平值越小，某方在席位分配中越有利，因此可以用使不公平值尽量小的分配方案来减少分配中的不公平。

确定分配方案：使用不公平值的大小来确定分配方案，不妨设11n p >22n p ，即对单位A 不公平，再分配一个席位时，关于11n p ,22n p 的关系可能有 1. 111+n p >22n p ,说明此一席给A 后,对A 还不公平;2. 111+n p <22n p ,说明此一席给A 后,对B 还不公平,不公平值为1)1(11),1(212111112221-⋅+=++-=+n p p n n p n p n p n n r B3. 11n p >122+n p ,说明此一席给B 后,对A 不公平,不公平值为1)1(11)1,(121222221121-⋅+=++-=+n p p n n p n p n p n n r A4.11n p <122+n p ,不可能上面的分配方法在第1和第3种情况可以确定新席位的分配，但在第2种情况时不好确定新席位的分配。

1引言席位分配是一个非常有趣而重要的问题，它在政治学管理和对策论等领域具有广泛的应用价值。

处理的方法最早的有尾数最大法；然后是Q值法；1974年引入了席位分配问题的公理体系研究方法，并于1982年证明了同时满足五个所用的比例分配方法存在较大缺陷分配为１１，７，３名额。

其结果是，单位增加一个先进名额后，丙部门反而减少了一个名额。

公理的席位分配方法是不存在的。

后又有一些新的算法，如：新值法，最大熵法，0-1规划法，法，值法最小极差法和最大概率法等。

但有时我们遇到大会上遇到少数情况，某个部门的人数较少，按上述方法分不到席位。

本文讨论的是“少数原则”下解决席位分配问题，在解决“少数原则”情况下较方便。

正文问题：2.1问题：在一次民族代表会中，有一个民族的人口在该国占有极少比例，但大会必须考虑政策给一个席位的分配资格。

如果我们遇到同样的问题该如何处理呢？下面我们给出少数分配的原则，并讨论在该特殊问题下的分配问题。

少数原则：在席位分配中，各部门都有分配资格，当席位数n大于单位（部门）数i时至少分配一个席位。

2.2问题的一般表述一个单位由m个部门组成，其中第i个部门的人数为ai (1)i m≤≤，学校总人数为a。

如果该单位需要召开一个由n个代表参加的代表大会,且每个部门尽可能分配一个名额，组织者必须把n个席位尽可能公平的分配到个部门中去。

记每个部门最后应分配到的席位数为ni ，试问ni是多少？模型假设要解决这样的问题首先必须舍弃原有的公平分配体系，让更多的部门拥有席位分配的资格,建立相对公平的指标。

建立数量指标首先我们必须讨论总席位数n和总部门数i之间的关系1）当n〈i时，由于不可能保证每个部门都可一分到席位，这时我们尽可能的让更多的部门分到席位，可以由D’Hondt法（备注2）中的ai/1来做比较，由值的大小来决定分配与否（由值的大小由大到小按顺序来排，依次给予一个席位直到分配完）2）当n=i时，由少数原则，每个部门必须分到，刚好每个部门分配一个3）当n〉i时，每个部门至少可以分到一个名额。

宴请礼仪桌次排列和工作流程的原则(4)酒桌上的礼仪和说话技巧一、席位安排1、中餐宴会席位安排首先确定主人位。

主人位置一般面朝宴会厅的出入口，可纵观全局，也可安排在宴会厅的重点装饰的前面，让客人一进宴会厅就可看见主人。

副主人安排在正主人的对面，一般背向出入口面朝主人，方便主人安排副主人具体事宜。

主宾安排在主人的右侧，方便主人照顾主宾。

如果主宾偕夫人出席，可把主宾夫人安排在主宾的边上，也可把主宾夫人安排在主人夫人右侧的位置，除此之外也需要把身份地位相近的客人安排在一起，方便交流。

副主宾安排在副主人的右侧，方便副主人照顾副主宾。

主宾和副主宾右侧可安排翻译入席，方便翻译向主宾和副主宾翻译，其他位置可安排陪同。

2、西餐宴会席位安排女士优先(女主人：主位/男主人：第二主位)恭敬主宾(男女主宾分别紧靠女主人和男主人)以右为尊(男主宾坐于女主人右侧，女主宾坐于男主人右侧)距离定位(距主位近的位子高于距主位远的位子)面门为上(面对餐厅门的位子高于背对餐厅门的位子)交叉排列(男VS女，生人VS熟人)二、礼仪1、餐前礼仪适度修饰、准点到场、各就各位、认真交际、认真倾听。

2、餐时礼仪不违食俗、不坏吃相、不胡布菜、不乱挑菜、不玩餐具、不吸香烟、不清嗓子、不作修饰、不瞎走动。

三、点菜原则主陪方点菜、买单者点菜、领导点菜、尊者点菜。

商务套餐“吃特色、吃文化、吃环境”、“洋人吃土、土人吃洋”、“中餐菜系、西餐菜系”。

四、上菜顺序1、中餐上菜顺序冷盘—热菜—甜食—水果。

2、西餐上菜顺序开胃菜(坚果、小块的鱼或肉)、面包(鲜面包、烤面包)、汤(红汤、白汤、清汤)、主菜(冻子、泥子、鱼、肉)、蔬菜沙拉、点心(饼干、馅饼、三明治、通心粉、土豆片、烤土豆)、甜品(布丁、冰激凌)、水果、咖啡/茶。

五、餐具使用1、中式餐具使用忌敲筷子、忌横竖交叉摆放、忌插筷子、忌筷子打架、忌舞筷子。

2、西式餐具使用几道菜会放置几套刀叉，每套餐具使用一次，刀叉由外向内取用;切割食物时，双肘下沉，不可弄出声响;被切割的食物刚好适合一次入口;餐刀的刀口永远朝内。