北京九中2017-2018学年第二学期初二期中试卷

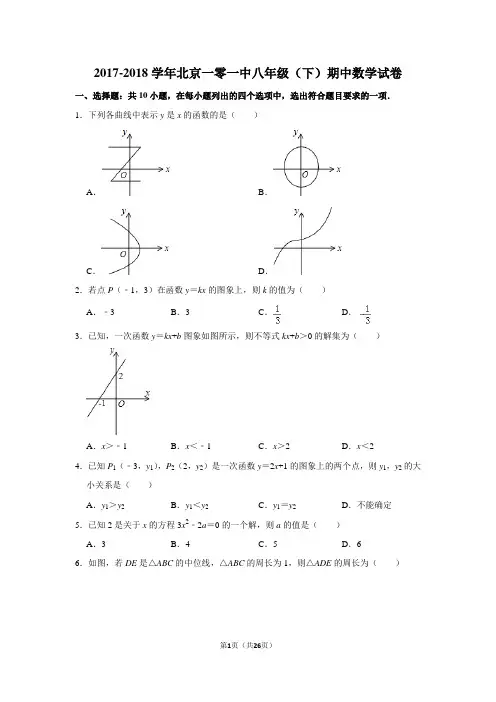
2017-2018学年北京一零一中八年级（下）期中数学试卷一、选择题：共10小题，在每小题列出的四个选项中，选出符合题目要求的一项．1．下列各曲线中表示y是x的函数的是（）A．B．C．D．2．若点P（﹣1，3）在函数y＝kx的图象上，则k的值为（）A．﹣3B．3C．D．3．已知，一次函数y＝kx+b图象如图所示，则不等式kx+b＞0的解集为（）A．x＞﹣1B．x＜﹣1C．x＞2D．x＜24．已知P1（﹣3，y1），P2（2，y2）是一次函数y＝2x+1的图象上的两个点，则y1，y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．不能确定5．已知2是关于x的方程3x2﹣2a＝0的一个解，则a的值是（）A．3B．4C．5D．66．如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（）A．1B．2C．D．7．若m＜﹣1，则一次函数y＝（m+1）x+m﹣1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限8．将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE＝30°，BE＝1，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则EC的长为（）A．B．2C．3D．29．如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE．下列结论：①∠CAD＝30°；②S▱ABCD＝AB•AC；③OB ＝AB；④OE＝BC，成立的个数有（）A．1个B．2个C．3个D．4个10．如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（）A．当x＝2时，y＝5B．矩形MNPQ的面积是20C．当x＝6时，y＝10D．当y＝时，x＝10二、填空题：共8小题．11．函数中自变量x的取值范围是．12．若一元二次方程x2﹣2x﹣m＝0无实根，则m的取值范围是．13．将函数y＝2x+1的图象向上平移2个单位，所得的函数图象的解析式为．14．如图，等边三角形EBC在正方形ABCD内，连接DE，则∠ADE＝度．15．在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3，若平行四边形ABCD的周长是16，则EC等于．16．根据如图所示的程序计算函数值，若输入x的值为，则输出的y值为．17．已知点A（2，﹣4），直线y＝﹣x﹣2与y轴交于点B，在x轴上存在一点P，使得P A+PB 的值最小，则点P的坐标为．18．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则点B3的坐标是；点B2018的坐标是．三、解答题共8小题．解答应写出文字说明、演算步骤或证明过程．19．（20分）解一元二次方程：（1）（2x+1）2＝9；（2）x2+4x﹣2＝0；（3）x2﹣6x+12＝0；（4）3x（2x+1）＝4x+2．20．（6分）已知，m是方程x2﹣x﹣3＝0的一个实数根，求代数式（m2﹣m）（m﹣+1）的值．21．（6分）已知直线l1的函数解析式为y＝x+1，且l1与x轴交于点A，直线l2经过点B，D，直线l1，l2交于点C．（1）求点A的坐标；（2）求直线l2的解析式；（3）求S△ABC的面积．22．（6分）如图，在△ABC中，AB＝AC，D是BC边的中点，点E，F分别在AD及其延长线上，且CE∥BF，连接BE，CF．（1）求证：四边形EBFC是菱形；（2）若BD＝4，BE＝5，求四边形EBFC的面积．23．（6分）已知：关于x的一元二次方程x2+（m+1）x+m＝0（1）求证：无论m为何值，方程总有两个实数根；（2）若x为方程的一个根，且满足0＜x＜3，求整数m的值．24．（7分）某游乐场普通门票价格40元/张，为了促销，新推出两种办卡方式：①白金卡售价200元/张，每次凭卡另收取20元；②钻石卡售价1000元/张，每次凭卡不再收费．促销期间普通门票正常出售，两种优惠卡不限次数，设去游乐场玩x次时，所需总费用为y元．（1）分别写出选择白金卡、普通门票消费时，y与x之间的函数关系式．（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点B，C的坐标．（3）请根据图象，直接写出选择哪种消费方式更合算．25．（7分）在平面直角坐标系xOy中，点P的坐标为（x1，y1），点Q的坐标为（x2，y2），且x1≠x2，y1≠y2．若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”，下图①为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，0），（1）若点B的坐标为（3，1），求点A，B的“相关矩形”的面积；（2）点C在直线x＝3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；（3）若点D的坐标为（4，2），将直线y＝2x+b平移，当它与点A，D的“相关矩形”没有公共点时，求出b的取值范围．26．（8分）在矩形ABCD中，AB＝1，BC＝2，点P是边BC上一点（点P不与点B，点C 重合），点C关于直线AP的对称点为C'．（1）如果C'落在线段AB的延长线上．①在图①中补全图形；②求线段BP的长度；（2）如图②，设直线AP与CC'的交点为M，求证：BM⊥DM．2017-2018学年北京一零一中八年级（下）期中数学试卷参考答案与试题解析一、选择题：共10小题，在每小题列出的四个选项中，选出符合题目要求的一项．1．下列各曲线中表示y是x的函数的是（）A．B．C．D．【分析】根据函数的意义求解即可求出答案．解：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，故D 正确．故选：D．【点评】主要考查了函数的定义．注意函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．2．若点P（﹣1，3）在函数y＝kx的图象上，则k的值为（）A．﹣3B．3C．D．【分析】利用待定系数法即可解决问题．解：∵点P（﹣1，3）在函数y＝kx的图象上，∴3＝﹣k，∴k＝﹣3，故选：A．【点评】本题考查一次函数图象上的点的坐标特征，待定系数法等知识，解题的关键是熟练掌握基本知识，属于中考基础题．3．已知，一次函数y＝kx+b图象如图所示，则不等式kx+b＞0的解集为（）A．x＞﹣1B．x＜﹣1C．x＞2D．x＜2【分析】不等式kx+b＞0的解集为直线y＝kx+b落在x轴上方的部分对应的x的取值范围．解：从图象得知一次函数y＝kx+b（k，b是常数，k≠0）的图象经过点（﹣1，0），并且函数值y随x的增大而增大，因而则不等式kx+b＞0的解集是x＞﹣1．故选：A．【点评】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y＝ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y＝kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．4．已知P1（﹣3，y1），P2（2，y2）是一次函数y＝2x+1的图象上的两个点，则y1，y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．不能确定【分析】先根据一次函数y＝2x+1中k＝2判断出函数的增减性，再根据﹣3＜2进行解答即可．解：∵一次函数y＝2x+1中k＝2＞0，∴此函数是增函数，∵﹣3＜2，∴y1＜y2．故选：B．【点评】本题开查的是一次函数图象上点的坐标特点及一次函数的性质，熟知一次函数的增减性是解答此题的关键．5．已知2是关于x的方程3x2﹣2a＝0的一个解，则a的值是（）A．3B．4C．5D．6【分析】利用一元二次方程解的定义，把x＝2代入方程3x2﹣2a＝0得12﹣2a＝0，然后解关于a的方程即可．解：把x＝2代入方程3x2﹣2a＝0得3×4﹣2a＝0，解得a＝6．故选：D．【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．6．如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（）A．1B．2C．D．【分析】根据三角形的中位线定理，DE是△ABC的中位线，△ABC的周长为1，得DE ＝，AD＝，AE＝而解得．解：∵DE是△ABC的中位线，△ABC的周长为1，∴DE＝，AD＝，AE＝∴△ADE的周长为．故选：C．【点评】根据三角形的中位线定理，得三角形ADE的边长是三角形ABC边长的．此题主要是根据三角形的中位线定理进行分析计算．7．若m＜﹣1，则一次函数y＝（m+1）x+m﹣1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据一次函数的性质，可得答案．解：当m＜﹣1时，m+1＜0，m﹣1＜2，一次函数y＝（m+1）x+m﹣1的图象不经过第一象限，故选：A．【点评】本题考查了一次函数的性质，利用一次函数的性质：y＝kx+b，k＜0，b＜0时，图象经过二三四象限是解题关键．8．将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE＝30°，BE＝1，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则EC的长为（）A．B．2C．3D．2【分析】根据直角三角形30°角所对的直角边等于斜边的一半求出AE＝2，再根据直角三角形两锐角互余求出∠AEB＝60°，根据翻折变换的性质可得∠AEB1＝∠AEB，根据两直线平行，内错角相等可得∠EAC1＝∠AEB1＝60°，然后判断出△AEC1是等边三角形，根据等边三角形的性质可得BC1＝AE，再根据翻折变换的性质可得EC＝BC1．解：∵矩形纸片ABCD，∠BAE＝30°，∴AE＝2BE＝2×1＝2，∠AEB＝90°﹣∠BAE＝90°﹣30°＝60°，∵AB沿AE翻折点B落在EC1边上的B1处，∴∠AEB1＝∠AEB＝60°，∵矩形对边AD∥BC，∴∠EAC1＝∠AEB1＝60°，∴△AEC1是等边三角形，∴BC1＝AE＝2，∵EC沿BF翻折点C落在AD边上的C1处，∴EC＝BC1＝2．故选：B．【点评】本题考查了翻折变换，直角三角形30°角所对的直角边等于斜边的一半，等边三角形的判定与性质，熟记翻折前后对应边相等，对应角相等是解题的关键．9．如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE．下列结论：①∠CAD＝30°；②S▱ABCD＝AB•AC；③OB ＝AB；④OE＝BC，成立的个数有（）A．1个B．2个C．3个D．4个【分析】由四边形ABCD是平行四边形，得到∠ABC＝∠ADC＝60°，∠BAD＝120°，根据AE平分∠BAD，得到∠BAE＝∠EAD＝60°推出△ABE是等边三角形，由于AB＝BC，得到AE＝BC，得到△ABC是直角三角形，于是得到∠CAD＝30°，故①正确；由于AC⊥AB，得到S▱ABCD＝AB•AC，故②正确，根据AB＝BC，OB＝BD，且BD ＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE＝AB，于是得到OE＝BC，故④正确．解：∵四边形ABCD是平行四边形，∴∠ABC＝∠ADC＝60°，∠BAD＝120°，∵AE平分∠BAD，∴∠BAE＝∠EAD＝60°∴△ABE是等边三角形，∴AE＝AB＝BE，∵AB＝BC，∴AE＝BC，∴∠BAC＝90°，∴∠CAD＝30°，故①正确；∵AC⊥AB，∴S▱ABCD＝AB•AC，故②正确，∵AB＝BC，OB＝BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE＝BE，CO＝OA，∴OE＝AB，∴OE＝BC，故④正确．故选：C．【点评】本题考查了平行四边形的性质，等边三角形的判定和性质，直角三角形的性质，平行四边形的面积公式，熟练掌握性质定理和判定定理是解题的关键．10．如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（）A．当x＝2时，y＝5B．矩形MNPQ的面积是20C．当x＝6时，y＝10D．当y＝时，x＝10【分析】根据图2可知：PN＝4，PQ＝5，然后根据三角形的面积公式求解即可．解；由图2可知：PN＝4，PQ＝5．A、当x＝2时，y＝＝＝5，故A正确，与要求不符；B、矩形的面积＝MN•PN＝4×5＝20，故B正确，与要求不符；C、当x＝6时，点R在QP上，y＝＝10，故C正确，与要求不符；D、当y＝时，x＝3或x＝10，故错误，与要求相符．故选：D．【点评】本题主要考查的是动点问题的函数图象，根据图2求矩形的长和宽是解题的关键．二、填空题：共8小题．11．函数中自变量x的取值范围是x≥﹣5．【分析】根据二次根式的性质，被开方数大于等于0可知：x+5≥0，解不等式求x的范围．解：根据题意得：x+5≥0，解得x≥﹣5．【点评】本题考查的是函数自变量取值范围的求法．函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．12．若一元二次方程x2﹣2x﹣m＝0无实根，则m的取值范围是m＜﹣1．【分析】根据方程的系数结合根的判别式△＜0，即可得出关于m的一元一次不等式，解之即可得出m的取值范围．解：∵关于x的一元二次方程x2﹣2x﹣m＝0无实根，∴△＝（﹣2）2﹣4×1×（﹣m）＜0，解得：m＜﹣1，故答案为：m＜﹣1．【点评】本题考查了根的判别式，牢记“当△＜0时，方程没有实数根”是解题的关键．13．将函数y＝2x+1的图象向上平移2个单位，所得的函数图象的解析式为y＝2x+3．【分析】根据一次函数图象平移时“上加、下减”的原则进行解答即可．解：由“上加下减”的原则可知，将函数y＝2x+1的图象向上平移2个单位所得函数的解析式为y＝2x+3．故答案为：y＝2x+3．【点评】本题考查的是一次函数的图象与几何变换，熟知“上加下减”的原则是解答此题的关键．14．如图，等边三角形EBC在正方形ABCD内，连接DE，则∠ADE＝15度．【分析】正方形ABCD中，BC＝CD，等边△BCE中，CE＝BC，即可得CD＝CE，然后依据等腰三角形的性质和三角形的内角和定理求解即可．解：正方形ABCD中，BC＝CD，等边△BCE中，CE＝BC，∴CD＝CE，∵∠DCE＝90°﹣60°＝30°，∴∠CDE＝＝75°．∴∠ADE＝90°﹣75°＝15°．故答案为：15°．【点评】本题考查了正方形各边长相等、各内角为直角的性质，考查了等边三角形各内角为60°、各边长相等的性质，考查了三角形内角和为180°的性质，本题中求CD＝CE是解题的关键．15．在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3，若平行四边形ABCD的周长是16，则EC等于2．【分析】由平行四边形的性质和已知条件证出∠BAE＝∠BEA，证出AB＝BE＝3；求出AB+BC＝8，得出BC＝5，即可得出EC的长．解：∵四边形ABCD是平行四边形，∴AD∥BC，AB＝CD，AD＝BC，∴∠AEB＝∠DAE，∵平行四边形ABCD的周长是16，∴AB+BC＝8，∵AE是∠BAD的平分线，∴∠BAE＝∠DAE，∴∠BAE＝∠AEB，∴AB＝BE＝3，∴BC＝5，∴EC＝BC﹣BE＝5﹣3＝2；故答案为：2．【点评】此题考查了平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，证出AB＝BE是解决问题的关键．16．根据如图所示的程序计算函数值，若输入x的值为，则输出的y值为．【分析】根据x的值选择相应的函数关系式，计算即可得解．解：x＝时，y＝﹣x+2＝﹣+2＝．故答案为：．【点评】本题考查了函数值，理解图表信息准确选择相应的函数关系式是解题的关键．17．已知点A（2，﹣4），直线y＝﹣x﹣2与y轴交于点B，在x轴上存在一点P，使得P A+PB 的值最小，则点P的坐标为．【分析】作点B关于x轴的对称点B′，连接AB′，交x轴于P，连接PB，此时P A+PB 的值最小．求出直线AB′的解析式即可解决问题；解：作点B关于x轴的对称点B′，连接AB′，交x轴于P，连接PB，此时P A+PB的值最小．设直线AB′的解析式为y＝kx+b，把A（2，﹣4），B′（0，2）代入得到，解得，∴直线AB′的解析式为y＝﹣3x+2，令y＝0，得到x＝，∴P（，0），故答案为（，0）．【点评】本题考查一次函数图象上的点的特征，轴对称最短问题等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．18．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则点B3的坐标是（7，4）；点B2018的坐标是（22018﹣1，22017）．【分析】首先求得直线的解析式，分别求得B1，B2，B3…的坐标，可以得到一定的规律，据此即可求解．解：∵B1的坐标为（1，1），点B2的坐标为（3，2），∴正方形A1B1C1O1边长为1，正方形A2B2C2C1边长为2，∴A1的坐标是（0，1），A2的坐标是：（1，2），代入y＝kx+b得，解得：．则直线的解析式是：y＝x+1．∵点B1的坐标为（1，1），点B2的坐标为（3，2），∴点B3的坐标为（7，4），…，∴Bn的横坐标是：2n﹣1，纵坐标是：2n﹣1．B n的坐标是（2n﹣1，2n﹣1）∴B2018的坐标是（22018﹣1，22017）．故答案为：（22018﹣1，22017）．【点评】此题考查的是一次函数图象上点的坐标特点及用待定系数法求函数解析式和坐标的变化规律，正确得到点的坐标的规律是解题的关键．三、解答题共8小题．解答应写出文字说明、演算步骤或证明过程．19．（20分）解一元二次方程：（1）（2x+1）2＝9；（2）x2+4x﹣2＝0；（3）x2﹣6x+12＝0；（4）3x（2x+1）＝4x+2．【分析】（1）利用直接开平方法解方程；（2）利用配方法解方程；（3）根据判别式的意义判断方程没有实数解；（4）先移项得到3x（2x+1）﹣2（2x+1）＝0，然后利用因式分解法解方程．解：（1）2x+1＝±3，所以x1＝1，x2＝﹣2；（2）x2+4x＝2，x2+4x+4＝6，（x+2）2＝6，x+2＝±，所以x1＝﹣2+，x2＝﹣2﹣；（3）△＝（﹣6）2﹣4×1×12＜0，所以方程没有实数解；（4）3x（2x+1）﹣2（2x+1）＝0，（2x+1）（3x﹣2）＝0，2x+1＝0或3x﹣2＝0，所以x1＝﹣，x2＝．【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了配方法解方程．20．（6分）已知，m是方程x2﹣x﹣3＝0的一个实数根，求代数式（m2﹣m）（m﹣+1）的值．【分析】根据一元二次方程解的定义得到m2﹣m﹣3＝0，则m2﹣2m＝3，把m2﹣m﹣3＝0两边都除以m得m﹣1﹣＝0，则m﹣＝1，然后利用整体代入的方法计算代数式的值．解：∵m是方程x2﹣x﹣3＝0的一个实数根，∴m2﹣m﹣3＝0，∴m2﹣2m＝3，m﹣1﹣＝0，即m﹣＝1，∴（m2﹣m）（m﹣+1）＝3×（1+1）＝6．【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．21．（6分）已知直线l1的函数解析式为y＝x+1，且l1与x轴交于点A，直线l2经过点B，D，直线l1，l2交于点C．（1）求点A的坐标；（2）求直线l2的解析式；（3）求S△ABC的面积．【分析】（1）在y＝x+1中，令y＝0，则x＝﹣1，即可得到点A的坐标；（2）利用待定系数法，即可得到直线l2的解析式；（3）解方程组求得C（，），即可得到S△ABC的面积．解：（1）在y＝x+1中，令y＝0，则x＝﹣1，∴A（﹣1，0）；（2）设直线l2的解析式为y＝kx+b，则，解得，∴y＝﹣2x+6；（3）解方程组，可得，∴C（，），∴S△ABC＝×（3+1）×＝．【点评】本题考查了两直线相交的问题，直线与坐标轴的交点的求解，待定系数法求一次函数解析式，要注意两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．22．（6分）如图，在△ABC中，AB＝AC，D是BC边的中点，点E，F分别在AD及其延长线上，且CE∥BF，连接BE，CF．（1）求证：四边形EBFC是菱形；（2）若BD＝4，BE＝5，求四边形EBFC的面积．【分析】（1）由D是BC边的中点，CE∥BF，利用ASA易证得△BDF≌△CDE，即可得CE＝BF，然后由一组对边平行且相等的四边形是平行四边形，证得四边形BFCE是平行四边形；由AB＝AC，D是BC边的中点，即可得AD⊥BC，又由四边形BFCE是平行四边形，根据对角线互相垂直的平行四边形是菱形，即可证得四边形BFCE是菱形．（2）求出BC、EF即可解决问题；（1）证明：∵D是BC边的中点，∴BD＝CD，∵CE∥BF，∴∠DBF＝∠ECD，在△BDF和△CDE中，，∴△BDF≌△CDE（ASA），∴CE＝BF，又∵CE∥BF，∴四边形BFCE是平行四边形；∵AB＝AC，D是BC的中点，∴AD⊥BC，又∵四边形BFCE是平行四边形，∴四边形BFCE是菱形．（2）解：在Rt△BDE中，BE＝5，BD＝4，∴DE＝＝3，∵四边形BECF是菱形，∴EF＝2DE＝6，BC＝2BD＝8，∴菱形BECF的面积＝×6×8＝24．【点评】此题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的性质以及菱形的判定．此题难度适中，注意掌握数形结合思想的应用．23．（6分）已知：关于x的一元二次方程x2+（m+1）x+m＝0（1）求证：无论m为何值，方程总有两个实数根；（2）若x为方程的一个根，且满足0＜x＜3，求整数m的值．【分析】（1）根据根的判别式求出△的值，再进行判断即可；（2）利用因式分解法求得x1＝﹣1、x2＝﹣m，利用0＜x＜3得出0＜﹣m＜3，据此求得m的取值范围，从而得出答案．解：（1）∵△＝（m+1）2﹣4×1×m＝m2+2m+1﹣4m＝m2﹣2m+1＝（m﹣1）2≥0，∴无论m为何值，方程总有两个实数根；（2）∵（x+1）（x+m）＝0，∴x+1＝0或x+m＝0，即x1＝﹣1、x2＝﹣m，∵0＜x＜3，∴0＜﹣m＜3，解得：﹣3＜m＜0，则整数m的值为﹣2、﹣1．【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式△＝b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△＝0，方程有两个相等的实数根；当△＜0，方程没有实数根．24．（7分）某游乐场普通门票价格40元/张，为了促销，新推出两种办卡方式：①白金卡售价200元/张，每次凭卡另收取20元；②钻石卡售价1000元/张，每次凭卡不再收费．促销期间普通门票正常出售，两种优惠卡不限次数，设去游乐场玩x次时，所需总费用为y元．（1）分别写出选择白金卡、普通门票消费时，y与x之间的函数关系式．（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点B，C的坐标．（3）请根据图象，直接写出选择哪种消费方式更合算．【分析】（1）根据白金卡售价200元/张，每次凭卡另收取20元，普通门票正常出售，设消费x次时，分别得出所需总费用为y与x之间的关系式即可；（2）利用函数交点坐标求法分别得出即可；（3）根据图象解答即可．解：（1）根据题意可得：白金卡：y＝20x+200．门票：y＝40x（2）将y＝40x代入y＝200+20x，得40x＝200+20x，解得x＝10，把x＝10代入y＝40x，得y＝400，所以B（10，400），把y＝1000代入y＝200+20x，得1000＝200+20x，解得x＝40，所以C（40，1000）；（3）当0＜x＜10时，选普通门票；当x＝10时，选普通门票和白金卡；当10＜x＜40时，选白金卡；当x＝40时，选白金卡和钻石卡；当x＞40时，选钻石卡【点评】本题考查了一次函数的应用，两函数交点坐标的求法．进行分类讨论是解题的关键．25．（7分）在平面直角坐标系xOy中，点P的坐标为（x1，y1），点Q的坐标为（x2，y2），且x1≠x2，y1≠y2．若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”，下图①为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，0），（1）若点B的坐标为（3，1），求点A，B的“相关矩形”的面积；（2）点C在直线x＝3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；（3）若点D的坐标为（4，2），将直线y＝2x+b平移，当它与点A，D的“相关矩形”没有公共点时，求出b的取值范围．【分析】（1）由相关矩形的定义可知：要求A与B的相关矩形面积，则AB必为对角线，利用A、B两点的坐标即可求出该矩形的底与高的长度，进而可求出该矩形的面积；（2）由定义可知，AC必为正方形的对角线，所以AC与x轴的夹角必为45，设直线AC 的解析式为；y＝kx+b，由此可知k＝±1，再（1，0）代入y＝kx+b，即可求出b的值；（3）分别把点A、D点的坐标代入y＝2x+b±2，求得b的数值即可．解：（1）∵A（1，0），B（3，1）由定义可知：点A，B的“相关矩形”的底与高分别为2和1，∴点A，B的“相关矩形”的面积为2×1＝2；（2）由定义可知：AC是点A，C的“相关矩形”的对角线，又∵点A，C的“相关矩形”为正方形∴直线AC与x轴的夹角为45°，设直线AC的解析为：y＝x+m或y＝﹣x+n把（1，0）分别y＝x+m，∴m＝﹣1，∴直线AC的解析为：y＝x﹣1，把（1，0）代入y＝﹣x+n，∴n＝1，∴y＝﹣x+1，综上所述，若点A，C的“相关矩形”为正方形，直线AC的表达式为y＝x﹣1或y＝﹣x+1；（3）把A（1，0），D（4，2）分别代入y＝2x+b±2，得出b＝0，或b＝﹣8，∴b＞0或b＜﹣8【点评】此题是一次函数综合题，主要考查了待定系数法，新定义的理解和应用，矩形的面积公式，找出分界点是解本题的关键．26．（8分）在矩形ABCD中，AB＝1，BC＝2，点P是边BC上一点（点P不与点B，点C 重合），点C关于直线AP的对称点为C'．（1）如果C'落在线段AB的延长线上．①在图①中补全图形；②求线段BP的长度；（2）如图②，设直线AP与CC'的交点为M，求证：BM⊥DM．【分析】（1）①根据要求画出图形即可；②连接AC，作PH⊥AC于H．则△APB≌△APH，同侧AB＝AH＝1，PB＝PH，设PB＝PH＝x，利用勾股定理构建方程即可；（2）如图②中，连接AC、BD交于点O．连接OM．只要证明A、B、M、C、D五点共圆，即可解决问题；解：（1）①如图①所示：②连接AC，作PH⊥AC于H．则△APB≌△APH，∴AB＝AH＝1，PB＝PH，设PB＝PH＝x，∵AC＝＝，∴CH＝﹣1，在Rt△PCH中，x2+（﹣1）2＝（2﹣x）2，解得x＝，∴PB＝．（2）如图②中，连接AC、BD交于点O．连接OM．∵四边形ABCD是矩形，∴OA＝OB＝OC＝OD，∵∠AMC＝90°，∴OM＝OA＝OB＝OC＝OD，∴A、B、M、C、D五点共圆，∵BD是直径，∴∠BMD＝90°，∴BM⊥DM．【点评】本题考查作图﹣轴对称变换，矩形的性质，五点共圆等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用辅助圆解决问题，属于中考常考题型．。

2017-2018学年第二学期九中教育联盟期中质量监测八年级物理试卷一、选择题（每题2分，共30分）1.关于力的作用,下列说法正确的是A.船桨向后划水,船会向前运动，说明物体间力的作用是相互的B.打篮球接球时,球对手有作用力,手对球没有作用力C.用拳头打棉花包,拳头不感到疼痛,说明棉花包对拳头没有力的作用D.鸡蛋碰石头,鸡蛋破了,说明鸡蛋对石头的力小于石头对鸡蛋的力2．宇宙飞船上的一颗螺丝进入太空后与在地面时相比，发生显著变化的是螺丝的A．长度B．质量C．密度D．重力3.下列实例中，为了增大摩擦的是A．拉杆旅行箱底部装有轮子B．向自行车的转轴处加润滑油C．骑自行车刹车时用力捏闸D．在气垫船底和水之间形成一层空气垫4.下列描述中达到了增大压强的是A．大型载重汽车有许多轮子B．缝衣服的针做的很光滑C．书包的肩带做的很宽D．菜刀的刃磨得很薄5.下列现象中，不属于利用惯性的是A．用手拍打衣服上的灰尘B．锤头松了，将锤柄在地上撞几下C．运动员采用助跑跳远D．驾驶汽车要系安全带6.如图所示的实例中,不是利用连通器原理的是A.活寒式抽水机B.锅炉水位计C.茶壶D.船闸7.如图装置中,不是利用大气压的是A.用注射器注射药液B.吸管吸饮料C.吸盘D.吸尘器吸尘8．一只空木箱，静止放在水平地面上，下列说法中正确的是A．木箱所受的重力和木箱对地面的压力为一对平衡力B．木箱所受的重力和地面对木箱的支持力为一对平衡力C．木箱对地面的压力和地面对木箱的支持力为一对平衡力D．木箱所受的重力和木箱对地球的吸引力为一对平衡力9. 如图所示，用F=150N的水平力把重50N的物体压在竖直墙壁上，当物体静止时受摩擦力的大小为A.0NB.50NC.150ND.200N10．如图甲所示，一块长木板放在水平桌面上．现用一水平力F1向右匀速推木板，使其一部分露出桌面如图乙所示，在推木板的过程中，木板对桌面的压力F、压强p和摩擦力f的变化情况是A．F、p不变，f变大B．F、f不变，p变小C．F变小，p、f变大D．F、f不变，p变大11．如图所示,以下四个关于“气体压强与流流速关系”的现象中压强p1＜p2的是A B C D12.物理兴趣小组的同学对图所示的现象进行讨论，其中错误的是A．图（甲）帕斯卡裂桶实验说明液体的压强与液体的深度有关B．图（乙）对沸腾的水停止加热，抽气减压，水再次沸腾，说明气压减小沸点降低C．图（丙）用吸管喝饮料时，瓶里的饮料是被嘴的吸力吸上来的D．图（丁）洗手盘下方弯管的水密封利用了连通器原理13．如图所示，底面积相同的甲、乙两容器中装有质量和深度均相同的不同液体，则甲、乙两容器中液体的密度ρ甲和ρ乙的关系以及液体对容器底部的压力F甲和F乙的关系，正确的是A.ρ甲=ρ乙，F甲＜F乙B.ρ甲＞ρ乙，F甲=F乙C.ρ甲＜ρ乙，F甲＞F乙D.ρ甲＞ρ乙，F甲＞F乙14.一个铜球浸没在水中受到的浮力为F 1 ，浸没在煤油中受到的浮力为F 2 ，比较铜球两次受到的浮力，则A.F1 ＞F2B.F 1 =F 2C.F 1 ＜F 2D.条件不足，无法确定15. 甲、乙、丙三个体积相同的球，分别放入三杯水中，如下图所示，它受浮力大小的情况应是A.F甲＞F乙＞F丙B. F甲=F乙＞F丙C. F甲＜F乙=F丙D. F甲＜F乙＜F丙二、填空题（每空1分，共16分）16．坐在小船中的人用力向前推动另一艘小船时，发现自己坐的船向后退，说明力可以改变物体的，还可说明物体间．17．如图是我国著名的花样滑冰运动员申雪、赵宏博在比赛中的精彩瞬间。

2016~2017学年北京石景山区北京九中初二上学期期中语文试卷一、基础与运用1.【答案】（1）D（2）B（3）A（4）C（5）D2.【答案】B二、默写3.【答案】（1）日暮乡关何处是（2）有良田美池桑竹之属（3）1．苔痕上阶绿2．草色入帘青（4）1．会当凌绝顶2．一览众山小三、名著阅读4.【答案】①；③5.【答案】1．拥有一辆自己的洋车2．好占便宜、穷困潦倒、麻木不仁、自私狡猾、自暴自弃3．为了置办虎妞的丧事，祥子又卖掉了车四、文言文阅读6.【答案】（1）1．“诎”同“屈”弯曲2．赠送3．表示约数，左右，上下4．全，都（2）①他们的互相靠近的两膝，各自隐藏在卷子下面的衣褶里。

②即使是狡猾（聪明）的人也不能够分辨它是真是假。

（3）灵怪（或“奇巧”）；做了一个长约一寸、能自动行走的木人。

五、现代文阅读7.【答案】（1）①听牛汉演讲② 具有强悍野性、豪迈激情③超越生命的极限，创造生命的奇迹和辉煌④聆听牛汉严肃的教导（2）（1）省略号表现了“我”难以言表的颓唐、苦闷的心情，同时也表现了“我”在牛汉面前不知如何说起的难堪。

（2）感叹号表现了牛汉对追寻有意义人生的坚定、执着的态度，同时也表现了他对“我”的劝诫和鼓励。

（3）画线句形象地写出了牛汉朗诵诗歌时的兴奋快乐心情，表现出他在经历了那么多苦难之后，依然保有对诗歌、对生命质朴赤诚的热爱。

（4）讨论题来自：阴冷的雨季，他佝偻着高大的身躯，拉着装载千斤以上的板车，艰难地挣扎在崎岖颠簸的山路上，嶙峋的瘦骨如蒙古骑士的一张弓，负担起压在身上的全部苦难。

你的讨论题：作者这句话起到了怎样的表达效果？或第四段中作者是如何将牛汉“创造了生命的奇迹和辉煌”写得生动形象的？8.【答案】（1）1．北京地名变化的情况2．导致北京地名变化的因素3．北京地名雅化的主要途径（2）“棺材胡同”“臭水街”改为“光彩胡同”“秀水街”，通过谐音将忌讳字改为典雅文秀的字眼，表现出老百姓对美好生活的向往，这与寻常人家的自尊心及图吉利的心态有关。

2017-2018学年北京十一学校第二学期期中数学练习初二年级一．选择题1. 下列线段能构成直角三角形的是( )A . 5, 12, 13B . 1, 3,5C . 3, 7, 5D . 2,2,3 2.关于函数 y =−3x ，判断正确的是 ( )A . 图象经过点 (0,0) 和点 (−1,−3)B . 图象经过第一、三象限C . y 随 x 的增大而减小D . 图象是一条射线3. △ABC 中, D 、E 、F 分别为AB 、AC 、BC 的中点, 若△DEF 的周长为6, 则△ABC 周长为( ) A . 3 B . 6 C . 12 D . 244.如图所示□ABCD , 再添加下列某一个条件, 不能．．判定□ABCD 是矩形的是( ) A . AC =BDB . AB ⊥BCC . ∠ABC =∠BCD D . ∠1=∠25.一次函数y = kx +b 的图象不经过第二象限, 则符合条件的k , b 的取值范围是( ) A . k < 0, b ≥0 B . k >0, b ≤0C . k < 0, b < 0D .k > 0, b > 06.如图，反映的过程是：小强从家跑步去体育馆，在那里锻炼了一段时间后，又去早餐店吃早餐，然后散步走回家，其中x 表示时间，y 表示小强离家的距离．根据图象提供的信息，以下四个说法正确的是( ) A . 小强在体育馆锻炼了 15 分钟B . 体育馆离早餐店 4 千米C . 体育馆离小强家 1.5 千米D . 小强从早餐店回到家用 50 分钟 7.正方形具有而矩形没有的性质是( ) A . 对角线互相平分B . 对边相等C . 对角线相等D . 每条对角线平分一组对角8.顺次连接对角线相等的四边形的各边中点，所形成的四边形是( ) A . 平行四边形B . 菱形C . 矩形D . 正方形9. 如图，两个一次函数图象的交点坐标为 (2,4)，则关于 x ，y 的方程组 {y =k 1x +b 1,y =k 2x +b 2 的解为 ( )A . {x =2,y =4B . {x =4,y =2C . {x =−4,y =0D . {x =3,y =010. 汽车由北京驶往相距 120 千米的天津，它的平均速度是 30 千米/时，则汽车距天津的路程 S （千米）与行驶时间 t （小时）的函数关系式及自变量的取值范围是( )A . S =120−30t (0≤t ≤4)B . S =30t (0≤t ≤4)C . S =120−30t (t >0)D . S =30t (t =4)二．填空题、11. 函数y 1x -x 的取值范围是__________12. 若 y =(m −2)x 3−∣m∣+2n −5 是正比例函数，则 m =_____，n =________ 13.如图，在平行四边形 ABCD 中，AE ⊥CD 于点 E ，∠B =65∘，则 ∠DAE 等于 ．14.若将直线 y =3x +2 沿 y 轴向下平移 5 个单位长度，则平移后的直线与 y 轴的交点坐标为 . 15. 如图，在 Rt △ABC 中，∠ACB =90∘，D ，E ，F 分别是 AB ，BC ，CA 的中点，若 CD =6 cm ，则 EF = cm ．16. P 1(−2,y 1)，P 2(3,y 2) 是一次函数 y =−2x +3 图象上的两个点，则 y 1，y 2 的大小关系是____ 17. 如图, 在周长为20cm 的□ABCD 中, AB ≠AD , AC 、BD 相交于点O , OE ⊥BD 交AD 于E , 则△ABE 的周长为________第17题 第18题18. 如图，正方形 ABCD 和正方形 CEFG 中，点 D 在 CG 上，BC =1，CE =3，点 H 是 AF 的中点，那么 CH 的长是 ___________ ．初二年级 数学学科 答题纸一．选择题 题目 1 2 3 4 5 6 7 8 9 10 答案二．填空题11.____________ 12.m =______,n =________. 13.______________ 14.____________ 15._____________ 16._______________ 17.______________ 18.______________ACOEB三．解答题19.已知一次函数的图象经过点A（-3，2）、B（1，6），求此函数的解析式．20.已知y1=−x+3，y2=3x−4.当x取何值时，y1<y2; 当x取何值时，y1>y2?21. 如图，已知□ABCD和□EBFD，求证：AE=CF．22. 作出．．象．并利用图像回答问题：．．y=．2．x-．6．的图（1）图象与坐标轴围成的三角形面积为。

2017-2018学年北京市昌平区临川育人学校八年级（下）期中物理试卷一、单项选择题下列各小题均有四个选项，其中只有一个符合题意．（每小题2分，共30分）1．（2分）力的单位是（）A．牛顿B．帕斯卡C．千克D．米2．（2分）如图所示的四个实例中，为了增大压强的是（）A．坦克有宽大的履带B．书包背带做得较宽C．斧刃磨得很锐利D．在铁轨下面铺枕木3．（2分）如图所示的四个实例中，目的是为了减小压强的是（）A．冰鞋上装有冰刀B．飞镖的箭头很尖C．载重车装有许多车轮D．压路机的碾子质量很大4．（2分）如图所示的实例中，不属于连通器应用的是（）A．茶壶B．锅炉水位计C．船闸D．潜水艇5．（2分）如图所示的实例中，目的是为了减小摩擦的是（）A．鞋底下的花纹B．车轮的防滑链C．瓶盖上的纹线D．旱冰鞋的滚轮6．（2分）下列措施中哪个是为了增大摩擦（）A．在机械内部的转动部分增加滚珠轴承B．在自行车的把手上做出凸凹花纹C．给自行车的轴加润滑油D．气垫船行驶时，在船体与水之间形成高压空气层7．（2分）下列关于力的说法，错误的是（）A．力是物体对物体的作用，力不能脱离物体而单独存在B．物体间力的作用是相互的，施力物体同时一定是受力物体C．力是维持物体运动状态的原因D．力是改变物体运动状态的原因8．（2分）下列数据比较符合实际情况的是（）A．乒乓球的质量约为2kgB．人体的正常体温为36.5℃左右C．教室地面到天花板的高度约为1.5mD．人脉搏跳动一次需要的时间约为2s9．（2分）下列估测数据，最接近实际情况的是（）A．你使用的物理课本的宽度约为16cmB．教学楼每一层的高度是20mC．一张课桌高度1.4mD．小明的鞋长度为43cm10．（2分）知识价值的体现之一是它可以帮我们避免事故发生。

在以下宣传语中与摩擦力知识有关的是（）A．车未停稳，请勿下车B．在地铁车站站台上候车的人必须站在安全线以外C．雨天路滑，小心驾驶D．为了您的安全，请系好安全带11．（2分）运动员投掷的标枪在出手后，仍能继续向前飞行，这是因为（）A．标枪受到向前的力B．标枪受到惯性C．标枪有惯性D．标枪不受力12．（2分）放在水平桌面上静止不动的电视机，受到彼此平衡的两个力是（）A．电视机受到的重力和桌面对电视机的支持力B．电视机受到的重力和电视机对桌面的压力C．桌面对电视机的支持力和电视机对桌面的压力D．桌面受到的重力和电视机对桌面的压力13．（2分）对静止在水平桌面上的书来说，下列各组力中属于相互作用力的是（）A．书的重力和书对桌面的压力B．书的重力和桌面对书的支持力C．书的重力和桌子的重力D．书对桌面的压力和桌面对书的支持力14．（2分）小静同学在乘坐校车上学途中，观察到了一些现象，并依据所学的物理知识做出了自己的判断，其中正确的是（）A．向窗外看时感觉到路边树木向后退，是以地面为参照物B．看到车上窗帘往外飘，是因为车外空气流速大压强小C．刹车时车能很快停下来，主要是因为车具有惯性D．刹车时感觉自己身体向前倾，是因为受到推力的作用15．（2分）小刚买了一瓶果酱，可是怎么也拧不开玻璃瓶上的铁皮盖。

2017-2018学年第二学期九中教育联盟期中质量监测（八）年级（数学）学科试卷时间：90分钟 分值：100分 命题人： 审题人：一、选择题（本大题共8小题，每小题2分，共16分）1．在平面直角坐标系中，点(2，－1)在（ ）.（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限2．如图所示，下列哪组条件能判别四边形ABCD 是平行四边形？（ ）.（A ）AB ∥CD ，AD ＝BC （B ）AB ＝AD ，CB ＝CD（C ）∠A ＝∠B ，∠C ＝∠D （D ）AB ＝CD ，AD ＝BC3．函数3＋＝x x y 中，自变量x 的取值范围是（ ）. （A ）3＞－x （B ）3＜－x （C ）x ≠-3 （D ）x ≠ 34．如图所示，在平行四边形ABCD 中，对角线AC 与 BD 相交于点O ，已知△BOC 与△AOB 的周长之差为3，平行四边形ABCD 的周长为26，则BC 的长度为（ ）.（A ）5 （B ）6 （C ）7 （D ）85．如图所示，已知点E 是矩形ABCD 的边BC 的中点，AB ＝6，若AE ⊥DE ，则矩形的周长是（ ）.（A ）24 （B ）30 （C ）36 （D ）42（第2题） （第4题） （第5题）6．小亮用作图象的方法解二元一次方程组时，在同一直角坐标系内作出了相应的两个一次函数的图象a 、b （如图），他解的这个方程组是（ ）.7．函数 y ＝x m 与y ＝mx －m （m ≠0）在同一平面直角坐标系中的大致图象是（ ）.8． 如图，函数y ＝－x 与函数y ＝－4x的图象相交于A 、B 两点，过A 、B 两点分别作y 轴的垂线，垂足分别为点C 、D ，则四边形ACBD 的面积为（ ）.（A ）2 （B ）4 （C ）6 （D ）8二、填空题（本大题共7小题，每小题3分，共21分）9 ．点P （-2，3）关于y 轴对称的点的坐标是 ．10．将直线13y x =-向下平移3个单位所得直线的解析式为 ． （第8题） 11．直线5y kx =+经过点(2,1)--，则k = ．12．如图所示，在▱ABCD中，对角线AC 、BD 相交于O ，AC+BD=10，BC=3，则△AOD的周长为________.（第12题）13. 如图所示，矩形ABCD 中，AB ＝2，BC ＝5，MN ∥AB 交AD 于点M ，交BC 于点N ，在MN 上任取两点P ，Q ，那么图中阴影部分的面积是________．14．如图所示，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AB=4㎝，则矩形对角线的长为．15．小明早晨从家骑车到学校，先上坡后下坡，行程情况如图，若返回时上、下坡的速度保持不变，那么小明从学校骑车回家用的时间是____分钟．/分（第13题）（第14题）（第15题）三、解答题（本大题共8小题，共63分）16．（6分）如图所示，已知在四边形ABCD中，AD＝BC，∠D＝∠DCE.求证：四边形ABCD是平行四边形．（第1617．（6分）已知一次函数的图象经过点（3，5）与（－4，－9）．（1）求这个函数的解析式.（2）判断点A（1，－1）是否在这个函数的图象上.18．（6分）如图：在平行四边形ABCD中，∠BAD的平分线AE交DC于E，若∠DAE=25°，求∠C、∠B的度数．（第18题）19．（8分）在△ABC中，AB＝AC，AD平分∠BAC，四边形CAED是平行四边形，DE交AB于点F，连结BE.求证：四边形AEBD是矩形.（第19题）20. （8分）如图，直线分别交x轴、y轴于点A、C，点P是直线AC与双曲线在第一象限内的交点，PB⊥x轴，垂足为点B，且OB=2，PB=4．（1）求k的值.（2）分别求A，C两点坐标.（3）在第一象限内，当x为何范围时一次函数的值大于反比例函数的值？（第20题）21.（8分）如图，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，BC=10，AB=8.求：(1)FC的长. (2)EC的长.（第21题）22．（9分）甲、乙两组工人同时开始加工某种零件，乙组在工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y （件）与时间x （时）之间的函数图象如下图所示．（1）求甲组加工零件的数量y 与时间x 之间的函数关系式．（2）求乙组加工零件总量a 的值．（第22题）23.（12分）如图，矩形ABCD 中，A （－3，0），B （6，0），C （6，3）．P 、Q 是线段AB 上的两动点，过点P 、Q 作AB 的垂线，分别交CD 于点S 、R ．C B ''与BC 关于PS 成轴对称，D A ''与AD 关于QR 成轴对称，连结D B ''．设BP=2AQ=x ，矩形B C PS ''与矩形D A RQ ''重合部分的面积为y ．（1）当B C ''与矩形D A RQ ''的一边重合时，求x 的值.（2）当3＜x ＜6时，求y 与x 的函数关系式.（3）在点P 由点B 运动到点A 的过程中，直接写出线段D B ''所扫过的面积．。

一、单选题1．沙滩上留有大人和小孩深浅相同大小不同的两对脚印，如图所示，则下列说法中正确的是A．大人对沙滩的压力大，压强大B．小孩对沙滩的压力小，压强小C．两个人对沙滩的压力相同D．两个人对沙滩的压强相同2．下列说法不正确的是A．船闸是利用连通器原理工作的B．海洋比陆地昼夜温差小是因为水的比热容大的缘故C．人在高山上呼吸困难是因为高山上气压比山下气压高D．并行的船不能靠得太近是因为流体中流速越大的位置压强越小3．如图所示，盛有水的容器静止在水平桌面上。

容器重1N，容器中的水重7N，顶部和底部的面积均为100cm2，顶部到底部的高度h2=6cm，侧壁上有一开口弯管，弯管内的水面高度h1=8cm；水的密度为1.0×103kg/m3，g取10N/kg。

下列选项中正确的是A．水对容器顶部的压强为200PaB．水对容器底部的压强为600PaC．水对容器底部的压力为7ND．容器对桌面的压力为9N4．如图所示，A，B为完全相同的两个容器，分别盛有7cm，5cm深的水，A，B之间用导管连接．若将阀门K打开后A．水从容器A内向B流动B．当水不流动时，A，B两容器底所受压强之比为1，1C．当水不流动时，A中液面高于B中液面D．当水不流动时，A，B两容器中液面相平，所以A，B容器底的深度均为6cm5．图中，A、B、C三个完全相同的杯子盛有不同体积的水，现将三个质量相同、材料不同的实心金属球甲、乙、丙分别浸没在A、B、C三个杯子的水中(水均未溢出)，且各杯中的水面达到同一高度。

下列关于甲、乙、丙对杯子底部压力的大小的判断正确的是A．甲最大B．乙最大C．丙最大D．无法判断6．有甲、乙两个完全相同的密闭圆台形容器一正一反放置在同一水平桌面上，甲、乙容器内装有质量相等的不同液体，且两容器内液体的深度相同，如图所示。

两容器底部受到液体的压强分别为p1和p2，桌面受到甲、乙两容器的压力分别为F甲和F乙。

则下列判断正确的是A．p1＜p2F甲＝F乙B．p1＝p 2F甲＞F乙C．p1＜p2F甲＞F乙D．p1＞p2F甲＝F乙7．如图为托里拆利实验的装置图，下列表述正确的是A．将玻璃管稍微倾斜，管内外水银面高度差将变大B．将玻璃管稍微向上提起但没有离开液面，管内外水银面高度差将变大C．向槽中继续注入少量水银，管内外水银面高度差将变小D．换用更粗一些的等长玻璃管，管内外水银面高度差将不变8．如图所示是力学的四个实验情景，下列关于每个实验的结果预测正确的是， ，A．甲图中：木块与小车一起向右匀速运动，小车受阻力停止时，木块一定停止B．乙图中：杠杆不能在水平位置保持平衡，杠杆的左端上升，杠杆的右端下降C．丙图中：当向玻璃管中吹风时，U形管A管中的水面上升，B管中水面下降D．丁图中：将容器侧壁的塞子同时拔出，水从a孔喷射最远，从c孔喷射最近9．如图所示，体积相同的甲、乙实心均匀圆柱体放在水平地面上，且对地面的压强p 甲=p 乙。

2017-2018学年北京理工大学附中分校八年级（下）期中物理试卷一．单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意．共30分，每小题2分）1．（2分）在国际单位制中，压强的单位是（）A．阿基米德B．托里拆利C．帕斯卡D．伽利略2．（2分）如图所示的实例中，目的是为了增大摩擦的是（）A．磁悬浮列车行驶时不接触轨道B．气垫船行驶时船体离开水面C．自行车轴承内部装有滚珠D．汽车轮胎表面刻有花纹3．（2分）如图所示的实例中，目的是为了减小压强的是（）A．削菠萝刀的刀尖做得很尖B．在行李箱的底部安装有小轮C．大型载重车安装有多个车轮D．压路机上的碾子质量很大4．（2分）下列物体运动状态没有发生变化的是（）A．加速升空的火箭B．被竖直向上抛出的石子C．沿光滑斜面滚下的小球D．水平公路上沿直线匀速行驶的汽车5．（2分）停在粗糙的水平地面上的汽车，受到的力有（）A．重力、摩擦力B．重力、支持力C．重力、支持力和摩擦力D．重力、压力、支持力和摩擦力6．（2分）将一个装有水的U型管倾斜放置，图中的水面状况符合实际的是（）A．B．C．D．7．（2分）如图所示，把装满水的量筒浸入水中，口朝下，将筒底向上提，在筒口离开水面之前，量筒露出的部分（）A．是空的B．有水，但不满C．充满水D．先是充满水，后来水会下降8．（2分）晓晗刚学完液体内部压强规律，一次喝完盒装酸奶后，想利用废纸盒做个小实验，他在空纸盒的侧面的不同高度处扎三个大小一样的孔，将纸盒装满水后，水从小孔喷出。

图中的几种水流现象最接近实际情况的是（）A．B．C．D．9．（2分）下列关于压力、压强，下列说法正确的是（）A．支持面所受的压力和物体所受的重力总是大小相等，所以物体越重，压力越大B．支持面所受的压力是由物体的重力产生，所以压力的方向总是竖直向下的C．支持面所受的压力越大，支持面所受的压强就一定越大D．往墙上按图钉时，钉尖和钉帽所受压力相同，但钉尖对墙壁的压强较大10．（2分）如图所示，天花板上的电线吊着一盏电灯，在下列各对力中，属于平衡力的是（）A．电线对电灯的拉力和电灯对电线的拉力B．电灯对电线的拉力和电灯受到的重力C．电线对天花板的拉力和它对电灯的拉力D．电线对电灯的拉力和电灯受到的重力11．（2分）如图7所示，小刚在做探究凸透镜成像规律的实验时，将焦距为10cm的薄凸透镜固定在光具座上50cm刻度线处，将点燃的蜡烛放置在光具座上25cm刻度线处，移动光屏至65cm刻度线处，在光屏上得到烛焰的像。

2017-2018第二学期期中阶段测试初二数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）第Ⅲ卷附加题三部分，其中第Ⅰ卷（选择题）和第Ⅱ卷共100分，第Ⅲ卷20分，考试时间100分钟。

第Ⅰ卷（共30分）一、选择题：(本大题共10小题，每小题3分，共30分. 在每小题的四个选项中，只有一个选项是符合题目要求的).1．下列各式中，运算正确的是（ ）．A ．3=B =．=D 2=-2．下列二次根式中，是最简二次根式的是（）．A ．3．下列各组数中，以它们为边长的线段不能构成直角三角形的是（ ）．A ．1．3，4，5C ．5，12，13D ．2，2，31．4．如图，矩形ABCD 中，对角线AC ，BD 交于O 点．若∠AOB ＝60°，AC ＝8，则AB 的长为（ ）.A ．4B ．．3D ．55．如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心，BC 、AB 长为半径画弧，两弧交于点D ，分别连接AB 、AD 、CD ，则四边形ABCD 一定是（ ）． A ．平行四边形 B ．矩形 C ．菱形 D ．正方形 6．用配方法解方程2230x x --=，原方程应变形为（ ）．A ．2(1)2x -=B ．2(1)4x +=C ．2(1)4x -= D ．2(1)2x +=7．如图，在平行四边形ABCD 中，∠BAD 的平分线交BC 于点E ，∠ABC 的平分线交AD 于点F ，若BF ＝12，AB ＝10，则AE 的长为（ ）．A ．13B ．14C ．15D ．168．下列命题中，正确的是（）．A ．有一组邻边相等的四边形是菱形B ．对角线互相平分且垂直的四边形是矩形C ．两组邻角相等的四边形是平行四边形D ．对角线互相垂直且相等的平行四边形是正方形9．如图，一根木棍斜靠在与地面（OM ）垂直的墙（ON ）上，设木棍中点为P ，若木棍A 端沿墙下滑，且B 沿地面向右滑行. 在此滑动过程中，点P 到点O 的距离（ ）． A ．不变B ．变小 C ．变大 D ．无法判断PFE DCB10．如图，在菱形ABCD 中，∠BAD ＝60°，AB ＝2，E 是DC 边上一个动点，F 是AB 边上一点，∠AEF ＝30°．设DE ＝x ，图中某条线段长为y ，y 与x 满足的函数关系的图象大致如图所示，则这条线段可能是图中的（ ）．A ．线段ECB ．线段AEC ．线段EFD ．线段BF第9题图 第10题图第Ⅱ卷(共70分)二、填空：（每小题2分，共10个小题，共20分）11．写出一个以0，1为根的一元二次方程．12．如果在实数范围内有意义，那么x 的取值范围是________． 13．一元二次方程2x ＋kx －3=0的一个根是x=1，则k 的值是．14．如图，为了检查平行四边形书架ABCD 的侧边是否与上、下边都垂直，工人师傅用一根绳子比较了其对角线AC ，BD 的长度，若二者长度相等，则该书架的侧边与上、下边都垂直， 请你说出其中的数学原理．15．某城2016年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，预计到2018年底增加到363公顷，设绿化面积平均每年的增长率为x ，由题意所列方程是 ． 16．如图，DE 为△ABC 的中位线，点F 在DE 上，且∠AFB ＝90°，若AB ＝5，BC ＝8，则EF 的长为．17．如果关于x 的一元二次方程210ax x +-=有实数根，则ａ的取值范围是________．18．如图，矩形ABCD 中，AB=3,BC=5.过对角线交点O 作OE ⊥AC 交AD 于E, 则AE 的长是． 19．如图，将矩形ABCD 沿对角线BD 所在直线折叠，点C 落在同一平面内，落点记为C’，BC’与AD 交于点E ，若 AB=3，BC ＝4，则DE 的长为．20．如图，正方形ABCD 的面积是2，E ，F ，P 分别是AB ，BC ，AC 上的动点， PE ＋PF 的最小值等于．A第18题图 第19题图 第20题图三、解答题：（21，22题每小题4分，23，24，25每题5分， 26，27每题6分，28题7分；共计50分） 21．计算（1）1)； （2）22．解方程： （1）2650x x -+=；（2） 22310x x --=．23．如图，在四边形ABCD 中，∠B ＝90º，AB=BC=2，AD ＝1，CD ＝3．求∠DAB 的度数．24．列方程或方程组解应用题如图，要建一个面积为40平方米的矩形花园 ABCD ，为了节约材料，花园的一边AD 靠着 原有的一面墙，墙长为8米（AD ＜8），另三 边用栅栏围成，已知栅栏总长为24米， 求花园一边AB 的长．25．如图，四边形ABCD 中，AB//CD ，AC 平分∠BAD ，CE//AD 交AB 于E.求证：四边形AECD 是菱形.26．已知关于x 的一元二次方程22(22)40x m x m +++-=有两个不相等的实数根． （1）求m 的取值范围；（2）若m 为负整数，且该方程的两个根都是整数，求m 的值．27．如图，四边形ABCD 是矩形，点E 在CD 边上，点F 在DC 延长线上，AE ＝BF ． （1）求证：四边形ABFE 是平行四边形（2）若∠BEF ＝∠DAE ，AE ＝3，BE ＝4，求EF 的长．D C B28．如图，在正方形ABCD 中，点M 在CD 边上，点N 在正方形ABCD 外部，且满足∠CMN ＝90°，CM ＝MN ．连接AN ，CN ，取AN 的中点E ，连接BE ，AC ，交于F 点． （1） ①依题意补全图形；②求证：BE ⊥AC ．（2）请探究线段BE ，AD ，CN 所满足的等量关系，并证明你的结论．（3）设AB ＝1，若点M 沿着线段CD 从点C 运动到点D ，则在该运动过程中，线段EN 所扫过的面积为______________（直接写出答案）．第Ⅲ卷附加题（共20分）附加题（1题6分，2题7分，3题7分，共20分）1. 如图1，将边长为1的正方形ABCD 压扁为边长为1的菱形ABCD ．在菱形ABCD 中，∠A 的大小为α，面积记为S ．30° 45°60° 90° 120°135°150° S12122由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A 大小的变化而变化，不妨把菱形的面积S 记为S (α)．例如：当α＝30°时，1(30)2S S =︒=；当α＝135°时，2(135)S S ο= (60)S S ︒=( ______°)；(150)S S ︒=( ______°)，…，由此可以归纳出(180)()S S α︒-=．（3） 两块相同的等腰直角三角板按图2的方式放置，AD 2AOB ＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．DACM图2图2 2．已知：关于x 的一元二次方程23(1)230(3)mx m x m m --+>-=． （1）求证：方程总有两个不相等的实数根；（2）设方程的两个实数根分别为1x ，2x ，且12x x <． ①求方程的两个实数根1x ，2x （用含m 的代数式表示）； ②若1284mx x <-，直接写出m 的取值范围．3. 阅读下列材料：问题：如图1，在平行四边形ABCD 中，E 是AD 上一点，AE=AB ，∠EAB=60°，过点E 作直线EF ，在EF 上取一点G ，使得∠EGB=∠EAB ，连接AG. 求证：EG =AG+BG.小明同学的思路是：作∠GAH=∠EAB 交GE 于点H ，构造全等三角形，经过推理解决问题. 参考小明同学的思路，探究并解决下列问题： （1）完成上面问题中的证明；（2）如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG 、AG 、BG 之间的数量关系，并证明你的结论. （1）证明：（2）解：线段EG 、AG 、BG 之间的数量关系为____________________________. 证明：图1图22017-2018第二学期期中阶段测试初二数学答案及评分标准＝(31)-…………………………………………………3分＝2……………………………………………………………4分（2）原式＝22⨯, ----2分＝＝3⨯3分＝＝ …………………………………………………………………4分 22．（1）解：2650x x -+=移项，得265x x -=-．配方，得26959x x -+=-+，…………………………………………………1分所以，2(3)4x -=．………………………………………………………………2分 由此可得32x -=±，所以，15x =，21x =．…………………………………………………………4分 （2）解：2a =，3b =-，1c =-．………………………………… 1分224(3)42(1)170b ac ∆=-=--⨯⨯-=>．………………………2分方程有两个不相等的实数根x==，1x2x ．……………………………………4分23．解：连接AC在Rt △ABC 中，∠B ＝90º，AB ＝BC ＝2，∴∠BAC ＝∠ACB ＝45°，………………………………………………1分 ∴222AC AB BC =+．∴AC=2分∵AD ＝1，CD ＝3，∴222AC AD CD +=．…………………………3分在△ACD 中，222AC AD CD +=，∴△ACD 是直角三角形，即∠DAC ＝90º．……………………………………4分 ∵∠BAD ＝∠BAC +∠DAC ，∴∠BAD ＝135º．………………………………………………………………5分 24．解：设AB 的长为x 米，则AD=BC=(242x -)米.(242)240x x -⋅=………………………………2分212200x x -+= (10)(2)0x x --=1210,2x x ==………………………………4分当110,4x AD == 当22,20x AD ==8,4AD AD <∴=10x ∴=………………………………5分答：AB 的长为10米．25．证明：∵AB ∥CD ，CE ∥AD∴四边形ADCE 是平行四边形…………………1分 ∵AC 平分∠BAD∴∠DAC=∠EAC ………………2分 ∵AB ∥CD∴∠DCA=∠EAC ………………3分 ∴∠DAC=∠DCA∴AD=DC …………………………4分 ∴四边形ADCE 是菱形…………5分26. 解：（1）∵一元二次方程22(22)40x m x m +++-=有两个不相等的实数根， ∴2224(22)41(4)b ac m m ∆=-=+-⨯⨯-………………………………1分8200m =+>……………………………………………………………2分∴52m >-．……………………………………………………………………3分（2）∵m 为负整数，∴1m =-或2-．……………………………………………………………4分C当1m =-时，方程230x -=的根为1x =2x =舍去．…………………………………………………………………………5分当2m =-时，方程220x x -=的根为10x =，22x =都是整数，符合题意．综上所述2m =-．…………………………………………………………6分27.（1）证明：∵四边形ABCD 是矩形,∴AD ＝BC , ∠D ＝∠BCD ＝90°. ∴∠BCF ＝180°－∠BCD ＝180°－90°＝90°.∴∠D ＝∠BCF .------------------------------------------------------------------1分 在Rt △ADE 和Rt △BCF 中,,.AE BF AD BC =⎧⎨=⎩ ∴Rt △ADE ≌Rt △BCF . ---------------------------------------------------------2分 ∴∠1＝∠F . ∴AE ∥BF . ∵AE ＝BF ,∴四边形ABFE 是平行四边形. ---------------------------------------------------3分（2）解：∵∠D ＝90°, ∴∠DAE ＋∠1＝90°.∵∠BEF ＝∠DAE , ∴∠BEF ＋∠1＝90°.∵∠BEF ＋∠1＋∠AEB ＝180°, ∴∠AEB ＝90°. --------------------------------------------------------------------------4分在Rt △ABE 中, AE =3，BE =4，AB 5. ∵四边形ABFE 是平行四边形,∴EF ＝AB ＝5. --------------------------------------------------------------------------6分28.（1）①依题意补全图形.---------------------------------------------------------1分②解法1： 证明：连接CE .∵四边形ABCD 是正方形, ∴∠BCD ＝90°, AB ＝BC . ∴∠ACB ＝∠ACD ＝12∠BCD ＝45°.∵∠CMN ＝90°, CM ＝MN , ∴∠MCN ＝45°.∴∠ACN ＝∠ACD ＋∠MCN ＝90°. ∵在Rt △ACN 中,点E 是AN 中点, ∴AE ＝CE ＝12AN . ----------------------------------------------------------------------------2分 ∵AE ＝CE ,AB ＝CB ,∴点B ，E 在AC 的垂直平分线上. ∴BE 垂直平分AC .∴BE ⊥AC . --------------------------------------------------------------------------------------3分 解法2： 证明：连接CE .∵四边形ABCD 是正方形, ∴∠BCD ＝90°, AB ＝BC . ∴∠ACB ＝∠ACD ＝12∠BCD ＝45°. ∵∠CMN ＝90°，CM ＝MN , ∴△CMN 是等腰直角三角形. ∴∠MCN ＝45°.∴∠ACN ＝∠ACD ＋∠MCN ＝90°. ∵在Rt △ACN 中,点E 是AN 中点, ∴AE ＝CE ＝12AN . 在△ABE 和△CBE 中,,,.AE CE AB CB BE BE =⎧⎪=⎨⎪=⎩∴△ABE ≌△CBE （SSS ）. -----------------------------------------------------------------2分 ∴∠ABE ＝∠CBE . ∵AB ＝BC ,∴BE ⊥AC . --------------------------------------------------------------------------------------3分 （2）BEAD ＋12CN （或2BE＋CN ）. -------------------------------------4分 证明：∵AB ＝BC , ∠ABE ＝∠CBE ,∴AF ＝FC . ∵点E 是AN 中点,∴AE ＝EN .∴FE 是△ACN 的中位线.∴FE ＝12CN . ∵BE ⊥AC ,∴∠BFC ＝90°.∴∠FBC ＋∠FCB ＝90°.∵∠FCB ＝45°,∴∠FBC ＝45°.∴∠FCB ＝∠FBC .∴BF ＝CF .在Rt △BCF 中,222BF CF BF +=,∴BF BC . -----------------------------------------------------------------------------5分 ∵四边形ABCD 是正方形,∴BC ＝AD .∴BF AD . ∵BE ＝BF ＋FE ,∴BE AD ＋12CN . -------------------------------------------------------------------6分 （3）34.---------------------------------------------------------------------------------------7分附加题：1.（1；12.（说明：每对两个给1分）----------------------------------2分 （2）120；30；α. -----------------------------------------------------------------------------------4分 （说明：前两个都答对给1分，最后一个α答对给1分）（3）答：两个带阴影的三角形面积相等.证明：将△ABO 沿AB 翻折得到菱形AEBO , 将△CDO 沿CD 翻折得到菱形OCFD .∴S △AOB ＝12S 菱形AEBO ＝12S (α)---------------------------------------------------5分 S △CDO ＝12S 菱形OCFD ＝12S (180α︒-)-----------------------------------------6分 由（2）中结论S (α)＝S (180α︒-)∴S △AOB ＝S △CDO .2.（1）证明：∵23(1)230(0)mx m x m m --+≠-=是关于x 的一元二次方程，∴2[3(1)]4(23)m m m ∆=---- ··························································· 1分 269m m =-+2(3)m =-． ······························································································· 2分 ∵3m >，∴2(3)0m ->，即0∆>．∴方程总有两个不相等的实数根． ·························································· 3分（2）①解：由求根公式，得3(1)(3)2m m x m-±-=． ∴1x =或23m x m-=． ∵3m >， ∴23321m m m-=->． ∵12x x <，∴11x =，22332m x m m-==-． ···························································· 5分②3m << ··································································································· 7分 3．（1）证明：如图1，作∠GAH=∠EAB 交GE 于点H ，则∠GAB=∠HAE ．……………………1分∵∠EAB=∠EGB ，∠AOE=∠BOF ，∴∠ABG=∠AEH ．在△ABG 和△AEH 中 GAB HAE AB AEABG AEH ⎧∠∠⎪⎨⎪∠∠⎩＝＝＝∴△ABG ≌△AEH ．……………………2分∴BG=EH ，AG=AH ．∵∠GAH=∠EAB=60°，∴△AGH 是等边三角形．∴AG=HG ．∴EG=AG+BG ；……………………3分（2）线段EG 、AG 、BG 之间的数量关系是EG+BG =AG ．………4分 证明：如图2，作∠GAH=∠EAB 交GE 的延长线于点H ，则∠GAB=∠HAE ． ∵∠EGB=∠EAB=90°，∴∠ABG+∠AEG=∠AEG+∠AEH=180°．∴∠ABG=∠AEH ．……………………5分在△ABG 和△AEH 中，∴△ABG ≌△AEH ．……………………6分∴BG=EH ，AG=AH ．∵∠GAH=∠EAB=90°，∴△AGH 是等腰直角三角形． ∴AG=HG ，∴EG+BG =AG ． (7)O。

北京市鲁迅中学2017-2018第二学期期中阶段测试初二数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）第Ⅲ卷附加题三部分，其中第Ⅰ卷（选择题）和第Ⅱ卷共100分，第Ⅲ卷20分，考试时间100分钟。

第Ⅰ卷（共30分）一、选择题：(本大题共10小题，每小题3分，共30分. 在每小题的四个选项中，只有一个选项是符合题目要求的). 1．下列各式中，运算正确的是（ ）．A ．3=B =．= D 2=- 2．下列二次根式中，是最简二次根式的是（ ）．A ．．3．下列各组数中，以它们为边长的线段不能构成直角三角形的是（ ）．A ．1．3，4，5 C ．5，12，13 D ．2，2，31．4．如图，矩形ABCD 中，对角线AC ，BD 交于O 点． 若∠AOB ＝60°，AC ＝8，则AB 的长为（ ）.A ．4B ．C ．3D ．55．如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心， BC 、AB 长为半径画弧，两弧交于点D ，分别连接AB 、AD 、CD ，则四边形ABCD 一定是（ ）．A ．平行四边形B ．矩形C ．菱形D ．正方形 6．用配方法解方程2230x x --=，原方程应变形为（ ）．A ．2(1)2x -=B ．2(1)4x +=C ．2(1)4x -= D ．2(1)2x +=7．如图，在平行四边形ABCD 中，∠BAD 的平分线交BC 于点E ，∠ABC 的平分线交AD 于点F ，若BF ＝12，AB ＝10，则AE 的长为（ ）． A ．13 B ．14 C ．15 D ．168．下列命题中，正确的是（）．A．有一组邻边相等的四边形是菱形B．对角线互相平分且垂直的四边形是矩形C．两组邻角相等的四边形是平行四边形D．对角线互相垂直且相等的平行四边形是正方形9．如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B 沿地面向右滑行. 在此滑动过程中，点P到点O 的距离（）．A．不变 B．变小 C．变大 D．无法判断10．如图，在菱形ABCD中，∠BAD＝60°，AB＝2，E是DC边上一个动点，F是AB边上一点，∠AEF＝30°．设DE＝x，图中某条线段长为y，y与x满足的函数关系的图象大致如图所示，则这条线段可能是图中的（）．A．线段EC B．线段AE C．线段EF D．线段BF第9题图第10题图第Ⅱ卷(共70分)二、填空：（每小题2分，共10个小题，共20分）11．写出一个以0，1为根的一元二次方程．12x的取值范围是________．13．一元二次方程2x＋kx－3=0的一个根是x=1，则k的值是．14．如图，为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直，工人师傅用一根绳子比较了其对角线AC，BD的长度，若二者长度相等，则该书架的侧边与上、下边都垂直，请你说出其中的数学原理．15．某城2016年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，预计到2018年底增加到363公顷，设绿化面积平均每年的增长率为x，由题意所列方程是．16．如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．PFEDCBA17．如果关于x 的一元二次方程有实数根，则ａ的取值范围 是________．18．如图，矩形ABCD 中，AB=3,BC=5.过对角线交点O 作OE ⊥AC 交AD 于E, 则AE 的长是 ．19．如图，将矩形ABCD 沿对角线BD 所在直线折叠，点C 落在同一平面内，落点记为C’，BC’与AD 交于点E ，若 AB=3，BC ＝4，则DE 的长为 ． 20．如图，正方形ABCD 的面积是2，E ，F ，P 分别是AB ，BC ，AC 上的动点， PE ＋PF 的最小值等于 ．第18题图 第19题图 第20题图三、解答题：（21，22题每小题4分，23，24，25每题5分， 26，27每题6分，28题7分；共计50分）21．计算（111)； （2）22．解方程： （1） 2650x x -+=； （2） 22310x x --=．23．如图，在四边形ABCD 中，∠B ＝90º，AB=BC=2， AD ＝1，CD ＝3．求∠DAB 的度数．24．列方程或方程组解应用题如图，要建一个面积为40平方米的矩形花园 ABCD ，为了节约材料，花园的一边AD 靠着 原有的一面墙，墙长为8米（AD ＜8），另三 边用栅栏围成，已知栅栏总长为24米， 求花园一边AB 的长．210ax x +-=C25．如图，四边形ABCD 中，AB//CD ，AC 平分∠BAD ，CE//AD 交AB 于E.求证：四边形AECD 是菱形.26．已知关于x 的一元二次方程22(22)40x m x m +++-=有两个不相等的实数根． （1）求m 的取值范围；（2）若m 为负整数，且该方程的两个根都是整数，求m 的值．27．如图，四边形ABCD 是矩形，点E 在CD 边上，点F 在DC 延长线上，AE ＝BF ． （1）求证：四边形ABFE 是平行四边形； （2）若∠BEF ＝∠DAE ，AE ＝3，BE ＝4，求EF 的长．28．如图，在正方形ABCD 中，点M 在CD 边上，点N 在正方形ABCD 外部，且满足∠CMN ＝90°，CM ＝MN ．连接AN ，CN ，取AN 的中点E ，连接BE ，AC ，交于F 点．（1） ①依题意补全图形；②求证：BE ⊥AC ．（2）请探究线段BE ，AD ，CN 所满足的等量关系，并证明你的结论．（3）设AB ＝1，若点M 沿着线段CD 从点C 运动到点D ，则在该运动过程中，线段EN 所扫过的面积为______________（直接写出答案）．BA第Ⅲ卷附加题（共20分）附加题（1题6分，2题7分，3题7分，共20分）1. 如图1，将边长为1的正方形ABCD 压扁为边长为1的菱形ABCD ．在菱形ABCD 中，∠A 的大小为α，面积记为S ．由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A 大小的变化而变化，不妨把菱形的面积S 记为S (α)．例如：当α＝30°时，1(30)2S S =︒=；当α＝135°时，(135)S S ο== 由上表可以得到(60)S S ︒=( ______°)；(150)S S ︒=( ______°)，…，由此可以归纳出(180)()S S α︒-=．（3） 两块相同的等腰直角三角板按图2的方式放置，AD AOB ＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．图2图22．已知：关于x 的一元二次方程23(1)230(3)mx m x m m --+>-=． （1）求证：方程总有两个不相等的实数根；（2）设方程的两个实数根分别为1x ，2x ，且12x x <． ①求方程的两个实数根1x ，2x （用含m 的代数式表示）； ②若1284mx x <-，直接写出m 的取值范围．3. 阅读下列材料：问题：如图1，在平行四边形ABCD中，E是AD上一点，AE=AB，∠EAB=60°，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG.求证：EG =AG+BG.小明同学的思路是：作∠GAH=∠EAB交GE于点H，构造全等三角形，经过推理解决问题.参考小明同学的思路，探究并解决下列问题：（1）完成上面问题中的证明；（2）如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG、AG、BG之间的数量关系，并证明你的结论.（1）证明：图1（2）解：线段EG、AG、BG之间的数量关系为____________________________.证明：图2北京市鲁迅中学2017-2018第二学期期中阶段测试初二数学答案及评分标准一、选择题（本题共30分每小题3分，）二、填空题（每小题2分，共20分请将答案写在横线上）21．（1；＝…………………………………………………3分……………………………………………………………4分（2）原式＝, ----2分 ＝＝……………………………………………………………3分 ＝＝. …………………………………………………………………4分22．（1）解：11)(31)-223⨯2650x x -+=移项，得．配方，得，…………………………………………………1分所以，．………………………………………………………………2分 由此可得，所以，，．…………………………………………………………4分 （2）解：2a =，3b =-，1c =-．………………………………… 1分224(3)42(1)170b ac ∆=-=--⨯⨯-=>．………………………2分方程有两个不相等的实数根x==1x =2x =．……………………………………4分 23．解：连接AC在Rt △ABC 中，∠B ＝90º，AB ＝BC ＝2，∴∠BAC ＝∠ACB ＝45°，………………………………………………1分∴．∴2分∵AD ＝1，CD ＝3，∴．…………………………3分在△ACD 中，，∴△ACD 是直角三角形，即∠DAC ＝90º．……………………………………4分 ∵∠BAD ＝∠BAC +∠DAC ，∴∠BAD ＝135º．………………………………………………………………5分 24．解：设AB 的长为x 米，则AD=BC=(242x -)米. (242)240x x -⋅= ………………………………2分265x x -=-26959x x -+=-+2(3)4x -=32x -=±15x =21x =222AC AB BC =+AC =222AC AD CD +=222AC AD CD +=C212200x x -+=(10)(2)x x --=1210,2x x ==………………………………4分当110,4x AD == 当22,20x AD ==8,4AD AD <∴=10x ∴= ………………………………5分答：AB 的长为10米． 25．证明： ∵AB ∥CD ，CE ∥AD∴四边形ADCE 是平行四边形…………………1分 ∵AC 平分∠BAD∴∠DAC=∠EAC ………………2分 ∵AB ∥CD∴∠DCA=∠EAC ………………3分 ∴∠DAC=∠DCA∴AD=DC …………………………4分 ∴四边形ADCE 是菱形…………5分26. 解：（1）∵一元二次方程22(22)40x m x m +++-=有两个不相等的实数根， ∴2224(22)41(4)b ac m m ∆=-=+-⨯⨯- ………………………………1分 8200m =+> ……………………………………………………………2分∴52m >-．……………………………………………………………………3分（2）∵m 为负整数，∴1m =-或2-． ……………………………………………………………4分当1m =-时，方程230x -=的根为1x 2x =不符合题意， 舍去． …………………………………………………………………………5分当2m =-时，方程220x x -=的根为10x =，22x =都是整数，符合题意．综上所述 2m =-． …………………………………………………………6分27.（1）证明：∵四边形ABCD 是矩形,∴AD ＝BC , ∠D ＝∠BCD ＝90°. ∴∠BCF ＝180°－∠BCD ＝180°－90°＝90°.∴∠D ＝∠BCF . ------------------------------------------------------------------1分在Rt △ADE 和Rt △BCF 中,∴Rt △ADE ≌Rt △BCF . ---------------------------------------------------------2分 ∴∠1＝∠F . ∴AE ∥BF .∵AE ＝BF ,∴四边形ABFE 是平行四边形. ---------------------------------------------------3分（2）解：∵∠D ＝90°,∴∠DAE ＋∠1＝90°.∵∠BEF ＝∠DAE , ∴∠BEF ＋∠1＝90°.∵∠BEF ＋∠1＋∠AEB ＝180°, ∴∠AEB ＝90°. --------------------------------------------------------------------------4分在Rt △ABE 中, AE =3，BE =4， AB. ∵四边形ABFE是平行四边形,∴EF ＝AB ＝5. --------------------------------------------------------------------------6分28.（1）①依题意补全图形.---------------------------------------------------------1分②解法1： 证明：连接CE .∵四边形ABCD 是正方形, ∴∠BCD ＝90°, AB ＝BC . ∴∠ACB ＝∠ACD ＝∠BCD ＝45°. ∵∠CMN ＝90°, CM ＝MN , ∴∠MCN ＝45°.∴∠ACN ＝∠ACD ＋∠MCN ＝90°.,.AE BF AD BC =⎧⎨=⎩5=12∵在Rt △ACN 中, 点E 是AN 中点,∴AE ＝CE ＝AN . ----------------------------------------------------------------------------2分 ∵AE ＝CE , AB ＝CB ,∴点B ，E 在AC 的垂直平分线上.∴BE 垂直平分AC .∴BE ⊥AC . --------------------------------------------------------------------------------------3分 解法2：证明：连接CE .∵四边形ABCD 是正方形,∴∠BCD ＝90°, AB ＝BC .∴∠ACB ＝∠ACD ＝∠BCD ＝45°. ∵∠CMN ＝90°，CM ＝MN ,∴△CMN 是等腰直角三角形.∴∠MCN ＝45°.∴∠ACN ＝∠ACD ＋∠MCN ＝90°.∵在Rt △ACN 中, 点E 是AN 中点,∴AE ＝CE ＝AN . 在△ABE 和△CBE 中,∴△ABE ≌△CBE （SSS ）. -----------------------------------------------------------------2分 ∴∠ABE ＝∠CBE .∵AB ＝BC ,∴BE ⊥AC . --------------------------------------------------------------------------------------3分（2）BEAD ＋CN （或2BE＋CN ）. -------------------------------------4分 证明：∵AB ＝BC , ∠ABE ＝∠CBE ,121212,,.AE CE AB CB BE BE =⎧⎪=⎨⎪=⎩12∴AF ＝FC .∵点E 是AN 中点,∴AE ＝EN .∴FE 是△ACN 的中位线.∴FE ＝CN . ∵BE ⊥AC ,∴∠BFC ＝90°.∴∠FBC ＋∠FCB ＝90°.∵∠FCB ＝45°,∴∠FBC ＝45°.∴∠FCB ＝∠FBC .∴BF ＝CF .在Rt △BCF 中, ,∴BFBC .-----------------------------------------------------------------------------5分 ∵四边形ABCD 是正方形,∴BC＝AD . ∴BF AD . ∵BE ＝BF ＋FE ,∴BE AD ＋CN . -------------------------------------------------------------------6分 （3）. ---------------------------------------------------------------------------------------7分附加题 ：1.（1；12.（说明：每对两个给1分） ----------------------------------2分 （2）120；30；α. -----------------------------------------------------------------------------------4分 （说明：前两个都答对给1分，最后一个α答对给1分）（3）答：两个带阴影的三角形面积相等.证明：将△ABO 沿AB 翻折得到菱形AEBO , 将△CDO 沿CD 翻折得到菱形OCFD .12222BF CF BF +=1234∴S △AOB ＝12S 菱形AEBO ＝12S (α) ---------------------------------------------------5分 S △CDO ＝12S 菱形OCFD ＝12S (180α︒-) -----------------------------------------6分 由（2）中结论S (α)＝S (180α︒-)∴S △AOB ＝S △CDO .2.（1）证明：∵是关于的一元二次方程，∴ ···························································· 1分． ······························································································· 2分 ∵，∴，即．∴方程总有两个不相等的实数根． ··························································· 3分（2）①解：由求根公式，得． ∴或． ∵，∴． ∵，∴，． ···························································· 5分 ②． ··································································································· 7分 3．（1）证明：如图1，作∠GAH=∠EAB 交GE 于点H ，则∠GAB=∠HAE ．……………………1分∵∠EAB=∠EGB ，∠AOE=∠BOF ，∴∠ABG=∠AEH ．在△ABG 和△AEH 中 23(1)230(0)mx m x m m --+≠-=x 2[3(1)]4(23)m m m ∆=----269m m =-+2(3)m =-3m >2(3)0m ->0∆>3(1)(3)2m m x m-±-=1x =23m x m -=3m >23321m m m-=->12x x <11x =22332m x m m-==-3m <<OGAB HAE AB AEABG AEH⎧∠∠⎪⎨⎪∠∠⎩＝＝＝∴△ABG ≌△AEH ．……………………2分∴BG=EH ，AG=AH ．∵∠GAH=∠EAB=60°，∴△AGH 是等边三角形．∴AG=HG ．∴EG=AG+BG ；……………………3分（2）线段EG 、AG 、BG 之间的数量关系是EG+BG =AG ．………4分 证明：如图2，作∠GAH=∠EAB 交GE 的延长线于点H ，则∠GAB=∠HAE ． ∵∠EGB=∠EAB=90°，∴∠ABG+∠AEG=∠AEG+∠AEH=180°．∴∠ABG=∠AEH ．……………………5分在△ABG 和△AEH 中，∴△ABG ≌△AEH ．……………………6分∴BG=EH ，AG=AH ．∵∠GAH=∠EAB=90°，∴△AGH 是等腰直角三角形．∴AG=HG ，∴EG+BG =AG ． (7)。

太原市2017-2018学年第二学期八年级阶段性测试（三）历史试卷（考试时间：下午4：30-6：00）说明：本试卷为闭卷笔答，做题时间90分钟，满分100分。

一、单项选择题（每小题2分，共30分）1.中华人民共和国的成立，开辟了中国历史的新纪元。

下列对“新纪元”理解正确的是A.彻底摧毁了我国两千多年的封建帝制B.中华民族由衰败到振兴的转折点C.推翻了三座大山压迫成为独立自主的国家2.1951年5月23日，中央人民政府和西藏地方政府在北京中南海正式签订了《关于和平解放西藏办法的协议》。

这意味着A.争取和平解放西藏取得了成功B.西藏从此走上了社会主义道路C.彻底废除了西藏封建土地制度D.废除了册封达赖、班禅的制度4.新中国成立初，中国人民银行组织设计新版人民币（1953版），下面是一分纸币的正面图案，图案所示为民用汽车，其型号为苏制。

这可以佐证A.工业化建设成果显著B.重工业体系初步确立C.社会主义建设全面展开①《义勇军进行曲》②《翻身农奴把歌唱》③《志愿军进行曲》④《学习雷锋好榜样》间的矛盾，已经是人民对于经济文化迅速发展的需要同当前经济文化不能满足人民需要的状况之间的矛盾。

”这一矛盾提出的主要依据是A.中华人民共和国成立B.第一个五年计划完成7.北京同仁堂是我国中药行业著名的老字号，创建于1669年，以配方奇特、制作精湛、药品货真价实而享誉海内外。

1954年，同仁堂的经理乐松生以大局为重，顺应历史潮流，带头进行公私合营，受到毛泽东主席的高度赞扬。

下面与此叙述相符合的措施是A.农业生产合作化的“社会主义改造”B.手工业生产合作化的社会主义改造C.资本主义工商业的社会主义改造8.1964年，周恩来与美国记者斯诺交谈时说：“15年中，有些事情我们是做对了，但也做了一些错事……只有敢于承认自己的缺点和错误，我们才能改正它们。

”周恩来所说的“错事”是指A.土地改革运动消灭了私有制B.社会主义建设事业急于求成C.为反对美国拒绝参加联合国D.派志愿军参加抗美援朝战争9.1959〜1961年，我国的国民经济发生严重困难。

2018北京九中初二（下）期中语文满分100分。

考试时间120分钟学校_______姓名_______准考证号_______一、基础·运用（共17分）阅读下面关于书法知识的语段，回答1——6题。

（共12分）行书是在楷书的基础上发展而来的，介于楷书和草书之间，较之楷书更为多姿，又弥补．．了草书不易识别的缺陷，写起来十分方便，在现代非常流行。

王羲之自幼跟随书法家卫夫人学习书法，后又游历名山名碑，广采众长，将各种书体róng(融溶)合提炼，逐渐形成自己的风格。

永和九年三月三日，王羲之与一群友人到兰亭踏青游玩，面对美好的春色，他们即兴．．赋诗，结成集子。

王羲之为这本诗集写了一篇序这就是流传千年被称作天下第一行书的《兰亭序》宋代书法四大家之一的黄庭坚说，《兰亭序》是王羲之平生最得意的作品。

其文通篇气息淡和空灵，潇洒自然，无雕琢之痕迹，自然天成。

最为后人称道的是通篇凡是相同的字，写法各不相同，如“之”、“以”、“为”等，各有变化。

特别是“之”字，变幻出二十几种不同的笔法，确实堪称王羲之书法艺术的最高境界。

这些文字①“______”，尽显魏晋士人洒脱的神韵。

其文也是一篇优美的散文，相传为王羲之当时醉酒后的作品，醒来后王又写多幅，却均无第一幅的神韵。

唐代楷书四大家之一的颜真卿行书也遒劲有力，开创了新的风格，具体可见他的《祭侄文稿》。

安史之乱爆发时，颜真卿正在安禄山管辖的平原郡做太守，他挺身而出，举兵讨伐，取得了重大胜利。

他的兄长颜杲卿也是抗击安禄山叛乱的重要人物，然而在一场战役中弹尽粮jué（绝决），与儿子颜季明一起被害。

安史之乱平定后，颜真卿开始四处寻找兄长和侄儿的尸首，并做了一篇悲痛的《祭侄文稿》，流传千古，紧随王羲之的《兰亭序》，被称为“天下第二行书”。

他用笔之际情感如潮涌，满篇狼藉，笔墨时而凝重，几处写到枯笔，可见他挥毫时不能自yǐ（以已）的悲情。

这第三行书的美誉则给了苏轼的《寒食帖》。

北京九中2019-2019学年第二学期初二期中试卷语文满分100分。

考试时间120分钟学校姓名准考证号一、基础·运用（共17分）阅读下面关于书法知识的语段，回答1——6题。

（共12分）行书是在楷书的基础上发展而来的，介于楷书和草书之间，较之楷书更为多姿，又弥补．．了草书不易识别的缺陷，写起来十分方便，在现代非常流行。

王羲之自幼跟随书法家卫夫人学习书法，后又游历名山名碑，广采众长，将各种书体ró(融溶)合提炼，逐渐形成自己的风格。

永和九年三月三日，王羲之与一群友人到兰亭踏青游玩，面对美好的春色，他们即．兴．赋诗，结成集子。

王羲之为这本诗集写了一篇序这就是流传千年被称作天下第一行书的《兰亭序》宋代书法四大家之一的黄庭坚说，《兰亭序》是王羲之平生最得意的作品。

其文通篇气息淡和空灵，潇洒自然，无雕琢之痕迹，自然天成。

最为后人称道的是通篇凡是相同的字，写法各不相同，如“之”、“以”、“为”等，各有变化。

特别是“之”字，变幻出二十几种不同的笔法，确实堪称王羲之书法艺术的最高境界。

这些文字①“”，尽显魏晋士人洒脱的神韵。

其文也是一篇优美的散文，相传为王羲之当时醉酒后的作品，醒来后王又写多幅，却均无第一幅的神韵。

唐代楷书四大家之一的颜真卿行书也遒劲有力，开创了新的风格，具体可见他的《祭侄文稿》。

安史之乱爆发时，颜真卿正在安禄山管辖的平原郡做太守，他挺身而出，举兵讨伐，取得了重大胜利。

他的兄长颜杲卿也是抗击安禄山叛乱的重要人物，然而在一场战役中弹尽粮é（绝决），与儿子颜季明一起被害。

安史之乱平定后，颜真卿开始四处寻找兄长和侄儿的尸首，并做了一篇悲痛的《祭侄文稿》，流传千古，紧随王羲之的《兰亭序》，被称为“天下第二行书”。

他用笔之际情感如潮涌，满篇狼藉，笔墨时而凝重，几处写到枯笔，可见他挥毫时不能自yǐ（以已）的悲情。

这第三行书的美誉则给了苏轼的《寒食帖》。

此贴是苏轼被贬黄州时，在寒食节所作。