材料力学第8章-弯曲剪应力分析及弯曲中心的概念

材料力学弯曲应力知识点总结弯曲应力是材料力学中重要的概念之一，它描述了材料在受到弯曲力作用时所承受的内部力状态。

了解和掌握弯曲应力的知识对于工程领域的设计和分析具有重要意义。

本文将对材料力学中弯曲应力的相关知识点进行总结。

一、弯曲应力的基本概念弯曲应力是指在材料受到弯曲作用时，在横截面上单位面积所承受的力的大小，通常用σ表示。

弯曲应力的大小与施加在材料上的弯曲力以及截面形状和尺寸有关。

二、弯矩和截面性质1. 弯矩：在弯曲过程中，作用在材料上的弯曲力会产生一个力矩。

弯矩的大小等于力矩除以截面法线距离。

弯矩的单位通常是N·m。

2. 惯性矩和截面模量：惯性矩描述了截面抵抗变形的能力，通常用I表示。

截面模量描述了材料在弯曲过程中的刚度，通常用W表示。

惯性矩和截面模量与截面的形状和尺寸有关。

三、材料的截面形状对弯曲应力的影响材料的截面形状对弯曲应力有着重要的影响，以下是几种常见截面形状的弯曲应力分析：1. 矩形截面：矩形截面的弯曲应力呈线性分布，最大弯曲应力出现在截面内边缘。

2. 圆形截面：圆形截面的弯曲应力均匀分布，在截面上的任意一点的弯曲应力都相同。

3. T型截面：T型截面的弯曲应力最大出现在截面顶部和底部的交接处。

4. I型截面：I型截面的弯曲应力主要集中在截面中轴线部分。

四、弯曲应力与应变的关系弯曲应力和应变之间的关系可以通过杨氏模量进行描述。

弯曲应力和应变的关系可以用以下公式表示：σ=M*y/I，其中M为弯矩，y为截面的纵向距离，I为截面的惯性矩。

五、弯曲应力的计算方法根据弯曲应力的定义和性质，可以采用以下方法来计算弯曲应力：1. 等效应力法：将弯矩和弯曲力矩转化为等效应力，然后根据截面形状计算弯曲应力。

2. 梁理论：基于材料的截面形状和尺寸，使用梁理论来计算弯曲应力。

通过计算截面的惯性矩和截面模量来获得弯曲应力。

六、弯曲应力的影响因素弯曲应力受到以下因素的影响：1. 弯曲力的大小和方向2. 材料的弹性模量3. 材料的截面形状和尺寸4. 材料的力学性质和力学行为5. 材料的应变率和应变历史七、弯曲应力的应用弯曲应力在工程设计和分析中具有广泛的应用，例如：1. 结构设计：通过对材料的弯曲应力进行分析，可以确定结构的合理尺寸和截面形状，以满足设计要求。

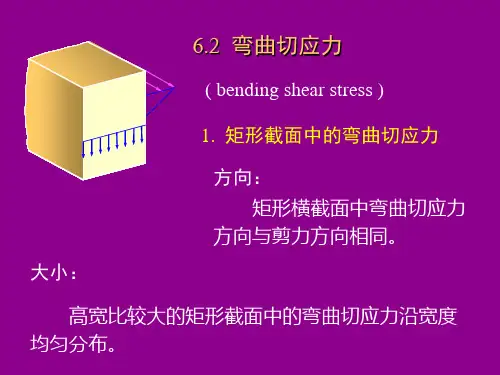
材料力学弯曲应力课件曲在工程中的应用。

这是一个厂房，这是一个大梁，这个吊车可以在这个大梁上运动。

对于这样一个问题，我们可以把它简化成一个简支梁，这个吊车的移动呢可以处理成一个移动荷载。

那么对于这个移动荷载而言，它所导致的应力如何计算行车移动时，它的应力如何变化这就是本章的内容之一。

我们再看看这个图片，这是我们拍摄的汽车的下部分，大家注意一些这个部分，这是就是汽车的板簧，它的模型就是这个样子，可以看成好几个钢板的组合，那么，为什么要设计成这个样子呢它有什么优点呢这也是本章要解决的问题。

这是一个运动员，撑杆跳，对吧。

大家常常见到，利用这个杆的助力，人可以跳的更高。

我们可以处理成这样一个模型。

她在跳高的过程中，杆就发生了弯曲。

那么，这个时候，跳杆横截面上的应力和杆曲率半径有什么关系这个杆在什么情况下才满足强度要求大家看看这个场面，对于这个场面，我们截面几何性质那章提到过，都是薄壁杆件，那么薄壁杆件有弯曲正应力和弯曲切应力，专门有一小节来讲解它的弯曲切应力，看看这些切应力有什么特点如何避免薄壁杆件的强度失效这也是本章的问题这个大家都熟悉，著名的比萨斜塔。

对于这个结构，初步计算，我们可以简化成这样一个均质圆筒，那么它有哪些变形效应它的危险截面、危险点在哪儿如何计算其应力这也是本章可以解决的问题。

因此，本章所涉及的问题是比较广的。

基本内容那么本章到底需要同学们掌握哪些内容呢1、熟练张博横截面上弯曲正应力和弯曲切应力的分布规律，并能正确熟练的进行梁的强度分析。

2、熟悉提高梁强度的主要措施。

、正确理解薄壁杆件横截面上弯曲切应力的分布规律，了解弯曲中心的概念。

4、熟悉掌握梁在组合变形中的应力的计算方法。

第一、第四条是很重要的。

这是以后大家经常需要处理的问题。

基本概念平面弯曲首先我们来看弯曲正应力。

在这章具体内容介绍之前呢，我们先介绍一些概念。

关于梁弯曲的基本概念。

梁的平面弯曲。

什么是梁的平面弯曲呢这是一个悬臂梁，截面是矩形截面，那么这个横截面就有一个中心对称轴，整个梁就存在一个对称面，如果我们的所有的外荷载都作用在这个平面之内，比如外荷载是这样的，那么发生变形后，梁的轴线仍然在这个平面内，像这样的弯曲，我们就叫做平面弯曲。

材料力学弯曲知识点总结材料力学是研究物质力学性质和力学行为的一门学科，其中弯曲是一个重要的研究方向。

本文将对材料力学中的弯曲知识点进行总结，包括弯曲的定义、应力、应变和杨氏模量等内容。

1. 弯曲的定义弯曲是指在作用力或力矩的作用下，物体发生形状的变化，使其变曲或曲度改变的现象。

在材料力学中，弯曲是指材料在受到外力作用下，产生弯曲应变和弯曲应力的行为。

2. 弯曲应力弯曲应力是指在材料发生弯曲时，单位面积上的内力。

在弯曲过程中，材料上的各点受到不同程度的拉伸或压缩，产生弯曲应力。

弯曲应力与外力以及横截面形状和尺寸有关。

3. 弯曲应变弯曲应变是指材料在受到弯曲作用时，单位长度上的变形量。

弯曲应变正比于弯曲的曲率半径和材料的长度，与材料的刚度有关。

4. 应力和应变的关系根据胡克定律，应力和应变之间存在线性关系。

在弯曲过程中，弯曲应力和弯曲应变近似满足线性关系，可以用杨氏模量来表示。

杨氏模量是材料的一个重要力学参数，可以衡量材料的刚度。

5. 计算弯曲应力和应变的公式在弯曲现象中，可以通过一些公式来计算弯曲应力和应变。

其中，弯曲应力的计算公式为σ = (M*y) / I，弯曲应变的计算公式为ε = (M*y) / (E*I)。

其中，M为弯矩，y为离中性轴的距离，I为惯性矩，E为杨氏模量。

6. 中性轴和惯性矩在材料弯曲过程中，中性轴是指曲率最小的轴线，即弯曲位置上的轴线。

惯性矩则是材料承受弯矩时，各点离中性轴距离的平方乘以截面积后的积分，用来量化材料的抗弯刚度。

7. 材料弯曲的应用材料弯曲的特性使其具有广泛的应用，比如在工程结构中的材料选择和设计中，弯曲强度和刚度是重要的考虑因素之一。

此外，弯曲还可用于制造各种曲线形状的构件和装饰品。

综上所述，材料力学中的弯曲是一种重要的力学行为，涉及到弯曲应力、弯曲应变和杨氏模量等知识点。

弯曲应力和应变的计算可以通过公式来完成，中性轴和惯性矩是描述材料弯曲过程中位置和抗弯刚度的重要概念。

工程力学（静力学与材料力学）习题第8章 剪应力分析8－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。

（A ）等截面圆轴，弹性范围内加载；（B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。

正确答案是 。

8－2 两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。

设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。

试判断下列结论的正确性。

（A ）max 1τ＞max 2τ；（B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ；（D ）若G 1＞G 2，则有max 1τ＜max 2τ。

正确答案是 。

8－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。

关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。

（A ）234)1(α-；（B ）)1()1(2234αα--；（C ）)1)(1(24αα--；（D ）)1/()1(2324αα--。

正确答案是 。

8－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。

圆轴尺寸如图所示。

圆轴受扭时，里、外层之间无相对滑动。

关于横截面上的切应力分布，有图中所示的四种结论，试判断哪一种是正确的。

正确答案是 。

8－5 等截面圆轴材料的切应力－切应变关系如图中所示。

圆轴受扭后，已知横截面上点)4/(d a a =ρ的切应变s γγ=a ，若扭转时截面依然保持平面，则根据图示的γτ-关系，可以推知横截面上的切应力分布。

试判断图中所示的四种切应力分布哪一种是正确的。

正确答案是 。

8－6图示实心圆轴承受外扭转力偶，其力偶矩T = 3kN ·m 。