八年级数学上册2.2轴对称的基本性质同步练习(1)(新版)青岛版

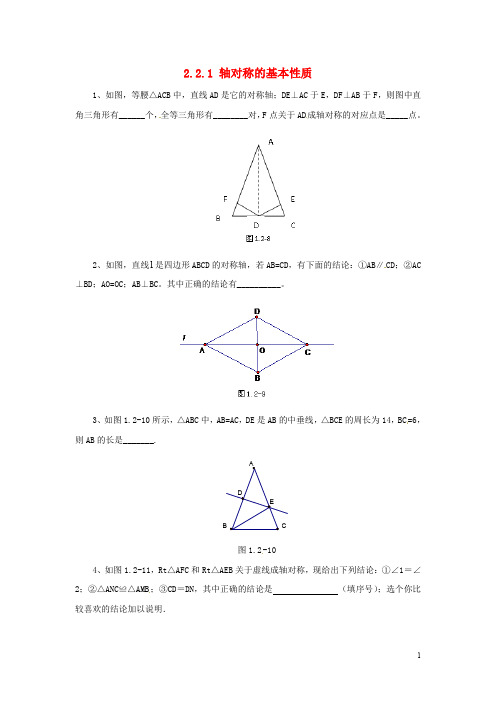
2.2.1 轴对称的基本性质1、如图，等腰△ACB中，直线AD是它的对称轴；DE⊥AC于E，DF⊥AB于F，则图中直角三角形有______个，全等三角形有________对，F点关于AD成轴对称的对应点是_____点。

2、如图，直线l是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC ⊥BD；AO=OC；AB⊥BC。

其中正确的结论有__________。

3、如图1.2-10所示，△ABC中，AB=AC，DE是AB的中垂线，△BCE的周长为14，BC=6，则AB的长是_______.图1.2-104、如图1.2-11，Rt△AFC和Rt△AEB关于虚线成轴对称，现给出下列结论：①∠1＝∠2；②△ANC≌△AMB；③CD＝DN，其中正确的结论是（填序号）；选个你比较喜欢的结论加以说明．5、如图1.2-13所示，在图形中标出点A 、B 、C 关于直线l 的对称点D 、E 、F 。

若M 为AB 的中点，在图中标出它的对称点N 。

若AB=5，AB 边上的高为4，则△D E F 的面积为多少？6、如图1.2-14，在两面成“八”字形放置的镜子中间放着塑料做的数字9，你在左右两面镜子中看到的像是怎么样的？请你把它们写出来。

BC参考答案1、6，3，E2、①②③.提示：由于直线l 是四边形ABCD 的对称轴，所以AC ⊥BD ，OD=OB ，由已知条件AB=CD ，所以△AOB ≌△COD （HL ）。

所以AO=OC ，∠OAB=∠OCD 。

由∠OAB=∠OCD 可得AB ∥CD 。

故正确结论有3个。

3、84、①②； ∠1＝∠2.∵R t △AFC 和Rt △AEB 关于虚线成轴对称， ∴∠E AD=∠FAD ，∠MAD=∠NAD. ∴∠EAD －∠MAD =∠FAD －∠NAD. 即：∠1＝∠2. 5、LB5题图△DEF 的面积为10. 6、。

2.2 轴对称的基本性质一、选择题1．一个图案上各点的横坐标都不变，纵坐标变为原来的相反数，但图案却未发生任何变化，则下列叙述正确的是（）A．原图案各点一定都在x轴上B．原图案各点一定都在y轴上C．原图案是轴对称图形，对称轴是x轴D．原图案是轴对称图形，对称轴是y轴2．有下列语句：①点A（5，-3）关于x轴对称的点A′的坐标为（-5，-3）；②点B（-2，2）关于y轴对称的点B′的坐标为（-2，-2）；③若点D在第二、四象限坐标轴夹角平分线上，则点D的横坐标与纵坐标相等．其中正确的是（）A．①B．②C．③D．①②③都不正确3．如图，若△OAB和△OA′B′关于直线OP对称，则下列说法错误的是（）（第3题图）A．OA=OA′B．线段AA′被直线OP平分C．∠A=∠A′D．OP不是BB′的垂直平分线4．下列说法正确的是（）A．有一条公共边的两个全等三角形关于共边所在的直线对称B．全等三角形是关于某直线对称的C．两个图形关于某直线对称，则这两个图形一定分别位于这条直线的两侧D．关于某直线对称的两个三角形是全等三角形5．若点A的坐标（x，y）满足条件（x-3）2+|y+2|=0，则点A关于y轴的对称点的坐标是（）A．（3，2）B．（-3，2）C．（3，-2）D．（-3，-2）6．如图，将△ABC沿AC所在的直线翻折得到△ADC，且顶点B的对应顶点是D，则下列结论正确的是（）（第6题图）A．AB=AC B．AB=AD C．∠ABC=∠CAD D．∠BAC=∠CDA7．点A（-3，5）与B（5，5）关于某一直线对称，则对称轴是（）A．x轴B．y轴C．直线x=1 D．直线y=18．如图，牧童家在B处，A，B两处相距河岸的距离AC，BD分别为500 m和300 m，且C，D两处的距离为600 m，天黑牧童从A处将牛牵到河边去饮水，在赶回家，那么牧童最少要走（）（第8题图）A．800 m B．1 000 m C．1 200 m D．1 500 m二、填空题9．如图，第一、三象限角平分线记为y=x，点（-1，-2）关于y=x对称点为，点（a，b）关于y=x对称点的坐标为．（第9题图）10．若△ABC和△A′B′C′关于直线l对称，∠A=55°，∠B′=45°，则∠C=．三、解答题11．如图，分别作点A（-3，0），B（-2，2）关于直线x=2的对称点A′，B′．（1）点A′的坐标为，点B′的坐标为；（2）四边形ABB′A′的面积为．（第11题图）答案一、1．C 【分析】根据一个图案上各点的横坐标都不变，纵坐标变为原来的相反数，但图案却未发生任何变化，则原图案是轴对称图形，对称轴是x轴．故选C．2．D 【分析】①点A（5，-3）关于x轴对称的点A′的坐标为（5，3），故不正确；②点B （-2，2）关于y轴对称的点B′的坐标为（2，2），故不正确；③若点D在第二、四象限坐标轴夹角平分线上，则点D的横坐标与纵坐标互为相反数，故不正确．故选D．3．D 【分析】∵△OAB和△OA′B′，关于直线OP对称，∴OA=OA′，故A选项正确；线段AA′被直线OP平分，故B选项正确；∠A=∠A′，故C选项正确；OP是BB′的垂直平分线，故D选项不正确．故选D．4．D 【分析】A．有一条公共边的两个全等三角形关于公共边所在的直线对称，错误，如答图（1），故此选项错误；B．全等三角形是关于某直线对称的错误，如答图（2），故此选项错误；C．两个图形关于某直线对称，则这两个图形一定分别位于这条直线的两侧错误，如答图（3），故此选项错误；D．关于某直线对称的两个三角形是全等三角形，此选项正确．故选D．（1）（2）（3）（第4题答图）5．D 【分析】由点A的坐标（x，y）满足条件（x-3）2+|y+2|=0，得x-3=0，y+2=0．解得x=3，y=-2．即A（3，-2）．点A关于y轴的对称点的坐标是（-3，-2）．故选D．6．B 【分析】∵将△ABC沿AC所在的直线翻折得到△ADC，且顶点B的对应顶点是D，∴△ABC≌△ADC，∴AB=AD，∠ABC=∠ADC，∠BAC=∠DAC，故选项A，C，D错误，选项B正确．故选B．7．C 【分析】∵点A（-3，5）与B（5，5），两点纵坐标相等，∴两点关于过线段中点的直线对称，即关于直线x=235=1对称．故选C．8．B 【分析】如图，作点A关于CD的对称点A′，连接A′B，则A′B的长即为AP+BP的最小值，过点B作BE⊥AC，垂足为E．∵CD=600 m，BD=300 m，AC=500 m，∴A′C=AC= 500 m，CE=BD=300 m，CD=BE=600 m，∴A′E=A′C+CE=500+300=800（m）．在Rt△A′EB中，A′B =6008002222+=+'BE E A =1 000（m ）．即牧童最少要走1 000米．故选B ．（第8题答图） 二、9．（-2，-1），（b ，a ） 【分析】点（-1，-2）关于y =x 对称点为（-2，-1），点（a ，b ）关于y =x 对称点的坐标为（b ，a ）．10．80° 【分析】∵△ABC 和△A′B′C′关于直线l 对称，∠A =55°，∠B′=45°，∴∠A =∠A′=55°，∠B =∠B′=45°，∴∠C =180°-∠A -∠B =180°-55°-45°=80°．三、11. 解：（1）由题意，得点A′的坐标为（7，0），点B′的坐标为（6，2）．（2）∵四边形ABB′A′是梯形，上底是8，下底为10，高为2，∴面积为（8+10）×2÷2=18．。

青岛版八年级上册数学第2章图形的轴对称含答案一、单选题(共15题，共计45分)1、如图，在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①BE= AC；②∠A=∠EBA；③EB 平分∠AED；④ED= AB中，一定正确的是（）A.①②③B.①②④C.①③④D.②③④2、在平面直角坐标系中，已知A（1，1），要在坐标轴上找一点P，使得△PAO 为等腰三角形，这样的P点有几个（）A.9B.8C.7D.63、下列图形中，既是中心对称图形，又是轴对称图形的是（）A. B. C. D.4、如图，在平面直角坐标系中，点A1， A2在x轴上，点B1， B2在y轴上，其坐标分别为A1(1，0)，A2(2，0)，B1(0，1)，B2(0，2)，分别以A1， A2，B 1， B2其中的任意两点与点O为顶点作三角形，所作三角形是等腰三角形的概率是( )A. B. C. D.5、如图，以Rt△ABC的斜边BC为一边作正方形BCDE，设正方形的中心为O，连结AO，如果AB＝3，AO＝，那么AC的长等于（）A.12B.7C.D.6、如图，已知正方形ABCD的边长为1，连结AC、BD，CE平分∠ACD交BD于点E，则DE长（）A. B. C.1 D.1﹣7、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC +S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A.1个B.2个C.3个D.4个8、如图，点C、D在线段AB的同侧，CA＝4，AB＝12，BD＝9，M是AB的中点，∠CMD＝120°，则CD长的最大值是（）A.16B.19C.20D.219、如图，把一张长方形纸片沿对角线折叠，若△EDF是等腰三角形，则∠BDC （）A.45ºB.60ºC.67.5ºD.75º10、如图，和都是等边三角形，是的角平分线，下列结论：①；②；③；④，其中结论正确的有（）A.4个B.3个C.2个D.1个11、下列图形中，既是轴对称图形，又是中心对称图形的是( )A. B. C. D.12、将一张正方形纸片，按如图步骤①，②，沿虚线对折两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（）A. B. C. D.13、如图，有一张△ABC纸片，AC=8，∠C=30°,点E在AC边上，点D在边AB 上，沿着DE对折，使点A落在BC边上的点F处，则CE的最大值为（）A. B. C.4 D.14、下列图案是轴对称图形的是( )A. B. C. D.15、如图，△ABC中，∠C=90°，AC=16cm，AB的中垂线MN交AC于点D，连接BD，若cos∠BDC= ，则BC=（）A.8cmB.4cmC.6cmD.10cm二、填空题(共10题，共计30分)16、如图，菱形ABCD中，AB=4，∠A=120°，点M、N、P分别为线段AB、AD、BD上的任意一点，则PM+PN的最小值为________17、等腰三角形的周长为30，腰长是12，则底边长为________.18、如图，矩形ABCD中，AB=6，BC=8，点E是BC边上一点，连接AE，把∠B 沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为________．19、如图，点A、B、C在⊙O上，弦AC与半径OB互相平分，那么∠OAC的度数为________度.20、如图，△A1B1A2，△A2B2A3，△A3B</i>3A4，…，△A n B n A n＋1都是等腰直角三角形，其中点A1， A2，…，An在x轴上，点B1， B2，…，Bn在直线y＝x上．已知OA1＝1，则OA2017的长为________．21、用一张斜边BC长为10的等腰直角三角形纸片进行折“狗脸”活动(如图1所示)第一步，如图2，沿MN向后折一个面积为1的等腰直角三角形△A'MN；第二步，在直角边AC，AB上各取一点E、F， D为BC的中点，将△CDE、△BDF 分别沿DE、DF折叠，使得点B、C对应点B'、C'落在直线MN上，DC'交AC于点P，DB'交AB于点Q，则“狗脸”(图形 DEC'PMNOB'F)的面积为________。

八年级数学上册《第二章轴对称的基本性质》同步练习题及答案(青岛版）学校:___________班级：___________姓名：___________考号：___________一、选择题1.下列说法正确的是( )A.两个全等的三角形一定关于某条直线对称B.关于某条直线的对称的两个三角形一定全等C.直角三角形是轴对称图形D.锐角三角形都是轴对称图形2.轴对称图形沿对称轴对折后，对称轴两旁的部分( )A.完全重合B.不完全重合C.两者都有D.不确定3.以下结论正确的是( ).A.两个全等的图形一定成轴对称B.两个全等的图形一定是轴对称图形C.两个成轴对称的图形一定全等D.两个成轴对称的图形一定不全等4.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )A.AM=BMB.AP=BNC.∠MAP=∠MBPD.∠ANM=∠BNM5.下列说法错误的是( )A.等边三角形是轴对称图形B.轴对称图形的对应边相等,对应角相等C.成轴对称的两条线段必在对称轴一侧D.成轴对称的两个图形对应点的连线被对称轴垂直平分6.已知点A（a，1）与点B（5，b）关于y轴对称，则实数a，b的值分别是（）A.5，1B.﹣5，1C.5，﹣1D.﹣5，﹣17.若点A（m，n）和点B（5，﹣7）关于x轴对称，则m+n的值是（）A.2B.﹣2C.12D.﹣128.如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )A.15B.20C.25D.30二、填空题9.成轴对称的两个图形.10.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 .11.若直角三角形是轴对称图形,则其三个内角的度数分别为________.12.如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为 .13.如图，Rt△AFC和Rt△AEB关于虚线成轴对称，现给出下列结论：①∠1=∠2；②△ANC≌△AMB；③CD=DN.其中正确的结论是.（填序号）14.小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时（机翼间无缝隙），∠AOB的度数是.三、解答题15.若|x＋2|＋|y－1|＝0，试问：P(x，y)，Q(2x＋2，y－2)两点之间有怎样的位置关系？16.已知点A(a－2，6)和点B(1，b－2)关于x轴对称，求(a＋b)2024的值.17.在直角坐标系中，已知点A(a＋b，2－a)与点B(a－5，b－2a)关于y轴对称.(1)试确定点A，B的坐标；(2)如果点B关于x轴的对称点是C，求△ABC的面积.18.如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.19.在平面直角坐标系中，直线1垂直于x轴，垂足为M(m，0)，点A(﹣1，0)关于直线的对称点为A′.探究：(1)当m=0时，A′的坐标为；(2)当m=1时，A′的坐标为；(3)当m=2时，A′的坐标为；发现：对于任意的m，A′的坐标为.解决问题：若A(﹣1，0)B(﹣5，0)，C(6，0)，D(15，0)，将线段AB沿直线l翻折得到线段A′B′，若线段A′B′与线段CD重合部分的长为2，求m的值.答案1.B2.A3.C4.B5.C6.B7.C8.D9.答案为：全等.10.答案为：8 cm2.11.答案为：90°，45°，45°.12.答案为：5cm.13.答案为：①②.14.答案为：45°；15.解：∵|x＋2|＋|y－1|＝0∴x＋2＝0，y－1＝0，解得x＝－2，y＝1.∴点P(－2，1)，Q(－2，－1)∴P，Q两点关于x轴对称.16.解：∵点A(a－2，6)和点B(1，b－2)关于x轴对称∴a－2＝1，b－2＝－6，解得a＝3，b＝－4.∴(a＋b)2024＝(3－4)2024＝1.17.解：由题意，得a+b=5-a，2-a=b-2a，解得a=1,b=3. ∴点A的坐标是(4，1)，点B的坐标是(－4，1).(2)∵点B关于x轴的对称点是C∴点C的坐标是(－4，－1).∴AB=8，BC=2.=8.∴S△ABC18.解:因为DE是△ABE的对称轴所以AE=BE.所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.因为BC=6,所以AC=8.所以AB=AC=8.19.解：探究：∵点A和A′关于直线l对称∴M为线段AA′的中点设A′坐标为(t，0)，且M(m，0)，A(﹣1，0)∴AM=A′M，即m﹣(﹣1)=t﹣m∴t=2m+1(1)当m=0时，t=1，则A'的坐标为 (1，0)，故答案为：(1，0)；(2)当m=1时，t=2×1+1=3，则A'的坐标为(3，0)，故答案为：(3，0)；(3)当m=2时，t=2×2+1=5，则A'的坐标为(5，0)，故答案为：(5，0)；发现：由探究可知，对于任意的m，t=2m+1，则A'的坐标为(2m+1，0) 故答案为：(2m+1，0)；解决问题：∵A(﹣1，0)B(﹣5，0)，∴A′(2m+1，0)，B′(2m+5，0)当B′在点C、D之间时，则重合部分为线段CB′，且C(6，0)∴2m+5﹣6=2，解得m=3 2；当A′在点C、D之间时，则重合部分为线段A′D，且D(15，0) ∴15﹣(2m+1)=2，解得m=6；综上可知m的值为32或6.。

青岛版八年级上册数学第2章图形的轴对称含答案一、单选题(共15题，共计45分)1、如图，△ABC与△A'B'C'关于直线L对称，∠A＝50°，∠C'＝30°，则∠B 的度数为（）A.30°B.50°C.90°D.100°2、下列图形中是中心对称图形但不是轴对称图形的是（）A. B. C. D.3、如图，在中，，是的平分线，，的面积为12，则的长度为（）A.3B.4C.5D.64、如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…按照此规律继续下去，则S2016的值为（）A. B. C. D.5、如图，DE是AC边的垂直平分线，AB＝5cm，BC＝4cm.那△BEC的周长是（）A.9cmB.8cmC.7cmD.6cm6、在△ABC中，AB=AC，∠A=80°，进行如下操作：①以点B为圆心，以小于AB长为半径作弧，分别交BA、BC于点E、F；②分别以E、F为圆心，以大于EF长为半径作弧，两弧交于点M；③作射线BM交AC于点D，则∠BDC的度数为（）A.100°B.65°C.75°D.105°7、如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )A.1个B.2个C.3个D.4个8、如图，△ABC中，AB，AC的垂直平分线分别交BC于D，E，若∠BAC=110°，则∠DAE的度数为( )A.40B.45C.50D.559、如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°；②∠AED=84°；③∠BFC=84°；④∠DGF=96°,其中正确的个数有( )A.4个B.3个C.2个D.1个10、Word文本中的图形，在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度，同一个图形随其放置方向的变化，所显示的绝对高度和绝对宽度也随之变化．如图①、②、③是同一个三角形以三条不同的边水平放置时，它们所显示的绝对高度和绝对宽度如下表，现有△ABC，已知AB=AC，当它以底边BC 水平放置时（如图④），它所显示的绝对高度和绝对宽度如下表，那么当△ABC 以腰AB水平放置时（如图⑤），它所显示的绝对高度和绝对宽度分别是（）图形图①图②图③图④图⑤绝对高度 1.50 2.00 1.20 2.40 ？绝对宽度 2.00 1.50 2.50 3.60 ？A.3.60和2.40B.2.56和3.00C.2.56和2.88D.2.88和3.0011、如图，在△ABC中，BD平分∠ABC，ED∥BC，已知AB=3，AD=1，则△AED的周长为（）A.2B.3C.4D.512、设等腰三角形（两底角相等的三角形）顶角的度数为y，底角的度数为x，则有（）A.y=180-2x（x为全体实数）B.y=180-2x（0≤x≤90）C.y=180-2x（0＜x＜90）D.y=180- x（0＜x＜90）13、如图，∠BAC=110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（）A.20°B.40°C.50°D.60°14、长方形的对称轴有（）A.2条B.4条C.6条D.无数条15、如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD; ②AD上任意一点到AB,AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是( )A.①B.①②C.①②③D.①②③④二、填空题(共10题，共计30分)16、如图，四边形ABCD中，∠B＝∠D＝90°，∠C＝50°，在BC、CD边上分别找到点M、N，当△AMN周长最小时，∠AMN＋∠ANM的度数为________.17、已知直线l经过点（0，2），且与x轴平行，那么点（6，5）关于直线l 的对称点为________18、如图，在长方形ABCD中，点E在边DC上，联结AE,将△ADE沿折痕AE翻EC=________度；折，使点D落在边BC上的D处，如果∠DEA= ，那么∠D119、把一张三角形的纸折叠成如图后，面积减少，已知阴影部分的面积是50平方厘米，则这张三角形纸的面积是________平方分米．20、如图，在平行四边形ABCD中，DE平分∠ADC，AD＝7，BE＝2，则平行四边形ABCD的周长是________．21、如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于D，PE⊥OB于E．若点Q是OC上与O、P不重合的另一点，则以下结论中，一定成立的是________（填序号）①PD=PE；②OC垂直平分DE；③QO平分∠DQE；④△DEQ是等边三角形．22、如果等腰三角形的一个外角是105°，那么它的顶角的度数为________．23、如图，在四边形ABCD中，AB=AD，CB=CD，对角线AC，BD相交于点O，下列结论中：①∠ABC=∠ADC；②AC与BD相互平分；③AC，BD分别平分四边形ABCD的两组对角；④四边形ABCD的面积S= AC•BD．正确的是________（填写所有正确结论的序号）24、如图，H是△ABC的边BC的中点，AG平分∠BAC，点D是AC上一点，且AG⊥BD于点G．已知AB=12，BC=15，GH=5，则△ABC的周长为________．25、如图，和关于直线对称，和关于直线对称，与交于点，若，，则的度数为________．三、解答题(共5题，共计25分)26、如图，在每个小正方形的边长为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上。

2.2 轴对称的根本性质◆根底训练一、选择题1．以下结论正确的选项是〔〕．A．两个全等的图形一定成轴对称B．两个全等的图形一定是轴对称图形C．两个成轴对称的图形一定全等D．两个成轴对称的图形一定不全等2．以下说法中正确的有〔〕．①角的两边关于角平分线对称;②两点关于连接它的线段的中垂线为对称;③成轴对称的两个三角形的对应点，或对应线段，或对应角也分别成轴对称．④到直线L距离相等的点关于L对称A．1个 B．2个 C．3个 D．4个3．以下说法错误的选项是〔〕．A．等边三角形是轴对称图形;B．轴对称图形的对应边相等，对应角相等;C．成轴对称的两条线段必在对称轴一侧;D．成轴对称的两个图形对应点的连线被对称轴垂直平分.二、填空题4．轴对称图形对应点连线被________，对应角对应线段都________．5．设A、B两点关于直线MN成轴对称，那么______垂直平分______．三、解答题6．找出图中是轴对称图形的图形，并找出两对对应点、两对对应线段、两对对应角．7．如图，将正方形ABCD绕A点按逆时针方向旋转60°至正方形AB′C′D′，那么旋转前后组成的图形是轴对称图形吗？假设是轴对称图形，画出它的对称轴，并求出∠DAB′的度数．◆能力提高一、填空题8．如图，矩形ABCD沿AE折叠，使点D落在BC边上的点F处，如果∠BAF=60°，那么∠DAE=_________．9．Rt△ABC中，斜边AB=2BC，以直线AC为对称轴，点B的对称点是B′，如下图，那么与线段BC相等的线段是______，与线段AB相等的线段是_______和_______．与∠B相等的角是_______和_______，因此，∠B=________．二、解答题10．如图，∠AOB内一点P，分别画出P关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N，假设P1P2=5cm，那么△PMN的周长为多少？参考答案1．C 2．C 3．C 4．略 5．直线MN，线段AB6．图A是轴对称图形．如图，假设以EF为对称轴，由点A与点B，点M与点N，点C与点D等是对称点，线段AG与BH，CM与DN，PG与PH等是对应线段，∠A与∠B，∠C与∠D，∠AMC与∠BND等是对应角．7．是轴对称图形，∠DAB′=30°8．15°9．B′C，BB′，AB′，∠BAB′，∠B′，60°10．∵P，P1，P，P2关于OA，OB对称，∴PM=P1M，PN=P2N，∴△PMN的周长=P1P2，∴△PMN的周长是5cm．4.4 数据的离散程度一、选择题〔每题6分，共36分〕1.如图是甲.乙两位同学5次数学考试成绩的折线统计图，你认为成绩较稳定的是〔〕2.某工厂为了选拔1名车工参加加工直径为10mm 的精密零件的技术比赛，随机抽取甲.乙两S 2甲.S 2乙的大小〔 〕 A.S 2甲＞乙甲乙 甲乙甲≤S 2 3.人数相等的甲.乙两班学生参加了同一次数学测验，班级平均分和方差如下：甲x =80，乙x =80，s 2甲=240，s 2乙 =180，那么成绩较为稳定的班级为〔 〕4.以下统计量中，能反映一名同学在7～9年级学段的学习成绩稳定程度的是〔 〕5.某车间6月上旬生产零件的次品数如下〔单位：个〕：0，2，0，2，3，0，2，3，1，2，那么在这10天中该车间生产零件的次品数的〔 〕6.在甲.乙两块试验田内，对生长的禾苗高度进行测量，分析数据得：甲试验田内禾苗高度数据的方差比乙实验田的方差小，那么〔 〕二、填空题〔每题6分，共36分〕7.5名同学目测同一本教科书的宽度时，产生的误差如下〔单位：cm 〕：0，2，－2，－1，1，那么这组数据的极差为__________cm.8.五个数1，2，4，5，a 的平均数是3，那么a= ，这五个数的方差为 . 9.一组数据1，2，1，0，－1，－2，0，－1，那么这组数据的平均数为 ，中位数为 ，方差为 .10.某校高一新生参加军训，一学生进行五次实弹射击的成绩〔单位：环〕如下：8，6，10，7，9，那么这五次射击的平均成绩是____环，中位数_____环，方差是______环2. 11. .12.数据a.b.c 的方差是1，那么4a ，4b ，4c 的方差是 . 三、解答题〔共28分〕13.〔8分〕某学生在一学年的6次测验中语文.数学成绩分别为〔单位：分〕：语文：80，84，88，76，79，85数学：80，75，90，64，88，95试估计该学生是数学成绩稳定还是语文成绩稳定？14.〔10分〕在某次体育活动中，统计甲.乙两班学生每分钟跳绳的成绩〔单位：次〕情况如下表：班级参加人数平均次数中位数方差甲班 55 135 149 190乙班 55 135 151 110 下面有三种说法：〔1〕甲班学生的平均成绩高于乙班的学生的平均成绩；〔2〕甲班学生成绩的波动比乙班成绩的波动大；〔3〕甲班学生成绩优秀的人数比乙班学生成绩优秀的人数〔跳绳次数≥150次为优秀〕少，试判断上述三个说法是否正确？请说明理由.15.〔10分〕某校要从小王和小李两名同学中挑选一人参加全国数学竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：根据上表解答以下问题：〔1姓名极差〔分〕平均成绩〔分〕中位数〔分〕众数〔分〕方差小王40 80 75 75 190小李〔2视为优秀，那么小王.小李在这五次测试中的优秀率各是多少？〔3〕历届比赛说明，成绩到达80分以上〔含80分〕就很可能获奖，成绩到达90分以上〔含90分〕就很可能获得一等奖，那么你认为应选谁参加比赛比拟适宜？说明你的理由.参考答案1.A2.A3.B4.D5.D6.B7.48.3 29.0 0 2310.8 8 2 11.乙13.语文平均分为82分，数学的平均分为82分，语文的极差为12分，数学的极差为31分，从极差上看，该同学语文成绩相对稳定些，当然也可通过求方差来判别.14.从表中可以看出，甲班学生平均成绩为135，乙班学生平均成绩也是135，因而甲.乙两班平均成绩相同，所以〔1〕的说法是错误的；因s 2甲=190> s 2乙=110，故甲的波动比乙大，所以〔2〕的说法是正确的；从中位数上看，甲班学生跳绳次数有27人少于149次，27人大于149次，而乙班学生跳绳次数151次的必有27人，故必有至少28人跳绳次数高于150次，因而甲班学生成绩的优秀人数比乙班少，从而知〔3〕是正确的. 15.〔1〕极差：90－70＝20平均成绩：〔70＋90＋80＋80＋80〕÷5＝80中位数：将这组数据按从小到大的顺序排列：70.80.80.80.90，就会得到中位数是80. 众数：在这组数据中80出现了3次，出现次数最多，因此这组数据的众数是80方差：2222221[(7080)(9080)(8080)(8080)(8080)]5s =-+-+-+-+-＝40〔2〕在这五次考试中，成绩比拟稳定的是小李，小王的优秀率为40%，小李的优秀率为80%〔3〕方案一：我选小李去参加比赛，因为小李的优秀率高，有4次得80分，成绩比拟稳定，获奖时机大方案二：我选小王去参加比赛，因为小王的成绩获得一等奖的机率较高，有2次90分以上〔含90分〕因此有可能获得一等奖.。

青岛版八年级上册数学第2章图形的轴对称含答案一、单选题(共15题，共计45分)1、下列图形具有两条对称轴的是（）A.等边三角形B.平行四边形C.矩形D.正方形2、已知等腰△ABC的周长为10，若设腰长为x，则x的取值范围是（）A. ＜x＜5B.0＜x＜2.5C.0＜x＜5D.0＜x＜103、如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（）A.80°B.60°C.50°D.40°4、如图，中，，是中点，下列结论中错误的是（）．A. B. C. 平分 D.5、如图，Rt△ABC中，∠BAC=90°，AB=AC，将△ABC绕点C顺时针旋转40°得到△A＇B＇C，CB＇与AB相交于点D，连接AA＇，则∠B＇A＇A的度数为（）A.10°B.15°C.20°D.30°6、如图，点P是∠AOB的角平分线上一点，过点P作PC⊥OA于点C，且PC=3，则点P到OB的距离为（）A.3B.4C.5D.67、如图，将四根长度相等的细木条首尾相连，用钉子钉成四边形，转动这个四边形，使它形状改变，当，时，等于（）A. B. C. D.8、等腰三角形底边长为6，周长为16，则三角形的面积为（）A.30B.25C.24D.129、下列图形中，既是轴对称图形又是中心对称图形的是（）A. 正方形B. 等边三角形C. 平行四边形D. 直角三角形10、如图，△ABC中，AB=AC，BC=5，，于D，EF垂直平分AB，交AC于F，在EF上确定一点P使最小，则这个最小值为（）A.3B.4C.5D.611、下列图形中，不是轴对称图形的是（）A. B. C. D.12、如图，在△ABC中，∠C=90°，∠CAB=50°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（）A.40°B.55°C.65°D.75°13、若等腰三角形的一个内角等于50°，则另外两个角的度数分别为A.50°、80°B.65°，65°C.50°、65°或65°，80° D.50°、80或65°，65°14、下列图形中，不是轴对称图形的是（）A. B. C. D.15、如图，△ABC 中，将∠A 沿 DE 翻折后，∠CEA′、∠BDA′、∠A 三者之间的关系是（）A.∠CEA′＝∠BDA′＋∠AB.∠CEA′－3∠A＝∠BDA′C.∠CEA′＝2(∠BDA′＋∠A)D.∠CEA′－∠BDA′＝2∠A二、填空题(共10题，共计30分)16、如图，在中，分别以点和为圆心，大于的长为半径画弧，两弧相交于，，作直线，交于点，连接。

2.2轴对称的基本性质同步训练题一、选择题（共10小题）1、正方形ABCD边长为a，点E、F分别是对角线BD上的两点，过点E、F分别作AD、AB的平行线，如图，则图中阴影部分的面积之和等于（）A、a2B、 0.25a2C、 0.5a2D、 2（1题图）（2题图）（3题图）（9题图）2、如图，若▱ABCD与▱BCFE关于BC所在直线对称，∠ABE=86°，则∠E等于（）A、137°B、104°C、94°D、86°3、如图，△ABC与△DEF关于直线MN轴对称，则以下结论中错误的是（）A、AB∥DFB、∠B=∠EC、AB=DED、AD的连线被MN垂直平分4、下列说法中不正确的是（）A、线段有1条对称轴B、等边三角形有3条对称轴C、角只有1条对称轴D、底与腰不相等的等腰三角形只有一条对称轴5、下列图形中对称轴最多的是（）A、等腰三角形B、正方形C、圆形D、线段6、点M（﹣2，1）关于x轴的对称点N的坐标是（）A、（2，1）B、（﹣2，1）C、（﹣2，﹣1）D、（2，﹣1）7、在平面直角坐标系中，点P（﹣2，3）关于y轴的对称点的坐标（）A、（﹣2，﹣3）B、（2，﹣3）C、（﹣2，3）D、（2，3）8、在平面直角坐标系中，已知点A（m，3）与点B（4，n）关于y轴对称，那么（m+n）2015的值为（）A、﹣1B、 1C、﹣72015D、 720159、如图，△ABC的顶点都在正方形网格格点上，点A的坐标为（﹣1，4）、将△ABC沿y轴翻折到第一象限，则点C的对应点C′的坐标是（）A、（3，1）B、（﹣3，﹣1）C、（1，﹣3）D、（3，﹣1）10、如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（）A、 B、 2 C、 2 D、二、填空题（共10小题）11、如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A 落在边CB上A′处，折痕为CD，则∠A′DB为。

八年级数学上册《第二章图形的轴对称》同步练习题及答案(青岛版）学校:___________班级：___________姓名：___________考号：___________一、选择题1.下列说法正确的是（）A.任何一个图形都有对称轴;B.两个全等三角形一定关于某直线对称;C.若△ABC与△A′B′C′成轴对称，则△ABC≌△A′B′C′;D.点A，点B在直线1两旁，且AB与直线1交于点O，若AO=BO，则点A与点B•关于直线l 对称.2.小明将一正方形纸片画分成16个全等的小正方形，且如图所示为他将其中四个小正方形涂成灰色的情形．若小明想再将一小正方形涂成灰色，使此纸片上的灰色区域成为线对称图形，则此小正方形的位置为 ( )A.第一列第四行B.第二列第一行C.第三列第三行D.第四列第一行3.如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是( )A.AB=A′B′B.BC∥B′C′C.直线l⊥BB′D.∠A′=120°4.如图所示,序号(1)(2)(3)(4)对应的四个三角形，都是△ABC这个图形进行了一次变换之后得到的，其中是通过轴对称得到的是( )ACB(1)(2)(3)(4)A.(1)B.(2)C.(3)D.(4)5.已知两条互不平行的线段AB和A′B′关于直线1对称，AB和A′B′所在的直线交于点P，下面四个结论：①AB=A′B′；②点P在直线1上；③若A、A ′是对应点，则直线1垂直平分线段AA′；④若B、B′是对应点，则PB=PB′.其中正确的是（）A.①③④B.③④C.①②D.①②③④6.如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是( )A.AB=A′B′B.BC∥B′C′C.直线l⊥BB′D.∠A′=120°7.如图，在3×3的正方形网格中有四个格点A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是( )A.A点B.B点C.C点D.D点8.如图，由4个小正方形组成的方格中，△ABC的顶点都在格点上，在这个方格中再画出一个三角形，使它的顶点都在格点上，且与△ABC关于某条直线成轴对称，这样的三角形共有( )A.1个B.2个C.3个D.4个二、填空题9.由一个平面图形可以得到它关于某条直线对称的图形，•这个图形与原图形的_________、___________完全一样.10.如图，∠A＝29°，∠C′＝62°，△ABC与△A′B′C′关于直线l对称，则∠B＝_____．11.如图是4×4的正方形网格，再把其中一个白色小正方形涂上阴影，使整个阴影部分成为轴对称图形，这样的白色小正方形有________个．12.如图，在正方形方格中，阴影部分是涂黑7个小正方形所形成的图案，再将方格内空白的一个小正方形涂黑，使得到的新图案成为一个轴对称图形的涂法有种.13.如图，正三角形网络中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有________种．14.如图，在△ABC中，AB=3，AC=4，AB⊥AC，EF垂直平分BC，点P为直线EF上一动点，则△ABP周长的最小值是．三、解答题15.下列图形是否是轴对称图形，画出轴对称图形的所有对称轴.思考：正三角形有条对称轴；正四边形有条对称轴；正五边形有条对称轴；正六边形有条对称轴；正n边形有条对称轴.当n越来越大时，正多边形接近于什么图形？它有多少条对称轴？16.认真观察图(1)的4个图中阴影部分构成的图案，回答下列问题：(1)请写出这四个图案都具有的两个共同特征.特征1：______________________________________________；特征2：______________________________________________.(2)请在图(2)中设计出你心中最美丽的图案，使它也具备你所写出的上述特征.17.如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.18.认真观察图①中的四个图中阴影部分构成的图案,其中每个小正方形的边长为1,回答下列问题:(1)请写出这四个图案都具有的两个特征.特征1:特征2:(2)请在图②中设计一个你心中最美丽的图案,使它也具备你所写出的上述特征.19.如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.试说明:点E,F关于AD对称.20.如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.(1)写出图中一对全等的三角形,并写出它们的所有对应角.(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)?(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.答案1.C2.B3.B4.A.5.D6.B.7.B8.D.9.答案为：形状；大小10.答案为：89°.11.答案为：412.答案为：3.13.答案为：3.14.答案为：7.15.解：正三角形有3条对称轴；正四边形有4条对称轴；正五边形有5条对称轴；正六边形有6条对称轴；正n边形有n条对称轴.当n越来越大时，正多边形接近于圆形，它有无数条对称轴.故答案为：3，4，5，6，n.作图如下：16.解：(1)特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些图形的面积都等于4个单位面积；(2)满足条件的图形有很多，只要画正确一个，都可以得满分.17.解:由折叠可知：∠ABH=∠EBH=12∠ABD,∠CDG=∠GDF=12∠CDB∠HEB=∠A=∠GFD=∠C=90°AB=BE,CD=FD.因为AB∥CD所以∠ABD=∠CDB.所以∠EBH=∠GDF.因为AB=CD所以BE=DF.所以△BHE≌△DGF.18.解:(1)都是轴对称图形;面积都是4(2)答案不唯一,只要画出一个满足条件的图案即可.如图.19.解:如图,连接EF交AD于点G因为AD平分∠BAC,所以∠EAD=∠FAD.又因为∠AED=∠AFD,AD=AD所以Rt△ADE≌Rt△ADF(AAS).所以AE=AF.又∠EAG=∠FAG,AG=AG,所以△AEG≌△AFG.所以EG=FG,∠AGE=∠AGF.又∠AGE+∠AGF=180°所以∠AGE=∠AGF=90°.所以AD垂直平分EF.所以点E,F关于AD对称.20.解:(1)△EAD≌△EA'D,其中∠EAD=∠EA'D∠AED=∠A'ED,∠ADE=∠A'DE.(2)∠1=180°-2x,∠2=180°-2y.(3)∠1+∠2=360°-2(x+y)=360°-2(180°-∠A)=2∠A. 规律为∠1+∠2=2∠A.。