第3章 机器人导论操作臂运动学
- 格式:ppt
- 大小:4.99 MB
- 文档页数:66




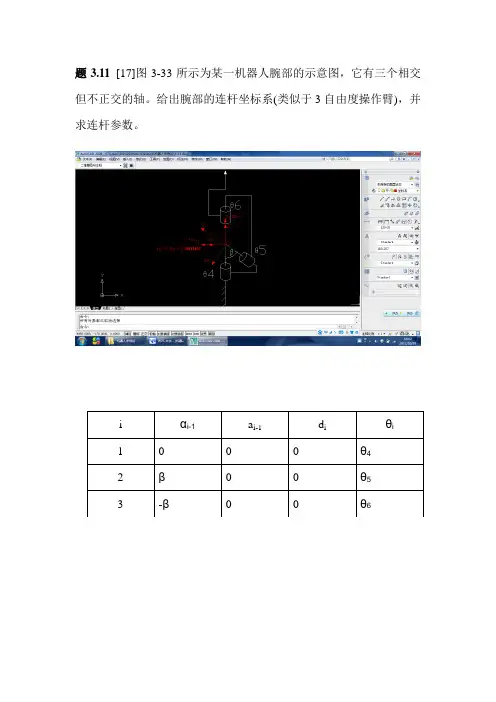
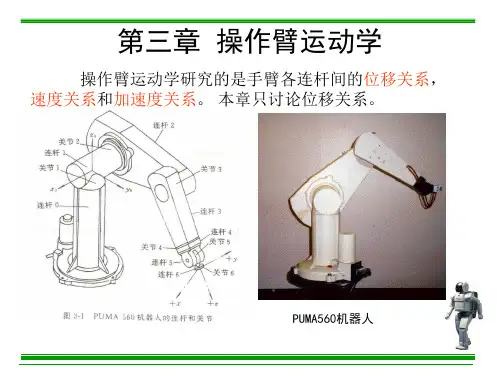
第3章工业机器人运动学和动力学机器人操作臂可看成一个开式运动链,它是由一系列连杆通过转动或移动关节串联而成。
开链的一端固定在基座上,另一端是自由的,安装着工具,用以操作物体,完成各种作业。
关节由驱动器驱动,关节的相对运动导致连杆的运动,使手爪到达所需的位姿。
在轨迹规划时,最感兴趣的是末端执行器相对于固定参考系的空间描述。
为了研究机器人各连杆之间的位移关系,可在每个连杆上固接一个坐标系,然后描述这些坐标系之间的关系。
Denavit和Hartenberg提出一种通用方法,用一个4*4的齐次变换矩阵描述相邻两连杆的空间关系,从而推导出“手爪坐标系”相对于“参考系”的等价齐次变换矩阵,建立出操作臂的运动方程。
称之为D-H矩阵法。
3.1 工业机器人的运动学教学时数:4学时教学目标:理解工业机器人的位姿描述和齐次变换;掌握齐次坐标和齐次变换矩阵的运算;理解连杆参数、连杆变换和运动学方程的求解;教学重点:掌握齐次变换及运动学方程的求解教学难点:齐次变换及运算教学方法:讲授教学步骤:齐次变换有较直观的几何意义,而且可描述各杆件之间的关系,所以常用于解决运动学问题。
已知关节运动学参数,求出末端执行器运动学参数是工业机器人正向运动学问题的求解;反之,是工业机器人逆向运动学问题的求解。
3.1.1 工业机器人位姿描述1.点的位置描述在选定的指教坐标系{A}中,空间任一点P的位置可用3*1的位置矢量表示,其左上标代表选定的参考坐标系。
2.点的齐次坐标如果用四个数组成4*1列阵表示三维空间直角坐标系{A}中点P,则该列阵称为三维空间点P的齐次坐标,如下:必须注意,齐次坐标的表示不是惟一的。
我们将其各元素同乘一个非零因子后,仍然代表同一点P,即其中:,,。
该列阵也表示P点,齐次坐标的表示不是惟一的。
3.坐标轴方向的描述用i、j、k分别表示直角坐标系中X、Y、Z坐标轴的单位向量,用齐次坐标来描述X、Y、Z轴的方向,则有,,从上可知,我们规定:4*1列阵中第四个元素为零,且,则表示某轴(某矢量)的方向。



机器人手臂的运动学与控制研究第一章:引言随着制造业、汽车工业、军事、医疗等领域的不断发展,机器人技术逐渐成为了人工智能领域的热门话题。
其中,机器人手臂是机器人中最常见的机械臂,其运动学和控制研究对于机器人技术的发展至关重要。
本文旨在深入探究机器人手臂的运动学与控制研究,为读者了解机器人手臂的基本结构、运动学、控制方式以及相关发展提供帮助。
第二章:机器人手臂的基本结构机器人手臂一般由底座、臂段、关节、末端执行器等主要组成部分构成。
其中,底座固定在地面或平台上,从而支撑机器人手臂的其他部分。
臂段是机器人手臂的主体,根据实际需要可以设置多个臂段。
每个臂段之间通过关节相互连接,在关节处用驱动器驱动,实现机械臂的运动。
末端执行器通常包括夹爪、工具、传感器等,用于完成特定的任务。
第三章:机器人手臂的运动学机器人手臂的运动学是指机器人手臂在三维空间中的运动方式。
机器人手臂的运动可以分为直线运动和旋转运动两种类型。
而机器人手臂的运动则是由机器人各个关节的运动所组成的。
对于机器人手臂的运动学研究,则主要包括正运动学与逆运动学两个方面。
正运动学是指已知机器人关节的转动角度,如何确定机器人末端执行器在三维空间中的位置和方向。
反之,逆运动学是指已知机器人末端执行器在三维空间中的位置和方向,如何确定机器人各关节的转动角度。
在机器人手臂运动学模型中,通常采用DH方法来建立解析式。
第四章:机器人手臂的控制机器人手臂的控制是机器人手臂的关键技术之一。
基于运动学模型的控制方法有点动控制、反馈线性化控制、自适应控制和非线性控制四种类型。
实际中,机器人手臂通常采用PID控制,通过控制机器人手臂的关节旋转角度,实现机器人手臂的精确定位、准确抓取等任务。
同时,近些年来机器学习技术的发展,也日趋应用于机器人手臂的控制之中。
第五章:机器人手臂的发展机器人手臂的发展正向着更加灵活、高效的方向不断发展。
近年来,增材制造、双臂机器人、软体机器人等技术的出现,为机器人手臂的发展提供了新的思路。