2019年广西防城港市防城区实验高级中学 (高中部)高考数学选择题专项训练(一模)

防城区高中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 若函数f （x ）=log a （2x 2+x ）（a ＞0且a ≠1）在区间（0，）内恒有f （x ）＞0，则f （x ）的单调递增区间为（ ）A ．（﹣∞，）B ．（﹣，+∞）C ．（0，+∞）D ．（﹣∞，﹣）2． 已知命题p ：对任意()0x ∈+∞，，48log log x x <，命题：存在x ∈R ，使得tan 13x x =-，则下列命题为真命题的是（ ）A ．p q ∧B ．()()p q ⌝∧⌝C ．()p q ∧⌝D ．()p q ⌝∧3． 已知向量(,1)a t = ，(2,1)b t =+ ，若||||a b a b +=-，则实数t =（ ） A.2- B.1- C. 1 D. 2【命题意图】本题考查向量的概念，向量垂直的充要条件，简单的基本运算能力．4． 已知函数22()32f x x ax a =+-，其中(0,3]a ∈，()0f x ≤对任意的[]1,1x ∈-都成立，在1和两数间插入2015个数，使之与1，构成等比数列，设插入的这2015个数的成绩为T ，则T =（ ） A ．20152B ．20153C ．201523D ．2015225． 若不等式1≤a ﹣b ≤2，2≤a+b ≤4，则4a ﹣2b 的取值范围是（ ）A ．[5，10]B ．（5，10）C ．[3，12]D ．（3，12）6． 半径R 的半圆卷成一个圆锥，则它的体积为（ ）A ．πR 3B ．πR 3C ．πR 3D ．πR 37． 若a ＜b ＜0，则下列不等式不成立是（ ）A ．＞B ．＞C ．|a|＞|b|D ．a 2＞b 28． 已知双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为21F F 、，过2F 的直线交双曲线于Q P ,两点且1PF PQ ⊥，若||||1PF PQ λ=，34125≤≤λ，则双曲线离心率e 的取值范围为（ ）.A. ]210,1(B. ]537,1(C. ]210,537[ D. ),210[+∞ 第Ⅱ卷（非选择题，共100分）9． 设函数的集合，平面上点的集合，则在同一直角坐标系中，P 中函数的图象恰好经过Q 中两个点的函数的个数是 A4 B6 C8 D1010．已知双曲线的方程为﹣=1，则双曲线的离心率为（ ）A ．B ．C ．或 D ．或11．函数y=x 2﹣2x+3，﹣1≤x ≤2的值域是（ ） A ．RB ．[3，6]C ．[2，6]D ．[2，+∞）12．函数sin()y A x ωϕ=+在一个周期内的图象如图所示，此函数的解析式为（ ） A ．2sin(2)3y x π=+B ．22sin(2)3y x π=+C ．2sin()23x y π=-D ．2sin(2)3y x π=-二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知各项都不相等的等差数列{}n a ，满足223n n a a =-，且26121a a a =∙，则数列12n n S -⎧⎫⎨⎬⎩⎭项中 的最大值为_________. 14．设全集______.15．设所有方程可以写成（x ﹣1）sin α﹣（y ﹣2）cos α=1（α∈[0，2π]）的直线l 组成的集合记为L ，则下列说法正确的是 ； ①直线l 的倾斜角为α；②存在定点A ，使得对任意l ∈L 都有点A 到直线l 的距离为定值； ③存在定圆C ，使得对任意l ∈L 都有直线l 与圆C 相交； ④任意l 1∈L ，必存在唯一l 2∈L ，使得l 1∥l 2； ⑤任意l 1∈L ，必存在唯一l 2∈L ，使得l 1⊥l 2．16．定义在R 上的可导函数()f x ，已知()f x y e=′的图象如图所示，则()y f x =的增区间是 ▲ ．70分。

同步测试一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

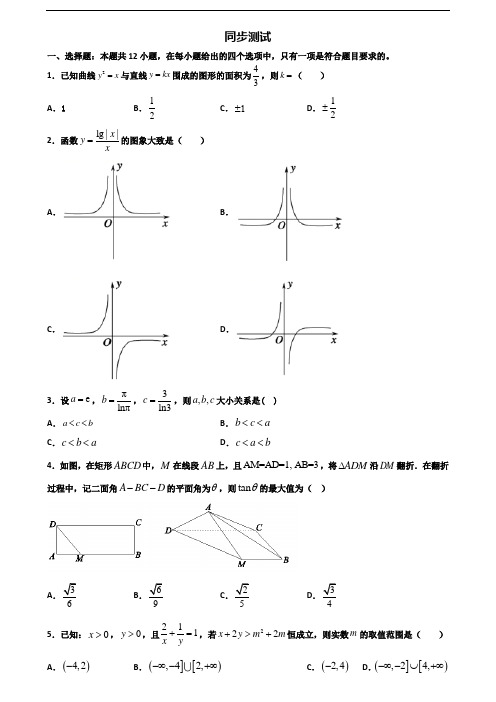
1．已知曲线2y x =与直线y kx =围成的图形的面积为43，则k =（ ） A ．1 B ．12C ．±1D ．12±2．函数lg ||x y x=的图象大致是（ ） A ． B ．C ．D ．3．设e a =，πln πb =，3ln3c =，则,,a b c 大小关系是( ) A ．a c b << B ．b c a << C ．c b a <<D ．c a b <<4．如图，在矩形ABCD 中，M 在线段AB 上，且AM=AD=1, AB=3，将ADM ∆沿DM 翻折．在翻折过程中，记二面角A BC D --的平面角为θ，则tan θ的最大值为（ ）A 3B 6C 2D 35．已知：0x >，0y >，且211+=，若222x y m m +>+恒成立，则实数m 的取值范围是（ ）6．抛物线214y x =的焦点到双曲线2213x y -=的渐近线的距离为（ ）A ．12B ．32C ．1D ．37．某同学家门前有一笔直公路直通长城，星期天，他骑自行车匀速前往旅游，他先前进了akm ，觉得有点累，就休息了一段时间，想想路途遥远，有些泄气，就沿原路返回骑了()bkm b a <, 当他记起诗句“不到长城非好汉”，便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为（ ）A ．B ．C ．D ．8．已知随机变量服从正态分布，且，则实数的值为（）A ．B ．C ．D ．9．已知函数f(x)是定义在R 上的增函数,f(x)+2>f ' (x),f(0)=1,则不等式ln[f(x)+2]>ln3+x 的解集为（ ） A ．(一∞,0)B ．(0,+∞)C ．(一∞,1)D ．(1,+∞)10．函数2()()41x x x e e f x x --=-的部分图象大致是（ ） A ． B ．C ．D ．2段MP 上，且满足2Q NP =N ，GQ 0⋅NP =，则点G 的轨迹方程是（ ）A ．22194x y +=B ．2213631x y +=C ．22194x y -=D ．2213631x y -=12．抛物线24y x =的焦点为F ，点(5,3)A ，P 为抛物线上一点，且P 不在直线AF 上，则PAF ∆周长的最小值为 A ．6B ．8C ．11D ．13二、填空题：本题共4小题13．用数字0，1，2，3，4，5组成没有重复数字的五位数，其中能被5整除的数共有______个． 14．函数f （x ）＝ax 3＋bx 2＋cx ＋d 的部分数值如下表：则函数y ＝lgf （x ）的定义域为__________．15．三角形ABC 中，D 是BC 边上一点，60BAD DAC ∠=∠=︒，7BC =，且三角形ABD 与三角形ADC 面积之比为53，则AD =__________． 16．如果关于x 的不等式|3||4|x x a -++<+a 的取值范围是______. 三、解答题：解答应写出文字说明、证明过程或演算步骤。

广西防城港市数学高三试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高二下·南山期末) 在复平面内，复数对应的点位于（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限2. （2分） (2018高二上·鞍山期中) 设不等式x2-2ax+a+2≤0的解集为A，若A⊆[1，3]，则实数a的取值范围是（）A .B .C .D .3. （2分）设函数f（x）（x∈R）是以2为最小正周期的周期函数，且x∈[0，2]时，f（x）=（x﹣1）2 ，则f（）=（）A .B . ﹣C .D . ﹣4. （2分） (2016高一下·益阳期中) 在四边形ABCD中，，，，则四边形ABCD的形状是（）A . 长方形B . 平行四边形C . 菱形D . 梯形5. （2分） (2018高一下·渭南期末) 下列函数中，最小正周期为且图像关于原点对称的函数是（）A .B .C .D .6. （2分）(2019·怀化模拟) 《镜花缘》是清代文人李汝珍创作的长篇小说，书中有这样一个情节：一座楼阁到处挂满了五彩缤纷的大小灯球，灯球有两种，一种是大灯下缀2个小灯，另一种是大灯下缀4个小灯，大灯共360个，小灯共1200个.若在这座楼阁的灯球中，随机选取一个灯球，则这个灯球是大灯下缀4个小灯的概率为（）A .B .C .D .7. （2分）已知抛物线的焦点与椭圆的一个焦点重合，它们在第一象限内的交点为，且与轴垂直，则椭圆的离心率为（）A .B .C .D .8. （2分）若角α的终边经过点（﹣3λ，4λ），且λ≠0，则等于（）A .B .C . ﹣7D . 79. （2分） (2019高二上·定远月考) 阅读如图的程序框图，运行相应的程序，则输出S的值为（）A . 3B . 4C . 6D . 710. （2分）(2019·南昌模拟) 平行六面体的底面是边长为4的菱形，且，点在底面的投影是的中点，且，点关于平面的对称点为，则三棱锥的体积是（）A . 4B .C .D . 811. （2分）曲线y= 在点（1，-1）处的切线方程为（）A . y=x-2B . y=-3x+2C . y=2x-3D . y= -2x+112. （2分）(2017·桂林模拟) 已知双曲线与双曲线的离心率相同，且双曲线C2的左、右焦点分别为F1 ， F2 ， M是双曲线C2一条渐近线上的某一点，且OM⊥MF2 ，，则双曲线C2的实轴长为（）A . 4B .C . 8D .二、填空题 (共4题；共4分)13. （1分） (2019高一上·柳州月考) 如图是正方体的平面展开图．在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个命题中，正确命题的序号是________．14. （1分）(2020·江西模拟) 已知实数x，y满足条件，则的取值范围为________．15. （1分） (2018高一上·河北月考) 以下说法中正确的是________．①函数在区间上单调递减；②函数的图象过定点；③若是函数的零点，且，则；④方程的解是16. （1分）(2018·南京模拟) 若不等式对任意都成立，则实数的最小值为________．三、解答题 (共7题；共75分)17. （10分） (2019高三上·广州月考) 已知为单调递增的等差数列，，，设数列满足， .（1）求数列的通项；（2）求数列的前项和 .18. （10分） (2020高一下·徐州期末) 手机支付也称为移动支付(Mobile Payment)，是当今社会比较流行的一种付款方式.某金融机构为了了解移动支付在大众中的熟知度，对15—65岁的人群作了问题为“你会使用移动支付吗？”的随机抽样调查，把回答“会”的100个人按照年龄分成5组，绘制成如图所示的频数分布表和频率分布直方图.（1）求x，a的值；（2）若从第1，3组中用分层抽样的方法抽取5人，求两组中分别抽取的人数；（3）在（2）抽取的5人中再随机抽取2人，求所抽取的2人来自同一个组的概率.19. （10分） (2018高二下·顺德期末) 已知函数，为自然对数的底数.（1）求曲线在处的切线方程；（2）求函数的单调区间与极值.20. （10分） (2019高二上·吉林期中) 已知，分别是椭圆：的左，右焦点，点在椭圆上，且抛物线的焦点是椭圆的一个焦点。

广西防城港市防城区实验高级中学2018-2019学年高二9月月考数学试题解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 高考临近，学校为丰富学生生活，缓解高考压力，特举办一场高三学生队与学校校队的男子篮球比赛．由于爱好者众多，高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队．首发要求每个班至少1人，至多2人，则首发方案数为（ ） A ．720 B ．270 C ．390 D ．3002． 已知集合{2,1,0,1,2,3}A =--，{|||3,}B y y x x A ==-∈，则A B =（ ）A ．{2,1,0}--B ．{1,0,1,2}-C ．{2,1,0}--D ．{1,,0,1}-【命题意图】本题考查集合的交集运算，意在考查计算能力．3． 已知集合},052|{2Z x x x x M ∈<+=，},0{a N =，若∅≠N M ，则=a （ ） A ．1- B ． C ．1-或 D ．1-或2- 4． 已知α，[,]βππ∈-，则“||||βα>”是“βαβαcos cos ||||->-”的（ ） A. 充分必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件【命题意图】本题考查三角函数的性质与充分必要条件等基础知识，意在考查构造函数的思想与运算求解能力.5． 已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y ，若目标函数mx y z -=取得最大值时有唯一的最优解)3,1(，则实数m 的取值范围是（ ）A ．1-<mB ．10<<mC ．1>mD ．1≥m【命题意图】本题考查了线性规划知识，突出了对线性目标函数在给定可行域上最值的探讨，该题属于逆向问题，重点把握好作图的准确性及几何意义的转化，难度中等. 6． 如右图，在长方体中，=11，=7，=12，一质点从顶点A 射向点，遇长方体的面反射（反射服从光的反射原理），将次到第次反射点之间的线段记为，，将线段竖直放置在同一水平线上，则大致的图形是（ ）ABCD7． 已知数列｛n a ｝满足nn n a 2728-+=（*∈N n ）.若数列｛n a ｝的最大项和最小项分别为M 和m ，则=+m M （ ）A ．211 B ．227 C ． 32259 D ．32435 8． 下列给出的几个关系中：①{}{},a b ∅⊆；②(){}{},,a b a b =；③{}{},,a b b a ⊆；④{}0∅⊆,正确的有（ ）个A.个B.个C.个D.个 9． 函数f （x ）＝kx ＋bx ＋1，关于点（－1，2）对称，且f （－2）＝3，则b 的值为（ ）A ．－1B ．1C ．2D ．410．将函数x x f ωsin )(=（其中0>ω）的图象向右平移4π个单位长度，所得的图象经过点 )0,43(π，则ω的最小值是（ ）A ．31B ．C ．35D ． 11．在《张邱建算经》中有一道题：“今有女子不善织布，逐日所织的布比同数递减，初日织五尺， 末一日织一尺，计织三十日”，由此推断，该女子到第10日时，大约已经完成三十日织布总量的（ ） A ．33% B ．49% C ．62% D ．88%12．设1m >，在约束条件,,1.y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数z x my =+的最大值小于2，则m 的取值范围为（ ）A ．(1,12)+B ．(12,)++∞ C. (1,3) D ．(3,)+∞二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知函数5()sin (0)2f x x a x π=-≤≤的三个零点成等比数列，则2log a = .14．等差数列{}n a 中，39||||a a =，公差0d <，则使前项和n S 取得最大值的自然数是________.15．已知圆22240C x y x y m +-++=：，则其圆心坐标是_________，m 的取值范围是________． 【命题意图】本题考查圆的方程等基础知识，意在考查运算求解能力.16．等比数列{a n }的前n 项和S n ＝k 1＋k 2·2n （k 1，k 2为常数），且a 2，a 3，a 4－2成等差数列，则a n ＝________．三、解答题（本大共6小题，共70分。

广西防城港市高级中学2018-2019学年高三上学期第三次月考试卷数学含答案班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知集合A={x|x ＜2}，B={y|y=5x }，则A ∩B=（ ） A ．{x|x ＜2} B ．{x|x ＞2} C ．{x|o ≤x ＜2} D ．{x|0＜x ＜2}2． 已知i z 311-=，i z +=32，其中i 是虚数单位，则21z z 的虚部为（ ） A ．1- B ．54 C ．i - D ．i 54 【命题意图】本题考查复数及共轭复数的概念，复数除法的运算法则，主要突出对知识的基础性考查，属于容易题.3． 复数满足2＋2z1－i ＝i z ，则z 等于（ ）A ．1＋iB ．－1＋iC ．1－iD ．－1－i 4． 已知m ，n 为不同的直线，α，β为不同的平面，则下列说法正确的是（ ） A ．m ⊂α，n ∥m ⇒n ∥αB ．m ⊂α，n ⊥m ⇒n ⊥αC ．m ⊂α，n ⊂β，m ∥n ⇒α∥βD ．n ⊂β，n ⊥α⇒α⊥β5． 已知向量(,2)a m =，(1,)b n =-（0n >），且0a b ⋅=，点(,)P m n 在圆225x y +=上，则|2|a b +=（ ）A B ． C ． D ．6． 已知函数()cos (0)f x x x ωωω=+>，()y f x =的图象与直线2y =的两个相邻交点的距离等于π，则()f x 的一条对称轴是（ ）A ．12x π=-B ．12x π=C ．6x π=-D ．6x π=7． 定义运算，例如．若已知，则=（ ）A ．B ．C ．D ．8． 已知全集I={1，2，3，4，5，6}，A={1，2，3，4}，B={3，4，5，6}，那么∁I （A ∩B ）等于（ ） A ．{3，4} B ．{1，2，5，6} C ．{1，2，3，4，5，6} D ．∅9． 若集合,则= ( )ABC D10．设曲线2()1f x x =+在点(,())x f x 处的切线的斜率为()g x ，则函数()cos y g x x =的部分图象 可以为（ ）A ．B ． C. D ．11．函数21()ln 2f x x x ax =++存在与直线03=-y x 平行的切线，则实数a 的取值范围是（ ） A. ),0(+∞ B. )2,(-∞ C. ),2(+∞ D. ]1,(-∞【命题意图】本题考查导数的几何意义、基本不等式等基础知识，意在考查转化与化归的思想和基本运算能力． 12．奇函数()f x 满足()10f =，且()f x 在()0+∞，上是单调递减，则()()210x f x f x -<--的解集为（ ）A ．()11-，B ．()()11-∞-+∞，，C ．()1-∞-，D ．()1+∞，二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知x ，y 为实数，代数式2222)3(9)2(1y x x y ++-++-+的最小值是 . 【命题意图】本题考查两点之间距离公式的运用基础知识，意在考查构造的数学思想与运算求解能力. 14． 设函数()xf x e =，()lng x x m =+．有下列四个命题：①若对任意[1,2]x ∈，关于x 的不等式()()f x g x >恒成立，则m e <；②若存在0[1,2]x ∈，使得不等式00()()f x g x >成立，则2ln 2m e <-；③若对任意1[1,2]x ∈及任意2[1,2]x ∈，不等式12()()f x g x >恒成立，则ln 22em <-； ④若对任意1[1,2]x ∈，存在2[1,2]x ∈，使得不等式12()()f x g x >成立，则m e <．其中所有正确结论的序号为 .【命题意图】本题考查对数函数的性质，函数的单调性与导数的关系等基础知识，考查运算求解，推理论证能力，考查分类整合思想.15．不等式()2110ax a x +++≥恒成立，则实数的值是__________.16．阅读下图所示的程序框图，运行相应的程序，输出的n 的值等于_________.三、解答题（本大共6小题，共17．（本题满分15分）已知抛物线C 的方程为22(y px p =>（1）求抛物线C 的方程；（2）过点(1,1)Q 作直线交抛物线C AR ，BR 分别交直线:22l y x =+于M ，N 两点，求MN 最小时直线AB 的方程．【命题意图】本题主要考查抛物线的标准方程及其性质以及直线与抛物线的位置关系等基础知识，意在考查运算求解能力.18．设不等式的解集为.（1）求集合； （2）若，∈，试比较与的大小。

提高练习一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若集合{}{}|23,|14A x x B x x x =-≤≤=-或，则集合A B ⋂=( ) A ．{}34x x x ≤或 B ．{}|13x x -≤≤ C ．{}|34x x ≤<D ．{}|21x x -≤<-2．若()2,1,3a x =-，()1,2,9b y =，如果a 与b 为共线向量，则（ ） A ．1x =，1y = B ．16x =-，32y =C ．1x =-，1y =D ．1x =-，1y =-3．用数学归纳法证明“()()()()12213...21nn n n n n ++⋅⋅⋅+=⋅⋅⋅⋅-”,从“k 到1k +”左端需增乘的代数式为( ) A ．21k +B ．()221k +C ．211k k ++ D ．231k k ++ 4．四大名著是中国文学史上的经典作品，是世界宝贵的文化遗产.在某学校举行的“文学名著阅读月”活动中，甲、乙、丙、丁、戊五名同学相约去学校图书室借阅四大名著《红楼梦》、《三国演义》、《水浒传》、《西游记》（每种名著至少有5本），若每人只借阅一本名著，则不同的借阅方案种数为（ ） A ．54B ．45C ．·45CD ．45A5．抛物线214y x =的焦点到双曲线2213x y -=的渐近线的距离为（ ）A ．12B ．3 C ．1D ．36．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（ ）A ．15B ．16C ．23D ．137．若曲线2y x mx n =++在点（0，n ）处的切线方程x-y+1=0，则（ ） A ．m 1=，n 1= B ．1m =-，n 1= C ．m 1=，n 1=-D ．m 1=-，n 1=-8．六安一中高三教学楼共五层，甲、乙、丙、丁四人走进该教学楼2~5层的某一层楼上课，则满足且仅有一人上5楼上课，且甲不在2楼上课的所有可能的情况有（ ）种 A ．27 B ．81C ．54D ．1089．函数ln xy x=的最大值为（ ） A ．1e -B ．1C ．2eD ．10310．已知空间不重合的三条直线l 、m 、n 及一个平面α，下列命题中的假命题．．．是（ ）． A ．若l m ，m n ，则ln B ．若l α，n α，则l nC ．若l m ⊥，m n ，则l n ⊥D ．若l α⊥，n α，则l n ⊥11．已知集合(){}3=|log 210A x x ≤-，{|B x y ==，全集U =R ，则()UA B ∩等于（ ）A ．1,12⎛⎤⎥⎝⎦B ．20,3⎛⎫ ⎪⎝⎭C ．2,13⎛⎤⎥⎝⎦D ．12,23⎛⎫⎪⎝⎭12．已知()f x 是可导函数，且()()f x f x '<对于x ∈R 恒成立，则 A ．2017(1)(0),(2017)(0)f ef f ef B ．2017(1)(0),(2017)(0)f ef f e f >> C ．2017(1)(0),(2017)(0)f ef f e f >< D ．2017(1)(0),(2017)(0)f ef f e f <<二、填空题：本题共4小题 13．在数列{}n a 中,1121,2nn na a a a +==+,通过计算234,,a a a 的值,可猜想出这个数列的通项公式为n a = 14．某校毕业典礼由6个节目组成，考虑整体效果，对节目演出顺序有如下要求：节目甲必须排在前三位，且节目丙、丁必须排在一起，则该校毕业典礼节目演出顺序的编排方案共有______种. 15．已知函数f （x ）是定义在R 上的偶函数，若对于x≥0，都有f （x+2）=﹣1()f x ，且当x ∈[0，2]时，f （x ）=log 2（x+1），则f （﹣2013）+f （2015）=_____． 16．已知z a bi =+(a b R i ∈，，是虚数单位),12z z C ∈，，定义:()()1212D z z a b D z z z z ==+=-，，，给出下列命题: (1)对任意z C ∈，都有()0D z ＞；(2)若z 是z 的共轭复数,则()()D z D z =恒成立； (3)若()()()1212D z D z z z C =∈，，则12z z =；(4)对任意123z z z C ∈，，，结论()()()131223+D z z D z z D z z ≤，，，恒成立. 则其中所有的真命题的序号是_____________.三、解答题：解答应写出文字说明、证明过程或演算步骤。

广西防城港市高考数学四诊试卷（文科）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）已知全集U={-1,0,1,2}，集合M={-1,2}，，N={0,2}则=A . {0}B . {2}C . {0,1,2}D .2. （2分）设复数z=+i（i为虚数单位），则|z|=（）A .B .C .D . 23. （2分）(2019高二下·长春期末) 设，则“ ”是“直线与平行”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件4. （2分）下列计算正确的是（）A .B .C .D .5. （2分）在内，不等式的解集是（）A .B .C .D .6. （2分）若函数y=f(x)的定义域为[0,1], 则下列函数中可能是偶函数的是（）.A . y=-f(x)B . y=f(3x)C . y=f(-x)D .7. （2分）计算机执行右边程序框图设计的程序语言后，输出的数据是，则判断框内应填（）A . n≤6B . n≤7C . n≤8D . n≤98. （2分）已知，则（）A .B .C .D .9. （2分）(2017·达州模拟) 如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（）A .B .C .D . 3π10. （2分）已知一个三棱锥的主视图与俯视图如图所示，则该三棱锥的侧视图面积为（）A .B .C . 1D .11. （2分）抛物线的标准方程是y2=﹣12x，则其焦点坐标是（）A . （3，0）B . （﹣3，0）C . （0，3）D . （0，﹣3）12. （2分）方程ex﹣x﹣2=0的一个根所在的区间（k，k+1）（k∈N），则k的值为（）A . 0B . 1C . 2D . 3二、填空题 (共4题；共6分)13. （1分）(2018·南宁模拟) 已知函数若，则实数的取值范围为________.14. （1分）已知是抛物线的焦点，点在该抛物线上且位于轴的两侧，（其中为坐标原点），则面积的最小值是________．15. （2分）若变量x，y满足约束条件，目标函数z=2x+y的最大值为7，则目标函数取最小值时的最优解为________ ，实数m的值为________16. （2分）(2019高三上·浙江期末) 在中，内角所对的边分别是 .若，，则 ________，面积的最大值为________.三、解答题 (共7题；共70分)17. （10分）(2017·白山模拟) 在数列{an}中，设f（n）=an ，且f（n）满足f（n+1）﹣2f（n）=2n（n∈N*），且a1=1．（1）设，证明数列{bn}为等差数列；（2）求数列{an}的前n项和Sn ．18. （15分）为了调查甲、乙两个交通站的车流量，随机选取了14天，统计每天上午8：00～12：00间各自的车流量（单位：百辆），得如图所示的统计图，试求：（1）甲、乙两个交通站的车流量的极差分别是多少？（2）甲交通站的车流量在[10，60]间的频率是多少？（3）甲、乙两个交通站哪个站更繁忙？并说明理由．19. （10分） (2019高三上·广州月考) 如图，在直三棱柱中，分别为的中点，， AB=BC=AA1=2 .（1）求证：平面；（2）求三棱锥的体积.20. （10分） (2017高二下·陕西期末) 已知椭圆C的对称中心为坐标原点O，焦点在x轴上，左右焦点分别为F，F，左右顶点分别为A，B，且|F1F2|=4，|AB|=4（1）求椭圆的方程；（2）过F1的直线l与椭圆C相交于M，N两点，若△MF2N的面积为，求直线l的方程．21. （15分）(2014·陕西理) 设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数．（1）令g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+ ，求gn（x）的表达式；（2）若f（x）≥ag（x）恒成立，求实数a的取值范围；（3）设n∈N+ ，比较g（1）+g（2）+…+g（n）与n﹣f（n）的大小，并加以证明．22. （5分）(2018高二下·巨鹿期末) 在平面直角坐标系xoy中，已知直线的参数方程为，直线与抛物线相交于A,B两点，求线段AB的长。

2019-2020学年高考数学模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．执行如图所示的程序框图，则输出的S 的值是（ ）A ．8B ．32C ．64D ．1282．天干地支，简称为干支，源自中国远古时代对天象的观测.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”称为十天干，“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”称为十二地支.干支纪年法是天干和地支依次按固定的顺序相互配合组成，以此往复，60年为一个轮回.现从农历2000年至2019年共20个年份中任取2个年份，则这2个年份的天干或地支相同的概率为（ ） A ．219B ．995C ．4895D ．5193．已知平面向量a ，b 满足()1,2a =-，()3,b t =-，且()a ab ⊥+，则b =（ ） A ．3B 10C ．23D ．54．若函数()()2(2 2.71828 (x)f x x mx e e =-+=为自然对数的底数)在区间[]1,2上不是单调函数，则实数m 的取值范围是( ) A ．510,23⎡⎤⎢⎥⎣⎦B ．510,23⎛⎫⎪⎝⎭C ．102,3⎡⎤⎢⎥⎣⎦D ．102,3⎛⎫⎪⎝⎭5．已知椭圆C 的中心为原点O ，(5,0)F -为C 的左焦点，P 为C 上一点，满足||||OP OF =且||4PF =，则椭圆C 的方程为（ ） A ．221255x y +=B ．2213616x y +=C ．2213010x y +=D ．2214525x y +=6．已知ABC ∆的内角,,A B C 的对边分别是,,,a b c 且444222222a b c a b ca b +++=+，若c 为最大边，则a b c +的取值范围是（ ）A．23 1⎛⎫⎪⎪⎝⎭,B．()1,3C．2313⎛⎤⎥⎝⎦,D．(1,3]7．2021年部分省市将实行“312++”的新高考模式，即语文、数学、英语三科必选，物理、历史二选一，化学、生物、政治、地理四选二，若甲同学选科没有偏好，且不受其他因素影响，则甲同学同时选择历史和化学的概率为A．18B．14C．16D．128．在复平面内，复数z a bi=+（a，b R∈）对应向量OZ（O为坐标原点），设OZ r=，以射线Ox 为始边，OZ为终边旋转的角为θ，则()cos sinz r iθθ=+，法国数学家棣莫弗发现了棣莫弗定理：()1111cos sinz r iθθ=+，()2222cos sinz r iθθ=+，则()()12121212cos sinz z rr iθθθθ=+++⎡⎤⎣⎦，由棣莫弗定理可以导出复数乘方公式：()()cos sin cos sinn nr i r n i nθθθθ+=+⎡⎤⎣⎦，已知()43z i=+，则z=（）A．23B．4 C．83D．169．已知集合{}{}22(,)4,(,)2xA x y x yB x y y=+===，则A B元素个数为( )A．1 B．2 C．3 D．410．已知某几何体的三视图如右图所示，则该几何体的体积为（）A．3 B．103C．113D．8311．数列{}n a的通项公式为()na n c n N*=-∈．则“2c<”是“{}n a为递增数列”的（）条件．A．必要而不充分B．充要C．充分而不必要D．即不充分也不必要12．已知01021:1,log;:,2xp x x q x R e x∃>>∀∈>，则下列说法中正确的是（）A．p q∨是假命题B．p q∧是真命题C ．()p q ∨⌝是真命题 D ．()p q ∧⌝是假命题二、填空题：本题共4小题，每小题5分，共20分。

防城区实验中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 在等比数列}{n a 中，821=+n a a ，8123=⋅-n a a ，且数列}{n a 的前n 项和121=n S ，则此数列的项数n 等于（ ）A ．4B ．5C ．6D ．7【命题意图】本题考查等比数列的性质及其通项公式，对逻辑推理能力、运算能力及分类讨论思想的理解有一定要求，难度中等.2． 已知直线l ⊥平面α，直线m ⊂平面β，有下面四个命题： （1）α∥β⇒l ⊥m ，（2）α⊥β⇒l ∥m ， （3）l ∥m ⇒α⊥β，（4）l ⊥m ⇒α∥β， 其中正确命题是（ ）A ．（1）与（2）B ．（1）与（3）C ．（2）与（4）D ．（3）与（4）3． 若集合A ＝{－1,1}，B ＝{0,2}，则集合{z|z ＝x ＋y ，x ∈A ，y ∈B}中的元素的个数为( )A5 B4 C3 D24． 设公差不为零的等差数列{}n a 的前n 项和为n S ，若4232()a a a =+，则74S a =（ ） A ．74 B ．145C ．7D ．14 【命题意图】本题考查等差数列的通项公式及其前n 项和，意在考查运算求解能力.5． 执行如图所示的程序框图，则输出结果S=（ ）A ．15B ．25C ．50D ．1006． 半径R 的半圆卷成一个圆锥，则它的体积为（ ）A ．πR 3B ．πR 3C ．πR 3D ．πR 37． 设α、β是两个不同的平面，l 、m 为两条不同的直线，命题p ：若平面α∥β，l ⊂α，m ⊂β，则l ∥m ；命题q ：l ∥α，m ⊥l ，m ⊂β，则β⊥α，则下列命题为真命题的是（ ）A ．p 或qB ．p 且qC ．￢p 或qD ．p 且￢q8． 已知函数()cos()3f x x π=+，则要得到其导函数'()y f x =的图象，只需将函数()y f x =的图象（ ）A ．向右平移2π个单位B ．向左平移2π个单位 C. 向右平移23π个单位 D ．左平移23π个单位9． 设集合3|01x A x x -⎧⎫=<⎨⎬+⎩⎭,集合(){}2|220B x x a x a =+++>,若 A B ⊆,则的取值范围（ ）A ．1a ≥B ．12a ≤≤ C.a 2≥ D ．12a ≤< 10．已知数列{}n a 为等差数列，n S 为前项和，公差为d ，若201717100201717S S -=，则d 的值为（ ） A ．120 B ．110C ．10D ．20 二、填空题11．已知过双曲线22221(0,0)x y a b a b-=>>的右焦点2F 的直线交双曲线于,A B 两点，连结11,AF BF ，若1||||AB BF =，且190ABF ∠=︒，则双曲线的离心率为（ ）A ．5-BC ．6- D【命题意图】本题考查双曲线定义与几何性质，意要考查逻辑思维能力、运算求解能力，以及考查数形结合思想、方程思想、转化思想．12．若数列{a n }满足：存在正整数T ，对于任意的正整数n ，都有a n+T =a n 成立，则称数列{a n }为周期为T 的周期数列．已知数列{a n }满足：a1＞=m （m ＞a ），a n+1=，现给出以下三个命题：①若 m=，则a 5=2；②若 a 3=3，则m 可以取3个不同的值；③若 m=，则数列{a n }是周期为5的周期数列．其中正确命题的序号是 ．13．已知两个单位向量,a b 满足：12a b ∙=-，向量2a b -与的夹角为，则cos θ= . 14．某高中共有学生1000名，其中高一年级共有学生380人，高二年级男生有180人.如果在全 校学生中抽取1名学生，抽到高二年级女生的概率为19.0，先采用分层抽样（按年级分层）在全校抽取 100人，则应在高三年级中抽取的人数等于 .15．抛物线24x y =的焦点为F ，经过其准线与y 轴的交点Q 的直线与抛物线切于点P ，则FPQ ∆ 外接圆的标准方程为_________.16．在平面直角坐标系中，(1,1)=-a ，(1,2)=b ，记{}(,)|M O M λμλμΩ==+a b ，其中O 为坐标原点，给出结论如下：①若(1,4)(,)λμ-∈Ω，则1λμ==；②对平面任意一点M ，都存在,λμ使得(,)M λμ∈Ω； ③若1λ=，则(,)λμΩ表示一条直线； ④{}(1,)(,2)(1,5)μλΩΩ=；⑤若0λ≥，0μ≥，且2λμ+=，则(,)λμΩ表示的一条线段且长度为 其中所有正确结论的序号是 ．三、解答题17．如图，四边形ABCD 与A ′ABB ′都是边长为a 的正方形，点E 是A ′A 的中点，AA ′⊥平面ABCD ． （1）求证：A ′C ∥平面BDE ；（2）求体积V A ′﹣ABCD 与V E ﹣ABD 的比值．18．已知数列{a n }满足a 1=，a n+1=a n +（n ∈N *）．证明：对一切n ∈N *，有（Ⅰ）＜；（Ⅱ）0＜a n ＜1．19．（本小题满分10分）选修4-1：几何证明选讲如图，直线PA 与圆O 相切于点A ，PBC 是过点O 的割线，CPE APE ∠=∠，点H 是线段ED 的中点.（1）证明：D F E A 、、、四点共圆； （2）证明：PC PB PF ⋅=2.20．已知A （﹣3，0），B （3，0），C （x 0，y 0）是圆M 上的三个不同的点． （1）若x 0=﹣4，y 0=1，求圆M 的方程；（2）若点C 是以AB 为直径的圆M 上的任意一点，直线x=3交直线AC 于点R ，线段BR 的中点为D ．判断直线CD 与圆M 的位置关系，并证明你的结论．21．（本题满分14分）在ABC ∆中，角A ，B ，C 所对的边分别为c b a ,,，已知cos (cos )cos 0C A A B +=． （1）求角B 的大小；（2）若2=+c a ，求b 的取值范围．【命题意图】本题考查三角函数及其变换、正、余弦定理等基础知识，意在考查运算求解能力．22．（本小题满分12分）如图, 矩形ABCD 的两条对角线相交于点()2,0M ,AB 边所在直线的方 程为360x y --=点()1,1T -在AD 边所在直线上. （1）求AD 边所在直线的方程； （2）求矩形ABCD 外接圆的方程.防城区实验中学2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1． 【答案】B2． 【答案】B【解析】解：∵直线l ⊥平面α，α∥β，∴l ⊥平面β，又∵直线m ⊂平面β，∴l ⊥m ，故（1）正确； ∵直线l ⊥平面α，α⊥β，∴l ∥平面β，或l ⊂平面β，又∵直线m ⊂平面β，∴l 与m 可能平行也可能相交，还可以异面，故（2）错误；∵直线l ⊥平面α，l ∥m ，∴m ⊥α，∵直线m ⊂平面β，∴α⊥β，故（3）正确；∵直线l ⊥平面α，l ⊥m ，∴m ∥α或m ⊂α，又∵直线m ⊂平面β，则α与β可能平行也可能相交，故（4）错误； 故选B ．【点评】本题考查的知识点是空间中直线与平面之间的位置关系，其中熟练掌握空间中直线与平面位置关系的判定及性质定理，建立良好的空间想像能力是解答本题的关键．3． 【答案】C【解析】由已知，得{z|z ＝x ＋y ，x ∈A ，y ∈B}＝{－1,1,3}，所以集合{z|z ＝x ＋y ，x ∈A ，y ∈B}中的元素的个数为3. 4． 【答案】C.【解析】根据等差数列的性质，4231112()32(2)a a a a d a d a d=+⇒+=+++，化简得1a d =-，∴1741767142732a dS d a a d d⋅+===+，故选C.5． 【答案】C【解析】解：根据程序框图，S=（﹣1+3）+（﹣5+7）+…+（﹣97+99）=50，输出的S 为50． 故选：C ．【点评】本题主要考查了循环结构的程序框图，模拟执行程序框图，正确得到程序框图的功能是解题的关键，属于基础题．6． 【答案】A【解析】解：2πr=πR ，所以r=，则h=，所以V=故选A7． 【答案】 C【解析】解：在长方体ABCD ﹣A 1B 1C 1D 1中命题p ：平面AC 为平面α，平面A 1C 1为平面β，直线A 1D 1，和直线AB 分别是直线m ，l ，显然满足α∥β，l ⊂α，m ⊂β，而m 与l 异面，故命题p 不正确；﹣p 正确；命题q ：平面AC 为平面α，平面A 1C 1为平面β，直线A 1D 1，和直线AB 分别是直线m ，l ， 显然满足l ∥α，m ⊥l ，m ⊂β，而α∥β，故命题q 不正确；﹣q 正确；故选C ．【点评】此题是个基础题．考查面面平行的判定和性质定理，要说明一个命题不正确，只需举一个反例即可，否则给出证明；考查学生灵活应用知识分析解决问题的能力．8． 【答案】B 【解析】试题分析：函数()cos ,3f x x π⎛⎫=+∴ ⎪⎝⎭()5'sin cos 36f x x x ππ⎛⎫⎛⎫=-+=+ ⎪ ⎪⎝⎭⎝⎭，所以函数 ()cos 3f x x π⎛⎫=+ ⎪⎝⎭，所以将函数函数()y f x =的图象上所有的点向左平移2π个单位长度得到5cos cos 326y x x πππ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭，故选B.考点：函数()sin y A x ωϕ=+的图象变换. 9． 【答案】A 【解析】考点：集合的包含关系的判断与应用.【方法点晴】本题主要考查了集合的包含关系的判定与应用，其中解答中涉及到分式不等式的求解，一元二次不等式的解法，集合的子集的相关的运算等知识点的综合考查，着重考查了转化与化归思想、分类讨论思想的应用，以及学生的推理与运算能力，属于中档试题，本题的解答中正确求解每个不等式的解集是解答的关键. 10．【答案】B 【解析】试题分析：若{}n a 为等差数列，()()111212n n n na S d a n n n -+==+-⨯，则n S n ⎧⎫⎨⎬⎩⎭为等差数列公差为2d , 2017171100,2000100,201717210S S d d ∴-=⨯==,故选B. 考点：1、等差数列的通项公式；2、等差数列的前项和公式.二、填空题11．【答案】B 【解析】12．【答案】 ①② ．【解析】解：对于①由a n+1=，且a 1=m=＜1，所以，＞1，，，∴a 5=2 故①正确；对于②由a 3=3，若a 3=a 2﹣1=3，则a 2=4，若a 1﹣1=4，则a 1=5=m ．若，则．若a 1＞1a 1=，若0＜a 1≤1则a 1=3，不合题意． 所以，a 3=2时，m 即a 1的不同取值由3个． 故②正确；若a1=m=＞1，则a2=，所a3=＞1，a4=故在a1=时，数列{an }是周期为3的周期数列，③错；故答案为：①②【点评】本题主要考查新定义题目，属于创新性题目，但又让学生能有较大的数列的知识应用空间，是较好的题目13．【答案】27-． 【解析】考点：向量的夹角．【名师点睛】平面向量数量积的类型及求法 （1）求平面向量的数量积有三种方法：一是定义cos a b a b θ⋅=；二是坐标运算公式1212a b x x y y ⋅=+；三是利用数量积的几何意义．（2）求较复杂的平面向量的数量积的运算时，可先利用平面向量数量积的运算律或相减公式进行化简 14．【答案】25【解析】考点：分层抽样方法．15．【答案】()2212x y -+=或()2212x y ++=【解析】试题分析：由题意知()0,1F ，设2001,4P x x ⎛⎫⎪⎝⎭，由1'2y x =，则切线方程为()20001142y x x x x -=-，代入()0,1-得02x =±，则()()2,1,2,1P -，可得PF FQ ⊥，则FPQ ∆外接圆以PQ 为直径，则()2212x y -+=或()2212x y ++=.故本题答案填()2212x y -+=或()2212x y ++=．1考点：1.圆的标准方程；2.抛物线的标准方程与几何性质． 16．【答案】②③④【解析】解析：本题考查平面向量基本定理、坐标运算以及综合应用知识解决问题的能力． 由(1,4)λμ+=-a b 得124λμλμ-+=-⎧⎨+=⎩，∴21λμ=⎧⎨=⎩，①错误；a 与b 不共线，由平面向量基本定理可得，②正确；记OA =a ，由OM μ=+a b 得AM μ=b ，∴点M 在过A 点与b 平行的直线上，③正确；由2μλ+=+a b a b 得，(1)(2)λμ-+-=0a b ，∵a 与b 不共线，∴12λμ=⎧⎨=⎩，∴2(1,5)μλ+=+=a b a b ，∴④正确；设(,)M x y ，则有2x y λμλμ=-+⎧⎨=+⎩，∴21331133x y x y λμ⎧=-+⎪⎪⎨⎪=+⎪⎩，∴200x y x y -≤⎧⎨+≥⎩且260x y -+=，∴(,)λμΩ表示的一条线段且线段的两个端点分别为(2,4)、(2,2)-，其长度为三、解答题17．【答案】【解析】（1）证明：设BD 交AC 于M ，连接ME ．∵ABCD为正方形，∴M为AC中点，又∵E为A′A的中点，∴ME为△A′AC的中位线，∴ME∥A′C．又∵ME⊂平面BDE，A′C⊄平面BDE，∴A′C∥平面BDE．（2）解：∵V E﹣ABD====V A′﹣ABCD．∴V A′﹣ABCD：V E﹣ABD=4：1．18．【答案】【解析】证明：（Ⅰ）∵数列{a n}满足a1=，a n+1=a n+（n∈N*），∴a n＞0，a n+1=a n+＞0（n∈N*），a n+1﹣a n=＞0，∴，∴对一切n∈N*，＜．（Ⅱ）由（Ⅰ）知，对一切k∈N*，＜，∴，∴当n≥2时，=＞3﹣[1+]=3﹣[1+]=3﹣（1+1﹣）=，∴a n ＜1，又，∴对一切n ∈N *，0＜a n ＜1．【点评】本题考查不等式的证明，是中档题，解题时要注意裂项求和法和放缩法的合理运用，注意不等式性质的灵活运用．19．【答案】（1）证明见解析；（2）证明见解析. 【解析】1111]试题解析：解：（1）∵PA 是切线，AB 是弦，∴C BAP ∠=∠，CPE APD ∠=∠， ∴CPE C APD BAP ∠+∠=∠+∠，∵CPE C AED APD BAP ADE ∠+∠=∠∠+∠=∠, ∴AED ADE ∠=∠，即ADE ∆是等腰三角形又点H 是线段ED 的中点，∴ AH 是线段ED 垂直平分线，即ED AH ⊥又由CPE APE ∠=∠可知PH 是线段AF 的垂直平分线，∴AF 与ED 互相垂直且平分， ∴四边形AEFD 是正方形，则D F E A 、、、四点共圆. （5分） （2由割线定理得PC PB PA ⋅=2，由（1）知PH 是线段AF 的垂直平分线，∴PF PA =，从而PC PB PF ⋅=2（10分）考点：与圆有关的比例线段． 20．【答案】【解析】解：（1）设圆的方程为x 2+y 2+Dx+Ey+F=0圆的方程为x 2+y 2﹣8y ﹣9=0…（2）直线CD 与圆M 相切O 、D 分别是AB 、BR 的中点 则OD ∥AR ，∴∠CAB=∠DOB ，∠ACO=∠COD ， 又∠CAO=∠ACO ，∴∠DOB=∠COD 又OC=OB ，所以△BOD ≌△COD ∴∠OCD=∠OBD=90°即OC ⊥CD ，则直线CD 与圆M 相切． … （其他方法亦可）21．【答案】（1）3B π=；（2）[1,2).【解析】22．【答案】（1）320x y ++=；（2）()2228x y -+=．【解析】试题分析：（1）由已知中AB 边所在直线方程为360x y --=，且AD 与AB 垂直，结合点()1,1T -在直线AD 上，可得到AD 边所在直线的点斜式方程，即可求得AD 边所在直线的方程；（2）根据矩形的性质可得矩形ABCD 外接圆圆心纪委两条直线的交点()2,0M ，根据（1）中直线，即可得到圆的圆心和半径，即可求得矩形ABCD 外接圆的方程.（2）由360320x y x y --=⎧⎨++=⎩解得点A 的坐标为()0,2-,因为矩形ABCD 两条对角线的交点为()2,0M ,所以M 为距形ABCD 外接圆的圆心, 又AM ==从而距形ABCD 外接圆的方程为()2228x y -+=.1考点：直线的点斜式方程；圆的方程的求解.【方法点晴】本题主要考查了直线的点斜式方程、圆的方程的求解，其中解答中涉及到两条直线的交点坐标，圆的标准方程，其中（1）中的关键是根据已知中AB边所在的直线方程以及AD与AB垂直，求出直线AD的斜率；（2）中的关键是求出A点的坐标，进而求解圆的圆心坐标和半径，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力.。

防城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 函数()2cos()f x x ωϕ=+（0ω>，0ϕ-π<<）的部分图象如图所示，则 f （0）的值为（ ） A.32-B.1-C.D.【命题意图】本题考查诱导公式，三角函数的图象和性质，数形结合思想的灵活应用.2．已知两不共线的向量，，若对非零实数m ，n 有m+n与﹣2共线，则=（ ）A ．﹣2B ．2 C．﹣ D．3． 已知函数f （x ）＝⎩⎨⎧a x －1，x ≤1log a1x ＋1，x ＞1（a ＞0且a ≠1），若f （1）＝1，f （b ）＝－3，则f （5－b ）＝（ ） A ．－14B ．－12C ．－34D ．－544． 已知α，[,]βππ∈-，则“||||βα>”是“βαβαcos cos ||||->-”的（ ） A. 充分必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件【命题意图】本题考查三角函数的性质与充分必要条件等基础知识，意在考查构造函数的思想与运算求解能力. 5． 等差数列{a n }中，已知前15项的和S 15=45，则a 8等于（ ） A．B ．6C．D ．36． 某几何体的三视图如图所示，该几何体的体积是（ ）A． B． C． D．7． 在正方体1111ABCD A B C D -中，M 是线段11AC 的中点，若四面体M ABD -的外接球体积为36p ， 班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________则正方体棱长为（ ）A ．2B ．3C ．4D ．5【命题意图】本题考查以正方体为载体考查四面体的外接球半径问题，意在考查空间想象能力和基本运算能力． 8． 执行如图的程序框图，若输出i 的值为12，则①、②处可填入的条件分别为（ ）A ．S 384,2i i ≥=+ C ．S 3840,2i i ≥=+9． a+2）y+1=0互相平行，则实数a 等于（ ）A ．1D ．﹣1或﹣310(4)()f x f x +=-,且在区间[0,2]上是增函数，则 A 、(25)(11)(80)f f f -<< B 、(80)(11)(25)f f f <<- C 、(11)(80)(25)f f f <<- D 、(25)(80)(11)f f f -<< 11．若f （x ）=sin （2x+θ），则“f （x ）的图象关于x=对称”是“θ=﹣”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件12．cos80cos130sin100sin130︒︒-︒︒等于（ ） A B ．12 C ．12- D ．二、填空题13．某几何体的三视图如图所示，则该几何体的体积为14．如图，在矩形ABCD 中，AB = 3BC =， E 在AC 上，若BE AC ⊥， 则ED 的长=____________15．已知A （1，0），P ，Q 是单位圆上的两动点且满足，则+的最大值为 ．16．△ABC中，，BC=3，，则∠C=．17．已知函数f（x）=cosxsinx，给出下列四个结论：①若f（x1）=﹣f（x2），则x1=﹣x2；②f（x）的最小正周期是2π；③f（x）在区间[﹣，]上是增函数；④f（x）的图象关于直线x=对称．其中正确的结论是．18．抛物线的准线与双曲线的两条渐近线所围成的三角形面积为__________三、解答题19．已知数列{a n}共有2k（k≥2，k∈Z）项，a1=1，前n项和为S n，前n项乘积为T n，且a n+1=（a﹣1）S n+2（n=1，2，…，2k﹣1），其中a=2，数列{b n}满足b n=log2，（Ⅰ）求数列{b n}的通项公式；（Ⅱ）若|b1﹣|+|b2﹣|+…+|b2k﹣1﹣|+|b2k﹣|≤，求k的值．2020142015CBA5场比赛中的投篮次数及投中次数如下表所示：3分球的平均命中率；（2）视这5场比赛中2分球和3分球的平均命中率为相应的概率．假设运动员在第6场比赛前一分钟分别获得1次2分球和1次3分球的投篮机会，该运动员在最后一分钟内得分ξ分布列和数学期望．21．【泰州中学2018届高三10月月考】已知函数()(),,xf x eg x x m m R ==-∈.（1）若曲线()y f x =与直线()y g x =相切，求实数m 的值； （2）记()()()h x f x g x =⋅，求()h x 在[]0,1上的最大值； （3）当0m =时，试比较()2f x e -与()g x 的大小.22．如图，四边形ABEF 是等腰梯形，,2,AB EF AF BE EF AB ====，四边形ABCD 是矩形，AD ⊥平面ABEF ，其中,Q M 分别是,AC EF 的中点，P 是BM 的中点．（1）求证:PQ 平面BCE ； （2）AM ⊥平面BCM .23．已知顶点在坐标原点，焦点在x 轴上的抛物线被直线y=2x+1截得的弦长为，求此抛物线方程．24．【2017-2018学年度第一学期如皋市高三年级第一次联考】设函数()1ln 1f x a x x=+-．（1）当2a =时，求函数()f x 在点()()11f ，处的切线方程； （2）讨论函数()f x 的单调性；（3）当102a <<时，求证：对任意1+2x ⎛⎫∈∞ ⎪⎝⎭，，都有1e x aa x +⎛⎫+< ⎪⎝⎭．防城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案） 一、选择题13． 2614．21215． ．16．17． ③④ ． 18．三、解答题19． 20．21．（1）1m =-；（2）当1e m e <-时，()()max 1h x m e =-；当1em e ≥-时，()max h x m =-；（3）()()2f x e g x ->. 22．（1）证明见解析；（2）证明见解析．23．24．（1）10x y --=；（2）见解析；（3）见解析.。