风荷载下悬臂挑蓬的整体疲劳分析

悬挑屋盖风荷载仿真分析论文悬挑屋盖风荷载仿真分析论文1模型设计及制作要求第四届全国结构设计竞赛的题目是“体育场悬挑屋盖结构”，需要制作的部分为挑棚结构，包括支承骨架和围护结构两部分(图1)。

要求使用长度为1250mm，截面规格为2mm×2mm、2mm×4mm、2mm×6mm、4mm×6mm、1mm×55mm的桐木条和502胶水，制作支承骨架;围护结构采用120g布纹纸，自行裁剪粘贴，要求围护材料在外观上必须全部覆盖挑篷上部及背部区域。

制作完成后，使用连接螺栓将挑棚结构固定在看台上。

采用在悬挑屋盖上加竖向静载和风荷载的方式测试模型的刚度和承载力。

以模型在1.88kg竖向静荷载作用下和9m/s风速作用下、悬挑端部竖向位移的加权平均值和模型自重综合评估模型优劣。

并且要求模型在12m/s风速作用下，模型不能发生破坏，充分考核了模型在正常使用条件下的刚度水平和极限承载力条件下的结构合理性。

2设计方案构思2.1结构选型根据本届结构设计大赛的竞赛规则，对设计制作要求、加载制度及评审规则等进行了认真分析，可以得到在考虑结构质量与结构位移所占分值比例不同的基础上(质量占得分的50%，位移占25%)，应尽可能减小结构质量，并在控制结构位移增加不大的情况下，采用桁架结构体系形式。

结构由两榀桁架组成，每榀桁架都采用三角形几何不变体系以提高结构的承载力、刚度及稳定性。

考虑竞赛对结构的加载方式以竖向静载为主，且在水平风荷载作用下结构满足强度及整体稳定性要求的情况下，依靠杆件自身截面强度即可提供抗力，这样可减少支撑数量从而减轻结构质量。

同时为了维持桁架自身的稳定性，设置了为维持结构稳定的竖向和斜向支撑。

另外，试验与计算分析结果均表明，风荷载对结构的影响没有静载显著，综合考虑到竞赛要求、工程的实际情况以及所提供材料的特点，在围护结构下部设置了分布均匀、规则的檩条，使结构能够满足使用的要求。

2013年（第35卷）第3期汽车工程Automotive Engineering2013（Vol．35）No．32013050悬架下摆臂的疲劳寿命分析**国家高技术研究发展计划（2008AA11A123）和吉林省科技厅科技发展计划重点项目（20086006）资助。

原稿收到日期为2011年9月21日，修改稿收到日期为2011年11月8日。

史建鹏1，管欣2(1.东风汽车公司技术中心，武汉430058 2.吉林大学，汽车动态模拟国家重点实验室，长春130025)［摘要］根据汽车悬架下摆臂所受的极限静载工况下的结构应力分析、道路载荷作用下的疲劳损伤分析和常用行驶工况下的疲劳寿命等分析，采用CAE 与台架和道路试验相结合的方法，从多体动力学得到载荷值，应用“惯性释放法”获得不同工况下，下摆臂的应力分布特征；据此确定易出现疲劳损伤的部位，为下摆臂探索出一种一体化疲劳寿命分析方法；采用该方法对某型汽车下摆臂进行分析的结果表明，受到的应力下降10MPa 时，疲劳寿命约能提高1倍。

关键词：悬架下摆臂；载荷；应力；疲劳寿命Fatigue Life Analysis of Lower Suspension ArmShi Jianpeng 1＆Guan Xin 21.Dongfeng Motor Corporation Technical Center ，Wuhan 430058；2.Jilin University ，State Key Laboratory of Automobile Dynamic Simulation ，Changchun 130025［Abstract ］Based on the analyses on the structural stress of static loads in extreme condition ，the fatigue damage under road loads and the fatigue life in normal driving conditions for lower suspension arm and combining CAE technique with road test ，the load values are obtained with multi-body dynamics ，and by applying inertia relief method the stress distribution features of lower suspension arm are acquired ，and based on which the locations are i-dentified where fatigue damages are easy to occur．Thus an integrated fatigue life analysis technique for lower sus-pension arm is explored ，using which the analysis on the lower suspension arm of a real vehicle is conducted with a result showing that for this specific situation a reduction of stress by 10MPa can lead to nearly a doubling in fatigue life．Keywords ：lower suspension arm ；load ；stress ；fatigue life前言关于下摆臂疲劳寿命的研究主要包括：应用结构有限元方法提升部件疲劳寿命和以台架试验为基础的多轴向疲劳寿命加载模式的分析方法。

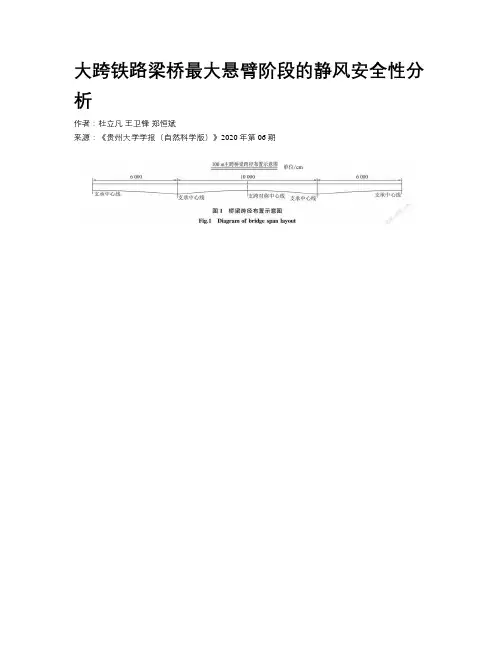
大跨铁路梁桥最大悬臂阶段的静风安全性分析作者：杜立凡王卫锋郑恒斌来源：《贵州大学学报（自然科学版）》2020年第06期摘要：在桥梁挂篮悬臂浇筑施工过程中，风荷载与桥梁结构的相互作用是一项工程风险因素。

为评估桥梁挂篮悬浇施工过程中结构的抗风安全性，同时为桥梁抗风设计提供有效依据，以某大跨铁路连续梁桥为背景，基于CFD数值模拟结合规范建议公式确定了桥梁关键截面的三分力系数，而后采用Midas Civil建立了考虑桥梁施工全过程的有限元模型。

针对主梁最大悬臂阶段将均匀对称、非均匀对称和龙卷风荷载分别与对称及非对称施工荷载工况组合，将结构预存状态与静风荷载效应叠加，以此全面分析主梁最不利施工阶段的静风安全性。

结果表明：静风荷载引起主梁横向位移最大值可达到6.98 mm，竖向位移最大值可达到5.03 mm，龙卷风工况对结构位移最为不利;各关键位置应力最大值，最小值均出现在对称均匀加载工况，对称均匀加载工况对结构应力最为不利。

为确保结构安全建议在桥梁挂篮悬臂浇筑施工过程中，考虑风荷载效应的影响。

关键词：桥梁工程;悬臂施工;静風荷载;CFD方法;三分力系数;安全性中图分类号：U441.2文献标识码： A桥梁结构的施工工程复杂庞大，工程建设过程中面临来自自然界气候条件、材料性能等不确定性因素影响，一旦发生事故，将会造成非常巨大的生命及财产损失。

风荷载引起的桥梁破坏发生面较广，桥梁结构在风荷载作用下可能发生失稳甚至破坏[1-3]。

在施工阶段下，桥梁结构对风荷载的作用更为敏感，结构过大的风响应会对施工及结构安全造成不利影响[4-5]。

而最大悬臂阶段是桥梁挂篮悬臂施工过程中最不利的阶段，结构在此阶段受风荷载的影响最大[6-8]。

所以，对桥梁的最大悬臂施工阶段进行风安全评估是有必要的。

由于在大跨梁桥悬臂浇筑的过程中，T构两侧悬臂难以做到完全对称，不平衡荷载是悬臂阶段风安全问题中一个需要考虑的因素[9]。

施工过程中结构状态有一个叠加的过程，静风荷载作用在叠加下可能导致结构产生更大的位移和内力，所以施工过程的结构状态与静风荷载效应的叠加也是需要考虑的问题。

基于现场实测的大跨钢桁悬索桥疲劳可靠度分析0 引言钢桁桥因跨越能力强、施工方便、外形优美、整体性好被广泛应用于大跨度桥梁，尤其是大跨度悬索桥。

在长期的车辆荷载和风荷载作用下，钢桁架主梁各杆件尤其是杆件的各个连接部位将长期处于累积疲劳损伤的状态[1-2]，进而影响桁架主梁结构的长期安全运营。

因此，对大跨度钢桁架悬索桥关键构件处的细节进行疲劳可靠度评估显得极为重要。

以往对钢桥疲劳的研究大多基于疲劳应力谱，因此，首先需要对处于正常运营期的大桥车流情况进行调查统计并分析，再通过确定不同车型荷载参数建立车辆荷载谱，最后得到只能反映大桥整体的车载特征，因此得到的局部应力分析结果将会在较大程度上与实际情况不符[3-5]。

为了更好地掌控大桥的服役情况，结构健康监测系统应运而生，目前已广泛地在大跨度桥梁领域使用[6-8]，应变时程可直接通过监测系统得到，用于疲劳分析的疲劳应力谱可由雨流计数法获得，随后便可对桥梁钢结构构件细节进行疲劳累积损伤及可靠度评估研究[9-10]。

但桥梁健康监测系统经济投入成本很大，而且以往基于现场实测的研究往往针对大跨度钢箱梁桥[11-14]，基于现场监测数据研究大跨度钢桁梁悬索桥关键构件的疲劳可靠度较少。

为节约成本，针对大跨度钢桁梁悬索桥，首先采用ANSYS软件建立了大桥的壳-梁混合单元空间桁架主梁有限元模型，随后通过分析确定了大桥的关键构件及关键点。

针对关键构件的关键点，进行为期6 d 的应变实时监测，通过对实测数据的预处理，获得了比较准确的应力响应，然后对于所测关键构件的关键点运用核密度估计法建立基于小子样的疲劳荷载谱概率分布模型，研究大桥所测关键构件关键点的疲劳可靠度，为大桥的安全运营提供保障。

1 有限元建模及关键截面确定本研究以某大跨度钢桁架悬索桥为工程背景，其主跨为1 176 m，主缆采用(242+1 176+116)m的孔跨布置方式。

加劲梁选用梁高为7.5 m且桁架节间距为7.25 m的钢桁梁。

连续刚构最大悬臂状态施工中的抗风分析摘要：由于山区自然风变化无常，桥梁建设周期较长，处于施工中的高墩大跨连续刚构最大悬臂状态刚度小，柔性大，通常为最不利的抗风状态。

以在建某高墩大跨连续刚构桥的最大悬臂施工状态为例，建立有限元模型围绕最大双薄壁状态高墩的抗风性能进行研究。

中图分类号： tu973+.32 文献标识码： a 文章编号：1 桥梁风害风是引起桥梁结构反应的的直接作用，由于它在自然界中变化无常，自身又携带着很大的能量，通常是桥梁结构最主要遭受的自然外力。

1940年，塔科马悬索桥在大风作用下出现主梁扭转振动而破坏，使得工程界和学界认识到风致振动的灾害性，于是把桥梁结构的抗风稳定性能纳入新的重要研究课题[1]。

目前，桥梁结构正朝着更大跨度、更纤柔的方向发展，桥梁工程师必须面对抗风稳定性能，充分认识风致振动问题。

风对结构的相互作用是一个十分复杂的现象，它受风的自然特性、结构的外形、结构的动力特性以及风与结构的相互作用等多方面因素制约。

这里把风与结构的相互作用也可分成[2-3]：①空气力受结构振动的影响很小，可忽略不计；②空气受结构振动的反馈制约，引起一种自激振动机制。

连续刚构通常建设在跨越沟壑的地方，沟壑本身对来流风有加速效应，会增大风对结构的作用。

而地形下垫面的实际情况对梯度风也有显著的影响，改变来流风的大小以及风向，都会对结构内力带来不同程度的作用。

连续刚构的最大双悬臂状态柔性大，此时稳定性差。

因此，工程师除考虑常规荷载作用下的稳定性以外还需根据当地风的自然情况分析对桥梁结构的作用，保证桥梁结构的施工安全性以及合拢施工时的精度。

虽然预应力混凝土连续刚构桥在成桥运营状态具有良好的抗风性能，但最大双悬臂施工状态时，抗风性能较薄弱，因此设计施工非常有必要进行风荷载对结构作用的研究，确保施工的安全和施工的精度。

在跨越沟壑时，并行双幅刚构桥受风荷载的作用不容忽视，尤其是最大悬臂施工状态时，结构处于t构状态刚度不足，对风荷载作用非常敏感，风荷载很大程度上起到控制荷载作用。

大气工程中风力发电塔筒结构的疲劳性能评估随着风力发电的快速发展，塔筒结构作为一个关键组成部分，有着重要的作用。

然而，在长期的风力作用下，塔筒结构容易出现疲劳破坏，影响风力发电的正常运行。

因此，对于风力发电塔筒结构的疲劳性能进行评估，具有重要的意义。

首先，我们需要了解什么是疲劳破坏。

疲劳破坏是指在循环载荷作用下，结构在未达到其静力强度的情况下发生破坏。

疲劳破坏是一种逐渐发展的过程，通常起始于微小的裂纹，然后沿着应力最大的位置扩展，最终导致结构破裂。

因此，疲劳性能评估的关键是确定结构中的疲劳破坏起始位置和扩展情况。

在风力发电塔筒结构的疲劳性能评估中，我们需要考虑到以下几个因素。

首先是塔筒结构的材料性能。

不同材料的疲劳特性存在差异，因此需要根据具体的材料选取合适的疲劳参数。

其次是结构的设计参数，包括截面尺寸、连接方式等。

这些设计参数会对结构的应力分布产生影响，从而影响疲劳寿命。

最后是外界环境因素，如风速、震动等。

这些因素会对塔筒结构产生不同程度的影响。

疲劳性能评估的方法主要包括实验研究和数值模拟两种。

实验研究通过在实验室中进行长期循环载荷试验，来模拟结构在实际运行条件下的疲劳行为。

这种方法对于验证理论模型和分析方法具有重要的作用。

然而，实验研究的成本较高且时间较长，无法涵盖所有的工况和边界条件。

因此，数值模拟成为研究人员常用的手段。

数值模拟采用计算机辅助工程软件，根据塔筒结构的几何形状和材料性能，通过有限元分析等方法，来模拟结构在不同工况下的应力分布和疲劳寿命。

数值模拟具有高效、经济和便捷的优点，可以在短时间内预测结构的疲劳性能。

疲劳性能评估的结果可以用疲劳寿命和安全系数来表示。

疲劳寿命是指结构在疲劳载荷下的使用年限，通常以循环数表示。

安全系数是指设计疲劳载荷与疲劳破坏强度之间的比值。

当安全系数大于1时，表示结构的设计寿命大于使用寿命，具有足够的安全性。

而当安全系数小于1时，表示结构的设计寿命小于使用寿命，存在疲劳破坏的风险。

第一章绪论１．１．２大跨度屋盖结构给风工程研究带来的严峻课题尽管工程界对结构风荷载的研究达到了非常高的重视，风灾仍然发生的频率很高、次生的灾难很大、带来的影响范围非常广泛。

表】１所列的是１９５０～１９９９年全球（特火型）重大自然灾害统计数据，可以看到风灾是自然灾害中影响最大的一种，给人类带来了巨大的生命和财产威胁。

表１１１９５０至１９９９年全球（特大型）重大自然灾害统计数据灾难种类地震风灾洪水其他台计灾难次数（次）６８８９６３１４２３４死亡人数（百万人）Ｏ，６６０．６３０．１Ｏ．Ｏｌ】．４经济损失（亿美元）３３６０２６８８２８８０６７２９６００保险损失（亿美元）２５４６８７８５８４１１１０在风灾肆虐的同时，人类用勤劳和智慧不断地发展现代文明。

大跨度屋盖结构由于建筑美学的提升和能够提供宽大的空闻等优势被广泛应用到重要的公共建筑中。

图１．１为２００２年韩日世界杯足球赛中的部分体育场建筑，可以看到悬臂挑篷凭借其风格明快的建筑外形、结构轻盈材料节省的优势在大跨度屋盖结构中占有重要地位。

在建筑形式上的特征使得悬臂挑篷柔度较大并且阻尼较小，这样的结构形式由于基频和风的卓越频率接近，必然对风荷载十分敏感。

（ａ）韩国水原世界杯露天体育场（ｂ）韩国西归浦济州体育场（ｃ）韩国光州世界杯露天体育场（ｂ）韩国全州世界杯体育场同济大学博七学位论文（ｅ）日本宫城世界杯体育场（ｂ）日本大阪世界杯体育场图１１２００２年韩日世界杯足球赛的部分体育场建毓图１．２和图１．３显示的是两个大跨度屋盖（英国某悬挑屋盖和苏卅Ｉ体育场屋盖）在风荷载下破坏的情况。

大跨度屋盖结构受风灾破坏的实例还有很多，如１９８８年８月８日“８８０７”号台风造成杭州笕桥机场航站楼、杭州市体育馆屋顶严重破坏：１９９４年８月１５日“９４１７”号台风在浙江温州登陆，造成温州机场屋盖严重受损等。

可以看到大跨度的屋盖结构对风荷载非常敏感，在建造这类结构之前如果对其表面风荷载分布特征及风致振动问题没有研究透彻，极易带来结构安全性方面的隐患。

悬臂梁的疲劳寿命预测与优化设计悬臂梁是一种常见的结构形式，在工程领域中被广泛应用。

然而，由于长时间的工作负荷和振动等外界因素的影响，悬臂梁常常出现疲劳破坏问题。

因此，研究悬臂梁的疲劳寿命预测与优化设计具有重要意义。

悬臂梁的疲劳寿命预测主要是通过疲劳分析方法来实现。

疲劳分析是一种根据载荷历史和材料特性等因素，对悬臂梁进行应力、应变分析，并结合疲劳损伤累积理论来预测其疲劳寿命的方法。

通过对悬臂梁的疲劳寿命进行预测，可以提前发现潜在的疲劳破坏问题，并采取相应的预防措施。

在进行疲劳寿命预测之前，首先需要对悬臂梁的载荷特性进行清晰准确的描述。

悬臂梁的载荷包括静载荷和动载荷两部分。

静载荷指悬臂梁受到的常数或变化缓慢的力的作用，如自身重量以及外部施加的静力。

动载荷则包括悬臂梁受到的频率较高、变化剧烈的往复运动力的作用，如振动载荷等。

在预测疲劳寿命时，需要同时考虑这两部分载荷的综合影响。

基于载荷特性的清晰描述，接下来需要进行悬臂梁的应力分析。

应力分析是疲劳分析的基础，其核心是计算悬臂梁在各种载荷作用下的应力分布情况。

通常情况下，悬臂梁的应力分布具有非均匀性，因此需要借助有限元分析等数值方法来求解。

通过应力分析，可以得到悬臂梁在工作负荷下的应力状态，从而为疲劳寿命预测提供了重要的基础参数。

除了应力分析之外，悬臂梁的材料特性也对疲劳寿命有着直接的影响。

不同材料的疲劳强度和疲劳寿命存在一定的差异，因此需要对材料的疲劳特性进行评估和选择。

疲劳特性的评估主要包括疲劳强度和疲劳寿命曲线等参数的确定。

通过对材料的疲劳特性进行准确的评估，可以提高疲劳寿命预测的准确性和可靠性。

在疲劳寿命预测的基础上，还可以进行悬臂梁的优化设计。

优化设计的目标是通过改变悬臂梁的几何形状、材料选型和结构参数等，以提高其疲劳寿命并满足特定的工作要求。

优化设计的方法包括多目标优化、遗传算法、粒子群算法等。

通过优化设计，可以在满足结构强度和刚度要求的前提下，尽可能延长悬臂梁的使用寿命。

《设置悬挂吊车平板网架结构的疲劳载荷谱及疲劳寿命研究》篇一一、引言随着现代建筑和工程技术的不断发展，悬挂吊车平板网架结构因其独特的优势在各类工程项目中得到了广泛应用。

然而，这种结构在长期使用过程中，会受到各种复杂载荷的作用，导致结构产生疲劳损伤，进而影响其使用寿命和安全性。

因此，对悬挂吊车平板网架结构的疲劳载荷谱及疲劳寿命进行研究具有重要的现实意义。

二、疲劳载荷谱的设置1. 载荷来源分析- 悬挂吊车平板网架结构的主要载荷包括自身重量、外部载荷（如设备、人员、货物等）、风载荷以及吊装过程中产生的动态载荷等。

- 这些载荷的组合和变化对结构的疲劳性能产生重要影响。

2. 载荷谱的建立- 通过实地测量和模拟分析，收集各种工况下的载荷数据。

- 利用统计分析方法，处理和筛选出对结构疲劳性能影响较大的载荷数据，形成载荷谱。

- 考虑不同方向、不同频率和不同幅值的载荷组合，建立多维度的载荷谱。

3. 载荷谱的应用- 将建立的载荷谱应用于有限元模型或实际结构中，进行疲劳分析。

- 通过不断调整和优化载荷谱，使其更贴近实际工况，提高分析的准确性。

三、疲劳寿命的研究1. 疲劳分析方法- 采用应力-寿命法、应变-寿命法或损伤力学法等方法，对结构进行疲劳分析。

- 利用S-N曲线、雨流计数法等工具，评估结构的疲劳性能。

2. 影响因素分析- 结构材料的选择和性能对疲劳寿命有重要影响，如材料的强度、韧性、抗疲劳性能等。

- 结构形式和尺寸也会影响其疲劳性能，如网格尺寸、吊车运行轨道等。

- 环境因素如温度、湿度、腐蚀等也会对结构的疲劳性能产生影响。

3. 疲劳寿命预测与优化- 基于上述分析，预测结构的疲劳寿命，并对其进行优化设计。

- 通过改变结构形式、材料选择、工艺方法等手段，提高结构的抗疲劳性能。

- 结合实际工程需求，制定合理的维护和检修计划，延长结构的使用寿命。

四、结论与展望通过对悬挂吊车平板网架结构的疲劳载荷谱及疲劳寿命进行研究，我们能够更准确地评估结构的性能和安全性。

·结构·抗震·文章编号:1009-6825(2009)31-0041-04钢结构雨篷静力动力分析收稿日期:2009-07-09作者简介:马少春(1982-),男,河南大学土木建筑学院硕士研究生,河南开封　475004鲍　鹏(1964-),男,博士,教授,河南大学土木建筑学院,河南开封　475004马少春　鲍　鹏摘　要:通过某具体工程,利用AN SYS 研究了静、动荷载作用下钢结构雨篷的力学性能,基于这种结构的非线性特征,并且考虑风与结构的耦合作用,对结构的选型、网格的划分及节点构造设计等问题进行了其强度、变形及稳定性分析,以推动钢结构雨篷的发展。

关键词:钢结构,静力分析,动力分析,反应谱法中图分类号:T U311文献标识码:A 目前制约我国钢结构雨篷发展的主要因素是:钢结构的直接造价高于钢筋混凝土结构。

因此如何在满足规范规定的前提下,在安全合理的基础上,对钢结构雨篷进行优化设计,减少用钢量,降低工程造价,对进一步推动钢结构雨篷的发展有重要的现实意义。

1　工程概况本工程是形状规则的悬挑钢结构雨篷,由钢框架、斜拉杆、水平撑杆、斜撑杆和装饰钢管等几部分构成。

雨篷尺寸7200mm ×12000mm ,主要平、剖面如图1,图2所示。

根据建筑外观要求,钢桁架梁水平撑杆、斜撑杆和装饰钢管均为 75×5mm 的圆钢管,上部斜拉杆由5根 89×4.0mm 的圆钢管组成。

钢桁架梁和斜拉杆与建筑物以固定铰支座的形式相连接,其余外悬部分为自由端。

本文运用有限元软件ANSYS 对本方案进行分析,建立了结2.2.3　运用“反规划”构建村镇生态基础设施1)交通廊道:沿城镇主要交通要道发展的交通绿道,既能降低和缓冲交通给城镇带来的不利影响,又能为生态城镇的建立创造有利条件。

2)农田防护绿带廊道:建立农田防风林,在保护国土生态安全和粮食生产的同时,也构建地区特有的大地景观特色。

第12卷第4期2006年12月空　间　结　构SP A T IA L ST RU C T U RESV ol.12No.4Dec .2006收稿日期:2005-08-20.作者简介:岑伟(1983—),男,浙江慈溪人,硕士研究生,主要从事钢结构及空间结构的研究.风机荷载下平板网架的整体疲劳分析岑　伟1,3,翁恩豪2,刘福祺3(1.浙江大学土木工程系,浙江杭州310027; 2.湖州市建筑设计研究院,浙江湖州313000;3.机械工业第三设计研究院,重庆400039)摘　要:针对风机交变荷载下平板网架产生整体疲劳的问题,采用总寿命法进行了分析.该方法考虑了Goodman 平均应力影响,运用雨流计数法统计应力-应变历程,并用M ine r 理论对不同应力幅值产生的损伤进行线性叠加,得到杆件的疲劳损伤程度,找出结构的疲劳薄弱区域.研究发现,平板网架的疲劳薄弱区域始终从放置风机的位置开始,随着风机荷载振幅的增大,疲劳薄弱区域逐步向四周扩散,疲劳损伤度呈指数增长.风机工作频率接近网架前几阶自振频率时,结构易出现疲劳;两风机竖向振动相位差在90°～135°及水平同步振动时,结构易出现疲劳.关键词:平板网架;疲劳;总寿命法;薄弱区域中图分类号:T U 356 文献标识码:A 文章编号:1006-6578(2006)04-0036-05Integral fatigue analysis of spatial trusses under fan loadsCEN Wei 1,3,W EN G En-hao 2,LIU Fu-qi 3(1.Department of Ctvil Engineering ,Zhejiang Univ erstity ,Hangzhou 310027,China ;2.Huzhou Architectural Design &Research Institute ,Huz hou 313000,China ;3.Third Design and Research Institute MI China ,Chongqing 400039,China )Abstract:To the problem o f integral fa tigue o f spatial trusses under fa n loads ,the tota l life m ethod w as adopted to solve it.Effects of Goodman av erag e stress w ere considered in the m ethod,and the stress-strain cy cle history was counted by the rain-flow co unting alg orithms.Fatig ue damage of members w as ac-cum ula ted linearly in the w hole stress -strain cycle histo ry with Miner dam ag e theory .Da mage deg rees of each member of the structure and fatig ue w eak a reas w ere obtained in the integral fa tigue analysis o f spa-tial trusses under fan loads.It w as show n that fa tigue areas alway s occur red fro m the sites of fans and ex-panded around,and the v alue o f fatigue damag e increased acco rding to the ex po nent law with the increase o f fan loads .The structure raised fa tigue easily w hen the fro nt several frequencies o f fans w ere near to those of structures.When the difference of phase o f two fans was between 90°a nd 135°in vertical v ibra-tion o r no difference of phase under ho rizontal v ibratio ns,fa tigue dam ag e arose easily.Key words :spa tial truss ;fatigue ;to tal life m ethod ;w eak a reas1　概　述疲劳失效是结构的主要破坏形式之一[1,2].在建筑结构工程领域,现行设计规范对结构由于动荷载的作用可能遭受的疲劳损伤考虑尚不全面[3].建筑结构中所采用的材料如结构用钢,也并非是均匀和连续的,实际上存在许多微小的缺陷,在循环荷载作用下,这些微小缺陷会逐渐发展、合并形成损伤,并逐步在材料中形成宏观裂纹.如果宏观裂纹得不到有效控制,极有可能会引起材料、结构的脆性断裂.早期疲劳损伤往往不易被检测到,但其带来的后果往往是灾难性的.目前采用的疲劳设计方法主要有总寿命法[4～6]和损伤容限法[7～9].总寿命法通过控制应力幅或应变幅来获得初始无裂纹的实验室试样产生疲劳破坏所需的应力循环数或应变循环数.以此为参考,并用各种方法处理平均应力、应力集中、环境、多轴应力和应力变幅的影响,估算结构的寿命.而损伤容限法以断裂力学[10,11]为基础,假定损伤为一切工程构件所固有,疲劳寿命则定义为主裂纹从原始尺寸扩展到某一临界尺寸所需的疲劳循环数或时间.对于空间结构来说,除了长期承受自重等恒荷载的作用外,也可能承受交变荷载,使结构的应力交替变化,从而发生整体疲劳破坏.为了通风需要,有些空间结构在屋盖上放置风机,风机的简谐强迫力使结构产生振动.在这种交变荷载作用下,结构中部分杆件的应力变化幅值是很大的.为了保证结构的安全使用,有必要对其进行整体疲劳分析.本文以风机荷载下的平板网架为例,采用总寿命法,得到杆件的疲劳损伤程度,预测结构可能出现疲劳的区域.2　疲劳寿命估算分析流程疲劳累积损伤理论是疲劳分析的主要原理之一[12],也是估算变应力幅值下疲劳寿命的主要理论.由于损伤是一个抽象的概念,不能直接度量,目前常用损伤度D 来反映裂纹扩展程度.疲劳累积损伤理论目前已提出了很多,本文采用Miner 线性累积损伤理论.Miner 认为如果试样承受幅值为S a 1的荷载,重复N 1次破坏,则在整个过程中材料所受的损伤线性地分配给各个循环,也就是每一循环材料的疲劳损伤度为D 1=1/N 1.显然,若S a 1荷载作用n 1次,则材料损伤度为D n 1=n 1/N 1.同样,在S a 2,S a 3,……下,各损伤分别为D n 2=n 2/N 2,D n 3=n 3/N 3,……(1)当材料整个损伤完毕时∑i(n i /N i )=1(2)就发生疲劳破坏.在实际工程中,对于某一构件来说,决定疲劳寿命的因素主要来自于三方面,即材料本身的疲劳特性、外荷载谱和构件本身的几何特征.图1给出了对结构进行整体疲劳分析的主要步骤.只要规定好构件的几何形状、材料的加载历史,便可分析构件的应力-应变响应.对于复杂的加载历史,可用循环计数法处理离散事件,然后采用合适图1　疲劳分析的主要步骤的部件或材料寿命曲线进行疲劳损伤分析,从而获得疲劳寿命的估算值.本文采用的疲劳寿命估计法包括以下主要步骤:(1)确定结构所承受的荷载谱,并通过有限元时程分析,得到结构每一杆件应力谱或应变谱;(2)通过程序把应力(应变)谱转化成应力(应变)峰值谱,并用雨流计数法[12,13]统计每根杆件的应力-应变循环历史;(3)选用合适的疲劳寿命估算模型,确定杆件的S -N 曲线或X -N 曲线.本文采用Basquin 疲劳寿命估算模型[4],考虑Goodman 平均应力[13]的影响,按式(3)计算每一应力应变循环下的疲劳寿命N f .Δe 2=e ′f (2N f )b(3)其中,e ′f 为疲劳强度系数,b 为疲劳强度指数,Δe 为应力幅值,N f 为疲劳寿命.(4)根据统计的应力-应变循环历史和S -N (X -N )曲线,计算杆件在每一应力-应变循环下的疲劳寿命N f ,按照Miner 线性累积损伤理论[13]计算疲劳损伤度D .一般规定,黑色金属及其合金经过2×106～107次循环仍不破坏,就认为它能承受无限次循环[13],因此假设疲劳损伤度D 大于1×10-7时,杆件发生疲劳.3　疲劳分析下面以一正放四角锥网架结构为例,对结构由于风机荷载的存在,可能产生的疲劳损伤进行分析.结构平面尺寸为42m ×21m ,网架厚度 1.5m ,上下弦杆长为 2.1m ,材料采用SAE -1015钢,结构支承于周边12根砼柱上,切向及法向的约束刚度均为K =15kN /mm ,如图2所示.首先进行自振特性分析,把结构自重和0.75kN /m 2的外荷载折算成质量块施加在结构上.把风机的自重也折算成质量块布置37　第2期岑　伟,等:风机荷载下平板网架的整体疲劳分析在相应的网架上弦节点上.图2中圆圈的位置各放置了1台风机.风机型号为D-1000,配套电机型号JK850,风机总重300kN,涡轮转速600～2950r/ min.选取钢材SAE-1015的疲劳参数[14],见表1.当网架上放置风机时,结构的各阶自振频率都有所下降,见表 2.这是由于放置风机时,结构的刚度基本不变,但网架上弦的局部节点增加了质量块,质量分布发生了变化,使网架的自振频率随着质量的增加而降低.图2　放置风机的正放四角锥网架表1　钢材疲劳参数表钢材型号Su(M Pa)K1(M Pa)n b c X f1e f1(M Pa) SAE-101541410830.243-0.133-0.5820.739946表2　网架有、无风机的前10阶自振频率比较(H z)12345678910频率(有风机) 3.29 3.63 4.784.90 6.858.0711.6612.4712.5813.17频率(无风机) 5.09 6.02 6.246.448.469.6413.1914.7415.0515.98 对该平板网架的前十阶振型特征进行分析可知,网架的第一、二阶以竖向振动为主,第一阶振型中,两风机位置处沿z向同侧振动,而第二阶振型中,两风机位置处沿z向反侧振动;第三、四阶振型以水平面内振动为主,分别沿水平面内两个相互垂直的方向振动;第五阶振型出现了水平面内的扭转.当风机正常工作时,由于转动偏心距的存在,产生一个正弦的扰力.扰力可按式(4)计算[15]:P=P0sin(k t+h)(4)P0= 1.1×10-5m0V0n20(5)式(5)中,m0为主要旋转部分质量(kg),V0为当量偏心距(mm),n0为转速(r/min).由式(5)可知,扰力振幅P0大小与旋转部分质量、当量偏心距成正比,与转速的平方成正比.在材料相同的情况下,疲劳损伤度的大小主要和应力幅值、平均应力等因素有关.风机竖向振动时,网架中出现疲劳的区域将随着荷载振幅的增大而逐步扩大,图3反映了相位差为零的两个竖向简谐荷载下,随着简谐振幅的增大,疲劳区域逐渐扩展的情况.图中用黑线标记的杆件即为出现疲劳的杆件,简谐振幅P0=16.37kN.从图中可以看出,当简谐振幅增大到 1.3P0时,两风机位置中心的下弦杆就出现疲劳,疲劳区域从这两点开始向外扩散,当振幅达到 1.5P0时,已发展为4个疲劳区域,振幅继续增大时,这四个区域逐渐连成一片,并向外扩展,而中心区域是相对安全的;当振幅达到1.8P0时,上弦杆件也开始可能出现疲劳,在振幅不超过2.0P0时,腹杆和纵向弦杆均未出现疲劳现象.两个简谐荷载同步时,由于荷载、结构形式、约束都是对称的,疲劳区域也表现出对称发展的特征.4　影响因素分析风机沿竖向简谐振动时,简谐振幅及风机相位差的影响.简谐振幅的变化与杆件疲劳损伤度最大值的关系如图4所示.在不同的相位差时,曲线的走势非常相似,随着简谐振幅的不断增大,杆件的最大疲劳损伤度呈现出指数增长的规律.然而在不同相位差时,最大疲劳损伤度的增长幅度各不相同,相位差为135°时增长最快,而相位差为270°时增长最缓(见图5),这主要是由于在不同相位差的简谐荷载作用下,结构的动力响应各不相同,杆件的应力变化幅值不同.风机的工作频率的影响.以上的分析都是基于风机在网架基频下振动的,当改变风机的工作频率时发现,随着工作频率的增大,杆件的最大疲劳损伤度下降很快,如图6所示.当风机的工作频率超过网架的前三阶自振频率时,网架已不会出现疲劳.显然,风机工作频率避开了网架的第一、二阶自振频率时,结构的动力响应已经变得很小.38空　间　结　构 第12卷　图3　风机竖向振动时疲劳区域的扩展图4　竖向振动时最大疲劳损伤度与简谐振幅的关系风机沿网架水平长方向振动时,经计算发现简谐振幅在3P0以上,结构才可能出现疲劳.从图7可以看出,在不同的相位差时,曲线的走势与图4完全相图5　竖向振动时最大疲劳损伤度与相位差的关系似,随着简谐振幅的不断增大,杆件的最大疲劳损伤度呈指数增长.不同相位差时,杆件最大疲劳损伤度呈现出不同的增长幅度,简谐荷载同步时增长最快,39　第2期岑　伟,等:风机荷载下平板网架的整体疲劳分析图6　竖向振动时最大疲劳损伤度与简谐频率的关系而相位差为180°时增长最缓(见图8).当简谐荷载同步时,对结构的作用同向叠加,杆件的内力变化很大;简谐荷载相位差为180°时,对结构的作用力正好相反,杆件的内力变化很小;而在其他相位差时,两个简谐荷载存在不同程度的抵消作用,杆件最大疲劳损伤度D 值在两者之间变化,图8很明显地反映了这一规律.图7　水平振动时最大疲劳损伤度与简谐振幅的关系图8　水平振动时最大疲劳损伤度与相位差的关系水平振动时风机工作频率与杆件最大疲劳损伤度D 的关系如图9所示.风机的工作频率在网架的前四阶自振频率内时,该网架结构会出现疲劳;而风机以网架的第二阶自振频率工作时,对该网架最不利;当风机的工作频率超过网架的前5阶自振频率时,网架不会出现疲劳.与风机的竖向振动不同的是,风机在第三、四阶网架自振频率范围内工作时,激起了结构较大的动力响应.图9　水平振动时最大疲劳损伤与简谐频率的关系5　结　论网架结构在风机荷载下的疲劳问题主要与风机的振动方向、振幅、频率以及风机振动的相位差等因素有关.本文分析了风机荷载下平板网架的整体疲劳,可以得到如下几点结论:(1)风机荷载是一种按正弦规律变化的荷载,风机竖向振动比水平振动时更易造成网架的疲劳.竖向振动时,网架的上下弦杆应力变化幅值较大,疲劳薄弱区域从风机位置的下弦杆开始,随着荷载振幅的增加,疲劳区域向周围扩展;水平振动时,由于网架的面内刚度很大,对杆件的影响较小.随着风机荷载振幅的增大,杆件疲劳损伤度呈指数增长.(2)风机振动频率靠近网架前几阶自振频率时对结构是危险的.风机竖向振动时,其工作频率靠近网架前两阶自振频率易造成结构的疲劳;水平振动时,工作频率靠近网架前四阶自振频率易造成结构疲劳.这与网架自身的振型特点有关,一、二阶振型以竖向振动为主,三、四阶则以水平振动为主.(3)两风机荷载存在不同相位差时,结构的动力响应差别很大.竖向振动时,相位差在90°～135°范围内,杆件的疲劳损伤度最大,而相位差为270°时,杆件的疲劳损伤度最小;水平向振动时,两风机荷载同步时,杆件的疲劳损伤度最大,而相位差为180°时,杆件的疲劳损伤度最小.(4)对放置风机的平板网架进行设计时,应选用合适的风机,使风机的工作频率避开网架前几阶自振频率.对风机位置处的杆件应加强,防止该处疲劳的过早出现.应根据具体情况,选择风机放置的方式,确定风机振动的方向.(下转第49页)40空　间　结　构 第12卷　图9　两种机构(单榀)5　结　论(1)对于环索水平的情况,桅杆之间的自平衡内力根据尺寸的不同存在一定的关系.(2)环索水平的情况下,结构上下不对称时,上下部分的桅杆长度必须满足同样的比例关系,这一点对于结构的找形以及建筑师、结构师的结构选型有重要意义.参考文献[1]C R Calladine.Buckminster Fuller's“Tenseg rity”Str uctur es a nd Cler k M a xw ell's Rulers for the Co n-structio n of Stiff Frames[J].Int ernatio na l J o urnal of Solids&Str uc tures,1978,14(2):161-172.[2]E N Kuznetsov.Underco nstr ained str uctur es[J].Inter-na tio nal Jour nal o f So lids&Structures,1988,24(2):153 -163.[3]De V eubeke.The num erical analy sis of str uc tures[A].Proceeding of.13th ICT AM,Spring er,Berlin,1973:20-28.[4]袁行飞.索穹顶结构的理论分析和实验研究[D]:[博士学位论文].杭州:浙江大学,2000.[5]S Pelleg rino.Structura l com putations with the singularv alue deco mpo sitio n o f the equilibrium ma trix[J].In-ter na tional J o urna l of So lids&Structures,1993,30(21):3025-3035.[6]罗尧治.索杆张力结构数值分析理论研究[D]:[博士学位论文].杭州:浙江大学,2000.[7]罗尧治,董石麟.索杆张力结构初始预应力分布计算[J].建筑结构学报,2000,21(5):59-64.(上接第40页)参考文献[1]Kr ajcinov ic D,Lemaitr e J.Continuum Da mage M e-chanics:T heor y a nd Applicatio n[M].Spring er V er lag, 1987.[2]Fuchs H O,Stephens R T.M etal Fa tigue in Engineer-ing[M].J oh n Wiley&Sons,1980.[3]GB50017-2003.钢结构设计规范[S].北京:中国计划出版社,2003.[4]Basquin O H.The ex ponential la w o f endur ance tests[A].Proceeding s of the American Society fo r T estinga nd M ate rials[C],1910:625-30.[5]Co ffin L F.A study of the effects o f cy clic ther malst resses o n a ductile metal[J].T ransac tio ns o f th e American Socie ty o f M echa nical Enginee rs,1954,76(1):931-950.[6]Ma nso n S S.Behav io r of materials under co nditions o fthe rmal stress[R].N atio na l Adv iso ry Co mmissio n o n Aer onautics:Repo rt1170.Clev ela nd:Lewis Fligh t Pro pulsio n Labo rato ry.1954.[7]Ritchie R O,Suresh S.Some co nsidera tio ns o n fatig uecrack clo sure at nea r-threshold st ress in tensities due to frac ture sur face mo rpholog y[J].M eta llurgical T ra nsac-tio ns,1981,13(1):937-940.[8]Suresh S.Crack deflectio n:implica tio ns fo r the g row thof lo ng and shor t fatig ue c racks[J].M etallur gical T ransac tio ns,1983,14(1):2375-2385.[9]Suresh S.M icr omechanisms o f fatig ue cr ack g ro w th r e-tar da tio n fo llow ing ov erloads[J].Eng ineering Fr acture M echanics,1983,18(1):577-593.[10]冈村弘之著,李顺林译.线性断裂力学入门[M].南京:江苏科学技术出版社,1980.[11]何庆芝,郦正能.工程断裂力学[M].北京:北京航空航天大学出版社,1993.[12]Miner M A.Cumula tiv e damag e in fa tig ue[J].Jour nalof Applied M echa nics,1945,12:159-164.[13]曾春华,邹十践.疲劳分析方法及应用[M].长沙:国防工业出版社,1991.[14]Safe Technolog y Limited2003[M].Fe-safewo r ks usermanual,2003.[15]许国良.+33.0m楼面上大型风机的振动影响问题[J].上海冶金设计,1991,4:24-33.49　第4期冯庆兴,等:大跨度环形索桁结构体系的找形。

大跨度连续桥梁悬臂施工监控与风荷载效应分析大跨度连续桥梁悬臂施工监控与风荷载效应分析近年来，随着我国快速发展的城市化进程，大跨度连续桥梁作为城市交通基础设施的重要组成部分，得到了广泛的应用。

对于这类桥梁的施工监控和风荷载效应的分析，具有重要的理论意义和实际应用价值。

本文将针对大跨度连续桥梁悬臂施工监控与风荷载效应进行详细探讨。

首先，我们来看大跨度连续桥梁悬臂施工监控的重要性。

随着桥梁建设规模的不断扩大，大跨度连续桥梁的悬臂施工也变得越来越常见。

悬臂施工是一种高风险的施工方法，对工程的成功完成和工人的人身安全具有重要的影响。

因此，进行悬臂施工的监控是必要的。

通过使用传感器和监控设备，可以实时监测悬臂构件的变形、应力等参数，及时发现潜在的问题，并采取相应的措施加以解决。

同时，悬臂施工监控也有助于提高工程质量和施工效率。

悬臂施工监控中的关键问题之一是桥梁的变形监测。

在悬臂施工过程中，由于外荷载和施工过程的影响，桥梁的变形会发生变化。

因此，及时、准确地监测桥梁的变形对于保证施工的安全和顺利进行至关重要。

常用的监测方法包括GPS监测、倾斜仪监测和多点测量等。

通过这些监测手段，可以获得桥梁变形的实时数据，并及时发现异常情况。

除了悬臂施工监控外，大跨度连续桥梁的风荷载效应也不容忽视。

由于大跨度桥梁的自重和外部风荷载，桥梁在使用过程中会受到风荷载的作用。

风荷载会引起桥梁的振动和变形，严重时可能导致桥梁的破坏。

因此，对桥梁的风荷载效应进行分析和评估是非常重要的。

风荷载效应分析涉及到桥梁结构的动力学和风洞试验等方面的知识。

通过运用相关理论模型和数值计算方法，可以计算出桥梁受到的风荷载大小和作用方式，为桥梁的设计和施工提供科学依据。

在实际工程中，大跨度连续桥梁的悬臂施工监控与风荷载效应分析也存在一些挑战和难点。

首先，悬臂施工监控需要大量的传感器和监测设备，且需要长期稳定地工作，这对设备的可靠性和稳定性提出了更高的要求。

悬臂施工中的刚构桥梁的风荷载计算方法说实话悬臂施工中的刚构桥梁的风荷载计算方法这事儿，我一开始也是瞎摸索。

我最开始就知道肯定要先考虑基本的风特性相关的东西，就像你得先知道风有多大力气，从哪个方向来的。

那风的速度肯定是关键因素，这个就需要实地测量或者根据当地气象数据来估算。

我试过到现场去用那种风速仪测量，但是会受到好多因素影响，周围的建筑啊地形啊啥的，测出来的数据有时候偏差好大，这算是一个失败的教训了。

在计算风荷载的时候，其中有一个形状系数的确定让我费了好大劲。

桥梁的截面形状不同，风流过的时候受到的力就不一样。

就好比拿一个平板和一个圆柱放在风中，肯定受到的力情况不同。

那刚构桥梁可能有各种复杂的截面形状。

我一开始就简单地按照最相似的标准形状去取值，后来发现误差不得了。

我才知道得更细致地考虑桥梁实际的结构部件对风的阻碍等情况，要把一些附属的结构，像栏杆什么的也算进去对形状系数的影响。

还有个空气密度这个因素，按道理说是有标准值，可实际现场情况可能会有变化。

有时候靠近水域的桥梁，那空气湿度大，感觉密度或许会有点变化，虽然我不知道确切会有多大影响，但总感觉这可能也是一个潜在的影响因素不确定的点。

那计算风荷载的时候，公式里还有一个风压高度变化系数。

这就好比风在地面的时候和在很高的桥梁位置的劲道不一样。

我开始是按照公式直接套，但是后来发现现场地形如果不是平坦的，比如说有山地起伏，这个系数就不是那么简单能确定的了。

我试着根据一些地形矫正的方法，参考旁边山坡的高度坡度这些去调整这个系数，但算起来很麻烦，而且也不确定准确不准确。

不过我觉得如果能多参考几个类似地形的成功桥例的计算方式会好很多。

再说到风振的影响，这个就更复杂了。

像颤振、抖振这类的，我光是查看资料就看了好久。

刚构桥梁悬臂施工的时候，结构是动态的、不断变化的，风振的情况就很难把握。

我当时的办法就是把悬臂部分近似看成一个悬臂梁的振动模型去先初步计算它的振动频率这些，再根据理论上去判断可能的风振情况，不过我也知道这只是个近似的，不是很精准的办法。